Closed-loop spontaneous baroreflex transfer function is inappropriate for system identification of neural arc but partly accurate for peripheral arc: predictability analysis

Non-technical summary

The arterial baroreflex is a closed-loop, negative feedback control system that senses baroreceptor pressure and controls systemic arterial pressure (AP) to attenuate perturbations in AP. The total arc of the baroreflex consists of two subsystems: the neural (baroreceptor pressure input to sympathetic nerve activity (SNA)) and peripheral (SNA input to AP) arcs. We show that although the spontaneous baroreflex transfer function obtained by closed-loop analysis has been believed to represent the neural arc function, it is inappropriate for system identification of the neural arc but is essentially appropriate for the peripheral arc under resting condition, when compared with open-loop transfer functions that have good predictabilities of time-series output dynamics from input signals. Our results indicate that in the spontaneous baroreflex system under closed-loop conditions, the peripheral arc (feedforward) function predominates over the neural arc (feedback) function, probably because of the SNA component that is independent of the baroreceptor pressure input.

Abstract

Abstract

Although the dynamic characteristics of the baroreflex system have been described by baroreflex transfer functions obtained from open-loop analysis, the predictability of time-series output dynamics from input signals, which should confirm the accuracy of system identification, remains to be elucidated. Moreover, despite theoretical concerns over closed-loop system identification, the accuracy and the predictability of the closed-loop spontaneous baroreflex transfer function have not been evaluated compared with the open-loop transfer function. Using urethane and α-chloralose anaesthetized, vagotomized and aortic-denervated rabbits (n = 10), we identified open-loop baroreflex transfer functions by recording renal sympathetic nerve activity (SNA) while varying the vascularly isolated intracarotid sinus pressure (CSP) according to a binary random (white-noise) sequence (operating pressure ± 20 mmHg), and using a simplified equation to calculate closed-loop-spontaneous baroreflex transfer function while matching CSP with systemic arterial pressure (AP). Our results showed that the open-loop baroreflex transfer functions for the neural and peripheral arcs predicted the time-series SNA and AP outputs from measured CSP and SNA inputs, with r² of 0.8 ± 0.1 and 0.8 ± 0.1, respectively. In contrast, the closed-loop-spontaneous baroreflex transfer function for the neural arc was markedly different from the open-loop transfer function (enhanced gain increase and a phase lead), and did not predict the time-series SNA dynamics (r²; 0.1 ± 0.1). However, the closed-loop-spontaneous baroreflex transfer function of the peripheral arc partially matched the open-loop transfer function in gain and phase functions, and had limited but reasonable predictability of the time-series AP dynamics (r², 0.7 ± 0.1). A numerical simulation suggested that a noise predominantly in the neural arc under resting conditions might be a possible mechanism responsible for our findings. Furthermore, the predictabilities of the neural arc transfer functions obtained in open-loop and closed-loop conditions were validated by closed-loop pharmacological (phenylephrine and nitroprusside infusions) pressure interventions. Time-series SNA responses to drug-induced AP changes predicted by the open-loop transfer function matched closely the measured responses (r², 0.9 ± 0.1), whereas SNA responses predicted by closed-loop-spontaneous transfer function deviated greatly and were the inverse of measured responses (r, −0.8 ± 0.2). These results indicate that although the spontaneous baroreflex transfer function obtained by closed-loop analysis has been believed to represent the neural arc function, it is inappropriate for system identification of the neural arc but is essentially appropriate for the peripheral arc under resting conditions, when compared with open-loop analysis.

Introduction

The arterial baroreflex plays a crucial role in circulatory control by its dynamic system characteristics (Eckberg & Sleight, 1992; Rowell, 1993). The baroreflex is a closed-loop, negative feedback control system that constantly senses arterial pressure (AP) by baroreceptors and quickly regulates systemic AP physiologically to attenuate perturbations in AP (Eckberg & Sleight, 1992; Rowell, 1993). The total arc baroreflex system consists of two subsystems: the neural and peripheral arcs (Kamiya et al. 2005b, 2008a, 2010; Kawada et al. 2010). The neural arc subsystem represents central processing from baroreceptor pressure to efferent sympathetic nerve activity (SNA), whereas the peripheral arc subsystem represents processing from SNA to systemic AP via peripheral circulatory organs including heart, kidney and blood vessels (Fig. 1) (Ikeda et al. 1996; Kamiya et al. 2005b).

Figure 1. Functional structure of arterial baroreflex system.

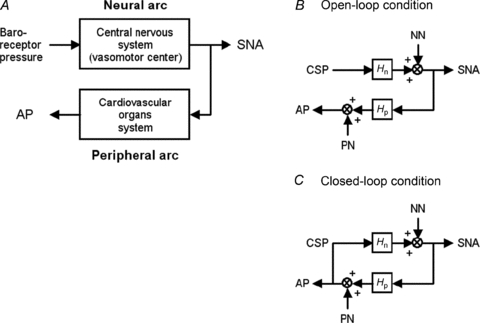
A, theoretical considerations of the coupling of baroreflex neural and peripheral arcs. Although baroreflex is a negative feedback control system that senses AP by baroreceptors and regulates AP, we opened the loop by changing baroreceptor pressure independent of AP. By measuring SNA, we divided the baroreflex system into the neural arc (from baroreceptor pressure input to efferent SNA via central nervous system) and the peripheral arc (from SNA input to AP via cardiovascular organs system). B, block diagram of open-loop baroreflex system. Because of vascular isolation of carotid-sinus regions, CSP is independent of systemic AP. Noise is introduced to the neural and/or peripheral arcs. C, block diagram of closed-loop-spontaneous baroreflex system, where CSP equals AP. Noise is introduced to the neural and/or peripheral arcs. Because of the closed-loop nature, changes in AP (and thus, in CSP) control SNA via neural arc transfer function (H_n), which in turn modulate AP via peripheral arc transfer function (H_p). CSP, carotid sinus pressure; SNA, sympathetic nerve activity; AP, arterial pressure; NN, unknown noise in the neural arc; PN, unknown noise in the peripheral arc.

Transfer function analysis is a powerful tool to determine the dynamic characteristics of biosystems. This analysis has revealed the dynamic causality mainly in ‘open-loop’ biosystems, including cerebral autoregulation (Zhang et al. 2002), renal vascular function (DiBona & Sawin, 2003, 2004), heart rate control (Ikeda et al. 1995) and cutaneous circulation (Kamiya et al. 2008b). We have applied the transfer function analysis to characterize the ‘closed-loop’ arterial baroreflex system, in which we used the open-loop and white-noise pressure perturbation techniques to overcome the difficulties of closed-loop system identification (see Appendix A) (Ikeda et al. 1996; Kawada et al. 2002; Kamiya et al. 2005b, 2008a). We have reported that the neural arc transfer function (H_n) has derivative and high-cut filter characteristics with a pure delay, indicating that more rapid change of arterial pressure results in greater response of SNA to pressure change (Kawada et al. 2002; Kamiya et al. 2005b), whereas the peripheral arc transfer function (H_p) has second-order low-pass filter characteristics with a pure delay (see Appendix B) (Kawada et al. 2002; Kamiya et al. 2005b). However, at least two important issues remain to be elucidated.

First, a hallmark of the transfer function, the predictability of time-series output dynamics from input signals (Ikeda et al. 1995; Kamiya et al. 2008b), has not yet been investigated in the baroreflex system. Accurate system identification of the transfer function yields good predictability, whereas inappropriate system identification results in poor predictability. In the present study, we tested the first hypothesis that the open-loop baroreflex transfer functions of the neural and peripheral arcs are capable of predicting time-series SNA and AP output dynamics from baroreceptor pressure and SNA inputs, respectively.

Second, identifying transfer functions is theoretically difficult under closed-loop and spontaneous resting baroreflex conditions. The reason is that unknown noises in the neural and peripheral arcs would interfere with the accuracy of system identification in closed-loop-spontaneous conditions, in contrast to open-loop transfer function identification where the interfering effects of noises would be eliminated by the open-loop and white-noise pressure perturbation techniques (Ikeda et al. 1996; Kawada et al. 2002; Kamiya et al. 2005b, 2008a) (see Appendix A). Although earlier interesting studies have applied a simplified (open-loop-like) calculation of transfer function to closed-loop-spontaneous resting baroreflex condition in humans (Cooke et al. 1999, 2009; Ogoh et al. 2009) and animals (Orea et al. 2007) without opening the loop, whether the reported transfer functions are actually capable of predicting time-series output dynamics has not been verified. In addition, the accuracy and limitation of closed-loop-spontaneous baroreflex transfer functions remain unclear from the viewpoint of comparing with open-loop transfer functions. In the present study, we tested the second hypothesis that the closed-loop-spontaneous baroreflex transfer function is limited to predict baroreflex dynamics compared with the open-loop transfer function.

In the present study, by artificially controlling intra-carotid sinus pressure (CSP) and recording renal SNA and systemic AP, we identified the open-loop baroreflex transfer functions by introducing CSP perturbation according to a binary random (white-noise) sequence. We also determined the closed-loop-spontaneous baroreflex transfer functions by matching CSP with systemic AP. We then compared the characteristics and predictability of these transfer functions. Our results confirmed good predictability of the open-loop baroreflex transfer functions, and unexpectedly indicated that the closed-loop-spontaneous transfer function approximately matched the open-loop transfer function for the peripheral arc but deviated markedly from the open-loop transfer function for the neural arc. Thus, the closed-loop-spontaneous baroreflex transfer function is inappropriate for system identification of the neural arc but is partially appropriate for the peripheral arc under resting condition, compared with the open-loop analysis. These findings may have great impact, because the closed-loop-spontaneous baroreflex transfer function has been believed to represent the neural arc function (Orea et al. 2007; Cooke et al. 2009; Ogoh et al. 2009).

Methods

Animal preparation

Animals were cared for in strict accordance with the Guiding Principles for the Care and Use of Animals in the Field of Physiological Science approved by the Physiological Society of Japan and the National Cerebral and Cardiovascular Center Research Institute, and the ethical regulations and policies of The Journal of Physiology (Drummond, 2009). Ten Japanese white rabbits weighing 2.4–3.3 kg were initially anaesthetized by intravenous injection (2 ml kg⁻¹) of a mixture of urethane (250 mg ml⁻¹) and α-chloralose (40 mg ml⁻¹). Anaesthesia was maintained by continuously infusing the anaesthetics at a rate of 0.33 ml kg⁻¹ h⁻¹ using a syringe pump (CFV-3200, Nihon Kohden, Tokyo). The rabbits were mechanically ventilated with oxygen-enriched room air. Bilateral carotid sinuses were isolated vascularly from the systemic circulation by ligating the internal and external carotid arteries and other small branches originating from the carotid sinus regions. The isolated carotid sinuses were filled with warmed physiological saline pre-equilibrated with atmospheric air, through catheters inserted via the common carotid arteries. CSP was controlled by a servo-controlled piston pump (model ET-126A, Labworks; Costa Mesa, CA, USA). Bilateral vagal and aortic depressor nerves were sectioned in the middle of the neck region to eliminate reflexes from the cardiopulmonary region and the aortic arch. Systemic AP was measured using a high-fidelity pressure transducer (Millar Instruments; Houston, TX, USA) inserted retrograde from the right common carotid artery below the isolated carotid sinus region. A catheter was inserted into the right femoral vein to infuse phenylephrine and nitroprusside. Body temperature was maintained at around 38°C with a heating pad.

The left renal sympathetic nerve was exposed retroperitoneally. A pair of stainless steel wire electrodes (Bioflex wire AS633, Cooner Wire) was attached to the nerve to record renal SNA. The nerve fibres peripheral to the electrodes were ligated tightly and crushed to eliminate afferent signals. The nerve and electrodes were covered with a mixture of silicone gel (Silicon Low Viscosity, KWIK-SIL, World Precision Instrument, Inc., FL, USA) to insulate and immobilize the electrodes. The pre-amplified SNA signal was band-pass filtered at 150–1000 Hz. These nerve signals were full-wave rectified and low-pass filtered with a cut-off frequency of 30 Hz to quantify the nerve activity.

Protocols

After the surgical preparation, all animals (n = 10) were maintained supine. The overall scheme of the experimental design is shown in Fig. 2. Protocols 1–4 were conducted in randomized order at intervals of at least 5 min, while protocol 5 was done finally. In all protocols, bilateral CSP was controlled by a servo-controlled piston pump (Kawada et al. 2002). The SNA, CSP and AP were recorded at a sampling rate of 200 Hz using a 12-bit analog-to-digital converter. Data were stored on the hard disk of a dedicated laboratory computer system.

Figure 2. Experimental design.

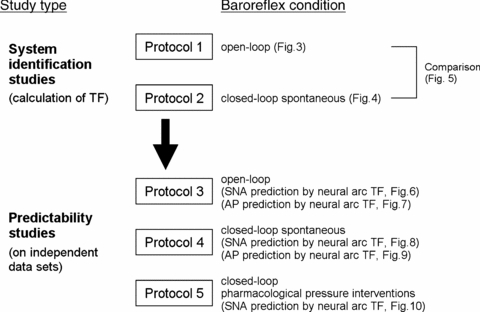
In system identification studies, open-loop (protocol 1, CSP was perturbed according to a binary random sequence) and closed-loop-spontaneous (protocol 2, CSP was matched with systemic AP) baroreflex transfer functions were identified from experimental data. In predictability studies, the predictive power of the above transfer functions was tested using independent data (protocols 3, 4 and 5). Protocol 3 and 4 were open-loop and closed-loop-spontaneous baroreflex conditions, respectively. Protocol 5 was pharmacological pressure intervention by phenylephrine and nitroprusside infusions in closed-loop condition. TF, transfer function; CSP, carotid sinus pressure; SNA, sympathetic nerve activity; AP, arterial pressure.

Before these protocols, operating AP and SNA in baroreflex closed-loop condition were determined. First, CSP was matched with systemic AP to close the baroreflex loop. After at least 5 min of stabilization, the variables were recorded for 10 min, and the average AP over 10 min was defined as the operating AP under closed-loop condition.

System identification studies

Protocol 1 was performed to identify the open-loop baroreflex transfer functions. After at least 5 min of stabilization, CSP was randomly assigned at 20 mmHg above or below the operating AP every 500 ms according to a binary random (white-noise) sequence, in which the input power spectrum of CSP was reasonably flat up to 1 Hz (Kawada et al. 2002). The variables were recorded for 10 min and stored for analysis.

Protocol 2 was performed to determine the closed-loop-spontaneous baroreflex transfer functions by a convenient method of applying the same calculation as that used in the open-loop condition of protocol 1 (see Appendix A). CSP was matched with systemic AP to close the baroreflex loop. After at least 5 min of stabilization, the variables were recorded for 10 min and stored for analysis.

Predictability studies

Protocols 3, 4 and 5 were performed to investigate the predictability of baroreflex transfer functions. In protocol 3 (open-loop), CSP was randomly assigned at 20 mmHg above or below the operating AP. The variables were recorded for 10 min and stored for analysis.

In protocol 4 (closed-loop), CSP was matched with systemic AP to close the baroreflex loop. After at least 5 min of stabilization, the variables were recorded for at least 10 min and stored for analysis.

Protocol 5 was also performed to investigate the predictability of baroreflex transfer functions during sequential pharmacological pressure interventions in the closed-loop condition. CSP was matched with systemic AP. After at least 2 min of stabilization, phenylephrine hydrochloride (3 μg kg⁻¹) was bolus infused through a venous catheter inserted into the right femoral vein, followed 1–2 min later by sodium nitroprusside (4 μg kg⁻¹) and then 1–2 min later by the second phenylephrine hydrochloride infusion (4 μg kg⁻¹). The variables were recorded continuously for at least 10–11 min and stored for analysis.

Data analysis

SNA signal was normalized by the following steps. First, 0 arbitrary unit (a.u.) was assigned to the post-mortem noise level. Second, 100 a.u. was assigned to the SNA signals averaged over 10 min before protocols. Last, the other SNA signals in protocols 1–5 were then normalized to these values.

In protocol 1, we calculated the open-loop transfer (gain and phase) and coherence functions from CSP input to SNA in the neural arc (H_n-open) and from SNA to AP in the peripheral arc (H_p-open). We re-sampled CSP and SNA at 10 Hz and segmented them into 10 sets of 50% overlapping bins of 2¹⁰ data point each. The segment length was 102.4 s, which yielded the lowest frequency bound of 0.01 (0.0097) Hz. We subtracted a linear trend and applied a Hanning window for each segment. We then performed fast Fourier transform to obtain frequency spectra of input (x) and output (y). The inputs are CSP and SNA, while the outputs are SNA and AP in the neural and peripheral arc subsystems, respectively. We ensemble averaged the input power (Sxx(f)), output power (Syy(f)), and cross power between input and output (Syx(f)) over the 10 segments. Then, we calculated the transfer function (H(f)) from input to output as follows:

(1)

Although individual noise may be present in the neural and peripheral arc subsystems, the effects of noise on the calculations of transfer functions are eliminated by open-loop operation and white-noise-like perturbation of CSP (see Appendix A, Fig. 1A).

To quantify the linear dependence between input and output in the frequency domain, we calculated the magnitude-squared coherence function (Coh(f)) as follows:

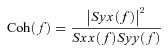(2)

The coherence values range from zero to unity. Unity coherence indicates a perfect linear dependence between input and output, whereas zero coherence indicates total independence of these two signals. To quantify the errors on individual gain and phase estimates, we calculated the normalized random error (ɛ(f)) as follows:

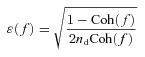(3)

where n_d is the number of distinct subrecord, when the error in gain factor estimate matches that in phase factor estimate (Julius & Allan, 2000).

To quantify the transfer characteristics in the time domain, step response was calculated by discrete from convolution integral as follows:

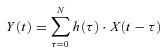(4)

where h(τ) is the impulse response obtained by inverse fast Fourier transform of the transfer function (H(f)); N is the total number of data elements; τ is the convolution parameter; t is time in increments of 0.1 s (or 10 Hz); X(t) = 0 for t < 0 and X(t) = 1 for t≥ 0.

It should be noted that since protocol 2 was a closed-loop and spontaneous baroreflex condition, unknown noise, if present in the neural and peripheral arc subsystems, would affect the accuracy of system identification (see Appendix A, Fig. 1B). Based on earlier studies (Cooke et al. 1999, 2009; Ogoh et al. 2009), we applied a simplified (open-loop-like) calculation of transfer function to the closed-loop-spontaneous resting baroreflex condition, and estimated the closed-loop-spontaneous baroreflex transfer functions from AP input to SNA in the neural arc (H_{n-closed-spon}) and from SNA to AP in the peripheral arc (H_{p-closed-spon}), together with coherence functions and step responses (see Appendix A).

In protocols 3 and 4, we calculated the predicted time-series output dynamics (SNA and AP) from measured input signals (CSP/AP and SNA in the neural and peripheral arc, respectively), using eqn (4) and impulse response obtained from the transfer functions in protocols 1 and 2. The predicted output was scatter-plotted, and compared with the actually measured output by calculating the linear correlation coefficient (r) and root mean square (RMS). The analysis was performed using the data at arbitrarily selected 1 and 3 min in protocols 3 and 4, respectively.

In protocol 5, similar to protocol 3 and 4, we calculated the predicted time-series output dynamics of SNA from measured pressure input signals (CSP/AP in the neural arc) during pharmacological interventions. The predicted SNA was scatter-plotted, and compared with the actual SNA measurements by calculating r and RMS. The analysis was performed using the data for 10–11 min. Since AP was determined by interventions (phenylephrine and nitroprusside infusions) and not by SNA, we did not calculate the predicted AP dynamics from the measured SNA signals.

Statistic analysis

All data are presented as means ± SD. Paired t test and repeated measures analysis of variance with post hoc multiple comparisons were used to compare variables as appropriate. Differences were considered significant when P < 0.05.

Results

Open-loop transfer function (protocol 2)

Figure 3 shows a typical example of the open-loop system identification of baroreflex transfer functions in protocol 2. CSP was perturbed according to a binary random (white-noise) sequence at 500 ms intervals (Fig. 3A, green line). When CSP was increased, SNA decreased, and vice versa. In the frequency domain, the input power spectrum of CSP was reasonably flat up to 1 Hz (Fig. 3B, green line).

Figure 3. Open-loop transfer function.

A, typical representative data of one rabbit in protocol 2, showing time series of carotid sinus pressure (CSP), sympathetic nerve activity (SNA) and systemic arterial pressure (AP) during CSP perturbation in open-loop baroreflex condition. CSP is changed according to a binary random (white-noise) signal with a switching interval of 500 ms. B, input power spectrum of CSP (green line) is reasonably flat up to 1 Hz. Autospectra of SNA (top line) and systemic AP (bottom line) are also shown. The arrowhead indicates a peak of SNA autospectrum at 0.4 Hz. C, open-loop transfer functions of the neural arc (H_n-open) from CSP input to SNA (left panels) and of the peripheral arc (H_p-open) from SNA input to AP (right panels) identified in the same animal as in A. The gain (top), phase (second), coherence (third) and normalized random error (Error, bottom) functions are shown. Units of gain are [a.u. mmHg⁻¹] for the neural arc and [mmHg a.u.⁻¹] for the peripheral arc, respectively. D, step responses (Step res.) derived from the transfer functions shown in C. The units are [a.u.] for the neural arc and [mmHg] for the peripheral arc, respectively. E, open-loop transfer functions of the total arc (H_total-open) from CSP input to AP identified in the same animal as in A. The gain (top), phase (second), coherence (third) and normalized random error (Error, bottom) functions are shown. Unit of gain is [mmHg mmHg⁻¹]. F, step response (Step res.) derived from the transfer function shown in E. The unit is [mmHg]. a.u., arbitrary unit.

The open-loop transfer function of the neural arc from CSP input to SNA (H_n-open; Fig. 3C, left panels) showed that the gain increased as the frequency of CSP perturbation increased between 0.01 Hz and 0.4 Hz, indicating dynamic high-pass characteristics. The phase approached –π at the lowest frequency, indicating a negative SNA response to CSP changes, and lagged as the frequency increased (Fig. 3C, left panels). The coherence was over 0.8 between 0.03 to 0.4 Hz except at around 0.35 Hz (Fig. 3C, left panels). The step response (Fig. 3D, left panel) of SNA in response to CSP consisted of an initial decrease followed by partial recovery and then steady state.

The open-loop transfer function of the peripheral arc from SNA input to AP (H_p-open, Fig. 3C, right panels) showed that the gain decreased as the frequency increased, indicating low-pass characteristics. The phase approached zero at the lowest frequency, indicating a positive AP response to SNA changes, and lagged as the frequency increased. The coherence was over 0.8 between 0.01 to 0.3 Hz except at around 0.2 Hz (Fig. 3C, right panels). The step response (Fig. 3D, right panel) of SNA to CSP was a gradual increase to steady state.

The transfer function of baroreflex total arc from CSP input to systemic AP identified in the open-loop condition (Fig. 3E) showed that the gain decreased as the frequency increased, indicating low-pass characteristics that were milder than H_p-open. The phase approached –π at the lowest frequency, indicating negative feedback system characteristics of baroreflex (negative AP response to CSP changes). The phase lagged as frequency increased. The transfer function of total arc was almost consistent with multiplication of tandemly arranged open-loop transfer functions of neural (H_n-open) and peripheral (H_p-open) arcs (Fig. 1A and B), at the frequency where their coherence functions were high.

Closed-loop-spontaneous transfer function (protocol 3)

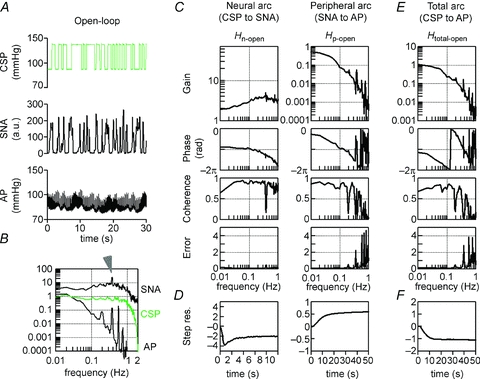
Figure 4 shows a typical example of the closed-loop-spontaneous transfer functions simplified, calculated in protocol 3 by applying open-loop-like calculations to closed-loop-spontaneous data. The data were obtained from the same animal as in Fig. 3.

Figure 4. Closed-loop-spontaneous transfer function.

A, typical representative data of protocol 3, showing time series of CSP, SNA and systemic AP in closed-loop-spontaneous baroreflex condition, where CSP is matched with systemic AP. The data were obtained from the same animal as in Figure 3. B–D show exactness of good match between CSP and systemic AP. B, autospectrum of CSP (green line) overlaps with that of AP (black line). Autospectrum of SNA (top line) is also shown. The arrowhead indicates a peak in the SNA autospectrum at 0.4 Hz. C, beat-to-beat waveform of CSP (green line) overlaps with that of AP (black line). D, the transfer functions from CSP to systemic AP. Gain (top), phase (middle) and coherence (bottom) functions are shown. Unit of gain is [mmHg mmHg⁻¹]. E, the closed-loop-spontaneous transfer functions of the neural arc (H_{n-closed-spon}) from CSP (=AP) input to SNA (left panels) and of the peripheral arc (H_{p-closed-spon}) from SNA input to AP (right panels) identified in the same animal as in A. The gain (top), phase (second), coherence (third) and normalized random error (bottom) functions are shown. Units of gain are [a.u. mmHg⁻¹] for the neural arc and [mmHg a.u.⁻¹] for the peripheral arc, respectively. F, step responses (Step res.) derived from the transfer functions. The units are [a.u.] for the neural arc and [mmHg] for the peripheral arc, respectively. a.u., arbitrary unit; CSP, carotid sinus pressure; SNA, sympathetic nerve activity; AP, arterial pressure; Step res., step response. In E and F, the open-loop transfer functions and derived step responses are included for reference (red lines).

We closed the baroreflex loop by matching CSP with systemic AP. The exact match of the two parameters was demonstrated by autospectrum (Fig. 4B) and beat-to-beat waveform (Fig. 4C), both showing overlapping of CSP (green line) and systemic AP (black line). The exact match was further confirmed by the transfer functions from CSP to systemic AP (Fig. 4D), which showed that the gain, phase and coherence functions were maintained constant at 1, zero and 1, respectively.

The closed-loop-spontaneous transfer function of the neural arc (H_{n-closed-spon}) from CSP (that equalled AP) to SNA (Fig. 4E, left panels, black line) was markedly different from the open-loop transfer function (H_n-open, red line) with respect to gain, phase, coherence and step response. The increase in gain versus frequency was steeper; the gain was thus higher and the coherence was lower in H_{n-closed-spon} compared with H_n-open. The phase led as frequency increased, while the step response oscillated (Fig. 4F, left panel) in H_{n-closed-spon}, which were markedly different from H_n-open.

In contrast to the neural arc, the closed-loop-spontaneous transfer function for the peripheral arc (H_{p-closed-spon}) from SNA to AP (Fig. 4E, right panels, black line) approximated that of the open-loop transfer function (H_p-open, red line). The gain (except at 0.02–0.05 Hz) and phase were similar up to 0.3 Hz, although the coherence was lower in H_{p-closed-spon} than in H_p-open (common feature for both neural and peripheral arcs). The step response was similar to that of H_p-open except for a slower time constant (Fig. 4F, right panel). Because of the closed-loop condition, the gain and phase functions of H_{p-closed-spon} were the inverse of those of H_{n-closed-spon}.

Since CSP exactly matched systemic AP in this closed-loop-spontaneous baroreflex condition, the transfer function of total arc baroreflex from CSP input to systemic AP was calculated as all-pass filter without modulating phase (Fig. 4D). This is greatly different from the transfer function of the total arc identified from open-loop experiments (Fig. 3E).

Comparison between open-loop and closed-loop-spontaneous transfer functions

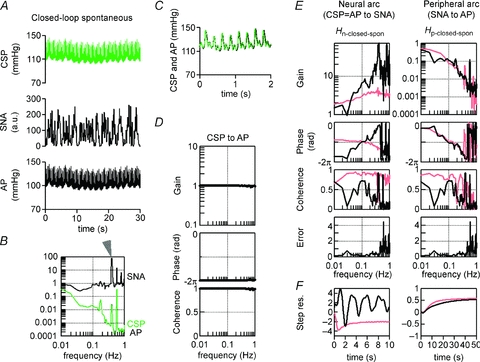
The closed-loop-spontaneous transfer functions (Fig. 5A, blue lines) (H_{n-closed-spon} and H_{p-closed-spon}) obtained from all animals (n = 10) in protocol 2 were compared with the open-loop transfer functions (Fig. 5A, red lines) in protocol 1. The step response was also compared between closed-loop-spontaneous (Fig. 5B, blue line) and open-loop experiments (Fig. 5B, red line).

Figure 5. Comparison between open-loop and closed-loop-spontaneous transfer functions.

Solid and dashed lines represent the mean and mean + SD, respectively, obtained from all animals (n = 10). A, red lines are open-loop transfer functions of the neural (H_n-open, left panels) and peripheral arcs (H_p-open, right panels) identified in protocol 1. Blue lines are closed-loop-spontaneous transfer functions (blue lines) of the neural (H_{n-closed-spon}, left panels) and peripheral arcs (H_{p-closed-spon}, right panels) identified in protocol 2. The gain (top), phase (second), coherence (third) and normalized random error (bottom) functions are shown. Units of gain are [a.u. mmHg⁻¹] for the neural arc and [mmHg a.u.⁻¹] for the peripheral arc, respectively. The closed-loop-spontaneous baroreflex transfer function for the neural arc is markedly different from the open-loop transfer function, whereas that for the peripheral arc partially matches the open-loop transfer function. B, step response (Step res.) calculated from the open-loop (red lines) and closed-loop-spontaneous (blue lines) transfer functions. The units are [a.u.] for the neural arc and [mmHg] for the peripheral arc, respectively. a.u., arbitrary unit; CSP, carotid sinus pressure; SNA, sympathetic nerve activity; AP, arterial pressure; Step res., step response.

In the neural arc (Fig. 5A and B, left panels; Table 1), closed-loop-spontaneous transfer functions (H_{n-closed-spon}, blue lines) were markedly different from open-loop transfer functions (H_n-open, red lines), similar to the example shown in Fig. 4E. The difference was characterized by an enhanced increase of gain versus frequency (slope), a phase lead and an oscillation of step response. In contrast, in the peripheral arc (Fig. 5A and B, right panels; Table 2), closed-loop-spontaneous transfer functions (H_{p-closed-spon}) were similar to open-loop transfer functions (H_n-open) in gain, phase and step response.

Table 1.

Transfer functions of the baroreflex neural arc (from CSP to SNA) in open-loop and closed-loop-spontaneous conditions

	Open-loop TF (Hn-open, CSP to SNA)	Closed-loop-spontaneous TF (Hn-closed-spon, CSP [= AP] to SNA)
Gain (a.u. mmHg−1)
0.01 Hz	1.2 ± 0.2	1.8 ± 0.1*
0.1 Hz	2.0 ± 0.3	5.3 ± 2.8*
0.3 Hz	2.6 ± 0.3	14.6 ± 5.7*
Phase (rad)
0.01 Hz	−2.7 ± 0.2	−5.4 ± 0.4*
0.1 Hz	−3.0 ± 0.1	−3.1 ± 0.4
0.3 Hz	−3.7 ± 0.1	−2.6 ± 0.11*
Coherence
0.01 Hz	0.8 ± 0.1	0.8 ± 0.2
0.1 Hz	0.9 ± 0.1	0.6 ± 0.2*
0.3 Hz	0.9 ± 0.1	0.4 ± 0.3*
Slope (dB per decade)
0.01 Hz to 0.3 Hz	4.7 ± 0.4	12.1 ± 6.1*
Step response
Initial response (a.u.)	−2.4 ± 0.2	Oscillating response
Steady-state level (a.u.)	−1.2 ± 0.2

Values are mean ± SD (n = 10).

^*P < 0.05; open-loop vs. closed-loop-spontaneous conditions. TF, transfer function.

Table 2.

Transfer functions of baroreflex peripheral arc (from SNA to AP) in open-loop and closed-loop-spontaneous conditions

	Open-loop TF (Hp-open, SNA to AP)	Closed-loop-spontaneous TF (Hp-closed-spon, SNA to AP)
Gain (mmHg a.u.−1)
0.01 Hz	0.7 ± 0.2	0.6 ± 0.2
0.1 Hz	0.1 ± 0.1	0.1 ± 0.1
0.3 Hz	0.03 ± 0.01	0.03 ± 0.02
Phase (rad)
0.01 Hz	−0.8 ± 0.2	−0.9 ± 0.2
0.1 Hz	−3.0 ± 0.2	−3.0 ± 0.2
0.3 Hz	−4.2 ± 0.1	−4.0 ± 0.3
Coherence
0.01 Hz	0.9 ± 0.1	0.8 ± 0.2
0.1 Hz	0.8 ± 0.2	0.6 ± 0.2*
0.3 Hz	0.9 ± 0.1	0.4 ± 0.3*
Step response
Steady-state level (mmHg)	−0.7 ± 0.2	−0.6 ± 0.2

Values are mean ± SD (n = 10).

^*P < 0.05; open-loop vs. closed-loop-spontaneous conditions. TF, transfer function.

The transfer function of the baroreflex total arc from CSP input to systemic AP in the open-loop condition was identified as having low-pass filter characteristics with negative feedback in all animals. In contrast, the total arc transfer function in the closed-loop-spontaneous condition had all-pass filter characteristics without modulating phase in all animals.

Predictability of open-loop and closed-loop-spontaneous transfer function compared with data measured in open-loop condition (protocol 3)

The ability of the neural arc transfer functions (determined by protocols 1 and 2) to predict output dynamics (SNA) from given input signals (CSP) in the open-loop condition was quantified by comparing with the actual measurements of SNA response to CSP changes in protocol 3. Figure 6 shows a typical example obtained from the same animal as in Figs 1 and 2. CSP was randomly assigned at 20 mmHg above or below the operating AP (changes according to binary random (white-noise) sequence; Fig. 6A, top panel). The SNA response to CSP changes predicted by the open-loop transfer function (H_n-open) (Fig. 6A; third panel) resembled the actually measured SNA (Fig. 6A, second panel) in both the timing (phase) and magnitude of neural burst. In contrast, the SNA response predicted by the closed-loop-spontaneous transfer function (H_{n-closed-spon}) (Fig. 6A, bottom panel) was different from the actually measured SNA (Fig. 6A, second panel), showing markedly exaggerated fluctuation and inconsistent burst timing. As a result, scatter plot analyses showed that the SNA predicted by H_n-open correlated significantly with the actually measured SNA (r², 0.83; RMS, 13 a.u.; P < 0.05) (Fig. 6B), whereas the SNA predicted by H_{n-closed-spon} showed no correlation (r², 0.04; RMS, 109 a.u.) (Fig. 6C). Using the data from all animals, the SNA predicted by H_n-open correlated with the measured SNA (r², 0.8 ± 0.1; RMS, 15 ± 4 a.u.; P < 0.05), whereas SNA predicted by H_{n-closed-spon} showed no correlation (r², 0.1 ± 0.1; RMS, 102 ± 24 a.u.).

Figure 6. Predictability of neural arc transfer functions in open-loop condition.

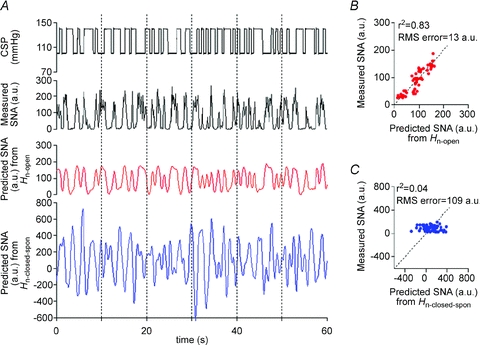
A, typical representative example of evaluating the predictability of SNA output from CSP input using the baroreflex transfer functions of the neural arc. The data were obtained from the same animal as in Fig. 3. The time-series SNA dynamics are predicted from CSP measured in protocol 4 (top panel), by the open-loop transfer function determined in protocol 1 (red line, third panel) and by the closed-loop-spontaneous transfer function determined in protocol 2 (blue line, bottom panel). CSP is changed according to a binary random (white-noise) signal with a switching interval of 500 ms under open-loop baroreflex condition. These predicted SNA changes are compared with the actual SNA measured in protocol 4 (second panel). SNA (red line, third panel) predicted by open-loop transfer function (H_n-open) appears to parallel the actually measured SNA, whereas SNA predicted by closed-loop-spontaneous transfer function (H_{n-closed-spon}) is markedly different from the measured SNA. B, scatter plot analysis of the SNA predicted by H_n-openversus the measured SNA. C, scatter plot analysis of the SNA predicted by H_{n-closed-spon}versus the measured SNA.

Table 3.

Predictive power of baroreflex transfer functions

	Open-loop TF (Hn-open, CSP to SNA)		Closed-loop-spontaneous TF (Hn-closed-spon, CSP [= AP] to SNA)
	r2	(Predicted condition)	r2	(Predicted condition)
Neural arc	0.8 ± 0.1*	(Open-loop)	0.1 ± 0.1	(Open-loop)
	0.1 ± 0.2	(Closed-loop-spon)	0.06 ± 0.1	(Closed-loop-spon)
	0.9 ± 0.1*	(Closed-loop-drug)	0.7 ± 0.1 (r < 0a)	(Closed-loop-drug)

	Open-loop TF (Hp-open, SNA to AP)		Closed -loop-spontaneous TF (Hp-closed-spon, SNA to AP)
	r2	(Predicted condition)	r2	(Predicted condition)
Peripheral arc	0.8 ± 0.1*	(Open-loop)	0.7 ± 0.1*	(Open-loop)
	0.7 ± 0.1*	(Closed-loop-spon)	0.7 ± 0.1*	(Closed-loop-spon)

Values are mean ± SD (n = 10).

^*P < 0.05; significant correlation between predicted and measured values.

^aRegarding the predictive power of closed-loop-spontaneous TF in neural arc closed-loop-drug condition, r is less than 0 (r =−0.8 ± 0.1). TF, transfer function; Open-loop, baroreflex open-loop condition where CSP was binary random (white-noise) sequence and independent of systemic AP; Closed-loop-spon, baroreflex closed-loop-spontaneous condition where CSP equalled systemic AP; Closed-loop-drug, sequential infusions of phenylephrine and nitroprusside in closed-loop condition where CSP equalled systemic AP.

In addition, the ability of the peripheral arc transfer functions (determined by protocols 1 and 2) to predict output dynamics (AP) from given input signals (SNA) in the open-loop condition was quantified by comparing with the actual measurements of AP response to SNA changes. Figure 7 shows an example obtained from the same animal as in Fig. 6. The AP response to SNA predicted by the open-loop transfer function (H_p-open) (third panel) resembled closely the actually measured AP (second panel). The AP response (bottom panels) predicted by the closed-loop-spontaneous transfer function (H_{p-closed-spon}) was also similar but with limitations. Scatter plot analyses showed that the AP predicted by H_p-open correlated well with the measured AP (r², 0.75; RMS, 2 mmHg; P < 0.05; Fig. 7B), whereas the AP predicted by H_{p-closed-spon} correlated partially with the measured values (r², 0.58; RMS, 3 mmHg; P < 0.05; Fig. 7C). Using the data from all animals, the H_p-open-predicted AP correlated well with the measured AP (r², 0.8 ± 0.1; RMS, 2 ± 2 mmHg; P < 0.05). The H_{p-closed-spon}-predicted AP similarly correlated with the measured AP, but with lower r² (0.7 ± 0.1) and higher RMS (3 ± 3 mmHg) compared with H_p-open (P < 0.05).

Figure 7. Predictability of peripheral arc transfer functions in open-loop condition.

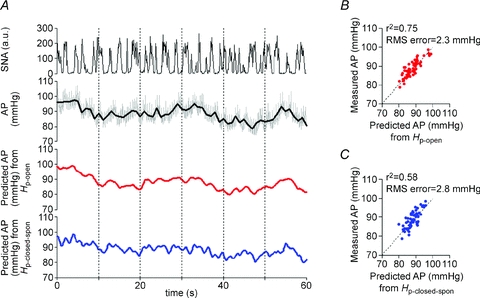
A, typical representative example of evaluating the predictability of AP output from SNA input using baroreflex transfer functions of the peripheral arc. The data were obtained from the same animal as in Fig. 3. The time-series AP dynamics are predicted from SNA measured in protocol 4 (top panel), by the open-loop transfer function determined in protocol 1 (red line, third panel) and by the closed-loop-spontaneous transfer function determined in protocol 2 (blue line, bottom panel). These predicted AP changes are compared with the actual AP measured in protocol 4 (the grey and black lines indicate AP re-sampled at 10 and 1 Hz, respectively; second panel). AP predicted by open-loop transfer function (H_p-open) appears to parallel the actually measured AP, whereas AP predicted by closed-loop-spontaneous transfer function (H_{n-closed-spon}) also correlates to some extent. B, scatter plot analysis of the AP predicted by H_p-openversus the measured AP. C, scatter plot analysis of the AP predicted by H_{p-closed-spon}versus the measured AP.

Predictability of open-loop and closed-loop-spontaneous transfer functions compared with data measured in the closed-loop-spontaneous condition (protocol 4)

The ability of neural arc transfer functions (determined by protocols 1 and 2) to predict SNA from CSP input in the closed-loop-spontaneous condition was quantified by comparing with the actual SNA measurements in protocol 4. Figure 8 shows a typical example. Since CSP was matched with systemic AP, spontaneous fluctuation of AP was observed (Fig. 8A, top panel). AP increased spontaneously for 60–90 s but SNA did not decrease but increased, indicating that AP changes did not induce a negative SNA response via the baroreflex neural arc (Fig. 8A, third panel). Indeed, SNA predicted by H_n-open (Fig. 8A, fourth panel) and H_{n-closed-spon} (Fig. 8A, bottom panel) were markedly different from the measured SNA (Fig. 8A, second and third panels). Scatter plot analyses indicated that these predicted SNAs did not correlate with the measured SNA (Fig. 8B and C).

Figure 8. Predictability of neural arc transfer functions in closed-loop-spontaneous condition.

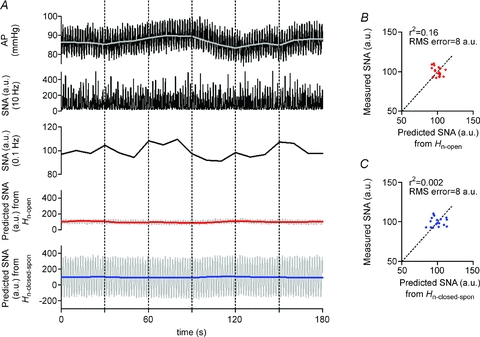
A, example of spontaneous changes in AP (resampled at 10 and 0.1 Hz represented by black and grey lines, respectively, in the top panel) and SNA (re-sampled at 10 and 0.1 Hz in second and third panels, respectively) in closed-loop baroreflex condition (protocol 5). Using the open-loop (H_n-open, identified in protocol 1) and the closed-loop-spontaneous transfer functions (H_{n-closed-spon}, identified in protocol 2) of the neural arc, a time-series of SNA output was predicted from the actual AP measured in protocol 5. However, the predicted SNA (re-sampled at 10 Hz represented by grey line, and at 0.1 Hz represented by red and blue lines in fourth and bottom panels, respectively) response is markedly different from the trend of measured SNA. B, scatter plot analysis of the SNA predicted by H_n-openversus the measured SNA. C, scatter plot analysis of the SNA predicted by H_{n-closed-spon}versus the measured SNA.

In addition, the ability of peripheral arc transfer functions (determined by protocols 1 and 2) to predict AP from SNA input in the closed-loop-spontaneous condition was also quantified by comparing with the actually measured AP. Figure 9 shows a typical example obtained from the same animal as in Fig. 8. The spontaneous changes in SNA (Fig. 9A, second panel) appeared to precede those in AP (Fig. 9A, third panel), suggesting that SNA changes induced a positive response of AP via the baroreflex peripheral arc. Indeed, the AP (grey lines, re-sampled at 0.1 Hz) predicted by H_p-open (Fig. 9A, fourth panel) and that predicted by H_{p-closed-spon} (bottom panel) resembled the measured AP (third panel). Scatter plot analyses indicated that these predicted APs correlated well with the measured AP (Fig. 9B and C).

Figure 9. Predictability of peripheral arc transfer functions in closed-loop-spontaneous condition.

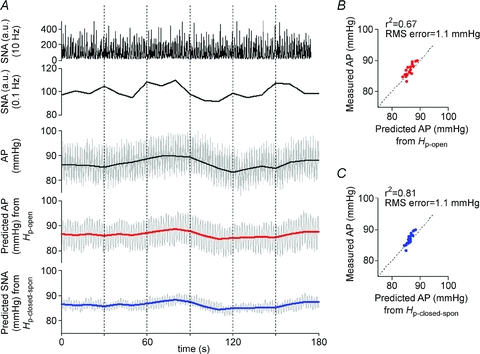
A, example of spontaneous changes in SNA (re-sampled at 10 and 0.1 Hz in top and second panels, respectively) and AP (re-sampled at 10 and 0.1 Hz represented by grey and black lines, respectively, in third panel) under closed-loop baroreflex condition measured in protocol 5. Using the open-loop transfer function (H_p-open, identified in protocol 1) and the closed-loop-spontaneous transfer function (H_{p-closed-spon}, identified in protocol 2) of the peripheral arc, a time-series of AP output was predicted (re-sampled at 10 Hz represented by grey line, and at 0.1 Hz represented by red and blue lines in fourth and bottom panels, respectively) from the actual SNA measured in protocol 5. The predicted APs re-sampled at 0.1 Hz appear similar to the measured AP to some extent. B, scatter plot analysis of the AP predicted by H_p-openversus the measured AP. C, scatter plot analysis of the AP predicted by H_{p-closed-spon}versus the measured AP.

Similar results were found in all animals in the closed-loop-spontaneous resting condition. Changes in SNA always preceded alterations in AP, and induced a positive AP response. The closed-loop peripheral arc transfer function predicted the time series of AP dynamics with some degree of accuracy, whereas the neural arc transfer function failed to predict SNA.

Predictability of open-loop and closed-loop-spontaneous transfer functions compared with data measured during pharmacological pressure intervention in the closed-loop condition (protocol 5)

The ability of neural arc transfer functions (determined by protocols 1 and 2) to predict SNA from CSP change induced by pharmacological intervention under closed-loop conditions was quantified by comparing with the actual SNA measurements in protocol 5. The intervention was sequential bolus infusions of phenylephrine, nitroprusside and phenylephrine. Figure 10 shows a typical example. CSP was matched with systemic AP (Fig. 10A, first and second panels). The phenylephrine–nitroprusside–phenylephrine bolus infusions produced an increase–decrease–increase and recovery changes in AP, which led to changes in SNA as follows. When AP (which equals CSP) increased, actually measured SNA decreased, and vice versa (Fig. 10A, third panel).

Figure 10. Predictability of neural arc transfer functions during pharmacological pressure interventions in closed-loop condition.

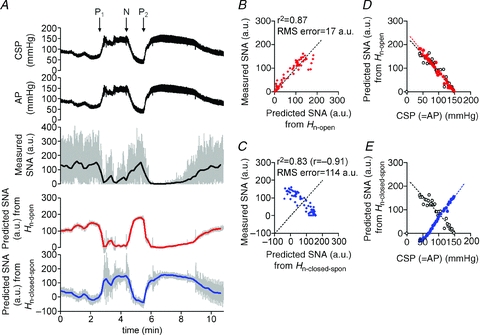
A, example of changes in CSP and AP (re-sampled at 10 Hz in the top and second panels, respectively) induced by pharmacological interventions and SNA responses (re-sampled at 10 and 0.1 Hz represented by grey and black lines, respectively, in third panel) in closed-loop baroreflex condition (protocol 5). Sequential bolus infusions of phenylephrine (P₁), nitroprusside (N) and phenylephrine (P₂) were administered. Using the open-loop (H_n-open, identified in protocol 1) and the closed-loop-spontaneous transfer functions (H_{n-closed-spon}, identified in protocol 2) of the neural arc, time-series of SNA output was predicted (re-sampled at 10 Hz represented by grey line, and at 0.1 Hz represented by red and blue lines in fourth and bottom panels, respectively) from the actual AP measured in protocol 5. SNA predicted by open-loop transfer function (H_n-open) appears to parallel the actually measured SNA, whereas SNA predicted by closed-loop-spontaneous transfer function (H_{n-closed-spon}) is markedly different from the measured SNA. B, scatter plot analysis of the SNA predicted by H_n-openversus the measured SNA. The identity line is shown. C, scatter plot analysis of the SNA predicted by H_{n-closed-spon}versus the measured SNA. D, relationship between CSP and SNA predicted by H_n-open (red filled circle, red broken line) is similar to that between CSP and actually measured SNA (open circle, black broken line) or E, relationship between CSP and SNA predicted by H_{n-closed-spon} (blue filled circle, blue broken line) is different from that between CSP and actually measured SNA (open circle, black broken line).

The SNA response to CSP changes predicted by the open-loop transfer function (H_n-open) (Fig. 10A; fourth panel) resembled the actually measured SNA (third panel) in both the timing (phase) and intensity of neural activity. In contrast, the SNA response predicted by the closed-loop-spontaneous transfer function (H_{n-closed-spon}) (bottom panel) showed oppositely directed neural response as compared with actually measured SNA (third panel). When AP (which equals CSP) increased, the predicted SNA increased whereas the measured SNA decreased, and vice versa. As a result, scatter plot analyses showed that the SNA predicted by H_n-open correlated significantly with the actually measured SNA (r², 0.87; RMS, 17 a.u.; P < 0.05; Fig. 10B), indicating a good predictability. However, the SNA predicted by H_{n-closed-spon} showed negative correlation (r, −0.91; RMS, 114 a.u.; Fig. 10C), indicating a lack of predictability. The relationship between CSP (= AP) and actually measured SNA (Fig. 10D and E, open circles) was similar to that between CSP (= AP) and SNA predicted by H_n-open (Fig. 10D, red circles) but different from that between CSP and SNA predicted by H_{n-closed-spon} (Fig. 10E, blue circles). Using the data from all animals, the SNA predicted by H_n-open correlated with the measured SNA (r², 0.9 ± 0.1; RMS, 16 ± 4 a.u.; P < 0.05), whereas SNA predicted by H_{n-closed-spon} showed negative correlation (r, −0.8 ± 0.1; RMS, 112 ± 35 a.u.).

Discussion

Good predictability of open-loop baroreflex transfer functions

Although baroreflex transfer functions have been identified by open-loop analysis (Ikeda et al. 1996; Kawada et al. 2002; Kamiya et al. 2005b, 2008a), whether the functions predict time-series output dynamics, which would confirm the accuracy of system identification of transfer function, remains to be elucidated. In the present study, we showed that the open-loop baroreflex transfer functions were able to predict output dynamics with high accuracy, even though the data set for determining the transfer functions (protocol 1) was different from that for investigating predictability (protocols 3, 4 and 5). The neural arc transfer function determined by the open-loop experiment (H_n-open) predicted SNA responses to measured CSP changes with r² of 0.8 ± 0.1. Likewise, the peripheral arc transfer function (H_p-open) also predicted the AP responses to measured SNA changes with r² of 0.8 ± 0.1 (Fig. 7). These results supported our first hypothesis that the open-loop baroreflex transfer functions for the neural and peripheral arcs are able to predict time-series SNA and AP outputs from baroreceptor pressure and SNA inputs, respectively. The good predictability indicates the accuracy of system identification of these transfer functions determined by open-loop experiments.

Inappropriate system identification and limited predictability of closed-loop spontaneous baroreflex transfer functions

Regarding the neural arc, our results showed that the transfer function determined under closed-loop-spontaneous conditions (H_{n-closed-spon}) was markedly different from that determined under open-loop conditions (H_n-open) (Fig. 5). In H_{n-closed-spon}, the increase in gain versus frequency was markedly enhanced (enhanced high-pass filter). A phase lead rather than phase lag indicates that the calculated phase may be incorrect since H_n-open showed a linear phase lag, reflecting a fixed pure time delay from baroreceptor pressure to SNA (Orea et al. 2007). Furthermore, the step response of SNA to CSP predicted by H_{n-closed-spon} oscillated, although an initial decrease followed by partial recovery was predicted by H_n-open (Fig. 5). These contradicting and strange characteristics of H_{n-closed-spon} were associated with less appropriate predictability of time-series SNA output dynamics. Although the SNA predicted by H_n-open in response to the measured changes in CSP was roughly similar to the actually measured SNA with respect to both amplitude and timing of the neural burst (Fig. 6A and B), the SNA predicted by H_{n-closed-spon} was greatly different from the measured SNA, showing increased amplitude and inconsistent timing of neural burst (Fig. 6A and C). Therefore, with regard to the neural arc, these results support our second hypothesis that the closed-loop-spontaneous baroreflex transfer function is limited in its ability to predict the baroreflex dynamics compared with the open-loop transfer function.

Regarding the peripheral arc, however, the present study showed unexpected results. In contrast to the neural arc, the closed-loop-spontaneous baroreflex transfer function for the peripheral arc (H_{p-closed-spon}) approximated the open-loop transfer function (H_p-open) not only in gain and phase functions but also in the step response (Fig. 5). The similar characteristics of H_{p-closed-spon} and H_p-open yielded high predictability of time-series AP dynamics. The AP predicted by H_{p-closed-spon} in response to the measured SNA changes was roughly the same as the actually measured AP (Fig. 7), although the correlation with measured data was lower than the AP predicted by H_p-open. Therefore, regarding the peripheral arc, these results support our second hypothesis and indicate that the closed-loop-spontaneous baroreflex transfer function is partially appropriate for system identification of the peripheral arc and is able to predict the time-series AP dynamics under resting conditions despite slightly limited accuracy compared with the open-loop transfer function. This finding may have great impact, because the closed-loop-spontaneous baroreflex transfer function has been believed to represent the neural arc function (Orea et al. 2007; Cooke et al. 2009; Ogoh et al. 2009).

Potential mechanism for the limitation of closed-loop-spontaneous baroreflex transfer functions

It is indeed difficult to understand why the closed-loop-spontaneous transfer function is inappropriate for system identification of the neural arc but is partially appropriate for the peripheral arc. As a possible mechanism, we examined the effects of noise on the calculation of the closed-loop-spontaneous transfer function using numerical simulations (Fig. 11). Noise is considered as a factor that modulates output dynamics independent of input. Figure 11 (upper panels in B, C and D) shows block diagrams of the closed-loop baroreflex system. H_n represents central processing from baroreceptor pressure input to SNA, while H_p represents peripheral processing from SNA input to systemic AP. According to our previous studies (Ikeda et al. 1996; Kawada et al. 2002), we modelled H_n using derivative and high-cut filter characteristics with a pure delay, and H_p using second-order low-pass filter with a pure delay (see Appendix B, Fig. 11A) (Kamiya et al. 2005b). In this closed-loop baroreflex system, CSP equals AP. As noise, Gaussian white-noise was introduced to the neural and/or peripheral arcs (Fig. 1C). As in protocol 2, closed-loop-spontaneous transfer functions were calculated by the simplified method, from AP to SNA as the neural arc (corresponding to the H_{n-closed-spon}) and from SNA to AP as the peripheral arc (corresponding to the H_{p-closed-spon}), while neglecting the noise (see Appendix A, Fig. 11B, C and D).

Figure 11. A numerical simulation of the effects of noise on calculation of baroreflex transfer functions.

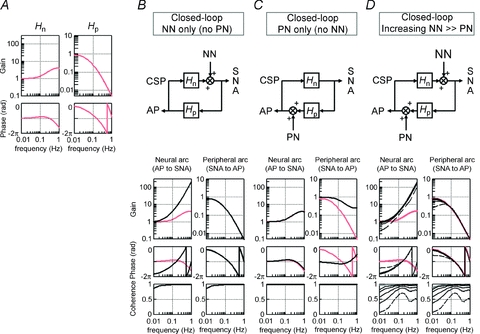
Noise (Gaussian white-noise) is introduced to the neural and/or peripheral arcs in closed-loop-spontaneous baroreflex condition, where CSP equals AP (see Figure 1C). A, the original baroreflex transfer functions of the neural (H_n, left panel) and peripheral (H_p, right panel) arcs. H_n is modelled using derivative and high-cut filter characteristics with a pure delay, and H_p using the second-order low-pass filter with a pure delay (see Appendix B). Units of gain are a.u. mmHg⁻¹ for H_n and mmHg a.u.⁻¹ for H_p, respectively. B–D, block diagrams (upper panels) and closed-loop-spontaneous transfer functions (lower panels); calculated from AP to SNA as the neural arc (left lower panel) and from SNA to AP as the peripheral arc (right lower panel). The open-loop transfer functions (H_n, H_p) are included as reference (gray lines). Units of gain are a.u. mmHg⁻¹ for the neural arc and mmHg a.u.⁻¹ for the peripheral arc, respectively. B, first simulation: noise (0.029, 0.117, 0.264, 0.732 and 2.928 × 10³ au²) is present only in the neural arc. The same results are obtained irrespective of the noise intensity. The closed-loop-spontaneous transfer function of the neural arc is totally different from the open-loop transfer function H_n, whereas that of the peripheral arc overlaps with H_p. C: Second simulation: noise (0.029, 0.117, 0.264, 0.732 and 2.928 × 10³ mmHg² is present only in the peripheral arc. The same results are obtained irrespective of the noise intensity. The closed-loop-spontaneous transfer function of the neural arc overlaps the open-loop transfer function H_n, whereas that of the peripheral arc is markedly different from H_n. D, third simulation: noise with incremental intensity [from 0.029 (broken line) to 0.117, 0.264, 0.732 and 2.928 (solid lines) × 10³ au²] is present in the neural arc, while a small constant noise (29 mmHg²) is present in the peripheral arc. The closed-loop-spontaneous transfer function of the neural arc is different from the open-loop transfer function of H_n, whereas that of the peripheral arc approaches H_p and the two become overlapped as the noise in the neural arc increases. H_n, neural arc transfer function; H_p, peripheral arc transfer function, NN, unknown neural noise; PN, unknown peripheral noise.

We next examined how the noise modifies the closed-loop-spontaneous transfer functions calculated by the simplified method and renders them different from the open-loop transfer functions by simulating three situations. Because of the closed-loop nature, changes in AP (thus, in CSP) modulate SNA via the neural arc transfer function (H_n), which in turn change AP via peripheral arc transfer function (H_p). In the first simulation, noise is present only in the neural arc (Fig. 11B). Regardless of the magnitude of the noise, the closed-loop-spontaneous transfer function for the neural arc is greatly different from the open-loop transfer function H_n (red lines), with markedly increased gain and phase lead versus frequency. In contrast, the closed-loop-spontaneous transfer function for the peripheral arc overlaps with the open-loop transfer function H_n. In the second simulation, noise is present only in the peripheral arc (Fig. 11C). Regardless of the magnitude of the noise, the closed-loop-spontaneous transfer function for the neural arc overlaps with the open-loop transfer function H_p, whereas that of the peripheral arc deviates markedly from the open-loop transfer function H_p (red lines). In the third simulation, an incremental noise is present in the neural arc and a small constant noise in the peripheral arc (Fig. 11D). Regardless of the magnitude of the noise, the closed-loop-spontaneous transfer function for the neural arc is different from the open-loop transfer function H_n (red lines). However, as the noise in the neural arc increases, the closed-loop-spontaneous transfer function for the peripheral arc approaches the open-loop transfer function H_p and becomes superimposed with respect to gain, phase and coherence functions. These simulations indicate that the presence of noise in the neural and peripheral arcs reduces the accuracy of identification of closed-loop-spontaneous transfer function for the neural and peripheral arc, respectively. Importantly, our experimental results (Fig. 5) may be consistent with the situation that noise is predominant in the neural arc rather than in the peripheral arc (Fig. 11B and D). This might reflect our experimental condition that had little or no noise in the peripheral arc (i.e. perturbation to AP), probably because the body did not move in closed-loop baroreflex and spontaneous resting conditions. Therefore, a noise predominantly in the neural arc may be a potential mechanism responsible for our experimental finding that the closed-loop-spontaneous transfer function is inappropriate in identifying the neural arc but partially appropriate in identifying the peripheral arc under resting conditions.

Physiological implication (1): Baroreflex is predominantly feedforward rather than feedback in the closed-loop-spontaneous condition

While we separate the total arc (CSP input to systemic AP) of the baroreflex system into the neural (CSP input to SNA) and peripheral (SNA input to systemic AP) arc subsystems, the neural and the peripheral arcs are equivalent to the feedback and feedforward arcs, respectively, as reported in earlier studies (Barres et al. 2004; Brychta et al. 2007). Using these terms, our data indicate that the baroreflex loop is predominantly feedforward rather than feedback in the closed-loop-spontaneous resting condition. This may be explained by the block diagram and simulation results shown in Fig. 11D. As the noise in the neural arc increases, SNA fluctuates more but becomes less dependent on CSP (baroreceptor pressure input), while the augmented SNA changes strongly the control systemic AP via the peripheral arc transfer function (H_p) with little interruption by noise in the peripheral arc. As a result, baroreflex control becomes feedforward-like, while the closed-loop-spontaneous transfer function for the peripheral arc approaches the open-loop transfer function H_p. This concept may explain our findings that the closed-loop-spontaneous baroreflex transfer function for the peripheral arc partially matched the open-loop transfer function, whereas that for the neural arc did not (Fig. 5). In addition, this concept may also explain other data that in the closed-loop-spontaneous condition, spontaneous changes in SNA appeared to precede changes in AP and induce positive AP responses (Fig. 9A), and that the closed-loop-spontaneous peripheral arc transfer function was capable of predicting the time-series AP dynamics from SNA (Fig. 9B and C).

Physiological implication (2): Potential mechanisms for AP and SNA fluctuations in the closed-loop-spontaneous condition

Our experiments of opening and closing the baroreflex loop in individual animals may help to suggest potential mechanisms responsible for AP and SNA fluctuations in the closed-loop condition. First, both SNA auto-rhythmicity (pacemaker) and baroreflex mechanisms may contribute to fluctuations of AP and SNA at approximately 0.4 Hz actually observed in the closed-loop-spontaneous baroreflex condition (Fig. 4B), which is often termed the Mayer wave (Malpas & Burgess, 2000; Barres et al. 2004). It is noteworthy that even in the baroreflex open-loop condition, the SNA autospectrum shows a small peak at approximately 0.4 Hz (arrowhead, Fig. 3B) despite no peak in CSP autospectrum, indicating the existence of SNA auto-rhythmicity at 0.4 Hz, which in turn produces systemic AP fluctuation at that frequency (Fig. 3B) via peripheral arc transfer function (Fig. 3C). This may explain the coherence drop at approximately 0.4 Hz (from CSP to SNA) in open-loop condition (Fig. 3C). Furthermore, since closing the baroreflex loop greatly increases the peak of the SNA autospectrum (arrowhead, Fig. 4B), interaction between the baroreflex neural and peripheral arcs is important for these fluctuations. This may be consistent with the report that bilateral denervation of aortic and carotid sinus baroreceptors eliminated 0.4 Hz oscillations of AP and SNA during sympathoexcitatory stress (Barres et al. 2004). Collectively, SNA auto-rhythmicity (which equals ‘origin’ activity) and its development and propagation by the baroreflex may partly be responsible for the 0.4 Hz fluctuations of AP and SNA in this experimental condition.

Second, although the baroreflex feedback system can theoretically generate oscillations of AP and SNA by itself without other factors (i.e. SNA auto-rhythmicity) in the closed-loop condition (Guyton & Harris, 1951; deBoer et al. 1987; Kamiya et al. 2005a), the baroreflex loop theory might not contribute to the 0.4 Hz AP and SNA fluctuations observed in the closed-loop-spontaneous condition, for the following reason. The key point of the baroreflex loop theory is that when the gain of total arc baroreflex transfer function is greater than 1 at the frequency where the phase reaches −2π radians (which we define as f₀), oscillations of AP and SNA will occur at around f₀. In our actual data, f₀ was approximately 0.13 Hz (Fig. 3E), which is consistent with a previous study (Malpas & Burgess, 2000) showing increased 0.1 Hz oscillation of AP during haemorrhage in rabbits. Moreover, the gain at f₀ was less than 1 (Fig. 3E), indicating no oscillations generated according to the baroreflex loop theory. Therefore, in the closed-loop-spontaneous condition, the baroreflex loop theory would not contribute to the 0.4 Hz fluctuations of AP and SNA.

Lastly, respiratory-mediated fluctuation of AP may contribute to SNA fluctuation via baroreflex mechanisms. In the baroreflex open-loop condition (Fig. 3B), SNA autospectrum shows no peak whereas systemic AP shows a large peak at the frequency of artificial respiration (approximately 0.57 Hz) (Fig. 3B). This indicates that AP fluctuation at that frequency is not mediated by SNA but by mechanical aspects of respiration (i.e. respiratory changes in intrathoracic pressure), consistent with an earlier report (Brychta et al. 2007). Since closing the baroreflex loop produces a peak in the SNA autospectrum at the respiratory frequency (Fig. 4B), a baroreflex mechanism may partly be responsible for respiratory-mediated SNA fluctuation in this experimental condition.

Physiological implication (3): open-loop baroreflex neural arc transfer function is able to predict closed-loop time-series SNA response to drug-induced AP change

The data discussed so far were obtained using mechanical interventions to change carotid sinus pressure, which arguably are not physiological changes. To validate whether the predictabilities of the open-loop and closed-loop-spontaneous transfer functions apply to more physiological conditions, we tested the neural arc transfer functions using pharmacological pressure intervention (phenylephrine and nitroprusside infusions) under closed-loop conditions. First, the SNA predicted by the open-loop baroreflex neural arc transfer function (H_n-open) in response to the measured changes in CSP (= AP) was roughly similar to the actually measured SNA with respect to both amplitude and timing of neural activity (Fig. 10A, third and fourth panel), showing high correlation (r²= 0.9, Fig. 10B). This result indicates that with regard to the neural arc, the open-loop transfer function is able to predict time-series SNA output from AP input even during pharmacological pressure interventions. A possible explanation for the good predictability is that since the pharmacological interventions exert a noise to the peripheral and not the neural arc, time-series SNA is almost determined by the pharmacologically induced changes in baroreceptor pressure (= systemic AP) via the neural arc transfer function (=H_n-open).

In contrast to the open-loop transfer function, the SNA predicted by the closed-loop-spontaneous baroreflex neural arc transfer function (H_{n-closed-spon}) was different from the measured SNA. The predicted SNA was an oppositely directed neural response: when AP (= CSP) increased, the predicted SNA increased whereas the measured SNA decreased, and vice versa. Therefore, with regard to the neural arc, the closed-loop-spontaneous transfer function is not able to predict SNA dynamics from AP. The failure in predicting SNA change may be explained by inappropriate system identification in the closed-loop condition. Because of the closed-loop condition, the calculated phase function of H_{n-closed-spon} was the inverse of that of H_{p-closed-spon}. Indeed, the phase led as frequency increased (Figs 5, 11B and D) in contrast to the phase lag of the open-loop transfer function (H_n-open). Furthermore, the calculated phase of H_{n-closed-spon} resulted in an oppositely directed response of predicted SNA as compared with actually measured SNA, in contrast to the good match of predicted SNA by H_n-open. These results indicate that with regard to the neural arc, the open-loop neural arc transfer function predicts time-series SNA response to changes in AP induced by pharmacological interventions, while the closed-loop-spontaneous transfer function cannot predict SNA response.

Although spontaneous baroreflex measures are believed to represent the neural arc function (baroreflex control of SNA), the present study raises potential methodological issues. First, since the baroreflex is a closed-loop feedback system, there is theoretical difficulty in identifying system characteristics in the closed-loop spontaneous condition. Since a relationship calculated from SNA input to AP during their spontaneous fluctuations is the inverse of that calculated from AP input to SNA, the calculation itself cannot determine the causality between them. Our present data clearly indicate limitation in estimating closed-loop-spontaneous transfer function of the neural arc, and that a good estimation requires opening the loop and introducing an intervention to the loop. Furthermore, although the spontaneous baroreflex transfer function obtained in the closed-loop condition (Orea et al. 2007; Cooke et al. 2009; Ogoh et al. 2009) has been used as a surrogate for the neural (feedback) arc function of the baroreflex loop, it actually represents the peripheral (feedforward) arc function since baroreflex loop is predominantly feedforward rather than feedback in the closed-loop-spontaneous condition.

Second, a recent study (Hart et al. 2010) has reported that spontaneous baroreflex measures (slope of strength of muscle SNA burst over-binned or non-binned AP) did not correlate (r²= 0.05–0.13) with the ‘gold standard’ modified Oxford analysis (nitroprusside and phenylephrine), whereas spontaneous threshold measure (slope of % occurrence of muscle SNA burst over 1 mmHg binned AP, eliminating strength of SNA burst) correlated with it mildly (r²= 0.5). Although we cannot directly compare the transfer function analysis in our present study with the spontaneous threshold measure reported by Hart et al. (2010) because of methodological differences, our open-loop transfer function of the neural arc was able to predict occurrence and magnitude of time-series SNA with a higher degree of accuracy (r²= 0.9, Fig. 10B) and reproduce the AP–SNA relationship during closed-loop, drug-induced AP changes (Fig. 10D).

Limitations

The present study has several limitations. First, we excluded the efferent effect of the vagally mediated arterial baroreflex, which could affect the properties of baroreflex control of SNAs. Second, artificial respiration and surgical procedures used in this study could affect baroreflex. Third, anaesthetic agents tend to inhibit efferent SNA and depress the gain of baroreflex control of SNA. Fourth, since the present study was animal research, it is limited in its applicability to humans. However, a problem of difficulty in identifying the ‘closed-loop’ system in contrast with the ‘open-loop’ system is common in animal and human studies. Lastly, we perfused the carotid sinuses with physiological saline pre-equilibrated with atmospheric. Local hypoxia could have occurred and somewhat affected baroreflex control of SNA. Further research to examine the relevance of the present findings to true physiological conditions is necessary.

Summary

In summary, the open-loop baroreflex transfer functions for the neural and peripheral arcs allowed good prediction of the time-series SNA and AP outputs from baroreceptor pressure and SNA inputs, respectively. In contrast, the closed-loop-spontaneous baroreflex transfer function for the neural arc deviated greatly from the open-loop transfer function, and could not predict the time-series SNA dynamics. However, the closed-loop-spontaneous baroreflex transfer function for the peripheral arc partially matched the open-loop transfer function, with reasonable predictability of the time-series AP dynamics although slightly inferior in accuracy. Furthermore, the predictabilities of open-loop and closed-loop-spontaneous transfer functions of the neural arc were validated by closed-loop pharmacological (phenylephrine and nitroprusside infusions) pressure interventions. Time-series SNA responses to drug-induced AP changes predicted by the open-loop transfer function matched closely the measured responses, whereas SNA responses predicted by the closed-loop-spontaneous transfer function deviated greatly and were the inverse of measured responses. Therefore, although the spontaneous baroreflex transfer function obtained by closed-loop analysis has been believed to represent the neural arc function, it is inappropriate for system identification of the neural arc but is partially appropriate for system identification of the peripheral arc under resting condition, compared with open-loop analysis.

Glossary

Abbreviations

AP

arterial pressure

CSP

intra-carotid sinus pressure

r

linear correlation coefficient

RMS

root mean square

SNA

sympathetic nerve activity

Appendix A

In a block diagram of the open-loop baroreflex system (Fig. 1A), CSP is independent of systemic AP because of vascular isolation of the carotid-sinus regions. In this framework, input–output relationships of these arcs are expressed in the frequency domain as:

(A1)

(A2)

where CSP(f), SNA(f) and AP(f) are the fast Fourier transforms of CSP, SNA and systemic AP, respectively. H_n(f) and H_p(f) denote the neural arc and the peripheral arc transfer functions, respectively. NN(f) and PN(f) represent unknown noise in the neural and peripheral arcs, respectively.

In the neural arc, calculating the ensemble averages of cross-powers between the terms of eqn (A1) and CSP(f) yields

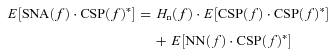(A3)

where E[] indicates an ensemble average operation. CSP(f)* denotes the complex conjugate of CSP(f). As H_n(f) is supposed to be time invariant during the observation period, H_n(f) is outside the ensemble average operation. When CSP is a white-noise signal, E[NN(f)·CSP(f)*] diminishes to zero asymptotically because the white noise is statistically independent of any other noise signal. Thus, we can estimate H_n(f) by the following equation, which we designate H_n-open(f).

(A4)

Similarly, in the peripheral arc, calculating ensemble averages of cross-powers between terms of eqn (A2) and SNA(f) yields

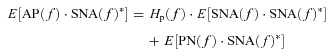(A5)

where SNA(f)* denotes the complex conjugate of SNA(f). As H_p(f) is supposed to be time invariant during the observation period, H_p(f) is outside the ensemble average operation. In the open-loop condition, since PN(f) cannot affect SNA(f) and is statistically independent of SNA(f) by definition, E[PN(f)·SNA(f)*] diminishes to zero asymptotically. Thus, we can estimate H_p(f) by the following equation, which we designate H_p-open(f).

(A6)

In contrast to the open-loop condition, CSP is matched with systemic AP in the closed-loop-spontaneous baroreflex condition (Fig. 1B). Thus, the input–output relationships of the arcs in the frequency domain are expressed as:

(A7)

(A8)

In the neural arc, calculating ensemble averages of cross-powers between the terms of eqn (A7) and AP(f) yields

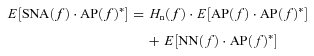(A9)

(A10)

However, in the baroreflex closed-loop conditions, the unknown noise in SNA (NN) can affect AP through the peripheral arc transfer function (H_p). In other words, AP(f) inevitably correlates with NN(f), and E[NN(f)·AP(f)*] does not diminish to zero. H_n(f) cannot be determined because the unknown noise NN is practically impossible to quantify. Therefore in protocol 3, we simplify eqn (A10) by neglecting the last term, and define the closed-loop-spontaneous transfer function by the following equation, which we designate H_{n-closed-spon}(f).

(A11)

However, from eqns (A4) and (A11), it is evident that H_{n-closed-spon}(f) should be different from H_n-open(f) when NN(f) is large and cannot be neglected.

In the peripheral arc, calculating ensemble averages of cross-powers between the terms of eqn (A8) and SNA(f) yields:

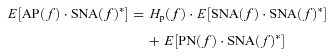(A12)

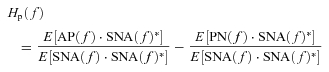(A13)

However, in the baroreflex closed-loop conditions, the unknown noise in AP (PN) can affect SNA through the neural arc transfer function (H_n). In other words, SNA(f) inevitably correlates with PN(f), and E[PN(f)·SNA(f)*] does not diminish to zero. H_p(f) cannot be determined because the unknown noise PN is practically impossible to quantify. Therefore in protocol 3, we simplify eqn (A13) by neglecting the last term and define the closed-loop-spontaneous transfer function by the following equation, which we designate H_{p-closed-spon}(f).

(A14)

However, from eqns (A6) and (A14), it is evident that H_{p-closed-spon}(f) should be different from H_p-open(f) when PN(f) is large and cannot be neglected.

Appendix B

In rabbits, the transfer function of the baroreflex neural arc (baroreceptor pressure/CSP to SNA) approximates derivative characteristics in the frequency range below 0.8 Hz, and high-cut characteristics of frequencies above 0.8 Hz (Kawada et al. 2002). Therefore, according to our previous study, we model the neural arc transfer function (H_n) using eqn (B1) as follows

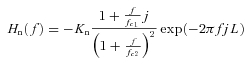(B1)

where f and j represent the frequency (in Hz) and imaginary units, respectively; K_n is static gain (in a.u. mmHg⁻¹); f_c1 and f_c2 (f_c1 < f_c2) are corner frequencies (in Hz) for derivative and high-cut characteristics, respectively; and L is a pure delay (in s), that would represent the sum of delays in synaptic transmission in the baroreflex central pathways and the sympathetic ganglion. The dynamic gain increases in the frequency range from f_c1 to f_c2, and decreases above f_c2. Based on the measured results, we set K_n, f_c1, f_c2 and L at 1, 0.1, 0.8 and 0.2, respectively, in all simulations in Fig. 11.

In addition, the transfer function of the baroreflex peripheral arc (SNA to systemic AP) approximates the second-order low-pass filter with a lag time in rabbits (Kawada et al. 2002). Therefore, we model the peripheral arc transfer function (H_p) using eqn (B2) as follows:

(B2)

where K_p is static gain (in mmHg a.u.⁻¹); fN and indicate a natural frequency (in Hz) and a damping ratio, respectively; and L is a pure delay (in s) that would represent the sum of delays in synaptic transmission in the neuroeffector junction and intracellular signal transduction in the effector organs. Based on the measured results, we set K_p, f_N, and L at 1, 0.07, 1.4 and 1.0, respectively, in all simulations in Fig. 11.

Author contributions

The experiments were performed at the Department of Cardiovascular Dynamics, National Cerebral and Cardiovascular Center Research Institute. A.K. absolutely contributed to: (1) Conception and design, (2) Collection, analysis and interpretation of data and (3) Drafting the article or revising it critically for important intellectual content. Other authors helped him particularly in (3). All authors approved the final version.