Characterization of a clinical polymer-drug conjugate using multiscale modeling

Abstract

The molecular conformation of certain therapeutic agents has been shown to affect the ability to gain access to target cells, suggesting potential value in defining conformation of candidate molecules. This study explores how the shape and size of poly-γ-glutamyl-glutamate paclitaxel (PGG-PTX), an amphiphilic polymer-drug with potential chemotherapeutic applications, can be systematically controlled by varying hydrophobic and hydrophilic entities. Eighteen different formulations of PGG-PTX varying in three PTX loading fractions of 0.18, 0.24, and 0.37 and six spatial arrangements of PTX (‘clusters’, ‘ends,’ even’, ‘middle’, ‘random’, and ‘side) were explored. Molecular dynamics (MD) simulations of all-atom (AA) models of PGG-PTX were run until a statistical equilibrium was reached at 100 ns and then continued as coarse-grained (CG) models until a statistical equilibrium was reached at an effective time of 800 ns. Circular dichroism spectroscopy was used to suggest initial modeling configurations. Results show that a PGG-PTX molecule has a strong tendency to form coil shapes, regardless of the PTX loading fraction and spatial PTX arrangement, although globular shapes exist at f_PTX = 0.24. Also, less uniform PTX arrangements such as ‘ends’, ‘middle’, and ‘side’ produce coil geometries with more curvature. The prominence of coil shapes over globules demonstrates that PGG-PTX may confer a long circulation half-life and high propensity for accumulation to tumor endothelia. This multiscale modeling approach may be advantageous for the design of cancer therapeutic delivery systems.

INTRODUCTION

There is a continuing interest in the development of new chemotherapeutic agents for cancer therapy.¹ Although many existing cancer therapeutics are known to be highly effective in destroying cancer cells in vitro, physiological barriers may prevent optimal access of the therapeutic to its target. Various investigators have argued that the ability of a therapeutic to successfully cross these barriers may depend on its physicochemical properties such as shape and size.^1,2 For instance, wormlike, filamentous polymeric micelles remain in the blood ten times longer than their spherical counterparts.^3,4 Ellipsoidal particles have shown to have a higher propensity to accumulate to the walls of tumor endothelia, than spherical particles.⁵ Also, it has been shown that nanoparticles within a size range of 2–100 nm altered intracellular signaling pathways associated with basic cell function.⁶ These intriguing observations suggest the shape and size of a therapeutic as a basis for design.

Since most therapeutic drugs are rigid, polar molecules, a flexible and hydrophilic entity is often attached to the drug to alter its physicochemical properties. As drug delivery agents, polymers are known to confer benefits such as targeting drugs to the tumor while simultaneously minimizing toxicity by limiting drug exposure to normal tissue, increasing blood circulation half-life of drugs, and increasing adsorption of drugs to tumor tissue.^7,8 The polymer-drug hybrid comprised of a rigid, hydrophobic therapeutic component and a flexible, biodegradable, and hydrophilic component may enhance the overall effectiveness of the drug.

This study focuses on developing a polymer-drug construct with potential applications for cancer chemotherapy: poly-γ-glutamyl-glutamate paclitaxel (PGG-PTX). A flexible, biocompatible, water-soluble polymer, poly-γ-glutamyl-glutamate (PGG) is covalently attached to paclitaxel (Taxol^®, C₄₇H₅₁NO₁₄), a widely used anticancer therapeutic known for its high efficacy in treating breast, ovarian, and lung cancers.^9–11 Due to paclitaxel’s high hydrophobicity and poor solubility, PGG, a hydrophilic, biodegradable carrier, is used to effectively deliver paclitaxel to tumors while minimizing adverse toxicity effects.¹² For comparison, a recent formulation of paclitaxel currently available on the market is paclitaxel bovine serum albumin, known as Abraxane^®.¹³ The traditional method of designing cancer therapeutics usually invokes an empirical approach of trial-and-error testing of chemical substances on animals and subsequently matching of apparent effects to treatments. While effective, this procedure can be time-consuming and expensive.¹⁴ We used multiscale modeling to elucidate the shape and size of various forms of a PGG-PTX molecule. Such information would aid in the ultimate effort to identify potentially useful conformational variants, which would be otherwise expensive and time-consuming to achieve by systematic synthesis. Our goal was to create a library of molecular conformations that can be biologically tested for potential advantages in chemotherapy.

In the field of molecular modeling, docking methods have been used to predict the activity and affinity of rigid small molecule drug candidates to their protein targets.^15–17 Although molecular modeling methods have been applied to flexible systems such as polymers in effort to predict their behavior,^4,18–20 modeling both rigid and flexible components poses new challenges and has yet to be attempted. Given the composite of the rigid paclitaxel molecule and the flexible PGG polymer, full equilibrium of the system will never be attained from running molecular dynamic (MD) simulations. Therefore, a PGG-PTX molecule is not expected to have a unique, singular equilibrated structure, but rather tend to a dynamic ensemble of molecular conformations, defined by a statistical equilibrium, a state representing ongoing structural movement with statistical similarity. At this point, there is little further change in the overall structure, although there may be minor movement on the molecular level. Our goal was to gain a general understanding of the range of candidate morphologies that can be generated from PGG-PTX, as well as demonstrate a novel and unique application of multiscale modeling for characterizing cancer therapeutics.

Given the practicalities of running MD simulations, there is a need for specifying the initial molecular structure. To construct the initial all-atom (AA) model of PGG-PTX, circular dichroism (CD) spectroscopy was used to gain information about the secondary structure of PGG-PTX in solution.²¹ However, a concern arises: since MD simulations can not be infinitely long, an acceptable approximation of the molecular structure is needed.²²

Computational modeling tools can be advantageous for understanding the dynamical and structural phenomena of molecular systems. Currently there exist a wide variety of methods suitable for molecular systems ranging from proteins, polymers, and nucleic acids.²³ However, AA MD simulations of relatively large systems (thousands to ten-thousands of atoms) can require a lot of CPU power and be very expensive. Therefore, to minimize computational costs, coarse-grained (CG) models are implemented by reducing the amount of structural information yet maintaining the integrity of the structural information conferred by AA models. Examples of such CG MD approaches have been applied to a wide range of molecular events, such as investigating protein folding and elucidating protein-protein interactions. Such CG simulation methods for polymer systems include Monte Carlo methods, dissipative particle dynamics, and Brownian dynamics.^24,25 In this study, multiscale MD simulations of PGG-PTX were carried out by first developing AA models and then CG models in order to access the hundreds of nanoseconds regime while minimizing CPU usage.

A PGG-PTX molecule is comprised of a 130-mer PGG backbone with PTX molecules covalently attached to a glutamate-glutamyl molecule via an ester linkage (see Fig. 1). There currently exist three different formulations of PGG-PTX varying in the number of PTX molecules attached to the PGG polymer, or PTX loading fraction (f_PTX):

$$f_{\mathit{\text{PTX}}}=\frac{{\mathit{\text{MW}}}_{\mathit{\text{PTX}}}}{{\mathit{\text{MW}}}_{\mathit{\text{PGG}}-\mathit{\text{PTX}}}}$$ (1)

where MW_PTX is the molecular weight of all paclitaxel molecules on a PGG-PTX molecule, and MW_PGG-PTX is the molecular weight of then entire PGG-PTX molecule.

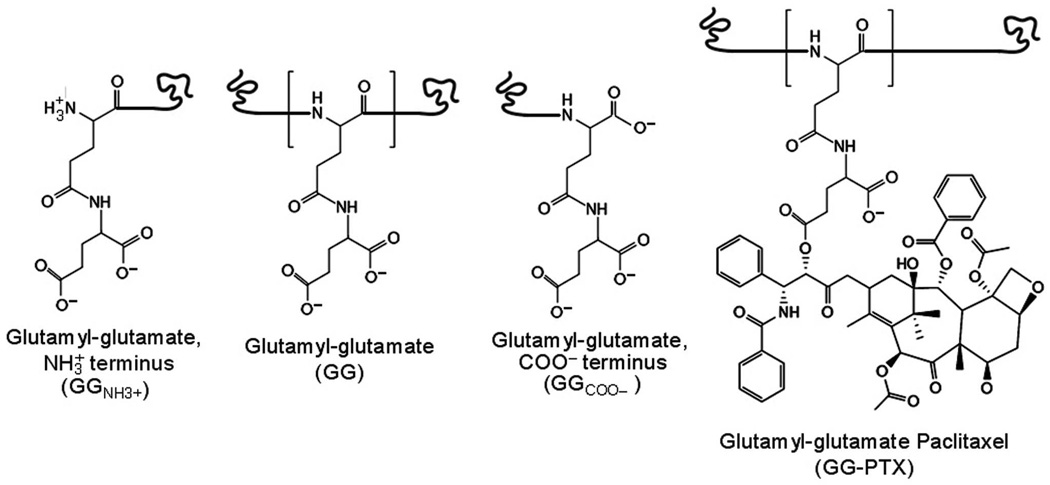
FIGURE 1.

Chemical structures of GG and GG-PTX. The GG residue differs slightly based on its position on the polymer, such as its position at the amino or carboxyl termini. For the GG-PTX residue, paclitaxel is covalently conjugated to a carboxylate group of glutamyl–glutamate via an ester linkage. GG_NH3+ and GG-PTX each has a charge of −1, GG a charge of −2, and GGCOO− a charge of −3. (Note: each twisted line represents the position to which a preceding or subsequent residue is covalently attached.)

The three PGG-PTX formulations are f_PTX = 0.18, 0.24, or 0.37, which correspond to 12, 19, and 26 paclitaxel molecules on the 130-mer PGG polymer, respectively. To explore the possible morphologies that each PGG-PTX formulation offers, it is of interest to test how the spatial positioning of hydrophobic PTX groups on the hydrophilic PGG backbone impacts the shape and size of a molecule. Therefore, for each f_PTX, the respective paclitaxel molecules were systematically positioned in a controlled manner on a 130-mer PGG polymer in six manners: ‘clusters’, ‘ends’, ‘even’, ‘middle’, ‘random’, and ‘side’ arrangements. Fig. 2 shows the six ways PTX can be spatially arranged on the PGG polymer for the f_PTX = 0.18 formulation. Applying this patterning scheme to the f_PTX = 0.24 and 0.37 formulations results in an array of 18 different PGG-PTX molecules for structural evaluation.

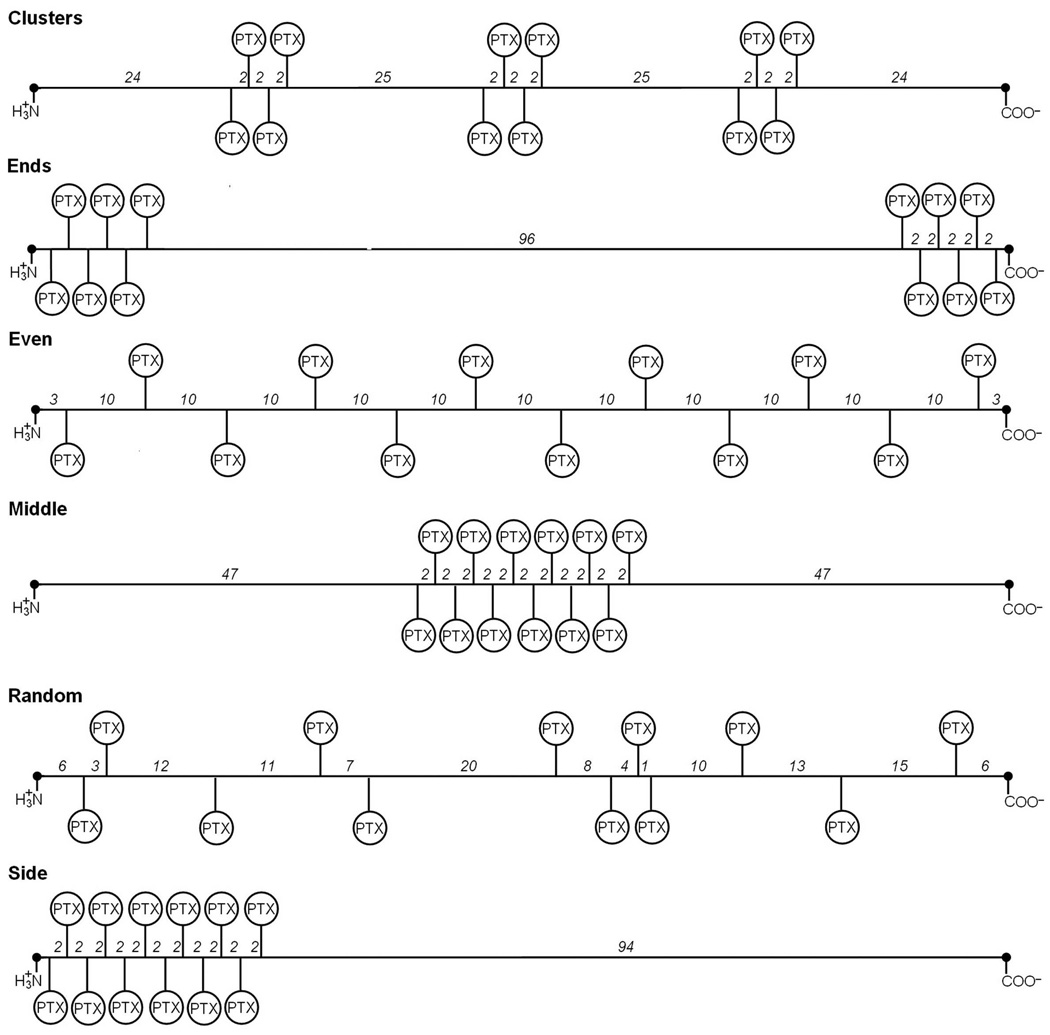
FIGURE 2.

Abstract representation of the spatial PTX positioning patterns on the PGG backbone for f_PTX = 0.18. Each PGG-PTX molecule is composed of 130 glutamyl–glutamate monomers and 12 paclitaxel molecules. Shows how 12 PTX are covalently attached to the PGG backbone in six arrangements: ‘clusters’ (3 PTX groups with 4 PTX per group, spaced an equal number of residues apart), ‘ends’ (2 PTX groups with 6 PTX each, located at both ends), ‘even’ (each PTX is spaced an equal number of residues apart along PGG), ‘middle’ (all PTX molecules positioned in the middle), ‘random’ (all PTX molecules located in random positions), and ‘side’ (all PTX molecules located at the amino terminus end). Numbers between residues denote number of repeating GG residues that are not amino- or carboxyl-termini GG residues. The amino- and carboxyl-termini GG residues are represented by black dots at the ends of each line. The abstract representations for the f_PTX = 0.24 and 0.37 molecules are shown in Figs. S2 and S3, respectively, in Supplementary Materials.

Multiscale modeling was then carried out as follows: AA MD simulations were run on the eighteen PGG-PTX molecules in the AMBER version 9.0 suite of programs²⁶ using the Cornell et al. parm99²⁷ and Generalized AMBER force fields²⁸ (GAFF) until each system reach a statistical equilibrium, which was usually attained by 100 ns, as indicated by root-mean-square deviation (RMSD) time evolutions. CG parameterization of the AA PGG-PTX models was done using the MARrink’s Toolkit INItiative (MARTINI) force field.²⁹ Subsequent CG MD simulations were run using GROningen Machine for Chemical Simulations (GROMACS) version 4.0.3 software package³⁰ for effective times of 800 ns.

EXPERIMENTAL METHODS

Sample preparation

Lyophilized samples of PGG-PTX varying in f_PTX = 0.18, 0.24, and 0.37 were provided by Nitto Denko Technical Corporation (Oceanside, CA). Each sample was weighed and then diluted to 1 mg/ml in 1X HyClone modified DPBS buffer (ThermoScientific, Cat. No. SH30028.03). The samples were then sonicated in a 37°C water bath for 15 min and vortexed at room temperature for 1 min. The samples were then allowed to settle at room temperature for an additional 10 min. Finally, the samples were then filtered using a 0.2 µm filter paper (Corning, Part No. 431215) and a 20G 1½ Precision Glide needle (Becton Dickinson).

Circular dichroism spectroscopy

CD spectroscopy measurements for PGG-PTX were carried out using an AVIV Model 202 spectrophotometer. CD spectra of pure 1X DPBS buffer and FD protein in 50% TFE/50% double distilled H₂O/0.1% TFA were also taken as the negative and positive controls, respectively. All measurements were done at 37°C. The far-UV CD spectra were recorded from 190 to 260 nm using a 1 cm rectangular quartz cuvette, and the CD spectra were collected at every 0.5 nm with 5 sec at each point. For each sample except pure 1X DPBS, the concentration was adjusted and diluted so that the dynode voltage corresponding to the ellipticity signal remained below 500 V throughout the entire spectra collection period. (It has been suggested by Greenfield et al. that the signal-to-noise ratio will greatly diminish once the dynode voltage exceeds 500 V.²¹) The optimum concentrations of each sample leading to optimum ellipticity signal and lowest signal-to-noise ratio were determined to be: 1 mg/ml of PGG-PTX at f_PTX = 0.18 in 1X DPBS, 1 mg/ml of f_PTX = 0.24 in 1X DPBS, 1 mg/ml of f_PTX = 0.37 in 1X DPBS, and 0.25 mg/ml of FD protein in 50% TFE/50% ddH₂O/0.1% TFA.

COMPUTATIONAL METHODS

All-atom modeling

Given the large size of each PGG-PTX molecule, AA MD simulations were carried out in implicit solvent. To run AA MD simulations of a PGG-PTX molecule in explicit solvent of the same system size would require an extraordinary amount of CPU power and computational time that are unfeasible for the scope of this study. Given the relatively flexible nature of PGG-PTX, we believe there would be minimal difference in the resulting structures from running AA MD simulations in implicit solvent vs. explicit solvent. In addition, GROMACS is only capable of running CG MD simulations with explicit solvent, not implicit solvent.

Model construction

The initial structures and input files were generated using the xleap module of AMBER 9.0. Paclitaxel was taken from the Protein Data Bank (PDB ID: IJFF).³¹ For the amino-terminus glutamyl-glutamate (GG_NH3+), glutamyl-glutamate (GG), carboxyl-terminus glutamyl-glutamate (GG_COO−), and glutamyl-glutamate paclitaxel (GG-PTX) residues, the atom-centered point charges were generated using the Gaussian (g03)³² program’s geometry optimization and restrained electrostatic potential fitting (RESP) calculations.³³ Specifically, hydrogen atoms were added to the carboxyl groups to achieve the ionization state of the protonated molecules. The molecules were then optimized using the AM1 geometry scheme followed by the HF/6-31G* and HF/6-31G** pop=mk iop(6/33=2) ab initio level calculations to obtain the electrostatic potential using Gaussian. Finally, RESP fitting was applied on the electrostatic potentials to derive the equivalent partial atomic charges for the molecules.

Energy minimization and MD simulation

These steps were carried out using the sander module. The starting structures were minimized in implicit solvent using the modified Generalized-Born model of IGB=2³⁴ and the LPCO model³⁵ using 250 steps of steepest descent followed by 1750 steps of conjugate gradient. To mimic the salt concentration of blood plasma and PBS buffer, the ionic strength of the implicit solvent was set to 140 mM. No periodic boundary conditions were applied. A non-bonded electrostatic cutoff of 16.0Å was used. Trajectory snapshots were saved every 100 steps for later reprocessing.

MD simulations were carried out using AMBER 9.0 with the modified version (ff99SB)³⁶ of the Cornell et al. parm99²⁷ and GAFF force fields.²⁸ MD simulations were carried out in the NVT ensemble (in which the number of atoms N, volume V, and temperature T were fixed) at 310K in an implicit solvent using the modified Generalized-Born model of IGB=2 and the LPCO model. No periodic boundary conditions were applied. Newton’s equations of motions were integrated with a time step of 2 fs. All bonds involving hydrogen atoms were constrained using the SHAKE algorithm³⁷. Constant temperature scaling was also applied with a time constant of 0.5 ps. Langevin dynamics was used with a collision frequency of 2.0 ps⁻¹. The rotational and translational degree of freedom about the center of mass was eliminated. Trajectory snapshots were saved every 100 steps for later reprocessing. Each cycle of the MD simulation was run for 0.1 ns, and this step was repeated until a statistical equilibrium was reached at 100 ns.

Coarse-grained modeling

For the sake of minimizing computational costs as well as accessing longer length and time scales, the level of information in each AA PGG-PTX molecule was reduced while striving to maintain the accuracy of the physicochemical information of each molecule. Given the amino acid-based nature of the glutamyl-glutamate backbone, the MARTINI force field was selected for the CG parameterization for its successful application to proteins by experimental validation of their structural properties as well as the reproduction of thermodynamics.^29,38–40 The MARTINI force field dictates that a group of roughly 4–5 atoms are represented as an interaction center, or bead. These beads interact through a set of short-ranged Lennard-Jones potentials to reproduce characteristic properties resulting from AA simulations. Charged groups interact via a Coulombic energy function, and bonded potentials are used to describe the chemical connectivity of the beads. Detailed parameterization of the GG_NH3+, GG, GG_COO−, and GG-PTX residues as well as water (W) and sodium (Na+) ions are described below.

Theory

The CG beads are considered as point masses, and their dynamics are described by Newton’s equations of motion. The effective bonded and nonbonded interactions among the beads are described by a potential of the form, adapted from Marrink et al.⁴⁰:

$$V={\displaystyle \sum _m}[V_{\mathit{\text{bond}}}^m+V_{\mathit{\text{angle}}}^m+V_{\mathit{\text{dihedral}}}^m]+V_{\mathit{\text{nonbonded}}}^m$$ (2)

where the index m denotes one of the six components in the system: GG_NH3+, GG, GG_COO−, GG-PTX, W, and Na+. The sum in Eqn. (2) describes the force potentials for the bonded CG beads: $V_{\mathit{\text{bond}}}^m$ describes the forces between two bonded CG beads; $V_{\mathit{\text{angle}}}^m$ accounts for the forces used to sustain angles between sets of three bonded CG beads; and $V_{\mathit{\text{angle}}}^m$ corresponds to the dihedral angle potential for quadruples of bonded CG beads. The $V_{\mathit{\text{nonbonded}}}^m$ term accounts for the nonbonded interactions between all of the CG beads in the system.

Bonded interactions are characterized as one of the following:

$$V_{\mathit{\text{bond}}}^m={\displaystyle \sum _{\mathit{\text{ij}}}}\frac{1}{2}{K}_{\mathit{\text{ij}}}^m{(R_{\mathit{\text{ij}}}^m-L_{\mathit{\text{ij}}}^m)}^2$$ (3)

$$V_{\mathit{\text{angle}}}^m={\displaystyle \sum _{\mathit{\text{ijk}}}}\frac{1}{2}{K}_{\mathit{\text{ijk}}}^m{[\text{cos}({\theta }_{\mathit{\text{ijk}}}^m)-\text{cos}({\mathrm{\Theta }}_{\mathit{\text{ijk}}}^m)]}^2$$ (4)

$$V_{\mathit{\text{dihedral}}}^m={\displaystyle \sum _{\mathit{\text{ijkl}}}}{K}_{\mathit{\text{ijkl}}}^m[1+\text{cos}(n{\chi }_{\mathit{\text{ijkl}}}^m-{\delta }_{\mathit{\text{ijkl}}}^m)]$$ (5)

where the indices i, j, k, and l represent four consecutive beads, $R_{\mathit{\text{ij}}}^m$ is the distance between two consecutive beads i and j, $L_{\mathit{\text{ij}}}^m$ is the equilibrium CG bond length (or the average of all the sampled conformations from the atomistic MD trajectory), ${\theta }_{\mathit{\text{ijk}}}^m$ is the angle between beads i, j, and k, and ${\mathrm{\Theta }}_{\mathit{\text{ijk}},0}^m$ is the equilibrium angle (the average of all the sampled conformations from the atomistic MD trajectory). The CG bead distance force constants $(K_{\mathit{\text{ij}}}^{\mathit{\text{GG}}}\text{and}{K}_{\mathit{\text{ij}}}^{\mathit{\text{GG}}-\mathit{\text{PTX}}})$ and the CG bead angle force constants $(K_{\mathit{\text{ijk}}}^{\mathit{\text{GG}}}\text{and}{K}_{\mathit{\text{ijk}}}^{\mathit{\text{GG}}-\mathit{\text{PTX}}})$ depend on the bead type and bead interaction.

The nonbonded interactions between two CG beads m and n at a distance r_mn interact via a van der Waals (vdW) characterized by a Lennard-Jones 12-6 potential energy function as well as a Coulombic potential for charged beads (bead type Q):

$$V_{\mathit{\text{nonbonded}}}={\displaystyle \sum _{m,n}}4{\epsilon }_{\mathit{\text{mn}}}\lfloor {\left(\frac{{\sigma }_{\mathit{\text{mn}}}}{r_{\mathit{\text{mn}}}}\right)}^{12}-{\left(\frac{{\sigma }_{\mathit{\text{mn}}}}{r_{\mathit{\text{mn}}}}\right)}^6\rfloor +{\displaystyle \sum _{m,n}}\frac{q_m{q}_n}{4\pi {\epsilon }_0\epsilon r_{\mathit{\text{mn}}}}$$ (6)

Where σ_mn refers to a typical closest distance of approach between two beads m and n, ε_mn denotes the strength of the interactions between beads m and n (one of five levels, I to V, for each bead type, and the full interaction matrix is provided in Marrink et al.²⁹ q_m and q_n are the charges of the mth and nth beads, ε₀ is the vacuum dielectric permittivity, and a relative dielectric constant of ε = 15 is assumed for all electrostatic interactions.

CG mapping

As aforementioned, the MARTINI force field dictates that approximately 4–5 heavy atoms are mapped to one interaction center (bead). An exception to this rule applies to aromatic groups, such as the benzene molecules in paclitaxel: in order to preserve the geometric symmetry of these groups, a 2 heavy atoms-to-1 bead mapping scheme is applied. The CG mapping of the GG_NH3+, GG, GG_COO−, and GG-PTX residues are depicted in Fig. 3. Given that the circular dichroism spectroscopy results show that PGG-PTX forms a random coil at 37°C (310 K), the bonded parameters of the GG backbone were assigned based on the values for a random coil, as dictated by the MARTINI force field. For the negative and positive controls, description of the CG mapping for glutamate (G) and glutamate-benzene (G-B) residues is provided in Fig. S1 in Supplementary Materials. In addition, four water molecules are represented as a single P₄ type bead, and each Na+ ion is represented by a single Q type bead with a +1 charge.

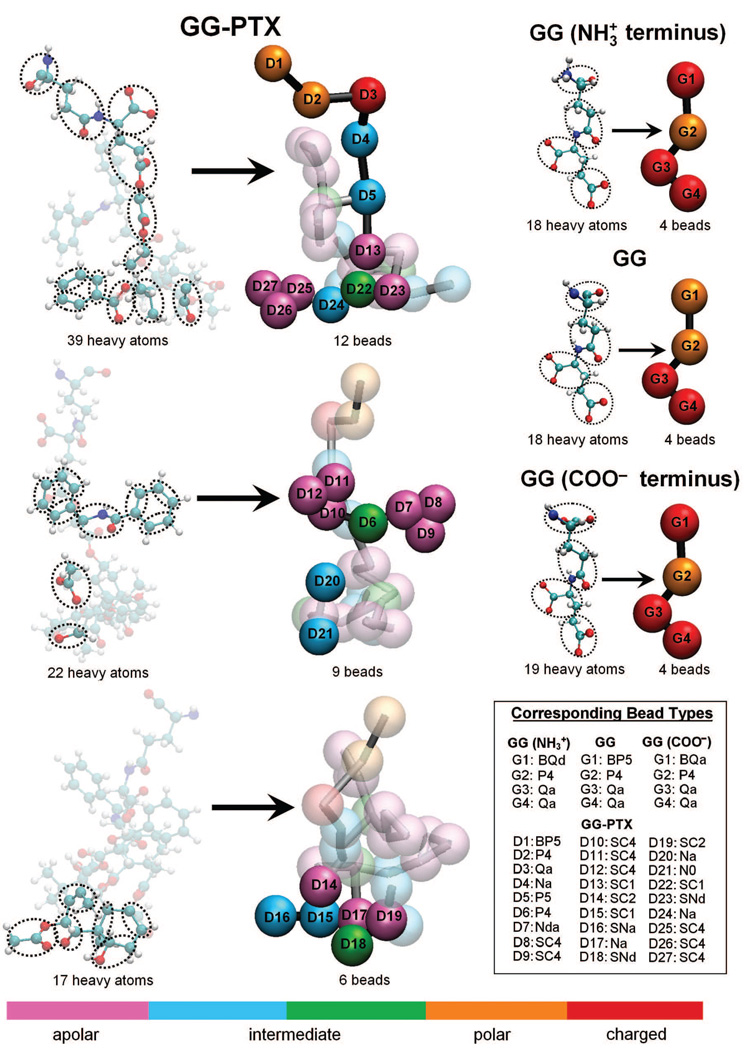
FIGURE 3.

Coarse-grained representations of GG and GG-PTX residues. Mapping of the AA models to CG models was done according to the MARTINI force field. Roughly 4–5 heavy atoms were assigned to one interaction center, or “bead”. (For the aromatic groups in Paclitaxel, the assignment was 2 heavy atoms to 1 bead.) GG was reduced from 18 or 19 heavy atoms to 4 beads, and GG-PTX was reduced from 148 heavy atoms to 27 CG beads. Differently colored beads represent different bead types, based on polarity and hydrogen-bonding capabilities. For each bead, four main types are considered: polar (P), nonpolar (N), apolar (C), and charged (Q). Each main type can subsequently be distinguished by its degree of polarity (from 1 = lowest polarity to = 5 highest polarity) and its hydrogen-bonding abilities (denoted by a letter: donor (d), acceptor (a), both (da), or none (0)). Beads with nomenclature beginning ‘B’ and ‘S’ letters denote a backbone bead and an aromatic bead, respectively.

Parameterization of bonded interactions for a PGG-PTX molecule

The equilibrium bond distances and angles were obtained from of the three ‘random’ PGG-PTX molecules (f_PTX = 0.18, 0.24, and 0.37) since they were the models that best mimic the experimental formulations of PGG-PTX. The parameterization was carried out by first extracting the time-dependent bond distances and angles from the 100 ns AA MD simulations using ptraj module of AMBER 9.0. Then, the bonded parameters were processed using the Boltzmann inversion procedure⁴¹ in MATLAB 7.0⁴² to determine the equilibrium bond distances and angles.

Energy minimization and MD simulation

CG PGG-PTX models were constructed in GROMACS 4.0.3. Each PGG-PTX molecule was solvated in the center of the box with explicit W beads of 2 nm thickness of surrounding the molecule. Due to the negative charges imparted by the GG and GG-PTX residues in each system, Na+ ions (usually 234) were added in place of W beads to neutralize the system. The simulations were carried out under NPT (the number of particles N, pressure P, and temperature T were fixed) conditions. For each simulation, the temperature was kept constant at 310 K with a coupling constant of τ_T = 0.1 ps, and the pressure was weakly coupled to 1 bar with a relaxation time of τ_P = 0.5 ps. The cutoff length for the nonbonded interactions is r_cut = 1.2 nm. Lennard-Jones forces were considered for r_cut < 0.9 nm and Coulombic forces for r_cut < 1.2 nm. The latter was computed every time step for 1.0 nm and once every 10 time steps for 0.9 nm < r_cut < 1.2 nm. The time step in the leap-frog integration scheme was 5 fs. The energies, coordinates and velocities were written every 0.5 ps. For each of the eighteen systems, MD simulations were run until a statistical equilibrium was obtained at 200 ns. It is worth noting that, due to the smoothness of the CG potentials, CG dynamics are actually faster than AA interactions. To account for this difference, researchers have approximated CG results by scaling the time axis by a conversion factor of four, the effective speed up factor in the diffusional dynamics of CG water compared to that of real water.^29,40,43 Therefore, the effective time sampled for each CG MD simulation was roughly 800 ns. Unless otherwise stated, the CG MD simulation times reported in this paper are effective times.

RESULTS AND DISCUSSION

Circular dichroism spectroscopy

To construct a theoretical model of PGG-PTX practical for clinical applications, its initial molecular configuration needs to be first defined. Circular dichroism spectroscopy was used to determine the general structure of a PGG-PTX molecule, and the resulting structure was regarded as the initial configuration for the AA PGG-PTX models.

Fig. 4 shows the CD spectra of 1 mg/ml PGG-PTX at f_PTX = 0.18, 0.24, and 0.37, all dissolved in 1X DPBS. All three curves are most representative of a random coil at physiological temperature of 37°C. The negative control of 1X DPBS at 37°C indicates that that there is no signal interference that may have influenced the conditions while CD spectra of PGG-PTX were being taken. For the positive control, the shape of the alpha-helical FD protein, a bZIP transcription factor in a floral pathway⁴⁴, in 50% TFE/50% ddH₂O/0.1% TFA buffer does indeed correspond to an alpha-helix, as compared with the CD spectrum of the alpha-helical poly-γ-tyrosine.⁴⁵ The lowest part of the curve is ~215nm and the highest point of the curve is ~200nm collectively indicate that the FD protein is indeed alpha-helical. This data shows that PGG-PTX exists as a random coil. For these three samples, it is most likely that the spatial PTX arrangement resembles the PTX arrangement in the ‘random’ configurations. Therefore, regardless of the PTX loading fraction, PGG-PTX lacks secondary structure and exists primarily as a random coil. Finally, the molecular configuration of PGG-PTX as a random coil does not impose any stipulations on construction of an AA model.

FIGURE 4.

CD spectra of samples. Shows the spectra for PGGPTX at f_PTX = 0.18 (blue line), PGG-PTX at f_PTX = 0.24 (red line), PGG-PTX at f_PTX = 0.37 (green line), FD protein (black line), and pure 1X DPBS (pink line).

Comparison of all-atom and coarse-grained models

Fig. 5 shows the initial structures of the AA and CG models at of PGG-PTX molecule at f_PTX = 0.37 with an ‘even’ PTX distribution. Neglecting the explicit solvent beads of the CG models, the size of the AA models (6189 heavy atoms) is roughly five times larger than its CG counterpart (1222 beads), which is apparent in that the AA model appears to have a higher image resolution than the CG model. Despite this difference, the structural integrity of the PGG-PTX molecule is still preserved in the CG model. From the perspectives of the xy and xz planes, the length and height of the AA and CG models are comparable, and the cross-sectional area is similar in AA and CG models from the yz plane. The paclitaxel molecules are arranged in a spiral fashion around the PGG backbone, similar to the spiral pattern in the AA model.

FIGURE 5.

AA and CG models of a PGG-PTX molecule. Shows the models for a f_PTX = 0.37 molecule with an ‘even’ PTX distribution. The GG (black) and PTX (grey) residues are portrayed.

AA and CG equilibrium bonded parameters

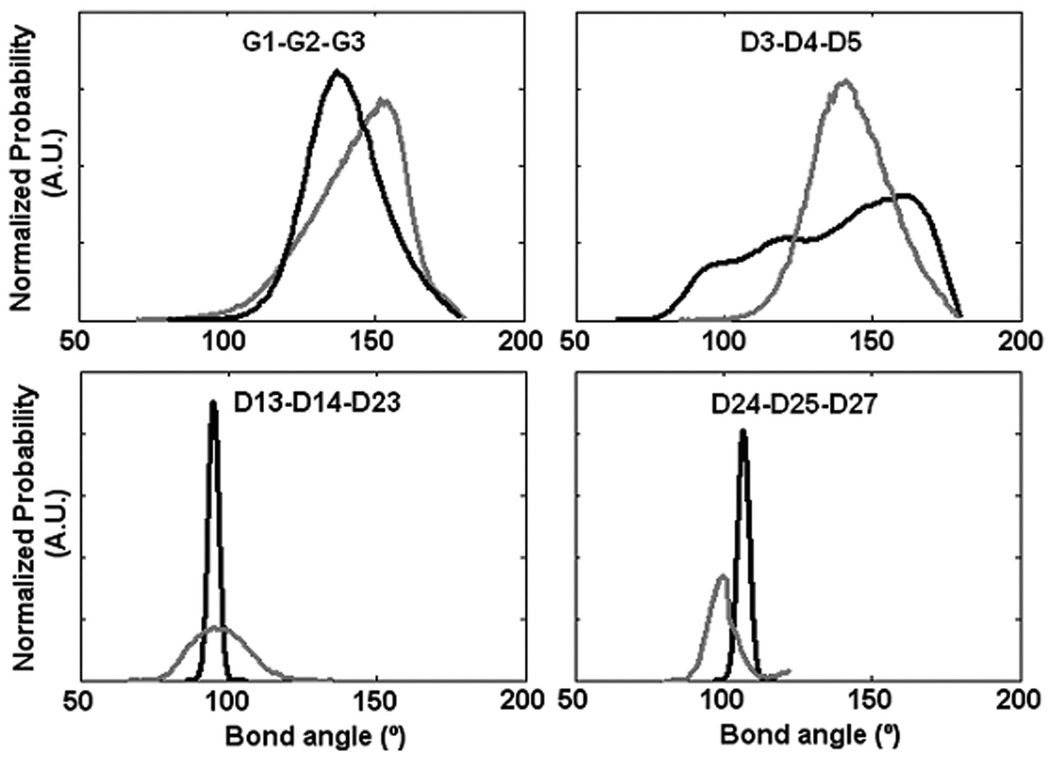
To assess the validity of the CG model of PGG-PTX, a few equilibrium bond angles (G1-G2-G3, D3-D4-D5, D13-D14-D23, and D24-D25-D37) of the AA and CG PGG-PTX models were selected and compared. As shown in Fig. 6, it is apparent that there is relatively good agreement between the AA and CG values. While there is not always a perfect overlap between the AA and CG curves, this behavior is to be expected for a system that has both flexible and rigid components. The AA and CG probability distributions for D13-D14-D23 and D24-D25-D27 are narrower than those for G1-G2-G3 and D3-D4-D5. An explanation for this difference is that the D13, D14, D23, D24, D25, and D27 beads are located in an area of the paclitaxel molecule with high sterical energy (D13, D14, D23, D25, and D26 are part of aromatic groups) thus limiting the range of orientations that the beads can sample. Contrariwise, G1, G2, G3, D3, D4, and D5 are not bound to any aromatic structures, not to mention that they are within close vicinity of the glutamyl-glutamate backbone. The positions of these beads allow for a larger range of accessible orientations. In all, the probability distribution curves show that more flexible components of a PGG-PTX molecule have a wider range of accessible conformations, while more rigid components of a PGG-PTX molecule have a limited range of accessible conformations.

FIGURE 6.

Selected probability distributions of AA and CG bond angles between PGG-PTX atom groups. Information was extracted from 100 ns AA MD and 100 ns CG MD simulations. Shows data for AA (black line) and CG models (grey line).

RMSD and RMSF values

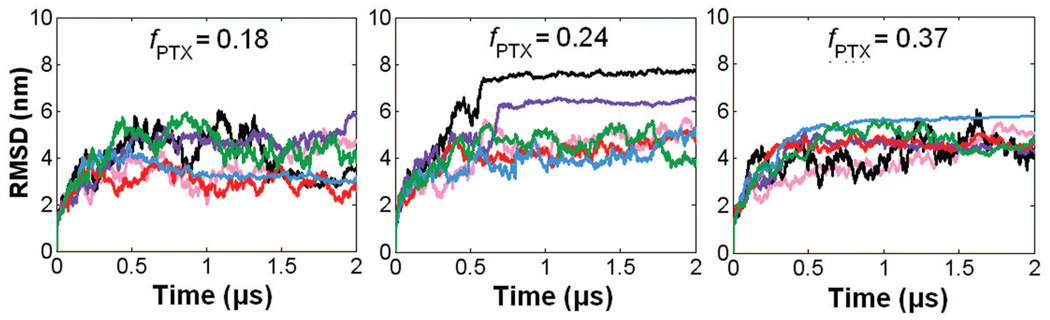
Figs. S4, S5, and S6 show the RMSD time evolutions from 100-ns AA MD and 100-ns (or 25 ns non-effective time) CG MD simulations of PGG-PTX molecules. It is apparent that there is relatively good agreement between the AA and CG RMSD values. Overall, the AA RMSD values rise to 3–5 nm by 100 ns, and CG RMSD values increase to 2–4 nm by 100 ns. Although these values are high, they are reasonable given the size of the PGG-PTX molecules. By 100 ns, most AA MD simulations have attained a steady-state level. (While certain systems such as the f_PTX = 0.18 ‘clusters’, f_PTX = 0.18 ‘even’, and f_PTX = 0.24 ‘even’ molecules have not yet attained a full steady-state level, they are adequately stabilized for this study.) On the other hand, the CG MD simulations did not attain a steady-state by 100 ns and were subsequently extended to 800 ns. To assess whether steady-state was reached by 800 ns, CG MD simulations were extended further to an effective time of 2 µs. Fig 7 shows the CG RMSD values for all eighteen systems; most plots show that there is minimal variation in RMSD between 800 ns and 2 µs, indicating that 800 ns was long enough for a statistical equilibrium to be reached.

FIGURE 7.

CG RMSD time evolutions of PGG-PTX molecules. PTX distributions include ‘clusters’ (pink line), ‘ends’ (black line), ‘even’ (purple line), ‘middle’ (red line), ‘random’ (blue line), and ‘side’ (green line).

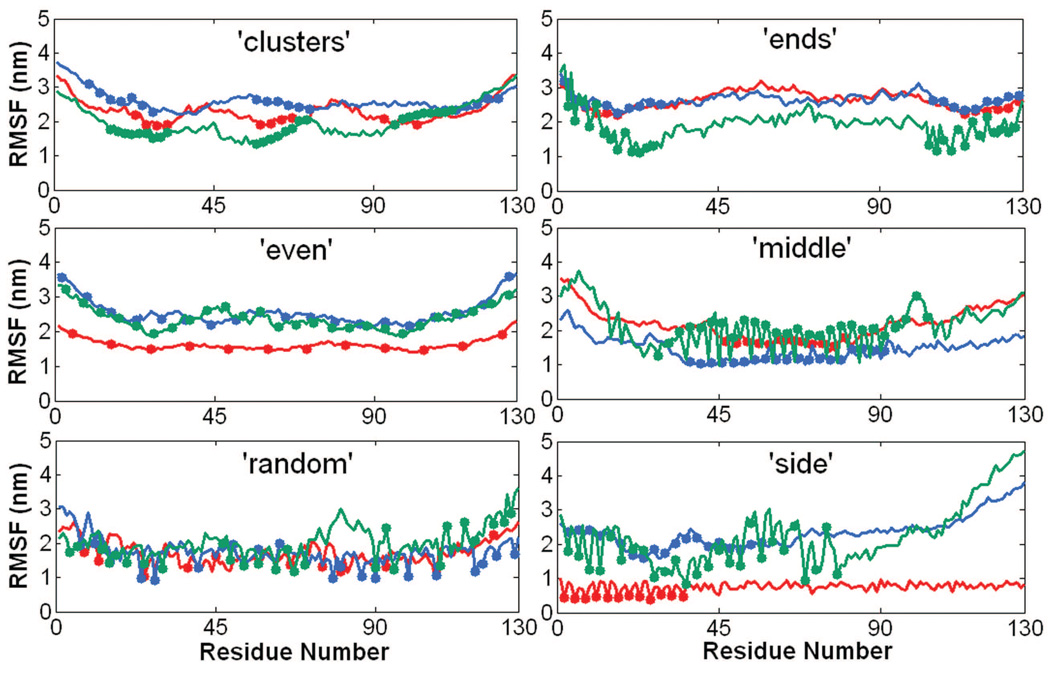
Figs. S7, S8, and S9 show the RMSF (by residue) values from 100 ns AA MD and 100 ns (or 25 ns non-effective time) CG MD simulations of PGG-PTX molecules. There is relatively good agreement between the AA and CG RMSF values. The AA RMSF values typically fluctuated between 2–4 nm, with a few molecules having RMSF values near 8 nm. The CG RMSF values are a bit lower by ~1–3 nm. This discrepancy is expected, given that some structural information was probably lost in the coarse-graining procedure and that the system is comprised of the flexible PGG polymer. Fig. 8 shows the CG RMSF values for all eighteen PGG-PTX molecules. Nearly all molecules fluctuate between 2–4 nm, regardless of the spatial PTX arrangement or PTX loading fraction. RMSF is also an indication of molecular flexibility; since higher RMSF values typically correspond to segments of PGG-PTX with unconjugated PGG (no paclitaxel molecules attached), those regions are the most flexible. The distribution of hydrophobic PTX on the PGG backbone influences the degree of residue fluctuation, which is further discussed below.

FIGURE 8.

CG RMSF trajectories of PGG-PTX molecules. Shows data for f_PTX = 0.18 (red line), f_PTX = 0.24 (blue line), and f_PTX = 0.37 (green line) molecules. All trajectories were extracted from the 800 ns effective time CG MD simulations.

Molecular conformation of a PGG-PTX molecule

Shape

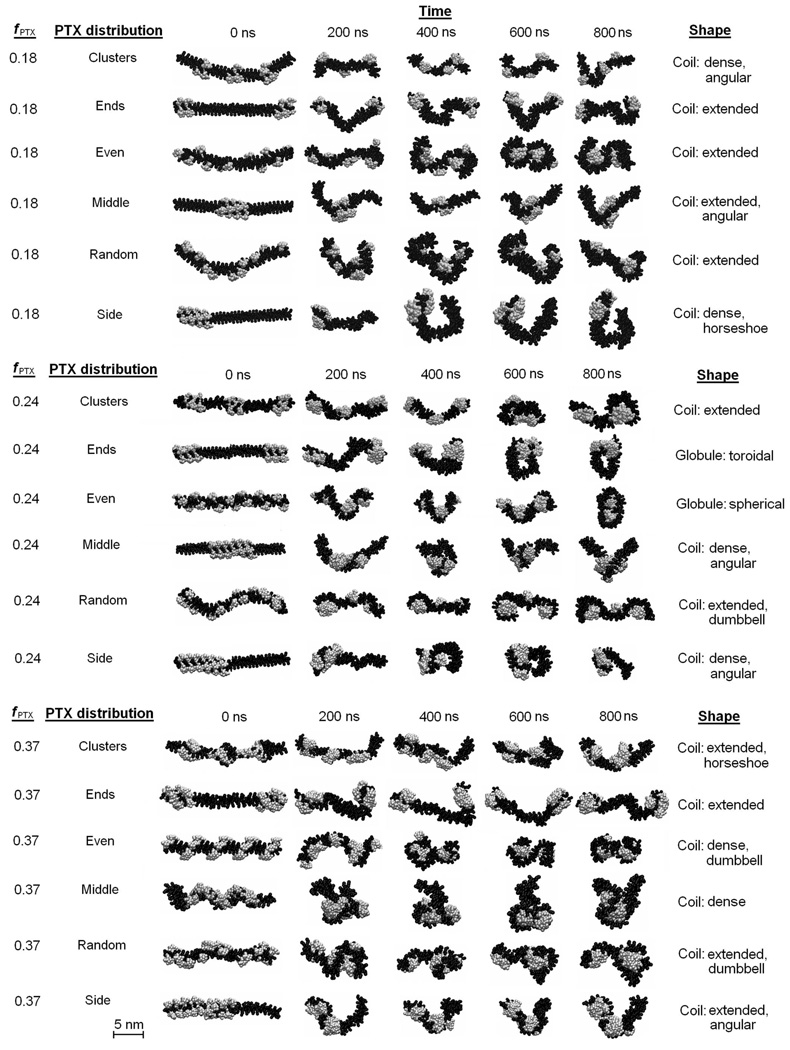
It was of interest to investigate whether the shape of PGG-PTX can be predicted using multiscale modeling. Fig. 9 shows the 800 ns CG MD simulations for the PGG-PTX molecules. All molecules start out as linear at 0 ns and eventually adopt a coil (filamentous) or globular (round) shape by 800 ns. Since steady-state was attained by all systems by 800 ns, the shape at this time was regarded as the official shape of each PGG-PTX molecule. There exists a wide variety of geometries among the molecules. The molecular shape of each molecule can be categorized into two main types: coil (filamentous, wormlike) and globular (round). For each type, the conformation can be further characterized as one or more subtypes (coil: angular, dense, extended, horseshoe, or dumbbell, globule: spherical and toroidal). Descriptions of the geometries are summarized in Table 2.

FIGURE 9.

CG MD simulations of PGG-PTX molecules. Portrays the glutamyl–glutamate (black) and paclitaxel (grey) molecules. Explicit water molecules and Na+ ions are not shown.

Table 2.

Descriptions of geometries of a PGG-PTX molecule

Coil (linear, filamentous)
Dense	Short, distance between NH3+ and COO− termini is < 10 nm
Extended	Long, distance between NH3+ and COO− termini is > 10 nm
Angular	Characterized by one sharp turn
Horseshoe	Characterized by one major curved turn
Dumbbell	Characterized by two linked spherical globules
Globule (round)
Spherical	Shaped like a ball
Toroidal	Shaped like a ring or donut

The coil was the most popular type of geometry among all PGG-PTX molecules. All molecules with PTX loading fractions of 0.18 and 0.37 are coils, and at f_PTX = 0.24, four of the six molecules are coils, whereas the other two are globules. The f_PTX = 0.24 set also has the most diverse set of subtype geometries. All six subtypes are prevalent in the f_PTX = 0.24 molecules, including the spherical globule and toroidal globule that are not apparent in the f_PTX = 0.18 and f_PTX = 0.37 molecules. This evidence suggests that, out of the three PTX loading fractions, PGG-PTX at f_PTX = 0.24 has the optimal balance of hydrophobic and hydrophilic forces to have the greatest concomitant effect on the geometry of the molecule. That is, at f_PTX = 0.24, the geometry of PGG-PTX is influenced more by the spatial positioning of PTX on the PGG backbone, rather than the PTX loading fraction. On the other hand, at f_PTX = 0.18 and 0.37, the geometries of PGG-PTX is more influenced by the mass fraction of hydrophobic PTX and hydrophilic PGG, rather than the spatial positioning of PTX on the PGG. In addition, there are certain spatial PTX arrangements for whose geometries are the least affected by the PTX loading fraction. Such are the ‘middle’ configuration, which maintains a dense coil for all three PTX loading fractions, and the ‘random’ configuration, which maintains an extended coil regardless of the PTX loading fraction. (This shape for the ‘random’ configuration is in good agreement with the previous circular dichroism spectroscopy data on PGG-PTX that indicate that the shape of PGG-PTX is a random coil.) It is also interesting that the ‘side’ and ‘middle’ configurations are unique in that they are characterized by sharp curvature: possessing an angled or curved turn. This behavior is most likely attributed to the spatial PTX arrangement on the PGG backbone, which has a major influence on the flexibility of a PGG-PTX molecule. What sets the ‘middle’ and ‘side’ configurations apart from the rest is that all of the PTX molecules are concentrated into one group such that it leaves long, uninterrupted portions of the PGG backbone unconjugated. These unconjugated portions are floppy and more flexible than the segments of the PGG backbone with PTX molecules attached. A similar pattern is also emergent in the f_PTX = 0.24 ‘ends’ molecule, a toroidal globule: two groups of paclitaxel molecules located at each end, thus leaving the middle portion of the PGG backbone unconjugated. As for other configurations like ‘clusters’, ‘random,’ and ‘even’, the paclitaxel molecules are arranged more uniformly along the PGG backbone such that the portions of unconjugated PGG are much shorter (see Fig. 2). This relatively equal dispersion of hydrophobic forces minimizes the movement or fluctuation of the PGG-PTX molecule as a whole. For the ‘middle’ and ‘side’ configurations, this absence of hydrophobic drug molecules removes the sterical hindrance imposed by the rigid PTX molecules and thus allows the unconjugated PGG portion to move about more freely. Generally speaking, configurations that have longer unconjugated PGG segments (‘middle’, ‘side’, and ‘ends’) tend to be more flexible and form more definitive, structured shapes as compared to configurations with a more even PTX distributions along the PGG backbone (‘clusters’, ‘random’, and ‘even’).

Size

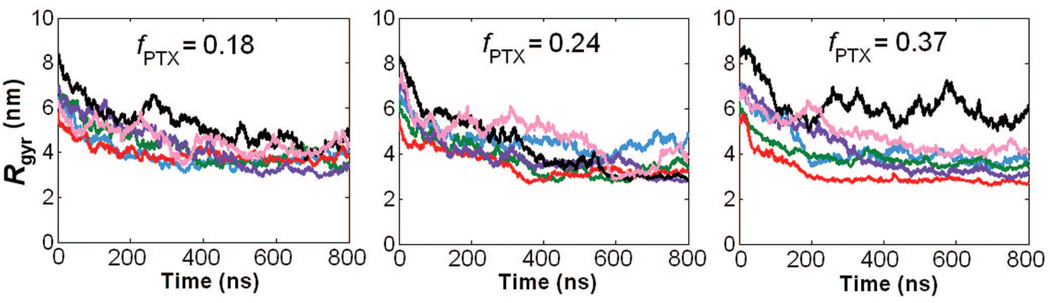
It was also of interest to examine the effects of PTX loading fraction and the spatial PTX arrangement on the size of a PGG-PTX molecule. Fig. 10 shows the 800 ns CG MD time evolutions of the radius of gyration (R_g) for all 18 PGG-PTX molecules. There are several interesting trends apparent. It is evident that, at t = 0 ns, the R_g of most molecules is ~6–8 nm, and over the 800 ns trajectory, each of the 18 PGG-PTX molecules decreased nearly 50% from its initial R_g. Fig. 9 confirms that, at t = 0 ns, all structures were stretched out and extended, but by t = 200 ns, all of them had shrunken in size. Also, it is interesting to see that, as the PTX loading fraction increases, the greater the variability in R_g among each set of six PGG-PTX configurations. As shown in Fig. 10, at f_PTX = 0.18, there is quite some overlap between the plots, especially at 800 ns, indicating that all six f_PTX = 0.18 configurations have more or less the same size. At f_PTX = 0.24, there is slightly less overlap in the plots, and at f_PTX = 0.37, there is nearly no overlap at all. Suffice to say, higher PTX loading fractions most likely results in a larger range of candidate sizes of PGG-PTX. In addition, the degree of influence the spatial PTX arrangement on PGG exerts over the size of a PGG-PTX molecule is quite minimal. Regardless of the hierarchy of initial R_g at t = 0 ns (from smallest to largest R_g: ‘middle’, ‘side’, ‘random’, ‘clusters’, ‘even’, and ‘ends’), once the molecules have stabilized, nearly all have a final R_g of ~4 nm.

FIGURE 10.

Radius of gyration time evolutions of PGG-PTX molecules. PTX distributions include ‘clusters’ (pink line), ‘ends’ (black line), ‘even’ (purple line), ‘middle’ (red line), ‘random’ (blue line), and ‘side’ (green line).

Influence of PTX on molecular conformation

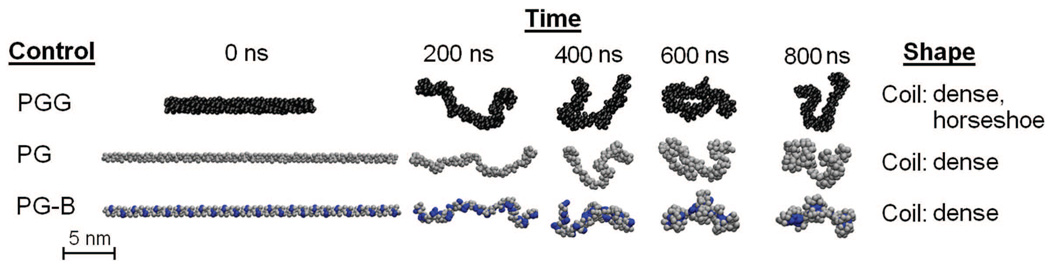
The effect of the presence of paclitaxel molecules on the conformation of a PGG molecule was also of interest. To examine the extent of this effect, two negative controls (CG models of hydrophilic polymers free of any hydrophobic entities) and a positive control (CG model of a hydrophilic polymer conjugated with hydrophobic entities) were constructed. The negative controls are: a 130-mer poly-γ-glutamate molecule (PG), and a 130-mer poly-γ-glutamyl-glutamate (PGG) molecule. The positive control is a 130-mer poly-γ-glutamate molecule with covalently conjugated benzene molecules (PG-B) with a benzene loading fraction of 0.37 (f_benzene = 0.37) and an ‘even’ benzene distribution. Fig. 11 shows the 800 ns CG MD simulations of the controls. During the 800 ns trajectory, both PG and PGG molecules wiggle around a lot, exhibiting flexible behavior. At 800 ns, they exhibit dense, horseshoe coil shapes. A similar behavior is observed in the PG-B molecule, as it also flexible and contorts before it finally adopts a dense coil at 800 ns. It is also worth noting that the benzene molecules self-assemble together to form three hydrophobic ‘cores’ located in the inner parts of the molecule.

FIGURE 11.

CG MD simulations of negative and positive controls. Shows the trajectories for PGG (black), PG (grey), and PG-B (blue). Explicit water molecules and Na+ ions are not shown.

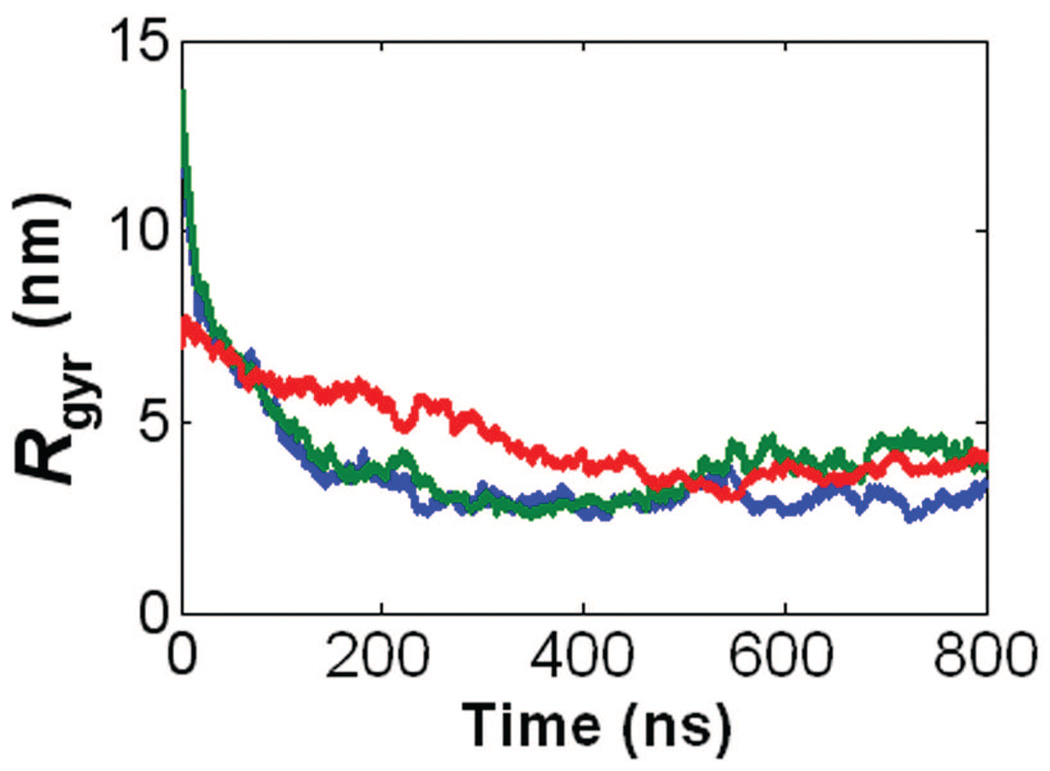
Fig. 12 shows the 800 ns CG MD time evolutions of R_g for the controls. The PG and PG-B molecules both have an initial R_g ~ 13 nm and final R_g ~ 4 nm. Given that they both have coil shapes, the benzene molecules have an insignificant effect on the coil geometry of a PG molecule. Similarly, the PGG molecule and PGG-PTX molecule (f_PTX = 0.37, ‘even’ PTX distribution) each has an initial R_g ~ 7 nm and final R_g ~ 4 nm. Since both molecules are dense coils, this data suggests that, for the PGG-PTX (f_PTX = 0.37 ‘even’) molecule, the presence of PTX on PGG only also has a minor influence on the conformation of PGG. It was also interesting to see how the PTX molecules in the PGG-PTX (f_PTX = 0.37 ‘even’) molecule also self-assemble to form multiple inner hydrophobic ‘cores’, similar to the PG-B molecule.

FIGURE 12.

Radius of gyration time evolutions for the negative and positive controls. Includes the negative controls, PG (red line) and PGG (green line), and the positive control, PG-B (blue line). All trajectories were extracted from the 800 ns CG MD simulations.

Ability to cross physiological barriers in drug delivery

Wormlike, filamentous micelles have been shown to result a longer circulation half-life than their spherical counterparts in drug delivery,^3,4 and discoidal particles have been shown to have a higher tendency to adhere and accumulate to the wall of tumor endothelia.⁵ By analogy, the shapes of the wormlike, filamentous micelles, and discoidal particles are structurally similar to the coil-shaped PGG-PTX molecules. Since all 18 molecules adopt a general coil shape (with a variety of coil subtypes), with exception to the f_PTX = 0.24 ‘ends’ and f_PTX = 0.24 ‘even’ molecules, it appears that the PTX loading fraction and spatial PTX arrangement have a minor concomitant influence on the molecular conformation of a PGG-PTX molecule. By analogy to the larger micelles and nanoparticles, we speculate that PGG-PTX formulations may confer a relatively long circulation half-life and propensity for accumulation, regardless of the PTX loading fraction and spatial PTX arrangement. Finally, the radius of gyration sizes of all PGG-PTX molecules range from 2–8 nm, implying that the actual molecular size is slightly greater. It has been shown that silver and gold nanoparticles of the 2–100 nm size range affects the intracellular signaling pathways implicated in basic cellular function.⁶ Therefore, PGG-PTX molecules may also possess the ability to control cellular signaling pathways of tumor cells.

CONCLUSIONS

There have been suggestions that the molecular conformation of a cancer therapeutic influences its ability to reach its intended site in the body. In this study, the conformation of PGG-PTX, a polymer-drug conjugate with potential applications in cancer therapy, was explored by systematically controlling the PTX loading fraction (f_PTX = 0.18, 0.24, and 0.37) and spatial patterning of PTX on PGG (‘clusters’, ‘ends’, ‘even’, ‘middle’, ‘random’, and ‘side’). Given that the CG models accurately reproduce the bonded parameters of the AA models and the good agreement between the AA and CG RMSD and RMSF trajectories, the CG models are suitable for accessing the nanosecond-microsecond regime. The 800 ns CG MD simulations have shown that, regardless of PTX loading fraction and PTX arrangement on PGG, a PGG-PTX molecule will most likely adopt a coil shape, suggesting that it has a long circulation half-life and high inclination to accumulate towards walls of tumor endothelia. PGG-PTX molecules with less homogeneous PTX arrangements (characterized by long, unconjugated PGG sections) tend to result in geometries with higher curvature. Also, the sizes of all PGG-PTX molecules fall within the 2–100 nm range, suggesting that they may affect the basic function of tumor cells. In terms of producing the widest variety of geometries, f_PTX = 0.24 is the PTX loading fraction at which the PTX arrangements are the most sensitive to morphological change.

Table 1.

Coarse-grained topologies for GG_NH3, GG, GG_COO−, and GG-PTX residues

GG Backbone topology
i j	Bond length $L_{\mathit{\text{ij}}}^m$ [nm]	Force constant $K_{\mathit{\text{ijk}}}^{\mathit{\text{GG}}}$ [kJ nm−2 mol−1]	i j k	Bond angle ${\mathrm{\Theta }}_{\mathit{\text{ijk}}}^m[\underset{¯}{°}]$	Force constant $K_{\mathit{\text{ijk}}}^{\mathit{\text{GG}}}$ [kJ nm−2 mol−1]
G1 G1	0.350*	200*	G1 G1 G1	127*	25*
GG Sidechain Topology (includes GGNH3+ and GGCOO−residues)
i j	Bond length $L_{\mathit{\text{ij}}}^m$ [nm]	Force constant $K_{\mathit{\text{ijk}}}^{\mathit{\text{GG}}}$ [kJ nm−2 mol−1]	i j k	Bond angle ${\mathrm{\Theta }}_{\mathit{\text{ijk}}}^m[\underset{¯}{°}]$	Force constant $K_{\mathit{\text{ijk}}}^{\mathit{\text{GG}}}$ [kJ nm−2 mol−1]
G1 G2	0.393	7500*	G1 G2 G3	143	100*
G2 G3	0.381	7500*	G2 G3 G4	85	100*
G3 G4	0.366	7500*
GG-PTX Sidechain Topology
i j	Bond length $L_{\mathit{\text{ij}}}^m$ [nm]	Force constant [kJ nm−2 mol−1]	i j k	Bond angle ${\mathrm{\Theta }}_{\mathit{\text{ijk}}}^m[\underset{¯}{°}]$	Force constant $K_{\mathit{\text{ijk}}}^{\mathit{\text{GG}}}$ [kJ nm−2 mol−1]
D1 D2	0.374	7500*	D1 D2 D3	153	100*
D2 D3	0.387	7500*	D2 D3 D4	94	100*
D3 D4	0.406	7500*	D3 D4 D5	130	100*
D4 D5	0.357	7500*	D4 D5 D6	84	100*
D5 D6	0.258	7500*	D4 D5 D13	146	100*
D6 D7	0.353	7500*	D5 D6 D7	107	100*
D6 D10	0.318	7500*	D5 D6 D10	75	100*
D5 D13	0.198	7500*	D5 D13 D14	80	100*
D13 D14	0.227	7500*	D5 D13 D23	158	100*
D7 D8	0.270*	1000*	D6 D7 D8	173	100*
D7 D9	0.270*	1000*	D6 D7 D9	109	100*
D8 D9	0.270*	1000*	D6 D10 D11	143	100*
D10 D11	0.270*	1000*	D6 D10 D12	105	100*
D10 D12	0.270*	1000*	D13 D14 D22	95	100*
D11 D12	0.270*	1000*	D13 D14 D15	127	100*
D13 D23	0.223	7500*	D13 D22 D24	85	100*
D14 D23	0.342	7500*	D14 D23 D22	60	100*
D14 D15	0.382	7500*	D14 D15 D16	52	100*
D15 D16	0.519	7500*	D14 D15 D17	36	100*
D15 D17	0.609	7500*	D15 D17 D22	53	100*
D17 D18	0.578	7500*	D15 D17 D18	85	100*
D18 D19	0.289	7500*	D15 D17 D19	48	100*
D17 D19	0.469	7500*	D16 D17 D24	31	100*
D17 D22	0.138	7500*	D17 D19 D21	120	100*
D19 D20	0.349	7500*	D18 D19 D20	115	100*
D19 D21	0.249	7500*	D18 D19 D21	121	100*
D22 D24	0.368	7500*	D18 D17 D19	30	100*
D22 D23	0.369	7500*	D22 D18 D19	54	100*
D24 D25	0.238	7500*	D22 D19 D20	105	100*
D25 D26	0.270**	1000*	D22 D24 D25	125	100*
D25 D27	0.270**	1000*	D23 D22 D13	75	100*
D26 D27	0.270**	1000*	D23 D22 D24	96	100*
			D24 D25 D26	128	100*
			D24 D25 D27	165	100*

^*Taken from the predetermined values for backbone or sidechain bonded parameters from the MARTINI force field.