Summary
We propose a phase I clinical trial design that seeks to determine the cumulative safety of a series of administrations of a fixed dose of an investigational agent. In contrast with traditional phase I trials that are designed solely to find the maximum tolerated dose of the agent, our design instead identifies a maximum tolerated schedule that includes a maximum tolerated dose as well as a vector of recommended administration times. Our model is based on a non-mixture cure model that constrains the probability of dose limiting toxicity for all patients to increase monotonically with both dose and the number of administrations received. We assume a specific parametric hazard function for each administration and compute the total hazard of dose limiting toxicity for a schedule as a sum of individual administration hazards. Throughout a variety of settings motivated by an actual study in allogeneic bone marrow transplant recipients, we demonstrate that our approach has excellent operating characteristics and performs as well as the only other currently published design for schedule finding studies. We also present arguments for the preference of our non-mixture cure model over the existing model.
Keywords: Adaptive design, Bayesian statistics, Dose finding study, Phase I trial, Weibull distribution
1. Introduction
Historically, phase I clinical trials are designed to determine the quantity of a new therapeutic agent (henceforth referred to as a ‘dose’) given to patients that leads to dose limiting toxicities (DLTs) in a limited proportion (usually 0.20–0.40) of patients. The largest dose examined that satisfies this criterion is known as the maximum tolerated dose (MTD). DLTs are side-effects of the dose whose severity is so great that general use of that dose would be unacceptable, regardless of its potential therapeutic benefit. For example, recombinant human keratinocyte growth factor (KGF) has been studied in allogeneic bone marrow transplant (BMT) recipients as prophylaxis against acute graft-versus-host disease. Unusually large increases in amylase and lipase, both of which are indicators of life-threatening pancreas dysfunction, have been seen in patients receiving KGF and are usually viewed as DLTs in phase I studies of KGF.
Various model-based, Bayesian adaptive phase I designs for identifying the MTD have been proposed, the first of which was the continual reassessment method (CRM) of O’Quigley et al. (1990) and later modifications proposed by Goodman et al. (1995). The CRM selects a parametric model (of which there are several; see O’Quigley et al. (1990)) for the association of dose and the probability of DLT and sequentially updates estimates for the parameters and the best estimate of the MTD continually during the study. Although the CRM was originally designed to estimate parameters with Bayesian methods, O’Quigley and Shen (1996) also proposed a maximum likelihood approach. There are other competing designs to the CRM; Rosenberger and Haines (2002) contains a comprehensive review of current phase I trial designs. As most model-based phase I designs assume complete follow-up for each patient, Cheung and Chappell (2000) recently proposed the time-to-event CRM, which allows patients to be enrolled when they are eligible, even if previously enrolled patients have not completed follow-up.
In many clinical settings, the agent will be given repeatedly in a sequence of administrations and patients will be followed to assess long-term cumulative effects of the agent. For example, in the aforementioned example, a trial in BMT patients might seek to determine how many consecutive 2-week series of KGF administrations can be given while keeping cumulative DLT rates below a desired threshold. The first attempt for designing such a trial was presented in Braun et al. (2003). In their approach, they treated each schedule as a single entity or ‘dose’ and applied a modified version of the time-to-event CRM that proved problematic. First, patients who received an incomplete schedule, e.g. 3.5 weeks instead of 4 weeks, had to be forced to ‘fit’ one of the planned biweekly schedules. Thus, in the given example, only the first 2 weeks of treatment for the patient could be used and the remaining 1.5 weeks had to be ignored. Second, each schedule was followed with additional follow-up, causing the doses to overlap, and leading to ambiguity about which dose contributed to a late onset DLT. This first attempt proved that a simple model of cumulative toxicity as a function of schedule is problematic and suggests that one should instead model how toxicity is related to each individual administration.
For this, Braun et al. (2005) constructed a new paradigm for schedule finding in which the hazard for the time to DLT is modelled as the sum of a sequence of hazards, each associated with one administration. The crux of this approach is to find a suitable model for the time to DLT for each administration. Braun et al. (2005) adopted a piecewise linear (triangle) model for the hazard, as it is reasonable to assume that the hazard of DLT for many cytotoxic agents increases steadily after administration, reaches a peak and then begins to decrease as the agent is cleared from the patient. This piecewise triangular model, although simple, has several limitations. First, none of the parameters have interpretations that relate directly to the overall probability of DLT. Second, the hazard function is not smooth and has finite support, both of which conflict with standard time-to-event models. Third, the model is inflexible for the inclusion of patient level or administration level covariates. Although one could conceive of a regression model for each parameter in the triangular hazard as a function of covariates, the direct relationship of each covariate to the probability of DLT would be difficult or impossible to discern.
To address these limitations, we propose a parametric non-mixture cure model for determining the maximum tolerated schedule (MTS), where in our setting ‘cured’ refers to patients who do not experience DLT. We shall model the total hazard of DLT as a sum of single administration hazards as done in Braun et al. (2005). However, because of the limitations that were described earlier, we shall instead model the hazard for each administration to be proportional to a standard two-parameter Weibull density function. Given the flexibility of the shape of this density, our model can accommodate a variety of hazard functions beyond the ‘up-and-down’ triangular hazard if so desired. Furthermore, this model includes parameters whose values can be directly interpreted in relationship to the probability of DLT, and we can model the marginal probability of DLT directly as a function of the number of administrations. In Section 2, we describe basic notation and develop our parametric cure model. Section 3 contains a method for developing prior distributions for our parameters, and Section 4 contains a specific outline of trial conduct using our design. Section 5 describes the performance of our algorithm and compares it with the approach of Braun et al. (2005). Section 6 contains concluding remarks.
2. Notation and cure model development
2.1. Notation
We seek a design for a phase I trial that will examine K different administration schedules of an agent. A maximum of N patients will be enrolled in the study, and each patient will be observed to the earlier of DLT or completion of ω days of follow-up without DLT. Medical investigators will select the value of ω as a clinically meaningful duration of time that is sufficiently late to accommodate the longest schedule. For example, in toxicity studies of possible treatments for acute graft-versus-host disease in allogeneic BMT patients, ω is often set at 100 days, as this is the duration that is required for acute graft-versus-host disease to develop. A fixed target probability pω is elicited from investigators and is defined as the targeted cumulative probability of DLT by time ω.
We denote schedule k, k = 1,2,…,K, with a vector of mk administration times s(k) = (s1k, s2k, …, smk). Without loss of generality, we set s1k = 0 for all k, i.e. patients receive their first administration when entering the study. Although we are not restricted by the number of administrations that are contained in each s(k) nor the timing of those administrations, medical investigators are often interested in examining schedules that have a natural order so that each s(k) is completely nested within s(k+1). Thus, the durations of the treatment schedules increase with k and m1<m2<…<mK. For example, if the first schedule was comprised of three weekly administrations after enrolment and the second schedule was a 3-week extension of the first schedule, s(1)={0, 7, 14} and s(2)={0, 7, 14, 21, 28, 35}={s(1), s(1)+21}.
We emphasize that the study is designed with the plan that each patient will receive a series of administrations at specific, fixed administration times as defined by s(1), …, s(K). However, in practice, patients may deviate from their assigned schedule after they begin treatment for a host of reasons, including clinician error or delay of treatment for medical reasons that are unrelated to toxicity, such as infection. Therefore, we let si={si,1, …, si,mi}, i=1,2,…,N, denote the actual times after enrolment at which patient i receives an administration, where si,1 = 0 and mi is the number of administrations received. Furthermore, although mk administrations are planned for patients who have been assigned to schedule s(k), it may be that mi<mk either because of administrative censoring (i.e. a new patient is enrolled, requiring an interim analysis), patient i has recurrence of disease and further administrations are cancelled, or because patient i experienced DLT at time si,mi and thus received no further administrations. If we were to model each schedule k as a single entity, rather than modelling its constituent administrations, patients with deviations from schedule that are unrelated to DLT would no longer provide information for the DLT profiles of the K schedules of interest. However, by modelling each administration separately, we develop an approach that will accommodate any administration schedule that is observed in the study and allow those schedules to contribute information about the K schedules that the study was designed to compare. Simply put, any patient who receives at least one administration, regardless of timing, provides useful data to our model.
We let Wi denote the duration of the entire study when patient i enters the study; by definition, W1 = 0. We also define Dij = Wj −Wi, for j>i, as the span of time between the enrolments of patient i and patient j. We let Ti denote the time after enrolment when patient i would experience DLT if followed for sufficiently long; note that Ti may be greater than the maximum amount of follow-up, ω. Thus, when each patient j>1 is enrolled, we have two quantities for each previously enrolled patient i=1,2, …, j−1:
Uij = min(Ti,Dij), the amount of follow-up for patient i, and
Cij = I(Uij = Ti), an indicator of whether patient i has experienced a DLT.
For example, suppose that we have enrolled two BMT patients in our KGF study on days 0 and 45 of the study. If the third patient is enrolled on day 75 of the study, and the other two patients have not had a DLT, we have (U13,C13)=(75, 0) and (U23,C23)=(30, 0). If instead the second patient had a DLT at day 60 of the study, we would have (U23,C23)=(15, 1), with U13 and C13 unchanged. The Uij and Cij will be incorporated in a parametric survival-type likelihood that will be described in the following section.
2.2. Cure model development
We first start by developing a probability model for the time to DLT for a single administration. A simple approach is to select a parametric probability density function f(ν|φ) consisting of parameters φ whose shape adequately describes the expected pattern for the hazard of DLT. We then define the hazard of DLT for each administration to be g(ν|φ, θ)=θf(ν|φ), where θ>0 quantifies the proportionality of g(·) to f(·). Then, V, the time to DLT after a single administration, has survival function
| (1) |
in which F(ν|φ) is the cumulative distribution function of f(ν|φ). Such a model is referred to as a non-mixture cure model (Chen et al., 1999; Tsodikov et al., 2003) because S(∞|φ, θ)=exp(−θ) and implies that a fraction of patients are cured, i.e. will never experience DLT after a single administration. Although a cured (non-DLT) fraction is also implied in the methods of Braun et al. (2005), it is not directly parameterized as it is in our current approach. Another benefit of our approach over that in Braun et al. (2005) is that the single-administration hazard can be as general as needed, provided that it is biologically plausible and is sufficiently tractable for parameter estimation.
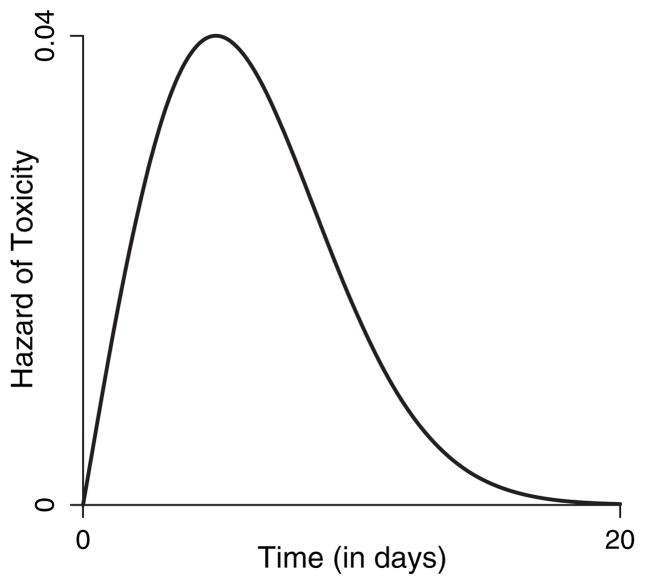
We recommend f(ν|φ)=exp(−γ)ανα−1exp{−να exp(−γ)}, which is a two-parameter Weibull density with φ=(α, γ), α>0 and −∞<γ <∞. This function implies a non-monotonic hazard when α≥2 and also allows for a monotonically decreasing hazard when 0≤α<2, which may be suitable when the agent is given as a bolus with immediate exposure to maximum toxicity that then decreases over time. In our application, we choose specifically to constrain α≥2 so that the resulting hazard function has our desired non-monotonic pattern. Fig. 1 displays an example of g(ν|φ, θ) with α=2, γ = 4 and θ=0.3 and demonstrates that, although an infinite support exists for the time to DLT, the hazard for one administration basically vanishes 20 days after administration.
Fig. 1.
Visual representation of a single-administration hazard based on a Weibull hazard with α=2 and γ=4, with θ=3
In our design, the form of g(·) is unchanged between administrations and all administrations have an additive cumulative effect on DLT. Therefore, if a patient has received administrations at times si = {si,1, …, si,mi}, we define the total and cumulative hazards of DLT for time to toxicity Ti to be
| (2) |
| (3) |
with corresponding survival function Pr(Ti > t|si) equal to
| (4) |
In equations (2)–(4), the parameter θ is now generalized to be a function of the number of administrations, which is necessary so that the limiting cumulative probability of DLT changes with the number of administrations and is equal to 1−exp{−θ(mi)}. We have also expressed equations (2) and (3) as an average of hazards among administrations; if scaling by mi were not done, then we would have S(∞)=exp{−mi θ(mi)}. Instead, scaling by mi maintains 1− exp{−θ(mi)} as the cumulative probability of DLT. We further adopt the regression model log{θ(mi)}=β0 +β1log(mi), β1 ≥ 0, so that the cumulative probability of DLT increases with the number of administrations. As a result, β0 quantifies a single administration’s effect on the probability of DLT. This model implies that the limiting cumulative probability of DLT is the same for two patients receiving the same number of administrations, regardless of when they receive those administrations. The administration times only impact the rate at which the limit is reached. Other models could certainly be adopted that allow θ to vary with the administration times. Most importantly, our model is much more flexible than that of Braun et al. (2005) and allows for the inclusion of additional covariates in both the cure fraction as well as the hazard function. For example, if doses were to vary between the patients, we could directly incorporate dose effects either in the cure fraction or the hazard function by using standard regression models.
The hazard and survival functions that were developed in equations (2)–(4) lead to a likelihood for β and φ as follows. Whenever patient j, j = 2,3,…,N, enters the study, we have an accumulated amount of follow-up Uij, for each patient i=1,2, …, j − 1. We also have Cij, an indicator of whether Uij corresponds to a DLT, and si, a vector of mi administration times. We let , so that the total data collected on all j −1 patients are . Using these data, the interim likelihood for our parameters before the enrolment of patient j is
| (5) |
On the basis of the priors for φ and β that were selected before the study began (as described next in Section 3), we can sample approximate values from the posterior distribution of φ and β by using Markov chain Monte Carlo techniques (Robert and Casella, 1999). Those posterior samples will be used to identify which schedule to assign to patient j as described in Section 4.
3. Developing priors for φ and β
We first describe the functional forms of each prior. As there are no constraints on γ and β0, we assume that both are normally distributed with respective means μγ and μβ0 and respective variances and . To reflect our need for α≥2 so that we have a non-monotonic hazard, we assume that α is equal in distribution to Zα+2, where Zα has a gamma distribution with mean μα −2 and variance . Note that there is no need to shift the distribution of α if we desire a monotonically decreasing hazard. To satisfy our constraint that β1 > 0, we assume that β1 has a gamma distribution with mean μβ1 and variance .
We now discuss how to select specific hyperparameter values for each prior. To identify mean hyperparameter values for β0 and β1, we ask the investigators to specify an a priori value Pk for the cumulative probability of DLT for schedule k, k=1,2, …,K. On the basis of the simple linear regression model E[log{−log(1−Pk)}]=b0 +b1 log(mk), we use ordinary least squares to find estimates of b0 and b1. We let μβ0 and μβ1 equal the estimates of b0 and b1 respectively.
To identify mean hyperparameter values for α and γ, we ask the investigators to specify an a priori value for the limiting cumulative probability of DLT for a single administration. We denote this value Q0 and note that Q0 must be less than the value of P1 that was elicited earlier. On the basis of equation (1), we first derive the value θ*=−log(1−Q0). We next ask investigators to select two time points t1 and t2 and to supply a priori values Q1 and Q2 for the cumulative probabilities of DLT at t1 and t2 respectively, for a single administration, such that Q1<Q2<Q0. Plugging θ* for θ(mk) into equation (4), the values Q1, t1,Q2 and t2 lead, with some algebra, to two equations in terms of two parameters a and g (in place of α and γ respectively):
If we let â and ĝ denote the respective solutions to a and g in the above equations, we set μα=max(2.01, â) and μγ = ĝ.
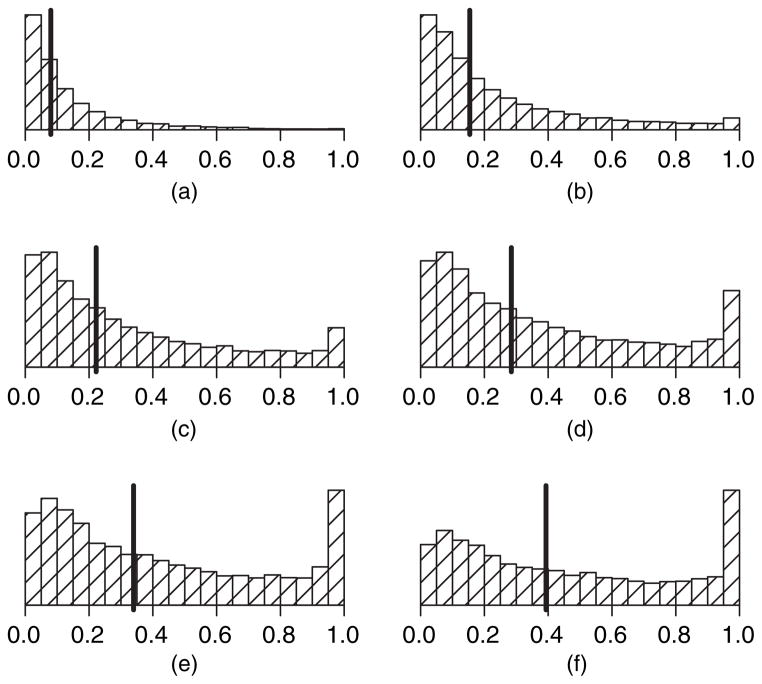
We do not derive variance hyperparameter values from elicited information; we choose rather to treat them as tuning parameters that will determine how informative the priors will be. The balance between ‘sufficiently informative’ and ‘not too informative’ is quite subjective but can be assessed through a thorough sensitivity analysis in settings where the prior means and the true distribution of DLT times greatly conflict. Specifically, we simulate the data of a handful of subjects in each of 100 simulations so that each patient experiences DLT after very few administrations. In each simulation, the prior means are set aggressively so that the longest schedule is tolerable (which is very contrary to the data) and each prior variance begins at a tenth of the magnitude of its corresponding prior mean. We then examine the operating characteristics of the design in the 100 simulations to determine how frequently the posterior reflects the data rather than the prior. We then repeat this process, continually tuning the four variance parameters until we find values in which the data can dominate the priors in a majority of 100 simulations. We then examine the final values of the variance hyperparameters with data that are simulated so that none of a handful of patients experience DLT after several administrations yet the prior means are set conservatively to indicate that only the lowest schedule is tolerable (again very contrary to the data). We then modify the prior variances as needed until all four values appear to work well with both conservative and liberal priors that are contrary to the data. As a final check, we draw 10000 samples from each of the selected priors and plug those values into equation (4) to generate 10000 prior estimates of the probability of DLT by ω for each schedule k. We then plot histograms of these values for each schedule k to inspect visually that the distributions have means tending to increase with mk and with a modest amount of variability around each of the means. Fig. 2 is an example of such a plot in the context of the numerical examples of Section 5. Note that the importance of this sensitivity analysis cannot be overemphasized, and the amount of time that is focused on this aspect of the design should constitute a significant portion of the overall time spent designing the study, as the prior cannot be altered once the study has begun.
Fig. 2.
Empirical prior distributions for cumulative probability of DLT by day for each schedule (❙, median): (a) schedule 1 (median 0.08); (b) schedule 2 (median 0.15); (c) schedule 3 (median 0.22); (d) schedule 4 (median 0.28); (e) schedule 5 (median 0.34); (f) schedule 6 (median 0.39)
4. Conduct of the trial
Once suitable prior distributions have been selected, we enrol the first patient on the lowest schedule (k = 1). With each additional patient j = 2,3,…,N, the following procedure is followed.
For each patient i=1,2, …, j−1, identify si, the timing of administrations received so far, Uij, the length of follow-up, and Cij, an indicator for the occurrence of DLT by Uij.
Use the prior distributions that are developed for φ and β and the likelihood in equation (5) to develop a posterior distribution for φ and β and use Markov chain Monte Carlo methods to sample from this posterior distribution.
Plug the posterior means φ̂ and β̂ into equation (4) and compute, for each schedule k=1,2, …,K, p̂k = 1−Sk(ω|φ̂, β̂, s(k)), the estimated probability of DLT by ω.
Compare all p̂k with pω, the target probability of DLT by ω. Then, determine the schedule k with p̂k closest to pω and denote the schedule as k̃.
Let k(j−1) denote the schedule that is assigned to patient j−1; assign patient j to schedule k*=min([k(j−1)+1], k̃).
Stop treating any patients i=1,2, …, j −1 who are still receiving administrations and have received administrations beyond those included in k*.
Reassign schedule k* to patients i=1,2, …, j−1 who are still receiving administrations and are assigned to a schedule other than k*.
Once all N patients have been enrolled and fully followed for a maximum of ω days, the MTS is defined as the schedule satisfying trial conduct rule (d) using the data of all N patients.
We now highlight some important aspects in the conduct of the trial. First, all future planned treatment for a patient is stopped once a DLT occurs. Second, conduct rule (d) uses a criterion, as a function of treatment schedule, that is identical to the CRM criterion as a function of dose (O’Quigley et al., 1990). If one were concerned with further limiting the rate of escalation, an alternative criterion that was proposed in Braun et al. (2005) could be used that reflects the point estimate p̂k, as well as the percentage of its corresponding posterior distribution lying above pω. One could further modify conduct rule (d) to terminate the study if all p̂k were greater than pω, subject to a minimum accrual requirement. Third, conduct rule (e) forbids non-incremental schedule escalation, so each patient can be assigned to at most the next longest schedule beyond that of the preceding patient. However, we do not put any constraint on schedule de-escalation, i.e. we enrol the next patient on the recommended schedule if it is shorter than the schedule that is assigned to the preceding patient. Fourth, conduct rules (f) and (g) are implemented to promote safety of the patient while increasing the likelihood that each patient is assigned to the actual MTS. For example, assume that six patients have been enrolled before an interim analysis in which two patients are assigned to each of the first three schedules. Suppose that the seventh patient is enrolled and assigned to the third schedule and a day later the fifth patient experiences toxicity. If our algorithm finds that the second schedule is the MTS (and the third schedule is overly toxic), we reassign the seventh patient to the second schedule. The number of patients who are impacted by such potential reassignments depends on the rate of accrual of patients. During rapid accrual, the number of reassigned patients may be potentially larger because those patients will have been enrolled before a substantial amount of data have been collected on previously enrolled patients. However, if the accrual rate is slow, a minimal number of patients will be reassigned because previously enrolled patients will have been monitored for the full observation period ω. Note that schedule reassignment was not described with the approach of Braun et al. (2005), but it can be easily incorporated.
5. Numerical studies
We compared the performance of our design with that of Braun et al. (2005) in a variety of settings via simulations programmed using SAS (SAS Institute, 1999). For our hypothetical schedule finding study, we continue with the motivating example of Braun et al. (2005): the study of KGF in BMT patients, in which investigators wished to study K=6 schedules corresponding to 2, 4, 6, 8, 10 and 12 weeks of KGF therapy. Each week of therapy consisted of three consecutive daily doses followed by four consecutive days of rest so that schedule k consisted of mk = 6k administrations. The maximum period to monitor DLT was specified to be ω=100 days. Our goal was to determine how long a patient could be treated while maintaining the cumulative probability of DLT by ω to be as close as possible to the threshold value pω = 0.40.
We studied the design with a maximum sample size of N = 30 patients, which is feasible in phase I trials and one that we have also found is sufficient to determine the MTS with reasonable accuracy. In each simulation, patient interarrival times were assumed to be uniformly distributed within 12–16 days. The first patient was assigned to the shortest schedule, with subsequent schedule assignments determined from the process that was described in Section 4. At each interim analysis, a single chain of 5000 observations, after a burn-in of 1000 observations, was drawn from the posterior distribution of each parameter. In all simulations, the 30 patients all follow their assigned administration schedule, i.e. there are no schedule deviations nor patients who drop out of the study because of progression of the disease. We do not present simulation results that incorporate schedule deviations, as there is little effect on the final decision of the trial when there are a handful of schedule deviations. This is because, as long as each patient receives their total number of administrations, the actual timing of those administrations is of lesser import for the overall probability of toxicity. Patients who fail to receive all their administrations will necessarily reduce the efficiency of our design, as censoring does to any study collecting time-to-event data. If substantial censoring is likely in a trial, then the planned sample size of the study will have to be increased to overcome the censoring and could be assessed via simulation.
We examined eight hypothetical scenarios which were selected so that we could numerically assess the performance of our design along a spectrum of possible ‘realities’, i.e. the eight scenarios were not selected from input with clinical investigators. The first six scenarios correspond to settings in which schedule k was the MTS in scenario k, k=1,2,…,6, and there is relatively small differential change in the DLT probabilities as the schedules increase. The final two scenarios correspond to settings in which there is a large jump in DLT probabilities near the MTS; the true MTS lay between schedules 3 and 4 in scenario 7 and was set at schedule 3 in scenario 8. The actual probabilities of DLT within 100 days for each schedule in all scenarios are shown in Table 1.
Table 1.
Numeric description of scenarios 1–8
| Scenario | Probability of DLT by ω
|
Δp | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | 0.40 | 0.64 | 0.79 | 0.87 | 0.92 | 0.95 | 0.36 |
| 2 | 0.23 | 0.40 | 0.54 | 0.64 | 0.72 | 0.79 | 0.21 |
| 3 | 0.16 | 0.29 | 0.40 | 0.49 | 0.57 | 0.64 | 0.14 |
| 4 | 0.12 | 0.23 | 0.32 | 0.40 | 0.47 | 0.54 | 0.12 |
| 5 | 0.10 | 0.19 | 0.26 | 0.34 | 0.40 | 0.46 | 0.13 |
| 6 | 0.08 | 0.16 | 0.23 | 0.29 | 0.35 | 0.40 | 0.15 |
| 7 | 0.10 | 0.20 | 0.30 | 0.60 | 0.70 | 0.80 | 0.25 |
| 8 | 0.20 | 0.30 | 0.40 | 0.70 | 0.80 | 0.90 | 0.25 |
The proximity of DLT probabilities for neighbouring schedules affects the ability of any algorithm to identify the target schedule. Therefore, we quantify the variability of the actual DLT probabilities around the target pω by using a measure Δp, which is the average absolute distance of pω from the true DLT probabilities in each scenario. Although many factors will contribute to the difficulty of finding the MTS, we find that Δp, although too simplistic as an absolute measure of difficulty, is very useful when comparing the relative difficulty of the scenarios. The value of Δp for each scenario is shown in the final column of Table 1, with smaller values indicating greater relative difficulty in locating the MTS. Thus, we predict that the MTS is easier to identify in scenarios 1, 2, 7 and 8 and more difficult to identify in scenarios 3–6.
In all simulations, DLT times were not simulated under our assumed model; instead, DLT times were simulated to occur uniformly over the interval [10+14(k−1), 10+14k] under schedule k. As a result, not only can we directly compare the two approaches; we can also examine the performance of our algorithm under model misspecification for the DLT times. We did perform simulations of our design when the DLT times occurred under the model assumed, but we have omitted those results for brevity; the results can instead be found in Liu (2007).
With regard to the prior distributions for φ and β, which are common to all scenarios, the investigators supplied the values P1 = 0.09, P2 = 0.17, P3 = 0.23, P4 = 0.29, P5 = 0.35 and P6=0.40. Thus, they believed that the longest schedule was the MTS, a belief that led to a misspecified prior for all except the sixth scenario. The investigators also believed that one administration had a limiting cumulative probability Q0=P1=6 (a sixth of the shortest schedule), with corresponding cumulative probabilities of DLT Q1=Q0=4 and Q2=Q0=2 at times t1=6 days and t2=9 days respectively. From these elicited values, we used the methods that were described in Section 3 to estimate the mean hyperparameter values μα = 2.2, μγ = 0.1, μβ0 = −4.3 and μβ1 = 1.1. Through a detailed sensitivity analysis, we identified variance hyperparameter values σα=0.50, σγ = 0.20, σβ0 = 1.2 and σβ1 = 0.3 that allowed for adequate performance of our algorithm. Fig. 2 displays histograms of 10000 draws from the resulting priors of F(100|φ, θ, s(j)) for j=1, …,6. As expected, the prior for schedule 6 is centred most closely to the target pω = 0.40 and the centres of the distributions increase with the number of administrations. The prior distributions that were used for the triangular model of Braun et al. (2005) were derived as they described, assuming that the longest schedule was the MTS and one administration had a hazard of 18 days and a peak at 2±2 days.
The results in Table 2 demonstrate that both approaches do an excellent job of identifying the MTS even when their corresponding assumed models do not reflect the actual DLT times. However, this result is not unexpected, as the MTS that was selected at the end of the study is impacted strongly by the overall rate of DLT and less so by the actual times of DLT. The times of DLT instead influence the schedule that was assigned to each patient during the study and influence the overall percentage of patients that were assigned to a neighbourhood of the MTS. And, with regard to that metric, we see that our approach does a slightly better job in some scenarios of assigning patients to schedules that are close to the MTS. For example, our approach assigned an average of 55% of patients within a neighbourhood of the MTS in scenario 2, compared with 43% with the approach of Braun et al. (2005); the corresponding percentages in scenario 6 are 60% and 52% respectively. However, no clear trend exists about which approach does a better job of assigning patients during a study. A worthy area for future research would be to assess formally whether one approach is more likely than the other to respond to the actual DLT times and to adjust patient assignments accordingly. Regardless, it is very encouraging that both approaches perform well in scenarios 7 and 8 when there is a drastic increase in the risk of DLT at schedules beyond the true MTS, even when DLTs have a very late time of onset. An interesting side note for our approach is in regard to the average number of patients out of 30 who received a reassignment to their originally assigned schedule. Overall, the number of patients with treatment reassignment increased as expected with the length of the true MTS. Specifically, the average number of patients who received reassignments were 1, 2, 4, 5, 6 and 7 for scenarios 1–6 respectively.
Table 2.
Comparison of the design proposed with that of Braun et al. (2005) with an incorrectly specified model†
| Scenario | Method | Results (%) for the following schedules (and number of weeks in parentheses):
|
|||||
|---|---|---|---|---|---|---|---|
| 1 (2) | 2 (4) | 3 (6) | 4 (8) | 5 (10) | 6 (12) | ||
| 1 | A | 90 (60) | 9 (26) | 1 (9) | 0 (3) | 0 (2) | 0 (0) |
| B | 88 (58) | 12 (33) | 0 (6) | 0 (2) | 0 (1) | 0 (0) | |
| 2 | A | 29 (33) | 61 (55) | 8 (10) | 2 (1) | 0 (1) | 0 (0) |
| B | 25 (20) | 60 (43) | 15 (24) | 0 (8) | 0 (3) | 0 (2) | |
| 3 | A | 9 (7) | 25 (25) | 41 (24) | 19 (22) | 6 (14) | 0 (8) |
| B | 8 (14) | 29 (23) | 45 (32) | 16 (18) | 2 (9) | 0 (3) | |
| 4 | A | 4 (10) | 20 (18) | 27 (22) | 32 (26) | 14 (13) | 3 (9) |
| B | 3 (9) | 18 (17) | 23 (18) | 34 (28) | 15 (16) | 7 (11) | |
| 5 | A | 0 (3) | 4 (4) | 19 (23) | 26 (30) | 34 (25) | 17 (15) |
| B | 0 (2) | 2 (14) | 22 (22) | 27 (20) | 33 (28) | 16 (14) | |
| 6 | A | 0 (2) | 0 (4) | 11 (9) | 22 (25) | 27 (28) | 40 (32) |
| B | 0 (3) | 0 (11) | 12 (16) | 20 (18) | 25 (22) | 43 (30) | |
| 7 | A | 10 (9) | 25 (25) | 37 (28) | 20 (15) | 6 (11) | 2 (10) |
| B | 4 (11) | 37 (27) | 41 (36) | 13 (13) | 4 (7) | 1 (6) | |
| 8 | A | 2 (2) | 27 (25) | 41 (30) | 19 (24) | 9 (11) | 2 (6) |
| B | 6 (5) | 30 (24) | 42 (33) | 13 (19) | 8 (11) | 1 (8) | |
For each scenario, each entry is the percentage of simulations in which each schedule was chosen as the MTS, with the average percentage of patients assigned to each schedule in parentheses. Rows A correspond to the results by using the model proposed; rows B correspond to the results by using Braun et al. (2005). Values in italics correspond to schedules within a 10-point neighbourhood of pω = 0.40.
6. Conclusion
In this paper, we have proposed a non-mixture cure model to identify a maximally tolerated schedule among a fixed number of possible nested treatment schedules. Via simulation, we have demonstrated the excellent operating characteristics of our algorithm when the model assumed is misspecified, as well as when the prior is incorrectly specified. By adopting a cure model framework, we have created a very flexible design that can be used in a variety of settings and allows for the adjustment of patient level characteristics as sample size permits. We re-emphasize that we did not seek to improve the results of Braun et al. (2005), but rather to develop a more flexible and appealing model for the cumulative hazard of DLT. On the basis of our arguments in Section 1 and the simulation results in Section 5, we feel that our approach is an extremely useful contribution to the design of schedule finding studies.
Our model can be used for the design of any clinical trial in which investigators wish to measure the effect of multiple administrations on a binary outcome. Thus, our algorithm could be used in a phase II study seeking to determine how many administrations are necessary for a desired rate of efficacy, or in a phase III study comparing two different schedules or doses of the same agent or two different agents in a large sample of (randomized) patients. Furthermore, if our methods were applied to a large cohort of patients like that in a phase III trial, we could model the single-administration hazard non-parametrically with standard techniques rather than forcing a parametric pattern on the event times.
We could also extend our models to allow for treatment schedule finding with combinations of two agents where both agents have a multiple-treatment schedule. In this scenario, our outcome remains the time to DLT; however, the non-mixture cure model would incorporate main effects of both agents in the cure fraction, as well as a term for any possible interaction between the agents. The more challenging aspect of this design is how to incorporate both agents into the time to DLT hazard, as the two agents will probably differ in both the number of administrations, as well as the times of administration. Nonetheless, once we have a reasonable model, the Bayesian estimation procedures that were developed in this paper could be used in the design for evaluating the combination therapies.
References
- Braun TM, Levine JE, Ferrara J. Determining a maximum cumulative dose: dose reassignment within the tite-crm. Contr Clin Trials. 2003;24:669–681. doi: 10.1016/s0197-2456(03)00094-1. [DOI] [PubMed] [Google Scholar]
- Braun TM, Yuan Z, Thall PF. Determining a maximum tolerated schedule of a cytotoxic agent. Biometrics. 2005;61:335–343. doi: 10.1111/j.1541-0420.2005.00312.x. [DOI] [PubMed] [Google Scholar]
- Chen MH, Ibrahim JG, Sinha D. A new bayesian model for survival data with a surviving fraction. J Am Statist Ass. 1999;94:909–919. [Google Scholar]
- Cheung Y, Chappell R. Sequential designs for Phase I clinical trials with late-onset toxicities. Biometrics. 2000;56:1177–1182. doi: 10.1111/j.0006-341x.2000.01177.x. [DOI] [PubMed] [Google Scholar]
- Goodman S, Zahurak M, Piantadosi S. Some pratical improvements in the continual reassessment method for Phase I studies. Statist Med. 1995;14:1149–1161. doi: 10.1002/sim.4780141102. [DOI] [PubMed] [Google Scholar]
- Liu CA. PhD Thesis. University of Michigan; Ann Arbor: 2007. Parametric likelihood approaches to determine a maximum tolerated schedule in phase I trials. [Google Scholar]
- O’Quigley J, Pepe M, Fisher L. Continual reassessment method: a practical design for Phase I clinical trials in cancer. Biometrics. 1990;46:33–48. [PubMed] [Google Scholar]
- O’Quigley J, Shen L. Continual reassessment method: a likelihood approach. Biometrics. 1996;52:673–684. [PubMed] [Google Scholar]
- Robert CP, Casella G. Monte Carlo Statistical Methods. New York: Springer; 1999. [Google Scholar]
- Rosenberger W, Haines L. Competing designs for phase I clinical trials: a review. Statist Med. 2002;21:2757–2770. doi: 10.1002/sim.1229. [DOI] [PubMed] [Google Scholar]
- SAS Institute. SAS Version 8 for Windows. Cary: SAS Institute; 1999. [Google Scholar]
- Tsodikov AD, Ibrahim JG, Yakovlev AY. Estimating cure rates from survival data: an alternative to two-component mixture models. J Am Statist Ass. 2003;98:1063–1078. doi: 10.1198/01622145030000001007. [DOI] [PMC free article] [PubMed] [Google Scholar]