In vitro-In vivo Correlation: Perspectives on Model Development

Abstract

In vitro – in vivo correlation (IVIVC) allows prediction of the in vivo performance of a drug based on the in vitro drug release profiles. To develop an effective IVIVC, the physicochemical and biopharmaceutical properties of the drug as well as the physiological environment in the body must be taken into consideration. Key factors include drug solubility, pKa, drug permeability, octanol-water partition coefficient and pH of environment. In general, construction of an IVIVC involves three stages of mathematical manipulation: construct a functional relationship between input (in vitro dissolution) and output (in vivo dissolution); establish a structural relationship using data collected; parameterize the unknowns in the structural model. Some key mathematical relationships used in IVIVC development are presented. The establishment of an effective IVIVC has important implications in quality control and regulatory compliance.

1. Introduction

An in vitro – in vivo correlation (IVIVC) is defined by the U.S Food and Drug Administration (FDA) as a predictive mathematical model describing the relationship between the in vitro property of an oral dosage form and relevant in vivo response. Generally the in vitro property is the rate or extent of drug dissolution or release, while the in vivo response is the plasma drug concentration or amount absorbed (FDA, 1997). An important objective of pharmaceutical product development is to gain better understanding of the in vitro and in vivo drug performances. Through the successful development and application of an IVIVC, in vivo drug performance can be predicted from its in vitro behavior. The establishment of a meaningful IVIVC can provide a surrogate for bioequivalence studies, improve product quality, and reduce regulatory burden. Since the pioneering works of Edwards (Edwards, 1951) and Nelson (Nelson, 1957) in correlating aspirin and theophylline dissolution rates with their respective in vivo appearances following oral administration, IVIVC has gained increasingly more significance in the pharmaceutical product development field. In particular, the emergence of new lipophilic drug candidates with low aqueous solubility demands special considerations during IVIVC model development.

The objective of the present review is to examine the various factors that need to be considered in the development of an IVIVC, including physicochemical factors, biopharmaceutical factors, and physiological factors. We will discuss general approaches to developing an IVIVC. In particular, the steps associated with the construction of an IVIVC including modeling and data analysis will be addressed in detail. Lastly, the various applications of a meaningful IVIVC will be briefly described.

2. Considerations in IVIVC development

While it is widely recognized that correlations exist between in vitro drug dissolution and in vivo drug absorption, limited progress has been made toward the development of a comprehensive model capable of predicting in vivo drug absorption based on dissolution. This is due to the existence of a complex array of factors that contribute to the process of drug dissolution and absorption. In general, these factors can be classified into three groups; physicochemical factors, biopharmaceutical factors, and physiological factors. In order to develop a model that can demonstrate good correlation between in vitro drug dissolution and in vivo drug absorption, these factors have to be taken into consideration.

2.1. Physicochemical Properties

Physicochemical properties play a major role in predicting the in vivo absorption of drug candidates. For almost all drugs administered orally, dissolution is a prerequisite to drug absorption and clinical efficacy. Dissolution is dependent on several physicochemical properties, including solubility, pH dependency, salt forms, and particle size. A classical mechanistic equation that attempts to model dissolution is the Noyes-Whitney dissolution equation given by equation 1, which incorporates several of the physicochemical factors mentioned before.

$$\frac{dM}{dt}=\frac{D\times S\times (C_s-C_b)}{h}$$ (1)

In this equation, M is the amount of the drug dissolved, t is time, D is the diffusion coefficient of the drug in the liquid, unstirred boundary layer surrounding the dissolving drug particle, S is the surface area of drug particle, h is the diffusion layer thickness, and C_s and C_b represent drug solubility and drug concentration in the bulk medium at time t, respectively. The Noyes-Whitney equation describes dissolution rate as a function of the change in drug concentration over time. If the sink condition is assumed, equation 1 can be transformed into the following form:

$$\frac{dM}{dt}=\frac{D\times S\times C_s}{h}$$ (2)

where C_s is approximated by the solubility of the drug substance. This concurs with our previous statement that the rate of dissolution is dependent on solubility. Although the Noyes-Whitney equation is a useful approach to model dissolution, it cannot be utilized to describe all types of dissolution data and may not apply in clinical settings (Dokoumetzidis et al., 2006). Another relatively simple model developed by Johnson and Swindell (Johnson and Swindell, 1996) presents the concept of maximum absorbable dose (MAD) as an initial guide to determine dissolution characteristics. In this approach, the MAD is calculated by:

$$MAD=S\times K_a\times SIWV\times SITT$$ (3)

where S is the solubility at pH 6.5, K_a is the intestinal absorption rate constant, SIWV is the small intestinal water volume, and SITT is the residence time of the drug in the small intestines. In general, the SIWV is considered to be 250 mL and the SITT is assumed to be 3 h. This rather simplistic approach has many limitations and can only be utilized as an initial assessment of drug dissolution.

To develop a more comprehensive model, all relevant physicochemical properties must be considered. In addition to solubility, another important factor is the compound's ionization constant or its logarithmic equivalent, the pK_a value. The pK_a values determine the stability, solubility and absorption of compounds under different environmental pH conditions. This is highly relevant because the human body contains inherent pH gradients, especially in the gastrointestinal (GI) tract, which give rise to pH-dependent absorption profiles in vivo (Carlson et al., 1983). The salt form of the drug compound is yet another important factor to be considered. In general, a salt form has a higher dissolution rate than that of its free acid or base form. However, under certain pH conditions in the GI tract, the reverse may also be true (Serajuddin and Jarowski, 1985). Perhaps a more obvious source of effect on dissolution is the particle size. It is commonly recognized that a reduction in particle size would increase surface area and enhance rate of dissolution. It is, however, less well established how particle size reduction affects the dissolution rate. In the study conducted by Johnson and Swindell (Johnson and Swindell, 1996), it was found that the effect of particle size on absorption is dependent on the drug dose and drug solubility. All these factors add to the complexity of the model building process.

2.2. Biopharmaceutical Properties

Drug permeability plays a major role in drug absorption, particularly in orally administered dosage forms. The transcellular permeability (P_m) of a compound is defined as:

$$P_m=\frac{K_p\times D_m}{L_m}$$ (4)

where K_p is the membrane-water partition coefficient, D_m is the membrane diffusivity, and L_m is the membrane thickness (Li et al., 2005). Various models have been developed to estimate membrane permeability. One such model is based on the pH-partition theory, which states that the membrane uptake of unionized solutes is favored over the ionized solutes (Shore et al., 1957). For weakly acidic compounds, ionization is suppressed at low pH values, resulting in relatively high absorption rate. At high pH values, equilibrium is shifted towards the ionization of the compound, resulting in decreased membrane permeability. The opposite conclusions can be deduced for weakly basic compounds. It is also predicted that the pH value at which the half maximal absorption occurs is approximately equal to the compound's pK_a value (Winne, 1976). This particular model is not without limitations and deviations have been observed, possibly due to factors such as microenvironmental pH and solubility issues.

Another parameter that may be useful in model development is the oil-water partition coefficient. In particular, octanol-water partition coefficient (P or logP) of neutral or unionized species is often used to provide insight into the ability of compounds to pass through membranes for absorption. Using computer and multiple linear regression, Hansch and Fujita (Hansch and Fugita, 1964) were able to quantitate the structure activity relationships based on lipophilicity. They discovered that in general, a bell-shaped distribution exists between absorption and logP values. Kramer was able to further establish that compounds with logP between 0 and 3 generally had high permeability, and those with logP values less than −1.5 or greater than 4.5 had lower membrane permeability (Kramer, 1999).

It is crucial to point out that although the octanol-water partition coefficient is a good indicator of membrane permeability, by itself it is not a sufficient parameter to predict in vivo absorption. Other measures of membrane permeability have been developed, such as absorption potential (AP) and polar surface area (PSA). The concept of absorption potential was developed by Dressman (Dressman et al., 1985) and is defined as:

$$AP=\text{log}\left(\frac{P\times F_{un}}{D_0}\right)$$ (5)

where P is the partition coefficient, F_un is the fraction of unionized drug at pH6.5, and D₀ is the dose number equal to the ratio of dose concentration to solubility. Studies indicate that AP correlates well with the fraction of drug absorbed. PSA is the surface area of a drug molecule occupied by polar atoms. The PSA value has demonstrated good correlation with the passive transport of molecules through membranes, making it a candidate parameter to include in an in vivo absorption model.

2.3. Physiological Properties

Besides physicochemical and biopharmaceutical considerations, physiological conditions are also important factors to consider for successful establishment of IVIVC, since physiological conditions can affect both drug dissolution as well as the rate and extent of drug absorption. In the previous sections, we have demonstrated the influence of pH on solubility, dissolution and membrane permeation. The effect of pH becomes particularly important in the human body, where there is an inherent pH gradient. The most well-known and commonly studied pH gradient is located throughout the GI tract, where it can range from values of 1 – 2 in the stomach to 7 – 8 in the colon. In the small intestine, where the vast majority of orally ingested substances are absorbed, the pH value ranges broadly from 5 to 8. These changes in GI pH profile can alter drug solubility, dissolution, stability and permeability. To further complicate the situation, the physiological environment is constantly adjusting and changing according to normal human activity such as food intake. Another important physiological property for oral dosage forms is the GI transit time, which affects the extent of drug release in the body. Typically, the gastric emptying time for liquids is 1 hour, while for solid materials it is approximately 2 to 3 hours. Consequently, the administration of drugs with liquid or with solid food will result in different drug transit times, leading to variations in extent of drug release. Additionally, food intake stimulates the release of enzymes and digestive fluids, and these may enhance or hinder drug absorption. As we can see, in order to accurately quantitate the relationship between in vitro data and in vivo response, the mathematical model must account for such changes.

3. Approaches to developing IVIVC models

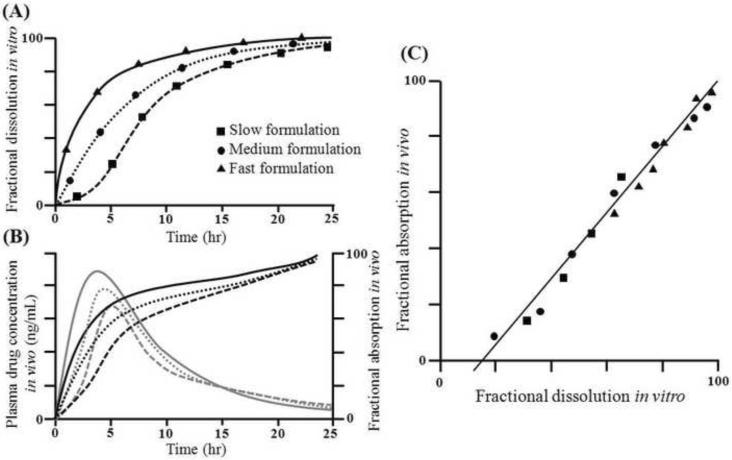
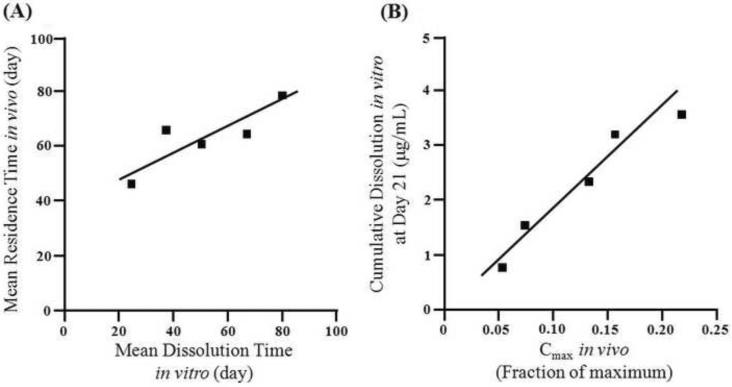
Under FDA guidance, there are four levels of IVIVC. Level A correlation is the point-to-point correlation between in vitro and in vivo profiles. This is generally considered as the highest level of correlation and allows prediction of the entire in vivo concentration time course from the in vitro dissolution profile (Fig. 1). Level B correlation compares a summary parameter from the mean in vitro profile with a summary parameter from the mean in vivo profile (Fig. 2A). This type of correlation is not considered useful. Level C correlation establishes a single time point correlation between a dissolution parameter and an in vivo parameter. An extension of this type of correlation is the multiple Level C correlation, which relates several in vitro parameters to in vivo parameters at multiple time points (Fig. 2B). Multiple Level C correlations are regarded as more useful than Level C correlations.

Figure 1.

Example of Level A IVIVC. (A) In vitro dissolution profiles of slow (square), medium (circle), or fast drug formulations (triangle). (B) In vivo studies provide plasma drug concentration of each formulation (gray lines), which can be converted to factional absorption profile (black lines) by deconvolution. (C) Level A IVIVC can be derived from the fractional dissolution in vitro and the fractional absorption in vivo. Figure shows a linear correlation, but FDA accepts non-linear correlation as well.

Figure 2.

Example of Level B (A) and Level C IVIVC (B).

Many case studies on different levels of IVIVC have been reported in the literature. In a study by Buch et al., for example, IVIVC for fenofibrate immediate release tablets was investigated (Buch et al., 2010). A linear relationship was established between in vitro drug solubility and permeability parameters and the in vivo C_max values. In another study, Amann et al. attempted to establish IVIVC for implants consisting of poly(lactic-co-glycolic acid) and the antipsychotic drug risperidone (Amann et al., 2010). Their analysis produced Level B correlation with high R² value (0.9585). Although they also obtained high R² value when performing linear regression in Level A analysis, the qualitative pattern of the fit indicated that a Level A correlation was not established. As another example, Ochoa et al. evaluated the in vitro and in vivo release profiles of theophylline formulations produced by one-step melt granulation (Ochoa et al., 2010). They observed Level A correlations between the dissolution and absorption profiles.

From a regulatory viewpoint, it is desirable to establish a Level A correlation. Such IVIVC can then be used to conduct bioequivalence studies between different dissolution profiles and play an important role in manufacturing quality control process. While the literature on Level A modeling and data analysis is extensive and the methods employed vary, in general they all follow common steps towards the establishment of a Level A correlation (Dunne, 2007). The first step is the construction of a functional relationship between the input and output quantities. Next a structural model is developed by connecting the data collected to the functional relationship previously established. The last step involves fitting the model parameters using data analysis.

3.1. Constructing a Functional Relationship

The goal of this step towards the development of an effective IVIVC is to find the relationship between the quantities of interest without considering any collected data. The framework of this approach is the linear time invariant dynamic (LTID) system (Finkelstein and Carson, 1985). LTID system is a system that contains an input i(t) and an output o(t), both as a function of time t. An important characteristic of such a system is that the output corresponding to the input i₁(t) + i₂(t) is equal to the sum of outputs from i₁(t) and i₂(t) calculated separately. In addition, shifting the input at time t by a period of Δt will result in a similar shift of the output. In other words, i(t + Δt) has an output of o(t + Δt). Having established these principles, it is easy to derive the following equation for all LTID systems:

$$o\left(t\right)={\int }_0^{t}i\left(\tau \right)r(t-\tau )d\tau$$ (6)

where the function r(t) represents the functional characteristic of the system and i(τ) is the unit input at an infinitely short period of time. This integral is known as the convolution integral. The purpose of forming an IVIVC is to use information from in vitro dissolution to predict the in vivo outcome. Usually in vitro dissolution is represented by the fraction of the dosage form dissolved, designated here by the function F₁(θ₁,t), where θ₁ consists of all the different parameters that contribute to the in vitro dissolution of the dosage form. Similarly, we can designate a function in the form of F₂(θ₂,t) to represent the fraction of drug dissolved in vivo, where θ₂ represents all parameters affecting the in vivo dissolution of the dosage form. In clinical settings, however, this function is rather difficult to observe directly. To solve this issue, the plasma drug concentration is used instead of in vivo drug dissolution. If we denote plasma drug concentration at time t as C(t), using the convolution integral we can obtain the following equation:

$$C\left(t\right)={\int }_0^{t}i\left(\tau \right)r(t-\tau )d\tau$$ (7)

Here the input function i(t) describes changes in the rate at which the drug enters the system. Since it is partly dependent on in vivo drug dissolution, we can express this function as:

$$i\left(t\right)=f_3({\theta }_3,t,F_2({\theta }_2,t))$$ (8)

where θ₃ consists of the parameters that affect the rate at which drug enters the system besides in vivo drug dissolution, such as drug absorption, distribution, metabolism and elimination. Equation 7 also contains the characteristic unit impulse response function r(t), which in itself is dependent on parameters that we inclusively define as θ₄. Therefore:

$$r\left(t\right)=f_4({\theta }_4,t)$$ (9)

Information about this function is often collected by inputting a unit input of infinitely small duration into the system and examining the corresponding output. The unit input can be of various dosage forms, such as intravenous and oral (Balan et al., 2001; Sirisuth et al., 2002). Depending on the type of dosage form administered, the parameters included in θ₃ and θ₄ may change. For example, if the unit input is administered intravenously, drug absorption would be bypassed and become an inherent part of the input. On the other hand, if the unit input is administered in the oral form, absorption would remain to be characterized.

The final step is the construction of a functional relationship between the input in vitro dissolution and the output in vivo dissolution. That is, we must establish the following relationship:

$$F_2({\theta }_2,t)=f_5({\theta }_5,t,F_1({\theta }_1,t))$$ (10)

This equation is what we ultimately want to achieve in IVIVC model development. Utilizing the approach outlined above, many models have been derived to describe the unit impulse response function r(t), the input function i(t), the in vitro dissolution function F₁(θ₁,t) and the in vivo drug dissolution function F₂(θ₂,t). As mentioned previously, r(t) and i(t) models take on different forms depending on the pharmacokinetics of the LTID system. For example, for one compartmental pharmacokinetics model without drug absorption in the LTID system would have a different r(t) than a multi-compartment pharmacokinetics model without drug absorption in the LTID system (Table 1). For processes that do not include absorption as part of the LTID system, the input function contains both absorption and in vivo dissolution. If the model does include absorption in the LTID system, the input function is simply the in vivo drug dissolution rate. The main disadvantage associated with using these models for r(t) is that assumptions are made about the structure of the LTID system. Alternatively, a deconvolution approach can be used but this model contains more parameters and is therefore more complex.

Table 1.

Some of the functions used to describe the unit impulse function.

Parameters	One compartment	Two compartments
V: apparent volume of distribution ke: first order elimination rate constant ka: first order absorption rate constant k12: rate constant for transfer from central to peripheral compartment k21: rate constant for transfer from peripheral to central compartment	·Single compartment = body ·Even distribution of drug throughout body ·Only applicable for rapidly distributed drug	·Central compartment (drug in and out) + peripheral compartment (drug distribution) ·Slow equilibration between compartments
Without absorption ·Very rapidly absorbed drug (almost ideal)	$r\left(t\right)=\frac{1}{V}{e}^{(-k_{e}t)}$	$r\left(t\right)=\frac{k_a}{V(k_a-k_e)}[e^{(-k_{e}t)}-e^{(-k_{a}t)}]$
With absorption ·Commonly applicable ·Severely influenced by physicochemical, biopharmaceutical, and physiological factors	$r\left(t\right)=\frac{k_a}{V}[\frac{k_{21}-k_a}{({\lambda }_1-k_a)({\lambda }_2-k_a)}{e}^{(-k_{a}t)}+\frac{k_{21}-{\lambda }_1}{(k_a-{\lambda }_1)({\lambda }_2-{\lambda }_1)}{e}^{(-{\lambda }_{1}t)}+\frac{k_{21}-{\lambda }_2}{(k_a-{\lambda }_2)({\lambda }_1-{\lambda }_2)}{e}^{(-{\lambda }_{2}t)}]$	$r\left(t\right)=\frac{A}{V}{e}^{(-{\lambda }_{1}t)}+\frac{1-A}{V}{e}^{(-{\lambda }_{2}t)}$

λ₁+λ₂ = k_e+ k₁₂+ k₂₁; λ₁ λ₂ = k_e k₂₁; A = (k₂₁ − λ₁)/(λ₂ − λ₁).

Similarly, various functional models can be derived for F₁(θ₁,t) and F₂(θ₂,t) (Table 2 and 3) (Bigora et al., 1997; Buchwald, 2003; Langenbucher, 2003; Mendell-Harary et al., 1997; Polli et al., 1996). The models listed in Table 2 have a common characteristic of predicting zero dissolution at time zero and complete dissolution at sufficient time t. By introducing a parameter that represents the degree of dissolution, these models can easily be modified to account for incomplete dissolution. Table 3 lists some of the commonly used models that relate in vivo drug dissolution to in vitro dissolution. However, a major limiting factor of these models is the assumption that in vitro – in vivo relationship does not vary with time.

Table 2.

Some of the functions describing in vitro drug dissolution.

Description	Function
Exponential	F1(θ1, t) = 1 − e(−θ11t)
Weibull	F1(θ1, t) = 1 − e(−θ11tθ12)
Logistic	$F_1({\theta }_1,t)=\frac{e^{({\theta }_{11}+{\theta }_{12}\text{log}\left(t\right))}}{1+e^{({\theta }_{11}+{\theta }_{12}\text{log}\left(t\right))}}$
Hill	$F_1({\theta }_1,t)=\frac{t^{{\theta }_{11}}}{{\theta }_{12}+t^{{\theta }_{11}}}$

θ_1i, (i = 1 and 2): parameter θ₁ at observation times t₁ and t₂.

Table 3.

Some of the functions describing the relationship between in vivo and in vitro drug dissolution.

Description	Function
Identity	F2(θ2, t) = F1(θ1, t)
Linear	F2(θ2, t) = θ51 + θ52F1(θ1, t)
Sigmoid	$F_2({\theta }_2,t)={\theta }_{51}+\frac{{\theta }_{52}{F}_1{({\theta }_1,t)}^{{\theta }_{53}}}{{\theta }_{54}+F_1{({\theta }_1,t)}^{{\theta }_{53}}}$
Higuchi	F2(θ2, t) = (θ51F1(θ1, t))0.5
Hixon-Crowell	$F_2({\theta }_2,t)={\theta }_{51}-{({\theta }_{51}^{0.33}-{\theta }_{52}{F}_1({\theta }_1,t))}^3$
Weibull	F2(θ2, t) = θ51 − θ52e(−θ53(F1(θ1,t))θ54

θ_5i (i = 1, 2, 3, 4): parameter θ₅ (see equation 10) at observation times t₁, t₂, t₃, t₄.

3.2. Constructing a Structural Model

The functional relationship described previously does not take into consideration any information gathered from actual data. The construction of a structural model connects the data collected to the functional models established earlier. The structural model can also be seen as a statistical model that forms a framework for parameterization, which is generally the last step in the development of a Level A IVIVC. Generally, the following approach is taken towards structural model development. In a previous statement, we denoted the plasma drug concentration at time t to be C(t). For any given data set, it contains a value Y(t) such that it is an approximation of the true value C(t). Statistically speaking, C(t) is the true value of plasma drug concentration at time t; it is a value that can never be precisely determined by experiments due to the presence of inevitable random errors. As a result, we can only estimate C(t) by the value of Y(t). The process of defining the statistical properties of Y(t) is the structural modeling process. Similarly, we can define a function that is capable of approximating the true value of in vitro dissolution data at time t.

In constructing a viable structural model, some form of data transformation may be necessary. For example, based on the previous definitions and properties of C(t) and Y(t), we can derive a simple relationship such that:

$$Y\left(t\right)=C\left(t\right)+{\epsilon }_1{\epsilon }_1~N(0,{\sigma }_1^2)$$ (11)

The term ε₁ represents the random differences between the true value C(t) and the estimate value Y(t). The errors are normally distributed around a mean of 0 and have a constant variance of σ₁². From this equation we can also see that Y(t) is also random and normally distributed, with both positive and negative values. However, we know that plasma concentration values cannot be negative, therefore a transformation of the data is necessary to ensure normality. One common transformation is to assume that the logarithm of plasma concentration is normally distributed such that:

$$\ln \left(Y\left(t\right)\right)=\ln \left(C\left(t\right)\right)+{\epsilon }_2{\epsilon }_2~N(0,{\sigma }_2^2)$$ (12)

However, this transformation presents the problem that equations 11 and 12 are not equivalent if ε₁ and ε₂ are not both equal to 0. Furthermore, the constant variance assumption in equation 11 may not hold as the function undergoes logarithmic transformations and vice versa. Other non-linear transformations will encounter similar situations. This clearly demonstrates that depending on the assumptions made and the methods used construct a structural model, the same functional relationship may result in different structural models, subsequently leading to different parameterization and predictions of in vivo results (Dunne, 2007).

Besides data transformations, there are other issues that must be taken into account when developing a structural model. One common practice is to collect in vitro and in vivo data across multiple dosage units and subjects at each time point, then averaging the data to construct a model (Eddington et al., 1998). This practice may lead to a loss in data information. In addition, it can be shown by simple simulation that a curve constructed from averages is not the same as curves constructed from averaging individual sets of data (Dunne, 2007). Another factor that needs to be considered is the discrepancy between theoretical and measured values. As we know the theoretical fraction of drug dissolved in vitro or in vivo should be a value between 0 and 1. In practice, the measured values may exceed 1 due to sampling errors or discrepancy between label claim and actual dose. An effective structural model may need to account for such deviations.

3.3. Model Fitting and Parameterization

After data collection and the development of a structural model, the unknown constants in the model have to be estimated. There are a number of statistical methods used for parameterization, including the method of maximum likelihood, the method of least squares and Bayesian analysis. The statistical characteristics of the data collected can be used to select the appropriate method for parameterization. For example, for a set of data values that are uncorrelated and have constant variance, the method of unweighted least squares is suitable; however, for data values that are correlated and have non-constant variance, weighted least squares have to be used (Kutner et al., 2004). Regardless of the method used, the ultimate goal is to produce a model that is in best agreement with the data collected. Previously, we mentioned the possibility of multiple structural models arising from a single functional relationship; during parameterization, different structural models will produce different parameter estimates. Thus it is important to be aware that the same functional relationship established early on in the process of IVIVC development can produce varying IVIVC models.

4. Applications of IVIVC

4.1. Biopharmaceutical Classification System

The biopharmaceutical classification system (BCS) is a way to categorize drug compounds based on their solubility and permeability properties. Under the BCS, drug substances can be grouped into four classes: Class 1 compounds are highly soluble and highly permeable; Class 2 substances have high permeability but relatively low solubility; Class 3 compounds are highly soluble but not very permeable; and Class 4 drug substances have both low solubility and low permeability. In general, it is recognized that the successful development and application of an IVIVC require dissolution to be the rate-limiting step in the process of drug administration and absorption. For Class 1 compounds, there are no rate-limiting steps for drug absorption, with the possible exception of immediate release dosage forms, for which gastric emptying could potentially become the rate-limiting step (Modi, 2007). For Class 2 compounds dissolution is the rate-limiting step in absorption, therefore the establishment of IVIVC is expected. For Class 3 compounds, IVIVC is generally regarded as unlikely but may be possible depending on the relative rates of dissolution and intestinal transit. For Class 4 compounds IVIVC is highly unlikely. Classification according to the BCS will enable early determination of whether IVIVC can be developed for a certain drug candidate.

4.2. Biowaivers

A biowaiver is an exemption granted by the FDA that allows in vivo bioavailability and/or bioequivalent studies to be avoided. A predictive and reliable IVIVC model can serve as a basis for biowaivers, allowing reductions in time and costs during pharmaceutical product development. For immediate release dosage forms, the successful development of IVIVC models may be limited to Class 2 and Class 3 compounds classified under the BCS, thereby restricting the application of biowaivers to these classes of drug compounds. However, according to FDA guidelines biowaivers can also be requested for Class 1 compounds provided the drugs are solubilized in the gastric fluid sufficiently rapidly that gastric emptying does not become the rate-limiting step. The situation for extended release (ER) dosage forms is more complex, since the factors considered in the BCS (i.e. solubility and intestinal permeability) are insufficient to predict the rate and extent of dissolution for ER drugs. Despite these limitations, the FDA has published important guidelines for establishing IVIVC for ER dosage forms. Readers should refer to the document “FDA Guidance for Industry – ER oral dosage forms: development, evaluation, and application of IVIVCs” (FDA, 1997) and “FDA Guidance for Industry – Waiver on in vivo bioavailability and bioequivalence studies for immediate-release solid oral dosage forms based on a Biopharmaceutics classification systems”(FDA, 2005) for more detailed information.

4.3. Non-oral Dosage Forms

Currently, regulatory guidance for IVIVC is mainly focused on oral dosage forms. However, similar principles of developing IVIVCs can be applied to non-oral dosage forms, with certain modifications to adjust for different modes and durations of drug delivery. Perhaps one of the most challenging aspects of developing IVIVCs non-oral drug delivery systems is how to design in vitro studies such that the in vivo behavior is reflected as much as possible. For example, it is difficult to apply classical IVIVC to drug-eluting stents because it is a local delivery system, not a systemic delivery system like oral dosage forms. Several publications have attempted to correlate in vitro pharmacokinetics of paclitaxel (Finkelstein et al., 2003) and dexamethasone (Lincoff et al., 1997) loaded stents with in vivo delivery into the artery wall with limited success. Another difficulty that may hinder the design of appropriate in vitro studies is the lack of suitable dissolution media that reflect the in vivo environment non-oral delivery systems are subjected to. This is particularly the case for implanted drug delivery devices and liposomal products. Liposomal formulations have traditionally demonstrated poor correlation between in vitro and in vivo performance, possibly due to the physiological presence of a lipid membrane `sink' to which released drugs may bind (Shabbits et al., 2002). To circumvent this problem, a novel drug release assay has been developed using excess multilamellar vesicles (Shabbits et al., 2002). This method demonstrated improved correlation between in vitro data and in vivo release of doxorubicin, verapamil and ceramide.

5. Conclusions

The development of a predictive and reliable IVIVC model is a complex process. Professor Takeru Higuchi, a pioneer in this field, developed one of the most important controlled release equations, known as the Higuchi's Equation. Since then this well-known and widely used equation has influenced drug delivery development and provided groundwork for subsequent IVIVC modeling. This review attempts to elucidate some of the general principles involved in the construction of IVIVC. Before the commencement of model building, it is important to consider the factors that may contribute to the in vitro and in vivo performance of the drug compounds. Since by definition the IVIVC is a mathematical model, various algebraic, calculi and statistical methods are employed in its development. Once a reliable IVIVC model has been developed, it can serve as regulatory guidance for pharmaceutical industry. With justified modifications, its applications can be expanded to include more dosage forms beside oral dosage forms. Currently numerous studies have been conducted that demonstrate the existence of relationships between in vitro dissolution and in vivo release data. However, most of these studies fail to provide mathematical models that describe these relationships. What's needed is not only more extensive research into IVIVC, but also better mathematical methods and simulation techniques.