Abstract
Dopaminergic neurons in the mammalian substantia nigra display characteristic phasic responses to stimuli which reliably predict the receipt of primary rewards. These responses have been suggested to encode reward prediction-errors similar to those used in reinforcement learning. Here, we propose a model of dopaminergic activity in which prediction-error signals are generated by the joint action of short-latency excitation and long-latency inhibition, in a network undergoing dopaminergic neuromodulation of both spike-timing dependent synaptic plasticity and neuronal excitability. In contrast to previous models, sensitivity to recent events is maintained by the selective modification of specific striatal synapses, efferent to cortical neurons exhibiting stimulus-specific, temporally extended activity patterns. Our model shows, in the presence of significant background activity, (i) a shift in dopaminergic response from reward to reward-predicting stimuli, (ii) preservation of a response to unexpected rewards, and (iii) a precisely timed below-baseline dip in activity observed when expected rewards are omitted.
Keywords: reinforcement learning, dopamine, STDP, neuronal excitability, prefrontal cortex, basal ganglia
1. Introduction
The mammalian dopamine (DA) system is implicated in a wide range of cognitive functions. Dopaminergic neurons have been shown to reliably respond to external stimuli both within task learning contexts (Schultz and Romo, 1990; Ljungberg et al., 1991, 1992; Pan et al., 2005), as well as outside of any specific task (Hyland et al., 2002). During conditioning, phasic DA responses appear to encode predictions about future events, either via an explicit reward prediction-error signal (Schultz, 1998, 2007; Sutton and Barto, 1998; Pan et al., 2005), or by a more generic signal for learning action-perception contingencies (Redgrave and Gurney, 2006; Redgrave et al., 2008). Most computational approaches to modeling DA responses during learning have focused on the “temporal difference” algorithm (Sutton and Barto, 1998; Pan et al., 2005, 2008; Hazy et al., 2010) which computes expected reward using an explicit temporal discount (Sutton and Barto, 1998). In contrast to these “top-down” approaches, “bottom-up” approaches seek to understand phasic DA responses by appeal to known features of neuroanatomy and physiology. For example, “dual-path” models (Brown et al., 1999; Tan and Bullock, 2008) investigate interactions between complementary excitatory and inhibitory pathways converging on DA neurons. These models involve spiking neural networks but do not rely on the precisely timed spiking activity patterns observed in prefrontal cortex (PFC) and striatum during reinforcement learning (Schultz, 1992; Durstewitz et al., 2000). By contrast, the model of Izhikevich (2007) does leverage precise spike timing but is unable to account for a full range DA responses (Schultz and Romo, 1990; Schultz, 1998). To advance the “bottom-up” approach, we describe and analyze a model of DA activity in which phasic prediction-error signals are generated through the joint action of excitatory and inhibitory pathways, in a spiking neural network undergoing DA modulation of both spike-timing dependent synaptic plasticity (DA–STDP) and neuronal excitability (DA-modulated post-synaptic facilitation, DA–PSF).
Our model accounts for the following key features of DA responses. First, DA neurons display phasic activation in response to unexpected primary rewards (unconditioned stimuli, US), such as food or water (Schultz and Romo, 1990; Schultz, 1998). Second, these neurons display phasic responses to reliably reward-predicting stimuli (conditioned stimuli, CS), yet do not respond to US (or CS) which are themselves predicted by earlier stimuli (Ljungberg et al., 1992). Third, reward-related DA responses reappear if a previously predictable reward occurs unexpectedly (Ljungberg et al., 1992). Fourth, DA neurons display a brief dip in activity at precisely the time of an expected reward, if that reward is omitted (Ljungberg et al., 1991). Finally, as contingencies in the environment change DA responses will shift to the time of the earliest reward-predicting CS (Ljungberg et al., 1992; Schultz, 1998; Pan et al., 2005).
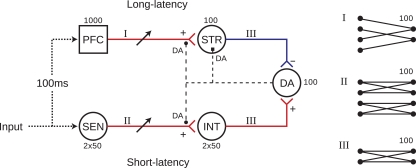
The model is depicted in Figure 1. Parallel pathways from peripheral sensory neurons (SEN) transmit signals to DA neurons either via PFC and striatum (STR) with 100 ms latency, or without latency via an intermediate group of excitatory neurons (INT) assumed to be within a fast relay such as the sub-thalamic nucleus (STN) or superior colliculus (Redgrave and Gurney, 2006). STR neurons project inhibitory synapses to DA neurons, such that a balance between STR and INT activities controls DA output. This balance is maintained by DA modulation of synaptic plasticity (DA–STDP) in PFC → STR and SEN → INT pathways. The model also includes DA modulation of neuronal excitability (DA–PSF) in STR neurons and stimulus-specific temporally extended PFC responses to sensory input. Note that we do not model either the SEN → PFC pathway or recurrent connectivity within the PFC; rather, stimulus-specific PFC responses to sensory input are represented by pre-computed temporally extended (1 s) activity patterns drawn from the same distribution as random background activity (Section 2.2).
Figure 1.
The model network is separated into short and long-latency channels. Input to the long-latency channel is delayed by 100 ms with respect to stimulus onset, representing upstream transmission delays to cortex. Each sub-group consists of 100 neurons (except PFC which contains 1000), with all neurons receiving input from 100 of their pre-synaptic afferents. Connectivity patterns are as depicted in I (sparse), II (parallel), and III (all-to-all). In the sparse PFC–STR pathway, afferent to each STR neuron are selected randomly from PFC modulation of STDP in both PFC → STR and SEN → INT pathways (filled circles), as well as post-synaptic facilitation of STR neurons (filled square) is enabled by DA release. DA output therefore controls, and is controlled by, a precisely timed balance of excitatory and inhibitory influences on DA neurons, resulting from DA modulation of synaptic efficacy and neuronal excitability at STR and INT neurons.
Our model combines features from two previous classes of model, extending both. It shares with previous “dual-path” models (Brown et al., 1999; Tan and Bullock, 2008) the architecture of complementary excitatory and inhibitory pathways converging on DA neurons. However, unlike these models we show that adaptive DA responses can be generated in the presence of substantial background activity, thereby addressing the so-called “credit assignment” problem (Sutton and Barto, 1998). Our model accomplishes this by sharing with another model (Izhikevich, 2007) the DA–STDP mechanism, according to which synapse-specific “eligibility traces” enable selective modulation of stimulus-related synapses. However, Izhikevich's model demonstrates only the US → CS shift in DA responses, and not the other key features described previously. In summary, by augmenting a dual-path model with DA–STDP, DA–PSF, and stimulus-specific temporally extended PFC responses, our model accounts for a broad range of adaptive DA responses in general conditions involving background neuronal activity. The model therefore provides an integrated account of DA neuromodulation and prediction-error signaling in the cortico-basal loop.
2. Materials and Methods
2.1. Spiking network model
Our model (Figure 1) consists of five groups of regular spiking (RS) neurons1, implemented using the phenomenological model of Izhikevich (2003) and integrated by the Euler method with a time-step of 1 ms. Our implementation was written in C and extends that of Izhikevich (2007).
Each neuron is modeled by two difference equations
| (1) |
| (2) |
where v is the membrane potential of a neuron and u is an abstract membrane recovery variable. Neurons are reset after spiking, according to:
| (3) |
I represents the total current input to each neuron; parameters a, b, c, and d define the type of neuron modeled. In our model, all neurons are RS having parameters a = 0.02, b = 0.2, c = −65, and d = 8 (Izhikevich, 2003).
The input I is computed as the linear summation of all active afferent synaptic weights (ω) in the model network, plus a term (ξ) which represents external synaptic input:
| (4) |
Here, ωij is the strength of the synapse connecting neuron i to neuron j, δ is the Dirac delta function, and tspike is the time of the last spike of neuron i. The external input term (ξ) is calculated for each j as a random current drawn from the uniform distribution
| (5) |
which is sufficient to causes neurons to fire irregular spike trains at 1–5 Hz without external stimulation (Softky and Koch, 1993).
Spikes are delivered to their post-synaptic targets after axonal conductance delay (L), uniformly distributed for all pairs of connected neurons in the range:
| (6) |
The network architecture and associated inter-cluster connectivity patterns are depicted in Figure 1. There is no intra-cluster connectivity. For all projections types, post-synaptic neurons receive exactly 100 randomly selected afferent connections from neurons in their associated pre-synaptic cluster. An exception to this uniform selection rule are connections in the SEN → INT pathway, which are separated into two distinct groups. Here, pre-synaptic neurons are selected randomly from either US- or CS-specific SEN neurons exclusively, such that functional anatomy in SEN is reflected in INT. In the PFC → STR pathway, where there are 10 times as many pre-synaptic neurons as post-synaptic targets, the uniform connectivity rule results in each PFC neuron having just 10 efferents to the SEN neurons´ afferents, 100 reflecting sparse connectivity.
Prefrontal cortex and SEN neurons project axons to plastic (modifiable) synapses at STR and INT neurons respectively, with strengths limited to within the range ω = [0, 10] mA (see Section 2.3). All other synapses in the network are non-plastic (INT → DA, ω = 0.6 mA; STR → DA, ω = 1 mA). We assume that synaptic dynamics do not play a role in the proposed mechanism and model pre-synaptic spikes as inducing instantaneous potentials at their post-synaptic targets (after axonal conductance delay).
2.2. Stimulation
Stimuli are presented as distinct patterns of current input to half the neurons in each of the two input groups, SEN and PFC, at times tsim and tsim + 0.1 s, respectively. tsim is the time at which a stimulus (either US or CS) impinges at the periphery and tsim + 0.1 s is the time at which the associated neural signal arrives at the PFC (i.e., after upstream transmission delay). Stimulation of SEN neurons occurs at stimulus onset and is transient (10 ms). Stimulus-specific activation of PFC neurons is delayed by 100 ms to simulate a longer latency in transmission to the cortex as compared to the short-latency (INT) pathway. PFC responses are sustained for 1 s representing self-sustained, recurrent excitation in the PFC rather than a continuation of the external stimulus (see below).
The SEN neurons respond to stimuli via a transient increase in the external current input to each affected neuron. Specifically, over the stimulation period of 10 ms, ξ is increased by a constant 0.2 mA:
| (7) |
which ensures that SEN neurons responding to a stimulus display a brief increase in their firing rate, but do not exhibit any particular spike ordering.
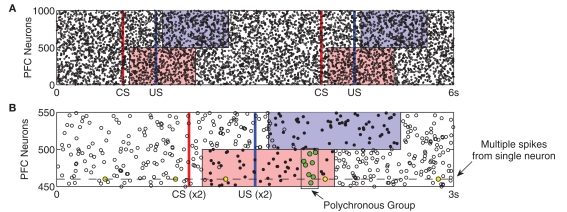
By contrast, PFC neurons respond to stimuli by exhibiting stimulus-specific spatio-temporal (polychronous) spike patterns, but without any increase in firing rate (see Figure 2). We pre-calculate a separate n × m matrix (C) of instantaneous currents for each stimulus (US/CS), where n = 500 (half the neurons in PFC) and m = 1000 (duration in ms of the PFC representation). During presentation of a stimulus, the external synaptic input ξ to the affected neurons is replaced by the input specified by the corresponding matrix C. Entries for each matrix are drawn from the same distribution as the external input (equation 5), ensuring that firing rates remain unchanged. We recognize that cortical neurons often fire between 5 and 20 Hz in task-related contexts (Funahashi et al., 1989), however we chose to keep firing rate constant in our model in order to ensure that the influence of PFC responses on DA neurons are due to spike-timing patterns rather than firing rate changes (see Section 4.3). The impact of PFC firing rate transitions on DA responses will be investigated in future work; see Section 4.6.
Figure 2.
Prefrontal cortex activity patterns. Stimulus-specific activities are shown by the shaded regions. (A) The same CS–US pair is presented at t = 1 s and t = 4 s. After a latency of 100 ms, injection of random currents into CS-associated PFC neurons (red) is replaced with CS-specific input. After a 500-ms ISI, US-specific input replaces random currents in US-associated neurons (blue). Both stimuli last for 1 s, after which random currents are reinstated. Stimulus-specific patterns are derived from the same probability distribution as the random currents (see Section 2) evoking spiking activity patterns which are statistically indistinguishable from background activity. (B) The superimposition of two US responses highlights how stimulus-specific activity is near-identical over repeated presentations. Here, a subset of the two CS–US responses in (A) are aligned with respect to CS onset and are displayed as dots (spikes are coincident) and open circles (spikes appear in only one response). The prevalence of dots reveals how activity patterns are near-identical only during the 1 s stimulus period. Also, because any individual neuron is equally likely to fire outside this period as within it (yellow dots), such activity cannot provide the temporal substrate for stimulus-specific reinforcement learning. In contrast, a polychronous group (green dots) occurs only at a specific time during stimulation.
2.3. Synaptic plasticity
Synaptic plasticity is modeled as in Izhikevich (2007) in which STDP modifies a variable (γ) that affects the derivative of synaptic strength. The variable γ therefore implements an “eligibility trace” (Sutton and Barto, 1998) at each synapse, enabling synaptic plasticity to be modulated by distal DA rewards (see below and Izhikevich, 2007) for a detailed explanation of this issue). Using an earliest-neighbor method, the firing of post-synaptic neuron j at time t increases γ by
| (8) |
where is the time of arrival (after axonal conductance delay) of the last spike of pre-synaptic neuron i. Similarly, when a spike arrives from pre-synaptic neuron i (again, after conductance delay) at time t the value of γ is reduced by
| (9) |
where is the time of last spike of post-synaptic neuron j. The variable γ otherwise decays exponentially with time constants τγ = 0.2 s (PFC) and τγ = 1 s (SEN). The parameters A+ = 0.1, A− = 0.15 (dimensionless), and τ± = 0.02 s determine the relative size of the STDP window for both causal and anti-causal firings.
2.4. Dopamine modulation of spike-timing dependent synaptic plasticity
Dopaminergic modulation of synaptic plasticity (DA–STDP) is implemented in the calculation of synaptic strength (ω) from its derivative
| (10) |
where α corresponds to the level of extracellular DA (in μM) and γ is the synaptic eligibility trace (Izhikevich, 2007). The value of α is step-increased by 0.05 μM for each spike of a DA neuron while otherwise diffusing with exponential time constant τα = 0.1 s. A baseline DA concentration of between 0.5 and 1 μM is therefore maintained by the background activity of DA neurons, allowing synaptic plasticity to occur at a slow rate at all times. Whenever DA neurons are phasically activated the increased firing of these neurons causes the value of α to transiently increase to between 2 and 3 μM.
2.5. Dopamine modulated post-synaptic facilitation
The DA–PSF (post-synaptic facilitation) mechanism enables DA responses to modulate the excitability of STR neurons on a millisecond timescale. Specifically, α modulates the parameter b in equation (2), which governs the rate of increase of the membrane potential. The modulation takes place according to:
| (11) |
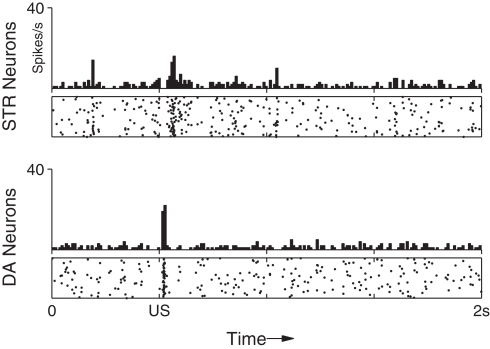
Under background DA activity, b remains at just under 0.2 which facilitates low-frequency spiking of STR neurons. However, immediately following phasic DA activation the value of b can rise to over 0.25, resulting in a transient burst in activity in STR neurons. Figure 3 (top) shows the effect of DA–PSF on STR neurons immediately following an unexpected reward (US), illustrating this mechanism.
Figure 3.
Maintenance of response to an unpredictable US. After training the response of the network to the presentation of a US is not suppressed if the preceding CS is omitted. The DA response immediately recovers to its original (pre-training) strength.
3. Results
We describe three experiments. Each experiment involves two stimuli: a CS and an US. Each stimulus is presented to the network as a distinct pattern of current applied to 50% of the neurons in each of SEN and PFC (Figure 2). Stimulus-related activity in SEN neurons is evoked by a transient (10 ms) increase in the background current, ξ, input to each affected neuron (Section 2.1). This causes an immediate increase in spike frequency, without inducing any specific spike ordering. In PFC neurons, stimuli are represented by replacing the background input with a stimulus-specific, pre-calculated pattern of currents (Section 2.2), for a sustained period of 1 s. This evokes a spatio-temporally extended pattern of activity which is near-identical over successive presentations of a given stimulus (Figure 2). Importantly, these pre-calculated patterns are drawn from the same distribution as ξ and are therefore statistically indistinguishable from background activity or concurrently active representations of other stimuli.
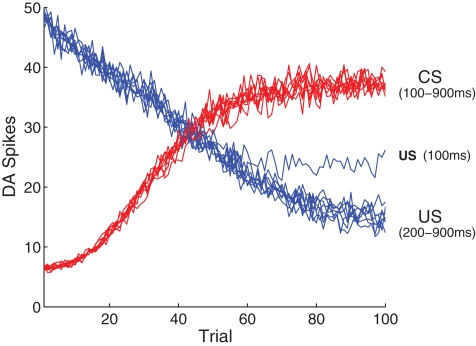
3.1. Shift in response
The first experiment (Figures 4 and 5) reproduces the shift in DA response from a US to an earlier CS (Ljungberg et al., 1992; Schultz, 1998; Pan et al., 2005). We recorded network activity over 100 conditioning trials, presented at 10 s intervals. Each trial begins with a presentation of the CS, followed 500 ms later by the US. Initially, we associate the US with intrinsic reward by setting all synapses projecting from US-specific SEN neurons to their maximum values, such that presentation of the US results in a strong phasic response in the short-latency pathway, from both INT and DA neurons (c.f. Figure 5A). All other modifiable synapses in the network are initialized to their minimum values.
Figure 4.
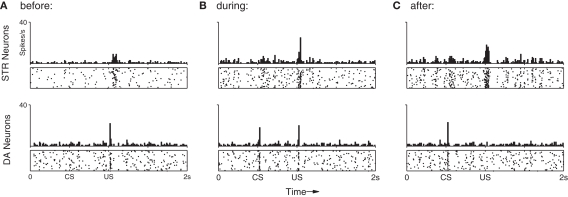
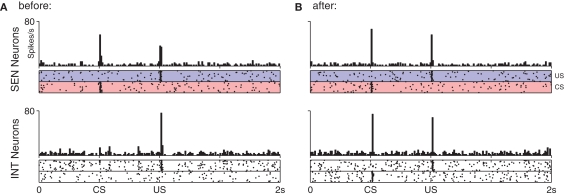
The shift in DA response from US to CS (bottom) relies upon a precisely timed inhibitory signal from STR neurons (top). (A) Before training DA neurons show a strong phasic response to the US only. This results in DA release which activates receptors on STR neurons, increasing their excitability and inducing a transient rise in their spontaneous activity immediately after the US. (B) After 50 trials DA neurons have begun to show a phasic response the CS, while some STR neurons now display well-timed activity immediately prior to the onset of the US, leading to a slight suppression of the response. (C) After 100 trials DA neurons show a strong phasic response to the CS, but not to the US. While excitatory afferents to DA neurons have been conditioned to produce a phasic response to the CS, the STR neurons now fire at exactly the time required to entirely suppress any DA response to the US.
Figure 5.
Response to stimulation in the short-latency pathway before (A) and after (B) conditioning of the CS–US pair. Parallel connectivity in the SEN → INT pathway preserves stimulus-specific regions in the post-synaptic (INT) group. No reduction in response to the US is seen at INT neurons even though plasticity occurs at their synapses.
Typical responses to stimuli via the long-latency pathway are shown in Figure 4. As expected, in the first trial (Figure 4A) the network shows no response to the CS in either DA or STR neurons, but produces a strong phasic DA response to the US. A small increase in STR spike frequency is induced immediately following presentation of the US. This increase is generated by the DA–PSF mechanism, whereby US-induced increases in DA concentration increase the excitability of STR neurons. This causes them to fire post-synaptically with respect to PFC neurons, just after presentation of the US, rendering their afferent synapses available for potentiation by DA–STDP.
Figure 4B shows the response of the network half-way through training. A DA response to the US is still easily identifiable, however, a response to the CS is now also established in the short-latency channel. Consistent with Pan et al. (2005), the simultaneous presence of separate DA responses to both CS and US excludes the possibility of a single response moving in a retrograde manner from US to CS over the course of the training period. Figure 4B also shows a response in STR neurons (upper panel, long-latency pathway) beginning just prior to US onset, eliciting a small inhibitory effect on DA neurons, and leading to a weakened DA response to the US (lower panel). The precise timing of this STR activity is ensured by sustained CS-specific activity in PFC neurons, combined with DA–PSF at STR neurons and DA–STDP at PFC → STR synapses.
After 100 trials the DA response has entirely shifted from the US to the CS (Figure 4C). Modification of synaptic efficacy in the short-latency channel by DA–STDP has led to a strong phasic response to the CS in nearly all DA neurons. Figure 5 shows how this is facilitated by a corresponding increase in CS-specific INT activity. Before conditioning, INT neurons respond only to the US (Figure 5A) whereas after conditioning a response to the CS has also developed (Figure 5B). Significantly, INT neurons maintain a response to the US. However, this no longer leads to DA activation because synaptic plasticity in the long-latency channel has also led to a strong phasic response in STR neurons, just prior to the US. Here the precisely timed wave of inhibition from STR entirely cancels INT activity, to result in the suppression of the previously observed US-specific DA response.
3.2. Response to unexpected rewards
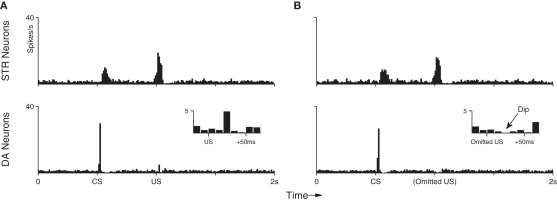
We next examined the behavior of the conditioned network obtained previously (i.e., after 100 trials involving US/CS pairing) to unexpected US presentations (Figure 3). Specifically, we remove the CS from the stimulus pair and present only the US in the 101st trial.
As just described, phasic responses of midbrain DA neurons will shift from US to CS when these stimuli are reliably paired. However, a response to the US will immediately return if the preceding CS is subsequently omitted (Ljungberg et al., 1992). This implies that DA responses do not become insensitive to US-signaled rewards in general. Rather, DA neurons remain sensitive to unpredictable rewards and utilize temporal information from preceding stimuli to actively suppress those which occur predictably. In agreement with in vivo observations (Ljungberg et al., 1992), Figure 3 shows a clear reappearance of the DA response. Reappearance of the DA response occurs in our model because, in the absence of a preceding CS, there is no stimulus-evoked activity in the PFC and therefore no anticipatory activation of inhibitory (STR) neurons prior to US onset (Figure 3, top).
3.3. Depression by reward omission
We next show how the model reproduces the below-baseline dip in DA activity which occurs at the time of a predicted reward, whenever that reward is unexpectedly omitted (Ljungberg et al., 1991). As before, we start with the fully conditioned network (Section 3.1). We now omit the US and present only the CS in the 101st trial; we repeat this procedure 10 times to allow ensemble averaging of DA responses.
Figure 6A shows the average (suppressed) DA response in the final conditioning trial (Section 3.1; trial 100) when both CS and US are presented in sequence for the last time. Here, the DA response to the US has clearly been suppressed (compare with Figure 4). In contrast, Figure 6B shows the DA response to the subsequent CS-only trials. A dip in DA response is clearly identifiable (inset). Importantly, the model captures both the negative (below baseline) response in this situation, as well as the precise timing of that signal. To assess the statistical significance of this dip a further 100 repetitions of the dip-inducing 101st trial were performed on a single fully conditioned network. This procedure yielded an average of 6.28 (σ = 2.65) DA spikes in the 50 ms preceding the US (baseline) compared to just 0.52 (σ = 0.70) in the 50 ms immediate following it; that is, over 2 SD below baseline. The DA response dip occurs in our model because STR neurons continue to exhibit precisely timed responses to the CS (Figure 6, top), however the resulting inhibition does not now encounter any corresponding excitatory signal from INT neurons. The below-baseline dip can be interpreted as a negative prediction-error with respect to the expected US (Schultz, 1998). We note here that repetition of CS-only trials was not investigated in respect of CS response extinction, as we consider that process to involve additional, active, mechanisms (see Pan et al., 2008 for a detailed model of the extinction process).
Figure 6.
Peri-event histograms reveal the dip in DA activity which occurs in response to omitted reward after training. (A) With the US still present, the average neuronal response to the final 10 training presentations of the CS–US pairing demonstrates an STR-mediated suppression of DA activity to near baseline (c.f. Figure 4). (B) Presentation of the CS alone in 10 trials immediately after training elicits the same STR response as in previous trials, but this now leads to a below-baseline suppression of DA activity at precisely the time of the expected (but omitted) US.
3.4. Sensitivity and robustness
To examine robustness, we investigated the model's performance under several perturbations. In each case we measure the mean number of DA spikes to occur in the 50 ms following either US or CS, over 50 runs of the original experiment described in Section 3.1. DA responses are expressed as a percentage of the maximum increase/decrease in mean spike count with respect to the original experiment.
3.4.1. Behavior over a range of ISIs
We first examined performance under different inter-stimulus intervals (ISI) separating US and CS presentations, over the entire range covered by the PFC representation (every 100 ms in the range [100, 900] ms, Figure 7). Consistent with the original experiment (Section 3.1), in each case DA responses to the US are initially strong, and responses to the CS are initially weak. As learning proceeds responses to the CS gradually increase, while responses to the US gradually decrease, asymptoting at 100% of the increase/decrease observed in the original experiment. These observations show that the model is robust across multiple ISIs.
Figure 7.
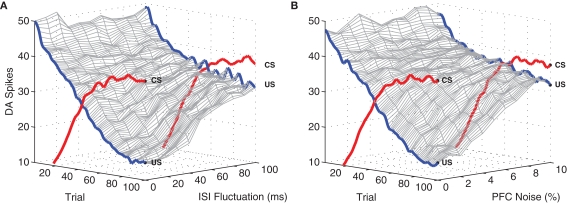
Model performance with respect to multiple ISIs. Here, the number of DA spikes in the 50 ms following stimulation are averaged over 50 simulation runs, for each ISI. Results from nine different ISIs (100–900 in 100 ms steps) are superimposed, demonstrating that development of a CS response and suppression of a US response is independent of any specific ISI. An exception is the extremely short ISI of 100 ms, where suppression of the US begins to break down because of overlap with the CS representation.
3.4.2. Inter-trial variation in ISI
We next examine model performance under inter-trial variation in ISI. For each CS + US presentation, ISI fluctuations were tested within a range of 500 ± [10, 100] ms. DA responses to the US degrade gracefully as inter-trial ISI variation increases (Figure 8A). With variation restricted to the narrower range (±10 ms) DA responses are eventually almost fully suppressed (>85%), as in the original experiment (see Figure 4. At higher levels, relative suppression decreases and CS/US responses become indistinguishable. We note that the manipulation of inter-trial ISI has no effect on DA responses to the CS (i.e., these responses develop as usual). This is expected, since CS responses in the short-latency pathway occur immediately after stimulation and are therefore independent of the ISI.
Figure 8.
Model performance with respect to fluctuating ISI timings and PFC noise. Again, plots show the number of DA spikes in the 50 ms following stimulation, averaged over 50 simulation runs. The data was smoothed with a 100 Hz low-pass (second-order) Butterworth filter. As trial-by-trial fluctuations around the mean ISI (μ = 500 ms) are increased, suppression of the US response undergoes graceful degradation (A). Similarly, performance degrades as the level of noise applied to PFC representations is increased (B). Development of associated CS responses are unaffected by either ISI fluctuation or PFC jitter.
3.4.3. PFC specificity
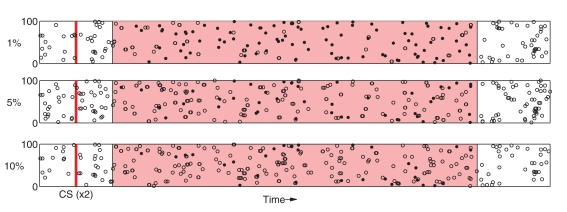
Finally, we examine sensitivity of the model to the specificity of PFC responses to sensory stimuli. At each time-step during stimulation, input to a random subset of stimulus-affected neurons in PFC is driven by the background current ξ instead of the stimulus-specific current pattern C. This has the effect of disrupting spike timing within PFC representations (Figure 9) and leads to significant degradation of the representation beyond 10% input noise.
Figure 9.
Relatively small amounts of noise induces degradation of PFC spike patterns. As in Figure 2, Responses to two separate presentations of the same stimuli are overlayed as dots (spikes are coincident) and open circles (spikes appear in only one response).
Figure 8B shows that model performance degrades gracefully as spike-timing disruption increases. PFC noise was incremented in 1% steps over the range [0%, 10%]. At 5%, DA responses to the US are suppressed by ≈75% as compared to the original experiment, while at above 10% CS and US responses become almost indistinguishable. As before, responses to the CS are unaffected as US suppression degrades. We note (see Figure 9) that 10% noise in PFC input does induce significant degradation of stimulus-specific activity patterns.
4. Discussion
We have described a spiking neural network model of DA activity in which phasic responses are adaptively transferred from primary rewards to earlier, reward-predicting stimuli. The model accounts for a broad range of features including; (i) the shift of the DA response from a US to an earlier predictive CS (Ljungberg et al., 1992; Schultz, 1998; Pan et al., 2005), (ii) the maintenance of a response to unpredicted rewards (Ljungberg et al., 1992), and (iii) the below-baseline suppression of background DA activity in response to omitted rewards (Ljungberg et al., 1991).
Our model combines a dual-path architecture (Brown et al., 1999; Tan and Bullock, 2008) with DA-modulated STDP (Izhikevich, 2007) to provide an integrated account of the neural computations underpinning adaptive DA responses to stimulus-reward contingencies, in the presence of uncorrelated background activity in participating neurons. It predicts specific roles, in this process, for both stimulus-specific temporally extended cortical activity (Goldman-Rakic, 1996; Fuster, 2009) and DA modulation of neuronal excitability (DA–PSF) in striatal neurons efferent to PFC.
4.1. Comparison with previous models
As in the present model, the dual-path models of Brown et al. (1999) and Tan and Bullock (2008) show how prediction-error signals can arise from a mismatch between excitatory and inhibitory pathways. While these models account for a similar range of phenomena as does the present model, they are not designed to do so in the presence of unrelated background activity of stimulus-affected neurons. In these previous models, incoming stimuli give rise to specific activity patterns in striosomal dendrites, however there is no mechanism by which unrelated activity in afferent neurons could be treated differently (i.e., “ignored”) by reward-related plasticity processes. By contrast, our model locates stimulus-specific activity in PFC (afferent to striatum) and incorporates a synaptic tagging mechanism in the plasticity rule, allowing selective synaptic modulation in the presence of irrelevant background (PFC) activity, via DA–STDP (see below). This aspect of our model is important inasmuch as it addresses the so-called “credit assignment” problem (Sutton and Barto, 1998), i.e., the problem of distinguishing between neuronal activity involved in generating a particular behavior or eliciting a particular reward, and other, unrelated, activity. In the context of reinforcement learning, credit assignment is essential to ensure that reward-relevant synapses can be identified, and that reward-unrelated activity of stimulus-affected neurons does not disrupt predictive DA responses.
The model of Izhikevich (2007) was designed to address precisely this credit assignment problem. In this previous model, prediction-error signals arise spontaneously in a network undergoing DA–STDP. The DA–STDP mechanism actively selects against irrelevant, background neural activity, allowing stimulus-specific responses to develop within a network that is neither quiet, nor constrained to respond to some particular set of task-related stimuli. Our model incorporates DA–STDP for just the same purpose. However, Izhikevich's model does not set out to capture the broad range of DA response features exhibited by our model. Unlike our model, Izhikevich's model is not able to reproduce either the below-baseline dip in DA activity observed when an expected reward is omitted (Figure 6), or the reappearance of a DA response to a US when a predictive CS is omitted (Figure 3). This is because Izhikevich's model does not incorporate any form of persistent “working memory” to enable active suppression of DA responses. Instead, the model relies upon spike-timing effects induced by the consecutive presentation of CS and US which have the effect of suppressing DA responses to any US, not just a US predicted by a preceding CS.
In short, by integrating the selective DA–STDP mechanism of Izhikevich (2007) into a dual-path architecture similar to Brown et al. (1999) and Tan and Bullock (2008), our model succeeds in reproducing a full range of reward-related DA responses, under general conditions in which neurons in the network may be concurrently activated outside of their specific task-context.
4.2. Network architecture
Our model is consistent with several features of mammalian cortico-basal anatomy and physiology. Consistent with the long-latency pathway, anatomical studies suggest that cortical signals arrive at DA neurons in the substantia nigra via medium spiny striatal neurons (Voorn et al., 2004). Also, striatal neurons display precisely timed phasic above baseline firing during the waiting period in conditioning tasks (Schultz, 1992). Here we model a subset of the cortico-striatal projection, in which PFC neurons converge on striatal neurons with a ratio of 10:1, consistent with experimental data (Zheng and Wilson, 2002). Consistent with the short-latency pathway, a variety of fast subcortical pathways connect peripheral sensory input to DA neurons. For example, visual input can arrive at DA neurons via the superior colliculus with a latency substantially shorter than the corresponding cortical pathway (McHaffie et al., 2005). In the model presented here, these asymmetric latencies ensure that CS cannot inhibit themselves.
There are multiple alternatives for neural instantiation of the short-latency pathway in our model via different subcortical nuclei; moreover, CS and US signals may flow through different pathways. Because conditioned responses involve plasticity, the corresponding short-latency pathways should undergo DA–STDP. In contrast, signals reflecting intrinsic primary rewards (US) need not involve plasticity mechanisms. Although our model is modality independent, candidate pathways may involve superior colliculus for US signals (Redgrave and Gurney, 2006), and STN for CS signals. In the latter case, STN may be activated directly as part of the so-called “hyperdirect” pathway (Nambu et al., 2002), or indirectly, via a process of disinhibition involving globus pallidus (external) and striatum (Albin et al., 1989).
Our model is consistent with suggestions that competition between excitatory and inhibitory pathways play a significant role in basal ganglia operation (Redgrave and Gurney, 2006), specifically in the generation of DA responses (Brown et al., 1999; Pan et al., 2008; Tan and Bullock, 2008), where their functional significance depends on their latency characteristics. Activity in the long-latency inhibitory channel that suppresses short-latency excitatory inputs to DA neurons can be interpreted as predictive; unsuppressed activity can be considered as a prediction-error. This interpretation is consistent with views of cortical dynamics suggesting that prediction-errors flow in a feedforward (bottom-up) direction, while predictions flow in a feedback (top-down) direction (Friston, 2010).
4.3. PFC activity
In our model, PFC neurons exhibit stimulus-specific temporally extended patterns of activity, enabling inhibitory projections in the striatum (STR) to suppress DA activity at precise times following stimulus offset. This implementation of PFC activity reflects the general role of PFC in working memory (Goldman-Rakic, 1996; Fuster, 2009), and is consistent with the existence of recurring, time-locked cortical spike patterns such as cell assemblies (Hebb, 1949; Harris, 2005), cognits (Fuster, 2009), synfire chains (Abeles, 1982), and polychronous groups (Izhikevich, 2006).
The framework of polychrony, which refers to time-locked but not synchronous activity (Izhikevich, 2006), is most appropriate for understanding the dynamics of our model. At any time post-stimulus (within the 1 s duration of stimulus-evoked activity), a specific and repeatable group of PFC neurons will have just fired, as determined by the corresponding matrix C (Section 2.2). These neurons project convergently and with varying delays to STR neurons. There is therefore a high probability that every such (polychronous) group will project to at least one specific target in STR such that incoming spikes arrive at the same time. By increasing the firing rate of STR targets at just the time of DA release, the DA–PSF mechanism ensures that only those synapses efferent to polychronous groups which fire immediately before US presentation are made available for potentiation via DA–STDP. In contrast to previous models (Brown et al., 1999; Tan and Bullock, 2008) background activity will not affect the specificity of potentiation because such activity will not reliably participate in polychronous grouping. The framework of polychrony therefore allows for selective strengthening of specific cortico-striatal synapses (in this case via DA–STDP), furnishing a mechanism for coincidence detection comparable to that suggested by Lustig et al. (2005). Moreover, the number of potentially coexisting polychronous groups typically far exceeds the number of neurons (Izhikevich, 2006), implying that our model has a very large memory capacity. Polychrony provides a distinctive framework for considering spike timing (Izhikevich, 2007). As compared to synfire chains (Abeles, 1982), polychrony emphasizes time-locked but synchronous activity, and unlike liquid state machines (Maass et al., 2002) polychronous groups exhibit sensitivity to previous inputs.
Prefrontal cortex neurons in our model fire in the range 1–5 Hz independently of whether stimuli are present or absent. Experimental observations, however, show that stimulus-related PFC activity is often in the range 5–20 Hz (Funahashi et al., 1989). We chose to maintain a constant PFC firing rate throughout the experiment in order to ensure that the influence of PFC on DA responses must be due to precise spike-timing patterns and cannot be explained by firing rate transitions at stimulus onset or offset, therefore validating the interpretation of our model in terms of polychronous groups. Future work will address firing rate transitions in explicit models of recurrent PFC activity (Szatmary and Izhikevich, 2010) in the context of DA-modulated plasticity.
4.4. Dopaminergic neuromodulation
Dopamine modulation of both STDP (Fino et al., 2005; Pawlak and Kerr, 2008; Shen et al., 2008; Di Filippo et al., 2009) and neuronal excitability (Nicola et al., 2000; Williams and Castner, 2006) have been reported for cortico-striatal projections. Both types of modulation are incorporated in our model.
4.4.1. Dopamine modulation of spike-timing dependent synaptic plasticity
Spike-timing dependent synaptic plasticity can take many forms, including both Hebbian (potentiation when post-synaptic activity follows pre-synaptic activity) and anti-Hebbian (the converse; Dan and Poo, 2004; Fino et al., 2005; Shen et al., 2008). We chose to implement the Hebbian form of DA–STDP, which has the network-level effect of increasing (decreasing) synaptic strengths under high (low) DA concentrations (Izhikevich, 2007). Because low DA concentrations tend to occur during random background activity, whereas high DA concentrations tend to occur immediately following stimulation, this mechanism results in weak long-term-depression (LTD) over prolonged periods of low (background) DA activation and strong long-term-potentiation (LTP) during brief periods of high (stimulus-evoked) DA activation, consistent with in vitro studies (Shen et al., 2008).
Dopamine modulation of spike-timing dependent synaptic plasticity depends on “eligibility traces,” implemented at each synapse as a simulated enzyme assumed to be important to plasticity (Izhikevich, 2007)2. Pre- and post-synaptic activity induces discrete changes in the concentration of this enzyme, which otherwise decays exponentially. DA modulates the extent to which this enzyme induces late LTP/LTD, thereby enabling DA-modulated plasticity to occur at synapses whose pre/post activity occur in the few ms prior to reward.
In our model, DA–STDP enables modification of SEN → INT synapses in the short-latency channel. Specifically, CS-induced (pre-synaptic) activity at SEN neurons is coupled with DA release at the time of the US (via eligibility traces) in the presence of stochastic, low-frequency (post-synaptic) INT activity, to induce plasticity in all synapses efferent to CS-specific SEN neurons. By this mechanism, repeated CS–US presentations lead to CS-specific responses in both INT and DA neurons (Ljungberg et al., 1992). In the PFC → STR pathway, DA–STDP is coupled with DA–PSF to induce plasticity (see below).
As mentioned, multiple forms of plasticity have been observed in the cortico-basal loop, especially in the prefrontal-striatal pathway (Dan and Poo, 2004; Fino et al., 2005; Shen et al., 2008). While in the present work we focus on the common Hebbian form, future work will address the interaction of alternative forms with DA modulation at the various timescales at which it has been shown to operate (Schultz, 2007).
4.4.2. Dopamine modulated post-synaptic facilitation
Modulation of neuronal excitability has been demonstrated in a variety of studies both in vitro and in vivo (see Nicola et al., 2000; Williams and Castner, 2006 for reviews). DA has a facilitatory effect on some but not all striatal neurons, specifically those receiving highly convergent synaptic input (Gonon, 1997), suggesting a process of DA–PSF. However as with DA–STDP, the precise mechanisms underpinning the observed phenomenology are not well understood. We implement DA–PSF here with a simple mechanism ensuring that DA up-regulates the excitability of STR neurons. As described in Section 2.5, this is accomplished by allowing DA to modulate the abstract parameter b, in the neuron model of Izhikevich (2007).
In our model, the modulation of neuronal excitability provides a temporal reference, contextualizing the effects of DA–STDP. That is, DA–PSF increases (post-synaptic) STR firing immediately after reward, therefore increasing the number synapses in the PFC → STR pathway that may be potentiated by DA–STDP. Because DA–STDP selects against non-specific firing in the PFC the combined DA–PSF/STDP mechanism allows stimulus-specific sub-groups of cortico-striatal synapses to be selectively reinforced in response to DA rewards.
In more detail, the mechanism operates as follows. When a US arrives the DA–PSF mechanism causes a phasic increase in STR activation. When reliably paired with a CS, the sub-population of (PFC → STR) synapses targeted by DA–STDP will be specific to that CS. Non-CS affected neurons continue to fire randomly with respect to increased STR activity and are therefore not targeted by DA–STDP. Over several trials, the STR response undergoes a retrograde shift, from just after the US, to just before it (Figure 4). The corresponding wave of inhibition accounts for the suppression of the DA response to the US. Importantly, STR activity in late trials does not occur in response to any US-induced DA–PSF (the US no longer elicits a DA response) but instead responds to specific CS-induced PFC activity. This process is inherently self-limiting; as the DA response extinguishes, both DA–PSF and DA–STDP shut off, STR activity ceases to regress, and suppression of the DA response is maintained at precisely the expected time of the US.
Modulation of neuronal excitability by DA–PSF enables DA–STDP to influence pathways that do not project directly onto DA neurons (i.e., the PFC → STR pathway). By modulating the excitability of post-synaptic neurons, this mechanism influences the relative firing rates of pre- and post-synaptic neurons, which in turn affects STDP. This mechanism ensures that DA responses to separate stimuli do not interfere at DA neurons, allowing multiple stimulus-response mappings to be maintained concurrently in the network (e.g., the CS response is maintained concurrently with the US response).
4.5. Predictions
Our model generates a number of predictions regarding DA responses in time-delayed reinforcement learning situations.
First, timely disruption of the phasic DA signal should impede learning of novel CS–US contingencies while having little effect on previously learned responses. This prediction arises because, in our model, phasic DA responses to a CS are not required for expression of previously learned responses, however phasic responses to the US are necessary for the induction of cortico-striatal plasticity underlying the acquisition of conditioned responses. To our knowledge, current evidence does not directly address this prediction, though it is consistent. Pharmacological disruption of DA receptor function in striatum does modulate cortico-striatal STDP (e.g., Fino et al., 2005; Shen et al., 2008 and see Di Filippo et al., 2009 for a review), yet it is still unclear exactly how phasic and tonic DA release differentially interact with other neurotransmitters to modulate plasticity in this pathway.
A second prediction, arising from the DA–PSF mechanism, is that during early conditioning trials a small increase in striatal activity should occur immediately after presentation of the US. Also, as learning progresses, this response should increase in strength and undergo a continuous retrograde shift (in virtue of DA–STDP) settling just prior to the US. This prediction furnishes a very specific test of the validity of our model. To our knowledge, existing studies have investigated striatal activity during delayed response tasks (Schultz, 1992, 1998) and have recorded the development of these signals during learning (Schultz, 2003). However, these recordings are often sparse (i.e., of only a few neurons, possibly masking ensemble activities) and do not report with sufficient temporal precision to directly evaluate our predictions.
Finally, we predict that disruption of stimulus-evoked prefrontal cortical activity [e.g., either pharmacologically or via transcranial magnetic stimulation (TMS)] during the delay period will disrupt the subsequent suppression of DA responses to the US. Current evidence shows that TMS to PFC can impede behavioral performance in delayed response tasks (Pascual-Leone and Hallett, 1994). To our knowledge, influence on DA responses in such situations have not been assessed. Our model would predict, in such cases, that previously suppressed DA responses would reappear, following PFC disruption. More generally, the dependence of our model on polychronous PFC activity raises the possibility that DA responses could be affected by fine-grained manipulation of PFC firing patterns, for example by micro-stimulation of PFC neurons.
4.6. Future work
The computational model described in this paper has provided an integrated account of cortico-basal neural computations accounting for a broad range of DA responses in reinforcement learning paradigms.
Our model has focused on combining competitive excitatory and inhibitory pathways with mechanisms of synaptic plasticity (DA–STDP) and post-synaptic facilitation (DA–PSF). Its results encourage a more detailed investigation of the biophysical properties of these mechanisms. For example Humphries (2009) describe a more accurate reduced model of DA-modulated striatal medium spiny neuron (MSNs) function which could be integrated into our own framework.
An additional key component of the model is the stimulus-specific and temporally extended (polychronous) PFC activity. However, in the present formulation we directly specified this activity using pre-computed activity patterns drawn from the same statistical distribution as random background activity. In future work, we intend to examine possible mechanisms underlying the generation of sustained, irregular, and repeatable activity patterns over a range of firing rates, that are consistent with prefrontal cortical anatomy and dynamics. We also hope to investigate the interaction of these mechanisms with the features of DA signaling described in the present work, specifically the interaction of DA signaling with self-sustained, above-baseline pre- and post-synaptic neural activity. Initial work in this direction suggests that DA plays a role in the stabilization of PFC representations (Durstewitz et al., 2000) and may implement a global feedback signal involved in maintaining PFC dynamics at a state comparable to self-organized criticality (Stassinoploulos and Bak, 1995).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Paul Chorley is supported by EPSRC doctoral studentship EP/C537912/1. Anil K. Seth is supported by EPSRC Leadership Fellowship EP/G007543/1 and by a donation from the Dr. Mortimer and Theresa Sackler Foundation.
Footnotes
1We omit detailed inter-group heterogeneity of neuron types (e.g., Medium spiny neurons in STR are modeled in the same way as pyramidal neurons in PFC) as this provides a significant reduction in computational overhead. Future work will address the issue of heterogeneity more fully (see Section 4.6).
2This enzyme could reflect autophosphorylation of CaMK-II, oxidation of PKC or PKA, or some other relatively slow process (Izhikevich, 2007).
References
- Abeles M. (1982). Local Cortical Circuits: An Electrophysiological Study. Berlin: Springer [Google Scholar]
- Albin R. L., Young A. B., Penney J. B. (1989). The functional anatomy of basal ganglia disorders. Trends Neurosci. 12, 366–375 10.1016/0166-2236(89)90074-X [DOI] [PubMed] [Google Scholar]
- Brown J., Bullock D., Grossberg S. (1999). How the basal ganglia use parallel excitatory and inhibitory learning pathways to selectively respond to unexpected rewarding cues. J. Neurosci. 19, 10502–10511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dan Y., Poo M. (2004). Spike timing-dependent plasticity of neural circuits. Neuron 44, 23–30 10.1016/j.neuron.2004.09.007 [DOI] [PubMed] [Google Scholar]
- Di Filippo M., Picconi B., Tantucci M., Ghiglierib V., Bagettab V., Sgobiob C., Tozzia A., Parnetti L., Calabresia P. (2009). Short-term and long-term plasticity at corticostriatal synapses: implications for learning and memory. Behav. Brain Res. 199, 108–118 [DOI] [PubMed] [Google Scholar]
- Ding M., Chen Y., Bressler S. (2006). Granger Causality: Basic Theory and Application to Neuroscience. Handbook of Time Series Analysis. Wienheim: Wiley, 438–460 [Google Scholar]
- Durstewitz D., Gabriel T. (2007). Dynamical basis of irregular spiking in NMDA-driven prefrontal cortex neurons. Cereb. Cortex 17, 894–908 [DOI] [PubMed] [Google Scholar]
- Durstewitz D., Seamans J. K., Sejnowski T. J. (2000). Dopamine-mediated stabilization of delay-period activity in a network model of prefrontal cortex. J. Neurophysiol. 83, 1733–1750 [DOI] [PubMed] [Google Scholar]
- Fino E., Glowinski J., Venance L. (2005). Bidirectional activity-dependent plasticity at corticostriatal synapses. J. Neurosci. 25, 11279–11287 10.1523/JNEUROSCI.4476-05.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K. (2010). The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127–138 [DOI] [PubMed] [Google Scholar]
- Funahashi S., Goldman-Rakic P. S. (1989). Mnemonic coding of visual space in the monkey's dorsolateral prefrontal cortex. J. Neurophysiol. 61, 331–349 [DOI] [PubMed] [Google Scholar]
- Fuster J. M. (1972). Cortex and memory: emergence of a new paradigm. J. Cogn. Neurosci. 21, 2047–2072 [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic P. S. (1996). Regional and cellular fractionation of working memory. Proc. Natl. Acad. Sci. U.S.A. 93, 473–480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonon F. (1997). Prolonged and extrasynaptic excitatory action of dopamine mediated by D1 receptors in the rat striatum in vivo. J. Neurosci. 17, 5972–5978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris K. D. (2005). Neural signatures of cell assembly organization. Nat. Rev. Neurosci. 6, 399–407 [DOI] [PubMed] [Google Scholar]
- Hazy T. E., Frank M. J., O'Reilly R. C. (2010). Neural mechanisms of acquired phasic dopamine responses in learning. Neurosci. Biobehav. Rev. 34, 701–720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hebb D. (1949). The Organization of Behavior. New York: Wiley and Sons [Google Scholar]
- Humphries M. D., Lepora N., Wood R., Gurney K. (2009). Capturing dopaminergic modulation and bimodal membrane behaviour of striatal medium spiny neurons in accurate, reduced models. Front. Comput. Neurosci. 3:26. 10.3389/neuro.10.026.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyland B. I., Reynolds N. J., Hay J., Perk C. G., Miller R. (2002). Firing modes of midbrain dopamine cells in the freely moving rat. Neuroscience 114, 475–492 10.1016/S0306-4522(02)00267-1 [DOI] [PubMed] [Google Scholar]
- Izhikevich E. M. (2003). Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572 10.1109/TNN.2003.820440 [DOI] [PubMed] [Google Scholar]
- Izhikevich E. M. (2006). Polychronization: computation with spikes. Neural Comput. 18, 245–282 10.1162/089976606775093882 [DOI] [PubMed] [Google Scholar]
- Izhikevich E. M. (2007). Solving the distal reward problem through linkage of STDP and dopamine signaling. Cereb. Cortex 17, 2443–2452 [DOI] [PubMed] [Google Scholar]
- Ljungberg T., Apicella P., Schultz W. (1991). Responses of monkey dopamine neurons during delayed alternation performance. Brain Res. 567, 337–341 10.1016/0006-8993(91)90816-E [DOI] [PubMed] [Google Scholar]
- Ljungberg T., Apicella P., Schultz W. (1992). Responses of monkey dopamine neurons during learning of behavioural reactions. J. Neurophysiol. 67, 145–163 [DOI] [PubMed] [Google Scholar]
- Lustig C., Matell M. S., Meck W. H. (2005). Not ‘just’; a coincidence: frontal-striatal interactions in working memory and interval timing. Memory 13, 441–448 10.1080/09658210344000404 [DOI] [PubMed] [Google Scholar]
- Maass W., Natschlager T., Markram H. (2002). Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 14, 2531–2560 10.1162/089976602760407955 [DOI] [PubMed] [Google Scholar]
- McHaffie J. G., Stanford T. R., Stein B. E., Coizet V., Redgrave P. (2005). Subcortical loops through the basal ganglia. Trends Neurosci. 28, 401–407 10.1016/j.tins.2005.06.006 [DOI] [PubMed] [Google Scholar]
- Nambu A., Tokuno H., Takada M. (2002). Functional significance of the cortico-subthalamo-pallidal ‘hyperdirect’ pathway. Neurosci. Res. 43, 111–117 [DOI] [PubMed] [Google Scholar]
- Nicola S. M., Surmeier J., Malenka R. C. (2000). Dopaminergic modulation of neuronal excitability in the striatum and nucleus accumbens. Annu. Rev. Neurosci. 23, 185–215 [DOI] [PubMed] [Google Scholar]
- Pan W., Schmidt R., Wickens J. R., Hyland B. I. (2005). Dopamine cells respond to predicted events during classical conditioning: evidence for eligibility traces in the reward-learning network. J. Neurosci. 26, 6242–6235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W., Schmidt R., Wickens J. R., Hyland B. I. (2008). Tripartite mechanism of extinction suggested by dopamine neuron activity and temporal difference model. J. Neurosci. 28, 9619–9631 10.1523/JNEUROSCI.0255-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual-Leone A., Hallett M. (1994). Induction of errors in a delayed response task by transcranial magnetic stimulation of the dorsolateral prefrontal cortex. Neuroreport 5, 2517–2520 10.1097/00001756-199412000-00028 [DOI] [PubMed] [Google Scholar]
- Pawlak V., Kerr J. N. (2008). Dopamine receptor activation is required for corticostriatal spike-timing-dependent plasticity. J. Neurosci. 28, 2435–2446 10.1523/JNEUROSCI.4402-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redgrave P., Gurney K. (2006). The short-latency dopamine signal: a role in discovering novel actions? Nat. Rev. Neurosci. 7, 967–975 [DOI] [PubMed] [Google Scholar]
- Redgrave P., Gurney K., Reynolds J. (2008). What is reinforced by phasic dopamine signals? Brain Res. Rev. 58, 322–339 [DOI] [PubMed] [Google Scholar]
- Schultz W. (1992). Neuronal activity in monkey ventral striatum related to the expectation of reward. J. Neurosci. 12, 4595–4610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W. (1998). Predictive reward signal of dopamine neurons. J. Neurophysiol. 80, 1–27 [DOI] [PubMed] [Google Scholar]
- Schultz W. (2003). Changes in behavior-related neuronal activity in the striatum during learning. Trends Neurosci. 26, 321–328 10.1016/S0166-2236(03)00122-X [DOI] [PubMed] [Google Scholar]
- Schultz W. (2007). Multiple dopamine functions at different time courses. Annu. Rev. Neurosci. 30, 259–288 [DOI] [PubMed] [Google Scholar]
- Schultz W., Romo R. (1990). Dopamine neurons of the monkey midbrain – contingencies of responses to stimuli eliciting immediate behavioral reaction. J. Neurophysiol. 63, 607–624 [DOI] [PubMed] [Google Scholar]
- Shen W., Flajolet M., Greengard P., Surmeier D. J. (2008). Dichotomous dopaminergic control of striatal synaptic plasticity. Science 321, 848–851 10.1126/science.1160575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Softky W. R., Koch C. (1993). The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 13, 334–350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stassinoploulos D., Bak P. (1995). Democratic reinforcement: a principle for brain function. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 51, 5033–5039 [DOI] [PubMed] [Google Scholar]
- Sutton R. S., Barto A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press [Google Scholar]
- Szatmary B., Izhikevich E. M. (2010). Spike-timing theory of working memory. PLoS Comput. Biol. 6, 20808877. 10.1371/journal.pcbi.1000879 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan C. O., Bullock D. (2008). A local circuit model of learned striatal and dopamine cell responses under probabilistic schedules of reward. J. Neurosci. 28, 10062–10074 10.1523/JNEUROSCI.0259-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voorn P., Vanderschuren L. J. M. J., Groenewegen H. J., Robbins T. W., Pennartz C. M. A. (2004). Putting a spin on the dorsal-ventral divide of the striatum. Trends Neurosci. 27, 468–474 10.1016/j.tins.2004.06.006 [DOI] [PubMed] [Google Scholar]
- Williams G. V., Castner S. A. (2006). Under the curve: critical issues for elucidating D1 receptor function in working memory. Neuroscience 139, 263–276 10.1016/j.neuroscience.2005.09.028 [DOI] [PubMed] [Google Scholar]
- Zheng T., Wilson C. J. (2002). Corticostriatal combinatorics: the implications of cortico-striatal axonal arborizations. J. Neurophysiol. 87, 1007–1017 [DOI] [PubMed] [Google Scholar]