Summary
NMR paramagnetic relaxation enhancement (PRE) measures long-range distances to isotopically labeled residues, providing useful constraints for protein structure prediction. The method usually requires labor-intensive conjugation of nitroxide labels to multiple locations on the protein, one at a time. Here a computational procedure, based on protein sequence and simple secondary structure models, is presented to facilitate optimal placement of a minimum number of labels needed to determine the correct topology of a helical transmembrane protein. Test on DsbB (4 helices) using just one label leads to correct topology prediction in four of five cases, with the predicted structures <6Å to the native structure. Benchmark results using simulated PRE data show we can generally predict correct topology for five and six-to-seven helices using two and three labels, respectively, with an average success rate of 76% and structures of similar precision, showing promises in facilitating experimentally constrained structure prediction of membrane proteins.
Keywords: transmembrane helical protein, helix packing topology, solution NMR, paramagnetic relaxation enhancement, distance geometry, structure prediction
Introduction
Transmembrane (TM) proteins play central roles in cellular transport processes, intercellular signaling, and growth regulation (Roosild et al. 2005). They comprise about 60% of all drug targets (Yildirim et al. 2007). Two fold classes have been observed for TM proteins: α-helical bundles and β-barrels, where α-helical proteins are substantially more abundant than β-barrel proteins with the latter largely limited to bacterial outer membrane proteins and their relatives (Koebnik et al. 2000). In humans, approximately 27% of all proteins are TM helical proteins (Almen et al. 2009) but only 1.6% of the determined structures (1,058 out of 65,075) in the PDB (Berman et al. 2000) (May 5th, 2010) are TM helical proteins, 226 of which are unique (Lomize et al. 2006). The scarcity of the TM helical structures reflects the difficulty in determining such protein structures using techniques such as X-ray crystallography or nuclear magnetic resonance (NMR) (Wiener 2004). The methods presented here attempt to facilitate solution NMR structure determination of membrane proteins by combining efficiently chosen small numbers of experimental constraints with computational structure prediction.
Solution NMR has only recently been used to determine the structures of polytopic helical membrane proteins. Successful examples of application, such as the structure determination of E. coli proteins DsbB (Zhou et al. 2008b) and DAGK (Van Horn et al. 2009), complement structures of oligomeric complexes of single pass TM helices in phospholamban (Oxenoid and Chou 2005; Traaseth et al. 2007) and the M2 viral protein (Marassi and Opella 2000; Nishimura et al. 2002; Cady and Hong 2008; Schnell and Chou 2008) determined using both solution and solid-state NMR methods. Because of the nature of membrane proteins, a combination of multiple sources of data is generally required to solve TM helical protein structures. In the cases of both DsbB and DAGK, extensive paramagnetic relaxation enhancement distance constraints, residual dipolar coupling data, and long-range NOEs were collected and used for solving the structures.
In the past few years, computational structure-prediction methods have improved to a point where predicted structures based on limited experimental data, possibly of low-resolution, become fairly useful for studying protein functions and associated mechanisms (Kang et al. 2008; Barth et al. 2009). Oftentimes a low-resolution structure is useful enough as it can serve as a starting point for more accurate structure determination using additional computational techniques. Barth et al. showed that, when coarse-grained decoy structures with near-native topologies (<4Å ) were generated, de novo methods can predict high-resolution structures (<2.5Å) for TM helical proteins with up to 145 residues (Barth et al. 2007). The major challenge in applying this approach for larger systems is in developing effective sampling procedures to consistently generate near-native topologies at a coarse-grained level. Our focus in this study is to develop a computational strategy that identifies a minimal set of NMR data that will be adequate to determine the correct packing topology of TM helical proteins.
Paramagnetic relaxation enhancement (PRE) can provide long range distance constraints (15–25Å) between a paramagnetic center and an NMR active nucleus such as a proton attached to a 15N or 13C enriched site (Bertini et al. 2001; Bertini et al. 2005; Otting 2010). Application of these constraints began with proteins that have native paramagnetic metal centers, but application has recently expanded with the use of cysteine mutagenesis and site-directed spin-labeling (SDSL) of cysteine sites with nitroxide labels (Cornish et al. 1994; Hubbell and Altenbach 1994; Battiste and Wagner 2000; Liang et al. 2006; Clore et al. 2007). While direct interaction between NMR active nuclei (NOEs) provides distance information that rarely goes beyond 5–6 Å, the much larger interaction energy between an electron and a nucleus makes PRE effective at significantly longer distances. For example, perturbation of proton spin relaxation rates by a nitroxide spin label can yield distance constraints of 15 to 25 Å with accuracies approaching ±15%. Thus PRE can be particularly helpful in determining the global fold of perdeuterated polypotic TM helical proteins.
There are a number of challenging issues associated with using this strategy for structure determination of TM helical proteins. Sample preparation is a major issue, including finding an expression system for producing a sufficient amount of isotopically labeled protein, solubilizing and refolding the protein in detergent micelles or other membrane mimetics, and dealing with the properties of the mimetics and the protein during purification. All of these together can make the production of a membrane protein sample a very lengthy process (Mobley et al. 2007).
In this study, we present a computational method for suggesting a minimal set of mutation sites in a given protein sequence for PRE data collection. The method is based on a theoretical analysis and it is validated through a computational study using a distance geometry-based algorithm. DsbB, a membrane protein with four TM helices is chosen as a test system; both a crystal structure and PRE data from nine Cysteine sites are available for this protein (Inaba et al. 2006; Zhou et al. 2008b). We demonstrate that it is possible to determine the correct packing topology by using PRE data collected on one specific Cysteine-mutation site or any two Cysteine-mutation sites within the protein if they are at the ends of helices and on the same side of the membrane. Using simulated PRE data, we extend the study to ten proteins ranging from 4 to 7 TM helices and with diverse topologies. The correct topology can be determined reliably for proteins with up to seven helices using PRE data collected on two or three sites, predicted by our program. These results show promise in predicting a minimal set of mutational sites needed for PRE data collection; this in turn can guide experimental design and improve efficiency of membrane protein structure determination.
Theoretical Analysis
3-D topology determination can be simplified to a 2-D problem
The two-step model for helix-bundle membrane protein folding (Popot and Engelman 1990) has been a general paradigm for membrane protein structure prediction. In the first step, independently stable helices are formed across the membrane bilayer. In the second, the helices optimally pack to form the final structure. Prediction of the boundaries of the TM helices and the helical orientation (i.e. which helix termini reside at the cytoplasm side of the membrane surfaces) from sequence, the first challenge, has achieved a better than 90% accuracy (Rost et al. 1996; Fleishman and Ben-Tal 2006). In this study, we focus on the second challenge, correctly packing the TM helices. We assume that the helices are ideal, i.e., they have no kinks. A further simplification is made that a helix can be treated as a symmetric cylinder when discussing PRE data collection. This is justified in that the helical backbone radius is around 3 Å while the measurement error of PRE can be of this magnitude or larger, especially for large proteins. Therefore PRE is not particularly sensitive to rotations around the helical axis. Despite the relatively low accuracy, the long-distance nature of PRE data makes it useful for defining the global topology of a polytopic helical membrane protein.
In the following, we assume that the helices are parallel and nearly perpendicular to the membrane surface. Therefore, the problem of finding the relative positions of n helices is reduced to identifying the geometry of the n termini on a plane. The lengths of the loops are also assumed to be long enough not to be a determinant of helix packing. The PRE spin labels will be attached to Cysteines at the ends of helices as the introduction of Cysteine mutations and nitroxide labels in the middle of helices are more likely to disrupt the structure. We are using PRE data to distinguish only among non-mirror structures since the pair-wise distance information is unable to distinguish mirror structures.
Four-helix bundles pack in a rhombus shape
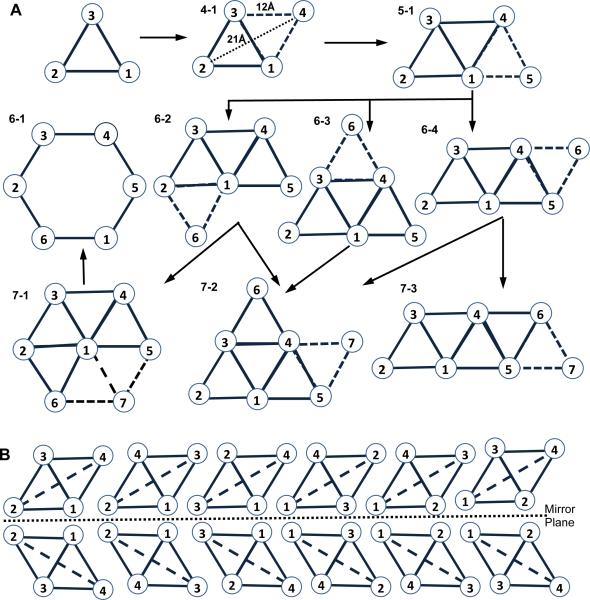
We first investigate the minimal number of PRE data needed for accurately packing a four-helix bundle, which consists of a simple structure motif and serves as a building block for more complex topologies consisting of more helices. In a non-channel forming helical bundle, helices will generally maximize interactions with other helices forming pair-wise interactions with two to six other helices (Harris et al. 1994). For four helices this generally implies a rhombus packing topology, where every pair of neighboring helices on the sides of a rhombus interact and the helices on the opposite sides of the short rhombus diagonal also interact with each other. Statistical analyses of helix-packing motifs in membrane proteins indicate that interacting helix pairs are in general approximately vertical to the membrane surface and are nearly parallel to one another with an average crossing angle of 151° (Walters and DeGrado 2006). In the core region they have an average inter-helical distance of 9 Å. Using the above crossing angle and assuming the length of a TM helix to be 30 Å, an average distance of 11–12 Å can be derived between the ends of two interacting helices on the same side of the membrane. Thus, the layout of a four-helix bundle on any side of the membrane can be modeled as an ideal rhombus, where the sides and the short diagonal are 12 Å and the long diagonal is about 21 Å (Figure 1A). To see how well the model superimposed on real structures, we constructed a 3-D model using ideal helices, which are parallel to each other and perpendicular to the membrane surface, assuming the correct helical arrangement. Structural alignment of the 3-D rhombus model to five unique four-helix bundles in our benchmark set, namely DsbB (2hi7B), ligand gated ion channel (2vl0A), Lekotriene C4 synthase (2uuhA), V-type Sodium ATPase (2bl2A), and Particulate Methane Monooxygenase (1yewC), shows the model has an RMSD over the Cα atoms to the natives at 4.1 Å, 3.9 Å, 5.0 Å, 3.3 Å, and 4.4 Å, respectively. Thus, we base the following analysis on this model.
Figure 1. Geometric models for the layouts of 4–7 helix bundles.
The view is from either side of the membrane. (A) The models for 4–7 helix bundles, derived by adding one helix at a time to the models of the previous set and assuming each new helix must interact with at least two existing helices. The one exception to this rule, the model 6–1 for six-helix channel, is generated by removing a central helix from 7–1 of the seven-helix models. (B) The 12 helix packing topologies forming 6 pairs of mirror images for the rhombus model of a 4-helix bundle.
One to two labels can determine packing topology of a four-helix bundle
For the four points forming a rhombus, there are 12 possible helix-packing topologies consisting of 6 pairs of mirror structures (Figure 1B). We now examine how to use PRE data to distinguish among the 6 pairs. The long diagonal of each rhombus has a unique distance different from all the other distances within the rhombus, i.e., 21Ǻ in this case. For example, in Figure 1B this distance is the distance between the helix termini 2 and 4 in the first model. Placement of a PRE spin-label on either of these two sites would provide the unique distance of 21Ǻ to an NMR observable nucleus at the other site, thus allowing for the identification of the topology. The other two sites, 1 and 3, can only provide the non-unique distances of 12Ǻ. Since only two of the four sites for PRE spin labeling have a 21Ǻ distance, one has 50% of chance to pick a site that will allow for the unique determination of the correct topology.
In the event when the first PRE label is not placed on a helix at one end of the long diagonal, the placement of a second label at the end of any helix on the same side of the membrane will allow for identification of the correct topology, regardless whether the second label provides the 21Ǻ distance measure (hence unique) or just a set of 12Ǻ distance measures. In the latter case, the two involved helices are on the opposite sides of the short diagonal and therefore the other two helices must be on the opposite sides of the long diagonal.
We conclude that we can uniquely determine the correct topology out of the six possible topologies with a 50% probability of success based on a placement of one PRE label and with a 100% probability of success based on placement of two PRE labels, as long as the labels are placed on the same side of the membrane. Restriction to the same side is easily done knowing the connectivity of TM helices in the protein sequence.
Five to seven helical bundles have one to three compact packing shapes
The analysis was extended to up to seven helix bundles since there is so much interest in seven helix GPCRs. Getting the PRE data may be feasible for seven helix bundles but will become increasingly more difficult as the number goes up, since expressing a protein at levels necessary for structural work is still a major hurdle for studying large membrane proteins (Mobley et al. 2007). At the same time, seven helix bundles may represent the upper limit for current membrane protein structure prediction methods (Barth et al. 2009). We observed in solved structures that helix bundles with more than 4 helices have rhombus-shape substructures, and most helices interact with at least two other helices from either the same protein monomer or other protein subunits. This motivated us to build the topologies for proteins with a higher-number of helices by adding one helix at a time to the rhombus-based models, assuming each new helix interacts with at least two existing helices. Figure 1A shows all possible geometric models for the layouts of five to seven helical bundles, as viewed from either side of the membrane. There is one exception to this rule, a six-helix channel, 6-1, which can be generated by removing a central helix from 7-1 of the seven helix models. Each model has a number of permutations of helix order (Table 1).
Table 1.
Theoretical analysis of the minimal number of mutation sites needed to determine the correct packing topology for 4–7 helix bundles
| Model | pairs of mirror topologies | Minimal sites needed: %combination | Minimal+1 Sites: %combination | Optimal sites |
|---|---|---|---|---|
| 4-1 | 6 | One: 2, 4 2 out of 4: 50% |
Two: any combination 6 out of 6: 100% |
2 or 4 Top 1 exposed helix |
| 5-1 | 60 | Two: 3+4, 2+5, 2+3, 4+5, (1+5, 1+2) 4–6 out of 10: 40–60% |
Three: any combination 10 out of 10: 100% |
2+5 Top 2 exposed helices |
| 6-1 | 60 | Two: 6 pairs like 2+4, (6 adjacent pairs like 2+3) 6–12 out of 15: 40–80% |
Three: any combination 20 out of 20: 100% |
Any two helices separated by 21Å |
| 6-2 | 360 | Two: 3+4, 2+3, 5+6 (4+5, 2+6) 3–5 out of 15: 20–33% |
Three: any non-collinear, excluding (or not) 4+5+1, 2+6+1. 16–18 out of 20: 80–90% |
5+6 Top 2 exposed helices |
| 6-3 | 120 | Two: 3 pairs like 2+5, (6 adjacent pairs like 2+1) 3–9 out of 15: 20–60% |
Three: any combination 20 out of 20: 100% |
2+5 Top2 exposed helices |
| 6-4 | 180 | Two: (3+6, 2+5, 2+6, 6 adjacent pairs like 3+4) 0–9 out of 15: 0–60% |
Three: any combination, except for (or not) 1+2+6, 1+5+6, 2+4+3, 2+4+6 16–20 out of 20: 80–100% |
2+6 Top 2 exposed helices |
| 7-1 | 420 | Two: (6 adjacent pairs) 0–6 out of 21: 0–29% |
Three: Any non-collinear combination except for (or not) 6 combinations like 1+2+3. 26–32 out of 35: 74–91% |
Any two helices separated by 21 Å, excluding the most buried helix, |
| 7-2 | 2520 | Two: (2+5, 2+7, 2+6, 1+5, 3+6, 3+2) 0–6 out of 21: 0–29% |
Three: Any combination except for 1+2+4, 4+5+6, 4+3+7, excluding (or not) 2+7+4, 2+7+1, 2+6+4, 2+6+3, 1+5+7, 3+6+4, 3+6+7, 3+2+4,5+6+7, 4+5+7, 4+6+7 21–32 out of 35: 60–91% |
2+6+(7) Top 3 exposed helices |
| 7-3 | 2520 | Two: (3+6, 3+4, 4+6, 1+5, 1+2, 5+7) 0–6 out of 21: 0–29% |
Three: Any combination without 2 or 7 except for 1+3+5, 1+5+6, plus 1+2+4, 1+2+7, 5+2+7, 5+4+7, 2+4+5, 1+4+7; (Any combination except for 2+4+7, 2+3+5, 1+6+7) 14–32 out of 35: 40–91% |
3+6 3rd and 4th most exposed helices |
The codes in “Model” column correspond to those in Figure 1A. The number of pairs of mirror topologies is derived as follows: a model with n-fold symmetry (rotation by 360°/n results in a molecule indistinguishable from the original) has m!/n topologies and m!/(2n) pairs of mirror images (m is the number of helices). In the 3rd and 4th columns, the combinations not in parentheses are obtained assuming the distances 21 Å and 24 Å are indistinguishable by PRE, while the combinations in parentheses are obtained assuming they are distinguishable. The percentage of combinations ranges between the values obtained by these two criteria. The optimal sites are the minimal number of sites that can correctly determine topology and are not adjacent to each other.
Adding one helix to the rhombus model with four helices leads to an isosceles trapezoid model for five-helix bundles. Besides the interactions between every pair of neighboring helices, the helix at the midpoint of the long base also interacts with the helices at both ends of the short base to form stable packing. Visual inspection of the benchmark protein structures indicates that the layouts of all five-helix bundles on any side of the membrane resemble this shape. There are 60 pairs of possible mirror topologies for this model (see Table 1 legend for detailed explanations of this and the numbers for other models). Adding one helix to the isosceles trapezoid model leads to three possible models for six-helix bundles (Figure 1A: 6-2, -3, -4). The number of possible pairs of mirror topologies for the model 6-2, 6-3, and 6-4 are 360, 120, and 180, respectively. In addition, six-helical proteins that transport substrates across the membrane can adopt a hexagonal shape with a helix missing from the middle to allow a transport channel (6-1) (Pebay-Peyroula et al. 2003). There are 60 pairs of mirror topologies for this model. These four models are all observed in the benchmark protein structures. Adding one helix to each model of six-helix bundles leads to three possible models for seven-helix bundles. The only seven-helix benchmark protein adopts the 7-3 model, which has 2,520 pairs of possible mirror packing topologies. The model that best depicts each benchmark protein is listed in Table 4 and the protein structure is shown in Figure 4.
Table 4.
Results of structure prediction for benchmark proteins using simulated PRE data
| Protein name | PDB chain | Model | Two labels | Three labels | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg. RMSD (Å) | Ratio corret topolg | Best sites (Å) | Pred. sites (Å/TM) | Avg. RMSD (Å) | Ratio corret topolg | Best sites (Å) | Pred. sites (Å/TM) | |||
| DsbB | 2hi7B | 4-1 | 5.0±1.1 | 1.00 | 3.4 | 4.6/0.49 | 4.7±0.5 | 1.00 | 3.8 | 4.5/0.47 |
| Ligand gated ion channel | 2vl0A | 4-1 | 6.5±1.0 | 0.75 | 4.9 | 4.9/0.47 | 4.8±1.0 | 1.00 | 3.0 | 3.5/0.56 |
| Lekotriene C4 synthase | 2uuhA | 4-1 | 4.8±0.9 | 0.75 | 3.4 | 3.9/0.50 | 4.1±0.7 | 1.00 | 3.0 | 3.2/0.56 |
| Particulatte Methane Monooxygenase | 1yewC (1–4) | 4-1 | 6.5±1.0 | 0.42 | 5.6 | 5.8/0.44 | 5.1±0.6 | 0.96 | 3.3 | 4.7/0.50 |
| Particulate Methane Monooxygenase | 1yewB (2–5) | 4-1 | 5.0±0.6 | 0.64 | 4.1 | 5.2/0.39 | 4.4±0.7 | 0.67 | 3.5 | 3.5/0.46 |
| Calcium ATPase | 1wpgA (5–8) | 4-1 | 4.4±0.8 | 1.00 | 3.4 | 3.5/0.54 | 4.1±0.5 | 1.00 | 3.4 | 3.5/0.54 |
| Average | 4 | 5.4 | 0.76 | 4.1 | 4.6/0.47 | 4.5 | 0.97 | 3.3 | 3.8/0.52 | |
|
| ||||||||||
| Calcium ATPase | 1wpgA (5–8,10) | 5-1 | 5.3±1.0 | 1.00 | 3.6 | 5.8/0.46 | 4.3±0.8 | 1.00 | 3.2 | 3.2/0.63 |
| Protease glpG | 2ic8A (1–5) | 5-1 | 6.4±0.9 | 0.55 | 4.7 | 6.2/0.36 | 5.1±0.6 | 0.95 | 4.1 | 5.2/0.47 |
| Particulate Methane Monooxygenase | 1yewB (2–5,7) | 5-1 | 5.4±0.9 | 0.70 | 4.1 | 5.2/0.43 | 4.6±0.8 | 0.86 | 3.5 | 4.3/0.47 |
| Bacteriorhodopsin | 1m01A (2–4,6–7) | 5-1 | 6.2±1.1 | 0.80 | 4.3 | 4.9/0.47 | 5.1±1.1 | 1.00 | 3.6 | 4.8/0.51 |
| Average | 5 | 5.8 | 0.76 | 4.2 | 5.5/0.43 | 4.8 | 0.95 | 3.6 | 4.4/0.52 | |
|
| ||||||||||
| Calcium ATPase | 1wpgA (5–10) | 6-2 | 6.1±0.9 | 0.60 | 4.0 | 4.5/0.54 | 4.8±0.8 | 0.93 | 2.8 | 3.3/0.65 |
| Aquaporin Aqpm | 2f2bA (1–2,4–6,8) | 6-1 | 6.4±1.1 | 0.30 | 4.0 | 6.2/0.43 | 5.4±1.2 | 0.75 | 3.3 | 5.4/0.53 |
| Protease glpG | 2ic8A | 6-3 | 6.4±0.9 | 0.37 | 4.7 | 6.5/0.44 | 5.2±0.8 | 0.85 | 4.4 | 4.7/0.52 |
| Particulate Methane Monooxygenase | 1yewB (1–5,7) | 6-2 | 6.4±1.3 | 0.37 | 4.6 | 6.1/0.38 | 5.4±1.2 | 0.68 | 3.8 | 4.2/0.54 |
| Bacteriorhodopsin | 1m01A (2–7) | 6-4 | 7.4±1.0 | 0.26 | 5.5 | 6.2/0.44 | 5.9±1.1 | 0.68 | 4.2 | 4.8/0.56 |
| Average | 6 | 6.5 | 0.38 | 4.6 | 5.9/0.45 | 5.3 | 0.78 | 3.7 | 4.5/0.56 | |
|
| ||||||||||
| Bacteriorhodopsin | 1m01A | 7-3 | 8.2±1.2 | 0.16 | 53 | 7.9/0.43 | 6.5±1.6 | 0.64 | 4.1 | 4.9/0.59 |
|
| ||||||||||
| V-type Sodium ATPase | 2bl2A* | 4-1 | 7.4±0.6 | 0.67 | 6.3 | 7.0/0.42 | 4.6±0.6 | 1.00 | 3.1 | 3.7/0.57 |
| Mitochondrial ADP/ATP carrier | 1okcA* | 6-1 | 7.3±0.8 | 0.30 | 5.4 | 6.7/0.45 | 6.1±0.8 | 0.80 | 5.0 | 5.4/0.55 |
In the “PDB chain” column, the numbers in parentheses in some entries indicate the transmembrane helical segments used. The two proteins with kinks are marked by “*”. The codes in “Model” column correspond to those in Figure 1.
Figure 4. Predicted structures for the benchmark proteins using the best three labels.
The structure (thick line) is aligned to the crystal structure (thin line) and colored from blue (N terminal) to red (C terminal).
Two to three labels can determine topology for five to seven helical bundles
We now examine the minimal number of sites needed to distinguish the correct topology for each model. Specifically, we examine all combinations consisting of a fixed number of sites to check which of them gives rise to the PRE data that can determine the correct topology. Table 1 lists all the correct combinations with the minimal number of sites needed for each model. From the table, we can see that the minimal number of sites for five to seven helical bundles is two, and the probabilities for selecting the correct two sites for five, six, and seven helical bundles are on average 50%, 40% and 15%, respectively. Adding one additional site significantly improves the percentage of correct combinations, specifically, the probabilities increase to 100%, 94% and 74%, for five, six and seven helical structure, respectively.
We now use the model for the five-helix bundle (Figure 1A:5-1) to illustrate a detailed procedure for finding the correct sites. Note that the isosceles trapezoid model consists of two overlapping rhombus shapes. If the first site is placed at one end of the long diagonal of one of the rhombus, say helix 2, the four distances to other helical ends are 24 Ǻ to helix 5, 21 Ǻ to helix 4, and 12 Ǻ to helices 1 and 3. The distances of 24 Ǻ and 21 Ǻ may be indistinguishable by PRE because the difference is within the measurement error. Thus, an additional site is needed to distinguish between the two non-unique pairs: helices 5 and 4, and helices 1 and 3. Placement of the second site on helix 5 or 3 (i.e., the long diagonal of the rhombus shape) will allow for identification of the correct topology. In the ideal case that the distances of 24 Ǻ and 21 Ǻ can be distinguished by PRE, an additional site only needs to distinguish between helices 1 and 3. Placement of the second site on helices 5, 3, or 1 will do. Of a total of ten possible combinations for selecting two sites for a five-helix bundle, four and six combinations are correct using the former strict criterion (i.e., distances of 24 Ǻ and 21 Ǻ are indistinguishable) and latter ideal criterion, respectively. Thus, the probability of selecting the correct two sites is 40–60% for a five-helix bundle.
Optimal mutation sites are on the most exposed helices
Examination of Table 1 led to a number of observations that can be useful for selection of the optimal sites for spin labeling. Of all combinations of the minimal number of sites leading to correct topology, those in which the sites are not adjacent to each other (i.e., distance ≥ 21 Ǻ) appear to give optimal results, possibly because the spin-labels attached to adjacent sites result in similar (redundant) coverage by PRE data.,
Among all the models except for 7-3, the optimal sites also occur on the two helices that have the least number of interactions with other helices, i.e., are most lipid accessible. The hexagonal models, 6-1 and 7-1, have six equivalent helices; hence any two helices separated by 21 Ǻ are equally good. For model 7-3, which has a more extended conformation than the others, the two most exposed helices are out of the PRE measurement range, thus the optimal sites occur on the 3rd and 4th most exposed helices. Hence, we should be able to improve our selection of the optimal sites by predicting lipid accessibility information (i.e., the fraction of lipid accessible surface area) from sequence.
Since spin-labeled samples used in collection of PRE data are usually prepared and analyzed one at a time, lipid accessibility information can be used to choose the first site. If data collected on the first sample are not adequate to determine topology based on patterns summarized in Table 1, the statistics given in the table can be used to optimize the choice for the second site.
The suggested protocol for selection of optimal spin labeling sites and the probabilities of deducing the correct topology for an experimentally targeted protein rest on several key assumptions; that helices can be represented by ideal cylinders, that helices pack in rhombic structures, that motion of spin labels can be ignored, and that PRE derived distances can be equated to center-to-center distances between cylinders. Concerns about some of these assumptions can be dismissed because PRE distances only need to be measured approximately (<17Å for a short distance, 17–25Å for a long diagonal, and >25Å for other elements. These ranges encompass most errors that come from spin-label motion and off-axis placement of nitroxides. A recent publication has presented a detailed analysis of the effects of motion (Iwahara and Clore 2010). Adopting their spherical model to a positional distribution for an MTSL group the distribution would have a radius 5Å and be centered 3.5Å off the helix axis. For the 12Å distance the range is 6.9–14.7; for the 21Å distance the range is 16.8–24.0. In real situations distributions are more localized, and may extend up to 6Å off the helix axis. But these distributions are skewed to the outside of the helical bundles where effects are minimized due to the longer distances involved. Some examples of the effects of these deviations, along with those that come from non-ideal helix geometry and non-ideal packing are given in an analysis of experimental data on the DbsB protein to follow.
It is, nevertheless, important to realize that there can be failures, and indicators of failure and measures of confidence can be valuable. It is clear from the above discussion, in combination with examination of the structures in Figure 1, that all labels should lead to at least 3 measureable inter-helix distances, three short (sss) or two short and one long (ssl), and that detection of one long distance (17–25Å) is more valuable in making a correct classification. One can therefore devise a quality score that approximates the predictions of Table 2 and allows for a penalty when observations inconsistent with the idealized models are made:
Table 2.
Experimental PRE data for DsbB
| Label site | Location on Helix | Number of constraints to helices1 | Distance to other helix ends (Å)2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| Intracellular side | |||||||||
| A14 | 1 | 13 (5,1,7) | 18 (0,10,8) | 14 (0,5,9) | 16 (4,8,4) | — | 16.6 | 19.7 | 16.6 |
| V72 | 3 | 15 (0,2,13) | 17 (4,8,5) | 7 (2,2,3) | 13 (0,5,8) | 21.6 | 16.3 | — | 18.6 |
| V161 | 4 | 18 (0,3,15) | 18 (0,9,9) | 5 (1,3,1) | 7 (0,1,6) | 19.8 | 16.9 | <15 | — |
| Extracellular side | |||||||||
| L30 | 1 | 10 (3,3,4) | 11 (3,6,2) | 11 (0,0,11) | 11 (0,0,11) | — | 20.1 | >25 | >25 |
| L87 | 3 | 14 (0,0,14) | 9 (1,3,5) | 4 (0,2,2) | 13 (0,9,4) | >25 | <15 | — | 18.4 |
| Y89 | 3 | 17 (0,0,17) | 18 (0,8,10) | 13 (3,4,6) | 14 (5,6,3) | >25 | 19.1 | — | <15 |
The total number and each number of constraints in the three ranges of distance of <15Å, 15–25 Å, > 25 Å.
Average PRE distances to the four residues at the helical end on the same side of membrane.
With these cautionary notes we conclude that a small number of strategically placed spin-labeled sites can provide sufficient distance constraints for prediction of the correct topology in most cases, and we anticipate that accurate structures for membrane proteins could be derived by coupling predicted topologies with experimental data and computational refinement.
Experimental Results and Discussion
Structure prediction of DsbB constrained by PRE data
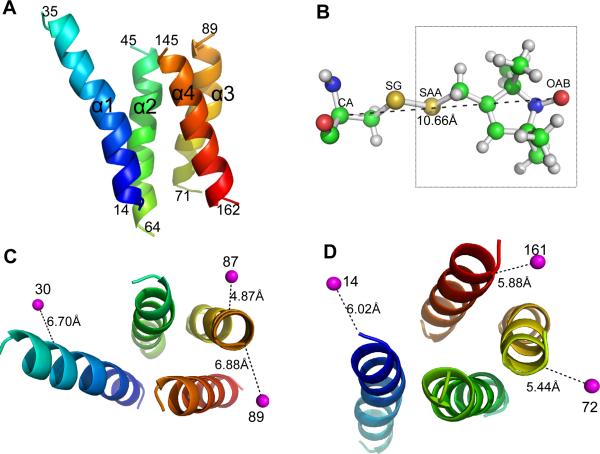
The utility of the above prediction capability can be examined by using both experimental and simulated PRE data and comparing predicted with observed structural topologies. The following shows an application of our prediction capability to protein DsbB, which has a crystal structure, an NMR solution structure and some PRE data (Inaba et al. 2006; Zhou et al. 2008b). The protein is 176 residues long and has four TM helices. The predicted TM residues using TMHMM2 (Krogh et al. 2001) are: TM1 (A14-V35), TM2 (I45-A64), TM3 (Y71-Y89), and TM4 (W145-I162). PRE data were collected from nine mutational sites, six of which are located at helix termini, i.e., A14, V72, and V161 on the intracellular side of the membrane, and L30, L87, and Y89 on the extracellular side. Three other sites (Q122, F137, and G139) are located in loops. Hence only the first six sites were used.
Experimental PRE data
Table 2 lists the number of PRE data from each site to the helices grouped into three ranges: [0, 15 Ǻ], [15, 25 Ǻ], and [25 Ǻ, 150 Ǻ], and the associated distances to the ends of helices on the same side of membrane as label-to-end distances. Only within the range of 15–25 Ǻ can a distance be measured with an error of 2–4 Ǻ while for the other two ranges, we can only say that the distance is below 15 Ǻ or above 25 Ǻ, respectively. We refer the first type of PREs as specific and the other two types as loose constraints.
To infer the helix-helix end distances from the experimental PRE label-to-nucleus data, both the relationships between the spin-label sites and the end of the label-attached helix and the relationships between the observed nucleus sites and the ends of various helices need to be considered. The latter relationships can be deduced from the crystal or NMR structures, but the label locations that best fit all the PRE data on the structure are computationally predicted since spin-labeled cysteine side-chains are not included in the DsbB structures. The crystal structure of the TM regions of DsbB (PDB: 2hi7B) and the predicted spin-label locations on the structure are shown in Figure 2. A spin label is on average 5–7 Ǻ away from its attached helix axis. Thus, the short inter-helical distances in the rhombus model could be as long as 19 Ǻ for the sides and the short diagonal, and the inter-helical distances along the long diagonal could be >21 Ǻ, as derived from the PRE distances. The deduced label-to-helix-end distances are listed in Table 2.
Figure 2. The DsbB structure and experimental PRE spin-label sites.
(A) Side view of the TM helices in the crystal structure of DsbB (2hi7B). The structure is colored by a spectrum running from blue (N terminal) to red (C terminal). The boundaries of the TM helices predicted by the TMHMM2 program (Krogh et al. 2001) are labeled. (B) The extended structure of the PRE tag molecule attached to a CYS residue. The PRE distances are measured from the spin label (OAB atom). (C) Top view of the TM helices from the extracellular side of the membrane. The average position of the spin-labels and the distance to the Cα atom of its attached CYS residue are shown. (D) Top view of the structure from the intracellular side of the membrane.
Topology predictions based on PRE data from a single PRE label
The label-to-end distances listed in Table 2 have been used to check if the correct topology can be determined by using a single PRE label. Note that four of the five labels placed on the ends of the long diagonal give rise to the correct topology. Three of the labels (72, 87, 89) provide a unique distance >21 Ǻ to the helix at the opposite side of the long diagonal. Another label, 14, uniquely determines its neighboring helices with two equal distances of 17 Ǻ, and the helix at its opposite side with a distance of 20 Ǻ. The label placed at an end of the short diagonal, 161, cannot uniquely determine the correct topology with three non-unique distances under 20 Ǻ as expected. The only unexpected one is label 30, which has two helices beyond the measurable range of PRE, due to the deviation of the 2D topology of DsbB from the ideal rhombus model (Figure 2C).
Generating residue-based models with native topology
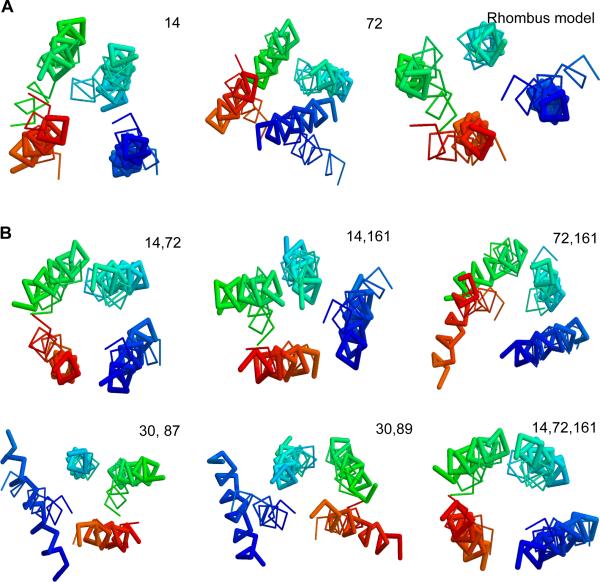
We computationally folded the structure using a distance geometry-based algorithm (Agrafiotis 2003) constrained by the PRE data and by the assumption that helices are approximately parallel with each other and perpendicular to the membrane surface (see Methods). The folding results are listed in Table 3. The models were compared with the crystal structure on the TM helical region using the TM-score program (Zhang and Skolnick 2004b). TM-score ranges in (0,1] with a higher value indicating a stronger structural similarity. TM-score ≥0.4 means statistically significant structural similarity (Zhang and Skolnick 2004a; Chen and Skolnick 2008; Xu and Zhang 2010). By visual examination, we found models with TM-score ≥0.4 generally give correct helical arrangement. Thus, TM-score=0.4 was used as cutoff for correct topology. The best model predicted by the algorithm has correct topology by using any label placed at the ends of the long diagonal and with specific constraints to all helices (i.e. label14, label72,), while the algorithm using any label without a specific constraint (i.e., label30, label87, label89) or placed on the end of the short diagonal (i.e., label161) did not lead to correct topology. For label87 and label89, a correct topology can be determined using the analytic solution (i.e., using the 3-D rhombus model with the predicted helical arrangement). The models based on label14 and label72 as well as the rhombus model are shown in Figure 3A.
Table 3.
Results of structure prediction for DsbB using experimental PRE data
| Label site | Rank of best cluster | Size of best cluster (%) | Best single structure RMSD(Å) | Best cluster centroid structure RMSD(Å)/TMscore |
|---|---|---|---|---|
| 14 | 4 | 16.1 | 5.64 | 5.37 / 0.40 |
| 72 | 4 | 13.0 | 5.46 | 5.69 / 0.43 |
| 161 | 4 | 12.9 | 6.12 | 6.31 / 0.36 |
| 30 | 6 | 10.9 | 6.28 | 9.36 / 0.31 |
| 87 | 2 | 17.0 | 5.44 | 6.74 / 0.30 |
| 89 | 1 | 20.3 | 4.31 | 6.97 / 0.32 |
| Average | 15.0±3.4 | 5.54±0.70 | 6.74±1.42 / 0.35±0.05 | |
| 14, 72 | 1 | 32.0 | 4.56 | 4.33 / 0.47 |
| 14, 161 | 1 | 30.1 | 4.53 | 4.38 / 0.45 |
| 72, 161 | 2 | 24.1 | 5.13 | 5.10 / 0.42 |
| 30, 87 | 1 | 37.0 | 5.41 | 4.85 / 0.41 |
| 30, 89 | 1 | 30.5 | 4.95 | 5.47 / 0.40 |
| Average | 30.7±4.6 | 4.92±0.38 | 4.83±0.48/ 0.43±0.03 | |
| 14, 72, 161 | 2 | 27.6 | 4.18 | 3.57 / 0.53 |
| Average | 31.5±8.6 | 4.11±0.46 | 4.65±0.67/0.43±0.05 | |
| 14,72,161,87 | 2 | 29.3 | 3.88 | 3.94/ 0.53 |
| Average | 34.4±8.2 | 4.17±0.34 | 4.30±0.44/ 0.46±0.06 | |
| 14,72,161,30,87 | 2 | 31.3 | 3.37 | 4.11/0.51 |
| 14,72,161,30,89 | 1 | 43.3 | 3.54 | 4.12/0.49 |
Figure 3. Predicted structures for DsbB constrained by experimental PRE data.
(A) Structures based on a single PRE label for label14 and label72, and the rhombus model. (B) Structures based on two PRE labels, compared to that based on the best three labels. The label sites are shown at the upper right corner. The predicted structure (thick line) is aligned to the crystal structure (thin line) and colored from blue (N terminal) to red (C terminal). See also Figure S1.
In summary, of the six experimental PRE labels, four labels placed at the ends of the long diagonal give rise to the correct topology, and the predicted models are <6Å of the native structure using either the distance geometry-based algorithm or the 3-D rhombus model.
Results based on PRE data from two labels
The DsbB structure was then folded using PRE data associated with any two labels on the same side of the membrane (except for label87 and label89 that are on the same helix terminus). The results are listed in Table 3 and the models are shown in Figure 3B. The models for all possible site combinations have the correct topology with an average RMSD 4.8 Ǻ to the crystal structure. We noted that the structures derived using two labels form two large clusters of similar structures in the derived structure space, with the centroid structure of one cluster having the correct topology and the centroid structure of the other being the mirror image of the first one (Figure S1), indicating that the PRE constraints from two labels are sufficient to uniquely determine the correct topology by using a distance geometry-based algorithm. In contrast, structures derived using a single label form a structure space with multiple small clusters of similar structures.
Results based on three or more PRE labels
The structure predictions using PRE data from any three or more labels from both sides of the membrane (except that label87 and label89 are not in the same combination) have also been tested. Table 3 lists the results of the best combination and the average results of all combinations from three to five labels. The best three-label combination gives a conformation with an RMSD of 3.6 Ǻ to the crystal structure. Adding more labels does not substantially improve the quality of the structure. The model for the best three-label combination is shown in Figure 3B. Considering that PRE derived specific distances have a measurement error of 2–4 Ǻ, plus additional errors caused by the motion of the spin-label and additional structural variations of the protein caused by adding the spin-label, we expect that a model with an RMSD at 4 Ǻ is likely to be near the upper limit in prediction accuracy when using a distance geometry algorithm solely based on PRE distance constraints and idealized helix geometry.
Overall, the distance-geometry based approach can produce starting models having the correct topology of DsbB if one label is placed at an end of the long diagonal and has specific distances to at least two other helices. The predicted structures can reach <5 Ǻ RMSD to the crystal structure with a uniquely determined topology if two labels are used on the same side of the membrane. More accurate structures (< 4 Ǻ) can be reached when using PRE data from three labels. Additional labels do not seem to improve the models based on idealized geometries. But it is worth noting that additional PRE data may allow further improvement if deviations from this ideal geometry are allowed. Also, it may be possible to resolve the mirror image issue with more precise PRE data or data from paired spin-label sites on the opposite sides of helices.
Tests on higher order helix bundles using simulated PREs
To extend the test to proteins with diverse topologies, simulated PRE data derived from crystal structures of a set of unique proteins with four to seven TM helices (see Methods) have been generated. All these proteins are folded using the distance geometry algorithm and the simulated PREs from every possible combination of two and three labels. The best of the top 10 models for each case is used as the prediction. In the following, a model with TMscore ≥ 0.4 is considered as having the correct topology. It should be noted that for proteins, PREs are subject to dynamic averaging due to local motions of the protein and the mobility of the nitroxide tag, so accurate simulation of the experimental PREs is nontrivial (Demarco et al. 2010). Thus, the simulated PREs used here are just a rough approximation of the experimental data, with the purpose of getting an estimate of the minimal number of sites needed and the probabilities in selecting the correct sites.
As shown in Table 4, the average percentages in selecting correct two-label combinations for four, five, six and seven helical bundles are 76%, 76%, 38% and 16%, respectively. The result for DsbB using simulated PRE data is the same as that using the experimental data. The two proteins with kinks are slightly worse: 67% for the one with 4 helices and 30% for the one with 6 helices. Using three labels, the average percentages of selecting the correct combinations for four, five, six and seven helical bundles are 97%, 95%, 78% and 64%, respectively. The percentages for the two kinked proteins are 100% and 80%, respectively, for the four and six helical bundles.
The results confirm the theoretical prediction that it is possible to use PRE data from a minimal two sites to predict the correct topology for up to seven-helix bundles if they are properly selected; however, the chance of selecting the correct two sites for six- or seven-helix bundles is relatively small. For these proteins, three sites should be generally adequate. If the best three sites are selected, a distance geometry-based algorithm constrained only by the PRE data can predict accurate (<4 Ǻ) structures for nearly all proteins. The models using the best three sites are shown in Figure 4. It is interesting to note that the chance for selecting correct two sites for kinked proteins is similar to that of non-kinked ones, although the resulting model quality could be worse due to the deviation from an ideal helix. It should be noted that it is possible to detect kinks in easily acquired RDC or PISEMA data (Mesleh et al. 2003; Nevzorov and Opella 2003; Kim and Cross 2004) or predict their occurrence based on sequence information (Yohannan et al. 2004; Bowie 2005).
Prediction of the optimal mutation sites
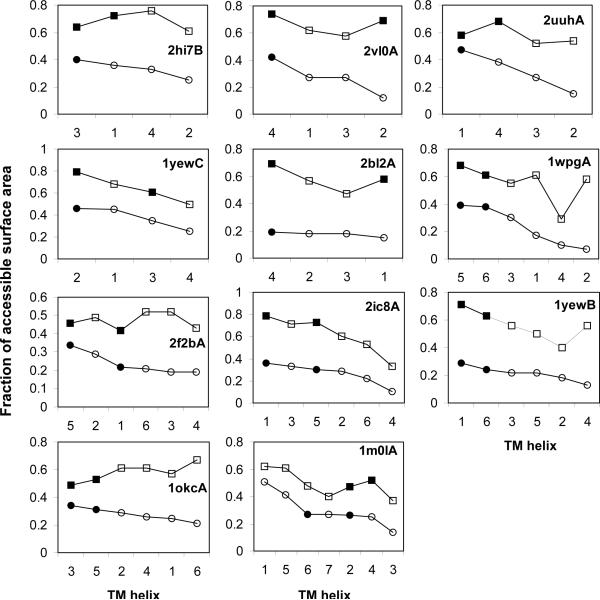
Performance in predicting the optimal sites for spin-labeling by estimating lipid accessibility of TM helices from the sequence information is now assessed (see Methods). The strategy for optimal site prediction is as follows: For 4–6 helical bundles, the most exposed helix by our prediction is selected as the first helix to label. For seven-helix bundles, if the 7–3 topology is identified by the lipid accessibility prediction (i.e., the top 2 lipid accessibilities are significantly higher than the others), the 3rd most exposed helix will be selected as the first site; otherwise, the most exposed helix will be selected as the first site. The second and subsequent sites (if needed) are selected iteratively based on the next most exposed helix and the site being >21 Ǻ away from the previous sites (as determined by sequential examination of PRE data).
Figure 5 shows the results of the optimal site prediction for DsbB and the other benchmark proteins. All the optimal single sites for the 5 four-helix bundles, and the optimal two-site combination for the 5 six-helix bundles are correctly predicted. For the seven-helix bundle, Bacteriorhodopsin (1m0lA), the top two exposed helices are also correctly identified, and the lipid accessibility prediction indicates the protein may adopt the 7–3 topology. However, the 3rd exposed helix as the first site is incorrect, resulting in the two-site combination being unable to determine the correct topology. Overall, the optimal site prediction is successful in 10 out of 11 cases, showing the effectiveness of using lipid accessibility prediction to select the optimal sites for PRE data collection.
Figure 5. Prediction of the optimal site for benchmark proteins.
The helices are ranked by the predicted lipid accessibility (in circles) with the predicted optimal labeling helices in filled circles (black). The lipid accessibility calculated from the crystal structure (the helix surface area in the protein structure / the surface area in the isolated helix) is shown with squares, with the real optimal labeling helices in filled squares (black).
Table 4 lists the results of the predicted structures using the distance geometry algorithm constrained by simulated PREs from the predicted sites. The structures have correct topologies in 15 out of 18 cases using PREs from two sites. One additional site is sufficient to predict correct topology for all cases with the structures <5Å of the native structures for up to seven helices.
Conclusion
We have theoretically analyzed and computationally verified that one to two PRE sites should be sufficient to constrain solution NMR structure prediction for four to seven helical bundles. Our approach for the optimal site prediction successfully predicts the minimal sites for up to six element helical bundles. Improving the lipid accessibility prediction will likely improve the prediction results for seven-helix bundles.
Since only a few structures of membrane protein families are currently available, template-based structure prediction methods do not work in general for membrane proteins (Fleishman and Ben-Tal 2006). At the same time, ab initio approaches suffer from a major hurdle in that a significant portion of conformation space must be sampled to derive a final structure (Schueler-Furman et al. 2005). This often makes the approach computationally infeasible. By determining the correct helix-packing topology of a membrane protein and producing a starting point having a native fold, the computational space can be significantly reduced (e.g., by 83.3% = 5/6 for a four-helix bundle to 99.96% = 2519/2520 for a seven-helix bundle (see Table 1 for the numbers of possible topologies for each model)) and an accurate structure may be determined using additional prediction methods. The study presented here provides a useful approach to deriving starting models for membrane proteins having a correct topology using a small number of experimental data and a simple structure prediction method.
Methods
Data set selection
A set of TM helical protein structures with diverse topologies were collected from the OPM database (Lomize et al. 2006) using the following criteria: (1) the structure was determined by X-ray crystallography with resolution <3.5 Ǻ ; (2) the structures have TM-scores < 0.5 (cutoff for removing structures sharing the same fold (Xu and Zhang 2010) ) on the TM helical region by pair-wise structure alignment using TM-align (Zhang and Skolnick 2005); (3) the protein has 4–7 TM helices forming a single bundle (i.e., each helix interacts with at least two other helices). The resulting set consists of 18 test cases from 11 proteins, including two proteins with kinks (Table 4). A detailed description of the procedure is provided in the Supplementary Information.
Simulation of PRE distance constraints
To simulate the PRE data from crystal structures, we mutated in silico the amino acids at the selected sites to a Cysteine residue carrying a PRE spin-label (Figure 2B) using AMBER (Case et al. 2005) LEaP. A PRE label-carrying Cysteine was added to the AMBER library as a new amino acid type to facilitate this procedure. The spin-labeled sites are those residues predicted by the TMHMM2 program (Krogh et al. 2001) to be at the ends of TM helices. An energy minimization step is carried out on each mutated residue to remove steric clashes and minimize the Van der Waals energy in AMBER. The distance between the spin-label (OAB atom) and any HN atom in the structure is calculated and grouped into three ranges: [0, 15 Ǻ), [15, 25 Ǻ], and (25 Ǻ, 150 Ǻ]. Only within the range of 15–25 Ǻ, is a distance specifically constrained (with an error of ±3 Ǻ).
Generation of structures from distance constraints
Our system consists of m amino acids (represented by the HN atoms) and n PRE labels, a total of m+n points. The distance constraints between the labels and the HN atoms are from either experimental or simulated PRE data. The distance constraints between pairs of HN atoms in the same helix are calculated from an ideal helical structure. Additional constraints are used to assure that the helices are roughly parallel to each other and perpendicular to the membrane surface. We implement the stochastic proximity embedding (SPE) procedure (Agrafiotis 2003) for a distance geometry search for structures that satisfy all the distance constraints. The detailed description of the procedure is provided in the Supplementary Information.
Structure selection by clustering
1,000 structures that satisfy all the constraints for each protein were generated and clustered using an in-house clustering method (Zhou et al. 2008a). For each cluster, a centroid structures was generated using the SPIKER program (Zhang and Skolnick 2004c). A model was created by superimposing the ideal helices to the centroid structure or the closest-to-centroid structure (the single structure with the best RMSD to the centroid structure) if steric clashes occur to the centroid structure. The models are ranked by the cluster density and the best of top 10 models are used as prediction for the benchmarking set. A more detailed description is provided in the Supplementary Information.
Prediction of lipid accessibility of TM helices
The lipid accessibility is the fraction of the surface area exposed to lipid. The lipid accessible surface area (ASA) for each residue was predicted from sequence using the ASAP server (Yuan et al. 2006), and the TM helical segments were predicted using the TMHMM2 program. The ASA of a TM helix is the sum of the ASA of all residues in the helix. The total surface area of the helix was calculated from the isolated ideal helical structure by the DSSP program (Kabsch and Sander 1983), as used in the ASAP server. The lipid accessibility of a TM helix was obtained by normalizing the ASA of the TM helix by its total surface area.
Supplementary Material
Acknowledgment
We thank Dr. Fang Tian, Dr. David D. Landau, Daniel T. Seaton and Ying-Wai Li for helpful discussions. This project is supported in part by grants from NIH grants (1R01GM075331 and 1R01GM081682), NSF grants (DBI-0354771, ITR-IIS-0407204, DBI-0542119, CCF-0621700), and a “Distinguished Scholar” award from the Georgia Cancer Coalition.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Agrafiotis DK. Stochastic proximity embedding. J Comput Chem. 2003;24:1215–1221. doi: 10.1002/jcc.10234. [DOI] [PubMed] [Google Scholar]
- Almen MS, Nordstrom KJ, Fredriksson R, Schioth HB. Mapping the human membrane proteome: a majority of the human membrane proteins can be classified according to function and evolutionary origin. BMC Biol. 2009;7:50. doi: 10.1186/1741-7007-7-50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth P, Schonbrun J, Baker D. Toward high-resolution prediction and design of transmembrane helical protein structures. Proc Natl Acad Sci U S A. 2007;104:15682–15687. doi: 10.1073/pnas.0702515104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth P, Wallner B, Baker D. Prediction of membrane protein structures with complex topologies using limited constraints. Proc Natl Acad Sci U S A. 2009;106:1409–1414. doi: 10.1073/pnas.0808323106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battiste JL, Wagner G. Utilization of site-directed spin labeling and high-resolution heteronuclear nuclear magnetic resonance for global fold determination of large proteins with limited nuclear overhauser effect data. Biochemistry. 2000;39:5355–5365. doi: 10.1021/bi000060h. [DOI] [PubMed] [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertini I, Claudio L, Parigi G. Current methods in inorganic chemistry. Elsevier Science Ltd, Amsterdam; New York: 2001. Solution NMR of paramagnetic molecules : applications to metallobiomolecules and models; p. 372. [Google Scholar]
- Bertini I, Luchinat C, Parigi G, Pierattelli R. NMR spectroscopy of paramagnetic metalloproteins. Chembiochem. 2005;6:1536–1549. doi: 10.1002/cbic.200500124. [DOI] [PubMed] [Google Scholar]
- Bowie JU. Solving the membrane protein folding problem. Nature. 2005;438:581–589. doi: 10.1038/nature04395. [DOI] [PubMed] [Google Scholar]
- Cady SD, Hong M. Amantadine-induced conformational and dynamical changes of the influenza M2 transmembrane proton channel. Proc Natl Acad Sci U S A. 2008;105:1483–1488. doi: 10.1073/pnas.0711500105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case DA, Cheatham TE, 3rd, Darden T, Gohlke H, Luo R, Merz KM, Jr., Onufriev A, Simmerling C, Wang B, Woods RJ. The Amber biomolecular simulation programs. J Comput Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H, Skolnick J. M-TASSER: an algorithm for protein quaternary structure prediction. Biophys J. 2008;94:918–928. doi: 10.1529/biophysj.107.114280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clore GM, Tang C, Iwahara J. Elucidating transient macromolecular interactions using paramagnetic relaxation enhancement. Curr Opin Struct Biol. 2007;17:603–616. doi: 10.1016/j.sbi.2007.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornish VW, Benson DR, Altenbach CA, Hideg K, Hubbell WL, Schultz PG. Site-specific incorporation of biophysical probes into proteins. Proc Natl Acad Sci U S A. 1994;91:2910–2914. doi: 10.1073/pnas.91.8.2910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demarco ML, Woods RJ, Prestegard JH, Tian F. Presentation of membrane-anchored glycosphingolipids determined from molecular dynamics simulations and NMR paramagnetic relaxation rate enhancement. J Am Chem Soc. 2010;132:1334–1338. doi: 10.1021/ja907518x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleishman SJ, Ben-Tal N. Progress in structure prediction of alpha-helical membrane proteins. Curr Opin Struct Biol. 2006;16:496–504. doi: 10.1016/j.sbi.2006.06.003. [DOI] [PubMed] [Google Scholar]
- Harris NL, Presnell SR, Cohen FE. Four helix bundle diversity in globular proteins. J Mol Biol. 1994;236:1356–1368. doi: 10.1016/0022-2836(94)90063-9. [DOI] [PubMed] [Google Scholar]
- Hubbell WL, Altenbach C. Investigation of Structure and Dynamics in Membrane Proteins Using Site-Directed Spin-Labeling. Curr Opin Struct Biol. 1994;4:566–573. [Google Scholar]
- Inaba K, Murakami S, Suzuki M, Nakagawa A, Yamashita E, Okada K, Ito K. Crystal structure of the DsbB-DsbA complex reveals a mechanism of disulfide bond generation. Cell. 2006;127:789–801. doi: 10.1016/j.cell.2006.10.034. [DOI] [PubMed] [Google Scholar]
- Iwahara J, Clore GM. Structure-independent analysis of the breadth of the positional distribution of disordered groups in macromolecules from order parameters for long, variable-length vectors using NMR paramagnetic relaxation enhancement. J Am Chem Soc. 2010;132:13346–13356. doi: 10.1021/ja1048187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabsch W, Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Kang C, Tian C, Sonnichsen FD, Smith JA, Meiler J, George AL, Jr., Vanoye CG, Kim HJ, Sanders CR. Structure of KCNE1 and implications for how it modulates the KCNQ1 potassium channel. Biochemistry. 2008;47:7999–8006. doi: 10.1021/bi800875q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S, Cross TA. 2D solid state NMR spectral simulation of 3(10), alpha, and pi-helices. J Magn Reson. 2004;168:187–193. doi: 10.1016/j.jmr.2004.02.009. [DOI] [PubMed] [Google Scholar]
- Koebnik R, Locher KP, Van Gelder P. Structure and function of bacterial outer membrane proteins: barrels in a nutshell. Mol Microbiol. 2000;37:239–253. doi: 10.1046/j.1365-2958.2000.01983.x. [DOI] [PubMed] [Google Scholar]
- Krogh A, Larsson B, von Heijne G, Sonnhammer EL. Predicting transmembrane protein topology with a hidden Markov model: application to complete genomes. J Mol Biol. 2001;305:567–580. doi: 10.1006/jmbi.2000.4315. [DOI] [PubMed] [Google Scholar]
- Liang B, Bushweller JH, Tamm LK. Site-directed parallel spin-labeling and paramagnetic relaxation enhancement in structure determination of membrane proteins by solution NMR spectroscopy. J Am Chem Soc. 2006;128:4389–4397. doi: 10.1021/ja0574825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lomize MA, Lomize AL, Pogozheva ID, Mosberg HI. OPM: orientations of proteins in membranes database. Bioinformatics. 2006;22:623–625. doi: 10.1093/bioinformatics/btk023. [DOI] [PubMed] [Google Scholar]
- Marassi FM, Opella SJ. A solid-state NMR index of helical membrane protein structure and topology. J Magn Reson. 2000;144:150–155. doi: 10.1006/jmre.2000.2035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mesleh MF, Lee S, Veglia G, Thiriot DS, Marassi FM, Opella SJ. Dipolar waves map the structure and topology of helices in membrane proteins. J Am Chem Soc. 2003;125:8928–8935. doi: 10.1021/ja034211q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley CK, Myers JK, Hadziselimovic A, Ellis CD, Sanders CR. Purification and initiation of structural characterization of human peripheral myelin protein 22, an integral membrane protein linked to peripheral neuropathies. Biochemistry. 2007;46:11185–11195. doi: 10.1021/bi700855j. [DOI] [PubMed] [Google Scholar]
- Nevzorov AA, Opella SJ. Structural fitting of PISEMA spectra of aligned proteins. J Magn Reson. 2003;160:33–39. doi: 10.1016/s1090-7807(02)00138-6. [DOI] [PubMed] [Google Scholar]
- Nishimura K, Kim S, Zhang L, Cross TA. The closed state of a H+ channel helical bundle combining precise orientational and distance restraints from solid state NMR. Biochemistry. 2002;41:13170–13177. doi: 10.1021/bi0262799. [DOI] [PubMed] [Google Scholar]
- Otting G. Protein NMR using paramagnetic ions. Annu Rev Biophys. 2010;39:387–405. doi: 10.1146/annurev.biophys.093008.131321. [DOI] [PubMed] [Google Scholar]
- Oxenoid K, Chou JJ. The structure of phospholamban pentamer reveals a channel-like architecture in membranes. Proc Natl Acad Sci U S A. 2005;102:10870–10875. doi: 10.1073/pnas.0504920102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pebay-Peyroula E, Dahout-Gonzalez C, Kahn R, Trezeguet V, Lauquin GJ, Brandolin G. Structure of mitochondrial ADP/ATP carrier in complex with carboxyatractyloside. Nature. 2003;426:39–44. doi: 10.1038/nature02056. [DOI] [PubMed] [Google Scholar]
- Popot JL, Engelman DM. Membrane protein folding and oligomerization: the two-stage model. Biochemistry. 1990;29:4031–4037. doi: 10.1021/bi00469a001. [DOI] [PubMed] [Google Scholar]
- Roosild TP, Greenwald J, Vega M, Castronovo S, Riek R, Choe S. NMR structure of Mistic, a membrane-integrating protein for membrane protein expression. Science. 2005;307:1317–1321. doi: 10.1126/science.1106392. [DOI] [PubMed] [Google Scholar]
- Rost B, Fariselli P, Casadio R. Topology prediction for helical transmembrane proteins at 86% accuracy. Protein Sci. 1996;5:1704–1718. doi: 10.1002/pro.5560050824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnell JR, Chou JJ. Structure and mechanism of the M2 proton channel of influenza A virus. Nature. 2008;451:591–595. doi: 10.1038/nature06531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schueler-Furman O, Wang C, Bradley P, Misura K, Baker D. Progress in modeling of protein structures and interactions. Science. 2005;310:638–642. doi: 10.1126/science.1112160. [DOI] [PubMed] [Google Scholar]
- Traaseth NJ, Verardi R, Torgersen KD, Karim CB, Thomas DD, Veglia G. Spectroscopic validation of the pentameric structure of phospholamban. Proc Natl Acad Sci U S A. 2007;104:14676–14681. doi: 10.1073/pnas.0701016104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Horn WD, Kim HJ, Ellis CD, Hadziselimovic A, Sulistijo ES, Karra MD, Tian C, Sonnichsen FD, Sanders CR. Solution nuclear magnetic resonance structure of membrane-integral diacylglycerol kinase. Science. 2009;324:1726–1729. doi: 10.1126/science.1171716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walters RF, DeGrado WF. Helix-packing motifs in membrane proteins. Proc Natl Acad Sci U S A. 2006;103:13658–13663. doi: 10.1073/pnas.0605878103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiener M. A pedestrian guide to membrane protein crystallization. Methods. 2004;34:364–372. doi: 10.1016/j.ymeth.2004.03.025. [DOI] [PubMed] [Google Scholar]
- Xu J, Zhang Y. How significant is a protein structure similarity with TM-score = 0.5? Bioinformatics. 2010;26:889–895. doi: 10.1093/bioinformatics/btq066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yildirim MA, Goh KI, Cusick ME, Barabasi AL, Vidal M. Drug-target network. Nat Biotechnol. 2007;25:1119–1126. doi: 10.1038/nbt1338. [DOI] [PubMed] [Google Scholar]
- Yohannan S, Faham S, Yang D, Whitelegge JP, Bowie JU. The evolution of transmembrane helix kinks and the structural diversity of G protein-coupled receptors. Proc Natl Acad Sci U S A. 2004;101:959–963. doi: 10.1073/pnas.0306077101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan Z, Zhang F, Davis MJ, Boden M, Teasdale RD. Predicting the solvent accessibility of transmembrane residues from protein sequence. J Proteome Res. 2006;5:1063–1070. doi: 10.1021/pr050397b. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Skolnick J. Automated structure prediction of weakly homologous proteins on a genomic scale. Proc Natl Acad Sci U S A. 2004a;101:7594–7599. doi: 10.1073/pnas.0305695101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Skolnick J. Scoring function for automated assessment of protein structure template quality. Proteins. 2004b;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Skolnick J. SPICKER: a clustering approach to identify near-native protein folds. J Comput Chem. 2004c;25:865–871. doi: 10.1002/jcc.20011. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Skolnick J. TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. 2005;33:2302–2309. doi: 10.1093/nar/gki524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou F, Olman V, Xu Y. Barcodes for genomes and applications. BMC Bioinformatics. 2008a;9:546. doi: 10.1186/1471-2105-9-546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y, Cierpicki T, Jimenez RH, Lukasik SM, Ellena JF, Cafiso DS, Kadokura H, Beckwith J, Bushweller JH. NMR solution structure of the integral membrane enzyme DsbB: functional insights into DsbB-catalyzed disulfide bond formation. Mol Cell. 2008b;31:896–908. doi: 10.1016/j.molcel.2008.08.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.