Measuring Surface Binding Thermodynamics and Kinetics by using Total Internal Reflection with Fluorescence Correlation Spectroscopy: Practical Considerations

Abstract

The combination of total internal reflection illumination and fluorescence correlation spectroscopy (TIR-FCS) is an emerging method useful for, among a number of things, measuring the thermodynamic and kinetic parameters describing the reversible association of fluorescently labeled ligands in solution with immobilized, nonfluorescent surface binding sites. However, there are many parameters (both instrumental and intrinsic to the interaction of interest) that determine the nature of the acquired fluorescence fluctuation autocorrelation functions. In this work, we define criteria necessary for successful measurements, and then systematically explore the parameter space to define conditions that meet the criteria. The work is intended to serve as a guide for experimental design; in other words, to provide a methodology to identify experimental conditions that will yield reliable values of the thermodynamic and kinetic parameters for a given interaction.

INTRODUCTION

Interactions between soluble ligands and membrane-bound species are an integral part of many, if not most, cellular processes. Many disease-causing microorganisms bind cell-surface molecules as a first step in pathogenesis and the subsequent immune response. A majority of pharmaceutical products target cell-surface receptors. Intercellular communication is often facilitated by soluble factors circulating between cells. Numerous intracellular mechanisms involve the interaction of soluble factors with the membranes of sub-cellular organelles, with the factors being present either in the cytosol or within the organelle. Consequently, to fully understand pathogenic processes, determine the mechanism of action of drugs, and characterize both intercellular and intracellular biological processes, the thermodynamic and kinetic parameters of relevant ligand-receptor interactions must be known. Total internal reflection with fluorescence correlation spectroscopy (TIR-FCS) is an emerging technique that allows one to study the reversible interaction between soluble and surface-associated species.^1–5

TIR-FCS combines two established techniques: total internal reflection fluorescence microscopy (TIRFM) and fluorescence correlation spectroscopy (FCS). In TIRFM, a laser beam approaching an interface between two media with different refractive indices, from the higher refractive index side and at an angle greater than the critical angle, is internally reflected. Total internal reflection gives rise to a thin, surface-associated light layer called the evanescent wave. This wave penetrates into the lower refractive index medium, and decays approximately exponentially with increasing distance from the interface. Evanescent illumination can therefore be used to achieve surface specificity and limit the size of the detection volume. In TIR-FCS, a pinhole or fiber optic, placed at a back image plane, is employed to further reduce this volume. A small detection volume ensures that a small number of fluorescent molecules are observed at a given time, not a large number that would only yield small fluorescence fluctuations. The fluorescence fluctuations arising from number fluctuations are auto-correlated. The magnitude of the fluorescence fluctuation autocorrelation function is inversely related to the average number of fluorescent molecules in the detection volume. The rate and shape of decay of the autocorrelation function contain information about the processes giving rise to the observed fluorescence fluctuations, such as diffusion through the evanescent wave or reversible association with the surface. To obtain values of the parameters describing these processes from TIR-FCS autocorrelation functions, knowledge of the appropriate theoretical form for a given optical arrangement and molecular process is required.

TIR-FCS has thus far been used primarily to investigate the mobility of small fluorescent molecules close to surfaces.^6–12 TIR-FCS has also been used to characterize the diffusion coefficients of fluorescently labeled proteins^13,14 and particles¹⁵ close to supported phospholipid membranes; molecular transport in sol-gel films,^16–18 and the mobility of intracellular vesicles very close to the basal membranes of live, adherent cells.^19,20 In addition, TIR-FCS has been used to study the reversible interaction of fluorescent species with surfaces; i.e., fluorescently labeled IgG and insulin with albumin-coated surfaces,²¹ rhodamine 6G with C₁₈-coated silica,^22–23 fluorescently labeled bovine serum albumin and Thermomyces lanuginosus lipase with C₁₈-coated glass in the presence of surfactants,²⁴ and fluorescently labeled IgG with Fc receptors reconstituted in supported planar membranes.²⁵ Applications to enzyme kinetics,²⁶ triplet state photo-physics,^27,28 and the association of cytosolic molecules with the basal membranes of live, adherent cells^7,29,30 have also been reported.

The use of TIR-FCS to examine the thermodynamic and kinetic parameters of soluble, fluorescent ligands reversibly associating with non-fluorescent surface binding sites is a promising method because it requires very small amounts of material. First, the fluorescence fluctuation autocorrelation functions obtained from FCS, in general, are roughly inversely proportional to the average number of fluorescent molecules within the observed volume. Therefore, TIR-FCS has the advantage of requiring low concentrations of fluorescent ligands. Second, because the non-fluorescent binding sites are present in a monomolecular layer on a surface, only small amounts of these molecules are also required. Another advantage of TIR-FCS is related to its recent combination with high-speed imaging detectors.^30–33 This arrangement, coupled with microfluidic devices, promises high throughput acquisition of numerous fluorescence fluctuation autocorrelation functions (e.g., as a function of the fluorescent ligand concentration and surface site density) from a single time-sequence of images and therefore rapid dissection of surface binding mechanisms.

TIR-FCS autocorrelation functions are predicted to depend on many different parameters; so many that it is difficult to readily identify experimental conditions that will yield autocorrelation curves that contain significant information about the thermodynamic and kinetic parameters which describe the interaction of fluorescent ligands with non-fluorescent surface binding sites. Therefore, in this work, we evaluate the parameter space in a systematic manner to identify viable experimental conditions. First, a set of criteria necessary for the autocorrelation curves to contain the desired information with high signal-to-noise ratios are defined. Then the previously derived theoretical form of the autocorrelation function is used to determine the experimental conditions that meet these criteria. The results are somewhat surprising in the inferred limitations on experimental parameters (primarily, upper limits on the allowed concentrations of fluorescent ligands given a defined equilibrium association constant). While many conditions are predicted not to yield viable TIR-FCS data, a number of conditions that are likely to yield productive data are identified. Thus, the results presented in this paper serve as a comprehensive guide to the design of TIR-FCS measurements aimed at measuring the kinetic and thermodynamic parameters describing the association of fluorescent ligands with non-fluorescent surface binding sites. Also, the work described here serves as a prerequisite for the design of measurements aimed at using a single, well characterized fluorescent reporter to scan non-fluorescent, soluble competitors for the thermodynamic and kinetic properties describing reversible association with the non-fluorescent surface binding sites.^34,35 Similarly, a single fluorescent reporter might be used to characterize non-fluorescent effectors that non-competitively interact with binding sites and enhance or reduce fluorescent reporter binding.

THEORETICAL BACKGROUND

Total Internal Reflection with Fluorescence Correlation Spectroscopy

Figure 1 illustrates the conceptual basis of TIR-FCS. Measurements are carried out on an inverted optical microscope. The sample plane, containing surface-binding sites for soluble fluorescent ligands, is the interface between optically transparent high and low refractive index materials (usually fused silica or glass and a buffered aqueous solution, respectively) and is placed at the focal plane of the microscope. Positions within the sample plane are described by polar coordinates (r, ϕ) and the distance from the sample plane into the lower refractive index medium is defined by coordinate z ≥ 0. An excitation source is internally reflected at the sample plane, creating a thin, surface-associated evanescent wave in the lower refractive index medium. Internal reflection may be generated by using either a through-prism or through-objective mechanism. The evanescent excitation intensity is assumed to decay exponentially with position z and characteristic distance d (usually ≈ 0.1 μm). Worth noting is that this assumption may not be completely accurate, as previously reviewed,¹ but that deviations from exponential behavior, if they occur, are expected to be minimal. The observed volume is further defined by a pinhole or fiber optic placed at a back image plane of the microscope. It is assumed that the observation area in the sample plane, as defined by the back image plane detection restriction, is circular with radius h ≈ 0.5 μm and area ≈ πh². Furthermore, the spatial extent of the evanescent intensity within the sample plane is assumed to be large enough so that the evanescent intensity within the observation volume does not depend on r. At chemical and thermal equilibrium, individual fluorescent molecules diffuse in solution within the observation volume, and also bind to and dissociate from surface binding sites. The fluorescence arising from the observation volume, defined by the evanescent excitation and projected area of the back image plane aperture on the sample plane, is collected through a high numerical aperture objective, detected by a sensitive photomultipler or silicon avalanche diode, and is denoted as F(t). Because only a small number of fluorescent molecules are within the observed volume, the fluorescence fluctuates significantly with time. The fluorescence fluctuations, δF(t) = F(t) - <F>, where the brackets denote equilibrium (i.e., time-averaged or ensemble-averaged) values, are auto-correlated. The normalized, dimensionless autocorrelation function is defined as

Figure 1. TIR-FCS.

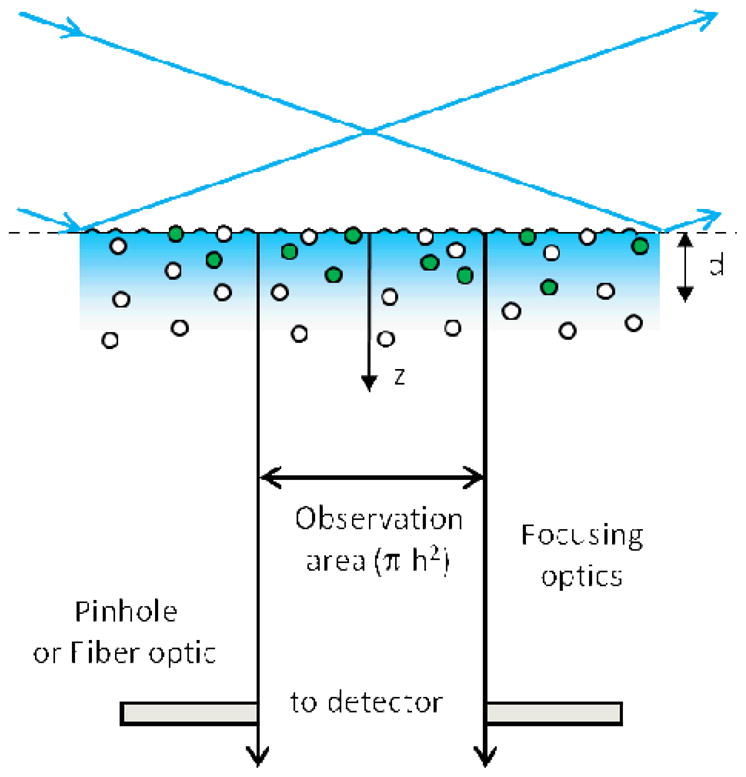
A laser beam is totally internally reflected at a planar interface between media with two different refractive indices, creating an evanescent field that penetrates a depth d into the lower refractive index medium. A small sample volume is defined by this depth in combination with a circular aperture or fiber optic placed at an intermediate image plane of the microscope that defines an area of radius h in the sample plane. The fluorescence measured from the small sample volume adjacent to the surface fluctuates with time as individual fluorescent ligands diffuse into the volume, bind to surface-associated receptors, dissociate, and diffuse out of the volume. These fluorescence fluctuations are autocorrelated and fit to theoretical expressions to obtain information about the dynamics at or near the surface.

$$G(\tau )=\frac{<\delta F(\tau )\delta F(0)>}{<F{>}^2}$$ (1)

and contains information about diffusion through the evanescent wave in addition to surface binding kinetics.

Reaction Mechanism

Consider a situation in which a single fluorescent species in solution interacts with binding sites on a surface through a simple, reversible bimolecular reaction (Figure 2). Fluorescent molecules in solution with average concentration A are in equilibrium with unoccupied, non-fluorescent surface binding sites of average density B, forming an average density of fluorescent, surface-bound complexes, C. The surface association and dissociation rate constants are denoted by k_a and k_d, respectively. The mechanism can be written as

Figure 2. Reaction Mechanism.

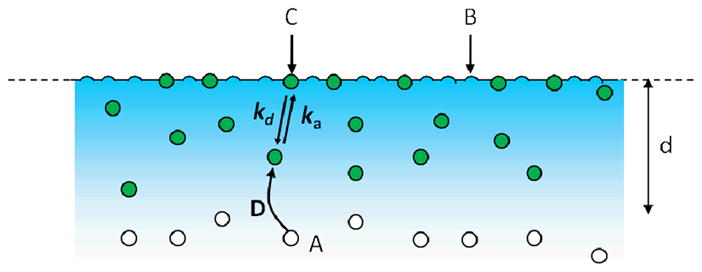
Fluorescent molecules in solution, A, reversibly bind to non-fluorescent surface sites, B, forming fluorescent complexes, C. The association and dissociation rates constants are k_a and k_d, respectively. The solution diffusion coefficient is D. The surface binding sites and surface-bound complexes are not laterally mobile.

$$A+B\underset{k_d}{\overset{k_a}{\leftrightarrow }}C$$ (2)

where the equilibrium association constant describing the reaction is

$$K=\frac{k_a}{k_d}=\frac{C}{AB}$$ (3)

The total surface site density is denoted by S. Thus,

$$S=B+CB=\frac{S}{1+KA}C=\frac{\mathit{KAS}}{1+KA}$$ (4)

The total number of surface binding sites within the observed area is defined as N. In this case,

$$N=\pi h^{2}S=N_B+N_C{N}_B=\frac{N}{1+KA}{N}_C=\frac{\mathit{KAN}}{1+KA}$$ (5)

where N_B is the average number of unoccupied binding sites in the observed area and N_C is the average number of surface-bound fluorescent molecules in the observed area.

Fluorescence Fluctuation Autocorrelation Function

A general expression for G(τ) which accounts for fluorescence fluctuations arising from diffusion through the evanescent field and from surface association and dissociation has previously been published.³⁶ In this work, it is assumed that the surface binding sites and surface-associated complexes are not laterally mobile along the surface. Furthermore, it is assumed that the excitation intensity is low enough so that photo-physical processes do not contribute significantly to G(τ). The first assumption can be proven by using fluorescence recovery after photobleaching and the second can be shown by acquiring data as a function of the excitation intensity. The published general expression is rather complex.³⁶ In the work described here, we consider the more simple form for G(τ) which is applicable when (1) the rates for diffusion in solution through the observation volume are much faster than the rates associated with surface association and dissociation and (2) rebinding of previously dissociated fluorescent molecules within the small observed area is negligible. In this case,

$$G(\tau )=G_s(\tau )+G_a(\tau )$$ (6)

where the first term describes contributions to the autocorrelation function from surface binding kinetics and the second term describes contributions from diffusion of fluorescent molecules in solution but within the evanescent wave.

Magnitude of the Fluorescence Fluctuation Autocorrelation Function

Because the observation volume is open with respect to coordinate z, fluctuations in the concentration of fluorescent molecules in solution obey Poisson statistics. However, because there is a finite number of surface binding sites in the observed area, fluctuations in the densities of surface-bound species obey binomial rather than Poisson statistics. These statements lead to the conclusion that³⁶

$$G_a(0)=\frac{N_A}{2{(N_C+N_A)}^2}{G}_s(0)=\frac{N_B{N}_C}{N{(N_C+N_A)}^2}$$ (7)

where the average number of unbound fluorescent molecules in the observed volume is

$$N_A=\pi h^{2}dA$$ (8)

It is convenient to define a dimensionless quantity proportional to the solution concentration, X = KA. In this case, Eqs. 7 can be rewritten as

$$G_a(0)=\frac{dK{(1+X)}^2}{2\pi h^{2}X{[KS+d(1+X)]}^2}{G}_s(0)=\frac{K^{2}S}{\pi h^{2}X{[KS+d(1+X)]}^2}$$ (9)

Time-Dependence of G_a(τ)

As shown previously,^9,36

$$\begin{array}{l}\frac{G_a(\tau )}{G_a(0)}=[(1-2R_z\tau )exp(R_z\tau )\mathit{erfc}(\sqrt{R_z\tau })+2\sqrt{\frac{R_z\tau }{\pi }}][\frac{1}{1+R_r\tau }]\\ R_z=\frac{D}{d^2}{R}_r=\frac{4D}{h^2}\end{array}$$ (10)

where D is the diffusion coefficient of the fluorescent molecules in solution, R_z is the rate associated with diffusion in solution perpendicular to the surface and through the depth of the evanescent wave, and R_r is the rate associated with diffusion in solution parallel to the surface and through the extent of the observed area. Both factors in the first expression in Eq. 10 equal one when τ = 0 and monotonically decay to zero as τ → ∞. For a protein with a molecular weight of ≈ 100 kD, D ≈ 50 μm²sec⁻¹. Typically, d ≈ 0.1 μm, and h ≈ 0.5 μm, so that, for this value of D, R_z ≈ (0.2 ms)⁻¹ and R_r ≈ (1.25 ms)⁻¹. The minimum decay rate of G_a(τ) is R_z; R_r only speeds the decay.¹

Time-Dependence of G_s(τ)

Given the assumptions that the rates for diffusion in solution through the observation volume are much faster than the rates associated with surface association and dissociation and that rebinding of previously dissociated fluorescent molecules within the small observed area is negligible, G_s(τ) has the form of an exponential decay:^36,37

$$\frac{G_s(\tau )}{G_s(0)}=exp(-\lambda \tau )\lambda =k_d+k_{a}A=k_d(1+X)$$ (11)

The first expression decays from one to zero with time.

RESULTS

Measurement of K by Steady-State TIRFM

Independent of TIR-FCS, the simplest method for measuring the value of the equilibrium association constant is by using steady-state TIRFM.^38–42 In this approach, the evanescently excited fluorescence is measured as a function of the concentration of fluorescent molecules in solution. The data are of the form

$$\begin{array}{l}{F}_{\mathit{pos}}(A)=Q[\frac{\mathit{KAS}}{1+KA}+dA]\\ F_{\mathit{neg}}(A)=\mathit{QdA}\end{array}$$ (12)

where F_pos(A) is the fluorescence measured for surfaces containing binding sites, the first term in F_pos(A) arises from fluorescent ligands bound to surface sites, the second term in F_pos(A) arises from fluorescent molecules in solution but close enough to the surface to be excited by the evanescent wave, F_neg(A) is the fluorescence measured for surfaces not containing binding sites, and Q is a proportionality constant.

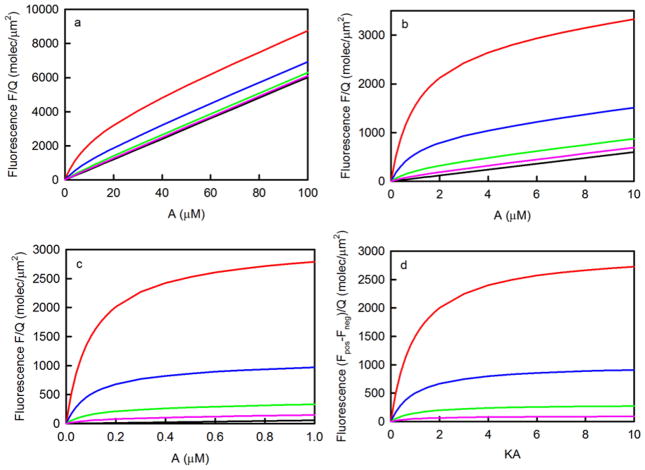
The difference between the fluorescence measured in the presence (S > 0) and absence (S = 0) of surface binding sites has the shape of a standard binding isotherm which can be curve-fit as a function of A to find the best value of K (and QS). The primary limitation of this type of measurement is that the surface site density in the positive samples must be high enough so that the first term in Eq. 12 is not overwhelmed by the second term. This feature is illustrated in Figure 3. As shown, higher binding site densities are required for lower values of K. If a general rule is set that the fluorescence measured in the presence of binding sites must be at least twice that measured in the absence of binding sites when A = K⁻¹, then one finds that S ≥ 2d/K. Thus, when d = 0.1 μm, the approximate lower limit for S ranges from 12,000 molecules/μm² for K = 10⁴M⁻¹ to 12 molecules/μm² for K = 10⁷M⁻¹. In addition, for adequate curve-fitting, because the value of QS and therefore the saturation point is usually unknown, data must be acquired for solution concentrations up to at least (approximately) 4/K, where the surface binding sites are 80% occupied.

Figure 3. Measurement of K by Steady-State TIRFM.

These plots show the values of Eq. 12 for d = 0.1 μm and K equal to (a) 10⁵M⁻¹, (b) 10⁶M⁻¹ or (c) 10⁷M⁻¹. The surface site densities S in units of molecules/μm² are (red) 3000, (blue) 1000, (green) 300, (pink) 100 or (black) zero. The difference between the values shown in (a-c) with S > 0 and with S = 0 have the same shape when plotted as a function of the product of K and A and are shown in panel (d).

Criteria for TIR-FCS

As shown in the previous section, G(τ) is predicted to depend on a rather large number of parameters, some of which are experimentally adjustable and some of which will be intrinsic to a given system of interest. Because so many parameters are present in the expression specifying the autocorrelation function and because all measured G(τ) will contain experimental uncertainties, identifying combinations of the parameter values which can be reasonably predicted to allow characterization of the mechanism shown in Figure 2 is not straightforward. Referring to Eqs. 6 and 9–11, one finds that the expression for G(τ) depends on seven independent parameters: K, k_d, X, d, h, D and S (Table 1). To make analysis tractable, we have set the values of d (0.1 μm), h (0.5 μm), and D (50 μm²s⁻¹), leaving four free parameters rather than seven. In addition, in many cases we have assumed that k_a = 10⁶ M⁻¹s⁻¹ as is common for processes at surfaces, thus fixing the value of k_d given a value for K, leaving three free parameters: K, X, and S. Although these selections may not apply to a given system being considered for investigation, the procedure we outline below is readily amenable to generalization.

Table 1.

Parameters Governing the Behavior of G(τ)

Parameter	Description
A	average concentration of fluorescent molecules in solution
K (*)	equilibrium association constant for fluorescent molecules and surface binding sites
X(*)	product of K andA
ka (***)	kinetic association rate constant for fluorescent molecules and surface binding sites
kd	kinetic dissociation rate for fluorescent molecules and surface binding sites
S (*)	total surface site density
d (**)	evanescent wave depth
h (**)	radius of observed area
D (**)	solution diffusion coefficient of fluorescent molecules
Rz	rate for diffusion in solution of fluorescent molecules through the evanescent wave
Rr	rate for diffusion in solution of fluorescent molecules through the observed area

There are three free (*), three fixed (**) and one partially fixed (***) parameters. The other four quantities depend on different subsets of these parameters as described in the text.

This work addresses combinations of the values of the three free parameters which will reasonably allow measurement by TIR-FCS of properties describing the thermodynamic and kinetic behavior of the mechanism shown in Figure 2. The criteria that we use are defined in Table 2: (A) G(τ) decays with reasonable rapidity so that data can be acquired in a reasonable amount of time. (B) Diffusion through the evanescent wave is fast enough so that Eqs. 6 and 11 are applicable;³⁶ worth noting is that R_r only increases the decay rate of G_a(τ) over that determined by R_z.¹ (C) G_s(0) is high enough so that G_s(τ) is measurable with high accuracy. Although fluorescence fluctuation autocorrelation functions with magnitudes much lower than the minimum given in Table 2 are often measurable, in all but the simplest case (Eq. 11), G_s(τ) is not a single exponential³⁵ and higher values of G_s(0) are required to resolve, for example, the rates and relative amplitudes associated with two exponentials. (D) The magnitude of G_s(τ) is high enough so that G(τ) is not dominated by G_a(τ). (E) Significant rebinding to the surface within the observed area does not occur so that Eqs. 6 and 11 are applicable.

Table 2.

Criteria

Criterion	Description	Quantification
A	fluorescence fluctuations must be fast enough	λ ≥ 0.1 s−1
B	diffusion through the evanescent wave must be fast enough	λ ≤ 500 s−1
C	magnitude of Gs(τ) is high enough	Gs(0) ≥ 0.05
D	Gs(τ) is not overwhelmed by Ga(τ)	Gs(0)/Ga(0) ≥ 0.1
E	surface rebinding is negligible	P ≤ 0.05

This table describes the criteria used to determine conditions for which TIR-FCS can measure thermodynamic and kinetic parameters describing the interaction of fluorescent molecules with surface binding sites given that the mechanism is a simple bimolecular reaction as defined in Eq. 2.

Experimental Conditions that Meet the Criteria

Criterion A requires that the fluorescence fluctuations be fast enough for G(τ) to be measurable with a good signal-to-noise ratio. We have quantified this criterion by specifying that G_s(τ) decays with a rate ≥ 0.1 s⁻¹. Referring to Eq. 11, one sees that the decay rate for G_s(τ) will always be ≥ k_d. Thus, assuming that k_a = 10⁶ M⁻¹s⁻¹ (see above), K ≤ 10⁷ M⁻¹ (Eq. 3).

Criterion B requires that the decay rate of G_s(τ) be at least ten times slower than R_z (5000 s⁻¹). To determine k_a, it would be far above sufficient to obtain G(τ) for values of k_aA = 4k_d (λ = 5k_d in Eq. 11). In this case, the decay rate of G_s(τ) for K = 10⁷ M⁻¹ would range from 0.1 to 0.5 s⁻¹, meeting criterion B. The minimum value of 5k_d is 500 s⁻¹, implying that (with k_a = 10⁶ M⁻¹s⁻¹) K ≥ 10⁴ M⁻¹.

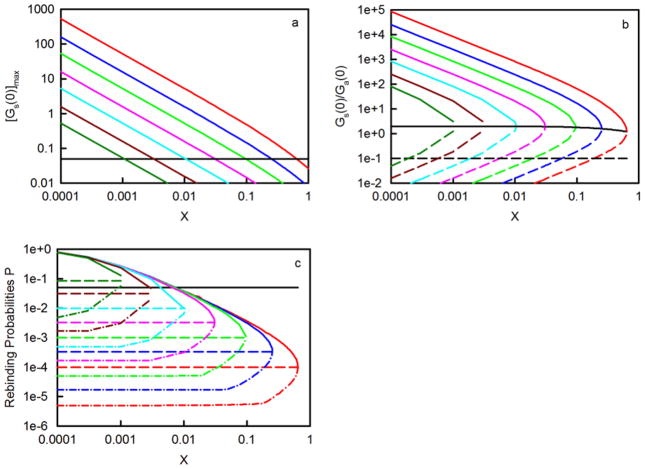
Criteron C requires that G_s(0) ≥ 0.05. Although this condition might seem to be too restrictive, it has been adopted primarily because we are ultimately interested in G_s(τ) that are more complex than Eq. 11 (see above). G_s(0) depends on three independent parameters (K, S and X) (Eq. 9), not including those that have been set at fixed values (h and d). Table 3 shows the conditions which conform to criterion C for different values of K, S and X. Worth noting first is that the partial derivative of G_s(0) with respect to X is negative, indicating that G_s(0) increases with decreasing X for set values of S and K. Second, the partial derivative of G_s(0) with respect to K is positive, indicating that G_s(0) increases with increasing K for set values of S and X. Third, the situation is a bit more complex when one considers the dependence of G_s(0) on S. In this case, each value of K and X has a value of S for which G_s(0) is maximized, found from the partial derivative of G_s(0) with respect to S. These values of S, denoted by S_max, are

Table 3.

Conditions for which Criteria A – E are satisfied

			S range			P range		ρ range		Gs(0)			Gs(0)/Ga(0)
K	X	A	lower	Smax	upper	lower	upper	lower	upper	lower	Smax	upper	lower	upper
107	0.0001	0.01	0.30	6.0	3300	5 × 10−6	0.05	0.050	550	95	530	3.8	0.10	1100
	0.300	30	0.90	7.8	68	1 × 10−5	9×10−4	0.15	11	0.050	0.14	0.050	:0.18	13
	0.643	64.3	9.9	9.9	9.9	1 × 10−4	1 × 10−4	1.6	1.6	0.050	0.050	0.050	1.2	1.2
3 × 106	0.0001	0.0333	1.0	20	3300	2 × 10−5	0.05	0.050	160	29	160	3.8	0.10	330
	0.100	33.3	2.3	22	210	4 × 10−5	0.003	0.11	10	0.050	0.14	0.050	0.19	17
	0.253	84.3	25	25	25	3× 10−4	3×10−4	1.2	1.2	0.050	0.050	0.050	1.6	1.6
106	0.0001	0.1	3.0	60	3300	5 × 10−5	0.05	0.050	55	9.5	53	3.7	0.10	110
	0.030	30	5.4	62	720	9 × 10−5	0.01	0.090	12	0.050	0.17	0.050	0.17	23
	0.0964	96.4	66	66	66	0.001	0.001	1.1	1.1	0.050	0.050	0.050	1.8	1.8
3 × 105	0.0001	0.33	10	201	3300	2× 10−4	0.05	0.050	16	2.9	16	3.4	0.10	33
	0.010	33.3	19	203	2100	3× 10−4	0.03	0.095	10	0.050	0.16	0.050	0.19	21
	0.0308	103	207	207	207	0.003	0.003	1.0	1.0	0.050	0.050	0.050	1.9	1.9
105	0.0001	1	30	602	3300	5 × 10−4	0.05	0.050	5.5	0.95	5.3	2.8	0.10	11
	0.003	30	50	604	3300	8 × 10−4	0.05	0.083	5.5	0.050	0.18	0.092	0.17	11
	0.0105	105	609	609	609	0.01	0.01	1.0	1.0	0.050	0.050	0.050	2.0	2.0
3 × 104	0.0001	3.33	100	2008	3300	0.002	0.05	0.050	1.6	0.29	1.6	1.5	0.10	3.3
	0.0010	33.3	190	2010	3300	0.003	0.05	0.094	1.6	0.050	0.16	0.15	0.19	3.3
	0.00316	105	2014	2014	2014	0.03	0.03	1.0	1.0	0.050	0.050	0.050	2.0	2.0
104	0.0001	10	301	6025	3300	0.005	0.05	0.050	0.55	0.096	0.53	0.48	0.10	1.1
	0.0003	30	502	6026	3300	0.008	0.05	0.083	0.55	0.050	0.18	0.16	0.17	1.1
	0.000965	96.5	3300	6030	3300	0.05	0.05	0.55	0.55	0.05	-	0.05	1.1	1.1
	0.00106	106	6030	6030	3300	-	-	-	-	-	-	-	-	-

K values are in units of M⁻¹, A values are in units of nM: and surface site densities are in units of molecules/μM². All other quantities are unitless. S_max was calculated by using Eq. 13. The allowed values of S range from the maximum of S₁ and S₃, to the minimum of S₂ and S₄. S₁ and S₂ were calculated by using Eq. 16, S₃ was calculated by using Eq. 18, and S₄ was found numerically as described in the text. P, ρ, G_s(0) and G_s(0)/G_a(0) were calculated for the lower and upper limits of S by using Eqs. 19 & 20, Eq. 23, Eq. 9 and Eq. 17, respectively. P, ρ, and G_s(0)/G_a(0) all increase monotonically with S. G_s(0) peaks when S = S_miK: these values were calculated by using Eq. 14.

$$S_{max}=\frac{d(1+X)}{K}$$ (13)

and are shown in Table 3. By using Eq. 13 in Eq. 9, one finds that, when S = S_max,

$${[G_s(0)]}_{max}=\frac{K}{4\pi h^{2}dX(1+X)}$$ (14)

These values are shown as upper limits in Table 3. Eq. 14 implies a maximum value of X, which is found by setting this expression equal to 0.05 and solving for X. The result is

$$X_{max}=\frac{1}{2}[-1+\sqrt{1+\frac{20K}{\pi h^{2}d}}]$$ (15)

The values of X_max are given as upper limits in Table 3. Fourth, there are two values of S for which G_s(0) = 0.05 (criterion C), denoted as S_1,2, which bracket the acceptable range of surface site densities. These values, found by setting G_s(0) in Eq. 9 equal to 0.05, are

$$S_{1,2}=\frac{10K-\pi h^{2}dX(1+X)\mp 10\sqrt{K^2-\frac{\pi }{5}{h}^2\mathit{dKX}(1+X)}}{\pi h^{2}KX}$$ (16)

S₁ and S₂ are real for X ≤ X_max. When X=X_max, the square root in Eq. 16 is zero and S₁=S₂=S_max. In some cases, the minimum value of S, S₁, is < 1 molecule/μm². Because h = 0.5 μm, the approximate size of the observed area is πh² = 0.8 μm² so that, for these low values of S, some observed areas will contain no binding sites. In other cases, the maximum value of S, S₂, is very high and may not be experimentally achievable. However, criterion E reduces these maximum values to experimentally reasonable ones (see below). The values of G_s(0) as a function of X, for different values of K and S = S_max are plotted in Figure 4a. As shown, in many cases G_s(0) ≫ 0.05.

Figure 4. Conditions Required for TIR-FCS.

In all panels, the colors denote (red) K = 10⁷ M⁻¹; (blue) K = 3 × 10⁶ M⁻¹; (green) K = 10⁶ M⁻¹; (pink) K = 3 × 10⁵ M⁻¹; (cyan) K = 10⁵ M⁻¹; (dark red) K = 3 × 10⁴ M⁻¹; and (dark green) K = 10⁴ M⁻¹. Panel (a) shows the values of [G_s(0)]_max calculated from Eq. 14 and as a function of X. In these plots, S = S_max (Eq. 13 and Table 3). The black line depicts the cutoff values of X for which G_s(0) ≤ 0.05 and criterion C is not satisfied. Panel (b) shows the values of G_s(0)/G_a(0) calculated from Eq. 17 and as a function of X. Solid, colored lines are for S = S₂ and dashed, colored lines are for S = S₁. The solid black line is for S = S_max and does not depend on K. The dashed black line shows the cutoff value below which the ratio is unacceptable according to criterion D. Panel (c) shows P calculated by numerically integrating Eq. 19 with Eq. 20. The value of k_a is taken to equal 10⁶ M⁻¹s⁻¹ and the values of S are (solid) S₂; (dash) S_max; and (dash-dot) the maximum of S₁ and S₃. The black line depicts the cut-off value for which P ≥ 0.05 and criterion E is not satisfied.

Criteron D requires that the ratio of G_s(0) and G_a(0) be ≥ 0.1, so that the long-time tail of G_a(τ) does not overlap too much with G_s(τ). This ratio (see Eqs. 9) is

$$\frac{G_s(0)}{G_a(0)}=\frac{2KS}{d{(1+X)}^2}$$ (17)

and, as shown, increases with K and S; and decreases with X and d. However, when S = S_max, G_s(0)/G_a(0) = 2/(1 + X) and depends only on X (Figure 4b). In this case, because X is always less than or approximately equal to 0.64 (Table 3), the ratio ranges from ≈ 2 at low X to 1.2, well above 0.1. In general, for a given value of K and X, an initial maximum value of G_s(0)/G_a(0) can be found with S = S₂. As shown in Figure 4b, these maximum values of the ratio are all much greater than 0.1, so that in these cases criterion D is always satisfied. However, for a given value of K and X, the minimum value of the surface site density, according to criterion C, is for S = S₁, and as shown in Figure 4b, the ratios G_s(0)/G_a(0) for S₁ are not all greater than the allowed value of 0.1. This result sets a new minimum for the site density, denoted by S₃, which is determined by setting the expression for the ratio in Eq. 17 equal to 0.1 and solving for the value of S. The values of S₃ are

$$S_3=\frac{d{(1+X)}^2}{20K}$$ (18)

The actual minimum site densities are thus equal to the maxima of S₁ and S₃ and are shown as the lower limits in the S ranges in Table 3.

Criterion E requires that rebinding to the surface after dissociation, within the observed area, is negligible. The purpose of this requirement is to ensure that Eqs. 6 and 11 are applicable, as their derivation depends on the assumption that the rates associated with rebinding are much lower than the intrinsic rates associated with the mechanism shown in Eq. 2.³⁶ As shown previously,^43,44 the probability that a molecule which dissociates from the origin at time zero has rebound at least once between positions r = 0 and r = h, and at time infinity, is

$$\begin{array}{l}P=-\underset{0}{\overset{\infty }{\int }}dt\underset{0}{\overset{2\pi }{\int }}d\varphi \underset{0}{\overset{h}{\int }}dr\frac{r}{4\pi Dt}exp(-\frac{r^2}{4Dt})\frac{\partial }{\partial t}[exp({\eta }^{2}t)\mathit{erfc}(\eta \sqrt{t})]\\ =\underset{0}{\overset{\infty }{\int }}dt[1-exp(-\frac{h^2}{4Dt})][-\frac{\partial }{\partial t}exp({\eta }^{2}t)\mathit{erfc}(\eta \sqrt{t})]\end{array}$$ (19)

In Eqs. 19, the parameter η describes the propensity for surface rebinding and is defined as

$$\eta =\frac{k_{a}S}{\sqrt{D}(1+X)}$$ (20)

Rebinding is more likely when the surface site density is higher, when the surface binding sites are less occupied, when the association kinetic rate constant is higher, and when the diffusion coefficient in solution is small. When h → ∞, the integral in Eq. 19 is⁴⁵

$${[P]}_{h\to \infty }=-\underset{0}{\overset{\infty }{\int }}dt[\frac{\partial }{\partial t}exp({\eta }^{2}t)\mathit{erfc}(\eta \sqrt{t})]={[-exp({\eta }^{2}t)\mathit{erfc}(\eta \sqrt{t})]}_0^{\infty }=1$$ (21)

A molecule which dissociates from an infinite plane always eventually rebinds somewhere on the surface. However, in the work described in this paper, h is small and the values of P are also (usually) small. Values of P as a function of X, with k_a = 10⁶ M⁻¹s⁻¹ and S = S₂, S_max, or the maximum of S₁ and S₃, were calculated by numerically integrating the second expression in Eq. 19 with Eq. 20. As shown in Figure 4c, P is usually much less than the cutoff value of 0.05. Exceptions are found for higher values of S, and lower values of X and K. For a given X value, an upper limit for S, denoted by S₄, can be found numerically for P = 0.05. These values range from 3300 – 5400 molecules/μm². The true maximum site densities are equal to the minima of S₂ and S₄ and are shown as upper limits in the S ranges in Table 3. [For the lowest K, S_max is greater than the upper limit and, when X=X_max (0.00106), the upper limit is less than the lower limit, and therefore no values of S meet all five criteria. These results set a new upper limit for X (9.65×10⁻⁴).]

Measurement of K by TIR-FCS

A first question, given that criteria A-E are satisfied, is how one might go about measuring the equilibrium association constant K by using TIR-FCS rather than steady-state TIRFM. This type of measurement might be useful for a number of situations. One class of such situations includes in vivo cases in which the parameters cannot be precisely controlled or known (e.g., when one is interested in examining reversible association of fluorescent molecules in the cytosol with sites on the cytoplasmic face of adherent cells illuminated by evanescent excitation). Another class includes those in which one finds it not to be possible to make steady-state in vitro TIRFM measurements up to A ≈ 4/K (see above) because the required higher concentrations of fluorescent ligands with good purity are not obtainable within a reasonable amount of time and expense, or precipitate and/or oligomerize at high concentrations. Thus, we define below two methods in which K might be measured by using TIR-FCS.

First, it should be noted that measures of F_pos(A) and F_neg(A) (Eq. 12) will be a natural consequence of acquiring TIR-FCS data. No extraneous steady-state TIRFM data acquisition is required. Then, from the two measured quantities, one can calculate

$$\frac{F_{\mathit{pos}}(A)-F_{\mathit{neg}}(A)}{F_{\mathit{neg}}(A)}=\frac{KS}{d}\frac{1}{1+KA}=\frac{\rho }{1+KA}$$ (22)

where the dimensionless parameter ρ is

$$\rho =\frac{KS}{d}$$ (23)

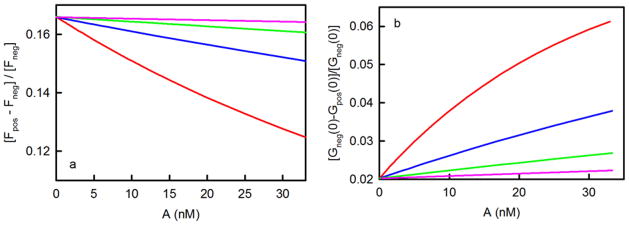
The wide range of ρ values (0.05 to 550) for different values of K and X are shown in Table 3. Curve-fitting the measured values of Eq. 22 to the form on the right side, as a function of A, will give a best-fit value for ρ and, if high enough A values are accessible, also for K. If one chooses to assume an approximate value for d,¹ then an approximate value for S can be found from ρ, K and d. Predicted data are illustrated in Figure 5a. As shown, this strategy for measuring K is more likely to be successful for higher K values. Because the accessible values of X are capped at very low values for smaller K (Table 3), in these cases Eq. 22 is approximately constant and equal to ρ. Thus, low K values are predicted to be measurable by this method only if the values of S and d are independently calibrated.

Figure 5. Measurement of K by using TIR-FCS.

In both panels, the colors denote (red) K = 10⁷ M⁻¹, (blue) K = 3 × 10⁶ M⁻¹, (green) K = 10⁶ M⁻¹, and (pink) K = 3 × 10⁵ M⁻¹; surface site densities are (red) 1, (blue) 3.33, (green) 10, and (pink) 33.3 molecules/μm²; and ρ = 0.166. Panel (a) shows the values of [F_pos(A)-F_neg(A)]/F_neg(A) calculated from Eq. 22. The intercepts equal ρ. The initial slopes equal −ρK; their magnitudes increase with K. These slopes are indicative of the ability of the proposed strategy to measure K. Panel (b) shows the values of [G_neg(0)-G_pos(0)]/[G_neg(0)] calculated from Eq. 25. The intercepts equal [ρ/(1+ρ)]². The initial slopes are 2Kρ/(1+ρ)³ and increase with K.

Because measuring equilibrium association constants by using only values of A that are less than K⁻¹ is vulnerable to potential artifacts, it is desirable to confirm the measured K value by using the information contained in the magnitudes of the acquired G(τ). There are two directly measurable quantities, G(0) in the presence and absence of surface binding sites, denoted as G_pos(0) and G_neg(0), respectively. Referring to Eqs. 6 and 9, one finds that

$$\begin{array}{l}{G}_{\mathit{pos}}(0)=\frac{2KS+d{(1+KA)}^2}{2\pi h^{2}A{[KS+d(1+KA)]}^2}\\ G_{\mathit{neg}}(0)=\frac{1}{2\pi h^{2}dA}\end{array}$$ (24)

To accurately measure these quantities, it may be necessary to account for photophysical effects that can occur at high excitation intensities and low time lags τ.^27,28 This correction is necessary only if the excitation intensity is high enough so that the measured G(τ) are dependent on it. In addition, the G(0) values must be extrapolated from G(τ) at low τ because when τ = 0 the autocorrelation functions contain contributions from shot noise. In analogy to Eq. 22, the following function can be defined:

$$\frac{[G_{\mathit{neg}}(0)-G_{\mathit{pos}}(0)]}{G_{\mathit{neg}}(0)}=\frac{KS[KS+2\mathit{dKA}]}{{[KS+d(1+KA)]}^2}=\frac{\rho (\rho +2KA)}{{(1+\rho +KA)}^2}$$ (25)

Eq. 25 is positive because G_neg(0) > G_pos(0). This at first counter-intuitive result is because, when comparing G_neg(0) to G_pos(0) for a given A value, there are fewer fluorescent molecules in the observed volume due to the lack of surface binding sites, and fewer fluorescent molecules in general translates into higher magnitudes for fluorescent fluctuation autocorrelation functions. Figure 5b shows the expected values of Eq. 25 as a function of K, A and set values of S. Curve-fitting the measured values of Eq. 25 to the form on the right side, as a function of A, will return best-fit values of ρ and, if high enough values of A are accessible, K.

Measurement of k_d, or k_d and k_a, by TIR-FCS

One way to measure k_d is by using evanescent illumination with fluorescence recovery after photobleaching.^{37,38,40,46,47} However, this method cannot directly report the value of k_a, which would need to be inferred from a previously measured value of K and the measured value of k_d (Eq. 3). TIR-FCS does not have this strict feature of reporting only k_d and not k_a; both rate constants are present in the theoretically predicted form for G(τ) (Eq. 11).

The above discussion defines conditions, as illustrated in Figures 4a-c and summarized in Table 3, for which criteria A, B, C, D and E (Table 2) are met, given assumed values of d, h, D and k_a (Table 1). Thus, for the conditions summarized in Table 3, we conclude that it is reasonable to expect that the rate associated with the exponential decay of G_s(τ) (Eq. 11) can be measured with sufficient accuracy. This rate equals k_d + k_aA and ranges from a minimum of k_d to infinity as the concentration of fluorescent molecules in solution, A, is increased. Plotting the measured rate vs. A and fitting to a line will in general yield an intercept of k_d and a slope of k_a.

The relaxation rate will increase fast enough with A for k_a to be directly measurable only if higher values of A are accessible. However, as shown in Table 3, it is the higher rather than lower values of A = X/K that limit the range of applicability. Rewriting the relaxation rate as k_d(1+ X) shows that the measurable rate will increase only by a percentage determined by X. In particular, the prediction is that the measured relaxation rate will exceed k_d only by ≈ 65% for K = 10⁷ M⁻¹; by ≈ 25% for K = 3 × 10⁶ M⁻¹s⁻¹; and by less than 10% for K = 10⁶ − 10⁴ M⁻¹. Thus, for low K values TIR-FCS will yield a measure of k_d, but not k_a. Subsequently, k_a can be inferred from the measured values of K and k_d (Eq. 3) in which K is measured either with steady-state TIRFM, TIR-FCS or with another method.

For higher values of K, k_a will be directly measurable by TIR-FCS. First, for K = 10⁷ M⁻¹, the relaxation rate is expected to be measurable through a range of k_d to 1.6 k_d and, given the accuracy of current FCS apparatuses, this range will most likely be wide enough for a direct measure of k_a. This optimal case is illustrated in Figures 6a-c. Figure 6a shows the predicted values of G(τ) as a function of τ, for four values of X and other defined experimental conditions. What is immediately obvious from this plot is that the main effect of increasing the solution concentration of fluorescent molecules is that G(0) is dramatically decreased. Figure 6b shows the predicted values of G(τ)/G(0) as a function of τ, for the same four values of X and the same other presumed experimental conditions. This plot shows that, when one changes A (and therefore X), the primary effect is that the fractional contributions to G(τ) arising from G_s(τ) and G_a(τ) change (Eq. 17); as expected, the contribution from G_s(τ) relative to that from G_a(τ) decreases with increasing X. This feature is a consequence of two effects (Eq. 5 and 7). As X is increased, both N_C/N_A and N_B/N decrease as (1+X)⁻¹. Figure 6c shows G_s(τ)/G_s(0) for the four chosen values of X. As shown, the decay rate increases with increasing concentrations of fluorescent reporter molecules. The case of K = 3 × 10⁶ M⁻¹ is illustrated in Figures 6d-f. The same features are present, except that G_s(τ)/G_s(0) changes only slightly with X. Thus, accurate measurement of k_a will be possible only for experimental situations in which both K and the signal-to-noise ratio of G(τ) are high.

Figure 6. Measurement of k_d, or k_d and k_a, by TIR-FCS.

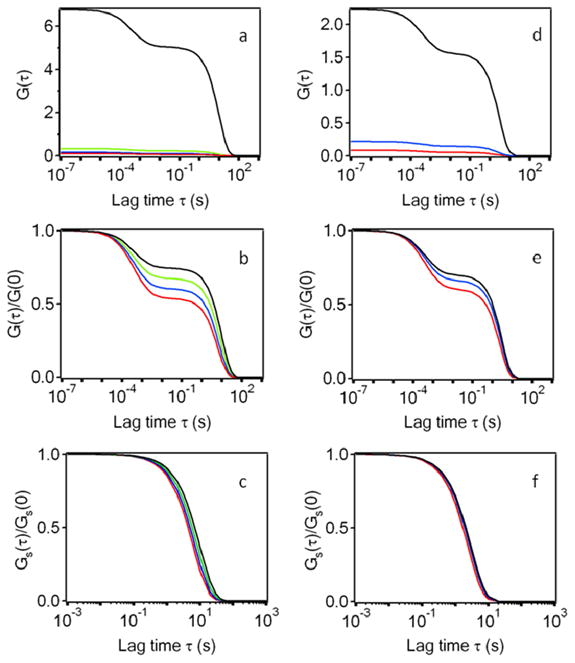
Panels (a) and (d) show G(τ) calculated from Eqs. 6 and 9–11. Panels (b) and (e) show G(τ)/G(0). Panels (c) and (f) show G_s(τ)/G_s(0). In all cases, D = 50 μm²s⁻¹, d = 0.1 μm, and h = 0.5 μm. In (a-c), K = 10⁷ M⁻¹, k_d = 0.1 s⁻¹, S= 9 molecules/μm² and X is (red) 0.6, (blue) 0.4, (green) 0.2 or (black) 0.01. In (d-f), K = 3 × 10⁶ M⁻¹, k_d = 0.33 s⁻¹, S= 24 molecules/μm² and X is (red) 0.25, (blue) 0.1, or (black) 0.01.

DISCUSSION

Summary of Results

Conditions for which TIR-FCS measurements aimed at quantifying the thermodynamic and kinetic parameters associated with a simple, reversible association of fluorescent ligands with immobilized, non-fluorescent surface binding sites have been defined in detail, for assumed values of the solution diffusion coefficient D (50 μm²s⁻¹), the evanescent wave depth d (0.1 μm), the radius of the observed area h (0.5 μm) and for a (usually) assumed value of the association rate constant k_a (10⁶ M⁻¹s⁻¹) (Table 1). The conditions are defined by five criteria as described in Table 2. Only values of the solution concentration of fluorescent molecules A which are greater than or equal to 10⁻⁴/K, where K is the equilibrium constant, were considered.

Meeting the criteria gave the following results, as shown in Table 3 and Figure 4: 1) K is limited to the range 10⁴ − 10⁷ M⁻¹. 2) For a given K, there is a maximum allowed value of A. These maximum values range from 64–100 nM and correspond to lower values of the product X = KA with decreasing K. For K = 10⁷ M⁻¹, the maximum value of X is 0.643 and for K = 10⁴ M⁻¹, the maximum value of X is 10⁻³. 3) Ranges of allowed total surface site densities, S, exist for given values of K and A. 4) G_s(τ), the quantity of interest, is maximized at a defined surface site density for given K and X values.

As illustrated in Figure 3, the most straightforward method of measuring K is to use steady-state TIRFM. However, this method is expected to be successful only for higher values of K and S. Measuring the lowest value of K (10⁴ M⁻¹) is expected to be possible only if a total surface site density ≥ 12,000 molecules/μm² can be experimentally generated. At the highest limit of K = 10⁷ M⁻¹, only very low total surface site densities, ≥ 12 molecules/μm², are predicted to be required. In addition, high A values must be experimentally accessible.

Two alternative methods for measuring K with TIR-FCS were also described. The first method uses the average fluorescence intensities in the presence and absence of binding sites, which will be found as a natural consequence of TIR-FCS measurements (Figure 5a). The second method uses G(0) values in the presence and absence of binding sites (Figure 5b). These methods are most likely to be successful either for high K or when S and d are independently calibrated.

It is desirable, in general, to independently measure all three parameters (K, k_a, and k_d) governing the mechanism shown in Eq. 2 and Figure 2 and to confirm their consistency (Eq. 3). However, as described in the text, both k_a and k_d are expected to be measurable only for higher K values (Figure 6). For lower values of K, TIR-FCS will yield only a measure of k_d. In these cases, k_a can be inferred from measured values of K and k_d.

Comparison with Experimental Results

Of interest is the comparison of the theoretical predictions described here with previously obtained experimental TIR-FCS data. The earliest attempt at characterizing surface binding kinetics by using TIR-FCS was carried out for the nonspecific, reversible interaction of fluorescently labeled IgG with albumin-coated surfaces.²¹ G(0) values were lower than those considered here (about 0.02) but were dominated by contributions from surface kinetics in that G_s(0)/G_a(0) was greater than 10. However, the characteristic time for the decay of G(τ) was fast (several ms), and theoretical considerations suggested that the autocorrelation functions were dominated by contributions from surface rebinding. Fitting the data to a form that accounted for this probable effect gave k_d = (0.4 ms)⁻¹. This first work demonstrated the feasibility of TIR-FCS and provided a basis for future development.

In a subsequent work, extrapolated G(0) values from TIR-FCS measurements were used to measure equilibrium association constants for rhodamine 6G with C-18 derivatized fused silica, with the intent of better understanding reversed-phase chromatography.²² Measurements were carried out for a range of water/methanol solutions and NaCl concentrations. The measured K values were very low, ranging from ≈ 3 to ≈ 20,000 M⁻¹. That such weak equilibrium association constants were measured is at first seemingly inconsistent with the results shown in Figure 5 and described in the associated text. One difference is that the probe concentrations were very low (50 pM − 1 nM) so that the values of X were much lower than those considered here (Table 3). Thus, the measured K values were obtained very far from the midpoint of the binding isotherm and must be taken as apparent K applicable to very low solution concentrations. However, the primary reason that such low K values were measurable (and with good accuracy) is not the low probe concentrations. The reason appears to be that a much different method than the ones considered here was used. The method incorporated direct calibration of Q (Eqs. 12) and the observation volume. In addition, the method did not use only the normalized fluorescence fluctuation autocorrelation function (Eq. 1) but instead used both the measured numerator extrapolated to τ = 0, <δF²>, and the measured average fluorescence, <F>, as independent quantities.

In a very elegant companion study, the kinetics of rhodamine 6G reversibly associating with C-18 derivatized fused silica were examined.²³ These measurements were also carried out for conditions of very low K (≈ 3 to 2000 M⁻¹) and A (50 pM − 1 nM). A number of features of this work are noteworthy. First, G(τ) were analyzed by using a more complex expression previously derived^36,37 which includes contributions arising from a rate related to surface rebinding,^43,44 and these contributions were not negligible. Second, in most cases, G(0) was much lower than considered in this work (≈ 5 × 10⁻⁴ to 5 × 10⁻³). Nonetheless, by estimating the rates associated with diffusion through the evanescent wave and with rebinding and fixing these rates before curve-fitting, values of the relaxation rate k_aA + k_d were measured. Not surprisingly, because the X values were so low, this rate was dominated by k_d, which ranged from ≈ 40 to 4000 s⁻¹. Previously measured values of K were then used to calculate k_a, which ranged from ≈ 10⁴ to 10⁵ M⁻¹s⁻¹. In comparison to the results described herein, this work highlights the fact that the criteria defined in Table 2 are more restrictive than is necessary. We have adopted the more restrictive criteria because of the goal of using a single fluorescent reporter to measure the thermodynamic and/or kinetic parameters associated with non-fluorescent species involved in more complex surface binding mechanisms (see below).

In a somewhat similar set of measurements, the kinetics of fluorescently labeled polyamidoamine dendrimers (with different sizes) at fused silica surfaces were characterized by using TIR-FCS.¹⁶ Equilibrium constants were found from G(0) values along with other calibrations, and ranged from 5 × 10⁴ to 2 × 10⁶ M⁻¹. The solution concentrations were very low, corresponding to much lower values of X than those considered here; the G(0) values were very low; and the surface site densities were also higher than the maximum values shown in Table 3. The low X values are predicted to preclude direct measurement of k_a, and this prediction was in fact observed. The high surface site densities should in theory result in significant rebinding, removing the ability of TIR-FCS to measure k_d. However, significant flow was included in this work, removing complications from rebinding, and values of k_d ranging from 6 to 70 s⁻¹ were measured. Association rate constants k_a were inferred from the measured values of K and k_d and ranged from 3 × 10⁶ to 10⁷ M⁻¹s⁻¹. Overall, the experimental results described in this work are consistent with our theoretical predictions. The results also provide a direct demonstration that flow can remove constraints arising from rebinding and that it is possible to work at very low G(0) values given adequate instrumentation.

The first use of TIR-FCS to examine the kinetics of the reversible association of fluorescent ligands with specific, molecular surface binding sites was carried out for fluorescently labeled IgG reversibly associating with the mouse Fc receptor FcγRII reconstituted into planar phospholipid bilayers formed on fused silica surfaces.²⁵ There is a difficulty in comparing the results with those described herein because a tracer amount of labeled IgG was combined with a large excess of unlabelled IgG so that the total ligand concentration was close to the mid-point of the binding isotherm. The effects of the presence of the non-fluorescent competitors on TIR-FCS data have been formally defined³⁵ but have not yet been fully explored theoretically in a manner comparable to the work described here. Nonetheless, the data conformed in a general manner with theoretical expectations.²⁵

TIR-FCS has recently been used to examine the kinetics of fluorescently labeled bovine serum albumin and Thermomyces lanuginosus lipase with C₁₈-coated glass in the presence of surfactants.²⁴ Again, it is difficult to compare the results reported in this work with the ones described herein, for several reasons. First, the surfactants can act as inhibitors of surface adsorption both by competitively occupying surface binding sites and by directly interacting with the proteins in solution. Also, in several of the measurements, free dye was present in addition to labeled proteins, photobleaching of tightly bound proteins was observed, the excitation intensities were high enough to produce photophysical effects at short times in the G(τ), and the systems were not at equilibrium. Nonetheless, this work provides a good deal of useful information about carrying out TIR-FCS when competitors are present (as well as providing information about the protein adsorption process itself) and highlights the need for a more thorough theoretical understanding of how TIR-FCS might be used to examine surface binding kinetics for mechanisms more complex than a simple, reversible association between fluorescent ligands in solution and non-fluorescent surface binding sites.

Enzyme kinetics at surfaces have also been investigated by using TIR-FCS.²⁶ In these measurements, the reduction of dihydrorhodamine 123 to the highly fluorescent rhodamine 123, as catalyzed by immobilized horseradish peroxidase (HRP), was followed. Single enzymes were located by using a CCD camera, and time-dependent fluorescence intensity data were obtained using a single-photon counting silicon avalanche photodiode. The autocorrelated fluorescence data were fit to a phenomenological expression for G(τ) which contained a term describing the diffusion of fluorophores through the observation volume and two terms describing the enzyme kinetics. For the last two terms, the multi-step enzyme mechanism was approximated as a unimolecular isomerization; one term was a stretched exponential with rate k₁ describing formation of the fluorescent enzyme-product complex and the other term was a simple exponential with rate k₂ describing all other steps in the mechanism. The total concentration of dihydrorhodamine 123 was ≈ 100–500 nM and the density of immobilized enzymes was 0.1 per μm². The value of R_z was measured in regions not containing enzymes and was found to be (18 μs)⁻¹, which is somewhat higher than theory predicts even for fast rhodamine diffusion, but not completely unreasonable. A result that is inconsistent with theoretical predictions was the measured G(0) values, which were higher in the presence relative to the absence of enzyme. This inconsistency may be a simple consequence that the work shows only representative G(τ) and not averages of G(0) from many positions. The ratios of G_s(0) to G_a(0) were greater than one, more than adequate for measuring surface kinetics, and the values of G(0) were quite high enough (0.2–0.4) for good signal-to-noise ratios. The measured values of k₂ were ≈ 1000 s⁻¹ and the measured values of k₁ were ≈ 15000 s⁻¹. Particularly the k₁ values do not comply with our criterion B, which may explain the somewhat fast measured value of R_z. Nonetheless, this work is seminal in that it demonstrates the ability of TIR-FCS to probe enzyme kinetics. The work also indicates that further work describing the nature of TIR-FCS kinetic data for different enzyme mechanisms is needed.

A series of three papers demonstrates the ability of TIR-FCS to probe the partitioning of fluorescent biomolecules between the cytoplasm and the inner face of the basal plasma membrane of adherent cells. In the first work, membrane binding of farnesylated EGFP in HeLa cells was examined.⁷ Autocorrelation data were analyzed with a model accounting for fast diffusion in solution coupled with slower diffusion on the membrane. The fractions of the magnitudes of the measured G(τ) associated with solution and membrane diffusion were found to be 0.72 and 0.28, respectively; and the times R_r⁻¹ associated with these fractions were 3.3 and 65 ms, respectively. In a similar work, membrane binding of EGFP-conjugated protein kinase C in HeLa cells was examined.⁸ The fractions of G(τ) associated with solution and membrane diffusion, and the associated times R_r⁻¹, were 2.5 ms (0.82) and 160 ms (0.18). After treatment with ATP, these parameters changed to 4.4 ms (0.69) and 140 ms (0.31), suggesting an ATP-induced shift towards membrane binding. The most important conclusion to be derived from these studies is that TIR-FCS can be successful in living cells. In the third paper, the work was extended by using seven different spatially separated observation volumes, each having its own photomuliplier as a detector.²⁹ This study represents a first step towards creating a kinetic map of intracellular dynamics occurring on or near basal cell membranes.

There is an important feature related to the application of TIR-FCS to live cells that becomes apparent when considering the results of these three studies in relation to the work described herein. Possible contributions to G(τ) arising from association/dissociation kinetics at the cell membrane were not considered. In its simplest form, TIR-FCS can provide information about association and dissociation kinetics only if the times related to these processes are faster than the times for diffusion on the surface through the observed area. Because this area is usually required to be small to limit the average number of fluorescent molecules in the observation volume, obtaining information about on/off kinetics will be possible only if the membrane diffusion coefficient is slow enough and only through careful analysis as a function of the size of the observed area, to separate contributions from lateral mobility and surface binding kinetics. In the work described above, the membrane diffusion coefficients were on the order of 10⁻⁹ cm²s⁻¹ and the associated transport times were ≈ 150 ms; thus, only kinetic processes on the order of or faster than this time would be detectable. However, in many cases, apparent membrane diffusion coefficients could be much slower, making measurement of dissociation rates and/or association kinetic rate constants more tractable.

An extensive study of paxillin dynamics in focal adhesions of migratory cells has recently been reported.³⁰ This work examined the behavior of EGFP-conjugated, cytosolic paxillin in adherent CHO cells by using a large variety of state-of-the art fluorescence microscopy methods. Of the many methods employed, one was TIR-FCS coupled not with a single-point detector but with a fast imaging camera. This approach allows calculation of G(τ) from very many positions by auto-correlating the fluorescence fluctuations from single pixels.³³ In the paxillin study, because the frame acquisition rate was ≈ 100 Hz, temporal contributions to the G(τ) from diffusion of the labeled paxillin through the depth of the evanescent wave were largely excluded. The G(τ) were fit to exponential decays (Eq. 11), yielding exchange rates that varied with position from 0.1 s⁻¹ to 10 s⁻¹. By combining these results with those found from a number of other methods, considerable information about the role of paxillin in migratory cells was obtained. This work demonstrates that imaging TIR-FCS is extremely promising in the context of creating “kinetic maps” for fluorescently labeled molecules reversibly associating with the inner face of the plasma membrane of adherent cells and correlating the observed kinetics with other molecular details of the plasma membrane.

Expanded Range

Upon review of the available experimental data, it becomes apparent that TIR-FCS has been successfully carried for conditions that do not conform to our criteria (Table 2). The most glaring discrepancy is in our definition of the minimum allowable value of G_s(0). Therefore, we have carried out calculations in which the minimum value of G_s(0) is not 0.05 but can also be 0.01, 0.005 or 0.001. The results of these calculations are given in the Supplementary Material. By comparing this material with Table 3 and Eqs. 13–18, the following conclusions can be made: 1) The values of X = KA can be considerably higher if it is possible to work at lower values of G_s(0) than those specified by Criterion C. For example, if the minimum allowed value of G_s(0) is 0.001, for K = 10⁷ M⁻¹, X values as high as 6.8 can be tolerated, and for K = 3 × 10⁴ M⁻¹, X values up to 0.14 are predicted to be tolerable. These higher values of X would make it more likely that k_a, in addition to k_d, could be measured. Higher X values would also facilitate measurement of a broader range of K values by using either F_pos(A) and F_neg(A), or G_pos(0) and G_neg(0). 2) The minimum and maximum values of the surface site densities set by the minimum value of G_s(0), S₁ and S₂, are lower and higher, respectively, for given values of K and X. 3) The surface site densities at which G_s(0) is maximized, S_max, do not change. 4) The minimum surface site densities set by Criterion D, S₃, do not change. 5) The rebinding probabilities P depend only on S, X, k_a and D. Thus, changing Criterion C does not change the maximum surface site densities S₄ set by Criterion E. 6) Reducing the minimum allowed value of G_s(0) changes the ratios G_s(0)/G_a(0) in a rather complex manner. However, this ratio is still always much greater than 0.1, for the conditions considered, when S = S_max. 7) The rebinding probabilities also change, but are often very low, remain equal to 0.05 when S = S₄, and are always less than 0.05 when S = S_max.

Future Directions

The use of TIR-FCS to quantify the thermodynamic and kinetic parameters governing the reversible association of fluorescent ligands with non-fluorescent surface binding sites shows great promise. However, the large number of parameters that affect the ability of TIR-FCS to provide information about surface binding kinetics complicates experimental design. The work described herein provides a comprehensive guide that addresses this issue. The theoretical predictions should be testable by careful in vitro measurements as a function of K, k_a, k_d, A, S, d, h, D and the excitation intensity. Only a simple reversible bimolecular reaction between soluble, fluorescent ligands and laterally immobile, non-fluorescent surface binding sites has been addressed here, but in many cases a more complex situation will be of interest. However, understanding this first simple mechanism in the context of TIR-FCS is a pre-requisite for extension to more complex processes, the need for which becomes evident after reviewing prior, related experimental results. Three extensions of interest are as follows: 1) the use of a single fluorescent reporter in solution to examine the thermodynamic and kinetic parameters describing the interaction of soluble, non-fluorescent molecules that compete with the fluorescent reporters for occupation of the surface binding sites; 2) the use of a single fluorescent reporter in solution to examine the thermodynamic and kinetic parameters describing the interaction of soluble, non-fluorescent molecules with the surface binding sites that subsequently inhibits or enhances the interaction of the fluorescent reporters with the surface binding sites; and 3) the use of a single fluorescent reporter in solution to investigate its interaction with soluble, non-fluorescent molecules that inhibit or enhance the interaction of the fluorescent reporter with the surface binding sites. All three of these extensions are quite important for processes in which the non-fluorescent molecules of interest are too small to be directly conjugated to a fluorophore without perturbing the values of the parameters of interest. As described above, additional extensions of interest include application of TIR-FCS to enzyme kinetics; multivalent, fluorescent ligands; and cellular or other processes in which the binding sites are laterally mobile.