Drosophila Gene Expression Pattern Annotation Using Sparse Features and Term-Term Interactions

Abstract

The Drosophila gene expression pattern images document the spatial and temporal dynamics of gene expression and they are valuable tools for explicating the gene functions, interaction, and networks during Drosophila embryogenesis. To provide text-based pattern searching, the images in the Berkeley Drosophila Genome Project (BDGP) study are annotated with ontology terms manually by human curators. We present a systematic approach for automating this task, because the number of images needing text descriptions is now rapidly increasing. We consider both improved feature representation and novel learning formulation to boost the annotation performance. For feature representation, we adapt the bag-of-words scheme commonly used in visual recognition problems so that the image group information in the BDGP study is retained. Moreover, images from multiple views can be integrated naturally in this representation. To reduce the quantization error caused by the bag-of-words representation, we propose an improved feature representation scheme based on the sparse learning technique. In the design of learning formulation, we propose a local regularization framework that can incorporate the correlations among terms explicitly. We further show that the resulting optimization problem admits an analytical solution. Experimental results show that the representation based on sparse learning outperforms the bag-of-words representation significantly. Results also show that incorporation of the term-term correlations improves the annotation performance consistently.

1. INTRODUCTION

Gene expression in a developing embryo is modulated in particular cells in a time-specific manner. This leads to the development of an embryo from an initially undifferentiated state to increasingly complex and differentiated form. The patterning of the model organism Drosophila melanogaster along the anterior-posterior and dorsal-ventral axes represents one of the best understood examples of a complex cascade of transcriptional regulation during development. Systematic understanding of the regulatory networks governing the patterning is facilitated by the atlas of patterns of gene expression, which has been produced by the in situ hybridization technique and documented as digital images [24, 10]. Such images capture the spatial and temporal patterns of gene expression at the cellular level and provide valuable resources for explicating the gene functions, interactions, and networks during Drosophila embryogenesis [12, 4]. To provide text-based pattern searching, the gene expression pattern images in the Berkeley Drosophila Genome Project (BDGP) high-throughput study are annotated with anatomical and developmental ontology terms using a controlled vocabulary (CV) [24, 25] (Figure 1). Currently, the annotation is performed manually by human curators. However, the number of available images is now rapidly increasing [11, 6, 27, 26]. It is therefore important to design computational methods to automate this task [8].

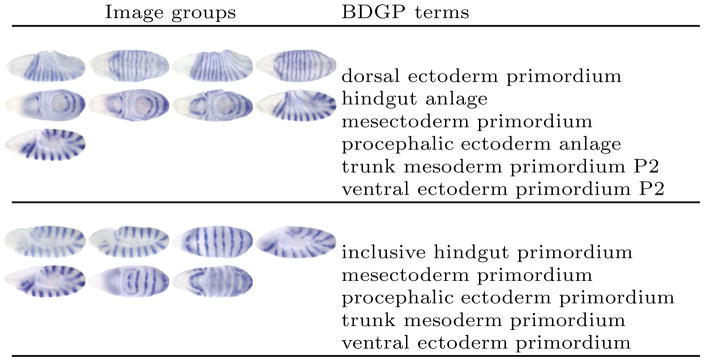
Figure 1.

Sample image groups and the associated terms in the BDGP database for the gene engrailed in stage ranges 7–8 (top) and 9–10 (bottom).

The gene expression pattern annotation problem can be formulated as an image annotation problem, which has been studied in computer vision and machine learning in the case of natural images. Although certain ideas from natural image annotation can be employed to solve this problem, significant challenges remain. Specifically, the gene expression pattern images are currently annotated collectively in small groups based on genes and developmental stages (time) using a variable number of terms in the original BDGP study (Figure 1). Since not all terms assigned to a group of images apply to every image in the group, we need to develop approaches that can retain the original group information of images. It has been shown that the annotation performance can be adversely affected if such groups are ignored, i.e., assuming that all terms are associated with all images in a group [8, 7, 13]. Moreover, images in the same group may share certain anatomical and developmental structures, hence, the terms in the CV are correlated. It is thus desirable to exploit this correlation information in the annotation process. In addition, the Drosophila embryos are 3D objects, and they are documented as 2D images taken from multiple views. Since certain embryonic structures can only be seen in specific two-dimensional projections (views), it is beneficial to integrate images with different views to make the final annotation.

In this paper, we present a systematic approach for annotating gene expression pattern images. We consider both improved feature representation and novel learning formulation to boost the performance of this annotation task. The proposed feature representation scheme is motivated from the bag-of-words scheme commonly used in visual recognition problems. In this approach, features are extracted from local patches on the images, and they are quantized to form the bag-of-words representation based on a pre-computed codebook. In our approach, visual features are extracted from local patches on each image in a group, so that the group information of images is retained as in the BDGP study. To integrate images with multiple views, we propose to construct a separate codebook for images with the same view and represent each image group as multiple bags. One major limitation of the bag-of-words approach is that each feature vector is only quantized to the closest code-book word, resulting in quantization errors. To overcome this limitation, we propose to encode each feature vector using multiple codebook words simultaneously. Specifically, we propose to determine the number of codebook words and their weights used to represent each feature vector automatically using the sparse learning framework.

In the design of learning schemes for the annotation task, we consider formulations that can incorporate the correlations among terms explicitly. Since not all terms are correlated and the degrees of correlation for different pairs of terms vary, we propose a regularization framework that imposes local constraints on the models so that only models for correlated terms are constrained to be similar. We further show that the resulting optimization problem admits an analytical solution. Experimental results on the images from the FlyExpress database (www.flyexpress.net) show that the representation based on sparse learning outperforms the bag-of-words representation significantly. Results also show that incorporation of the term-term correlations improves the annotation performance consistently.

2. FEATURE EXTRACTION AND CODEBOOK CONSTRUCTION

2.1 Feature Extraction

The images in the FlyExpress database [10] have been standardized semi-automatically, including alignment. We propose to use local features extracted from local patches on the images for the annotation task, since such features are more robust than global features [16]. The methods for localizing patches on images can be categorized into three classes including affine-region-detector-based methods [17], sampling-based methods [19], and regular-patch-based methods [3]. We extract dense features on regular patches on the images, since such features are commonly used for aligned images. Due to the limitations of the image processing techniques, local variations may exist on the images. Thus, we extract invariant features from each regular patch. In this paper, we apply the SIFT descriptor [14] to extract local visual features, since it has been applied successfully to other image-related applications [16]. Specifically, each feature vector is computed as a set of orientation histograms on 4 × 4 pixel neighborhoods, and each histogram contains 8 bins. This leads to a SIFT feature vector with 128 (4 × 4 × 8) dimensions on each patch. Note that although the invariance to scale and orientation no longer exists since we do not apply the SIFT interest point detector, the SIFT descriptor is still robust against the variance of position, illumination and viewpoint.

2.2 Codebook Construction

The images in the BDGP high-throughput study are annotated collectively in small groups based on the genes and the developmental stages. We propose to encode each image group as a feature vector based on the bag-of-words and the sparse coding representations. Both of these two schemes are based on a pre-computed codebook, which consists of representative local visual features computed on the images. The codebook is usually obtained by applying a clustering algorithm on a subset of the local features, and the cluster centers are then used as the visual words of the codebook.

The 3D nature of the embryos and the 2D layout of the images determine that certain body parts can only be captured by images taken from certain views. We propose to construct a separate codebook for images with the same view. In particular, we consider images taken from the lateral and the dorsal views, since the number of images from other views is small. For each stage range, we build a separate codebook for images with each view. Since the visual words of the codebooks are expected to represent the embryonic structures, the images used to build the codebooks should contain all the embryonic structures that the system is expected to annotate. Hence, we extract codebook images in a way so that each embryonic structure appears in at least 10 and 5 images for lateral and dorsal views, respectively, based on the total number of images with each view. The SIFT features computed from regular patches on the code-book images are then clustered using the k-means algorithm. Since this algorithm depends on the initial centers, we repeat the algorithm with ten random initializations from which the one resulting in the smallest summed within-cluster distance is selected. The number of clusters (i.e., the codebook size) is set to 2000 and 1000 for lateral and dorsal images in the experiments, respectively.

3. IMAGE GROUP REPRESENTATION

The proposed image group representation scheme is motivated from the bag-of-words approach commonly used in image and video analysis problems [21, 18]. In this approach, invariant features are extracted from local patches on images or videos, and each feature in a test image or video is then quantized based on a pre-computed codebook. Hence, an entire image or video is represented as a global histogram counting the number of occurrences of each word in the code-book. To integrate images taken from multiple views of the 3D embryos, we propose to extract local visual features from each image in a group and represent the images in the same group with the same view as a bag of visual words. Groups that contain images with multiple views can thus be represented as multiple bags of visual words, one for each view. The bags for multiple views can then be concatenated to annotate the image groups collectively. One limitation of the bag-of-words approach is that features are only quantized to the closest visual words, which may cause quantization errors. We thus propose to enhance the bag-of-words approach using sparse coding techniques. Experiments in Section 5 show that such technique improves the annotation performance consistently.

3.1 The Bag-of-Words Approach

After the codebooks for both views are constructed, the images in each group are quantized separately for each view. In particular, features computed on regular patches on images with a certain view are compared with the visual words in the corresponding codebook, and the word closest to the feature in terms of Euclidean distance is used to represent it. Then the entire image group is represented as multiple bags of words, one for each view. Since the order of the words in the bag is irrelevant as long as it is fixed, the bag can be represented as a vector counting the number of occurrences of each word in the image group.

Let a₁, ···, a_d ∈ ℝ^r be the d cluster centers (codebook words) and let u₁, ···, u_s ∈ ℝ^r be the s features extracted from images in a group with the same view, where r is the dimensionality of the local features (r = 128 for SIFT). Then the bag-of-words vector x is d-dimensional, and the i-th component x_i of x is computed as

$$x_i=\sum _{j=1}^s\delta (i,arg\underset{p}{min}||u_j-a_p||),$$

where δ(a, b) = 1 if a = b, and 0 otherwise, and ||·|| denotes the vector 2-norm. Note that ${\sum }_{i=1}^m{x}_i=s$, since each feature is assigned to exactly one word.

Based on this construction, the vector representation for each view can be concatenated so that the images in a group with different views are integrated. Let x^l and x^d be the bag-of-words vector for images in a group with lateral and dorsal views, respectively. Then the bag-of-words vector x for the entire image group can be represented as

$$x=[x^l,x^d].$$

The length of the final vector representing an image group is 3000 (2000+1000) in our implementation. To account for the variability in the number of images in each group, we normalize the bag-of-words vector to unit length.

3.2 The Sparse Coding Approach

One major limitation of the bag-of-words approach is that the representation is obtained by the hard assignment approach in which a local feature vector is only assigned to its closest visual word. It could be the case that a feature vector is very close to multiple words in the codebook, and it is thus desirable to represent this feature vector using all of them. Indeed, a recent study has shown [20] that the soft assignment approach that assigns each feature vector to multiple visual words based on their distances usually results in improved performance. However, there is no principled way to determine the number of visual words to which a feature vector should be assigned. In the following, we propose to address this issue by relying on the sparse learning framework.

Let A = [a₁, ···, a_d] ∈ ℝ^r×d denote the codebook matrix in which ${\{a_i\}}_{i=1}^d$ are the visual words. Given a feature vector u, the traditional bag-of-words approach assigns u to the closest visual words and represents u as a d-dimensional vector x in which the entry corresponding to the closest visual word is one, and all other entries are zero. This reduces to computing x by solving the following optimization problem:

$$\underset{x}{min}\frac{1}{2}{\left|\right|Ax-u\left|\right|}^2$$ (1)

subject to the constraint that only one entry in x is one, and all other entries are zero. A natural extension of this hard assignment approach is to remove the constraint on x. This, however, may yield x that is not sparse at all, i.e., the local feature u is mapped to a large number of visual words simultaneously.

To achieve a compromise between these two extreme cases, we propose to compute x by solving the following optimization problem:

$$\begin{array}{ll}\underset{x}{min}& \frac{1}{2}{\left|\right|Ax-u\left|\right|}^2+\lambda {\left|\right|x\left|\right|}_1\\ \text{subject}\text{to}& x_i\ge 0,\text{for}i=1,\cdots ,d,\end{array}$$ (2)

where λ > 0 is a tunable parameter and ${\left|\right|x\left|\right|}_1={\sum }_{i=1}^d\mid x_i\mid$ denotes the vector 1-norm. The problem in Eq. (2) is the ℓ₁-regularized regression problem called “lasso” [22] with the additional nonnegativity constrain. It is well-known the solution to this problem is sparse in the sense that many entries in x will be set to zero. Recently, many algorithms for solving the lasso problem have been proposed such as the coordinate descent algorithm [5].

4. A LOCAL REGULARIZATION FORMULATION

Given the bag-of-words and the sparse coding representations of image groups, we develop a framework for annotating the gene expression pattern images in this section. The proposed framework can incorporate the correlations among different terms by constraining the models for correlated terms to be similar. We further derive an analytical solution to the resulting problem.

4.1 The Proposed Formulation

Let $X=[x_1^T,\cdots ,x_n^T]\in {\mathbb{R}}^{n\times d}$ be the data matrix derived from the bag-of-words or the sparse coding representations, where x_i ∈ ℝ^d is the representation for the ith image group (sample), and let Y ∈ ℝ^n×k be the label indicator matrix defined as

$$Y_{ij}=\{\begin{array}{ll}1\hfill & \text{if}\text{the}i-\text{th}\text{sample}\text{has}\text{the}j\text{th}\text{label}\hfill \\ -1\hfill & \text{otherwise},\hfill \end{array}$$ (3)

where n is the number of training samples, d is the data dimensionality, and k is the number of terms. Given a prescribed loss function ℓ(·, ·), we propose to build k models ${\{f_i\}}_{i=1}^k$ by minimizing the following regularized empirical risk function:

$$\sum _{i=1}^k\sum _{j=1}^n\ell (f_i(x_j),Y_{ji})+\lambda \mathrm{\Omega }(f),$$ (4)

where $f\triangleq {\{f_i\}}_{i=1}^k$, Ω(·) is some regularization functional, and λ > 0 is the regularization parameter. Many multi-task learning formulations constrain the multiple models by employing different forms of regularization on f [2, 1].

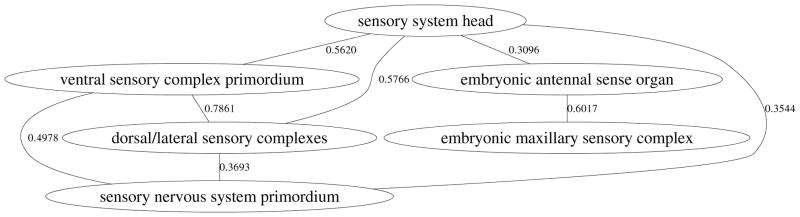
We build a model for each term in the one-against-rest manner. Since certain groups of terms from the CV are highly correlated, it is desirable to constrain the models for correlated terms to be similar. In this paper, we use the Pearson’s correlation coefficient computed on columns of the label indicator matrix Y as our measure of term correlation. Figure 2 shows the Pearson’s correlation coefficients computed on two data sets from stage ranges 11–12 and 13–16 with 50 and 60 terms, respectively. It can be observed that a significant number of terms show different degrees of correlation. To visualize the correlation graph, we show in Figure 3 one of the connected components in the correlation graph in stage range 13–16 after removing correlations below 0.3. We can observe that all terms in this graph are related to the sensory system. Based on these observations, we propose a particular form of regularization that can constrain the models for correlated terms to be similar.

Figure 2.

The Pearson’s correlation coefficients computed on the columns of the label indicator matrix using two data sets from stage ranges 11–12 (left figure) and 13–16 (right figure) with 50 and 60 terms, respectively.

Figure 3.

The term-term interaction graph computed using the Pearson’s correlation coefficient for terms in stage range 13–16. The vertices represent terms and edges represented the correlations between terms. The graph shown in this figure is one of the connected components after the correlation coefficients are thresholded at 0.3.

In the following, we consider linear models:

$$f_i(x_j)=w_i^T{x}_j+b_i,\text{for}i=1,\cdots ,k,$$

which is parameterized by the weight vector w_i ∈ ℝ^d and the bias b_i ∈ ℝ. Let C ∈ ℝ^k×k be the term-term correlation matrix in which C_pq measures the correlation between the pth and the qth term. Note that the proposed formulation is independent of the methods used to measure the correlations among terms, and any other methods can be used for this purpose. Since terms can be positively or negatively related, the entries in C can be either positive or negative. To capture the correlations among terms encoded into C, we propose to solve the following optimization problem:

$$\underset{W}{min}\sum _{i=1}^k\sum _{j=1}^n\ell (f_i(x_j),Y_{ji})+{\lambda }_1{\left|\right|W\left|\right|}_F^2+{\lambda }_2\sum _{(p,q)\in G}g(C_{pq})·{\left|\right|w_p-\text{sign}(C_{pq})w_q\left|\right|}^2,$$ (5)

where W = [w₁, ···, w_k] ∈ ℝ^d×k, G denotes the index set with the magnitudes of the corresponding entries in C above a pre-specified threshold μ, i.e., G = {(p, q): |C_pq| ≥ μ}, ||·||_F denotes the Frobenius norm, λ₁ > 0 and λ₂ > 0 are two regularization parameters, and g(C_pq) is the weight for the regularization on terms p and q. In this paper, we set $g(C_{pq})=C_{pq}^2$. In this model, the weight vectors for models corresponding to correlated terms are constrained to be similar, weighted by the strength of the correlation. Moreover, negatively-related terms are also taken into account by considering the sign of the correlation coefficient.

4.2 An Equivalent Formulation

In the following, we consider the least squares loss

$$\ell (f_i(x_j),Y_{ji})={(f_i(x_j)-Y_{ji})}^2$$

for the formulation in Eq. (5). This leads to the following optimization problem:

$$\underset{W}{min}{\left|\right|XW-Y\left|\right|}_F^2+{\lambda }_1{\left|\right|W\left|\right|}_F^2+{\lambda }_2\sum _{(p,q)\in G}{C}_{pq}^2·{\left|\right|w_p-\text{sign}(C_{pq})w_q\left|\right|}^2.$$ (6)

Note that we have assumed that both X and Y are centered in terms of rows, and thus the bias term can be ignored. We show in the following that the optimal W admits an analytical solution, which only involves the singular value decomposition (SVD) and matrix and vector operations.

Note that $C_{pq}^2·{\left|\right|w_p-\text{sign}(C_{pq})w_q\left|\right|}^2={\left|\right|\mid C_{pq}\mid w_p-C_{pq}{w}_q\left|\right|}^2$. To reformulate the problem in Eq. (6) into a compact matrix form, we need to introduce an additional variable. For the mth constraint in G, which encodes the correlation between the pth and the qth terms, define h_m ∈ ℝ^k as a vector whose pth and qth entries are nonzero, and all other entries are zero as:

$$h_m={(\cdots ,0,\cdots ,\underset{p\text{th}}{\underbrace{\mid C_{pq}\mid }},\cdots ,0,\cdots ,\underset{q\text{th}}{\underbrace{-C_{pq}}},\cdots ,0,\cdots )}^T.$$ (7)

Based on this definition, it is easy to verify that the problem in Eq. (6) can be expressed equivalently as:

$$\underset{W}{min}{\left|\right|XW-Y\left|\right|}_F^2+{\lambda }_1{\left|\right|W\left|\right|}_F^2+{\lambda }_2{\left|\right|WH\left|\right|}_F^2,$$ (8)

where H = (h₁, ···, h_g) ∈ ℝ^k×g and g = |G| is the size of the set G.

4.3 The Main Algorithm

We show that the problem in Eq. (8) admits an analytical solution. Taking the derivative of the objective function in Eq. (8) with respect to W and setting it to zero, we obtain that

$$X^{T}XW-X^{T}Y+{\lambda }_{1}W+{\lambda }_{2}WH{H}^T=0.$$ (9)

Let $X=U_1{\mathrm{\sum }}_1{V}_1^T$ and $H=U_2{\mathrm{\sum }}_2{V}_2^T$ be the SVD of X and H, respectively, where U₁ ∈ ℝ^n×n, V₁ ∈ ℝ^d×d, U₂ ∈ ℝ^k×k and V₂ ∈ ℝ^g×g are orthogonal, and Σ₁ ∈ ℝ^n×d and Σ₂ ∈ ℝ^k×g are diagonal. Then the equality in Eq. (9) can be expressed as

$$V_1({\mathrm{\sum }}_1^T{\mathrm{\sum }}_1+{\lambda }_{1}I)V_1^{T}W+{\lambda }_2{WU}_2{\mathrm{\sum }}_2{\mathrm{\sum }}_2^T{U}_2^T=X^{T}Y.$$ (10)

Multiplying $V_1^T$ and U₂ from the left and right, respectively, on both sides of Eq. (10), we obtain that

$$({\mathrm{\sum }}_1^T{\mathrm{\sum }}_1+{\lambda }_{1}I)V_1^T{WU}_2+{\lambda }_2{V}_1^T{WU}_2{\mathrm{\sum }}_2{\mathrm{\sum }}_2^T=V_1^T{X}^T{YU}_2.$$ (11)

Denote

$$\begin{array}{l}{\mathrm{\sum }}_1^T{\mathrm{\sum }}_1+{\lambda }_{1}I={\mathrm{\sum }^{\sim }}_1=\text{diag}({\sigma }_1^{(1)},\cdots ,{\sigma }_1^{(d)})\in {\mathbb{R}}^{d\times d},\\ {\lambda }_2{\mathrm{\sum }}_2{\mathrm{\sum }}_2^T={\mathrm{\sum }^{\sim }}_2=\text{diag}({\sigma }_2^{(1)},\cdots ,{\sigma }_2^{(k)})\in {\mathbb{R}}^{k\times k},\\ V_1^T{WU}_2=\stackrel{\sim }{W},\\ V_1^T{X}^T{YU}_2=D.\end{array}$$

Then Eq. (11) can be expressed as

$${\mathrm{\sum }^{\sim }}_1\stackrel{\sim }{W}+\stackrel{\sim }{W}{\mathrm{\sum }^{\sim }}_2=D.$$ (12)

Note that Σ̃₁ is positive definite, and hence ${\sigma }_1^{(i)}>0$ for all i. It follows that W̃ can be obtained as

$${\stackrel{\sim }{W}}_{ij}=\frac{D_{ij}}{{\sigma }_1^{(i)}+{\sigma }_2^{(j)}}.$$ (13)

After W̃ is computed, the original weight matrix W can be recovered as $W=V_1\stackrel{\sim }{W}{U}_2^T$. This leads to the main algorithm in Algorithm 1 for computing the optimal W.

Algorithm 1.

The main algorithm

Input: X, Y, H, λ1, and λ2

Output: W Compute SVD as $X=U_1{\mathrm{\sum }}_1{V}_1^T$ and $H=U_2{\mathrm{\sum }}_2{V}_2^T$ ${\mathrm{\sum }^{\sim }}_1={\mathrm{\sum }}_1^T{\mathrm{\sum }}_1+{\lambda }_{1}I=\text{diag}({\sigma }_1^{(1)},\cdots ,{\sigma }_1^{(d)})$ ${\mathrm{\sum }^{\sim }}_2={\lambda }_2{\mathrm{\sum }}_2{\mathrm{\sum }}_2^T=\text{diag}({\sigma }_2^{(1)},\cdots ,{\sigma }_2^{(k)})$ $D=V_1^T{X}^T{YU}_2$ ${\stackrel{\sim }{W}}_{ij}=\frac{D_{ij}}{{\sigma }_1^{(i)}+{\sigma }_2^{(j)}}$ $W=V_1\stackrel{\sim }{W}{U}_2^T$

In Algorithm 1, the dominant computational cost is the SVD’s of X and H. The two regularization parameters λ₁ and λ₂ can be tuned using double cross-validation. Note that for different values of λ₁ and λ₂, the SVD’s of X and H need to be computed only once. Thus, the overall procedure for parameter tuning is efficient.

4.4 Discussion

The proposed formulation is related to the fused lasso [23], which encourages the sparsity of the difference between coefficients in single-response regression problems. In particular, the sum of the absolute values of differences between consecutive coefficients are regularized in fused lasso. Motivated by fused lasso, the graph-guided fused lasso (GFlasso) was proposed in [9] to constrain the weight vectors of correlated tasks in multiple-response regression problems. A key difference between our formulation and those based on fused lasso is that we regularize the two norm of the differences between the weight vectors for related tasks, while those based on the fused lasso use the one norm regularization. This leads to different procedures for solving the resulting problem. In particular, it has been shown [9] that the GFlasso formulation involves a quadratic programming problem, which is computationally expensive for problems such as the annotation of gene expression patterns. In contrast, our formulation results in an analytical solution, and the parameter tuning is efficient, since the computationally dominant part needs to be performed only once for different values of the regularization parameters.

5. EXPERIMENTS

In this section, we report and analyze the annotation results obtained by applying the proposed approach to images in the Fly Express database (http://www.flyexpress.net/).

5.1 Experimental Setup

The size of images in the FlyExpress database is standardized to 128 × 320 pixels, and the radius and spacing of the regular patches to extract local features are set to 16 pixels in the experiments. The non-negative lasso problem in Eq. (2) is solved by adapting the coordinate descent algorithm [5] to incorporate the non-negativity constraint. The continuous process of Drosophila embryogenesis is divided into 16 stages, which are then grouped into 6 stage ranges (1–3, 4–6, 7–8, 9–10, 11–12, and 13–16) [24, 25]. Since most of the CV terms are stage-range specific, we annotate the image groups according to their stage ranges separately. The first stage range contains only 2 terms, and we do not report the performance in this stage range. For other stage ranges, we begin with the 10 terms that appear in the largest number of image groups, and then we add additional terms in the order of their frequencies with a step size of 10. This results in different numbers of data sets in each stage range, depending on the number of CV terms in that stage range. The extracted data sets are randomly partitioned into training and test sets using the ratio 1:1 for each term. For each data set, we randomly generate 30 training/test partitions, and the average performance is reported. We use the AUC and F1 score as the performance measures. To assess the performance across multiple terms, we report both the macro-averaged and the micro-averaged F1 scores. The threshold value μ for the correlation coefficient is tuned empirically, and it is fixed to 0.3 in the experiments. The regularization parameters λ₁ and λ₂ are tuned using double cross-validation. Note that for different values of λ₁ and λ₂, the SVD of X and H need to be computed only once. The code for the proposed formulation is available at http://www.public.asu.edu/~sji03/annotation/.

5.2 Evaluation of Annotation Performance

We assess the performance of the proposed local regularization formulation on 18 data sets from 5 stage ranges. We evaluate the effectiveness of the bag-of-words and the sparse feature representations in the following subsection, which shows that the sparse feature representation yields significantly higher performance in all cases. Hence, we use the sparse feature representation in this experiment. To demonstrate the effectiveness of this formulation, we report the results obtained by applying linear support vector machines (SVM) separately for each term in the one-against-rest manner. To compare the performance achieved by the proposed formulation based on the sparse feature representation with existing approaches, we report the performance of the methods in [8] based on pyramid match kernels (PMK). All three formulations proposed in [8], denoted as PMK_star, PMK_clique and PMK_kcca are reported. All the model parameters are tuned using cross-validation. The performance in terms of AUC, macro F1 and micro F1 for the five methods is reported in Tables 1, 2 and 3, respectively.

Table 1.

Comparison of the performance achieved by the five methods in terms of AUC. LR_soft denotes the proposed formulation, and SVM_soft denotes the independent SVM, both based on the sparse feature representation. PMK_star, PMK_clique, and PMK_kcca denote the three methods based on pyramid match kernels. In each case, the average performance and standard deviations over 30 random trials are reported.

Stage range	# of terms	LRsoft	SVMsoft	PMKstar	PMKclique	PMKkcca
4–6	10	82.86 ± 0.67	80.61 ± 0.68	77.67 ± 0.82	76.97 ± 0.91	77.47 ± 0.80
	20	84.20 ± 0.54	82.34 ± 0.52	77.44 ± 0.75	76.84 ± 0.71	77.46 ± 0.72
	30	81.63 ± 1.12	78.81 ± 1.47	74.18 ± 0.86	73.40 ± 0.90	74.71 ± 0.84
7–8	10	77.38 ± 0.90	75.21 ± 0.91	71.78 ± 0.97	72.41 ± 0.84	72.27 ± 0.78
	20	76.78 ± 1.36	73.48 ± 2.56	69.28 ± 1.17	69.01 ± 1.22	69.79 ± 1.18
9–10	10	79.04 ± 0.55	76.60 ± 0.74	71.90 ± 0.80	72.38 ± 0.79	72.28 ± 0.72
	20	80.41 ± 0.94	77.87 ± 1.03	72.10 ± 0.94	71.61 ± 1.18	72.75 ± 0.99
11–12	10	86.02 ± 0.49	82.67 ± 0.48	78.55 ± 0.63	78.54 ± 0.57	78.64 ± 0.57
	20	86.60 ± 0.26	83.48 ± 0.31	76.62 ± 0.68	76.39 ± 0.68	76.97 ± 0.67
	30	83.86 ± 0.42	80.40 ± 0.55	71.94 ± 0.60	71.36 ± 0.51	72.90 ± 0.63
	40	82.85 ± 0.55	79.37 ± 0.63	71.16 ± 0.65	70.28 ± 0.68	72.12 ± 0.64
	50	81.70 ± 0.62	78.06 ± 0.77	69.64 ± 0.86	68.24 ± 0.64	70.73 ± 0.83
13–16	10	89.44 ± 0.31	86.49 ± 0.35	82.22 ± 0.42	82.58 ± 0.64	81.87 ± 0.76
	20	87.05 ± 0.33	83.40 ± 0.36	76.74 ± 0.33	77.36 ± 0.54	77.03 ± 0.52
	30	85.72 ± 0.32	81.86 ± 0.38	73.80 ± 0.48	74.07 ± 0.53	74.05 ± 0.68
	40	84.55 ± 0.33	80.66 ± 0.38	71.02 ± 0.56	71.19 ± 0.50	71.49 ± 0.45
	50	83.15 ± 0.36	79.22 ± 0.51	68.74 ± 0.51	68.92 ± 0.57	69.15 ± 0.73
	60	82.34 ± 0.43	78.52 ± 0.60	67.33 ± 0.57	67.34 ± 0.63	68.24 ± 0.48

Table 2.

Comparison of the performance achieved by the five methods in terms of macro F1. See the caption of Table 1 for explanations.

Stage range	# of terms	LRsoft	SVMsoft	PMKstar	PMKclique	PMKkcca
4–6	10	50.93 ± 1.46	49.55 ± 1.13	33.68 ± 1.41	38.94 ± 1.57	30.23 ± 1.55
	20	43.21 ± 1.19	42.48 ± 1.23	22.76 ± 0.84	24.79 ± 1.37	22.79 ± 1.34
	30	32.63 ± 1.42	31.45 ± 1.27	17.80 ± 1.02	17.05 ± 1.13	16.92 ± 1.23
7–8	10	51.51 ± 1.33	47.24 ± 1.55	40.43 ± 1.24	42.15 ± 1.33	32.94 ± 1.32
	20	34.10 ± 1.37	33.77 ± 1.24	22.83 ± 1.04	23.13 ± 0.93	19.91 ± 1.16
9–10	10	54.91 ± 1.02	52.48 ± 1.41	42.00 ± 1.06	41.84 ± 0.96	33.96 ± 0.98
	20	37.71 ± 1.24	35.83 ± 1.43	25.57 ± 0.97	24.38 ± 0.97	21.79 ± 1.11
11–12	10	63.80 ± 0.92	58.88 ± 0.91	47.93 ± 0.87	50.21 ± 1.27	35.85 ± 0.88
	20	51.82 ± 0.99	47.26 ± 0.88	28.97 ± 0.84	31.92 ± 1.29	22.42 ± 0.98
	30	38.66 ± 0.97	34.90 ± 0.82	19.69 ± 0.61	22.12 ± 0.89	16.34 ± 0.47
	40	31.39 ± 0.88	28.25 ± 0.85	15.15 ± 0.55	16.73 ± 0.69	12.48 ± 0.51
	50	26.16 ± 1.01	23.58 ± 0.94	12.27 ± 0.42	13.52 ± 0.65	10.49 ± 0.47
13–16	10	67.47 ± 0.75	63.69 ± 0.81	55.03 ± 0.94	55.34 ± 1.09	38.84 ± 0.86
	20	54.12 ± 0.87	48.41 ± 0.87	34.42 ± 1.00	34.20 ± 0.82	24.94 ± 1.29
	30	47.21 ± 0.88	40.73 ± 0.78	25.92 ± 0.75	25.73 ± 0.90	19.53 ± 0.92
	40	40.26 ± 0.65	34.63 ± 0.80	19.84 ± 0.42	19.38 ± 0.73	14.85 ± 0.76
	50	33.98 ± 0.64	28.58 ± 0.64	16.35 ± 0.46	15.55 ± 0.61	12.85 ± 0.61
	60	29.50 ± 0.74	24.99 ± 0.76	14.05 ± 0.41	13.20 ± 0.46	11.44 ± 0.49

Table 3.

Comparison of the performance achieved by the five methods in terms of micro F1. See the caption of Table 1 for explanations.

Stage range	# of terms	LRsoft	SVMsoft	PMKstar	PMKclique	PMKkcca
4–6	10	52.87 ± 1.40	51.31 ± 1.07	44.06 ± 1.20	45.21 ± 1.18	36.57 ± 1.36
	20	47.11 ± 1.12	45.48 ± 1.10	37.31 ± 0.91	36.06 ± 1.12	30.43 ± 1.16
	30	44.63 ± 1.21	40.91 ± 4.02	36.14 ± 1.27	34.20 ± 1.18	32.77 ± 1.41
7–8	10	57.93 ± 1.18	55.39 ± 1.44	52.42 ± 1.11	52.84 ± 1.13	48.66 ± 1.06
	20	54.97 ± 1.36	47.89 ± 6.09	49.04 ± 1.07	48.73 ± 1.05	46.66 ± 1.05
9–10	10	60.83 ± 0.74	56.47 ± 1.26	54.21 ± 0.74	54.72 ± 0.79	51.33 ± 0.89
	20	56.73 ± 1.01	53.42 ± 2.51	49.68 ± 0.82	49.00 ± 1.15	47.39 ± 1.00
11–12	10	69.16 ± 0.74	64.44 ± 1.00	60.95 ± 0.58	60.73 ± 0.80	55.21 ± 0.97
	20	62.19 ± 0.75	56.76 ± 0.94	51.72 ± 0.69	51.68 ± 0.87	46.05 ± 0.78
	30	57.50 ± 0.74	51.59 ± 1.73	47.49 ± 0.72	46.58 ± 0.66	43.30 ± 0.79
	40	56.31 ± 0.67	49.56 ± 2.24	45.90 ± 0.75	45.24 ± 0.78	42.26 ± 0.90
	50	54.98 ± 0.84	47.44 ± 2.98	45.17 ± 0.58	44.70 ± 0.68	43.55 ± 0.93
13–16	10	70.60 ± 0.59	66.73 ± 0.68	61.12 ± 0.71	61.21 ± 0.89	52.38 ± 0.72
	20	61.37 ± 0.70	56.11 ± 0.89	48.31 ± 0.57	48.56 ± 0.60	41.04 ± 0.69
	30	56.81 ± 0.71	49.70 ± 0.94	43.87 ± 0.64	43.17 ± 0.62	36.55 ± 0.67
	40	54.07 ± 0.51	47.08 ± 0.89	40.89 ± 0.73	40.09 ± 0.86	33.86 ± 0.80
	50	52.68 ± 0.57	44.65 ± 2.31	39.54 ± 0.61	38.65 ± 0.65	33.63 ± 0.96
	60	51.92 ± 0.58	42.08 ± 2.67	38.55 ± 0.69	37.57 ± 0.67	34.57 ± 1.05

We can observe from the results that among the five methods, LR_soft outperforms the other four methods in all cases. In particular, LR_soft outperforms SVM_soft significantly in almost all cases. Since both of these methods are based on the sparse feature representation, this shows that the proposed local regularization formulation is effective in exploiting the correlations among terms. Both LR_soft and SVM_soft outperform the three methods based on pyramid match kernels. This demonstrates that the sparse feature representation is more effective than the pyramid match kernel method.

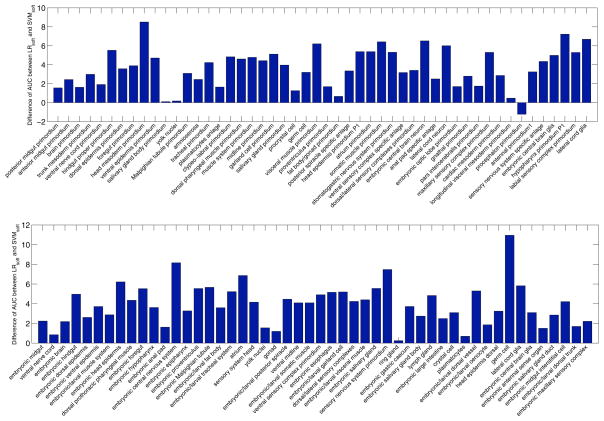
To assess the relative performance of LR_soft and SVM_soft on individual terms, we show the differences of AUC achieved by these two methods for each term on two data sets from stage ranges 11–12 and 13–16 in Figure 4. In these two figures, the reported performance is the average values over 30 random trials, and positive bar values show that LR_soft outperforms SVM_soft, while negative bar values show that SVM_soft outperforms LR_soft. We can observe that among the 100 terms reported, LR_soft outperforms SVM_soft on 99 terms except for the term procephalon primordium. A detailed analysis on this term shows that this term is not related to any other terms after the correlations are thresholded. Thus, no local regularization is imposed on this term.

Figure 4.

Performance differences on individual terms in terms of AUC between LR_soft and SVM_soft on two data sets from stage ranges 11–12 (top) and 13–16 (bottom) with 50 terms. Positive bar values show that LR_soft outperforms SVM_soft, while negative bar values show that SVM_soft outperforms LR_soft.

5.3 Evaluation of Feature Representation

We compare the performance obtained by the bag-of-words and the sparse learning representations on three data sets from stage range 4–6 with 10, 20 and 30 terms, respectively. For each data set, we report the performance of the local regularization formulation based on the bag-of-words (LR_hard) and the sparse learning (LR_soft) representations in Table 4. We can observe that the proposed sparse feature representation outperforms the bag-of-words scheme significantly on all three data sets. We observe a similar trend in other data sets. This shows that the soft assignment approach based on the sparse learning formulation can potentially reduce the quantization error of the bag-of-words scheme.

Table 4.

Comparison of the performance achieved by the proposed formulation based on the bag-of-words (LR_hard) and the sparse learning feature representations (LR_soft) on three data sets from the stage range 4–6 with 10, 20, and 30 terms. The reported performance is the average value obtained from 30 random trials.

	AUC		macro F1		micro F1
k	LRhard	LRsoft	LRhard	LRsoft	LRhard	LRsoft
10	81.06	82.86	47.61	50.93	50.71	52.87
20	82.54	84.20	40.02	43.21	44.42	47.11
30	79.99	81.63	30.07	32.63	42.13	44.63

5.4 Evaluation of Local Regularization

To assess the effectiveness of the local regularization in constraining the models for correlated terms, we visualize the weight matrices on a data set in stage range 13–16 with 60 terms as the regularization parameter λ₂ increases gradually in Figure 5. When λ₂ = 0, the models for different terms are decoupled, and thus no regularity is observed in the weight matrix. As λ₂ increases, the weight vectors for correlated models are increasingly constrained to be similar. This can be observed from the increasingly similar patterns in certain columns of the weight matrix. This demonstrates that the local regularization formulation is effective in constraining the models for correlated terms to be similar.

Figure 5.

Visualization of the weight matrices on a data set in stage range 13–16 with 60 terms as the regularization parameter λ₂ increases gradually. The weight matrix on this data set is of size 3000 × 60, and only the first 50 rows are shown in each case. Each column in the matrix corresponds to a model for a term. There are 8 connected components (of sizes 10, 6, 3, 3, 2, 2, 2, and 2) after the correlation coefficients are thresholded at 0.3. For better visualization, the columns of the weight matrices shown here are grouped according to the connected components to which they belong, and the groups are shown in decreasing order of size.

6. CONCLUSION AND DISCUSSION

In this paper, we propose a systematic approach for annotating Drosophila gene expression pattern images. For the feature representation, we propose to reduce the quantization error associated with the bag-of-words scheme using the sparse learning technique. Based on this improved feature representation, we propose a classification formulation using a local regularization, which accounts for the correlations among different CV terms. We further show that the resulting regularized formulation admits an analytical solution. The effectiveness of the feature representation and the local regularization formulation is evaluated using images from the FlyExpress database.

The codebooks used in this paper are constructed by un-supervised methods. Recent studies have shown [18, 15] that incorporation of the label information in constructing the codebook usually results in improved performance. We will explore the supervised codebook construction in the future. In the current work, we only consider the least squares loss in the local regularization formulation. We will explore other loss functions, such as the hinge loss, in the future.