On the Relationship Between the Apparent Diffusion Coefficient and Extravascular Extracellular Volume Fraction in Human Breast Cancer

Abstract

MRI techniques have been developed that can noninvasively probe the apparent diffusion coefficient (ADC) of water via diffusion weighted MRI (DW-MRI). These methods have found much application in cancer where it is often found that the ADC within tumors is inversely correlated with tumor cell density, so that an increase in ADC in response to therapy can be interpreted as an imaging biomarker of positive treatment response. Dynamic contrast enhanced MRI (DCE-MRI) methods have also been developed and can noninvasively report on the extravascular extracellular volume fraction of tissues (denoted by v_e). By conventional reasoning the ADC should therefore also be directly proportional to v_e. Here we report measurements of both ADC and v_e obtained from breast cancer patients at both 1.5T and 3.0T. The 1.5T data were acquired as part of normal standard-of-care, while the 3.0T data were obtained from a dedicated research protocol. We found no statistically significant correlation between ADC and v_e for the 1.5T or 3.0T patient sets on either a voxel-by-voxel or ROI basis. These data, combined with similar results from other disease sites in the literature, may indicate that the conventional interpretation of either ADC, v_e, or their relationship are not sufficient to explain experimental findings.

1. Introduction

The microscopic thermally-induced behavior of molecules moving in a random pattern is referred to as self-diffusion or Brownian motion. The rate of diffusion in cellular tissues is described by means of an apparent diffusion coefficient (ADC), which largely depends on the number and separation of barriers that a diffusing water molecule encounters in a specified time interval [1]. Diffusion weighted magnetic resonance imaging (DW-MRI) methods sensitive to water diffusion have been developed to map the ADC, and in well-controlled situations the variations in ADC have been shown to correlate inversely with tissue cellularity [2]. More specifically, as the number and density of barriers increases, the ADC will decrease because water molecules are not able to diffuse as far per unit time as they would in a free solution. This interpretation has been of particular (recent) interest to the cancer imaging community where changes in the ADC have been interpreted to report on the ability of various anti-cancer therapies to kill tumor cells. There are mounting pre-clinical and clinical data indicating that exposure of tumors to both chemotherapy and radiotherapy consistently leads to measurable increases in conventional measurements of ADC in cases of favorable treatment response [3–6]. Studies in humans have shown that ADCs in both normal tissues and benign lesions have significantly higher ADCs compared to those of malignant breast lesions [7,8]. Furthermore, recent results indicate that the ADC is a promising quantitative biomarker for assessing the response of breast tumors to neoadjuvant chemotherapy [9,10].

In parallel with developments of DW-MRI, there have been advances in tissue characterization based on the quantification of the kinetics of injectable MRI contrast agents. The most common MRI contrast agents are gadolinium-based chelates which are pharmaceuticals administered intravenously to patients and are designed to change the contrast between different tissues by decreasing a tissue’s native T₁ and/or T₂ relaxation times. Except in the healthy brain, these agents pass from the circulation into the extravascular, extracellular interstitial volume of normal tissues. Studies designed to exploit the change in T₁ are referred to as dynamic contrast enhanced MRI (DCE-MRI; reviewed in [11]). In a typical DCE-MRI procedure, MR images are collected before, during, and after a CA is injected into an appropriate peripheral vein of a patient. Each image corresponds to one time point, and each pixel in each image set gives rise to its own signal time course which can be analyzed with a mathematical model. The parameters that are typically returned from such analysis are the volume transfer constant (K^trans), the extravascular extracellular volume fraction (v_e) into which the agent distributes, and the blood plasma volume fraction (v_p).

In this contribution, we compare and correlate the DW-MRI measure of cellularity (ADC) with the DCE-MRI derived measure of extravascular volume fraction (v_e) for multiple voxels in a series of patients. Conventional models of ADC and DCE parameters would suggest that these two parameters should be directly related; that is, as the volume of extracellular space increases (as v_e increases) water diffusion should be less restricted and therefore the ADC should also increase. However, in the one paper studying this relationship in the literature (to the best of our knowledge) there was no relationship found between these two parameters [12]. Moreover, our own previous study of treatment effects in breast tumors found the converse relationship [13]. Using two different DCE protocols, we were able to explore the relationship between ADC and v_e using a number of pharmacokinetic models to return estimates of v_e. Our overall goal is to establish whether ADC and v_e are related in the case of invasive ductal carcinomas in human breast cancer patients.

2. Methods

Patient data were acquired at 1.5T as part of a clinical standard-of-care exam and at 3.0T as part of a research study, so we have divided the following sections along those lines.

2.1 Data acquisition at 1.5T

Data were acquired from 13 patients as part of the clinical, standard-of-care, breast MRI for diagnostic and staging purposes. DW-MRI and DCE-MRI were performed using a Philips 1.5T Achieva MR scanner (Philips Healthcare, Best, The Netherlands) prior to neoadjuvant chemotherapy and following completion of the first cycle of chemotherapy. A 4-channel receive double-breast coil covering both breasts was used for all imaging (In-vivo Inc., Gainesville, FL).

DW-MRIs were acquired with a single-shot spin echo (SE) echo planar imaging (EPI) sequence in three orthogonal diffusion encoding directions (x, y, and z), with two b-values (0 and 500 s/mm²), FOV = 320×320 (bi-lateral), and an acquisition matrix of 100×97 reconstructed to 160×160. SENSE parallel imaging (acceleration factor = 2) and spectral presaturation with inversion recovery (SPIR) fat saturation were implemented to reduce image artifacts. Subjects were breathing freely, with no gating applied. The patient DWIs consisted of 20 transverse slices with slice thickness = 5 mm (no slice gap) and TR\TE = 4280\43 ms, Δ = 20.6 ms, and δ = 10.9 ms, respectively, number of signal averages (NSA) = 6, for a total scan time of 5 min and 43 s.

Data for a T₁ map were acquired with a 3D RF-spoiled gradient echo multi-flip angle approach with a TR = 7.9 ms, TE = 1.3 ms, and ten flip angles from 2 to 20 degrees in two degree increments. The acquisition matrix was 240×240×30 over the same FOV as above. There was one signal acquisition, and a SENSE factor of 2 for an acquisition time of 5 min and 37 sec. The dynamic scans used a TR\TE = 5.3\2.6 ms with a flip angle of 10° and an acquisition matrix of 448×448×150 over the same FOV as above. Each 150-slice set was collected in 90 seconds at eight time points for approximately twelve minutes of scanning. A catheter placed within an antecubital vein delivered 0.1 mmol/kg of the contrast agent gadopentetate dimeglumine, Gd-DTPA, (Magnevist, Wayne, NJ) over 20 seconds (followed by a saline flush) after the acquisition of one baseline dynamic scan.

2.2 Data acquisition at 3.0T

Data were acquired from nine patients with locally advanced breast cancer who were enrolled in an ongoing clinical trial. The patients provided informed consent and the study was approved by the ethics committee of our cancer center. DW-MRI and DCE-MRI were performed using a Philips 3T Achieva MR scanner (Philips Healthcare, Best, The Netherlands) prior to neoadjuvant chemotherapy and four patients were also scanned following completion of the first cycle of chemotherapy; thus, we had 13 total data sets. A 4-channel receive double-breast coil covering both breasts was used for all imaging (In-vivo Inc., Gainesville, FL).

DW-MRIs were acquired with a single-shot spin echo (SE) echo planar imaging (EPI) sequence in three orthogonal diffusion encoding directions (x, y, and z), with two b-values (0 and 600 s/mm²), FOV = 192×192 (uni-lateral), and an acquisition matrix of 96×96. SENSE parallel imaging (acceleration factor = 2) and spectrally-selective adiabatic inversion recovery (SPAIR) fat saturation were implemented to reduce image artifacts. Subjects were breathing freely with no gating applied. The patient DWIs consisted of 12 sagittal slices with slice thickness = 5 mm (no slice gap), TR = 2255 ms, TE = ‘shortest’ (43, 48, or 51 ms), Δ = 20.7, 23.2, or 24.9 ms, and δ = 11.6, 10.6, or 10.2 ms, respectively, NSA = 10, for a total scan time of 2 min and 42 s.

Data for a T₁ map were acquired with a 3D RF-spoiled gradient echo multi-flip angle approach with a TR\TE of 7.9\1.3 ms and ten flip angles from 2 to 20 degrees in two degree increments. The acquisition matrix was 192×192×20 (full-breast) over a sagittal square field of view (22 cm²) with slice thickness of 5 mm, one signal acquisition, and a SENSE factor of 2 for an acquisition time of just under 3 minutes. The dynamic scans used identical parameters and a flip angle of 20°. Each 20-slice set was collected in 16.5 seconds at 25 time points for approximately seven minutes of scanning. A catheter placed within an antecubital vein delivered 0.1 mmol/kg of Magnevist over 20 seconds (followed by a saline flush) after the acquisition of three baseline dynamic scans for the DCE study. The diffusion, T₁, and dynamic image volumes were all acquired with the same center location, making them inherently co-registered.

2.3 Data analysis for 1.5T data

The diffusion data sets were fit to Eq. (1) to return ADC values on a voxel-by-voxel basis:

$$\text{ADC}=-ln[S(b)/S_0]/b,$$ (1)

where S₀ denotes the signal intensity in the absence of diffusion gradients, b reflects the strength and duration of a diffusion-sensitizing gradient, and S(b) is the signal intensity in the presence of the diffusion-sensitizing gradient. Voxels for which Eq. (1) could not fit the data were set to zero and not included in the subsequent analysis.

The dynamic and multi-flip angle T₁ data were down-sampled to match the resolution of the DWI data. Pre-contrast T₁ values, T₁₀, were computed from the multi-flip angle data by fitting to Eq. (2):

$$S=S_{0}sin\alpha \frac{1-exp-TR/T_1}{1-cos\mathit{a}exp-TR/T_1},$$ (2)

where α is the flip angle, S₀ is a constant describing the scanner gain and proton density, and we have assumed that TE ≪ T₂^*. Voxels for which Eq. (2) could not fit the data were set to zero and not included in the subsequent analysis. The T₁₀ values were then used in conjunction with T₁-weighted images to obtain a T₁ time course for pharmacokinetic analysis.

The 1.5T data were acquired in the clinical setting, so the temporal resolution was not optimal for kinetic modeling, and therefore a model that requires characterization of only the washout portion of the arterial input function (AIF) was selected; the model is given by:

$$\mathrm{\Delta }{R}_1(t)=D•K^{\mathit{trans}}•r_1\sum _{i=1}^2\frac{a_i(exp(-K^{\mathit{trans}}/v_e)t)-exp(-m_{i}t)}{m_i-(K^{\mathit{trans}}/v_e)},$$ (3)

where D = dose of contrast agent in mmol/kg, R₁ = 1/T₁ and we set, as has been done previously for breast cancer studies, a₁ = 3.99 kg⁻¹, a₂ = 4.78 kg⁻¹, m₁ = 0.144 min⁻¹, m₂ = 0.011 min⁻¹ [14]. The ΔR₁ time courses are then fit to Eq. (3) to extract K^trans and v_e on a voxel-by-voxel basis. This model (and variations thereof) has previously been used in the analysis of low temporal resolution DCE-MRI data of the breast (see, e.g., [15]–[17]). The fitting routine employs a standard gradient-expansion, nonlinear, least-squares, curve-fitting algorithm written in the Interactive Data Language (Research Systems, Boulder, CO, USA). Voxels for which the fitting algorithm did not converge, or converged to non-physical values (i.e., K^trans > 5.0 min⁻¹, v_e > 1.0, or any parameter below 0.0) were set equal to zero.

2.4 Data analysis for 3.0T data

ADC values were computed in a similar fashion as described above in section 2.3. The data obtained at 3.0 T were part of a dedicated research study, so we were able to acquire the DCE data at a much higher temporal resolution which afforded more rigorous quantification than the 1.5 T data.

DCE-MRI data were analyzed by the fast exchange limit formalism [11]. With this assumption, the longitudinal relaxation rate constant, R₁ (≡1/T), is given by Eq. (4):

$$R_{1}t=r_1•C_{t}t+R_{10},$$ (4)

where r₁ is the CA longitudinal relaxivity, R₁₀ is the pre-CA longitudinal relaxation rate constant, and C_t is the time course of the concentration of CA in tissue. To compute C_t, we use the standard model both with and without a plasma term. The standard model without a plasma term computes C_t as follows:

$$C_t(T)=K^{\mathit{trans}}{\int }_0^T{C}_p(t)exp(-(K^{\mathit{trans}}/v_e)•(T-t))dt,$$ (5)

where K^trans is the CA volume transfer rate constant, v_e is the extravascular-extracellular volume fraction, and C_p(t) is the concentration of CA in blood plasma (i.e., the AIF). A more complex “extended” model incorporates the blood plasma volume fraction, v_p:

$$C_t(T)=K^{\mathit{trans}}{\int }_0^T{C}_p(t)exp(-(K^{\mathit{trans}}/v_e)(T-t))dt+v_p{C}_{p}t.$$ (6)

DCE-MRI data were also analyzed with the fast exchange regime formalism [18,19]. With this assumption, the longitudinal relaxation rate constant, R₁ (≡1/T), is given by Eq. (7):

$$R_1(t)=(1/2)•(2R_{1i}+r_1•K^{\mathit{trans}}\underset{0}{\overset{T}{\int }}{C}_p(t)exp(-(K^{\mathit{trans}}/v_e)+(T-t))dt+(R_{10}-R_{1i}+1/{\tau }_i)/(v_e/f_w)\}-(1/2)•[(2/{\tau }_i-r_1•K^{\mathit{trans}}\underset{0}{\overset{T}{\int }}{C}_p(t)exp(-(K^{\mathit{trans}}/v_e)+(T-t))dt-{(R_{10}-R_{1i}+1/{\tau }_i)/v_e/f_w)}^2+4•(1-v_e/f_w)/{\tau }_i^2•{(v_e/f_w)}^{1/2}]\},$$ (7)

where R_1i is the intracellular R₁, τ_i is the average intracellular water lifetime of a water molecule, and f_w is the fraction of water that is accessible to mobile CA. In the analysis below, R_1i was set equal to R₁₀ and f_w was set to 0.8 as has been done previously [20]. The AIF was derived on an individual patient basis from the signal intensity time obtained from the axillary artery [21].

Data from each DCE-MRI study were fit on a voxel-by-voxel basis with Eqs. (4) and (5) or Eqs. (4) and (6) or Eqs. (5) and (7) to yield estimates of K^trans, v_e (Eqs. (5) and (6)), and v_p (Eq. (6)) or τ_i (Eq. (7)). As described in Section 2.3, voxels for which the fitting algorithm did not converge or converged to non-physical values were set equal to zero.

2.5 Statistical analysis

Correlation and linear regression analysis were performed on the ADC and v_e maps to test the hypothesis that these parameters are directly correlated. We computed the Pearson correlation coefficient, and the slope and intercept of the best fit line when v_e was regressed on ADC for both ROI and voxel level data. The ROI was selected as the volume of tissue showing enhancement greater than 25% above baseline after injection of the contrast agent. This was done for the ADC and v_e data computed for each patient at 1.5 T, as well as the ADC and v_e data computed by all three models employed in the 3.0T DCE-MRI analysis.

3. Results

3.1 Results at 1.5T

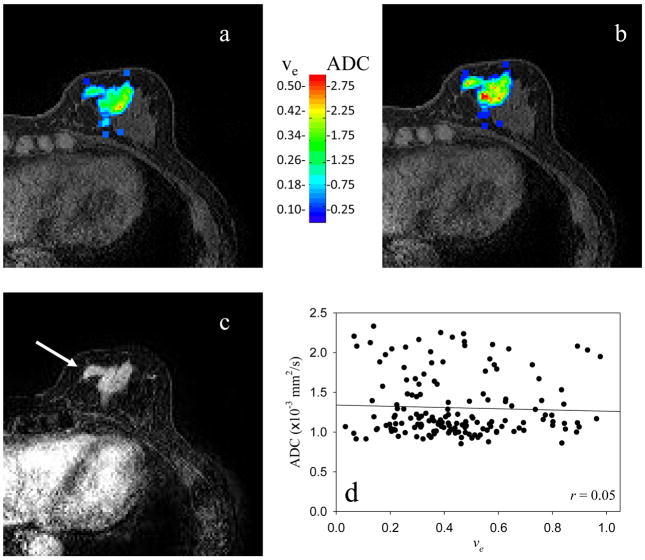
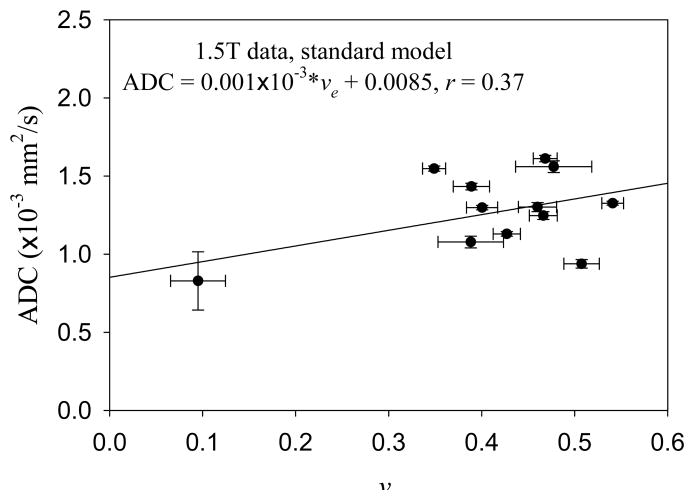
Figure 1 displays the central slice of a representative patient. The parametric v_e (obtained using Eq. (3)) and ADC maps are displayed in panels a and b, respectively, while panel c is the initial area under the curve map using the data from the first 120 seconds to identify the lesion (arrow). The model fit approximately 75% of the enhancing signal intensity time courses. Visually, there does not appear to be a spatial relationship between the two maps, and this is confirmed in Panel d where the Pearson correlation value (r = 0.05) is displayed. While plotting all data from all slices for a particular patient is too cumbersome to examine, all the data were used when computing the overall correlation coefficient. When this was done, none of the patients displayed a significant relationship between these two parameters, as summarized in the far right column of Table 1 (the 95% confidence intervals on the correlation coefficient are also presented). The Pearson correlation values range from r = −0.34 to 0.28, showing an extremely weak relationship between these parameter values; the changes in v_e explain a maximum of only 12% of the variance in the ADC values. Averaging over each patients’ individual voxels to yield one ADC and one v_e value per patient and then performing a group analysis also did not yield a strong correlation, as summarized by Figure 2, where the Pearson correlation value (r = 0.37; approximately 14% of the variance in ADC explained by v_e values), the slope (1×10⁻³), and intercept (0.0085) are presented.

Figure 1.

Panels a and b depict the parametric maps of the extravascular extracellular volume fraction and the apparent diffusion coefficient, respectively, of the central slice of a representative patient. (Note the color bar where the ADC values are given in units of 10⁻³ mm²/s.) Panel c depicts the initial area under the contrast enhanced curve so that the enhancing lesion is easily visualized (arrow). Panel d depicts the scatter plot of the data presented in panels a and b, and it is clear that there is not a strong correlation between the data sets. These data were obtained in the clinical setting on a 1.5T scanner.

Table 1.

Patient #	# slices	# voxels	CC (95% CI)
1	8	918	0.058 (−0.0067, 0.12)
2	4	184	−0.086 (−0.23, 0.060)
3	11	1234	0.16 (0.11, 0.22)
4	13	815	−0.13 (−0.20, 0.066)
5	8	213	0.28 (0.15, 0.40)
6	5	640	−0.024 (−0.011, 0.053)
7	9	1629	−0.017 (−0.0066, 0.032)
8	10	1090	−0.029 (−0.088, 0.031)
9	11	1781	0.18 (0.13, 0.22)
10	4	124	0.27 (0.10, 0.43)
11	9	563	0.13 (0.050, 0.21)
12	9	1423	0.25 (0.21, 0.30)

Figure 2.

The figure displays data similar to that found in Figure 1d, except these points represent the average of all voxels for a given patient; the error bars denote the standard error of the mean. Again, there is not a strong relationship between ADC and v_e data obtained at 1.5T.

3.2 Results at 3.0T

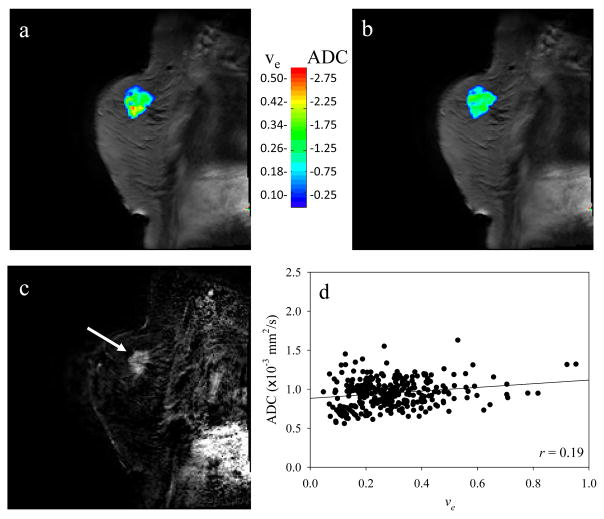
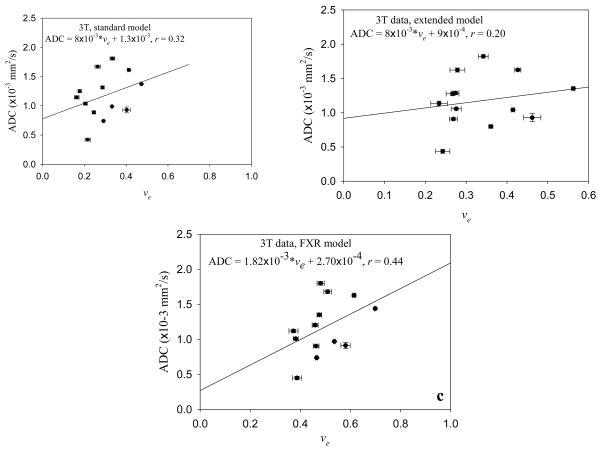
Figure 3 displays the central slice of a representative patient. The parametric v_e (obtained using Eqs. (4) and (5)) and ADC maps are displayed in panels a and b, respectively, while panel c is the initial area under the curve map using the data from the first 120 seconds to identify the lesion (arrow). This model also fit approximately 80% of the enhancing signal intensity time courses. Again, there does not appear to be a spatial relationship between the two maps, and this is confirmed in Panel d where the Pearson correlation value (r = 0.19) is displayed for this patient. Similar to the 1.5T data, none of the patients displayed a strong correlative relationship between these two parameters, as summarized in the second to last column on the right of Table 1. (The first column of the Table indicates which patient and which scan in the format of ‘Patient x-y’, where x is the patient number and y is the scan number’ y=1 is the pre-treatment scan, and y=2 is the post-one cycle of therapy scan.) The Pearson correlation values range from r = −0.24 to 0.31, also showing an extremely weak relationship between these parameter values; the changes in v_e explain a maximum of only 10% of the variance in the ADC values. Similar to the 1.5T data, averaging over each patients’ individual voxels to yield one ADC and one v_e value per patient and then performing a group analysis also did not yield a strong correlation, as summarized by Figure 4a where the Pearson correlation value (r = 0.32, approximately 10% of the variance in ADC explained by v_e values), slope (8×10⁻³), and intercept (1.3×10⁻³) are presented.

Figure 3.

This figure is the 3T data analogous to the 1.5T data displayed in Figure 1. Panels a and b depict the extravascular extracellular volume fraction and the apparent diffusion coefficient maps, respectively, and panel c presents the initial area under the contrast enhanced curve to highlight the lesion (arrow). Panel d shows that, just as in the 1.5T case, there is not a strong relationship between the two parameters.

Figure 4.

Just as in the Figure 2 data, when ADC and v_e are averaged over all voxels for each patient scanned at 3T, there is not a strong correlation between the two. Panel a depicts the correspondence when the standard model (Eqs. (3) and (4)) is used, while panel b depicts the correspondence when the extended model (Eqs. (3) and (5)) is used. There is little change in the relationship between the parameters based on the model used to estimate v_e.

The middle column of Table 2 shows that analyzing the DCE data with the extended model (Eq. (6)) yields very little change in the correlation coefficients for each patient data set. The extended model was able to fit 66% of the enhancing voxels. Again, just as with the previous two analyses, averaging over each patients’ individual voxels to yield one ADC and one v_e value per patient and then performing a group analysis also did not yield a strong correlation, as summarized by Figure 4b where the Pearson correlation value (0.20; approximately 4% of the variance in ADC explained by v_e values), slope (8×10⁻³), and intercept (9×10⁻⁴) are presented.

Table 2.

Patient #	# slices	# voxels	CC (95% CI, standard)	CC (95% CI, extended)	CC (95% CI, FXR)
1-1	10	11964	0.14 (0.13, 0.16)	0.14 (0.12, 0.16)	0.083 (0.068, 0.098)
1-2	9	7557	0.31 (0.29, 0.32)	0.32 (0.30, 0.34)	0.29 (0.27, 0.31)
2-1	4	441	0.21 (0.14, 0.28)	0.20 (0.11, 0.29)	0.20 (0.13, 0.27)
2-2	4	648	−0.21 (−0.27, −0.14)	−0.24 (−0.31, −0.17)	−0.18 (−0.24, −0.12)
3-1	8	1252	0.25 (0.21, 0.29)	0.25 (0.20, 0.31)	0.25 (0.221, 0.29)
4-1	10	8425	0.17 (0.15, 0.18)	0.14 (0.12, 0.16)	0.08 (0.067, 0.096)
5-1	4	339	−0.24 (−0.33, −0.15)	−0.33 (−0.43, −0.24)	−0.14 (−0.056, −0.22)
6-1	4	943	0.24 (0.20, 0.29)	0.23 (0.17, 0.29)	0.23 (0.18, 0.28)
6-2	5	648	−0.06 (−0.12, −0.0016)	−0.10 (−0.18, −0.026)	−0.076 (−0.14, −0.0096)
7-1	3	764	0.2 (0.15, 0.25)	0.10 (0.033, 0.17)	−0.19 (−0.23, −0.15)
7-2	2	425	−0.023 (−0.087, 0.041)	−0.058 (−0.15, 0.037)	0.18 (0.11, 0.24)
8-1	8	3883	−0.03 (−0.059, −0.0016)	−0.0091 (−0.041, 0.022)	0.03 (0.002, 0.059)
9-1	5	1617	0.21 (0.18, 0.25)	0.17 (0.12, 0.21)	0.21 (0.18, 0.25)

The far right column of Table 2 presents the results of analyzing the DCE data with the FXR model (Eq. (7)); in this final case, the model fit 73% of the enhancing voxels. Again there is very little correlation between the two parameters. And just as in the previous three analysis, averaging over each patients’ individual voxels to yield one ADC and one v_e value per patient and then performing a group analysis also did not yield a strong correlation, as summarized by Figure 4c where the Pearson correlation value (0.44; approximately 19% of the variance in ADC explained by v_e values), slope (1.82×10⁻³), and intercept (2.7×10⁻⁴) are presented.

4. Discussion

While in vivo measurements of water diffusion in tissues via MRI is a mature field, the explanation of why ADC values change and our knowledge of how contrast agents perfuse and diffuse through tissue spaces is not complete. DCE-MRI analyses are typically built on compartmental models which make a number of assumptions that may not be always valid, potentially leading to errors in the estimation of v_e. In particular, in some regions the delivery of contrast agents may not rely entirely on perfusion via the vasculature but instead at least some of the contrast agent may diffuse into the voxel or into adjacent regions, and the compartmental models do not account for this. Current models assume that each voxel has a single intravascular compartment that introduces the contrast agent and that the only volume with which it mixes is the extracellular volume of the same voxel. In situations where these assumptions break down, the results returned from the models may not be correct.

While there have been several efforts aimed at validating K^trans (reviewed in [22]), there have been very limited published studies attempting to validate v_e by comparison with histology. In general, these studies have focused on well-controlled pre-clinical mouse studies where histological sections can be compared to the corresponding in vivo imaging data. One such study actually found no significant difference between DCE-MRI and histological estimates of v_e in four mouse melanoma cell lines [23]. The authors did note, however, that there were a number of important limitations to their study; namely, that the tumor lines employed were well vascularized and did not develop large necrotic regions. Furthermore, the investigators were careful to eliminate any areas that included necrosis based on the histological slices. Another pre-clinical study [24] also found that there was no statistical difference between histology and DCE-MRI estimates of v_e. However, this result was only reported for the “top five” volume normalized K^trans values; that is, a relationship held between DCE-MRI and histological estimates of v_e when looking at the most well-vascularized regions. Though such a relationship did not exist in our study (data not shown), it is possible that the elimination of necrotic regions can improve the relationship between v_e and ADC; but this would be very difficult to assess without ex vivo (post-mortem) alignment of histological data to imaging data—data that is difficult to acquire in clinical studies. However, another pre-clinical study did not find a strong correlation between v_e (or K^trans) and histomorphological parameters [25]. The authors concluded this was mostly likely due the heterogeneity of tumor tissue found at the sub-voxel level. The fact that v_e cannot be accurately measured in areas that are poorly perfused means there could be sections of tumor tissue with inaccurate v_e estimates and a wide range of ADC values [12], and this would hinder any attempts at testing for a statistical relationship between the two parameters.

Diffusion weighted MRI also is not without its limitations and is also incompletely understood. The above mentioned issue of subvoxel heterogeneity on ADC estimates was also noted in the Mills et al study [12] where the authors pointed out that glioblastoma multiforme (the disease in their paper) has areas of microvascular proliferation, necrosis, edema, increased cellularity can influence ADC measurements in multiple ways. Such characteristics are found in many tumors (including breast). Additionally, perfusion can mimic diffusion at low diffusion weighting values (b < ~200 s/mm²), resulting in an artificial increase in the measured ADC value. In this study, a low b-value of 0 s/mm² was used, so there could be varying contributions from perfusion within the tumor, causing any increase in ADC to be non-uniform. However, it seems unlikely that this would cause a lack of correlation between ADC and v_e. As mentioned earlier, the relationship between the ADC and extracellular volume has been studied in a controlled manner [2] and is much more straightforward than the relationship between extracellular volume and v_e, as measured by DCE-MRI. There are also numerous other factors that may affect the ADC other than cell density (e.g., cell membrane permeability [26]), but in tumors over the time scales relevant here we would anticipate a strong correlation between ADC and v_e. Additional factors that affect the accuracy of ADC calculation include patient motion, incomplete suppression of the signal from adipose tissue, artifacts from biopsy markers, and susceptibility-induced distortions, which worsen as field strength increases, but the values reported here accord with other and expected values of ADC.

5. Conclusion

We have studied the relationship between the apparent diffusion coefficient returned by the analysis of diffusion weighted MRI and the extravascular extracellular volume fraction returned by analysis of dynamic contrast enhanced MRI. We were unable to find a significant relationship between the parameters even though a variety of common DCE analyses were explored. As stated in Mills et al. [12], this negative result is of importance because it indicates that our fundamental understanding of these two imaging parameters must not be complete. Given the simpler and strong evidence for explanation of ADC, we postulate that current DCE estimates of v_e in corporate assumptions into the data analysis that are not rigorously valid.