Abstract
Creep is a time-dependent viscoelastic deformation observed under a constant prolonged load. It has been indicated that progressive vertebral deformation due to creep may increase the risk of vertebral fracture in the long-term. The objective of this study was to examine the relationships of creep with trabecular architecture and tissue mineral density (TMD) parameters in human vertebral cancellous bone at a physiological static strain level. Architecture and TMD parameters of cancellous bone were analyzed using microcomputerized tomography (micro-CT) in specimens cored out of human vertebrae. Then, creep and residual strains of the specimens were measured after a two-hour physiological compressive constant static loading and unloading cycle. Creep developed (3877±2158 με) resulting in substantial levels of non-recoverable post-creep residual strain (1797±1391 με). A strong positive linear correlation was found between creep and residual strain (r=0.94, p<0.001). The current results showed that smaller thickness, larger surface area, greater connectivity of trabeculae, less mean tissue mineral density (TMD, represented by gray levels) and higher variability of TMD are associated with increasing logarithmic creep rate. The TMD variability (GLCOV) was the strongest correlate of creep rate (r=0.79, p<0.001). This result suggests that TMD variability may be a useful parameter for estimating the long-term deformation of a whole vertebral body. The results further suggest that the changes in TMD variability resulting from bone remodeling are of importance and may provide an insight into the understanding of the mechanisms underlying progressive failure of vertebral bodies and development of a clinical fracture.
Keywords: Human cancellous bone, Viscoelastic creep, Tissue mineral density, Architecture, Vertebral deformation
1. Introduction
Many clinical studies have indicated that progressive vertebral deformation of elderly patients results in long-term vertebral height loss and back pain (Briggs et al., 2004; Fechtenbaum et al., 2005; Keller et al., 2003; Melton III and Kallmes, 2006) and can eventually lead to a clinically established vertebral fracture (Keller et al., 2003; Sone et al., 1997). This loss of height implies that permanent deformations during prolonged mechanical loading of vertebral bodies are relevant to the tendency of a vertebra to collapse.
Creep is a continuous, time-dependent deformation observed in viscoelastic materials under a constant load (Lakes, 1999). Bone is a viscoelastic material in which mechanical properties change over the duration of loading (Currey, 1965; George and Vashishth, 2005; Kim et al., 2004b; Lynch and Silva, 2008; Rimnac et al., 1993; Sasaki and Enyo, 1995). Yamamoto et al. (2006) applied a physiological static creep (1500 με) on human vertebral cancellous bone and found a substantial creep development up to approximately 180% of the applied initial elastic strain. Of post-creep deformation, about half was not recovered, remaining as a residual strain. Furthermore, similar levels of creep and residual strain were measured during a physiological creep loading (1kN, corresponding to a range of strains between 1246 and 2018 με)-unloading cycle on whole human vertebrae (Pollintine et al., 2009). These findings suggested that progressive vertebral deformation would develop even at the physiological loading level over years, which may increase the risk of vertebral failure. However, very little is known about the factors that determine creep and recovery behavior of cancellous bone.
Bone mass or bone mineral density (BMD) is the strongest single determinant of cancellous bone mechanical properties (Keaveny et al., 2001; Kopperdahl and Keaveny, 1998). Thus, it is not surprising that less bone mass is associated with higher fracture risk of bone. However, it was indicated that bone mass alone can not fully explain bone fragility (Heaney, 2003; McCreadie and Goldstein, 2000) and creep of trabecular bone (Yamamoto et al., 2006). While BMD is defined to be the mineral content within an apparent volume of bone (including porosity and bone marrow, as well as bone matrix), the tissue mineral density (TMD) represents mineral content contained only in the matrix of bone (Tassani et al., 2011). Previous studies showed that TMD distribution of trabecular bone is altered after antiresorptive treatment with bisphosphonates in postmenopausal osteoporosis patients (Boivin et al., 2003; Borah et al., 2006). It has been also reported that TMD distribution is an important parameter in determining strength and elastic mechanical properties of bone matrix (Busse et al., 2009; Jaasma et al., 2002; van der Linden et al., 2001; van Ruijven et al., 2007; Yao et al., 2007). In addition to the bone tissue mineralization parameters, trabecular architectural parameters were also widely investigated for their association with mechanical properties of cancellous bone (Hernandez and Keaveny, 2006). However, to date, association of physiological creep behavior with architectural and TMD parameters of trabecular bone has not been investigated.
Because microstructural organization and tissue mineralization are strong determinants of the apparent and hard tissue mechanical properties of bone, we expect that the microstructural and mineralization parameters can contribute in determining the time-dependent mechanical behavior of bone. Therefore, we hypothesized that creep parameters strongly correlate with microstructure and TMD parameters in cancellous bone. The objective of this study was to examine the relationship of creep with trabecular architecture and mineralization in human vertebral cancellous bone at a physiological load level.
2. Materials and Methods
Thirteen vertebrae (T10: 1, T12: 3, L1: 3, L2: 3, L4: 2, and L5: 1) were prepared from 6 human cadavers (63~85 yrs, 3 males, and 3 females). Sixteen cylindrical cancellous bone specimens (∅ 7.54±0.13 mm × 9.39±0.2 mm) were obtained from the 13 vertebral cancellous centrums (one specimen per vertebra using 10 vertebrae and two specimens per vertebra using 3 vertebrae) under irrigation (Fig. 1a). The cored cylindrical specimens were stored at −21°C until utilized. After thawing at room temperature, the marrow and inter-trabecular water were removed by water- and air-jetting. Specimens were scanned by an in-house micro-CT scanner (20 μm) following previously developed protocols (Hou et al., 1998; Reimann et al., 1997). Bone voxels were digitally segmented from background noise in the three-dimensional (3D) reconstructed (20 μm) micro-CT images using commercial micro-CT software (Microview, GE). In the process of segmentation, the CT attenuation value (gray level (GL)) of a bone voxel, which is equivalent to bone tissue mineral density (TMD), was maintained in the micro-CT image (Fig. 1a and b). After segmentation, gray level density (GLD) and mean gray level (GLMean) were calculated by dividing the sum of gray levels of bone voxels by an apparent total volume (TV) of the cylindrical specimen and by the total number of bone voxels, respectively. Variability (coefficient of variation) of gray levels (GLCOV) was determined by dividing GL standard deviation (GLSD) by GLMean for each specimen. A customized code for morphological analysis was used to compute trabecular bone volume fraction (BV/TV), trabecular number (Tb.N), thickness (Tb.Th), separation (Tb.Sp), surface-to-volume ratio of bone (BS/BV), and connectivity density (Conn.D) using the segmented micro-CT images of cylindrical cancellous bone specimens (Kim et al., 2004a).
Fig. 1.
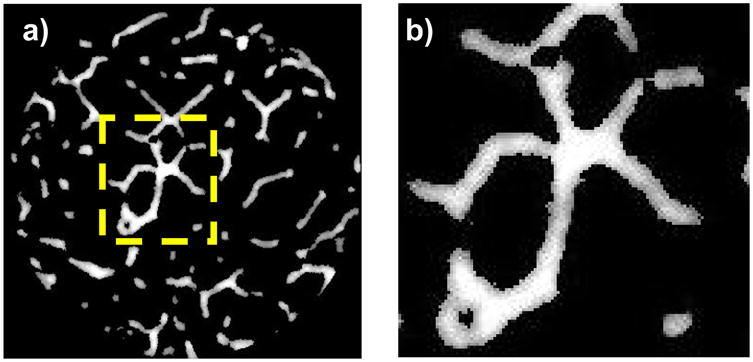
a) An axial view after micro-CT scanning and reconstruction, and b) a detailed view of the gray levels of bone-only voxels. More gray color represents less TMD.
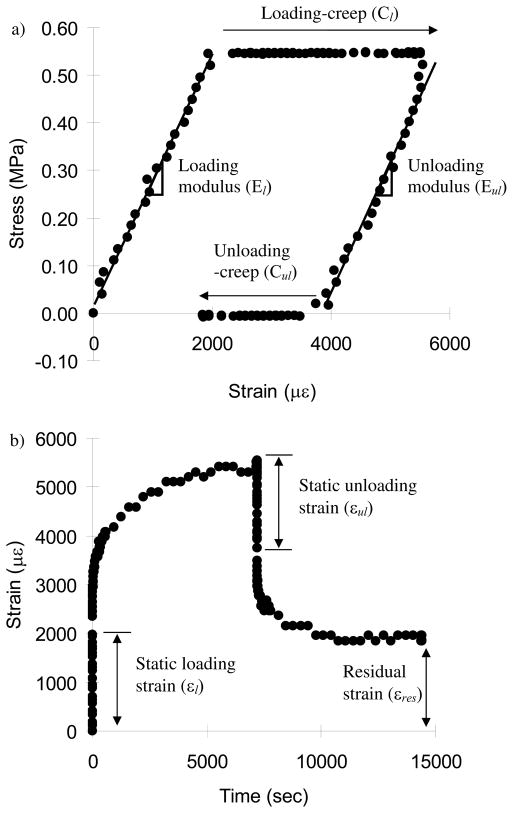
Following micro-CT scanning, creep tests were performed using a loading device (ELF 3200, EnduraTec, MN) with a 450 N load cell. An environmental chamber system installed on the loading machine was used to control temperature (37°C) and specimen moisture during creep tests. Before mechanical testing, machine compliance was measured following a previous study (Kalidindi et al., 1997) and accounted for later in calculation of creep displacements. After thawing, each specimen was mounted on a flat compressive loading jig. To avoid a sliding artifact during mechanical testing, both ends of the cancellous bone specimen were glued on metal jigs (Yeni and Fyhrie, 2001). The specimens were preloaded up to 0.01 MPa in order to glue the specimen on the metal jig surface. The initial compressive modulus (E0) of each bone specimen was determined by conducting 10 pre-cycles at a small elastic compressive strain range up to about 2000 με under displacement control. All other mechanical tests were performed under load control. The specimens were compressed at the stress level corresponding to 2000 με with a loading rate corresponding to a strain rate of 0.01 ε/sec. Using the initial modulus, an apparent stress corresponding to an apparent strain of 2000με (σ= 2000με × E0) was prescribed. This strain value was estimated as close to in vivo strains of human vertebral trabecular bone (Kopperdahl and Keaveny, 1998; Yamamoto et al., 2006). Following 2 hour compressive creep loading, the specimen was fully unloaded with the same loading rate and allowed to recover for 2 hours (Fig. 2). These durations for the loading-unloading cycle were the same as used for the whole vertebral body creep tests (Pollintine et al., 2009). The data sampling rates were 100 Hz for the static loading/unloading periods and down to 0.003 Hz for the creep periods. We did not use a smoothing process. Specimen moduli were determined using slopes of stress-strain curves during the whole static loading (El) and unloading (Eul) ranges of the creep cycle (Fig. 2a), and static strains were measured during loading (εl) and unloading (εul) (Fig. 2b). Loading creep (Cl) was computed by subtracting the initial strain from the strain measured at the end of 2 hours of creep loading and unloading creep recovery (Cul) was obtained by subtracting the final strain at the end of 2 hours of unloading recovery from the strain measured at the end of static unloading. Residual strain (εres) was measured as the final strain at the end of a 2 hour unloading recovery process. Slopes of logarithmic time-to-creep curve for the 2 hour loading and unloading creep cycles were separately measured to obtain creep rates for loading (al) and unloading (aul) processes (Fig. 3).
Fig. 2.
a) A typical stress-strain curve of creep and b) strain development with time during loading and unloading periods. The terms related to mechanical creep testing were defined using the typical creep curves.
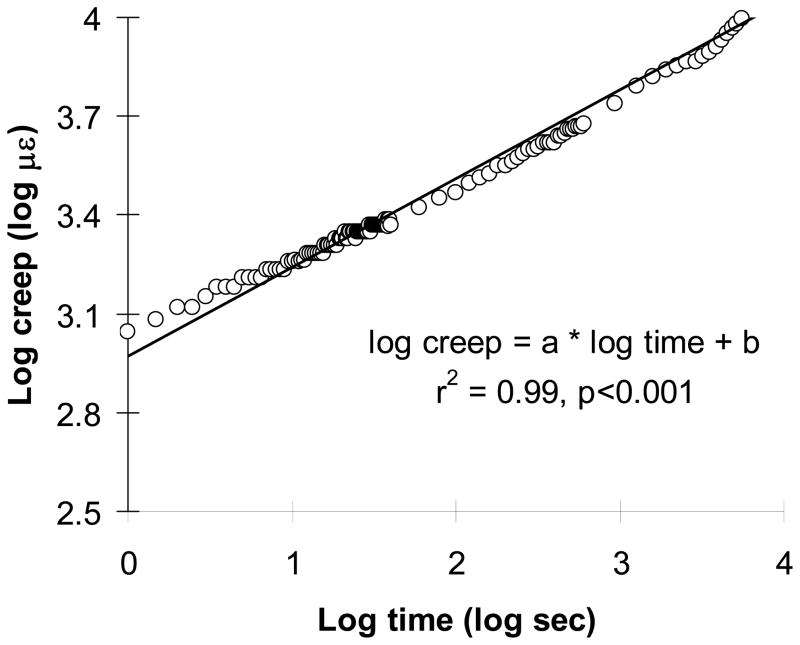
Fig. 3.
A typical log-log plot for a time-to-creep curve (al=0.22±0.03 (με/sec) and bl=2.67±0.17 με, and aul=0.16±0.02 (με/sec−1) and bul=2.65±0.16 με for all specimens (n=16)).
Paired t-tests were performed to compare between loading and unloading periods for modulus (El vs Eul), static strain (εl vs εul), creep (Cl vs Cul) and creep rate (al vs aul). Linear regression was used to characterize the logarithmic time-to-creep curve. Pearson’s correlation coefficients were used to examine correlations between creep parameters (El, Eul, Cl, Cul, al, aul and εres) and correlations of the creep parameters with architectural (BV/TV, Tb.N, Tb.Th, Tb.Sp, BS/BV, and Conn.D) and TMD (GLD, GLMean, GLSD, and GLCOD) parameters. For the architectural and TMD parameters that had significant correlations with the creep parameters, stepwise regressions were performed to find the best parameter to explain the creep behavior. Significance was set at p<0.05 for all statistical tests.
3. Results
The initial static loading strain (εl) values (1998±148 με) were close to the targeted value (2000 με). The initial static stresses to achieve these strain values were 0.53±0.26 MPa. Creep (Cl) increased with time for all cancellous bone specimens under loading for 2 hours (3877±2158 με) (Fig. 2). The unloading modulus (Eul) was significantly higher than the loading modulus (El) (p<0.013) (Table 1). The static unloading strain (εul) was significantly lower than the static loading strain (εl) (p<0.041). The creep was not fully recovered after a two-hour unloading, as indicated by the significantly lower value of unloading creep recovery (Cul) than that of loading creep (Cl) (p<0.001). Combination of these incomplete recoveries of static strain and creep resulted in substantial residual strain (1797±1391 με) after the loading-unloading creep cycle. A linear fit to the log-log plot of creep vs. time curves was used for both creep loading and unloading creep recovery for each specimen (Fig. 3, r2=0.95~0.99, p<0.001). The loading creep rate (al) was significantly higher than the unloading recovery rate (aul) (p<0.001).
Table 1.
The paired t-test between loading and unloading periods for modulus (El vs Eul), static strain (εl vs εul), creep (Cl vs Cul) and logarithmic creep rates (al vs aul) (n=16).
| Modulus (MPa) | Static Strain (με) | Creep (με) | Log creep rate (με/sec) | |||||
|---|---|---|---|---|---|---|---|---|
| El | Eul | εl | εul | Cl | Cul | al | aul | |
| Mean ±SD | 251±126 | 274±132 | 1998±148 | 1855±300 | 3877±2158 | 2223±820 | 0.22±0.03 | 0.16±0.02 |
| p-value | <0.013 | <0.041 | <0.001 | <0.001 | ||||
Significant positive correlations were found between loading and unloading moduli (El vs Eul), creep (Cl vs Cul), unloading creep recovery and loading creep rate (Cul vs al), and creep and residual strain (Cl vs εres and Cul vs εres) (r=0.52~97, p<0.04) (Table 2) while the correlations between other creep parameters were not significant (p>0.086).
Table 2.
The correlation coefficient (r) and p-values of significant correlation between mechanical parameters (n=16).
| Y | X | r | p-values |
|---|---|---|---|
| Eul (MPa) | El (MPa) | 0.97 | <0.001 |
| Cul (με) | Cl (με) | 0.89 | <0.001 |
| Cul (με) | al (με/sec) | 0.52 | <0.039 |
| εres (με) | Cl (με) | 0.94 | <0.001 |
| εres (με) | Cul (με) | 0.70 | <0.003 |
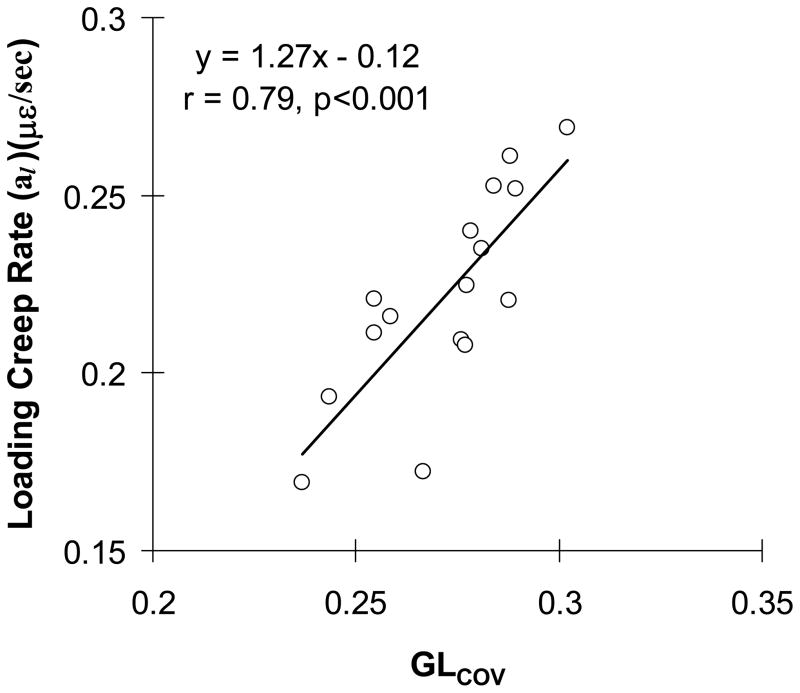
The unloading modulus (Eul) had a significant negative correlation with variability of gray levels (GLCOV) (r=−0.52, p<0.038). The creep rate (al) had significant or marginally significant positive correlations with BS/BV, Conn.D, GLSD and GLCOV (p<0.001 to p<0.067) but negative correlations with Tb.Th and GLMean (p<0.054 for both) (Table 3). All other correlations of creep parameters with architectural and gray level parameters were not significant (p>0.095). The GLCOV had the strongest correlation with al (r=0.79, p<0.001) (Fig. 4). The stepwise regression including all of the architectural and TMD parameters that had significant correlations with al in Table 3 confirmed that the GLCOV was the only parameter to explain al (p<0.001). The GLCOV significantly correlated with the parameters that had significant or marginal correlations with al (Table 3).
Table 3.
The correlation coefficient (r) and p-value of significant or marginal correlations of loading-creep rate (al) and variability of gray levels (GLcov) with architectural and gray level (TMD) parameters (n=16).
| Y | X
|
||||||
|---|---|---|---|---|---|---|---|
| Tb.Th (mm) | BS/BV (mm−1) | Conn.D (mm−3) | GLMean (mm−3) | GLSD (mm−3) | GLcov | ||
| al (με/s) | r | −0.50 | 0.47 | 0.49 | −0.62 | 0.51 | 0.79 |
| p-value | <0.05 | 0.067 | 0.053 | <0.01 | <0.05 | <0.001 | |
|
| |||||||
| GLcov (mm−1) | r | −0.72 | 0.71 | 0.62 | −0.87 | 0.52 | 1 |
| p-value | <0.002 | <0.003 | <0.011 | <0.001 | <0.045 | ||
Fig. 4.
Correlation of loading creep rate (al) with variability of gray levels (GLcov) (n=16).
4. Discussion
The creep (Cl) was observed in human vertebral cancellous bone under the physiological compressive loading level resulting in the substantial non-recoverable post-creep residual strain (εres). The strong positive linear correlation between creep and residual strain indicated that the physiological creep could determine the permanent decrease in ancellous bone height. We found that smaller thickness, larger surface area of trabeculae, greater connectivity, less mean tissue mineral density (TMD, represented by gray levels), and higher variability of TMD, are associated with increasing logarithmic creep rate (al). Of the architectural and TMD parameters, the TMD variability (GLCOV) turned out to be the strongest parameter that correlated with the creep rate. It was previously indicated that higher rates of bone turnover increase the variability of TMD (Yao et al., 2007). Combined together, these observations suggest that increased variability of TMD in association with high bone matrix turnover would contribute to the long-term deformation of cancellous bone under physiological creep.
The initial static strains used in this study was higher than those used in the previous study (Yamamoto et al. (2006)) but the creep loading duration was shorter. Despite these differences in loading protocols, we found substantial residual strain after the creep-recovery loading cycle of bone consistent with those observed in the previous studies (Currey, 1965; Pollintine et al., 2009; Yamamoto et al., 2006). Yamamoto et al. (2006) measured creep and residual strains of human L3 vertebral cancellous bone developed under prolonged static loading corresponding to 750 με (169 με for creep and 515±255 με for residual strain) and 1500 με (1198 με for creep and 1565±590 με for residual strain) static strains for a 125,000 sec load-unload period. They estimated that the residual strain would be recovered within 26 days and 63 days in the 750 με and 1500 με loading groups, respectively. Compared with their study, the current creep tests applied higher loading corresponding to a higher static strain (1998 με) and a shorter load-unload period (7200 sec). The loading conditions of the current study produced higher creep and residual strains (3877±2158 με and 1797±1391 με, respectively) than those of the previous study (Yamamoto et al. (2006)). However, the full recovery time for the higher amount of strain resulting from the current loading condition was estimated shorter (11 days) based on the unloading equation in Fig 3. Overall, these results indicate that the amount of creep and residual strains would strongly depend on the applied initial loading level whereas full recovery time would depend on combination of loading-unloading duration and the initial loading level. This finding suggests that a complex interaction between activity level and duration, and rest periods in determining long-term creep in real life.
The amount of residual strain was dependent on the level of creep development. No traditional parameters related to mechanical properties of cancellous bone including modulus (El and Eul), bone volume fraction (BV/TV) and bone mineral density (GLD) could explain the creep parameters measured in the current study. This result agreed with Yamamoto et al. (2006) who found no significant correlations between apparent density and any outcome variables of creep in human vertebral cancellous bone. On the other hand, the logarithmic creep rate (al) was significantly associated with trabecular thickness (Tb.Th) and all of TMD parameters examined in the current study. Increase in the logarithmic creep rate accounts for non-linear (power law) acceleration of creep in a given duration of loading. The stronger correlations of TMD parameters with the creep rate suggests that degree of mineralization at the tissue level is involved in the time-dependent creep mechanisms and may be a significant source of the apparent viscoelastic behavior in trabecular bone.
Perhaps most noteworthy is the finding that TMD variability (GLCOV) showed a strong positive linear correlation with the creep rate independent of architectural measures. It was previously found that the TMD variability of bone increased by active bone remodeling that produces more newly forming (less mineralized) bone matrix (Ames et al., 2010; Roschger et al., 2008; Ruffoni et al., 2007; Yao et al., 2007). Yao et al. (2007) observed that estrogen deficiency elevated bone turnover of ovariectomized (OVX) rat vertebral trabeculae resulting in higher TMD variability, mineralizing surface and connectivity density, and lower mean TMD and trabecular thickness compared to sham surgery. Similar changes of the architectural and TMD parameters were also observed in association with active bone remodeling in postmenopausal human patients (Borah et al., 2005; Parfitt et al., 1997; Roschger et al., 2001; Seeman, 2003; Sornay-Rendu et al., 2009). Although many studies indicated that increase in TMD variability leads to inferior static mechanical properties of bone (Jaasma et al., 2002; van der Linden et al., 2001; van Ruijven et al., 2007; Yao et al., 2007), no study has investigated the correlation of the TMD variability with a viscoelastic property of bone. To our knowledge, the current study is the first experiment that examined the effect of TMD variability on time-dependent viscoelastic creep behavior of human trabecular bone. The current results reinforce the notion that residual strains due to the compressive creep of vertebral trabecular bone may be a mechanical cause for the progressive height loss vertebrae observed postmenopause. The strong positive correlation between the TMD variability with the creep rate suggests changes in bone turnover rate and/or targeted remodeling that may result in increased TMD variability could cause acceleration of creep and contribute to the development of vertebral deformities.
Mechanism of creep behavior of bone under a small physiological load level has not been fully understood. It was indicated that trabecular bone damage may start at the load level corresponding to as small as 2000 με (Morgan et al., 2001; Morgan et al., 2005). If the bone specimens were damaged by loading, the unloading modulus should decrease relative to the loading modulus (Joo et al., 2007). In contrast, we found that the post-creep unloading modulus of the specimen was significantly greater than the pre-creep loading modulus. This increase of post-creep modulus was accompanied by, as expected under a constant load level, a significantly lower post-creep unloading static recovery strain (εul) than the static loading strain (εl). These results imply that a reorganization of micro- or ultrastructural components of bone matrix is caused by compressive creep and this new organizational state is not fully released at unloading. Lakes and Saha (1979) showed that creep developed at cement lines of bone under a prolonged constant loading. They suggested that internal friction at cement lines would be a source of the creep (Lakes and Saha, 1979). The number of inter-packet cement lines inherently increases while more new trabecular packets are produced by rapid bone turnover (Boyde, 2002; Marcus, 1996; van der Linden et al., 2001). It was found that newly forming bone matrix develops more creep than existing bone matrix (Kim et al., 2010). These observations suggest that creep behavior of trabecular bone also would be controlled by the degree of bone remodeling. This suggestion is supported by the current finding of the strong positive correlation between the creep rate and the TMD variability that is likely accelerated by active bone remodeling.
Although vertebral cortex would substantially share mechanical stress applied on vertebra with trabecular centrum (Eswaran et al., 2006), the current measurements did not include the creep behavior of cortex. Recently, Pollintine et al. (2009) applied 2 hour creep-unloading cycles corresponding to physiological strain (1246~2018 με) on a whole vertebral body. They measured creep (2867~3133 με) and residual strain (up to 2540 με) values in the anterior vertebral region, which are comparable to those from the current creep tests of vertebral cancellous bone only. These results suggest that the cancellous centrum rather than the cortex is largely responsible for the creep behavior of the anterior vertebral region in which a greater creep was observed in comparison to other vertebral regions as the previous study measured (Pollintine et al., 2009).
Some limitations must be noted. First, the sample size of 16 used in the current study was small but it was comparable with that in Yamamoto et al. (2006) who succeeded to show the creep development with a sample size of 12 human vertebral cancellous bones. However, larger scale studies are necessary for further confirmation of the significant observations found in the current study. Second, the specimens were preloaded (0.01 MPa) to ensure the contact between the surfaces of loading jig and trabecular bone. As the amount of preload was less than 2% of loading stress, we ignored the effect of preload on creep development. Third, we did not apply cyclic loading which would be more realistic for simulating daily activities. We feel our static loading condition was justified because Yamamoto et al. (2006) clearly demonstrated that no significant differences in creep and residual strain developed between static loading corresponding to 1500 με and cyclic loading corresponding between 0 and 1500 με at 8Hz for the same loading duration. Fourth, this study was not designed to examine the possible biological activities including bone remodeling that may be stimulated while creep develops. Pattin et al. (1996) suggested that 4000 με in compression is within a strain range to trigger bone remodeling (Pattin et al., 1996). As such, the sum of compressive static strain and creep that was measured 5875 με in the current study likely stimulates bone remodeling in a live patient. The newly forming bone matrix during the bone remodeling may accelerate local creep development leading to increase in overall apparent creep. If the structure of cancellous centrum bone deformed due to creep becomes permanent by continuous bone remodeling, the accumulation of such deformation may contribute to the development of clinically observable whole vertebral deformities. On the other hand, it is possible that the residual creep deformation is released by bone remodeling. Pollintine et al. (2009) noted that creep deformation can not always lead to bone fracture because bone creep can be reversed in living tissues (Lynch and Silva, 2008). However, investigating these biological activities during creep in vivo was beyond the scope of the current study.
In conclusion, viscoelastic creep development in vertebral trabecular bone caused residual strain, accumulation of which could be a mechanical cause of time-dependent vertebral height loss. We examined several architectural and mineralization parameters and identified TMD variability as a possible determinant of creep rate in cancellous bone. This result suggests that the changes in TMD variability, potentially resulting from bone remodeling, is of importance in providing a useful parameter for estimating the long-term deformation and understanding the mechanisms underlying progressive failure of a whole vertebral body.
Acknowledgments
The project described was, in part, supported by Grant Number AG033714 from National Institute on Aging (Kim, D-G). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Institute on Aging. Human tissue used in the presented work was provided by NDRI (National Disease Research Interchange).
Footnotes
Conflict of Interest Statement None declared.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ames M, Hong S, Lee H, Fields H, Johnston W, Kim DG. Estrogen deficiency increases variability of tissue mineral density of alveolar bone surrounding teeth. Arch Oral Biol. 2010;55:599–605. doi: 10.1016/j.archoralbio.2010.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boivin G, Lips P, Ott SM, Harper KD, Sarkar S, Pinette KV, Meunier PJ. Contribution of Raloxifene and Calcium and Vitamin D3 Supplementation to the Increase of the Degree of Mineralization of Bone in Postmenopausal Women. J Clin Endocrinol Metab. 2003;88:4199–4205. doi: 10.1210/jc.2002-022020. [DOI] [PubMed] [Google Scholar]
- Borah B, Ritman EL, Dufresne TE, Jorgensen SM, Liu S, Sacha J, Phipps RJ, Turner RT. The effect of risedronate on bone mineralization as measured by micro-computed tomography with synchrotron radiation: Correlation to histomorphometric indices of turnover. Bone. 2005;37:1–9. doi: 10.1016/j.bone.2005.03.017. [DOI] [PubMed] [Google Scholar]
- Borah B, Dufresne TE, Ritman EL, Jorgensen SM, Liu S, Chmielewski PA, Phipps RJ, Zhou X, Sibonga JD, Turner RT. Long-term risedronate treatment normalizes mineralization and continues to preserve trabecular architecture: sequential triple biopsy studies with micro-computed tomography. Bone. 2006;39:345–352. doi: 10.1016/j.bone.2006.01.161. [DOI] [PubMed] [Google Scholar]
- Boyde A. Morphologic detail of aging bone in human vertebrae. Endocrine. 2002;17:5–14. doi: 10.1385/ENDO:17:1:05. [DOI] [PubMed] [Google Scholar]
- Busse B, Hahn M, Soltau M, Zustin J, Puschel K, Duda GN, Amling M. Increased calcium content and inhomogeneity of mineralization render bone toughness in osteoporosis: mineralization, morphology and biomechanics of human single trabeculae. Bone. 2009;45:1034–1043. doi: 10.1016/j.bone.2009.08.002. [DOI] [PubMed] [Google Scholar]
- Currey JD. Anelasticity in Bone and Echinoderm Skeletons. J Exp Biol. 1965;43:279–292. [Google Scholar]
- Eswaran SK, Gupta A, Adams MF, Keaveny TM. Cortical and trabecular load sharing in the human vertebral body. J Bone Miner Res. 2006;21:307–314. doi: 10.1359/jbmr.2006.21.2.307. [DOI] [PubMed] [Google Scholar]
- George WT, Vashishth D. Damage mechanisms and failure modes of cortical bone under components of physiological loading. J Orthop Res. 2005;23:1047–1053. doi: 10.1016/j.orthres.2005.02.008. [DOI] [PubMed] [Google Scholar]
- Heaney RP. Is the paradigm shifting? Bone. 2003;33:457–465. doi: 10.1016/s8756-3282(03)00236-9. [DOI] [PubMed] [Google Scholar]
- Hernandez CJ, Keaveny TM. A biomechanical perspective on bone quality. Bone. 2006;39:1173–1181. doi: 10.1016/j.bone.2006.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou FJ, Lang SM, Hoshaw SJ, Reimann DA, Fyhrie DP. Human vertebral body apparent and hard tissue stiffness. J Biomech. 1998;31:1009–1015. doi: 10.1016/s0021-9290(98)00110-9. [DOI] [PubMed] [Google Scholar]
- Jaasma MJ, Bayraktar HH, Niebur GL, Keaveny TM. Biomechanical effects of intraspecimen variations in tissue modulus for trabecular bone. J Biomech. 2002;35:237–246. doi: 10.1016/s0021-9290(01)00193-2. [DOI] [PubMed] [Google Scholar]
- Joo W, Jepsen KJ, Davy DT. The effect of recovery time and test conditions on viscoelastic measures of tensile damage in cortical bone. J Biomech. 2007;40:2731–2737. doi: 10.1016/j.jbiomech.2007.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalidindi SR, Abusafieh A, El-Danaf E. Accurate characterization of machine compliance for simple compression testing. Experimental Mechanics. 1997;37:210–215. [Google Scholar]
- Keaveny TM, Morgan EF, Niebur GL, Yeh OC. Biomechanics of trabecular bone. Annu Rev Biomed Eng. 2001;3:307–333. doi: 10.1146/annurev.bioeng.3.1.307. [DOI] [PubMed] [Google Scholar]
- Keller TS, Harrison DE, Colloca CJ, Harrison DD, Janik TJ. Prediction of osteoporotic spinal deformity. Spine. 2003;28:455–462. doi: 10.1097/01.BRS.0000048651.92777.30. [DOI] [PubMed] [Google Scholar]
- Kim DG, Christopherson GT, Dong XN, Fyhrie DP, Yeni YN. The effect of microcomputed tomography scanning and reconstruction voxel size on the accuracy of stereological measurements in human cancellous bone. Bone. 2004a;35:1375–1382. doi: 10.1016/j.bone.2004.09.007. [DOI] [PubMed] [Google Scholar]
- Kim DG, Miller MA, Mann KA. Creep dominates tensile fatigue damage of the cement-bone interface. J Orthop Res. 2004b;22:633–640. doi: 10.1016/j.orthres.2003.09.007. [DOI] [PubMed] [Google Scholar]
- Kim D-G, Huja SS, Lee HR, Tee BC, Hueni S. Relationships of viscosity with contact hardness and modulus of bone matrix measured by nanoindentation. J Biomech Eng. 2010;132(2):024502, 1–5. doi: 10.1115/1.4000936. [DOI] [PubMed] [Google Scholar]
- Kopperdahl DL, Keaveny TM. Yield strain behavior of trabecular bone. J Biomech. 1998;31:601–608. doi: 10.1016/s0021-9290(98)00057-8. [DOI] [PubMed] [Google Scholar]
- Lakes R, Saha S. Cement line motion in bone. Science. 1979;204:501–503. doi: 10.1126/science.432653. [DOI] [PubMed] [Google Scholar]
- Lakes RS. Viscoelastic Solid. CRC Press; New York: 1999. p. 267. [Google Scholar]
- Lynch JA, Silva MJ. In vivo static creep loading of the rat forelimb reduces ulnar structural properties at time-zero and induces damage-dependent woven bone formation. Bone. 2008;42:942–949. doi: 10.1016/j.bone.2008.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcus R. The nature of osteoporosis. J Clin Endocrinol Metab. 1996;81:1–5. doi: 10.1210/jcem.81.1.8550734. [DOI] [PubMed] [Google Scholar]
- McCreadie BR, Goldstein SA. Biomechanics of fracture: Is bone mineral density sufficient to assess risk? J Bone Miner Res. 2000;15:2305–2308. doi: 10.1359/jbmr.2000.15.12.2305. [DOI] [PubMed] [Google Scholar]
- Morgan EF, Yeh OC, Chang WC, Keaveny TM. Nonlinear behavior of trabecular bone at small strains. J Biomech Eng. 2001;123:1–9. doi: 10.1115/1.1338122. [DOI] [PubMed] [Google Scholar]
- Morgan EF, Yeh OC, Keaveny TM. Damage in trabecular bone at small strains. Eur J Morphol. 2005;42:13–21. doi: 10.1080/09243860500095273. [DOI] [PubMed] [Google Scholar]
- Parfitt AM, Han ZH, Palnitkar S, Rao DS, Shih MS, Nelson D. Effects of ethnicity and age or menopause on osteoblast function, bone mineralization, and osteoid accumulation in iliac bone. J Bone Miner Res. 1997;12:1864–1873. doi: 10.1359/jbmr.1997.12.11.1864. [DOI] [PubMed] [Google Scholar]
- Pattin CA, Caler WE, Carter DR. Cyclic mechanical property degradation during fatigue loading of cortical bone. J Biomech. 1996;29:69–79. doi: 10.1016/0021-9290(94)00156-1. [DOI] [PubMed] [Google Scholar]
- Pollintine P, Luo J, Offa-Jones B, Dolan P, Adams MA. Bone creep can cause progressive vertebral deformity. Bone. 2009;45:466–472. doi: 10.1016/j.bone.2009.05.015. [DOI] [PubMed] [Google Scholar]
- Reimann DA, Hames SM, Flynn MJ, Fyhrie DP. A cone beam computed tomography system for true 3D imaging of specimens. Appl Radiat Isot. 1997;48:1433–1436. doi: 10.1016/s0969-8043(97)00139-5. [DOI] [PubMed] [Google Scholar]
- Rimnac CM, Petko AA, Santner TJ, Wright TM. The effect of temperature, stress and microstructure on the creep of compact bovine bone. J Biomech. 1993;26:219–228. doi: 10.1016/0021-9290(93)90360-q. [DOI] [PubMed] [Google Scholar]
- Roschger P, Rinnerthaler S, Yates J, Rodan GA, Fratzl P, Klaushofer K. Alendronate increases degree and uniformity of mineralization in cancellous bone and decreases the porosity in cortical bone of osteoporotic women. Bone. 2001;29:185–191. doi: 10.1016/s8756-3282(01)00485-9. [DOI] [PubMed] [Google Scholar]
- Roschger P, Paschalis EP, Fratzl P, Klaushofer K. Bone mineralization density distribution in health and disease. Bone. 2008;42:456–466. doi: 10.1016/j.bone.2007.10.021. [DOI] [PubMed] [Google Scholar]
- Ruffoni D, Fratzl P, Roschger P, Klaushofer K, Weinkamer R. The bone mineralization density distribution as a fingerprint of the mineralization process. Bone. 2007;40:1308–1319. doi: 10.1016/j.bone.2007.01.012. [DOI] [PubMed] [Google Scholar]
- Sasaki N, Enyo A. Viscoelastic properties of bone as a function of water content. J Biomech. 1995;28:809–815. doi: 10.1016/0021-9290(94)00130-v. [DOI] [PubMed] [Google Scholar]
- Seeman E. Reduced bone formation and increased bone resorption: rational targets for the treatment of osteoporosis. Osteoporos Int. 2003;14(Suppl 3):S2–8. doi: 10.1007/s00198-002-1340-9. [DOI] [PubMed] [Google Scholar]
- Sone T, Tomomitsu T, Miyake M, Takeda N, Fukunaga M. Age-related changes in vertebral height ratios and vertebral fracture. Osteoporos Int. 1997;7:113–118. doi: 10.1007/BF01623685. [DOI] [PubMed] [Google Scholar]
- Sornay-Rendu E, Boutroy S, Munoz F, Bouxsein ML. Cortical and trabecular architecture are altered in postmenopausal women with fractures. Osteoporos Int. 2009;20:1291–1297. doi: 10.1007/s00198-009-1008-9. [DOI] [PubMed] [Google Scholar]
- Tassani S, Ohman C, Baruffaldi F, Baleani M, Viceconti M. Volume to density relation in adult human bone tissue. J Biomech. 2011;44:103–108. doi: 10.1016/j.jbiomech.2010.08.032. [DOI] [PubMed] [Google Scholar]
- van der Linden JC, Birkenhager-Frenkel DH, Verhaar JA, Weinans H. Trabecular bone’s mechanical properties are affected by its non-uniform mineral distribution. J Biomech. 2001;34:1573–1580. doi: 10.1016/s0021-9290(01)00146-4. [DOI] [PubMed] [Google Scholar]
- van Ruijven LJ, Mulder L, van Eijden TM. Variations in mineralization affect the stress and strain distributions in cortical and trabecular bone. J Biomech. 2007;40:1211–1218. doi: 10.1016/j.jbiomech.2006.06.004. [DOI] [PubMed] [Google Scholar]
- Yamamoto E, Crawford RP, Chan DD, Keaveny TM. Development of residual strains in human vertebral trabecular bone after prolonged static and cyclic loading at low load levels. J Biomech. 2006;39:1812–1818. doi: 10.1016/j.jbiomech.2005.05.017. [DOI] [PubMed] [Google Scholar]
- Yao W, Cheng Z, Koester KJ, Ager JW, Balooch M, Pham A, Chefo S, Busse C, Ritchie RO, Lane NE. The degree of bone mineralization is maintained with single intravenous bisphosphonates in aged estrogen-deficient rats and is a strong predictor of bone strength. Bone. 2007;41:804–812. doi: 10.1016/j.bone.2007.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeni YN, Fyhrie DP. Finite element calculated uniaxial apparent stiffness is a consistent predictor of uniaxial apparent strength in human vertebral cancellous bone tested with different boundary conditions. J Biomech. 2001;34:1649–1654. doi: 10.1016/s0021-9290(01)00155-5. [DOI] [PubMed] [Google Scholar]