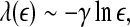Abstract
To understand the nature of brain dynamics as well as to develop novel methods for the diagnosis of brain pathologies, recently, a number of complexity measures from information theory, chaos theory, and random fractal theory have been applied to analyze the EEG data. These measures are crucial in quantifying the key notions of neurodynamics, including determinism, stochasticity, causation, and correlations. Finding and understanding the relations among these complexity measures is thus an important issue. However, this is a difficult task, since the foundations of information theory, chaos theory, and random fractal theory are very different. To gain significant insights into this issue, we carry out a comprehensive comparison study of major complexity measures for EEG signals. We find that the variations of commonly used complexity measures with time are either similar or reciprocal. While many of these relations are difficult to explain intuitively, all of them can be readily understood by relating these measures to the values of a multiscale complexity measure, the scale-dependent Lyapunov exponent, at specific scales. We further discuss how better indicators for epileptic seizures can be constructed.
Keywords: Brain dynamics, Complexity measures of EEG signals, Epileptic seizure
Introduction
Electroencephalographic (EEG) signals provide a wealth of information about the brain dynamics, especially related to cognitive processes and pathologies of the brain such as epileptic seizures (Napolitano and Orriols 2008; Plummer et al. 2008; Holmes 2008). To understand the nature of brain dynamics as well as to develop novel methods for the diagnosis of brain pathologies, recently, a number of complexity measures from information theory, chaos theory, and random fractal theory have been applied to analyze the EEG data. They include the Lempel–Ziv (LZ) complexity (Lempel and Ziv 1976), the permutation entropy (PE) (Bandt and Pompe 2002; Cao et al. 2004), the Lyapunov exponent (LE) (Wolf et al. 1985), the Kolmogorov entropy (Grassberger and Procaccia 1983b), the correlation dimension D2 (Grassberger and Procaccia 1983a; Martinerie et al. 1998), and the Hurst parameter (Peng et al. 1994; Hwa and Ferree 2002; Robinson 2003).
The above complexity measures and the associated models are crucial for quantifying some of the key notions of neurodynamics, including determinism, stochasticity, causation, and correlations (Atmanspacher and Rotter 2008). For example, if one can infer low-dimensional chaos from EEG data analysis (Pijn et al. 1991; Babloyantz and Destexhe 1986), then the notion of determinism would be favored. Otherwise, stochasticity would be favored. When developing stochastic models for EEG signals, one important task would be to address what kind of causation and/or correlation structure the model has to possess. With this respect, 1/fα noise has attracted much attention (Freeman 2009). The defining parameter for 1/fα noise is the Hurst parameter, which characterizes the correlation structure of the EEG. Therefore, finding and understanding the relations among these complexity measures for EEG is an important issue, both theoretically and clinically.
This above issue is difficult to solve, however, for two basic reasons: (1) The dynamics of the brain is highly complicated, having multiple spatial-temporal scales (Gao et al. 2007; Deco et al. 2008). At present, however, it is unknown whether a certain measure is characterizing the EEG dynamics on a specific or on multiple spatial-temporal scales. (2) The foundations of information theory, chaos theory, and random fractal theory are very different: Chaos theory is mainly concerned about apparently irregular behaviors in a complex system that are generated by nonlinear deterministic interactions with only a few degrees of freedom, where noise or intrinsic randomness does not play an important role, while random fractal theory and information theory both assume that the dynamics of the system are inherently random (Gao et al. 2007). Even though the latter two theories are both about randomness, their focus is fundamentally different: random fractal theory focuses on long-range correlations while information theory focuses on short-range correlations (Gao et al. 2006b, 2007). As a consequence of the 2nd reason, although a lot of efforts have been made to determine whether EEGs are chaotic or random (Rombouts et al. 1995; Pritchard et al. 1995; Theiler and Rapp 1996; Fell et al. 1996; Andrzejak et al. 2001; Lai et al. 2003; Aschenbrenner-Scheibe et al. 2003), no systematic efforts have been made to compare among the different complexity measures of EEG.
In this paper, we aim primarily to understand the relations of different complexity measures of EEG, by examining how different complexity measures vary with time. Our purpose can be best served by analyzing long EEG signals containing special events, such as epileptic seizures or strokes, or events related to special stimulations or cognitive processes. We choose data with seizures so that our analysis presented here can be directly useful for clinical monitoring of seizures. We emphasize, however, that this shall only be our secondary purpose, but not the primary one, and therefore, no animal models will be considered here. In fact, we shall point out in due time that far away from seizure events, a complexity measure can still have nontrivial temporal variations. We also emphasize that signal analyses presented here are not the same as physiology-based modeling of the brain dynamics. For an exquisite exposition of this point, we refer to Deco et al. (2008).
The remainder of the paper is organized as follows. In Sect. "EEG data with epileptic seizures", we briefly describe the EEG data analyzed here. In Sect. "Analysis of EEG by a variety of complexity measures", we compare six major complexity measures for EEG. In Sect. "Concluding remarks", we summarize our findings and understandings.
EEG data with epileptic seizures
Epilepsy is one of the most common disorders of the brain. Seizure onset is often associated with simultaneous occurrence of transient EEG signals such as spikes, spike and slow wave complexes or rhythmic slow wave bursts. It is also associated with either abnormal running/bouncing fits, clonus of face and forelimbs, or tonic rearing movement. These activities may be recorded by videotapes.
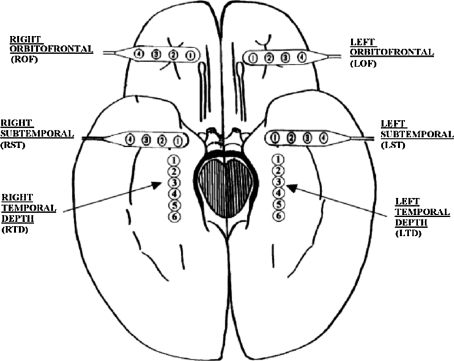
The EEG recordings analyzed here were obtained from implanted electrodes placed in the hippocampus and over the inferior temporal and orbitofrontal cortex, as well as coverage of the temporal lobes by a limited number of scalp electrodes (scalp EEG). Figure 1 shows our typical 28 electrode montage used for subdural and depth recordings. For more details about EEG recording collection, please refer to Iasemidis et al. (1999).
Fig. 1.
Schematic diagram of the depth and subdural electrode placement. This view from the inferior aspect of the brain shows the approximate location of depth electrodes, oriented along the anterior–posterior plane in the hippocampi (RTD—right temporal depth, LTD—left temporal depth), and subdural electrodes located beneath the orbitofrontal and subtemporal cortical surfaces (ROF—right orbitofrontal, LOF—left orbitofrontal, RST—right subtemporal, LST—left subtemporal). Figure adapted from Iasemidis et al. (1999)
Altogether, we have analyzed 7 patients’ multiple channel EEG data, sampled with a sampling frequency of 200 Hz. The exact length of the EEG signals and the number of seizures contained in the signals are shown in Table 1.
Table 1.
Performance of the LE-based method for seizure monitoring
| Data set | Length (Hours) | Total number of seizures | Sensitivity overall: 74 (%) | False alarm per hour mean: 0.05 |
|---|---|---|---|---|
| P92 | 35 | 7 | 100 | 0.09 |
| P93 | 64 | 23 | 78 | 0.02 |
| P148 | 76 | 17 | 58 | 0.07 |
| P185 | 47 | 19 | 73 | 0.02 |
| P40 | 5.3 | 1 | 100 | 0.00 |
| P256 | 4.5 | 1 | 100 | 0.00 |
| P130 | 5.7 | 2 | 50 | 0.18 |
The total number of seizures was determined by examining clinical symptoms and all 28 channel video-EEG data by medical experts. Note the 5 missed seizures for patient P93 are all subclinical seizures, whose information does not appear to be reflected by the EEG dynamics
When analyzing EEG for epileptic seizure prediction/detection, it is customary to partition a long EEG signal into short windows of length W points, and calculate the measure of interest for each window. The criterion for choosing W is such that the EEG signal in each window is fairly stationary, is long enough to reliably estimate the measure of interest, and is short enough to accurately resolve localized activities such as seizures. Since seizure activities usually last about 1–2 min, in practice, one often chooses W to be about 10 s. When applying methods from random fractal theory such as the detrended fluctuation analysis (DFA) (Peng et al. 1994), it is most convenient when the length of a sequence is a power of 2. Therefore, we have chosen W = 2,048 when calculating the measures considered here. We have found, however, that the variations of these measures with time are largely independent of the window size W (such as W = 512 or 1,024). The relations among the measures studied here are the same for all the 7 patients’ EEG data. In this paper, for illustration purpose, we illustrate the generic results based on two patients’ data, and summarize the results for seizure detection in Table 1.
Analysis of EEG by a variety of complexity measures
In this section, we analyze EEG signal using LZ complexity, the PE, the LE, the correlation dimension, the correlation entropy, the Hurst parameter, and the SDLE. Our main emphasis will be to identify some curious relations among these complexity measures, and resolve them. We shall also make an effort to shed some new light on the meaning of the four waves of EEG, the β, α, θ and δ waves. Before we go into details of each complexity measure, we note that theoretically, to compute LZ complexity, the PE, the LE, the correlation dimension, and the correlation entropy, the data have to be stationarity. As is well-known, EEG can be highly nonstationary. We hope this problem has been mitigated by working with short EEG segments. On the other hand, the detrending fluctuation analysis, which will be used to estimate the Hurst parameter from EEG, can remove some nonstationarity from EEG, such as linear trends (which could be as a form of baseline drifts). The SDLE is the most powerful in dealing with nonstationarity. This point will be made clearer below.
The LZ complexity
The LZ complexity is closely related to the Kolmogorov complexity and the Shannon entropy. It is the foundation of a commonly used compression scheme, gzip. Being easily implementable and very fast, the LZ complexity and its derivatives have found numerous applications in characterizing the randomness of complex data.
To compute the LZ complexity, the signal has to be transformed into a symbol sequence first. One popular approach is to convert the signal into a 0–1 sequence by comparing the signal with a threshold value Sd (Zhang et al. 2001). That is, whenever the signal is larger than Sd, one maps the signal to 1, otherwise, to 0. To ensure that Sd is well defined, the underlying data have to be stationary.
Under the assumption that data are indeed stationary, a simple and effective choice of Sd is the median of the signal (Nagaragin 2002). Denote the 0–1 sequence obtained by 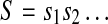 . It is sequentially scanned and rewritten as a concatenation
. It is sequentially scanned and rewritten as a concatenation 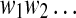 of words wk chosen in such a way that
of words wk chosen in such a way that 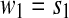 and wk+1 is the shortest word that has not appeared previously. In other words, wk+1 is the extension of some word sj in the list,
and wk+1 is the shortest word that has not appeared previously. In other words, wk+1 is the extension of some word sj in the list, 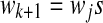 , where
, where 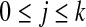 , and s is either 0 or 1. For example, the string
, and s is either 0 or 1. For example, the string 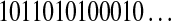 is parsed as
is parsed as 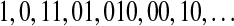 . The 1st and the 2nd words are the extensions of the empty word with the symbol 1 and 0, respectively. Let c(n) denote the number of words in the parsing of the input n—sequence. For each word, we need log2c(n) bits to describe the location of the prefix to the word and 1 bit to describe the last bit. For our example, we can let 000 describe an empty prefix. Then the above sequence can be described as (000, 1)(000, 0)(001, 1)(010, 1)(100, 0)(010, 0)(001, 0). The length L(n) of the encoded sequence is then L(n) = c(n)[log2c(n) + 1]. The LZ complexity can be defined as
. The 1st and the 2nd words are the extensions of the empty word with the symbol 1 and 0, respectively. Let c(n) denote the number of words in the parsing of the input n—sequence. For each word, we need log2c(n) bits to describe the location of the prefix to the word and 1 bit to describe the last bit. For our example, we can let 000 describe an empty prefix. Then the above sequence can be described as (000, 1)(000, 0)(001, 1)(010, 1)(100, 0)(010, 0)(001, 0). The length L(n) of the encoded sequence is then L(n) = c(n)[log2c(n) + 1]. The LZ complexity can be defined as
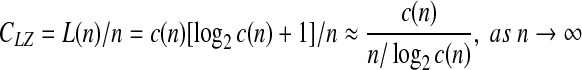 |
1 |
Theoretically, it can be proven (Cover and Thomas 1991) that when 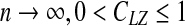 , and CLZ approaches to the Shannon entropy. However, when a sequence is of finite length, CLZ can be significantly larger than 1 for a random sequence, and larger than 0 for constant or periodic sequences without any randomness. In Hu et al. (2006), based on analytic results for constant, periodic, and fully random sequences of finite length, we proposed a simple normalization scheme. That is the basis of our analysis here. For simplicity, we shall denote the normalized LZ score by LZ.
, and CLZ approaches to the Shannon entropy. However, when a sequence is of finite length, CLZ can be significantly larger than 1 for a random sequence, and larger than 0 for constant or periodic sequences without any randomness. In Hu et al. (2006), based on analytic results for constant, periodic, and fully random sequences of finite length, we proposed a simple normalization scheme. That is the basis of our analysis here. For simplicity, we shall denote the normalized LZ score by LZ.
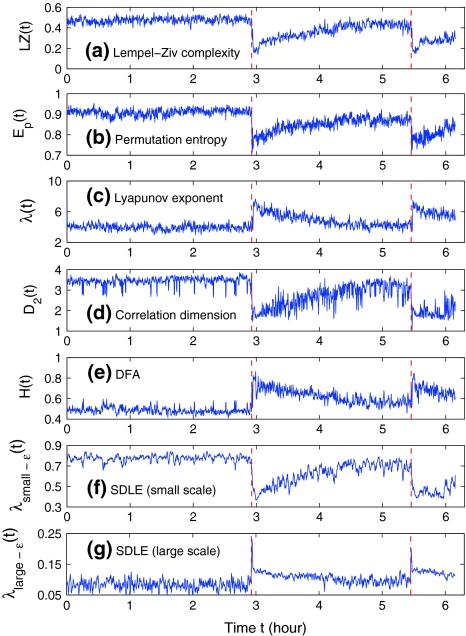
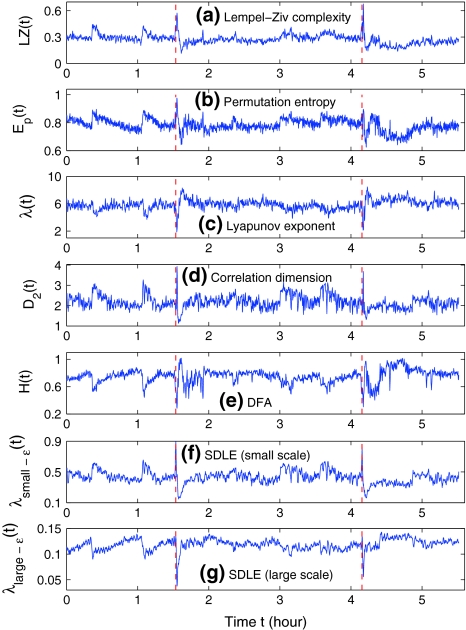
Figures 2a and 3a show the variation of LZ with time for two patients. Let us examine the variation of LZ with time near the seizures as well as away from the seizures. (i) Slightly after the seizure, the LZ has a sharp drop, followed by a gradual increase. This indicates that the dynamics of the brain first becomes more regular right after the seizure, then its irregularity returns as it approaches the normal state. This also suggests that transient EEG signals such as spikes, spike and slow wave complexes or rhythmic slow wave bursts that are associated with seizures are usually less random than normal background EEGs. However, at the onset of seizure, LZ may increase before it decreases, as shown in Fig. 3a. (ii) When away from the seizure, Fig. 2a does not show much variability. However, Fig. 3a has shown some very non-trivial variability. Will these variabilities be also captured by other complexity measures? We shall find this out momentarily.
Fig. 2.
The variation of a the LZ complexity, b the PE, c the LE, d the D2, e the Hurst parameter, f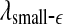 , and g
, and g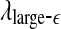 with time for part of the EEG signals of patient #P185. The EEG signal is from the electrode LTD 1. The vertical red dashed lines indicate seizure occurrence time determined by medical experts. On average, a seizure lasts about 1–2 min, which is equivalent to 6–10 sample points in these plots
with time for part of the EEG signals of patient #P185. The EEG signal is from the electrode LTD 1. The vertical red dashed lines indicate seizure occurrence time determined by medical experts. On average, a seizure lasts about 1–2 min, which is equivalent to 6–10 sample points in these plots
Fig. 3.
The variation of a the LZ complexity, b the PE, c the LE, d the D2, e the Hurst parameter, f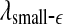 , and g
, and g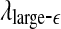 with time for part of the EEG signals of patient #P93. The EEG signal is from the electrode RTD 1. The vertical red dashed lines indicate seizure occurrence time determined by medical experts. On average, a seizure lasts about 1–2 min, which is equivalent to 6–10 sample points in these plots
with time for part of the EEG signals of patient #P93. The EEG signal is from the electrode RTD 1. The vertical red dashed lines indicate seizure occurrence time determined by medical experts. On average, a seizure lasts about 1–2 min, which is equivalent to 6–10 sample points in these plots
EEG analysis by chaos theory
We now examine measures from chaos theory. For illustrative purpose, we shall focus on the PE, the LE, the Kolmogorov entropy, and the correlation dimension D2. Before analysis, we first embed the EEG signal 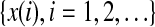 to a phase space (Packard et al. 1980; Takens 1981; Sauer et al. 1991):
to a phase space (Packard et al. 1980; Takens 1981; Sauer et al. 1991):
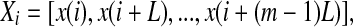 |
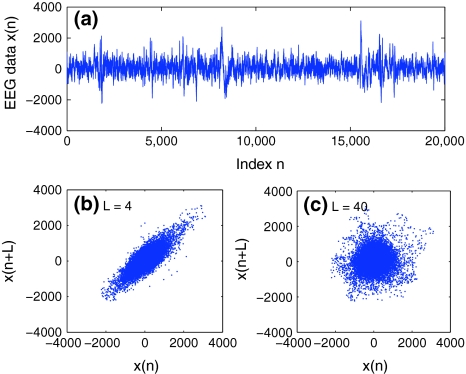
where the embedding dimension m and the delay time L are chosen according to certain optimization criterion (Gao and Zheng 1993, 1994; Gao et al. 2007). For graphical displays, one may choose m to be 2, and plot x(t + L) vs. x(t). This is called 2-D phase diagram. For the EEG signal shown in Fig. 4a, two examples of phase diagrams are shown in Fig. 4b, c, for L = 4 and 40, respectively. Note that when one computes the LE, the Kolmogorov entropy, and the correlation dimension D2 from a dataset, one assumes the existence of an underlying chaotic attractor. Therefore, the dataset has to be stationary. The same assumption has to be made as well when computing the PE, since the PE is based on sorting of the elements of the embedding vector.
Fig. 4.
a An example to show a segment of one EEG data with seizure. The data was sampled with a frequency of 200 Hz. The phase diagrams of the EEG data are shown in (b, c), where the delay time L is chosen as 4 (b) or 40 (c)
We first examine the PE. It is introduced in (Bandt and Pompe 2002; Cao et al. 2004) as a convenient means of analyzing a time series. It works as follows. For a given, but otherwise arbitrary i, the m number of real values of Xi = [x(i), x(i + L), ..., x(i + (m − 1)L)] are sorted in an increasing order: 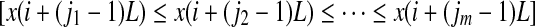 . When an equality occurs, e.g.,
. When an equality occurs, e.g., 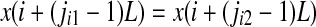 , we order the quantities x according to the values of their corresponding j’s, namely if
, we order the quantities x according to the values of their corresponding j’s, namely if 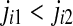 , we write
, we write 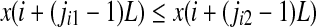 . This way, the vector Xi is mapped onto
. This way, the vector Xi is mapped onto 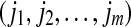 , which is one of the m! permutations of m distinct symbols
, which is one of the m! permutations of m distinct symbols  . When each such permutation is considered as a symbol, then the reconstructed trajectory in the m-dimensional space is represented by a symbol sequence. Let the probability for the
. When each such permutation is considered as a symbol, then the reconstructed trajectory in the m-dimensional space is represented by a symbol sequence. Let the probability for the 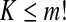 distinct symbols be
distinct symbols be 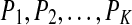 . Then PE, denoted by Ep, for the time series
. Then PE, denoted by Ep, for the time series 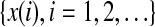 is defined (Bandt and Pompe 2002; Cao et al. 2004) as
is defined (Bandt and Pompe 2002; Cao et al. 2004) as
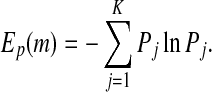 |
2 |
The maximum of EP (m) is 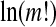 , when Pj = 1/(m!). For convenience, we work with
, when Pj = 1/(m!). For convenience, we work with
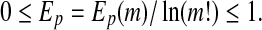 |
3 |
Thus Ep gives a measure of the departure of the time series under study from a complete random one: the smaller the value of Ep, the more regular the time series is. Following Cao et al. (2004), we choose m = 6, L = 3. Figures 2b and 3b have shown the Ep (t) for the 2 patients. We observe that the variation of Ep (t) with t is similar to that of LZ(t) with t: the dynamics of the brain first becomes more regular right after the seizure, then its irregularity returns as it approaches the normal state. This is as expected. Also note that the variabilities of LZ away from seizures shown in Fig. 3a are not only also captured by PE, but also in a similar way and slightly better. In fact, such variabilities will also be captured by other complexity measures, as we shall see.
Next we examine three commonly used measures from chaos theory, the LE, the correlation entropy, and the correlation dimension.
The LE is a dynamic quantity. It characterizes the exponential growth of an infinitesimal line segment,
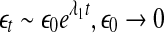 |
4 |
It is often computed by the algorithm of Wolf et al. (1985), which assumes exponential divergence between a reference and a perturbed trajectory. Using the schematic shown in Fig. 5, this amounts to assuming that 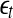 grows exponentially, according to Eq. 4. (In reality, this is often not the case; this is emphasized by the schematic shown in Fig. 5.) For truly chaotic signals, 1/ λ 1 gives the prediction time scale of the dynamics. Also, it is well-known that the sum of all the positive Lyapunov exponents in a chaotic system equals the Kolmogorov-Sinai (KS) entropy. The KS entropy characterizes the rate of creation of information in a system. It is zero, positive, and infinite for regular, chaotic, and random motions, respectively. It is difficult to compute, however. Therefore, one usually computes the correlation entropy K2, which is a tight lower bound of the KS entropy. Similarly, the box-counting dimension, which is a geometrical quantity characterizing the minimal number of variables that are needed to fully describe the dynamics of a motion, is difficult to compute with finite data, and one often calculates the correlation dimension D2 instead. Again, D2 is a tight lower bound of the box-counting dimension. Both K2 and D2 can be readily computed from the correlation integral through the relation (Grassberger and Procaccia 1983a, b),
grows exponentially, according to Eq. 4. (In reality, this is often not the case; this is emphasized by the schematic shown in Fig. 5.) For truly chaotic signals, 1/ λ 1 gives the prediction time scale of the dynamics. Also, it is well-known that the sum of all the positive Lyapunov exponents in a chaotic system equals the Kolmogorov-Sinai (KS) entropy. The KS entropy characterizes the rate of creation of information in a system. It is zero, positive, and infinite for regular, chaotic, and random motions, respectively. It is difficult to compute, however. Therefore, one usually computes the correlation entropy K2, which is a tight lower bound of the KS entropy. Similarly, the box-counting dimension, which is a geometrical quantity characterizing the minimal number of variables that are needed to fully describe the dynamics of a motion, is difficult to compute with finite data, and one often calculates the correlation dimension D2 instead. Again, D2 is a tight lower bound of the box-counting dimension. Both K2 and D2 can be readily computed from the correlation integral through the relation (Grassberger and Procaccia 1983a, b),
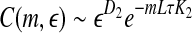 |
5 |
where m and L are the embedding dimension and the delay time, τ is the sampling time, 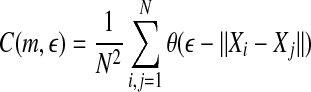 is the correlation integral, θ is the Heaviside step function, Xi and Xj are reconstructed vectors, N is the number of points in the reconstructed phase space, and
is the correlation integral, θ is the Heaviside step function, Xi and Xj are reconstructed vectors, N is the number of points in the reconstructed phase space, and 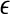 is a prescribed small distance. Equation 5 means that in a plot of
is a prescribed small distance. Equation 5 means that in a plot of 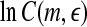 versus
versus 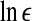 with m as a parameter, for truly low-dimensional chaos, one observes a series of parallel straight lines, with the slope being D2, and the spacing between the lines estimating K2 (where lines for larger m lie below those for smaller m). Note that when K2 is evaluated at a fixed scale
with m as a parameter, for truly low-dimensional chaos, one observes a series of parallel straight lines, with the slope being D2, and the spacing between the lines estimating K2 (where lines for larger m lie below those for smaller m). Note that when K2 is evaluated at a fixed scale 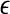 (say, 15% or 20% of the standard deviation of the data), the resulting entropy is called sample entropy (Richman and Moorman 2000). In our calculations, we have used m = 4,5 and L = 1.
(say, 15% or 20% of the standard deviation of the data), the resulting entropy is called sample entropy (Richman and Moorman 2000). In our calculations, we have used m = 4,5 and L = 1.
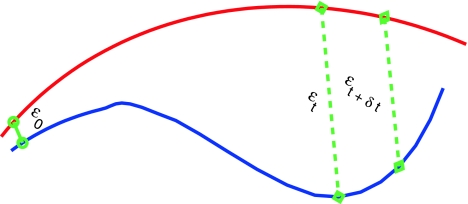
Fig. 5.
A schematic showing 2 arbitrary trajectories in a general high-dimensional space, with the distance between them at time 0, t, and t + δt being 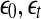 , and
, and 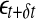 , respectively
, respectively
From the above descriptions, one would expect that λ1 (t) and K2 (t) are similar, while D2 (t) has little to do with either λ1 (t) or K2 (t). We have found that the variation of K2 with t is very similar to that of LZ(t) and Ep(t), as one would expect (and thus not shown here). However, the variation of λ(t) with t is reciprocal to those of entropies, as shown in Figs. 2c and 3c. This is rather puzzling. Equally puzzling is the variation of D2 with t, which is always reciprocal to that of λ with t, or similar to that of entropies, as shown in Figs. 2d and 3d. We shall try to understand these curious relations shortly.
Fractal scaling analysis of EEG
As pointed out earlier, the Hurst parameter H characterizes the long-term correlations in a time series. There are many different ways to estimate H. We choose DFA (Peng et al. 1994), since it can remove certain type of nonstationarity in the data, such as linear trends, which could appear as some kind of baseline drifts in EEG. It is also more reliable (Gao et al. 2006b), and has been used to study EEG (Hwa and Ferree 2002; Robinson 2003).
DFA is an effective method for the analysis of 1/fα noise, a type of temporal or spatial fluctuation characterized by a power-law decaying power spectral density. The prototypical model for 1/fα noise is the fractional Brownian motion (fBm), which is a Gaussian random walk process with mean 0 and stationary increments. Its variance, covariance, and power spectral density (PSD) are given by 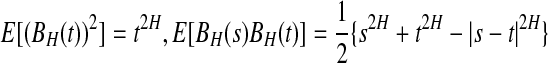 , and E(f) ∼ f−(2H+1), respectively, where 0 < H < 1 is often called the self-similar or Hurst parameter. Depending on whether H is smaller than, equal to, or larger than 1/2, the fBm process is said to have anti-persistent correlation, short-range correlation, and persistent long-range correlation (Gao et al. 2006b, 2007; Mandelbrot 1982). When applying DFA, EEG is treated as a random walk process (Hwa and Ferree 2002; Robinson 2003). Denote the EEG signals under study by
, and E(f) ∼ f−(2H+1), respectively, where 0 < H < 1 is often called the self-similar or Hurst parameter. Depending on whether H is smaller than, equal to, or larger than 1/2, the fBm process is said to have anti-persistent correlation, short-range correlation, and persistent long-range correlation (Gao et al. 2006b, 2007; Mandelbrot 1982). When applying DFA, EEG is treated as a random walk process (Hwa and Ferree 2002; Robinson 2003). Denote the EEG signals under study by 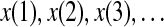 , DFA works as follows: First divide a given time series of length N into ⌊N/l⌋ non-overlapping segments, each containing l points. Then define the local trend in each segment to be the ordinate of a linear least-squares fit of the time series in that segment; this is schematically shown in Fig. 6. Finally compute the “detrended walk”, denoted by xl(n), as the difference between the original “walk” x(n) and the local trend. One then examines the following scaling behavior,
, DFA works as follows: First divide a given time series of length N into ⌊N/l⌋ non-overlapping segments, each containing l points. Then define the local trend in each segment to be the ordinate of a linear least-squares fit of the time series in that segment; this is schematically shown in Fig. 6. Finally compute the “detrended walk”, denoted by xl(n), as the difference between the original “walk” x(n) and the local trend. One then examines the following scaling behavior,
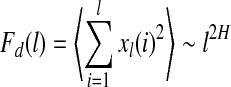 |
6 |
where the angle brackets denote ensemble averages of all the segments. From our EEG data, we have found that the power-law fractal scaling breaks down around l ≈ 26. This is caused by distinct time scales defined by the α rhythm (Hwa and Ferree 2002) or the dendritic time constants (Robinson 2003). Therefore, we used the scale range of l ∼ 22 to 26 to calculate H. Figures 2e and 3e show H(t) for the 2 patients. We notice that the pattern of H(t) is very similar to that of λ (t), but reciprocal to other measures. Such relations cannot be readily understood intuitively, since the foundations for the chaos theory and the random fractal theory are entirely different.
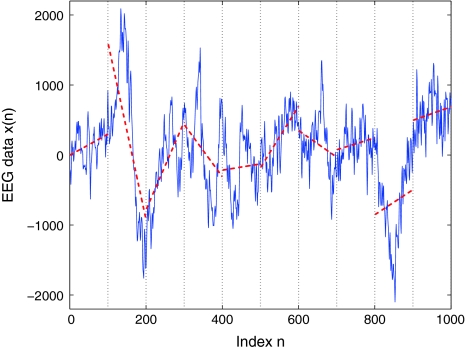
Fig. 6.
A schematic showing local detrending in the DFA method. Shown is a segment of an EEG data. The vertical dotted lines indicate segments of length l = 100, and the dashed straight line represents the local trend estimated in each segment by a linear least-squares fit
Multiscale analysis of EEG by scale-dependent Lyapunov exponent
To understand the relations among the measures considered above, we now carry out a multiscale analysis of EEG by computing the scale-dependent Lyapunov exponent (SDLE) (Gao et al. 2006a, 2007; Hu et al. 2009, 2010).
SDLE as a multiscale analysis measure
SDLE is defined in a phase space through consideration of an ensemble of trajectories (Gao et al. 2006a, 2007; Hu et al. 2009, 2010). When one is only given a scalar time series, one can use the time delay embedding to reconstruct a suitable phase space, as explained before. Now denote the initial distance between two nearby trajectories by 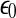 , and their average distances at time t and
, and their average distances at time t and 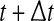 respectively, by
respectively, by 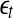 and
and 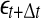 , where
, where 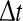 is small. This is schematically shown in Fig. 5. The SDLE
is small. This is schematically shown in Fig. 5. The SDLE 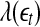 is defined by (Gao et al. 2006a, 2007)
is defined by (Gao et al. 2006a, 2007)
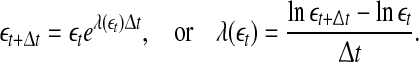 |
7 |
Or equivalently by,
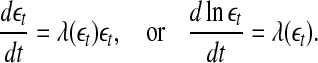 |
8 |
To compute SDLE, we can start from an arbitrary number of shells,
 |
9 |
where 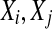 are reconstructed vectors,
are reconstructed vectors, 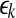 (the radius of the shell) and
(the radius of the shell) and 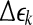 (the width of the shell) are arbitrarily chosen small distances (
(the width of the shell) are arbitrarily chosen small distances (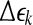 is not necessarily a constant). Then we monitor the evolution of all pairs of points
is not necessarily a constant). Then we monitor the evolution of all pairs of points 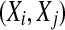 within a shell and take average. Equation 7 can now be written as
within a shell and take average. Equation 7 can now be written as
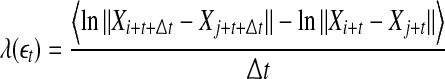 |
10 |
where t and 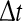 are integers in unit of the sampling time, and the angle brackets denote average within a shell.
are integers in unit of the sampling time, and the angle brackets denote average within a shell.
Note that the initial set of shells serve as initial values of the scales; through evolution of the dynamics, they will automatically converge to the range of inherent scales. This is emphasized by the subscript t in 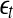 —when the scales become inherent, t can then be dropped. Also note that when analyzing chaotic time series, the condition
—when the scales become inherent, t can then be dropped. Also note that when analyzing chaotic time series, the condition
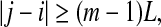 |
11 |
needs to be imposed when finding pairs of vectors within a shell, to eliminate the effects of tangential motions (Gao et al. 2007). To understand this, it is beneficial to take j = i + 1, and image how different Xi+t and Xj+t, where t is an integer denoting a time in future, can be. A moment of thinking would convince one that so far as t is not huge, Xi+t and Xj+t will stay close together, just as a car following another car on a freeway. Note that this condition is also often sufficient for an initial scale to converge to the inherent scales (Gao et al. 2007).
To better understand SDLE, it is instructive to point out a relation between SDLE and the largest positive Lyapunov exponent λ1. It is given by (Gao et al. 2007)
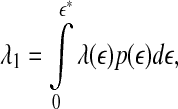 |
12 |
where 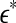 is a scale parameter (for example, used for re-normalization when using Wolf et al.’s algorithm (Wolf et al. 1985)),
is a scale parameter (for example, used for re-normalization when using Wolf et al.’s algorithm (Wolf et al. 1985)), 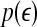 is the probability density function for the scale
is the probability density function for the scale 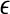 given by
given by
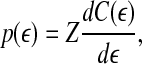 |
13 |
where Z is a normalization constant satisfying 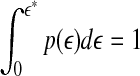 , and
, and 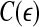 is the well-known Grassberger-Procaccia’s correlation integral (Grassberger and Procaccia 1983b).
is the well-known Grassberger-Procaccia’s correlation integral (Grassberger and Procaccia 1983b).
SDLE has distinctive scaling laws for different types of time series. Those most relevant to EEG analysis are listed here.
- For clean chaos on small scales, and noisy chaos with weak noise on intermediate scales,
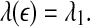
14 - For white noise, when the evolution time
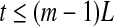 , where (m − 1)L is the embedding window length, we have a scaling described by Eq. 15 (Gao et al. 2006a, 2007; Gaspard and Wang 1993); when t > (m − 1)L,
, where (m − 1)L is the embedding window length, we have a scaling described by Eq. 15 (Gao et al. 2006a, 2007; Gaspard and Wang 1993); when t > (m − 1)L,
Note that noisy chaos usually has the scaling of Eq. 15 on a much longer time scale range, and therefore, noisy chaos is quite different from white noise. Also note that Eq. 12 gives a positive largest Lyapunov exponent for white noise, when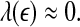
16 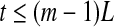 , since
, since 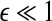 . This is the case when using Wolf et al.’s algorithm (Wolf et al. 1985; Gao et al. 1999a).
. This is the case when using Wolf et al.’s algorithm (Wolf et al. 1985; Gao et al. 1999a). - For random 1/f2H+1 processes, where 0 < H < 1 is called the Hurst parameter which characterizes the correlation structure of the process: depending on whether H is smaller than, equal to, or larger than 1/2, the process is said to have anti-persistent, short-range, or persistent long-range correlations (Gao et al. 2006b, 2007),
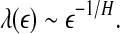
17
To appreciate the above properties, it is helpful to examine the following model with chaotic behavior on small scales and diffusive fractal behavior on large scales (Gao et al. 2006a, 2007):
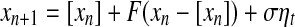 |
18 |
where [xn] denotes the integer part of 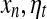 is a noise uniformly distributed in the interval [−1, 1], σ is a parameter quantifying the strength of noise, and F(y) is given by
is a noise uniformly distributed in the interval [−1, 1], σ is a parameter quantifying the strength of noise, and F(y) is given by
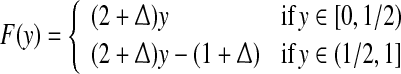 |
19 |
The map F(y) gives a chaotic dynamics with a positive Lyapunov exponent 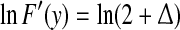 . On the other hand, the term [xn] introduces a random walk on integer grids. This system is very easy to analyze. When
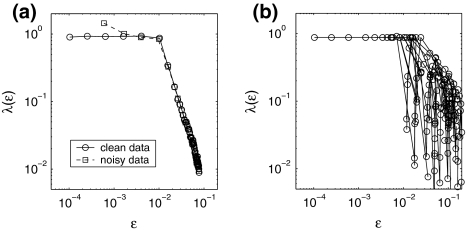
. On the other hand, the term [xn] introduces a random walk on integer grids. This system is very easy to analyze. When 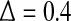 , with only 5,000 points and m = 2, L = 1, all the interesting behaviors of the system are resolved, as is evident in Fig. 7a: (1) for the clean system, there is a chaotic behavior described by Eq. 14 on small scales and diffusive behavior (Eq. 17 and H = 1/2) on large scales; (2) for the noisy system, there is scaling of Eq. 15 on small scales, scaling of Eq. 14 on intermediate scales, and finally diffusive scaling on large scales. In fact, the clean chaotic behavior can be readily resolved using only a few hundred points, as shown in Fig. 7b.
, with only 5,000 points and m = 2, L = 1, all the interesting behaviors of the system are resolved, as is evident in Fig. 7a: (1) for the clean system, there is a chaotic behavior described by Eq. 14 on small scales and diffusive behavior (Eq. 17 and H = 1/2) on large scales; (2) for the noisy system, there is scaling of Eq. 15 on small scales, scaling of Eq. 14 on intermediate scales, and finally diffusive scaling on large scales. In fact, the clean chaotic behavior can be readily resolved using only a few hundred points, as shown in Fig. 7b.
Fig. 7.
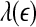 for the model described by Eq. 18. a 5,000 points were used; for the noisy case, σ = 0.001. b 500 points were used
for the model described by Eq. 18. a 5,000 points were used; for the noisy case, σ = 0.001. b 500 points were used
To facilitate EEG analysis, we now make a comment. For an irregular time series, if the dataset is large enough, in principle, one can calculate the distances between all the pairs of points and estimate the probability distribution for these distances. In particular, one can calculate the mean, 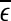 , of these distances.
, of these distances. 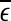 defines a characteristic scale that is closely related to the total variations. For example, for a chaotic system,
defines a characteristic scale that is closely related to the total variations. For example, for a chaotic system, 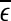 defines the size of the chaotic attractor. If one starts from
defines the size of the chaotic attractor. If one starts from 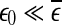 , then, regardless of whether the data is deterministically chaotic or simply random,
, then, regardless of whether the data is deterministically chaotic or simply random, 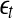 will initially increase with time and gradually settle down around
will initially increase with time and gradually settle down around 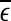 . Consequentially,
. Consequentially, 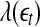 will be positive before
will be positive before 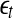 reaches
reaches 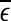 . On the other hand, if one starts from
. On the other hand, if one starts from 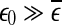 , then
, then 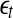 will simply decrease, again regardless of whether the data is chaotic or random. When
will simply decrease, again regardless of whether the data is chaotic or random. When 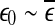 , then
, then 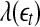 will stay around 0.
will stay around 0.
The notion of the characteristic scale can help one readily understand the ability of SDLE in coping with an important type of nonstationarity of bio-signals—fractal/chaotic components coexist with periodic components. The periodic components only affect the behavior of SDLE near the characteristic scale, but not the fractal/chaotic scalings (Gao et al. 2007; Hu et al. 2009). At this point, we also like to note that when nonstationarity reveals itself as amplitude variations in the signal, then all the scaling laws expressed by Eqs. 14, 15, 16 and 17 are still valid, except they are shifted a little bit on the axis for the scale 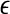 . This is because amplitude variations amount to a change in
. This is because amplitude variations amount to a change in 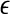 (Hu et al. 2010).
(Hu et al. 2010).
Analysis of EEG by SDLE
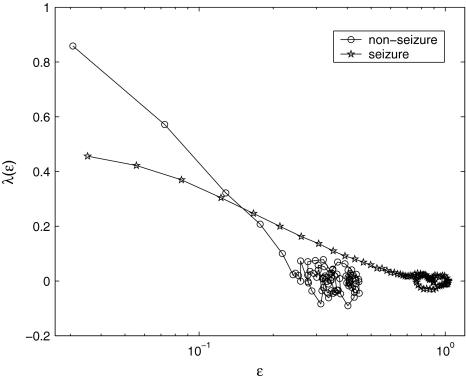
To compute SDLE from EEG, we have used m = 4, L = 1, and a shell of size 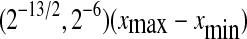 , where xmax and xmin denote the maximal and minimal value of the entire time series. We have examined the variation of λ with
, where xmax and xmin denote the maximal and minimal value of the entire time series. We have examined the variation of λ with 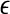 for each segment of the EEG data. Two representative examples for seizure and non-seizure segment are shown in Fig. 8. We observe that on a specific scale
for each segment of the EEG data. Two representative examples for seizure and non-seizure segment are shown in Fig. 8. We observe that on a specific scale 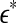 , the two curves cross. Loosely, we may term any
, the two curves cross. Loosely, we may term any 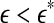 as small scale, while any
as small scale, while any 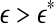 as large scale. Therefore, on small scales,
as large scale. Therefore, on small scales, 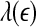 is smaller for seizure than for non-seizure EEG, while on large scales, the opposite is true. The variations of
is smaller for seizure than for non-seizure EEG, while on large scales, the opposite is true. The variations of 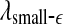 and
and 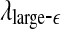 with time for the 2 patients’ EEG data, where
with time for the 2 patients’ EEG data, where 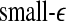 and
and 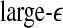 stand for (more or less arbitrarily) chosen fixed small and large scales, are shown in Figs. 2f, g and 3f, g, respectively. It is observed that the pattern of variation of
stand for (more or less arbitrarily) chosen fixed small and large scales, are shown in Figs. 2f, g and 3f, g, respectively. It is observed that the pattern of variation of 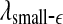 with t is similar to those of LZ, EP and D2, while the pattern of variation of
with t is similar to those of LZ, EP and D2, while the pattern of variation of 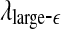 is similar to the LE and the Hurst parameter.
is similar to the LE and the Hurst parameter.
Fig. 8.
Representative 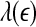 vs.
vs. 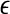 for a seizure and non-seizure EEG segment
for a seizure and non-seizure EEG segment
We are now ready to understand the curious relations among all the complexity measures examined here. (i) Generally, entropy measures the randomness of a dataset. This pertains to small scale. Therefore, the variation of entropy with time should be similar to 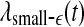 . This is indeed the case. (ii) To understand why the variation of the LE by the Wolf et al’s algorithm (Wolf et al. 1985) corresponds to
. This is indeed the case. (ii) To understand why the variation of the LE by the Wolf et al’s algorithm (Wolf et al. 1985) corresponds to 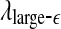 , we note that the Wolf et al’s algorithm (Wolf et al. 1985) involves a scale parameter that whenever the divergence between a reference and a perturbed trajectory exceeds this chosen scale, a renormalization procedure is performed. When the Wolf et al’s algorithm (Wolf et al. 1985) is applied to a time series of only a few thousand points, in order to obtain well-defined LE, the chosen scale parameter has to be fairly large. This is the reason that the LE and
, we note that the Wolf et al’s algorithm (Wolf et al. 1985) involves a scale parameter that whenever the divergence between a reference and a perturbed trajectory exceeds this chosen scale, a renormalization procedure is performed. When the Wolf et al’s algorithm (Wolf et al. 1985) is applied to a time series of only a few thousand points, in order to obtain well-defined LE, the chosen scale parameter has to be fairly large. This is the reason that the LE and 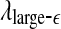 is similar. (iii) It is easy to see that if one fits the
is similar. (iii) It is easy to see that if one fits the 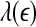 curves shown in Fig. 8 by a straight line, then the variation of the slope with time should be similar to
curves shown in Fig. 8 by a straight line, then the variation of the slope with time should be similar to 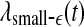 but reciprocal to
but reciprocal to 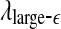 . Such a pattern will be preserved even if one takes logarithm of
. Such a pattern will be preserved even if one takes logarithm of 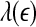 first and then does the fitting. Such a discussion makes it clear that even if EEG is not ideally of 1/f2H+1 type, qualitatively, the relation
first and then does the fitting. Such a discussion makes it clear that even if EEG is not ideally of 1/f2H+1 type, qualitatively, the relation 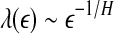 holds. This in turn implies D2∼1/H. With these simple arguments, it is clear that the seemingly puzzling relations among the measures considered here can be readily understood by the
holds. This in turn implies D2∼1/H. With these simple arguments, it is clear that the seemingly puzzling relations among the measures considered here can be readily understood by the 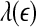 curves.
curves.
Accuracy of seizure detection
We have systematically evaluated the accuracy of seizure detection using the complexity measures considered here. Specifically, we have computed positive detection (or equivalently, sensitivity) and false alarm per hour for all these measures, where positive detection is defined as the ratio between the number of seizures correctly detected and the total number of seizures, while the false alarm per hour is simply the number of falsely detected seizures divided by the total time period. It turns out the accuracy for different measures is very similar, and does not appear to depend on the electrodes much. Therefore, we illustrate the main results using the LE-based method. Table 1 summarizes the results. We observe that accuracy varies considerably among different patients. This may be due to the different noise levels (such as motion artifacts).
Further comparison with frequency domain analysis
To make our discussions complete, in this subsection, we try to understand if the four waves of EEG—β, α, θ and δ, are related to the complexity measures considered here.
The β wave is associated with the brain’s being aroused and actively engaged in mental activities. The α wave represents the nonarousal state of the brain. The θ wave is associated with drowsiness/idling, and the δ wave is associated with sleep/dreaming. They are not characterized by sharp spectral peaks in the frequency domain, but instead are defined by frequency bands. While the exact frequency ranges for the four waves may vary among researchers, they are fairly close. For example, the four waves may correspond to frequency ranges 14–40, 7.5–13, 3.5–7.5, and <3 Hz (i.e., cycles per second), respectively. Or, they could correspond to the frequency ranges 15–40, 9–14, 5–8, and 1.5–4 Hz. The results shown below are largely independent of the exact choice of the frequency bands.
Since the four waves of EEG are not defined by sharp spectral peaks, it would make more sense to find the total energy of each type of wave. Denote them by 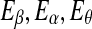 , and Eδ, respectively. They can be obtained by integrating the power-spectral density over their defining frequency bands. Furthermore, we normalize them by the total energy in the frequency band (0, 40) Hz. Denote the normalized energy, or fraction of energy, by
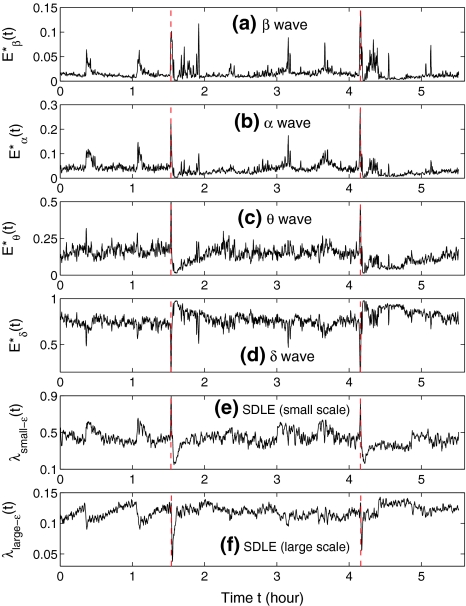
, and Eδ, respectively. They can be obtained by integrating the power-spectral density over their defining frequency bands. Furthermore, we normalize them by the total energy in the frequency band (0, 40) Hz. Denote the normalized energy, or fraction of energy, by 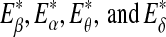 . Note that normalization does not change the functional form for temporal variations of the energy of each type of wave. The variations of these normalized energies with time for the EEG data analyzed in Fig. 3 are shown in Fig. 9a–d, where for convenience of comparison, the curves for SDLE shown in Fig. 3f, g are re-plotted in Fig. 9e, f. We observe that, overall, the variations of
. Note that normalization does not change the functional form for temporal variations of the energy of each type of wave. The variations of these normalized energies with time for the EEG data analyzed in Fig. 3 are shown in Fig. 9a–d, where for convenience of comparison, the curves for SDLE shown in Fig. 3f, g are re-plotted in Fig. 9e, f. We observe that, overall, the variations of 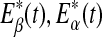 , and E*θ(t) are similar to that of
, and E*θ(t) are similar to that of 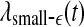 , while the variation of E*δ (t) is similar to that of
, while the variation of E*δ (t) is similar to that of 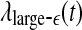 . This suggests that
. This suggests that 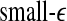 corresponds to high frequency, or small temporal scales, while
corresponds to high frequency, or small temporal scales, while 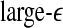 is related to low frequency, or large temporal scales. It should be emphasized, however, that the features uncovered by spectral analysis are not as good as those uncovered by the complexity measures discussed here. Furthermore, when the high-frequency bands, such as the β wave band, are used for seizure detection, the variation of the corresponding energy with time shows activities that are not related to seizures but are related to noise such as motion artifacts. Therefore, for the purpose of epileptic seizure detection/prediction, spectral analysis (or other methods, such as wavelet-based methods, for extracting equivalent features) may not be as effective as the complexity measures discussed here, especially the SDLE.
is related to low frequency, or large temporal scales. It should be emphasized, however, that the features uncovered by spectral analysis are not as good as those uncovered by the complexity measures discussed here. Furthermore, when the high-frequency bands, such as the β wave band, are used for seizure detection, the variation of the corresponding energy with time shows activities that are not related to seizures but are related to noise such as motion artifacts. Therefore, for the purpose of epileptic seizure detection/prediction, spectral analysis (or other methods, such as wavelet-based methods, for extracting equivalent features) may not be as effective as the complexity measures discussed here, especially the SDLE.
Fig. 9.
The variation of the normalized energies of four waves and the SDLE with time for part of the EEG signals of patient #P93
Let us now quantitatively understand the relation between 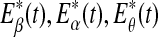 , and
, and 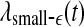 . Assuming that EEG signals may be approximated as a type of 1/f2H+1 process. Integrating 1/f2H+1 over a frequency band of
. Assuming that EEG signals may be approximated as a type of 1/f2H+1 process. Integrating 1/f2H+1 over a frequency band of 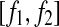 , we obtain the energy
, we obtain the energy
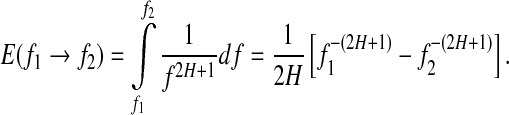 |
This suggests that the variation of 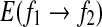 is similar to 1/H(t). Since the variation of H with t is reciprocal to that of
is similar to 1/H(t). Since the variation of H with t is reciprocal to that of 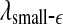 , as can be seen in Fig. 3e, f (or Fig. 9a), we thus see that β, α, and θ waves can indeed be approximated by 1/f2H+1-type processes. The δ wave, however, is not of the 1/f2H+1 type.
, as can be seen in Fig. 3e, f (or Fig. 9a), we thus see that β, α, and θ waves can indeed be approximated by 1/f2H+1-type processes. The δ wave, however, is not of the 1/f2H+1 type.
The above observation is consistent with our earlier discussion that fractal scaling is only valid up to 26 sample points—with a sampling frequency of 200 Hz, this translates to a fractal scaling above about 3 Hz. In other words, β, α, and θ waves together constitute the 1/f process, but the δ wave is a different process.
Concluding remarks
In this work, aimed at understanding the relations among different complexity measures for EEG, we have examined a number of complexity measures from information theory, chaos theory, and random fractal theory for characterizing EEG. We have found that the variations of these complexity measures with time are either similar or reciprocal. While some of these findings are expected, many are counter-intuitive and puzzling, since the foundations of information theory, chaos theory, and random fractal theory are fundamentally different. Fortunately, We are able to understand all these relations through a new multiscale complexity measure, the SDLE. We are also able to shed some new light on the meaning of the four waves of EEG, the α, γ, β, and δ waves of EEG.
Our analysis has important implications to the understanding of EEG dynamics in general and prediction/detection of epileptic seizures from EEG in particular. (i) For truly low-dimensional chaos, 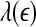 is constant over a wide range of scales. Since
is constant over a wide range of scales. Since 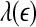 for seizure is flatter than that for non-seizure EEG, therefore, seizure EEG is closer to chaos. However, seizure EEG is not truly chaotic, since
for seizure is flatter than that for non-seizure EEG, therefore, seizure EEG is closer to chaos. However, seizure EEG is not truly chaotic, since 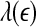 is not constant over any scale. This is evident from Fig. 8. (ii) To comprehensively characterize the complexity of EEG, a wide range of scale has to be considered, since the complexity is different on different scales. For this purpose, the entire
is not constant over any scale. This is evident from Fig. 8. (ii) To comprehensively characterize the complexity of EEG, a wide range of scale has to be considered, since the complexity is different on different scales. For this purpose, the entire 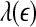 curve, where
curve, where 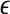 is such that
is such that 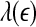 is positive, provides a good solution. This point is particularly important when one wishes to compare the complexity between two signals—the complexity for one signal may be higher on some scales, but lower on other scales. The situation shown in Fig. 8 may be considered one of the simplest possible. (iii) Observing Figs. 2 and 3, we notice that for the purpose of detecting seizures,
is positive, provides a good solution. This point is particularly important when one wishes to compare the complexity between two signals—the complexity for one signal may be higher on some scales, but lower on other scales. The situation shown in Fig. 8 may be considered one of the simplest possible. (iii) Observing Figs. 2 and 3, we notice that for the purpose of detecting seizures, 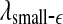 and
and 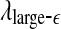 appear to provide better defined features. This may be due to the fact that
appear to provide better defined features. This may be due to the fact that 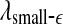 and
and 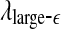 are evaluated at fixed scales, while the LZ, the PE, the LE, and D2, and the Hurst parameter are not. In other words, scale mixing blurs the features for seizure. Also note that in certain situations, seizure-related features from SDLE are 5–15 s earlier than from other measures. (iv) As we have pointed out, around the characteristic scale
are evaluated at fixed scales, while the LZ, the PE, the LE, and D2, and the Hurst parameter are not. In other words, scale mixing blurs the features for seizure. Also note that in certain situations, seizure-related features from SDLE are 5–15 s earlier than from other measures. (iv) As we have pointed out, around the characteristic scale 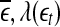 is always close to 0. The behavior of the EEG around
is always close to 0. The behavior of the EEG around 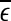 may carry important information about the structured components of the data, such as oscillatory components. Such structured components may be helpful for seizure prediction/detection. Indeed, by observing Fig. 8, we notice that the patterns of
may carry important information about the structured components of the data, such as oscillatory components. Such structured components may be helpful for seizure prediction/detection. Indeed, by observing Fig. 8, we notice that the patterns of 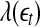 around
around 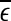 for seizure and non-seizure EEG segments are very different—in fact, they are typical. Better seizure prediction/detection algorithms may be obtained by simultaneously characterizing both the complexity as well as the structured components of the data.
for seizure and non-seizure EEG segments are very different—in fact, they are typical. Better seizure prediction/detection algorithms may be obtained by simultaneously characterizing both the complexity as well as the structured components of the data.
We have emphasized that signal analysis modeling and physiology-based dynamical modeling are different (Deco et al. 2008). Being based on real data, signal analysis may provide powerful constraints on dynamical modeling, when analysis is done in a mathematically rigorous and systematic manner.
Finally, we would like to note that it would be interesting to extend our analysis to EEG data collected in animal models to check if the relations among different complexity measures can still be observed.
Acknowledgments
This work is partially supported by US NSF grants CMMI-1031958 and 0826119.
Contributor Information
Jianbo Gao, Phone: +1-765-418-8025, FAX: +1-765-463-2189, Email: jbgao@pmbintelligence.com.
Jing Hu, Email: jing.hu@gmail.com.
Wen-wen Tung, Email: wwtung@purdue.edu.
References
- Andrzejak R, Lehnertz K, Mormann F, Rieke C, David P, Elger C. Indications of nonlinear deterministic and finite dimensional structures in time series of brain electrical activity: dependence on recording region and brain state. Phys Rev E. 2001;64:061,907. doi: 10.1103/PhysRevE.64.061907. [DOI] [PubMed] [Google Scholar]
- Aschenbrenner-Scheibe R, Maiwald T, Winterhalder M, Voss H, Timmer J, Schulze-Bonhage A. How well can epileptic seizures be predicted? An evaluation of a nonlinear method. Brain Behav Evol. 2003;126:2616. doi: 10.1093/brain/awg265. [DOI] [PubMed] [Google Scholar]
- Atmanspacher H, Rotter S. Interpreting neurodynamics: concepts and facts. Cogn Neurodyn. 2008;2:297–318. doi: 10.1007/s11571-008-9067-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babloyantz A, Destexhe A. Low-dimension chaos in an instance of epilepsy. Proc Natl Acad Sci. 1986;83:3513–3517. doi: 10.1073/pnas.83.10.3513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandt C, Pompe B. Permutation entropy: a natural complexity measure for time series. Phys Rev Lett. 2002;88:174,102. doi: 10.1103/PhysRevLett.88.174102. [DOI] [PubMed] [Google Scholar]
- Cao Y, Tung W, Gao J, Protopopescu V, Hively L. Detecting dynamical changes in time series using the permutation entropy. Phys Rev E. 2004;70:046,217. doi: 10.1103/PhysRevE.70.046217. [DOI] [PubMed] [Google Scholar]
- Cover T, Thomas J. Elements of information theory. New York: Wiley; 1991. [Google Scholar]
- Deco G, Jirsa V, Robinson P, Breakspear M, Friston K. The dynamic brain: from spiking neurons to neural masses and cortical fields. PLoS Comput Biol. 2008;4:e1000,092. doi: 10.1371/journal.pcbi.1000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fell J, Roschke J, Schaffner C. Surrogate data analysis of sleep electroencephalograms reveals evidence for nonlinearity. Biol Cybern. 1996;75:85–92. doi: 10.1007/BF00238742. [DOI] [PubMed] [Google Scholar]
- Freeman W. Deep analysis of perception through dynamic structures that emerge in cortical activity from self-regulated noise. Cogn Neurodyn. 2009;3:105–116. doi: 10.1007/s11571-009-9075-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J, Zheng Z. Local exponential divergence plot and optimal embedding of a chaotic time series. Phys Lett A. 1993;181:153–158. doi: 10.1016/0375-9601(93)90913-K. [DOI] [Google Scholar]
- Gao J, Zheng Z. Direct dynamical test for deterministic chaos and optimal embedding of a chaotic time series. Phys Rev E. 1994;49:3807–3814. doi: 10.1103/PhysRevE.49.3807. [DOI] [PubMed] [Google Scholar]
- Gao J, Chen C, Hwang S, Liu J. Noise-induced chaos. Int J Mod Phys B. 1999;13:3283–3305. doi: 10.1142/S0217979299003027. [DOI] [Google Scholar]
- Gao J, Hwang S, Liu J. When can noise induce chaos. Phys Rev Lett. 1999;82:1132–1135. doi: 10.1103/PhysRevLett.82.1132. [DOI] [Google Scholar]
- Gao J, Hu J, Tung W, Cao Y. Distinguishing chaos from noise by scaledependent lyapunov exponent. Phys Rev E. 2006;74:066,204. doi: 10.1103/PhysRevE.74.066204. [DOI] [PubMed] [Google Scholar]
- Gao J, Hu J, Tung W, Cao Y, Sarshar N, Roychowdhury V. Assessment of long range correlation in time series: how to avoid pitfalls. Phys Rev E. 2006;73:016,117. doi: 10.1103/PhysRevE.73.016117. [DOI] [PubMed] [Google Scholar]
- Gao J, Cao Y, Tung W, Hu J. Multiscale analysis of complex time series-integration of chaos and random fractal theory, and beyond. New York: Wiley; 2007. [Google Scholar]
-
Gaspard P, Wang X. Noise, chaos, and (
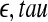 )-entropy per unit time. Phys Rep. 1993;235:291–343. doi: 10.1016/0370-1573(93)90012-3. [DOI] [Google Scholar]
)-entropy per unit time. Phys Rep. 1993;235:291–343. doi: 10.1016/0370-1573(93)90012-3. [DOI] [Google Scholar] - Grassberger P, Procaccia I. Characterization of strange attractors. Phys Rev Lett. 1983;50:346–349. doi: 10.1103/PhysRevLett.50.346. [DOI] [Google Scholar]
- Grassberger P, Procaccia I. Estimation of the kolmogorov entropy from a chaotic signal. Phys Rev A. 1983;28:2591–2593. doi: 10.1103/PhysRevA.28.2591. [DOI] [Google Scholar]
- Holmes M. Dense array eeg: methodology and new hypothesis on epilepsy syndromes. Epilepsia. 2008;49(Suppl.3):3–14. doi: 10.1111/j.1528-1167.2008.01505.x. [DOI] [PubMed] [Google Scholar]
- Hu J, Gao J, Principe J. Analysis of biomedical signals by the lempel-ziv complexity: the effect of finite data size. IEEE Trans Biomed Eng. 2006;53:2606–2609. doi: 10.1109/TBME.2006.883825. [DOI] [PubMed] [Google Scholar]
- Hu J, Gao J, Tung W. Characterizing heart rate variability by scale-dependent lyapunov exponent. Chaos. 2009;19:028506. doi: 10.1063/1.3152007. [DOI] [PubMed] [Google Scholar]
- Hu J, Gao J, Tung W, Cao Y. Multiscale analysis of heart rate variability: a comparison of different complexity measures. Ann Biomed Eng. 2010;38:854–864. doi: 10.1007/s10439-009-9863-2. [DOI] [PubMed] [Google Scholar]
- Hwa R, Ferree T. Scaling properties of fluctuations in the human electroencephalogram. Phys Rev E. 2002;66:021901. doi: 10.1103/PhysRevE.66.021901. [DOI] [PubMed] [Google Scholar]
- Hwang K, Gao J, Liu J. Noise-induced chaos in an optically injected semiconductor laser. Phys Rev E. 2000;61:5162–5170. doi: 10.1103/PhysRevE.61.5162. [DOI] [PubMed] [Google Scholar]
- Iasemidis L, Principe J, Sackellares J (1999) Measurement and quantification of spatiotemporal dynamics of human epileptic seizures. In: In nonlinear signal processing in, Press
- Lai Y, Harrison M, Frei M, Osorio I. Inability of lyapunov exponents to predict epileptic seizures. Phys Rev Lett. 2003;91:068102. doi: 10.1103/PhysRevLett.91.068102. [DOI] [PubMed] [Google Scholar]
- Lempel A, Ziv J. On the complexity of finite sequences. IEEE Trans Inf Theory. 1976;22:75–81. doi: 10.1109/TIT.1976.1055501. [DOI] [Google Scholar]
- Mandelbrot B. The fractal geometry of nature. San Francisco: Freeman; 1982. [Google Scholar]
- Martinerie J, Adam C, Quyen MLV, Baulac M, Clemenceau S, Renault B, Varela F. Epileptic seizures can be anticipated by non-linear analysis. Nat Med. 1998;4:1173–1176. doi: 10.1038/2667. [DOI] [PubMed] [Google Scholar]
- Nagaragin R. Quantifying physiological data with lempel-ziv complexity—certain issues. IEEE Trans Biomed Eng. 2002;49:1371–1373. doi: 10.1109/TBME.2002.804582. [DOI] [PubMed] [Google Scholar]
- Napolitano C, Orriols M. Two types of remote propagation in mesial temporal epilepsy: analysis with scalp ictal eeg. J Clin Neurophysiol. 2008;25:69–76. doi: 10.1097/WNP.0b013e31816a8f09. [DOI] [PubMed] [Google Scholar]
- Packard N, Crutchfield J, Farmer J, Shaw R. Gemomtry from time-series. Phys Rev Lett. 1980;45:712–716. doi: 10.1103/PhysRevLett.45.712. [DOI] [Google Scholar]
- Peng C, Buldyrev S, Havlin S, Simons M, Stanley H, Goldberger A. On the mosaic organization of dna sequences. Phys Rev E. 1994;49:1685–1689. doi: 10.1103/PhysRevE.49.1685. [DOI] [PubMed] [Google Scholar]
- Pijn J, Vanneerven J, Noest A, LopesDaSilva F. Chaos or noise in eeg signals—dependence on state and brain site. Electroencephalogr Clin Neurophys. 1991;79:371–381. doi: 10.1016/0013-4694(91)90202-F. [DOI] [PubMed] [Google Scholar]
- Plummer C, Harvey S, Cook M. Eeg source localization in focal epilepsy: where are we now. Epilepsia. 2008;49:201–218. doi: 10.1111/j.1528-1167.2007.01381.x. [DOI] [PubMed] [Google Scholar]
- Pritchard W, Duke D, Krieble K. Dimensional analysis of resting human eeg ii: surrogate data testing indicates nonlinearity but not low-dimensional chaos. Psychophysiology. 1995;32:486–491. doi: 10.1111/j.1469-8986.1995.tb02100.x. [DOI] [PubMed] [Google Scholar]
- Richman J, Moorman J. Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circ Physiol. 2000;278:H2039–H2049. doi: 10.1152/ajpheart.2000.278.6.H2039. [DOI] [PubMed] [Google Scholar]
- Robinson P. Interpretation of scaling properties of electroencephalographic fluctuations via spectral analysis and underlying physiology. Phys Rev E. 2003;67:032,902. doi: 10.1103/PhysRevE.67.032902. [DOI] [PubMed] [Google Scholar]
- Rombouts S, Keunen R, Stam C. Investigation of nonlinear structure in multichannel eeg. Phys Lett A. 1995;202:352–358. doi: 10.1016/0375-9601(95)00335-Z. [DOI] [Google Scholar]
- Sauer T, Yorke J, Casdagli M. Embedology. J Stat Phys. 1991;65:579–616. doi: 10.1007/BF01053745. [DOI] [Google Scholar]
- Takens F (1981) Detecting strange attractors in turbulence. In: Rand DA, Young LS (eds) Dynamical systems and turbulence, lecture notes in mathematics, vol 898. Springer, p 366
- Theiler J, Rapp P (1996) Re-examination of the evidence for low-dimensional, nonlinear structure in the human electroencephalogram. Electroencephalogr Clin Neurophysiol 98:213–222 16 [DOI] [PubMed]
- Wolf A, Swift J, Swinney H, Vastano J. Determining lyapunov exponents from a time series. Physica D. 1985;16:285. doi: 10.1016/0167-2789(85)90011-9. [DOI] [Google Scholar]
- Zhang X, Roy R, Jensen E. Eeg complexity as a measure of depth of anesthesia for patients. IEEE Trans Biomed Eng. 2001;48:1424–1433. doi: 10.1109/10.966601. [DOI] [PubMed] [Google Scholar]