Skip to main content
PMC home page
Cognitive Neurodynamics logoLink to Cognitive Neurodynamics
. 2011 Mar 1;5(2):209–220. doi: 10.1007/s11571-011-9152-2

Fast and robust image segmentation by small-world neural oscillator networks

Chunguang Li 1,✉, Yuke Li 1
PMCID: PMC3100468  PMID: 22654991

Abstract

Inspired by the temporal correlation theory of brain functions, researchers have presented a number of neural oscillator networks to implement visual scene segmentation problems. Recently, it is shown that many biological neural networks are typical small-world networks. In this paper, we propose and investigate two small-world models derived from the well-known LEGION (locally excitatory and globally inhibitory oscillator network) model. To form a small-world network, we add a proper proportion of unidirectional shortcuts (random long-range connections) to the original LEGION model. With local connections and shortcuts, the neural oscillators can not only communicate with neighbors but also exchange phase information with remote partners. Model 1 introduces excitatory shortcuts to enhance the synchronization within an oscillator group representing the same object. Model 2 goes further to replace the global inhibitor with a sparse set of inhibitory shortcuts. Simulation results indicate that the proposed small-world models could achieve synchronization faster than the original LEGION model and are more likely to bind disconnected image regions belonging together. In addition, we argue that these two models are more biologically plausible.

Keywords: Image segmentation, Small-world network, Neural oscillator, Synchronization

Introduction

Human beings have the ability to effortlessly identify objects (patterns) in a visual scene. In fact, our visual system is the most important sensory system for information gathering and visual perception significantly helps us to understand the world. However, a robot can not easily know what is in sight. It is an old issue that how computers or intelligent machines could share the ability of mankind to perceive distinct objects.

Image segmentation is a fundamental step in computer vision. By partitioning an image into multiple segments, tasks such as automatic target recognition can be much easier to perform. Psychological studies on perceptual organization in vision point to several sensory cues that determine grouping and segregation. In particular, Gestalt psychology has listed a number of key principles for perceptual organization, such as similarity, proximity, and constancy (Wertheimer 1938). Many researchers regard these Gestalt principles as sensory cues when they approach the problem of visual scene segmentation.

In pattern analysis, image segmentation has been extensively studied and various methods have been proposed over the years (Pal and Pal 1993; Zhu et al. 1995; Dal Maso et al. 1992; Vese and Chan 2004; Shi and Malik 2000). Though some partially parallel methods have been developed, most of these algorithms are computationally serial. Since some ambiguous factors exist, ways to achieve perfect visual scene segmentation remain tough and no general solution to the image segmentation problem is available.

In neural networks, a few of studies were reported in image segmentation (Wang 2003). The parallel computation attribute of these approaches is favorable in engineering (Egmont-Petersen et al. 2002; Kuntimad and Ranganath 1999). Theoretical studies on the brain function of feature binding lead a number of scholars to neural oscillator networks and some achievements in this field are attractive (Wang and Terman 1995; Liu and Wang 1999; Sporns et al. 1991; Ursino et al. 2003, 2009; Yu and Slotine 2009). After von der Malsburg put forward the correlation theory, which asserted that an object is represented by the temporal correlation of distributed firing neurons encoding different features of the object (von der Malsburg 1981; von der Malsburg and Schneider 1986), Wang and his colleagues proposed an innovative oscillator network called locally excitatory and globally inhibitory oscillator network—LEGION (Wang 1995; Wang and Terman 1995). LEGION is based on the mechanism that neurons coding the same feature fire synchronously while neuron groups representing different features are desynchronized. This mechanism is known as the oscillatory correlation, which is a special form of temporal correlation. The oscillators of the LEGION model are limit cycle oscillators, and the coupling of this model consists of locally excitatory connections and a global inhibitor. The LEGION approach offers some unique advantages; for example, oscillators can be computed in parallel and the model organization is simple.

Recent studies found that biological neural networks have the typical properties of small-world networks (Watts and Strogatz 1998; White et al. 1986; Humphries et al. 2006; Song et al. 2005; Sporns and Zwi 2004; Micheloyannis et al. 2006; Stam 2004; Stam et al. 2007; Bassett and Bullmore 2006; Rubinov and Sporns 2009), characterized by short path length and high clustering coefficient. It is interesting to study how the small-world topology affects the dynamics and functions of neural networks. Recent modeling studies showed that the small-world neural networks (SWNN) has many advantages, such as enhancing signal propagation speed, learning speed, and synchronization (Lago-Fernandez et al. 2000; Li and Chen 2003; Masuda and Aihara 2004; Hasegawa 2005; Simard et al. 2005; Li 2009; Guo and Li 2010; Li and Zheng 2010; Kwok et al. 2007). Specifically, many researchers have studied the effects of network topology on the synchronization of SWNN. Since existing results showed that small-world topology has significant effects on synchronization (Barahona and Pecora 2002; Hong et al. 2002; Masuda and Aihara 2004; Hasegawa 2005; Li and Zheng 2010), and segmentation by oscillatory correlation is tightly related to network synchronization, it is interesting to investigate how the small-world network topology affects image segmentation. In this paper, we add unidirectional shortcuts (both excitatory and inhibitory shortcuts are considered) on the basis of the original LEGION model to form a small-world network. Due to long-range connections, oscillators on the network could obtain more information for feature binding. According to the simulations, excitatory random long-range connections assist the network to achieve faster and better synchronization. Besides, unlike local connections, shortcuts can cluster separated parts that belong to a single object as well. This characteristic is advantageous because one object in a visual scene may be separated by other objects or large noise. Furthermore, the global inhibitor could be replaced with the inhibitory random long-range connections.

In this paper, we gradually modify the original LEGION to improve the performance of the model and enhance neural plausibility. The rest of this paper is organized as follows. Section “Model 1: LEGION with excitatory shortcuts” presents a basic LEGION model with unidirectional excitatory shortcuts and describes its performance. Section “Model 2: Neural oscillator networks with excitatory and inhibitory shortcuts” introduces a novel small-world model that replaces the global inhibition with unidirectional inhibitory shortcuts. Finally, conclusions and discussions are given in Sect. “Conclusion and discussion”.

Model 1: LEGION with excitatory shortcuts

Model description

According to the original LEGION model, a single oscillator i is the building block, which is defined in the simplest form as a feedback loop between an excitatory unit xi and an inhibitory unit yi (Wang and Terman 1995):

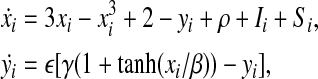graphic file with name M1.gif 1

where Ii represents external stimulation to the oscillator i. One oscillator will receive an external input if it is stimulated by an object. Si represents coupling from other oscillators on the network. Details about Si will be presented later. ρ denotes the noise term. The noise term can be used to verify that LEGION is robust and, more important, effectively assist the desynchronization of different input patterns. The parameter 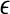Inline graphic is chosen to be a small positive number. Without any coupling or noise, (1) corresponds to a standard relaxation oscillator. The x-nullcline of (1) is a cubic curve, and the y-nullcline is a sigmoid function. The parameter β specifies the steepness of the sigmoid. If Ii > 0, these curves intersect along the middle branch of the cubic and the oscillator is enabled, whose periodic solution alternates between silent and active phases of near steady-state behavior. The parameter γ is introduced to control the relative times that the solution spends in these two phases. If Ii < 0, then the nullclines of (1) intersect at a stable fixed point along the left branch of the cubic. In this case, the oscillator is inactive.

The coupling of the original LEGION model is only based on local excitatory and global inhibitory connections. Each oscillator of LEGION is coupled to its nearest four neighbors by excitatory connections. The global inhibitor receives excitation from all oscillators on the network and in turn inhibits them to desynchronize the oscillations of distinct patterns.

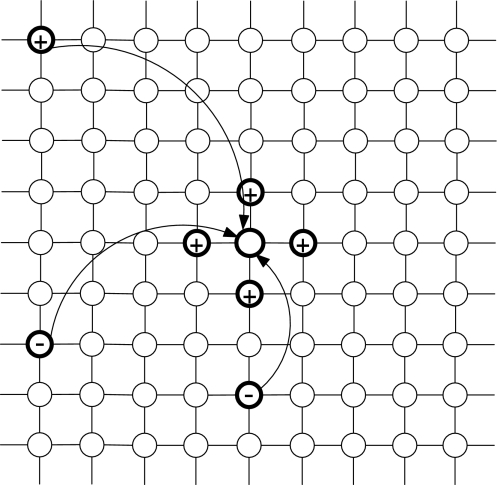
Wang has pointed out that more extensive connections can speed up the synchronization process (Wang 1995), but he didn’t treat this problem in greater detail, and didn’t show how network topology affects the performance of the model. The coupling type of model 1 is changed in order to form a small-world network. In addition to local excitatory connections, some excitatory shortcuts (random long-range connections) are added among oscillators, so as to facilitate phase entrainment of oscillations. In detail, besides each neuron is bidirectionally connected to its four nearest neighbors, a unidirectional excitatory shortcut is added uniformly with a small probability pE between each unconnected pair of neurons. Note that a neuron being coupled with itself is not allowed. Thus, this two-dimensional network combines a regular graph and a random one, which has the properties of a small-world network (Newman et al. 2002; Guo and Li 2010). The architecture of model 1 is shown in Fig. 1, and this model is named as small-world excitatory and globally inhibitory oscillator networks (SWEGION) in this work.

Fig. 1.

Fig. 1

Open in a new tab

Architecture of a two dimensional SWEGION with 4 nearest neighbor connections and random long-range connections. The black circle on the bottom indicates the global inhibitor connected to every oscillator on the network. Circles with a plus sign denote oscillators connected to the center oscillator

One oscillator of SWEGION can not only cooperate with its immediate four neighbors through local excitatory connections but also communicate with several remote nodes by excitatory shortcuts. Therefore, once one oscillator representing a certain pattern becomes active, these oscillators representing the same pattern will rapidly be activated no matter they are near or far away from the active source.

The coupling term Si in (1) is given by

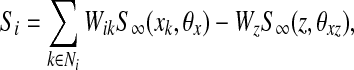graphic file with name M3.gif

where

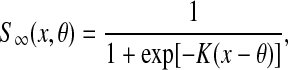graphic file with name M4.gif

and Wik is an connection (synaptic) weight from oscillator k to oscillator i. This weight is described as excitatory and Wik is a positive number. If oscillator k is connected to oscillator i by an excitatory connection and they represent the same object, the excitatory connection between them is effective and Wik is an appropriate positive number. Such two oscillators are called a pair of cooperators. Thus, once one oscillator is in the active phase, it rapidly spreads activation to its cooperators. On the contrary, if two oscillators coupled with each other represent different objects, their excitatory connection is ineffective and Wik = 0. Since random long-range connections have been introduced to SWEGION, connections to each oscillator on the network are no longer identical. In order to avoid distortions to the stability of synchronous oscillations caused by this asymmetry, an approach called dynamic normalization is utilized (Wang 1995; Wang and Terman 1995). The result of dynamic normalization is that overall effective excitatory connection weights WEtotal are equal. Ni is the set of oscillators connected to oscillator i, including the adjacent oscillators and the distant partners. As shown in Fig. 1, adjacent oscillators are four immediate neighbors on the two-dimensional grid, except on the boundaries where adjacent oscillators may be either two or three immediate neighbors. K is a positive parameter. θx is a threshold above which an oscillator can affect its cooperators. Wz (positive) is the weight of inhibition from the global inhibitor z, whose activity is defined as

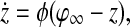graphic file with name M5.gif

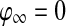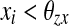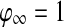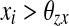where Inline graphic if Inline graphic for every oscillator, and Inline graphic if Inline graphic for at least one oscillator i. Thus, if the activity of every oscillator is below this threshold, the global inhibitor will not receive any input and the oscillators on the grid can not receive any inhibition from z. Otherwise, if the activity of at least one oscillator is above this threshold, the global inhibitor will receive input and every oscillator on the grid will receive inhibition from z when z is above the threshold θxz. The parameter ϕ determines the rate at which the inhibitor reacts to such simulation.

Examples and simulations

In this section, firstly we choose a synthetic image with three patterns as an example to show the synchrony of SWEGION. Figure 2a illustrates a synthetic 32 × 32 image contaminated by white Gaussian noise with standard deviation σ = 10 and the gray level of the black, gray, and white parts are 0, 128, and 255. A SWEGION with the same size is built as described in the previous section. As in most papers on LEGION, see e.g. Chen et al. (2000), we don’t represent the image by the input Ii in (1), instead, we use the weight, which depends on the difference between two pixels (two oscillators), to represent the input image. The external inputs of all oscillators are equal, Ii = 0.2. The noise ρ is uniformly distributed in the range [ − 0.02, 0.02]. Parameter values are chosen as follows: 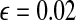Inline graphic, γ = 6.0, β = 0.1, K = 50, θx =  − 0.5, 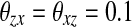Inline graphic, and ϕ = 3.0. In the simulations of this paper, we always use these parameters unless otherwise stated. The initial phases of all 32 × 32 oscillators on the network are random in a certain range. Two excitatory-linked oscillators are a pair of effective cooperators as long as their gray level difference is below 40; otherwise, their excitatory connection is not effective and Wik = 0. The overall effective excitatory connection weights WEtotal are normalized to 7.5 and pE is set to be 0.004. The differential equations are solved numerically by the fourth-order Runge-Kutta method.

Fig. 2.

Fig. 2

Open in a new tab

Segmentation by SWEGION. a A 32 × 32 noisy synthetic image. The gray levels of the black, gray and white patterns are 0, 128, 255, respectively. The standard deviation of Gaussian noise is 10. b Segmentation in three patterns. c Initial x activity, different gray levels represent different x activity. d–f Three segments are illustrated by black regions

Three patterns of the synthetic image are segmented by SWEGION as illustrated in Fig. 2b. Figure 2c shows the instantaneous activity of the oscillators at the beginning of dynamic evolution. Here the gray level of each pixel indicates the x activity of the corresponding oscillator. The gray level corresponding to oscillator i is set to be proportional to the initial xi. In Fig. 2d–f, a black region represents a certain pattern of the synthetic image.

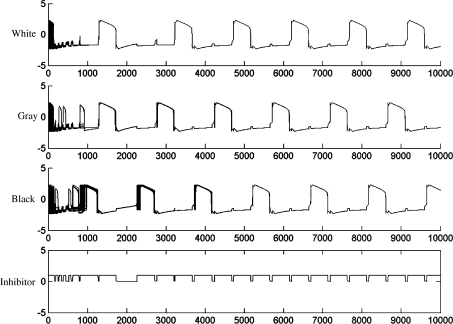
Figure 3 displays the temporal evolution of all 32 × 32 oscillators. In the figure the activities of the oscillators representing the same pattern are combined into a single trace and the activities of different oscillator groups are in different phases. The desired synchronization is stabilized quickly. Figure 4 shows the temporal evolution of the oscillators of the original LEGION model whose input is also the 32 × 32 synthetic image in Fig. 2a. The dynamics are solved with the same parameters set above. Simulation results in Figs. 3 and 4 show that a small portion of excitatory long-range connections between non-local oscillators can shorten the total time during which all oscillators representing the same pattern are completely synchronized while different oscillator groups are desynchronized. In SWEGION, the traces of oscillators that belong to the same pattern are more synchronous and the desynchronization of different patterns is completed faster. We have performed the simulations more than 20 times, and we have obtained similar results as those shown in Figs. 3 and 4 in each time. The results are unsurprising since excitatory shortcuts could provide additional pathways to spread phase information which plays a major role in synchronization. With a larger synthetic input image (64 × 64 for instance), the distinction between the synchronization performances of LEGION and SWEGION should be more significant. The fast synchrony is meaningful since in the brain visual perception should arise in a very limited time (Biederman 1987). Besides, this small-world model is likely to provide a solution to real-time problems in engineering.

Fig. 3.

Fig. 3

Open in a new tab

Traces of all 32 × 32 oscillators of SWEGION converge into three groups. The four panels show traces of white, gray, black and the global inhibitor, respectively

Fig. 4.

Fig. 4

Open in a new tab

Traces of all 32 × 32 oscillators of LEGION

Choosing a proper proportion of global excitatory connections pE is necessary for this proposed small-world model. In fact, a large number of global excitatory connections provide a noise source that could synchronize oscillator groups representing different objects, which leads to a failing segmentation. To avoid distortions and obtain desired synchronization, we should keep pE small. In this simulation we set pE = 0.004 and slight disturbances of this value do not damage the desired oscillations. However, as pE increases by a large margin, the performance of the model becomes worse. On the contrary, if pE is far fewer than 0.004, the performance of SWEGION would be similar to that of the original LEGION model.

To segment real images with a large number of pixels by the above-mentioned oscillator network models involves integrating a large number of differential equations, which is time-consuming. Wang and his colleagues developed an algorithm of LEGION to reduce numerical computations (Wang and Terman 1997). This LEGION algorithm exhibits the essential properties of oscillators on the network, such as the properties of synchrony and desynchrony in a population of oscillators. According to the LEGION algorithm, lateral potential is proposed as a solution to the problem of fragmentation. Each oscillator has a corresponding lateral potential in this algorithm and an oscillator located in the interior of a pattern can receive a high lateral potential. At the very start, oscillators which can jump up without stimulation from other oscillators are called leaders. After jumping up, a leader spreads activity within its own block and oscillators representing the leader’s pattern are referred to as followers. When a leader jumps up firstly, its followers will all jump up in next several periods. After that a leader of another pattern is selected to be active and then it will activate its followers. The step will be iterated until all patterns are found.

Figure 5 presents a gift box tied by a piece of ribbon with a white background (the background shown in Fig. 5 is not purely white in order to be visible on the white paper). We can easily obtain three parts from this image, the gift box, the white background and the ribbon. In LEGION, taking into account the principle of proximity, oscillators which are not connected to each other can not be synchronized. If the LEGION algorithm is applied to segment this image, unconnected parts are segmented as individual objects. Thus, we will obtain six segments. Figure 6 shows the six parts of Fig. 5 segmented by the original LEGION algorithm. In each figure, oscillators corresponding to black pixels are in the active phase and white pixels are silent. Figure 6a, b present instantaneous activities of oscillators when the oscillators representing the gift box jump up. The gift box are segmented into two distinct parts. As shown in Fig. 6a, some pixels representing the ribbon are grouped into the upper part of the box. Figure 6c–e are instantaneous activities of oscillators when different parts of the background jump up. Figure 6f shows the main part of the ribbon.

Fig. 5.

Fig. 5

Open in a new tab

A picture of a gift box tied by a piece of ribbon with a white background

Fig. 6.

Fig. 6

Open in a new tab

Six patterns grouped by the LEGION algorithm, in which black regions indicate the segments. a, b Two parts of the gift box. c–e Three parts of the background. c The ribbon

However, in this case, although the gift box is separated, our brain will not recognize the separated box as two objects. In addition, three white parts on the corner should be perceived as one background. Since excitatory shortcuts could help one oscillator to communicate with cooperators far away, SWEGION may be capable of grouping unconnected parts of one object into a single pattern. According to the principle of proximity, connectedness is not necessary and unconnected but close parts sometimes represent the same pattern. From the biological perspective, these unconnected parts that are perceived as one object should be recognized as a single pattern. In this paper, we call this recognition capability robustness.

In order to demonstrate the robustness of SWEGION, we also choose Fig. 5 as an example for segmentation. On the basis of the LEGION algorithm, a SWEGION algorithm is presented. Since the SWEGION algorithm is very similar to the LEGION algorithm, details about the SWEGION algorithm are provided in the Appendix.

Figure 7 shows the segmentation by the SWEGION algorithm. Due to the excitatory shortcuts, the gift box is segmented from the background as a single object though it is tied by a piece of ribbon. In this case, the separated gift box is a single object in human vision and the ribbon can be regarded as interference. The segmentation by SWEGION is much closer to the human visual perception. On the other hand, some wrongly grouped pixels can be found in Fig. 7a and c. These small errors are usually in the lines made by folding or on the boundaries of distinct objects. We consider these errors as the small cost of the robustness. In short, the SWEGION model concentrates on the principle of similarity and provides an approach to extract main information from the background.

Fig. 7.

Fig. 7

Open in a new tab

Three patterns grouped by the SWEGION algorithm, in which black regions indicate the individual segments. a The gift box is segmented as a single object. b The background. c The ribbon

Although SWEGION is a slightly modified version of LEGION, it produces some interesting outcomes. Depending on the simulation results shown above, the advantages of excitatory small-world coupling are summarized as follows:

  1. Fastness The simulations imply that a small number of long-range connections could provide more pathways to broadcast information and help oscillators far away to synchronize in a short time. This advantage appears when Figs. 3 and 4 are compared.

  2. Robustness In accordance with Gestalt principles, proximity occurs when elements are placed close. Connectedness is just a special case of closeness and some separated parts of an image may together express a single pattern. Particularly, one pattern may be split by noise or another object. In this case, long-range connections could set up links between these partitions. This advantage could be found when Figs. 5 and 6 are in contrast.

Model 2: Neural oscillator networks with excitatory and inhibitory shortcuts

On the basis of SWEGION, in this section, we go further to present a new oscillator network model.

Model description

In either the original LEGION model or SWEGION, a global inhibitor receives inputs from the entire network and feeds back with inhibition to the entire network to produce desynchronization of oscillator groups. The global inhibitor is quite helpful in such a globally inhibitory mechanism. However, from the biological perspective, it is not economical to produce global inhibition which influences neurons universally. Besides, it is unlikely that there exists such a global feedback inhibitor in the biological neural system especially in the visual cortex. Recent experimental results show that excitation dominates the extrastriate feedback pathways to the primary visual cortex V1 (Johnson and Burkhalter 1996, 1997; Shao and Burkhalter, 1996). To imitate the biological neural networks, a two dimensional neural oscillator network including both excitatory shortcuts and inhibitory shortcuts is developed. The global inhibitor of this model is entirely removed. Besides excitatory shortcuts introduced to SWEGION, unidirectional inhibitory long-range connections are added to replace the global inhibitor. Simulation results show that inhibitory shortcuts can desynchronize different patterns alone. Architecture of model 2 is showed in Fig. 8. We named this new class of networks small-world oscillator networks (SWON). SWON can be viewed as an upgraded version of SWEGION.

Fig. 8.

Fig. 8

Open in a new tab

Architecture of SWON. Circles with a plus sign excite and circles with a minus sign inhibit the central oscillator

As shown in Fig. 8, each oscillator has excitatory connections to its four nearest neighbors; in addition, with probability pE a unidirectional excitatory shortcut is added between one oscillator and a randomly selected node on the network. Thus, as explained in SWEGION, excitatory connections of each oscillator are composed of two parts. On the other hand, unidirectional inhibitory shortcuts are added uniformly with probability pI between each unconnected pair of neurons. Inhibitory connections of oscillators could spread inhibition to facilitate the desynchronization between oscillator groups representing different objects.

As stated above, in such a mechanism, one oscillator can cooperate with its immediate four neighbors through local excitatory connections and communicate with several remote nodes by excitatory shortcuts. Therefore, once one oscillator representing a certain pattern becomes active, these oscillators representing the same pattern will rapidly be activated no matter where they are. Furthermore, when a specific oscillator group gets active, members of this group deliver inhibition to other groups by inhibitory shortcuts. Due to this framework, visual scenes can be segmented.

The SWON model is described by the following equations

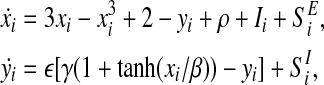graphic file with name M12.gif

where SEi is the excitatory coupling and SIi is the inhibitory coupling. The coupling term SEi and SIi are given by

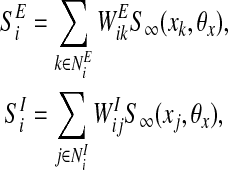graphic file with name M13.gif

where NEi is the set of oscillators connected to oscillator i by excitatory connections and NIi is the set of oscillators connected to oscillator i by inhibitory connections. On this proposed network, if oscillator k is connected to oscillator i by an excitatory connection and these two oscillators represent the same object, the excitatory connection between them is effective and we call oscillator k a cooperator of oscillator i. On the other hand, if oscillator j is connected to oscillator i by an inhibitory connection and they represent different objects, their inhibitory connection takes effect and we call oscillator j a competitor of oscillator i. Dynamic normalization is used to ensure that both overall effective excitatory connection weights WEtotal and overall effective inhibitory connection weights WItotal of each oscillator are equal. The weights WEtotal > 0 and WItotal > 0 are normalized to two constants. CEi is the number of cooperators of oscillator i and CIi is the number of competitors of oscillator i. In detail, the excitatory connection weight from oscillator k to oscillator i, WEik, and the inhibitory connection weight from oscillator j to oscillator i, WIij, are given by

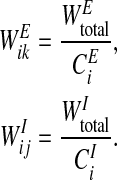graphic file with name M14.gif

Simulations

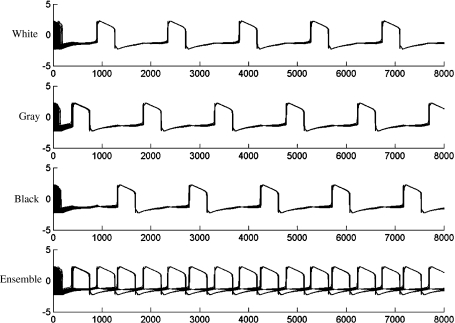
The effectiveness of SWON is illustrated by grouping Fig. 2a, as described before. In this simulation, we let WEtotal = 6.3, WItotal = 0.042, pE = 0.004 and pI = 0.04. If oscillator k is connected to oscillator i by an excitatory connection and their gray level difference is below 40, oscillator k becomes a cooperator of oscillator i. Besides, if oscillator j is connected to oscillator i by an inhibitory connection and their gray level difference is above 70, oscillator j becomes a competitor of oscillator i. The differential equations are solved using the fourth-order Runge-Kutta method. The segmentation result is similar to Fig. 2, and we do not show it again here. Figure 9 shows the traces of all 32 × 32 oscillators, which successfully separate into three groups. Although the traces of oscillators representing the same pattern are not as synchronous as those of SWEGION, it is satisfactory and sufficient to segment the image. In addition, these three oscillator groups are totally desynchronized at the first cycle of oscillation, which implies that SWON could be faster than SWEGION in image segmentation. The reason is that in LEGION and SWEGION all oscillators are inhibited when at least one oscillator is in the active phase while in SWON only oscillators that do not belong to the group of active oscillators can be inhibited. In other words, inhibitory targets of SWON are selective.

Fig. 9.

Fig. 9

Open in a new tab

Traces of all 32 × 32 oscillators of SWON converge into 3 groups

The proportion of global connections (pE and pI) should be appropriate. A too small value of pI is helpless to desynchronize different oscillator groups. An overlarge value of pI seems uneconomical and would provide excessive inhibition that destabilizes the desired synchronization. In this simulation, we keep pE = 0.004 as in SWEGION and pI = 0.04.

In Sect. “Model 1: LEGION with excitatory shortcuts”, a real image of a gift box is segmented by the SWEGION algorithm and the original LEGION algorithm. Similarly, we develop a SWON algorithm and apply it to segment the same image. In the SWON algorithm, oscillators no longer receive global inhibition. Instead, they are inhibited when one of their competitors becomes active. Details of the SWON algorithm are shown in the Appendix.

Figure 10 shows the result of simulation which is similar to Fig. 6. The result indicates that by SWON, as by SWEGION, separated regions with the same gray level could be detected as a single object.

Fig. 10.

Fig. 10

Open in a new tab

Three patterns grouped by the SWON algorithm, in which black regions indicate the segments. a The gift box is composed of two parts. b The background. c The ribbon

Simulation results above demonstrate that SWEGION and SWON share the feature of fast synchrony and robustness. SWON has advantages over SWEGION in two aspects:

  1. Biologically Plausibility Since the inhibitory shortcuts on the small-world network take the place of the global inhibitor, SWON does not need to inhibit oscillators all over the network as LEGION and SWEGION do.

  2. Faster Speed The inhibitory shortcuts would make the model faster to achieve desired synchronization.

Conclusion and discussion

In conclusion, we have proposed two models derived from LEGION. As stated in Sect. “Model 1: LEGION with excitatory shortcuts”, excitatory shortcuts help the SWEGION model to achieve fast and robust segmentation. Oscillators on the network can both exchange information with local neighbors and obtain extra information from cooperators far away. Thus, in a short time, oscillators belonging to the same pattern are synchronized and different oscillator groups are desynchronized. Furthermore, separated parts that belong together would be recognized as a single object. In fact, one pattern may be separated by noise or other patterns. In SWON, the global inhibitor is removed and inhibitory shortcuts are introduced. The simulations show that SWON also has the ability to quickly segment an image including different patterns and exhibits the feature of robustness. Compared with SWEGION, SWON possesses a biologically plausible mechanism of inhibitory control and to some extent could achieve faster synchronization. SWEGION and SWON perform well to synchronize similar but far away regions. However, in LEGION, such synchronization can never take place after connected regions are first organized. In Fig. 6, disjoint regions can not be synchronized at a later stage based on the results of Fig. 6.

Based on Gestalt principles, proximity occurs when elements are close to each other. However, it is difficult to put forward a criterion determining how close elements are to cause proximity. Connectedness is not the only situation of proximity. Meanwhile, maybe elements too far away with the same feature should not be considered as the situation of proximity. For an image like Fig. 5, SWEGION and SWON are more suitable methods than LEGION. These proposed models in this paper keep local excitatory coupling to obey the proximity principle and utilize long-range coupling to beyond locality. From another point of view, long-range connections, to some extent, destroy the principle of proximity and emphasize similarity, which is also among the Gestalt principles. If the input image is characterized by portions of quite similar grayscale that do not belong together, the two proposed models (SWEGION and SWON) will also group these portions as a single object. In this situation, the principle of similarity is subordinate in segmentation and the original LEGION is preferable. In this paper, we pay more attention to images in which portions of similar grayscale indicate the same object; for example, images of bacteria, fingerprints and numbers. This grouping characteristic of SWEGION and SWON is similar to that of another kind of oscillator network (Yu and Slotine 2009). On the other hand, as we described in the introduction, ways to achieve perfect segmentation of visual scene remain tough and a general algorithm suitable for all kinds of images is still unavailable. In fact, we could firstly detect the properties of the input images and then choose the most suitable algorithm for segmentation. In biological vision, there should be a dynamic balance of using the proximity and similarity criteria when analyzing visual scenes.

In this paper, we do not consider noise suppression. In (Chen et al. 2000; Chen and Wang 2002), weight adaptation is used in LEGION to remove noise and preserve significant discontinuities. Because we concentrate on the ability of small-world coupling, weight of each synapse on the oscillator network is calculated in a simple method. Weight adaptation may be beneficial to improve the performance of SWEGION and SWON in noise suppression.

As future work, the proposed network models and algorithms might be applied to real image segmentation, e.g. fMRI images, as well as auditory segregation, as was done by LEGION (Wang and Brown 1999; Wang and Chang 2008).

Acknowledgments

We gratefully acknowledge D. Q. Guo, L. Sheng, and Q. X. Zheng for valuable comments on an early version of this paper. We gratefully acknowledge the anonymous reviewers for their valuable comments and suggestions, which greatly improved our paper. This work was supported by the National Natural Science Foundation of China (Grant No. 60871094), the Fundamental Research Funds for the Central Universities (Grant No. 1A5000-172210126), and the Foundation for the Author of National Excellent Doctoral Dissertation of PR China (Grant No. 2007B42).

Appendix

The SWEGION algorithm and SWON algorithm are developed from the LEGION algorithm proposed by Wang (Wang and Terman 1997). Here Ii denotes the value of pixel i, and IM denotes the maximum possible pixel value. LKx, RKx and LCx represent the x values of three corner points of a typical limit cycle (please refer to Fig. 2 in Wang and Terman 1997). The values of them are LKx =  − 1, RKx = 1 and LCx =  − 2.

SWEGION algorithm

The SWEGION algorithm is described as follows:

  1. Initialize
    1. Set z(0) = 0;
    2. Form effective connections
      graphic file with name M15.gif
      where Ni contains local coupling and long-range coupling.
    3. Find leaders
      graphic file with name M16.gif
      where pi is the lateral potential, θp is the threshold and H is the Heaviside function.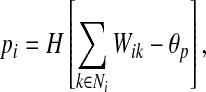
    4. Place all the oscillators randomly on the left branch. Namely xi(0) takes a random value between LCx and LKx.
  2. Find one oscillator j so that (i) 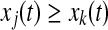Inline graphic, where k is currently on the left branch; and (ii) pj = 1. Then
    graphic file with name M18.gif
    In this step, the leader on the left branch which is closet to the left knee is selected. This leader jumps up to the right branch, and all the other oscillators move towards LK.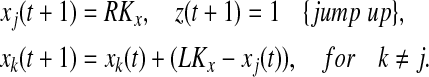
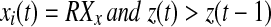
  3. Iterate until stop If Inline graphic
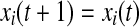
    graphic file with name M20.gif

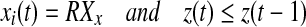
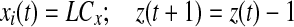
    else if Inline graphic

          Inline graphic

          if z(t + 1) = 0 go to step 2

    else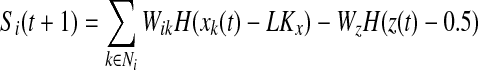
    graphic file with name M23.gif

          if Si(t + 1) > 0

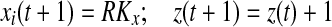
                Inline graphic

          else

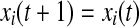
                Inline graphic

SWON algorithm

The SWON algorithm is stated below where the inhibitory long-range coupling is added:

  1. Initialize
    1. Set z(0) = 0; z counts members of a group.
    2. Form effective connections
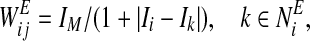
      graphic file with name M26.gif
    3. Find leaders
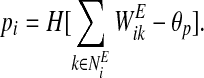
      graphic file with name M27.gif
    4. Place all the oscillators randomly on the left branch.
  2. Find one oscillator j so that (i) 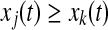Inline graphic, where k is currently on the left branch; and (ii) pj = 1. Then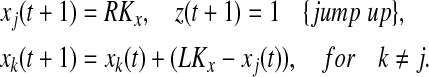
    graphic file with name M29.gif

  3. Iterate until stop

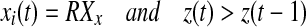
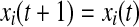
    if Inline graphic

          Inline graphic

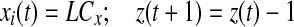
    else if Inline graphic

          Inline graphic

          if z(t + 1) = 0 go to step 2

    else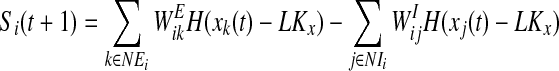
    graphic file with name M34.gif

          if Si(t + 1) > 0

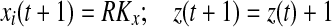
                Inline graphic

          else

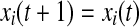
                Inline graphic

References

  1. Barahona M, Pecora LM. Synchronization in small-world systems. Phys Rev Lett. 2002;89(5):054101. doi: 10.1103/PhysRevLett.89.054101. [DOI] [PubMed] [Google Scholar]
  2. Bassett DS, Bullmore E. Small-world brain networks. Neuroscientist. 2006;12(6):512–523. doi: 10.1177/1073858406293182. [DOI] [PubMed] [Google Scholar]
  3. Biederman I. Recognition-by-components: a theory of human image understanding. Psychol Rev. 1987;94(2):115–147. doi: 10.1037/0033-295X.94.2.115. [DOI] [PubMed] [Google Scholar]
  4. Chen K, Wang D, Liu X. Weight adaptation and oscillatory correlation for image segmentation. IEEE Trans Neural Netw. 2000;11(5):1106–1123. doi: 10.1109/72.870043. [DOI] [PubMed] [Google Scholar]
  5. Chen K, Wang D. A dynamically coupled neural oscillator network for image segmentation. Neural Netw. 2002;15(3):423–439. doi: 10.1016/s0893-6080(02)00028-x. [DOI] [PubMed] [Google Scholar]
  6. DalMaso G, Morel JM, Solimini S. Variational methods in image segmentation: existence and approximation results. Acta Mathematica. 1992;168(1):89–151. doi: 10.1007/BF02392977. [DOI] [Google Scholar]
  7. Egmont-Petersen M, Ridder D, Handels H. Image processing with neural network—a review. Pattern Recogn Lett. 2002;35(10):2279–2301. [Google Scholar]
  8. Guo D, Li C. Self-sustained irregular activity in 2-D small-world networks of excitatory and inhibitory neurons. IEEE Trans Neural Netw. 2010;21(6):895–905. doi: 10.1109/TNN.2010.2044419. [DOI] [PubMed] [Google Scholar]
  9. Hasegawa H. Synchronizations in small-world networks of spiking neurons: diffusive versus sigmoid coupling. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72(5 Pt 2):056139. doi: 10.1103/PhysRevE.72.056139. [DOI] [PubMed] [Google Scholar]
  10. Hong H, Choi MY, Kim BJ. Synchronization on small-world networks. Phys Rev E. 2002;65:026139. doi: 10.1103/PhysRevE.65.026139. [DOI] [PubMed] [Google Scholar]
  11. Humphries MD, Gurney K, Prescott TJ. The brainstem reticular formation is a smallworld, not scale-free, network. Proc R Soc B Biol Sci. 2006;273(1585):503–511. doi: 10.1098/rspb.2005.3354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Johnson R, Burkhalter A. Microcircuitry of forward and feedback connections within rat visual cortex. J Comp Neurol Psychol. 1996;368(3):383–398. doi: 10.1002/(SICI)1096-9861(19960506)368:3<383::AID-CNE5>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
  13. Johnson R, Burkhalter A. A polysynaptic feedback circuit in rat visual cortex. J Neurosci. 1997;17(18):7129–7140. doi: 10.1523/JNEUROSCI.17-18-07129.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kuntimad G, Ranganath HS. Perfect image segmentation using pulse coupled neural networks. IEEE Trans Neural Netw. 1999;10(3):591–598. doi: 10.1109/72.761716. [DOI] [PubMed] [Google Scholar]
  15. Kwok HF, Jurica P, Raffone A, Leeuwen C. Robust emergence of small-world structure in networks of spiking neurons. Cogn Neurodyn. 2007;1(1):39–51. doi: 10.1007/s11571-006-9006-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lago-Fernandez LF, Huerta R, Corbacho F, Siguenza JA. Fast response and temporal coherent oscillations in small-world networks. Phys Rev Lett. 2000;84(12):2758–2761. doi: 10.1103/PhysRevLett.84.2758. [DOI] [PubMed] [Google Scholar]
  17. Li C. Memorizing morph patterns in small-world neuronal network. Phys A Stat Mech Appl. 2009;388:240–246. doi: 10.1016/j.physa.2008.10.004. [DOI] [Google Scholar]
  18. Li C, Chen G. Stability of a neural network model with small-world connections. Phys Rev E. 2003;68:052901. doi: 10.1103/PhysRevE.68.052901. [DOI] [PubMed] [Google Scholar]
  19. Li C, Zheng Q (2010) Synchronization of the small-world neuronal network with unreliable synapses. Phys Biol 7 (in press) [DOI] [PubMed]
  20. Liu X, Wang D. Range image segmentation using a LEGION network. IEEE Trans Neural Netw. 1999;10(2):564–573. doi: 10.1109/72.761713. [DOI] [PubMed] [Google Scholar]
  21. von der Malsburg C (1981) The correlation theory of brain functions. Internal Report 81-2 Max-Planck-Institut for Biophysical Chemistry Göttungen FRG
  22. Malsburg C, Schneider W. A neural cocktail-party processor. Biol Cybern. 1986;54:29–40. doi: 10.1007/BF00337113. [DOI] [PubMed] [Google Scholar]
  23. Masuda N, Aihara K. Global and local synchrony of coupled neurons in small-world networks. Biol Cybern. 2004;90:302–309. doi: 10.1007/s00422-004-0471-9. [DOI] [PubMed] [Google Scholar]
  24. Micheloyannis S, Pachou E, Stam CJ, Breakspear M, Bitsios P, Vourkas M, Erimaki S, Zervakis M. Small-world networks and disturbed functional connectivity in schizophrenia. Schizophr Res. 2006;87(1–3):60–66. doi: 10.1016/j.schres.2006.06.028. [DOI] [PubMed] [Google Scholar]
  25. Newman MEJ, Jensen I, Ziff RM. Percolation and epidemics in a two-dimensional small world. Phys Rev E. 2002;65:02194. doi: 10.1103/PhysRevE.65.021904. [DOI] [PubMed] [Google Scholar]
  26. Pal NR, Pal SK. A review on image segmentation techniques. Pattern Recogn Lett. 1993;26(9):1277–1294. [Google Scholar]
  27. Rubinov M, Sporns O. Complex network measures of brain connectivity: uses and interpretations. NeuronImage. 2009;52(3):1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
  28. Shao Z, Burkhalter A. Different balance of excitation and inhibition in forward and feedback circuits of rat visual cortex. J Neurosci. 1996;16(22):7353–7365. doi: 10.1523/JNEUROSCI.16-22-07353.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Shi J, Malik J. Normalized cuts and image segmentation. IEEE Trans Pattern Anal Mach Intell. 2000;22(8):888–905. doi: 10.1109/34.868688. [DOI] [Google Scholar]
  30. Simard D, Nadeau L, Kroger H. Fastest learning in small-world neural networks. Phys Lett A. 2005;336:8–15. doi: 10.1016/j.physleta.2004.12.078. [DOI] [Google Scholar]
  31. Song S, Sjötröm PJ, Reigl M, Nelson S, Chklovskii DB. Highly nonrandom features of synaptic connectivitly. Plos Biol. 2005;3:0507–0519. doi: 10.1371/journal.pbio.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sporns O, Zwi JD. The small world of the cerebral cortex. Neuroinformatics. 2004;2(2):145–162. doi: 10.1385/NI:2:2:145. [DOI] [PubMed] [Google Scholar]
  33. Sporns O, Tononi G, Edelman GM. Modeling perceptual grouping and figure-grpund segregation by means of active reentrant connections. Proc Natl Acad Sci USA. 1991;88:129–133. doi: 10.1073/pnas.88.1.129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Stam CJ. Functional connectivity patterns of human magnetoencephalographic recordings: a “small-world” network? Neurosci Lett. 2004;355(1–2):25–28. doi: 10.1016/j.neulet.2003.10.063. [DOI] [PubMed] [Google Scholar]
  35. Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P. Small world networks and functional connectivity in Alzheimer’s disease. Cereb Cortex. 2007;17(1):92–99. doi: 10.1093/cercor/bhj127. [DOI] [PubMed] [Google Scholar]
  36. Ursino M, Cara GEL, Sarti A. Binding and segmentation of multiple objects through neural oscillators inhibited by contour information. Biol Cybern. 2003;89:56–70. doi: 10.1007/s00422-003-0410-1. [DOI] [PubMed] [Google Scholar]
  37. Ursino M, Magosso E, Cuppini C. Recognition of abstract objects via neural oscillators: interaction among topological organization, associative memory and gamma band synchronization. IEEE Trans Neural Netw. 2009;20(2):316–335. doi: 10.1109/TNN.2008.2006326. [DOI] [PubMed] [Google Scholar]
  38. Vese LA, Chan TF. A multiphase level set framework for image segmentation using the Mumford and Shah model. Int J Comput Vis. 2004;50(3):271–293. doi: 10.1023/A:1020874308076. [DOI] [Google Scholar]
  39. Wang D. Visual scene segmentation. The handbook of brain theory and neural networks, 2nd edn. Cambridge: MIT Press; 2003. pp. 1215–1219. [Google Scholar]
  40. Wang D. Emergent synchrony in locally coupled neural oscillators. IEEE Trans Neural Netw. 1995;6(4):941–948. doi: 10.1109/72.392256. [DOI] [PubMed] [Google Scholar]
  41. Wang D, Terman D. Locally excitatory globally inhibitory oscillator network. IEEE Trans Neural Netw. 1995;6(1):283–286. doi: 10.1109/72.363423. [DOI] [PubMed] [Google Scholar]
  42. Wang D, Terman D. Image segmentation based on oscillatory correlation. Neural Comput Appl. 1997;9(4):805–836. doi: 10.1162/neco.1997.9.4.805. [DOI] [PubMed] [Google Scholar]
  43. Wang D, Brown GJ. Separation of speech from interfering sounds based on oscillatory correlation. IEEE Trans Neural Netw. 1999;10(3):684–697. doi: 10.1109/72.761727. [DOI] [PubMed] [Google Scholar]
  44. Wang D, Chang P. An oscillatory correlation model of auditory streaming. Cogn Neurodyn. 2008;2(1):7–19. doi: 10.1007/s11571-007-9035-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nat Biotechnol. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
  46. Wertheimer M. Laws of organization in perceptual forms (partial translation) In: Ellis W, editor. A source book of gestalt psychology. London: Routledge & Kegan Paul; 1938. pp. 71–88. [Google Scholar]
  47. White JG, Southgate E, Thompson JN, Brenner S. The structure of the nervous system of the nematode Caenorhabditis elegans. Phil Trans R Soc London B. 1986;314(1165):1–340. doi: 10.1098/rstb.1986.0056. [DOI] [PubMed] [Google Scholar]
  48. Yu G, Slotine J. Visual grouping by neural oscillator networks. IEEE Trans Neural Netw. 2009;20(12):1871–1884. doi: 10.1109/TNN.2009.2031678. [DOI] [PubMed] [Google Scholar]
  49. Zhu S, Lee TS, Yuille AL (1995) Region competition: unifying snakes, region growing, energy/Bayes/MDL for multi-band image segmentation. In: ICCV, fifth international conference on computer vision (ICCV’95), p 416

Articles from Cognitive Neurodynamics are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES