An integrated neural model of semantic memory, lexical retrieval and category formation, based on a distributed feature representation

Abstract

This work presents a connectionist model of the semantic-lexical system. Model assumes that the lexical and semantic aspects of language are memorized in two distinct stores, and are then linked together on the basis of previous experience, using physiological learning mechanisms. Particular characteristics of the model are: (1) the semantic aspects of an object are described by a collection of features, whose number may vary between objects. (2) Individual features are topologically organized to implement a similarity principle. (3) Gamma-band synchronization is used to segment different objects simultaneously. (4) The model is able to simulate the formation of categories, assuming that objects belong to the same category if they share some features. (5) Homosynaptic potentiation and homosynaptic depression are used within the semantic network, to create an asymmetric pattern of synapses; this allows a different role to be assigned to shared and distinctive features during object reconstruction. (6) Features which frequently occurred together, and the corresponding word-forms, become linked via reciprocal excitatory synapses. (7) Features in the semantic network tend to inhibit words not associated with them during the previous learning phase. Simulations show that, after learning, presentation of a cue can evoke the overall object and the corresponding word in the lexical area. Word presentation, in turn, activates the corresponding features in the sensory-motor areas, recreating the same conditions occurred during learning, according to a grounded cognition viewpoint. Several words and their conceptual description can coexist in the lexical-semantic system exploiting gamma-band time division. Schematic exempla are shown, to illustrate the possibility to distinguish between words representing a category, and words representing individual members and to evaluate the role of gamma-band synchronization in priming. Finally, the model is used to simulate patients with focalized lesions, assuming a damage of synaptic strength in specific feature areas. Results are critically discussed in view of future model extensions and application to real objects. The model represents an original effort to incorporate many basic ideas, found in recent conceptual theories, within a single quantitative scaffold.

Introduction

A fundamental problem in cognitive neuroscience is how the meaning of objects is stored in mind, recollected from partial cues and related with lexical items. Tulving (1972) first introduced the term “semantic memory” to denote a type of declarative memory which contains concepts on objects, is culturally shared and is context independent. The fundamental importance of semantic memory, and its strict relation with language, motivated the formulation of several theories aimed at understanding its organization in the brain and at providing a deeper insight on the behavior of patients with lexical deficits. Most fundamental ideas have been formulated in qualitative ways, although some computational studies have also appeared recently. The same ideas may also permeate artificial systems for object recognition (such as in robotics or in multimodal pattern recognition).

A common viewpoint in the literature is that semantic and lexical aspects are memorized in separate regions of the brain, i.e., the brain possesses distinct (but reciprocally linked) semantic and lexical stores (Anderson 1983; Collins and Loftus 1975; Seidenberg and McClelland 1989). Furthermore, most semantic memory models assume that knowledge of concrete objects is constituted by a collection of primitive features (Collins and Loftus 1975; Shallice 1988; Smith and Medin 1981). Traditional theories in Artificial Intelligence were based on the idea that these features are represented as amodal symbols, and that knowledge exploits a variety of amodal representations (such as frames, symbolic lists, semantic networks) [see Barsalou and Hale (1993) for a review]. More recent data, however, collected from observation of patients with neurological deficits and from neuroimaging studies, challenged this viewpoint and focused attention on the neural representations in the different modalities (Barsalou 2008; Martin 2007; Martin and Chao 2001). These data support the idea that semantic knowledge of concrete objects is not merely symbolic, but rather is grounded on concrete experience (Barsalou 2008; Borghi and Cimatti 2010; Gibbs 2003). This means that the multimodal representation acquired during experience (such as perception, action and emotion) is re-activated in the brain during the representation of a concrete object. A direct consequence of this idea, is that object meaning is described by means of a distributed representation, which spreads over different cortical areas [some located in the lateral and ventral temporal cortex, see Martin (2007)] and matches the organization of sensory, motor and emotional systems.

In the following, some conceptual models based on these ideas will be described briefly: the interested reader can find more details in an excellent recent review paper (Hart et al. 2007).

One of the first theories which have been proposed to explain the neural organization of semantic memory is the “sensory-functional theory” by Warrington and McCarthy (1987), Warrington and Shallice (1984), which was motivated by the observation of patients with selective impairment in category representation. This theory assumes that semantic memory consists of multiple channels of processing within the sensory and motor systems. An extension of this model, more strictly based on neuroanatomical data, is the “sensory-motor model of semantic knowledge” proposed by Gainotti (2006). Similarly, the “Hierarchical Inference Theory” (Humphreys and Forde 2001) assumes that semantic memory is organized by modality-specific stores for features, and that concepts derive from an interactive process between the semantic and perceptual levels of representation. Alternatively, the “property-based model” (Caramazza and Shelton 1998) assumes that conceptual knowledge is organized in distinct domains (such as animals, plants, tools, conspecifics) which reflect the presence of evolutionary constraints. Another model which emphasizes the organization of semantic memory via features is the “conceptual structure account” (Tyler and Moss 2001): in this model, categories emerge as a consequence of correlated features, while distinctive features allow discrimination of individual concepts within categories. Models more strictly based on neuroimaging data, laying emphasis on the grounded cognition idea, were formulated by Barsalou et al. (2003), Simmons and Barsalou (2003), and Martin and Chao (2001). Finally, Hart and coworkers formulated a complex theory, which incorporates several previous aspects: Their model (named “hybrid model of semantic object memory”), assumes that different cortical regions embody not only sensory-motor representations of objects, but also higher cognitive aspects (lexical, emotional,…). This information is then integrated by means of synchronized neural activity in the gamma-range modulated by the thalamus (Hart et al. 2002; Kraut et al. 2003, 2004).

The models mentioned above were essentially formulated in qualitative terms. As explicitly pointed out by Barsalou (2008), an important goal for future research is to formalize and implement these theories. Moreover, rather than using manipulation of amodal symbols, as in Artificial Intelligence, these theories should be implemented using dynamical systems and connectionist neural networks.

A few connectionist mathematical models have been proposed in recent years, to explore aspects of the neural semantic organization (see the “Discussion” for a brief review). In recent years, we developed an original model, which aspires to explore several important issues of semantic memory, laying emphasis on the possible organization of the neural units involved, and on synapse learning mechanisms (Cuppini et al. 2009; Ursino et al. 2009). The model assumes that objects are represented via multimodal features, encoded through a distributed representation among different cortical areas. This semantic representation is then linked with the lexical representation via recurrent synapses. Furthermore, the model implements some original aspects compared with former studies: (1) each feature is organized according to a topological map, to implement a similarity principle. This means that an object can be recognized even in the presence of a moderate distortion in some features (a property which is not implemented in classical Hopfield nets); (2) neurons in the semantic network oscillate in the gamma band. Synchronization of γ-band oscillations allows different concepts to be simultaneously restored in memory with a correct solution of the binding and segmentation problem; (3) the conceptual representation of objects and the lexical aspects are learned during training phases, in which the object features and the corresponding word are given together. After learning, a word can be evoked from its features (word production task) and features can be evoked from the corresponding word (word recognition task).

The previous model, however, exhibited some important limitations. First, all simulated objects had the same number of features. Conversely, in a real semantic memory, some concepts can contain more features than others (for instance, artifacts have usually fewer properties than living things, see Moss et al. (2007) for a clear analysis). Differences in the number of features play an essential role in semantic memory, for instance in problems like simulation of semantic deficits and category formation. Furthermore, the previous model made use of a complex “decision network” to establish whether a correct concept is recognized and the corresponding word must be active in the lexical area. This network was not physiologically motivated.

In the present work, we propose a new version of the model, in which significant improvements are incorporated. The main improvement is that a concept can now be represented by a different number of features. Moreover, different objects can have common features (thus allowing the formation of categories) and we can distinguish between words denoting a category and words denoting the individual members within a category. To achieve these objectives, we modified the learning rules adopted during the training phases, with the inclusion of inhibitory mechanisms. With these rules, a word can be recognized when all its features have been correctly evoked in the semantic network, without the use of any “ad hoc” decision network. Furthermore, synapses among features are now asymmetric, allowing distinctive features to play a greater role for object recognition than shared features.

In the following, the main aspects of the model are first presented in a qualitative way, followed by equations and parameter numerical values. Simulations on a few exemplary cases and the discussion are aimed at investigating the following points: how can a coherent and complete object representation be retrieved starting from partial or corrupted information? How can this representation be linked to lexical aspects (word forms or lemmas) of language? How can different concepts be simultaneously recalled in memory, together with the corresponding word? How can categories be represented? How can category-specific deficits be at least approximately explained?

Model description

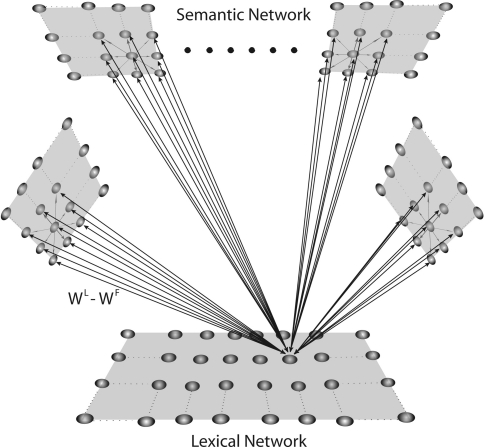
The model incorporates two networks of neurons, as illustrated in the schematic diagram of Fig. 1. These are first described in a qualitative way, and then all equations and parameters are given.

Fig. 1.

Schematic diagram describing the general structure of the network. The model presents a “semantic network” and a “lexical network”. The semantic network consists of 9 distinct Feature Areas (upper shadow squares), each composed of 20 × 20 neural oscillators. Each oscillator is connected with other oscillators in the same area via lateral excitatory and inhibitory intra-area synapses, and with oscillators in different areas via excitatory inter-area synapses. The Lexical Area consists of 20 × 20 elements (lower shadow square), whose activity is described via a sigmoidal relationship. Moreover, elements of the feature and lexical networks are linked via recurrent synapses (W^F, W^L)

The semantic network

Qualitative description

The first network, named “semantic network” is devoted to a description of objects represented as a collection of sensory-motor features. We assume that different cortical areas (both in the sensory and motor cortex as well as in other regions) are devoted to the representation of different features of an object, and that each feature is organized topologically according to a similarity principle. This means that two similar features (for instance two similar colors, or two similar motions) activate proximal neural groups in the same area of the semantic network.

Accordingly, the network is composed of N neural oscillators, subdivided into F distinct cortical areas (see Fig. 1). Each area in the model is composed of N₁xN₂ oscillators and is devoted to the representation of a single feature. An oscillator may be silent, if it does not receive enough excitation, or may oscillate in the γ-frequency band, if excited by a sufficient input. γ-band synchronization has been proposed as an important mechanism in high-level cognitive tasks, including language recognition and semantic processing (Kraut et al. 2004; Slotnick et al. 2002; Steriade 2000). In particular, the presence of oscillators in this network allows different objects to be simultaneously held in memory (i.e., it favors the solution of the binding and segmentation problem) (Ursino et al. 2009).

Previous works demonstrated that, in order to solve the segmentation problem, a network of oscillating units requires the presence of a “global separator” (Ursino et al. 2009). For this reason, the model incorporates a inhibitory unit which receives the sum of the whole excitation from the semantic network, and sends back an inhibitory signal as soon as this input exceeds a given threshold. In this way, when a single object pops out in the network, all other objects are momentarily inhibited.

During the simulation, a feature is represented by a single input localized at a specific coordinate of the network, able to trigger the oscillatory activity of the corresponding unit. We assume that this input is the result of an upstream processing stage, that extracts the main sensory-motor properties of the objects. In previous works each object was described by a fixed number of features (four features in (Cuppini et al. 2009; Ursino et al. 2009)). Conversely, we now consider that the number of features can vary from one object to the next. The way these features are extracted and represented in the sensory and motor areas is beyond the aim of the present model. The use of authentic objects with realistic features may represent a further evolution of the model.

In the present network, the maximum number of features is nine; this constraint has been imposed just to reduce the simulation computational cost.

A topological organization in each cortical area is realized assuming that each oscillator is connected with the others in the same area via lateral excitatory and inhibitory synapses (intra-area synapses). These have a Mexican hat disposition, i.e., proximal neurons excite reciprocally and inhibit more distal ones. This disposition produces an “activation bubble” in response to a single localized feature input: not only the neural oscillator representing that individual feature is activated, but also the proximal ones linked via sufficient lateral excitation. This has important consequences for object recognition: neural oscillators in proximal positions share a common fate during the learning procedure and are subject to a common synapse reinforcement. Hence, they participate to the representations of the same objects. In this way, an object can be recognized even in the presence of a moderate alteration in some of its features (similarity principle).

Throughout the following simulations, lateral intra area synapses and the topological organization will not be trained, i.e., they are assigned “a priori”. This choice is convenient to maintain a clear separation between different processes in our model (i.e. implementation of the similarity principle on one hand and implementation of object semantics on the other). Of course, topological maps can be learned via classical Hebbian mechanisms too (Hertz et al. 1991) but probably this mechanism develops in early life and precedes object semantic learning.

Besides the intra-area synapses, we also assumed the existence of excitatory long-range synapses between different cortical areas (inter-area synapses). These are subject to a training phase (see “Training the network” below) and implement the conceptual (i.e., semantic) knowledge of the object.

Model equations

In the following, each oscillator will be denoted with the subscripts ij or hk. In the present study we adopted an exemplary network with 9 areas (F = 9) and 400 neural groups per area (N₁ = N₂ = 20).

Each single oscillator consists of a feedback connection between an excitatory unit, x_ij, and an inhibitory unit, y_ij while the output of the network is the activity of all excitatory units. This is described with the following system of differential equations

1

2

where H() represents a sigmoidal activation function defined as

3

and T is a parameter that sets the central slope of the sigmoidal relationship.

The other parameters in Eqs. 1 and 2 have the following meaning: α and β are positive parameters, defining the coupling from the excitatory to the inhibitory unit, and from the inhibitory to the excitatory unit of the same neural group, respectively. In particular, α significantly influences the amplitude of oscillations. Parameter γ is the reciprocal of a time constant and affects the oscillation frequency. The self-excitation of x_ij is set to 1, to establish a scale for the synaptic weights. Similarly, the time constant of x_ij is set to 1, and represents a scale for time t. φ_x and φ_y are offset terms for the sigmoidal functions in the excitatory and inhibitory units. I_ij represents the external stimulus for the oscillator in position ij, coming from the sensory-motor processing chain which extracts features. E_ij and J_ij represent coupling terms (respectively excitatory and inhibitory) from all other oscillators in the semantic network (see Eqs. 5–8), while 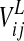is the stimulus (excitatory) coming from the lexical area (Eq. 9). z(t) represents the activity of a global inhibitor whose role is to ensure separation among the objects simultaneously present. This is described with the following algebraic equation:

4

According to Eq. 4, the global inhibitor computes the overall excitatory activity in the network, and sends back an inhibitory signal (z = 1) when this activity overcomes a given threshold (say θ_z). This inhibitory signal prevents other objects from popping out as long as a previous object is still active.

The coupling terms between elements in cortical areas, E_ij and J_ij in Eqs. 1 and 2 are computed as follows

5

6

where ij denotes the position of the postsynaptic (target) neuron, and hk the position of the presynaptic neuron, and the sums extend to all presynaptic neurons in the semantic network. The symbols 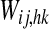represent inter-area synapses, subjects to Hebbian learning (see next paragraph), which favour synchronization. The symbols and represent lateral excitatory and inhibitory synapses among neurons in the same area. It is worth noting that all terms and 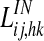with neurons ij and hk belonging to different areas are set to zero. Conversely, all terms 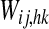, linking neurons ij and hk in the same area, are set to zero.

The Mexican hat disposition for the intra-area connections has been realized by means of two Gaussian functions, with excitation stronger but narrower than inhibition. Hence,

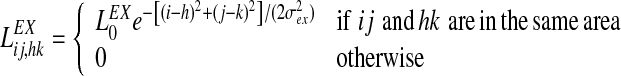7

8

where and are constant parameters, which establish the strength of lateral (excitatory and inhibitory) synapses, and and 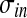determine the extension of these synapses.

Finally, the term 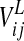coming from the lexical area is calculated as follows

9

where 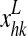represents the activity of the neuron hk in the lexical area and the symbols are the synapses from the lexical to the semantic network (which are subject to Hebbian learning, see below).

The lexical network

Qualitative description

In order to represent lexical aspects, the model includes a second layer of neurons, denoted “lexical network”. Each computational unit in this network codes for a lemma or a word form (see (Howard et al. 2006) for another example) and is associated with an individual object representation. Even in this case, the input must be considered as the result of an upstream processing stream, which recognizes the individual words from phonemes or from orthographic processing. Description of this processing stream is well beyond the aim of this model: some exempla can be found in recent works by others (see Hopfield and Brody (2001) for word recognition from phonemes, and (Farah and McClelland 1991; Hinton and Shallice 1991) for orthographic processing models).

Of course, units in this network can also be stimulated through long-range synapses coming from the semantic network; hence this network constitutes an amodal convergence zone, as hypothesized in the anterior temporal lobe (Damasio 1989; Damasio et al. 1996; Gainotti 2006; Snowden et al. 2004). Long-range synapses between the lexical and the semantic networks are subjected to Hebbian learning (see below) and may be either excitatory or inhibitory. In particular, as demonstrated below, the presence of inhibitory synapses from the semantic network to the lexical one is necessary to avoid that presentation of a member from a category evokes the word representing the overall category.

For the sake of simplicity, computational units in this network are described via a simple first-order dynamics and a non-linear sigmoid relationship. Hence, if stimulated with a constant input, these units do not oscillate but, after a transient response, reach a given steady-state activation value (but, of course, they oscillate if stimulated with an oscillating input coming from the semantic network).

Model equations

In the following each element of the lexical area will be denoted with the subscripts ij or hk (i, h = 1, 2, …, M₁; j, k = 1,2,…, M₂) and with the superscript L. In the present study we adopted M₁ = M₂ = 20. Each single element is described via the following differential equation:

10

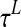is the time constant, which determines the speed of the answer to the stimulus, and 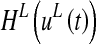is a sigmoidal function. The latter is described by the following equation:

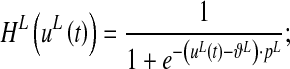11

where defines the input value at which neuron activity is half the maximum (central point) and p^L sets the slope at the central point. Equation 11 conventionally sets the maximal neuron activity at 1 (i.e., all neuron activities are normalized to the maximum).

According to the previous description, the overall input, 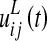, to a lexical neuron in the ij-position can be computed as follows

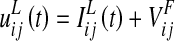12

is the input produced by an external linguistic stimulation. represents the intensity of the input due to synaptic connections from the semantic network; this synaptic input is computed as follows:

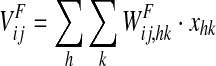13

where 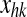represents the activity of the neuron hk in the Feature Areas (see Eq. 1) and 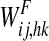the strength of synapses. These synapses may have both an excitatory and an inhibitory component (say and , respectively) which are trained in different ways (see section “synapse training: phase 2”, below). Hence, we can write

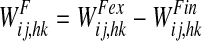14

Training the network

Training the network is subdivided in two distinct phases.

First training phase—qualitative description

During the first phase, individual objects (described by all their features) are presented to the network one by one, and inter area synapses linking the different features are learned. Recent experimental data suggest that synaptic potentiation occurs if the pre-synaptic inputs precede post-synaptic activity by 10 ms or less (Abbott and Nelson 2000; Markram et al. 1997). Accordingly, in previous works (Cuppini et al. 2009; Ursino et al. 2009) we used a time-dependent Hebbian rule, based on the correlation between the activity in the post-synaptic unit, and the activity in the pre-synaptic unit mediated over a previous 10 ms time-window. However, this rule produces a symmetric pattern of synapses. Conversely, an asymmetric pattern of synapses may be useful in case of objects with common features. Let us consider an object which shares common features with other objects, and has some distinctive features (examples will be considered in section “Results”). One can expect that distinctive features are highly important to recognize an object and evoke the remaining features (including all common ones). Conversely, one can expect that common features (shared with other objects) do not evoke distinctive features. In order to obtain this behavior, one needs asymmetrical synapses: synapses from common features to distinctive features must be weaker, whereas synapses from distinctive features to common features must be stronger. This asymmetrical pattern of synapses may be obtained assuming that a synapse reinforces whenever the postsynaptic and the presynaptic neurons are active, but weakens when the presynaptic neuron is active and the postsynaptic neuron is inhibited (homosynaptic depression). In this way, synapses from common features to distinctive features weaken at any presentation of a new object which shares the same common features.

First training phase—model equations

In this phase, the network is trained with objects but without the presence of words. We start with the rule used in previous works. This rule is then modified with a forgetting factor.

Rule (1)—In previous works (Cuppini et al. 2009; Ursino et al. 2009), we used a Hebbian rule which depends on the present value of post-synaptic activity, x_ij(t), and on the moving average of the pre-synaptic activity (say m_hk(t)) computed during the previous 10 ms. We define a moving average signal, reflecting the average activity during the previous 10 ms, as follows

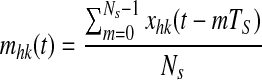15

where T_S is the sampling time (in ms), and N_S is the number of samples contained within 10 ms (i.e., Ns = 10/T_S). The synapses linking two neurons (say ij and hk) are then modified as follows during the learning phase

16’

where β_ij.hk represents a learning factor (see below).

Rule (2)—The previous rule does not consider any forgetting factor, i.e., synapses are just reinforced whenever an object is presented during the training phase. Moreover, synapses resulting from Eq. 16′. are symmetrical. In order to obtain asymmetric synapses between common and distinctive features, we assume that the Hebb rule depends on the average activity of both the post synaptic and the pre-synaptic neurons, but the post-synaptic activity is compared with a threshold, to determine whether this neuron is (on the average) in the off or in the on state. Hence, Eq. 16′ is replaced with the following equation

16’’

where λ is a threshold for comparing the post synaptic activity. The moving average of the post-synaptic activity (m_ij(t)) is computed with an equation analogous to Eq. 15. Symbols []⁺ in the right-hand member of Eq. 16″ denotes the positive part, which is used to avoid that synapses among features become negative.

In order to assign a value for the learning factor, β_ij,hk, we assumed that inter-area synapses cannot overcome a maximum saturation value. This is realized assuming that the learning factor is progressively reduced to zero when the synapse approaches its maximum saturation. Furthermore, neurons belonging to the same area cannot be linked by a long-range synapse. We have

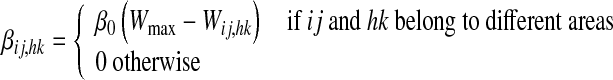17

where W_max is the maximum value allowed for any synapse, and is the maximum learning factor (i.e., the learning factor when the synapse is zero).

It is worth noticing that Eqs. 16′ and 16″ provide analogous synapses in the case of uncorrelated objects, that is objects without common features (since in this case synaptic depression never occurs); on the contrary, in case of correlated objects, the two rules furnish different pattern of synapses.

Second training phase—qualitative description

Words are associated with their object representation during a second training phase, in which the model receives a single input to the lexical network (i.e., a single word form) together with the features of a previously learned object. Synapses linking the objects with words, in both directions (i.e., from the lexical network to the semantic network and viceversa) are learned with Hebbian mechanisms too.

While synapses from words to features ( in Fig. 1) are simply excitatory and are trained on the basis of the pre and post synaptic correlation, when computing the synapses from features to words (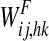 in Fig. 1) we tried to address two major requirements, that are essential for correct object recognition. First, a word must be evoked from the corresponding object representation only if all its features are simultaneously on. This corresponds to a correct solution of the binding problem. Second, a word must not be evoked if spurious features (not originally belonging to the prototypical object) are active. This second situation may occur when two or more objects, simultaneously present, are not correctly segmented, and some of their features pop up together. Hence, the second requirement corresponds to a correct solution of the segmentation problem. The second requirement also avoids that a member of a category evokes the word representing the whole category (assuming that features in a category are shared by its members).

In order to address these two requirements, in previous works we implemented a complex “decision network” (see (Cuppini et al. 2009; Ursino et al. 2009)). Conversely, in the present model we adopted a more straightforward and physiologically realistic solution. First, we assumed that, before training, all units in the semantic network send strong inhibitory synapses to units in the lexical network. Hence, activation of any feature potentially inhibits lexical units. These synapses are then progressively withdrawn during the training phase, on the basis of the correlation between activity in the feature unit and in the lexical unit. Moreover, feature units can send excitatory synapses to lexical units: these are initially set at zero and are reinforced via a Hebbian mechanism. The consequence of this choice is that, after training, a word receives inhibition by all features that do not belong to its object representation, but excitation from its own feature units. Finally, we assumed that excitatory synapses from features to words are subject to an upper saturation, i.e., the sum of all synapses reaching a lexical unit must not overcome a maximum level (say W_max). This rule warrants that, after prolonged training, the sum of synapses entering a lexical unit is constant, independently of the number of its associated features.

Using quite a sharp sigmoidal characteristic for lexical units, the previous two rules ensure that a word in the lexical network is excited if and only if all its features are simultaneously active: if even a single feature is not evoked, the word does not receive enough excitation (failure of the binding problem); if even a spurious feature pops up, the lexical unit receives excessive inhibition (failure of the segmentation problem): in both conditions it does not jump from the silent to the excited state.

Second training phase—model equations

Long-range synapses among the Lexical and the Semantic networks are trained during a second phase, in which an object is presented to the network together with its corresponding word.

Synapses from the lexical network to the semantic network (i.e., parameters in Eq. 9) are learned using an Hebbian rule similar to that used in Eqs. 16′ and 17. We can write

18

where represents the learning factor and is the averaged signal:

19

20

Conversely, synapses from the semantic network to the lexical network (i.e., parameters 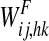in Eq. 13) include both excitatory and inhibitory contributions:

21

The excitatory portion is trained (starting from initially null values) using equations similar to 16′ and 17, but assuming that the sum of synapses entering a word must not overcome a saturation value (say 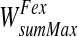). Hence

22

23

where the average activity m_hk(t) is defined as in Eq. 15, and the sum in the right-hand member of Eq. 23 is extended to all synapses from the semantic network entering the neuron ij in the lexical network.

The inhibitory synapses start from a high value (say 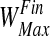) and are progressively withdrawn using an Hebbian mechanism:

24

The function “positive part” ([]⁺) is used in the right hand member of Eq. 24 to avoid that these synapses become negative (i.e., that inhibition is converted to excitation).

All equations have been numerically solved in the software environment MATLAB with the Euler integration method (step 0.2 ms) and using the parameter values reported in Table 1.

Table 1.

Model parameters used during the simulations

Wilson-Cowan oscillators
α	0.3
β	2.5
γ	0.6 ms−1
T	0.025
φx	0.7
φy	0.15
Lateral intra-area connections in features network
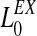
	11
σex	0.8
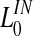
	3
σin	3.5
Global inhibitor
ϑz	1.3
Lexical area
ϑL	50
pL	1
τL	1
Hebbian rule for synapses within the semantic network (phase i)
Wmax	1
	0.25
λ	0.07
Hebbian rule for synapses between Features network and Lexical network (phase ii)
	0.125/5
	5
	0.125/2
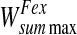
	2
	0.06
	0.125/2

Results

Objects with no semantic correlation

The first set of simulations has been performed using three distinct objects: the first (named obj1) with three features, the second (obj2) with five features, the third (obj3) with seven features. These objects have no common feature (i.e., there is no correlation between their semantic representations); hence, training inter-area synapses within the semantic network by using Eqs. 16′ or 16″ does not affect the results (since in case of uncorrelated objects the two rules provide similar patterns of synapses). The learning rate and the number of iteration steps during the training phase have been chosen so that each object could be reconstructed using more than half of its features as input (hence, obj1 could be recovered using 2/3 of its features, obj2 using 3/5 of its features and obj3 using 4/7 of its features). The position of the individual features in the semantic network, and the position of the corresponding word forms in the lexical network are given in Table 2 for each object.

Table 2.

Position of the features in the semantic network for the seven simulated objects and for the three categories (second column), and position of the corresponding word-forms in the lexical network (third column)

Object	Feature positions	Word-form position
Obj1	[6 17] [6 26] [38 16]	[5 5]
Obj2	[50 15] [50 30] [30 30] [50 45] [30 45]	[5 10]
Obj3 (dog)	[15 5] [15 35] [55 5] [25 5] [45 55] [5 55] [25 55]	[15 5]
Obj4 (cat)	[15 5] [30 30] [55 13] [25 5] [45 55] [50 30] [25 55]	[15 10]
Obj5 (cattle)	[15 5] [15 45] [25 25] [25 15] [55 55] [45 25] [25 55]	[3 3]
Obj6 (goat)	[15 5] [15 55] [35 35] [25 15] [55 55] [55 35] [25 55]	[7 7]
Obj7	[10 15] [10 30] [30 55] [50 5] [5 45]	[5 15]
Ctg1 (pet)	[15 5] [25 5] [45 55] [25 55]	[15 15]
Ctg2 (ruminant)	[15 5] [25 15] [55 55] [25 55]	[13 13]
Ctg3 (animal)	[15 5] [25 55]	[11 11]

The first object has three features, the second five features, the third seven features. The fourth object has seven features, four of them shared with Obj3 (positions of the four features shared by Obj3 and Obj4 are indicated in italics). These four features represent the category Ctg1 (“pet”). Obj5 and Obj6 have seven features, four in common (in italics), which represent a category Ctg2 (“ruminant”). Finally, Obj3, Obj4, Obj5 and Obj6 have two shared features (upper category, Ctg3, “animal”). The last object is constituted by five features, most located in different regions of space compared with Obj2

An example of the synapses entering into one neural unit in the semantic network, and of synapses entering into one neural unit in the lexical network are shown in Fig. 2. These have been obtained using Eqs. 16–24 described above.

Fig. 2.

An example of the synapses which connect feature and lexical units in the semantic network after training. The synapses refer to Obj2 described in Table 2, with five features. Each panel represents a matrix of synapses targeting into a post synaptic neuron. The color in each figure represents the strength of the synapses which reach a given post-synaptic neuron, coming from different pre-synaptic neurons. The position of the post-synaptic neuron is marked with a grey circle. Arrows have been included for clarity. The left upper panel represents the matrix W_3030,hk in Eqs. 5 and 6, i.e., the strength of synapses which reach a feature at position [30 30] from the other four features. The right upper panel represents the matrix 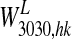in Eq. 9, i.e., the strength of synapses which reach the feature at position [30 30] from the lexical word (i.e., from the word form at position [5 10]). The bottom panel represent the matrix in Eq. 13, i.e., the strength of synapses which reach the word-form at position [5 10] in the lexical area originating from the five features in the semantic area. It is worth noting that synapses in the semantic network originate not only from neurons coding for the “exact” feature of an object, but also from proximal neurons which constitute an “activation bubble”. This implements a similarity principle

After training, the three objects and the related words can be simultaneously restored in memory, and oscillate in time division, even if objects are lacking some properties or if some properties are moderately modified compared with the original version.

A first example is shown in Fig. 3, where some properties of the three objects (in a number sufficient to recover the overall object representation) are given to the semantic network (object recognition task). In particular, in this example two objects lack one property, while the third object receives all properties but one is shifted compared with the exact one. After a transient period, the network can correctly segment the three objects, recovers all lacking properties and the correct word forms are activated in the lexical area.

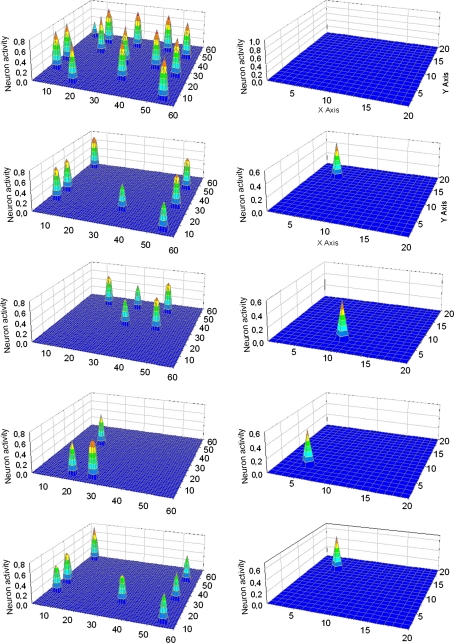
Fig. 3.

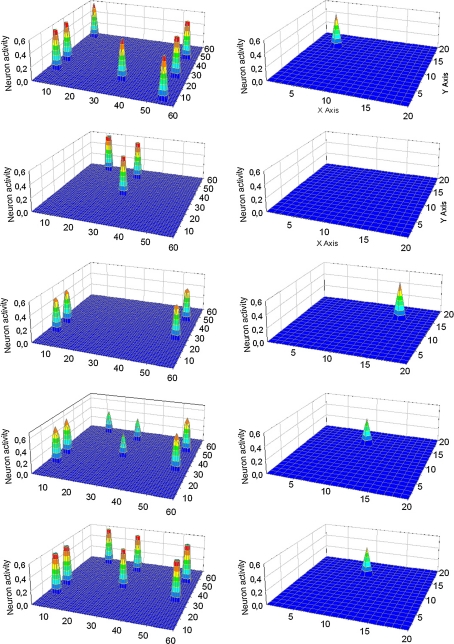
Simulation of an “object recognition task” in which properties of three objects are given simultaneously to the network. In particular, Obj1 received 2/3 of its features, Obj3 received 6/7 of its features while Obj2 received all its five features, but one of them was shifted by one position compared with the original one. The five lines represent activity in the semantic network (left panels) and in the lexical network (right panels) at steps 71, 227, 262, 284 and 304 of the simulation (duration of each step: 0.2 ms). At step 71 (first line) all features appear simultaneously in the semantic network, and no word is detected in the lexical network. Starting from step 227, the three objects are correctly reconstructed and segmented in the semantic network, and the corresponding words become active in the lexical network

The previous example was concerned with a three-object recognition task. Figure 4 shows a second example, in which the network receives two words as inputs in the lexical area, together with the conceptual representation of a third object in the semantic area (two-word recognition and one object recognition task). Results show that the three semantic representations oscillate in time division in the semantic area (one directly stimulated by the external inputs, the other two evoked by the corresponding words). It is worth noting that, in a short interval when no representation is present in the semantic network (see, for instance, step 60 in Fig. 4), the two external words are coactive in the lexical area. However, as soon as a representation appears in the semantic network, all words that do not match this semantic representation are inhibited and just the correct word remains active.

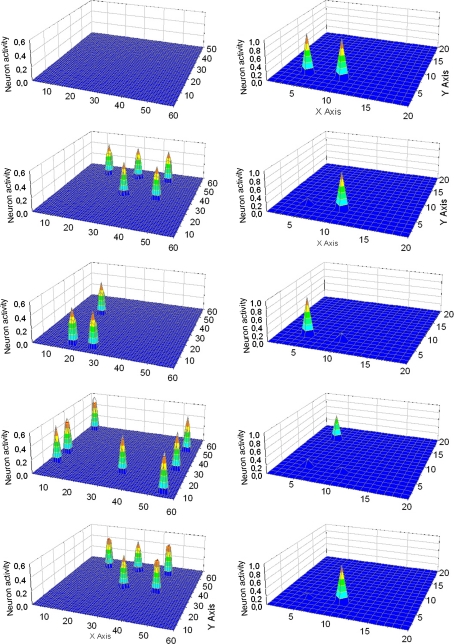
Fig. 4.

Simulation of a “word recognition task” and of an “object recognition task” performed simultaneously. In particular, 6/7 features of Obj3 were given to the semantic network, while the two words representing Obj1 and Obj2 were given to the lexical network. The five lines represent activity in the semantic network (left panels) and in the lexical network (right panels) at steps 60, 99, 122, 144 and 166 of the simulation (duration of each step: 0.2 ms). At step 60 (first line) when no feature is present in the semantic network, the two externally given words are simultaneously active in the lexical network. Subsequently, objects and words are correctly segmented. It is worth noting that, as soon as a conceptual representation appears in the semantic network, all other words are inhibited in the lexical network

The effect of noise

A further set of simulations has been carried out to test how the algorithm performs in the presence of noise superimposed to the features. Different levels of noise were used, and the capacity of the model to achieve correct object reconstruction tested by computing the output of the lexical net. Results show that, during the first simulation steps after input presentation, the model exhibits an excellent capacity to reconstruct objects and to evoke the corresponding words even in the presence of significant noise; however, if simulation is protracted with time, the different features of the same object tends to lose their synchronism, until the object is progressively lost. A summary is reported in Fig. 5, with reference to the reconstruction of an object (Obj2) with five properties (four were given as input, the fifth was lacking and reconstructed). The capacity to reconstruct the object rapidly deteriorates after 150–200 simulations steps. Similar results were obtained with the other objects. The reason is that the frequency of the Wilson Cowan oscillators depends on the input, hence, in the presence of noise, oscillators exhibit a different frequency. This difference engenders a progressive loss of synchronization.

Fig. 5.

Effect of noise (white Gaussian, zero mean value, assigned standard deviation) superimposed on the input features, at different steps after the presentation of the inputs. The panel represents the average response in the lexical network, mediated over 10 random trials, during an object recognition task in which four features of Obj2 are given to semantic network and a fifth feature is lacking. The abscissa represent the percentage of noise compared with the input. The object is detected with good accuracy during the first steps, despite the presence of significant noise. However, within 200 steps, the object is lost as a consequence of desynchronization

Objects with semantic correlation and the formation of categories

The previous examples were concerned with objects with no semantic overlapping. Let us now consider the case of two objects having a significant semantic correlation. In order to simulate this case, we trained two objects (say Obj3 and Obj4) with seven features each. Moreover, the two objects share four features (named “common features” or “shared features” in the following) and have three different features each (named “distinctive features” in the following). We can think that the two objects are members of the same category, and that the four common features represent this category. During the first training phase the conceptual object representation is first learned (using either Eqs. 16′ or 16″). During the second training phase, two distinct words are associated to Obj3 and Obj4 (say “cat” and “dog” just to fix our ideas), while a third word is associated to the category represented by the four common features (say “pet”).

In the case of correlated objects the rules (16′) and (16″) furnish different patterns of synapses. Hence, results obtained with the two rules will be considered separately.

First, let us consider the case in which Eq. 16′ is used to train the semantic network. Synapses linking two features of an object are reinforced whenever the object is presented, until a maximum saturation is reached. This rule does not consider a forgetting factor. Hence, the order of object presentation is not relevant but only the duration of the presentation affects the final value of synapses. After training the semantic network with Obj3 and Obj4, the four features denoting the common category are reciprocally linked with stronger synapses, whereas synapses which involve a distinctive feature are weaker. The reason is that distinctive features have been seen less frequently than common features, hence these synapses have been learned for a shorter period. This same effect occurs when using Eq. 16″.

However, the main drawback from using Eq. 16′ is that synapses from a “common feature” to a “distinctive feature” have the same strength as synapses from a “distinctive feature” to a “common feature” (since this rule provide symmetrical synapses). This signifies that, if the learning period is too long, the common features become able to evoke the distinctive features (in practice, if the word “pet” is given to the network, a hybrid object is evoked in the semantic network including all ten properties of “cat” and “dog” together). This undesired behavior can be avoided by reducing the training period (or the learning rate) but in this case providing all distinctive features to the semantic network (for instance the distinctive features of the cat) does not evoke the common features (i.e., we cannot reconstruct the overall conceptual representation using distinctive features only).

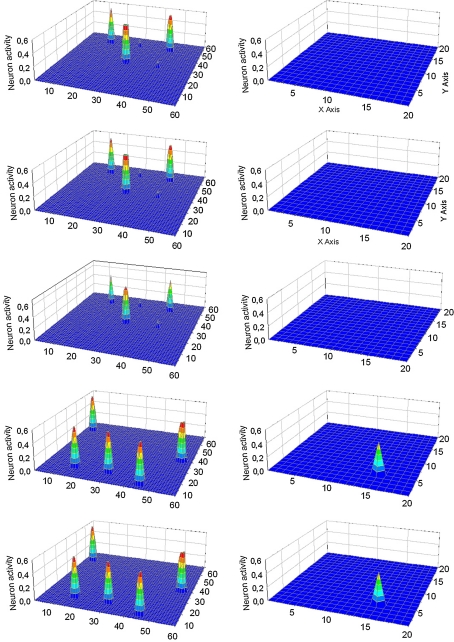
A better behavior (which we claim closer to reality) can be obtained if Eq. 16″ is used to train the semantic network. This rule, in fact, considers a “forgetting factor” (homosynaptic depression) which realizes asymmetrical synapses among features, making the synapses from common features to distinctive features much weaker than the synapses from distinctive features to common features. An example of the asymmetric synapses obtained using Eq. 16″ is illustrated in Fig. 6. In this case, the two objects have been presented alternately during the training phase (eight presentations of 100 steps for each object) to make the effect of the forgetting factor almost equivalent.

Fig. 6.

An example of differences in the synaptic strength within the semantic network, in case of shared and distinctive features. These synapses have been obtained by training the network with Obj3 and Obj4, which share four features, and using both homosynaptic potentiation and homosynaptic depression. The left panel represents synapses entering a common feature at position [15 5] (i.e., the figure represents the content of the matrix W_155,hk in Eqs. 5 and 6). The right panel represents synapses entering a distinctive feature of Obj4 at position [30 30] (i.e., the figure represents the content of the matrix W_3030,hk in Eqs. 5 and 6). The figure content can be explained as follows: (1) a common feature (left panel) receives synapses from all features in Obj3 and Obj4. The synapses coming from the other three common features are stronger (red color) than those coming from the six distinctive features (yellow color), since common features are more often encountered during training; ii) a distinctive feature (right panel) receive synapses only from the other six features of the same object (Obj4). Synapses from the distinctive features have the same strength as in the left panel (yellow color), whereas synapses from common to distinctive features are weaker (cyan color) as a consequence of depression (see text for details)

Since this pattern of synapses provides better results, all following simulations have been performed with it.

A first set of simulations concerns the possibility to recover the entire information (conceptual meaning and words) from a partial cue during object-recognition and word-recognition tasks. A further set concerns priming. Finally, we will describe a last set of simulations, including two additional objects (“cattle” and “goat”) to have a simple taxonomy of categories (“animal”, “pet” and “ruminant”). Results can be summarized as follows.

Object recognition tasks

1. If three common features are given to the semantic network, the model recovers the fourth common feature; consequently, the correct word denoting a category (“pet”) appears in the lexical area. Hence, category information remains confined and does not spreads toward distinctive features.

2. If all three distinctive features (for instance those of cat) are given to the semantic network, this information spreads toward the common features, and all seven features of the cat are activated, together with the corresponding word. Information does not spread toward the distinctive features of “dog”.

3. The individual object can also be evoked by giving two distinctive features and one common feature. In this condition too, all seven features are evoked together with the correct word, without spreading information toward other members of the same category.

4. If the ten features of “cat” and “dog” are given simultaneously, the network can segment the two objects correctly and evoke the correct words in the lexical area (despite the presence of four common features). However, between each word appearance, there is a transient period in which a few features appear isolated. These features, however, do not evoke any word.

Word recognition tasks

1. If a word denoting a category member (“dog” or “cat”) is given to the lexical network, the seven features representing its conceptual meaning oscillate synchronously in the semantic network, without spreading to features of other category members.

2. If the word denoting the category (“pet”) is given to the lexical network, the four common features oscillate synchronously in the semantic network, without spreading to the other features.

3. If the two words (“dog” and “cat”) are given simultaneously, the behavior of the semantic network is a little strange. The four common features oscillate in synchronism, and the word “pet” appears in the lexical network. Hence, the model seems able to generalize from two words to a category. However, the three distinctive features of cat, and the three distinctive features of dog oscillate independently, without a synchronization with the remaining four features. The behavior is illustrated in Fig. 7.

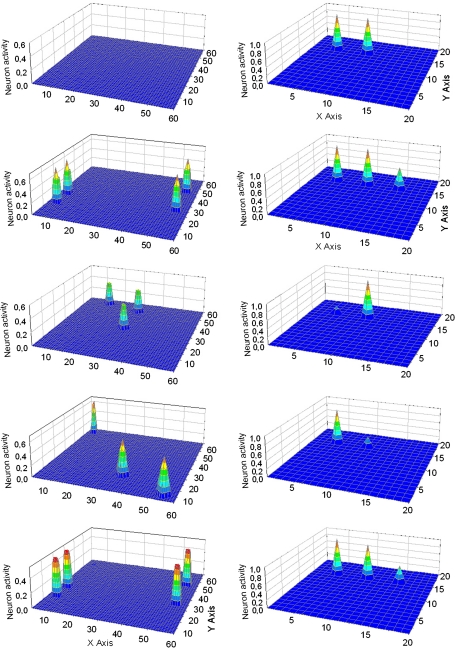
Fig. 7.

Simulation of a “word recognition task”. Two words, with four common features (i.e., words denoting Obj3 and Obj4) are simultaneously given to the lexical network. In this case the subject must recognize two words in the same category. The five lines represent activity in the semantic network (left panels) and in the lexical network (right panels) at steps 41, 60, 81, 99 and 119 of the simulation (duration of each step: 0.2 ms). As evident from the figure, the two words initially evoke the four shared properties in the semantic network and consequently the word denoting the category is activated in the lexical area (second line). Hence, the network can generalize from the two members of the category to the category name. The three distinctive features of the two objects oscillate in time division (third and fourth lines) causing the momentarily inhibition of the alternative word. Hence, the three words (two members and their category) oscillate in time division in the gamma range

Priming

The model can also be used to study the effect of an object (the prime) on recognition of a second correlated object (the target). To this end, the two objects, the two words or one object and the other word are given to the network, with a small interval between them, to study the effect on recognition. The recognition time is then compared with the time required by the presentation of the second object alone.

A first simulation was performed by providing all features of a first object (say cat) in the semantic area; after 200 steps (40 ms), when the model is in a stable oscillatory condition, the features have been replaced with the features of “dog”. An example of the obtained results is shown in Fig. 8. The interesting aspect is that the second object is not immediately recognized. The semantic network exhibits a transient period, in which the three new features initially appear, followed by the four common features (hence, the category “pet” appears in the lexical area). Only after this transient period, the seven features of “dog” are synchronized in the semantic network, and the word “dog” is activated in the lexical area. Hence, it seems that the semantic network first recognizes the category and requires approximately 30 ms (the duration of a gamma cycle) to move to a new member. This 30 ms delay does not occur if the seven features are given to the network without the previous presentation of a prime.

Fig. 8.

Simulation of a negative priming. The seven features of Obj3 are initially given to the semantic network, causing activation of the corresponding word in the lexical network. Then, at step 200, the seven features of Obj3 are replaced with the seven features of Obj4 (four are shared among the two objects). The five lines represent activity in the semantic network (left panels) and in the lexical network (right panels) at steps 197, 241, 295, 341 and 401 of the simulation (duration of each step: 0.2 ms). Initially the three distinctive properties (step 241) and the four shared properties (step 295) oscillate out of phase, and the word denoting the common category is produced. Subsequently (from step 341) the seven properties of Obj4 are correctly bound and the corresponding word produced in the lexical area. This corresponds to a delay of approximately 30 ms

Conversely, if the first word (the prime) is given in the lexical area and the second word is given after 200 steps, we cannot observe any priming effect. Similarly, no evident priming effect occurs if the first word (prime) is initially given, followed by the semantic meaning of the second object (in both cases, the prime was removed from the input at step 200 and the second input immediately given)

Finally, a very strong negative priming is seen when the semantic representation of a first object is initially given, followed (at step 200) by the word denoting the second concept. In this case, the three distinctive properties of the second object do not synchronize with the four common features, and only the category emerges (i.e., the four common features are synchronized). The second object, however, can be correctly reconstructed if the frequency of gamma oscillations is increased (i.e., parameter γ in Eq. 2 is raised from 0.6 to 0.8 ms⁻¹).

The previous results, taken together, suggest that the use of semantic information as a prime induces a delay in the recognition of a second correlated object and, even more evident, on recognition of a second correlated word. This delay can be ascribed to the difficulty of the semantic network to synchronize all features of the new object; indeed, there is some tendency of the network to synchronize only common features of the category. Conversely, in the present network the use of a word as a prime has no relevant effect on recognition of a second correlated word or on recognition of a second correlated object. These results will be commented in section “Discussion”.

A taxonomy of categories

In the previous exempla we used just a small number of objects and categories (four objects and just one category). An important problem is whether the network can manage a taxonomy of categories and exploit similarity when retrieving words. To test this condition, we incorporated two new objects in the network (Obj5 and Obj6, see Table 2). These, together with the previous objects Obj3 and Obj4, now generate a simple taxonomy: a category (say “animal”) now includes four objects (say dog, cat, cattle and goat) with two shared features; another two categories (say “pet” and “ruminant”), included within “animal”, have two objects each with four shared features. All objects were first trained separately in the semantic network, then objects and categories were associated with the corresponding word-forms in the lexical network (see Table 2).

Simulations show that the model can correctly discriminate between these categories and individual members, and correctly evoke the corresponding words. In particular, a word in the lexical network evokes the correct conceptual representation in the semantic network, both when the word represents a member and when it represents a category. For instance, the word “goat” evokes all its seven features; the word “ruminant” evokes only the four features common to cattle and goat; the word “animal” evokes just the two features shared by dog, cat, cattle and goat. Similarly, providing a number of features to the semantic net causes the correct object reconstruction and evokes the corresponding word. In particular, neural activity does not spread from a category to an individual member, if no distinctive feature of the member is provided as input to the model. Conversely, a category name can help reconstruction of a member in the presence of some more specific cues. An example is shown in Fig. 9, where the word “ruminant” is given to the lexical net together with some specific features of goat to the semantic net (let us image, for instance, the feature beard). The overall goat representation is reconstructed, and so the word “goat” appears in the lexical net together with the word “ruminant”. It is worth noting that the individual feature alone (beard) would not be able to evoke the overall member representation (“goat”) if not associated with the category name (“ruminant”).

Fig. 9.

Simulation of an object recognition task helped by a category word. One feature of Obj6 (for instance the feature “beard”) is given to the semantic network, while the word denoting its category (“ruminant”) is given to the lexical network. The overall representation of Obj6 is restored in the semantic network and the word (“goat”) correctly evoked. The three lines represent activity in the semantic network (left panels) and in the lexical network (right panels) at steps 70, 71, 73 and 76 of the simulation (duration of each step: 0.2 ms)

Simulation of semantic deficits

A last set of simulations has been performed to study whether the behavior of patients with category-specific lexical deficits (i.e., patients unable to recognize certain categories of objects) can be mimicked assuming a synaptic damage in certain localized regions of the semantic network. To this end, one may suppose that only synapses in certain feature areas are weakened (for instance, as a consequence of a local lesion) thus resulting in a deficit for those concepts which make an intensive use of these areas.

In order to simulate category-specific deficits, we trained the network with two distinct objects (Obj2 and Obj7, see Table 2) each with five features and each trained for the same number of iterations (we assumed that the number of features and the training period are the same, so that the capacity of the network to recognize objects depends on the lesion only, and is not affected by differences in semantic complexity). Moreover, the two objects have no common feature. A significant difference between the two objects is in the location of features: the first has four features in a region of the semantic network defined as follows; S: = {x_ij with 20 ≤ i ≤ 60, 20 ≤ j ≤ 60}. This regions includes four areas. Conversely, the second object has just one feature in this region (see Fig. 10 upper panel). To simulate semantic deficits, we assumed that a given percentage of synapses emerging from neurons in the region S are damaged in a random fashion (i.e., they have been randomly set at zero). The damage interests all synapses, both lateral intra-area synapses and long-range inter-area synapses, as well as synapses directed to the lexical area. This may reflect a loss of neurons in the damaged region. For each level of synapse damage (from 0 to 50%) we repeated 10 simulations for each object presentation, and computed the average response of the corresponding word in the lexical area. Results (Fig. 10, bottom panel) show that, by increasing the percentage of damaged synapses, the network progressively looses the capacity to recognize the first object (an object is recognized when all its features are synchronized, and the corresponding word appears in the lexical area). When 30% of synapses are damaged, only a small activity in the lexical area appears after presentation of the first object. Conversely, response to the second object in the lexical area is just moderately affected even when 50% of synapses are damaged in region S.

Fig. 10.

Simulation of a patient with selective category impairment. Two objects (Obj2 and Obj7), with five features each, are used during the trials (upper panels). A given percentage of synapses originating from the shaded regions are set to zero in a random fashion to simulate a localized neurological deficit. The bottom panel represents the average response in the lexical network, mediated over 10 random trials, during an object recognition task using Obj2 or Obj7, as a function of the percentage of damaged synapses. The object with four features in the damaged area is almost completely lost with a percentage of damaged synapses as high as 30%, whereas the object with just one feature in the damaged area is detected with good accuracy despite the damage

An example of simulation results, concerning the presentation of the first object, followed by the presentation of the second object (assuming 30% of damage in the region S) is illustrated in Fig. 11. Simulation results show that the first object is not correctly reconstructed (its features can hardly pop out), whereas the second can be reconstructed easily, despite the presence of one feature in the damaged region.

Fig. 11.

An example of simulation with 30% of damaged synapses, in accordance with Fig. 10. During this trial, the five features of Obj2 were initially given to the semantic networks: Then, at step 250, these were replaced with the five features of Obj7. The five lines represent activity in the semantic network (left panels) and in the lexical network (right panels) at steps 127, 188, 248, 310 and 372 of the simulation (duration of each step: 0.2 ms). The network fails to recover two features of Obj2, as a consequence of the synaptic damage, and so the corresponding word is not evoked in the lexical network. Conversely, all five features of Obj7 are bound, and the word is evoked in the lexical network

Discussion

The present study describes a new model of the semantic-lexical system, based on connectionist neural networks, and justifies the main choices via a few schematic exempla. Of course, this is not the first model that investigates neural semantic organization. Two main classes of connectionist models have been applied in past years: multilayered networks based on backpropagation, and attractor networks (such as the Hopfield net). Most of them are aimed at analyzing how the statistical relationships between features and categories can be incorporated in a semantic memory model, to explore the consequences for language processing (for instance, semantic priming) and to simulate semantic deficits through damages in network connection weights.

Among the others, Farah and McClelland (1991) developed a model in which differences between living and non-living things were simulated using a different amount of functional and perceptual features for each concept. The model was able to explain selective category impairment by removing some features. Hinton and Shallice (1991) and Plaut and Shallice (1993) used a backpropagation network with a feedforward from orthography to semantics, and a feedback loop from semantics to hidden units. The damaged network exhibits behavior which emulates several phenomena found in deep dyslexia. Randall et al. (2004) trained a feed-forward three-layer back-propagation model to map words from semantic features, and studied the role of shared and distinctive features.

Alternative models used attractor networks to simulate phenomena such as semantic priming in normal subject and in schizophrenia (Siekmeier and Hoffman 2002) or to study the type of errors made by dyslexic patients (Cree et al. 2006; McLeod et al. 2000; McRae 2004; McRae et al. 1997) and by patients with dementia (Gonnerman et al. 1997). In these networks, semantic memory consists of a number of nodes representing features. Features belonging to the same concept are mutually connected according to past experience (using Hebbian mechanisms to train synapses). Activity thus spreads from one feature to another, and a concept is represented by a stable set of features. These models demonstrate that attractor basins are crucial to understand phenomena such as priming, deep dyslexia and ambiguity resolution (Kawamoto 1993).

Further models tried to integrate semantic and lexical aspects to simulate word retrieval and speech production from concepts (Dell 1986; Dell et al. 1997; Goldrick and Rapp 2002; Levelt et al. 1999; McRae et al. 1997). These models generally assume separate semantic and lexical networks. Semantic representation is distributed over different units (Dell 1986; Dell et al. 1997)) while lexical units generally represent lemma or lexical word forms. Howard et al. (2006) recently developed a model consisting of a feed forward connection from semantic units to lexical units, and a competition mechanism between lexical units. An additional learning mechanism was included to reinforce synapses form semantic to lexical units. With this model, the authors were able to simulate long lasting inhibition priming. Rogers et al. (2004) developed a model in which perceptual, linguistic and motor representations communicate via an heteromodal region (probably located in the anterior temporal cortex), which encodes semantic aspects and reminds the “convergence zone” hypothesized by Damasio (1996). The model has been used to differentiate between semantic dementia (which causes a generalized semantic impairment) and other pathologies characterized by category-specific deficits (Lambon Ralph et al. 2007). Mikkulainen (1993, 1997) developed a model consisting of two self-organizing maps (one for lexical symbols and the other for word meaning) and of associative connections between them based on Hebbian learning. The latter model is perhaps that more similar to the model presented in this work.

The previous partial review underlines the increasing impact that computational models are playing in the study of semantic memory and word comprehension.

Despite the presence of previous contributions, we claim the present study introduces several important new aspects which distinguish our model from previous attempts, and makes it particularly suitable to interact with modern conceptual theories of semantic memory. Indeed, the philosophy of the model is substantially similar to that used in autoassociative networks, but is original for what concerns several aspects:

1. Autoassociation does not occur among all elements in the semantic network, but only between elements in distinct areas. Each area, in turn, is devoted to the representation of a distinct feature of the object. Although we did not use real objects in the present simulation, model implicitly assumes that the conceptual meaning of objects is grounded on the different sensory modalities, spreads over different brain regions (visual, auditory, tactile, action areas, emotional areas and so on) and recreates the same multimodal representation which was originally present during object perception and action. This model formulation agrees with the so called “emobodied cognition” or “grounded cognition” viewpoint (Barsalou 2008; Borghi and Cimatti 2010; Gibbs 2003). This organization of conceptual knowledge is supported by several recent results obtained with neuroimaging techniques, some reviewed in (Barsalou 2008; Martin 2007; Martin and Chao 2001). For instance, dealing with information on food or smell causes activation of gustatory and olfactory areas, respectively (Gonzalez et al. 2006; Simmons et al. 2005). Regions of the posterior temporal cortex involved in object representation become active during conceptual processing of pictures and words, as well as during auditory sentence comprehension (Davis and Johnsrude 2003; Giraud et al. 2004; Rodd et al. 2005). Reading action words activates regions in the premotor cortex that are active when the subject perform the corresponding movement (Hauk et al. 2004).

   This model organization is also indirectly supported by anatomical studies performed in the rodent hippocampus. Burvell’s et al. (Furtak et al. 2007; Kerr et al. 2007) report that cortical afferents to the hippocampus (and efferent from the hippocampus) separately convey complementary visual and spatial, polymodal sensory and emotional information. All this information is then linked in the hippocampus to realize episodic memory and participate to other cognitive processes. Further studies in the hippocampus support the representation of abstracts and physical quantities assumed at the basis of our model. Of particular interest is the research by Teyler et al. (Teyler and DiScenna 1986; Teyler and Rudy 2007). These authors proposed the “indexing theory” according to which the hippocampus is anatomically positioned to integrate information coming from the neocortex and other subcortical areas, and is functionally designed to capture information generated by the individual features of behavioral episodes. Although devoted to episodic memory instead of semantic memory, the mentioned works support several aspects of the organization of our model.

2. Within individual areas of the semantic network, we used a topological structure, in order to implement a similarity principle. In this way, while features of the same objects tend to create reciprocal links, according to classic autoassociation memories, neurons coding for the same feature within the same area (for instance, color, shape, motion, etc.) tends to interact with a competitive mechanism (similar to that used in Kohonen maps). The idea that features may be topologically organized has been suggested by Barsalou et al. in their conceptual model (named “Conceptual Topography Theory”) (Barsalou et al. 2003) and finds several important supports, not only for what concerns elementary features, but also more abstract ones [see (Pulvermuller 2005; Thivierge and Marcus 2007)]. A consequence is that similar features may be involved in the representation of the same object and that an object can be recognized even in the presence of moderate changes in some of its features (for instance, the color of an object can be modified within a certain range in the topological map of colors, without jeopardizing recognition). It is worth noting that, in the present model, we assumed that all features exhibit this topological representation. Of course, forthcoming versions of the model may consider that just some features are topologically organized, while others lack this organization. This can be implemented in a straightforward way by eliminating lateral synapses within some feature areas.

3. Synapses which link different features in the semantic network are asymmetrical [whereas a typical property of most autoassociative networks is the symmetry of synapses (Hertz et al. 1991)]. Asymmetrical synapses play a pivotal role in our model, to characterize the role of distinctive features from that of shared features. This distinction is obtained using a modified learning rule, in which we incorporate both homosynaptic potentiation and homosynaptic depression, not including heterosynaptic depression (whereas both homosynaptic and heterosynaptic depression are included in classic autoassociative nets). As a consequence of this choice, distinctive features send stronger synapses to shared features (see Fig. 6), thus evoking the complete object representation; conversely, a shared feature sends weak synapses to distinctive features, thus leading to the restoration of the semantic content of a given category, without evoking individual members of that category. The idea that distinctive features play an essential role in object recognition, and that the presence of shared features establishes the category membership, has been stressed by Humphrey and Forde in their conceptual model named “Hierarchical Interference Theory” and by Tyler et al. in the “Conceptual Structure Account”. We think the auto-associative network proposed in this work may represent a first step toward the numerical implementation of several ideas contained in (Humphreys and Forde 2001; Tyler and Moss 2001). Although this mechanism has been tested here only on very simple schematic objects, and a very limited taxonomy of categories, it is very promising to build more complex self-trained semantic networks which can deal with multiple categories altogether.

   Furthermore, the learning rules implemented in this work to train the semantic net may be exploited, in future works, not only to arrive at a distinction between categories and individual members of a category, but also to differentiate between features with greater and smaller saliency. Indeed, in the present work we trained all objects with the complete set of features: the only way to modify the saliency of a feature for object recognition was to assume that some features are shared with other objects, hence some synapses are depotentiated during presentation of other elements in the same category. A different conditions for training may assume that some features are lacking during the training phase, i.e., that some features occur more frequently than others. Using the present rules, this kind of training would lead to a more complex object semantics, in which features have a different saliency on the basis of their frequency. A further question is that word meaning may not be a fixed content, but different features may be activated depending on the context (Barsalou 1982). This opens new perspectives for future studies.

4. The model assumes two distinct networks to memorize the semantic content of an object and its word-form. This division has a long tradition in the cognitive literature (Anderson 1983; Collins and Loftus 1975), and is further supported by results on bilingual or multilingual subjects (who exhibit a single semantic store, but different word-forms in different languages (Kroll and Stewart 1994; Potter et al. 1984)).

   Further learning rules have been adopted to train the relationships between the semantic and the lexical nets. Here, two fundamental problems had to be solved: first, a word must be able to evoke its semantic content, which spreads over multiple areas according to the grounded cognition assumption (word recognition task); second, an object must be recognized, and the corresponding word produced (word production task) avoiding confusion with other objects and avoiding the inclusion of uncorrect features (features which do not belong to the object).

   The solution of the first problem was quite easy, requiring just the presence of excitatory synapses which spread out from the lexical items to target the overall semantic content (i.e., the correct features). This can be realized using Hebbian potentiation.

   Conversely, the second problem required a more sophisticate learning strategy. The main difficulty was that different objects can contain a different number of features, and an object cannot contain a spurious feature (i.e., a feature which does not belong to its conceptual description). The solution that we propose is that all correct features must be bound together in the semantic net (i.e., the object must be completely reconstructed in the semantic net) without any spurious feature, before its identification can occur in the lexical network. This is realized using a rule which normalizes the excitatory synapses entering into a lexical item, and assuming the presence of inhibitory mechanisms from spurious features. In this regard, the lexical network represents a kind of multimodal “convergence zone”, where all embodied information converges. This strategy works adequately, at least with reference to the simple exempla we present here. In particular, it allows words to be used to represent a category or to denote individual members of that category, still avoiding confusion.

5. A further peculiarity of the present model, compared with previous autoassociative nets, is the presence of gamma-band synchronization. According to a celebrated hypothesis (Singer 1993; von der Malsburg and Schneider 1986) rhythmic synchronization in the gamma-band would permit the solution of the binding and segmentation problem, i.e., it allows different objects to be simultaneously held in memory avoiding misinterpretations. Experimental evidence supporting this hypothesis for object recognition has been given, not only for what concerns bottom-up processing but also internally driven representations (Bertrand and Tallon-Baudry 2000). Furthermore, gamma-band synchronization agrees with recent temporal rules of Hebbian potentiation (Abbott and Nelson 2000; Markram et al. 1997).

   The presence of oscillations in gamma-band is essential to segment multiple objects simultaneously in the network. This is shown, for instance, in the simulation depicted in Fig. 3, where three objects, with incomplete inputs, are given simultaneously to the network and correctly separated, and in Fig. 4 where an object representation and two words are used all together. Without gamma band oscillations, these segmentations would not be possible, i.e., the model would have no possibility to distinguish features of one object from features of another concurrent object. Actually, the present model can manage different objects (and the corresponding word-forms) simultaneously, a property that can be very important in language processing (for instance, when several words must be held in memory to recognize the meaning of a sentence). This aspect shares some ideas with the “Neural Hybrid Model of semantic Object Memory” by Hart et al. (2007), Kraut et al. (2003, 2004).

Of course, if one assumes that objects are always given separately (or have been correctly segmented in a previous computational layer) a network similar to the present but without oscillations could be used, with a significant simplification in computation time.

In the present simulations, binding is realized in the γ-band only. However, as summarized in Buzsàki (2006), Singer (2009) binding by oscillations may involve a much broader frequency range, from <2 Hz (thetha) to >40 Hz (gamma, ultra gamma and ripples). For instance, high-frequency network oscillations are well documented in the hippocampus (Nguyen et al. 2009; Ylinen et al. 1995) where they may facilitate the transfer of stored information to the cortex (Ylinen et al. 1995). Hence, it is of value to discuss whether the time scale of the present model can be modified by acting on some parameters, to mimic the presence of different brain rhythms.

A significant change in the oscillation frequency can be achieved in our model by acting on parameter γ (Eq. 2), which establishes the time constant of the inhibitory mechanisms. In a previous work (Ursino et al. 2009) we have shown that modulation of this parameter in the range 0.3–0.5 (which approximately corresponds to a frequency change between 30 and 45 Hz) is essential to allow the solution of segmentation problems with different complexity: a slower frequency is necessary to segment many objects with incomplete information, whereas a higher frequency is better in case of simpler tasks. Such modulation can occur in vivo trough D4 dopamine, or cholinergic (acetylcholine and muscarinic) receptors (Hentschke et al. 2007; Kuznetsova and Deth 2008; Rodriguez et al. 2004). A much slower oscillation, as in alpha and theta rhythms, can be realized by modifying the time constant of the excitatory unit too (Eq. 1) which was arbitrarily set at one in the present study.

Unfortunately, the Wilson Cowan oscillator is not flexible enough to mimic the presence of multiple rhythms (such as theta + gamma, which play an essential role to produce a precession of states in a given order (Lisman and Redish 2009), or alpha + gamma often observed in the occipital cortex). To simulate these “multiple rhythms” one needs a more complex neural mass model which incorporates connections among different excitatory and inhibitory sub-populations with various synaptic kinetics [see, for instance, (Ursino et al. 2010)]. The use of these models for object storage, binding and segmentation may represent an interesting challenge for future studies.

As a consequence of the previous assumptions, the model permits several aspects of interest for cognitive neuroscience to be simulated: these include the occurrence of neurological deficits with category selective impairment, and the effect of a previous concept (a prime) on network dynamics.

Of course, the formation of semantic-lexical associations could be obtained using much simpler models than that proposed here, like those based on feature vector templates, in which a word is represented by a template. However, these techniques are not based on neural computation but on more traditional artificial intelligence techniques, and so are less indicate to study how the brain really deals with lexical-semantic problems.

The possibility to simulate patients with selective category deficits descends on the idea, frequently proposed in the literature (Caramazza and Shelton 1998; Gainotti 2000; Warrington and McCarthy 1987; Warrington and Shallice 1984), that objects in similar categories exploit similar features (for instance, visual vs. action features) and these features occupy proximal regions in the cortex (for instance, visual features occupy regions in the ventral temporal lobe, space and action features in the parietal cortex, etc.). Our simulations clearly demonstrate that object recognition depends on the number of damaged areas in the semantic network, whose feature participate in the conceptual object description. Future studies may test this idea simulating concrete objects with a realistic feature description, possibly associated with specific cortical regions. This may constitute a quantitative way to implement existing theories and verify their reliability.

The problem of priming is certainly very complex, and cannot be exhaustively analyzed with a simple model as the present one. Indeed, both positive and negative priming effects have been documented in the cognitive literature, with different characteristics and time dynamics [see (Howard et al. 2006)]. However, some considerations can be drawn. In past years, autoassociative networks with attractor dynamics have frequently been used to explain priming (Kawamoto 1993; McRae and Boisvert 1998; Plaut and Booth 2000). A typical idea in these models is that a first object (the prime) which has some semantic similarity with a second object (the target) would place the network in a position of the state space close to the attractor of the target. This would reduce the settling time of network dynamics necessary to reveal the target. Hence, these models generally try to explain a positive priming effect. Conversely, in our model a prime causes a delay in the convergence of the target, since shared features, which were oscillating in phase during detection of the prime, must reset their phase to synchronize with the distinctive features of the target. During a transient period, the shared features and the distinctive features show the tendency to oscillate out of phase, thus increasing the time required for object recognition (indeed, it is possible that during a short transient period, the category is detected before the target, see Fig. 8). Of course, this behavior depends on the dynamics of Wilson-Cowan oscillators, and is strictly reliant on the choice of gamma-band synchronization as a way to solve the binding and segmentation problem.

We think that a complete approach to priming requires the inclusion of additional mechanisms in the model. This leads us to a discussion of the main limitations of the present study and of possible lines for forthcoming research.

First, in order to simulate real experimental results [such as event related potentials, which are commonly used to study the dynamics of semantic activation and priming, (Bermeitinger et al. 2008; Deacon et al. 2000; Kounios et al. 2009)), or lexical-semantic integration (Graben et al. 2008)] a more complex dynamics should be included in the network. In the present model, all neural units reach their activation state (either oscillatory or static) with a time constant of a few milliseconds, which is typical of the dynamics of individual neurons. In order to simulate real EEG activities, a more complex dynamics should be included with a longer activation period following a stimulus and an adaptation period, simulating a fatigue, after stimulus removal. This may help a description of the different phases of EPRs (Deacon et al. 2000; Graben et al. 2008) and a description of both positive and negative priming. Neural mass models instead of Wilson Cowan oscillators may be used to simulate such a more sophisticate dynamics (Ursino et al. 2010).

A further model limitation, which may preclude simulations of some types of priming, is the absence of any connection between word-forms in the lexical network. In the present model, words in the lexical area can interact only indirectly, via the presence of shared features in the semantic store. This is the reason why the use of a word as a prime does not introduce significant effects in model dynamics. It is probable that direct synapses exist among word-forms, for instance as a consequence of their frequent co-occurrence within a sentence; these links may be responsible for further priming effects (see [Howard et al. 2006]).

Model results demonstrate that synchronization is affected by noise superimposed on feature inputs. A possible way to improve model performance with noise may be the use of greater synaptic strength among features, to reinforce synchronization; however, in this case even one or two features would be sufficient to reconstruct the entire object, with a dramatic increase of false positives. The observation that the object is immediately reconstructed during the first steps, independently of noise, and only subsequently lost, suggests a possible strategy to improve model robustness still maintaining a high specificity: long term synapses, as those used in this work, would ensure the permanent storage of an object in long-term memory and its initial reconstruction despite noise; short-term synapses, immediately reinforced during the first steps, would maintain feature synchronization despite noise, but would be rapidly forgotten after object use. This strategy might be implemented in future works.

Finally, another limitation of this work consists in having used just schematic exempla (i.e., vector of features). In the present study concepts and words are described by random vectors, i.e., we are not using real exempla from semantic databases. Indeed, our aim was to expound the main mathematical characteristics of the model, and to verify the capacity of the network and of learning rules to provide the desired behavior; hence, we separated the mechanisms included in the model from any real dataset. Starting from the present results, future studies will consider real objects with reasonable features, and will test the possibility to simulate more complex subdivisions in categories and more sophisticate priming effects.