Silicon-Neuron Design: A Dynamical Systems Approach

Abstract

We present an approach to design spiking silicon neurons based on dynamical systems theory. Dynamical systems theory aids in choosing the appropriate level of abstraction, prescribing a neuron model with the desired dynamics while maintaining simplicity. Further, we provide a procedure to transform the prescribed equations into subthreshold current-mode circuits. We present a circuit design example, a positive-feedback integrate-and-fire neuron, fabricated in 0.25 μm CMOS. We analyze and characterize the circuit, and demonstrate that it can be configured to exhibit desired behaviors, including spike-frequency adaptation and two forms of bursting.

I. Silicon Neurons

Neuromorphic engineering aims to reproduce the spike-based computation of the brain by morphing its anatomy and physiology into custom silicon chips, which simulate neuronal networks in real-time (i.e., emulate). The basic unit of these chips is the silicon neuron, designed using analog circuits for spike generation and digital ones for spike communication. Engineers have built many silicon neuron chips, ranging in complexity from simple current-to-spike frequency generators to multicompartment, multichannel models, and ranging in density from a single neuromorphic neuron to arrays of ten thousand neurons [1, 2, 3, 4, 5, 6, 7]. Systems of silicon neurons have realized numerous computations, such as visual orientation maps, echolocation, and winner-take-all selection [1, 8, 9, 10].

A fundamental choice in designing silicon neurons is selecting the appropriate level of abstraction, with the field segregated into two design styles, a top-down approach and a bottom-up approach. The top-down approach aims to copy neurobiology, building every possible detail into silicon neurons. In this manner, designers aim to ensure that they include all of neurobiology’s computing power. This approach comes with a high price; engineers are unable to build large arrays of such complex neurons. Further, even small arrays are difficult to use, suffering from large variations among neurons, pushing them off the precipice into the Valley of Death.¹ On the other hand, the bottom up approach aims to build minimal neuron models, exploiting the inherent features of a technology. Engineers are able to build dense arrays of simple neurons, often expressing little variation, compared to complex models; however, these simple models often fail to reflect the properties of neurobiology. Unable to behave like their biological counterparts, these models fail to compute like them as well.

To avoid the precipice leading into the Valley of Death, we aim to design silicon neurons that realize the simplest complete model for intended tasks, keeping in mind that once a chip is fabricated we can tune neuron properties (e.g., thresholds, time constants, etc.) but cannot modify structure (i.e., we cannot add missing components). Models should be complex enough to express the same qualitative behavior and neurocomputational properties as their biological counterparts, in contrast to simple integrate-and-fire models; but they must accomplish this goal without superfluous detail and complexity, in contrast to biophysically detailed models [15, 16]. Recent work suggests that simple phenomenological models can not only reproduce the qualitative properties of biological neurons, but also their precise spike times [14]. The tool we use to select the appropriate level of abstraction between integrate-and-fire and biophysical models is dynamical systems theory (DST).

DST prescribes how a system’s states evolve, focusing on qualitative transitions among dynamical regimes as inputs and other parameters vary. DST achieves this function by finding equilibrium points, analyzing stability, and determining bifurcations [17]. For example, from the DST perspective, a bifurcation is responsible for a neuron’s transition from resting to spiking, and can aid us in deducing a neuron’s computational properties as they are linked to the type of bifurcation(s) a neuron undergoes. Experimental and computational neuroscientists have used DST to study the behavior of both individual neurons [18, 19] and neural networks [20], providing insight into how neural systems move among behavioral regimes (for a review see [21]). Engineers have used DST to analyze silicon models, elucidating their behavior [22, 23] and showing similarities between silicon and neurobiology [5]. In addition, one group has used DST to as a tool to transform a neuron with one type of dynamics into another type with distinct qualitative behavior [24].

In this paper, we use DST to design a neuron with simple but rich dynamics realized compactly in silicon. Until now, no formal procedure existed to choose the appropriate level of abstraction for a silicon neuron, and once the level of abstraction is selected no systematic process existed to design the neuron circuit. These challenges are particularly daunting in designing neurons for large-scale models of the brain, as they must optimize silicon area while maintaining flexibility. Following the philosophy that the simplest capable neuron results in the least variance, we limit our scope to single-compartment neurons with two degrees of freedom:

$$\begin{array}{l}\stackrel{.}{x}=f_1(x,y)\\ \stackrel{.}{y}=f_2(x,y)\end{array}$$ (1)

Such models have been studied from computational [25, 26] and dynamical [21] perspectives, and are sufficient to produce all the (practical) bifurcations between resting and spiking. However, we do provide one example with three variables.

In Section II, we introduce the concept of dynamical systems design, focusing on neuron bifurcations and their influence on behavior. In Section III, we describe the design process, focusing on how we use DST to create a positive-feedback integrate-and-fire neuron. In addition, we describe how we synthesize the neuron using log-domain circuits. In Section IV, we analyze and characterize the neuron, focusing on the neuron’s frequency-current relationship and showing the match between the theoretical behavior and the silicon neuron’s behavior. In Sections V through VII, we reapply the design procedure, enabling the neuron to exhibit bursting and spike-frequency adaptation by augmenting it with model ion-channel populations, and we verify its behavior in silicon. In Section VIII, we discuss the implications of our work, focusing on neuron variation and the future of silicon neuron design.

II. Dynamical System Theory

To design our silicon neuron, we employ DST to achieve the desired neuron properties while maintaining simplicity—dynamical system design (DSD). First, we determine the appropriate bifurcation(s) for the neuron to transition from resting to spiking. Second, we select whether the neuron should support bistability, monostability, or both. Third, we include additional properties that are important for a given neuron’s application, or that relate to a property we wish to study (e.g., spike-frequency adaptation). In general, a neuron’s required degree of complexity would depend strongly on the application(s) for which it is intended; however application-driven specifications are outside the scope of this paper.

Though biological and silicon neurons realize their transitions from resting to spiking in a myriad of ways, from a dynamical systems perspective, they all transition via two bifurcation types: saddle node or Androv–Hopf [21]. A saddle-node bifurcation occurs when two equilibrium points, one stable and one unstable, collide and annihilate each other. An Androv–Hopf bifurcation occurs when a stable equilibrium point transforms into an unstable one. In both cases, the elimination of the stable point causes the neuron’s potential to increase, eliciting a spike. These two bifurcation types result in different behaviors: Neurons expressing a saddle-node bifurcation integrate; excitatory input promotes spiking and inhibitory input represses spiking [27]. In contrast, neurons expressing a Androv–Hopf bifurcation resonate; excitatory or inhibitory input promotes or represses depending on timing [28].

In addition to the bifurcation type, we must choose whether the neuron expresses bistability. Each bifurcation type comes in two varieties, depending on whether a stable (spiking) limit cycle exists before the bifurcation occurs or only after. If the stable limit cycle exists before the bifurcation, the neuron is bistable since both resting and spiking are simultaneously stable. In addition, this bistability results in hysteresis: If the input current increases enough to cause spiking, the neuron will continue to spike even after it decreases below the bifurcation point. On the other hand, for a monostable neuron, the same input may cause a single spike, rather than continuous spiking.

The four combinations of bifurcation types and stability yield different neuron membrane (black) behaviors when driven with an increasing ramp of current (gray), followed by a decreasing one (Table I). Neurons expressing a monostable saddle-node bifurcation integrate, exhibiting a continuous current-frequency curve. They spike at a near-zero frequency when the current surpasses a threshold. As the current drops below this threshold, they cease spiking. Neurons expressing a bistable saddle-node bifurcation also integrate, but exhibit a discontinous current-frequency curve. They spike at a nonzero frequency when the current surpasses a threshold. As the current drops below the original threshold, they continue spiking, until it decreases further to a new threshold. Neurons expressing a monostable Androv–Hopf bifurcation resonate, expressing increasing subthreshold oscillations until spikes reach their full amplitude. As the current drops, their spikes cease and the oscillation’s amplitudes decrease. Neurons expressing a bistable Androv–Hopf bifurcation resonate, but express only low-amplitude subthreshold oscillations until spikes jump to their full amplitude. As the current drops below the original threshold, they continue spiking, until it decreases further to a new threshold.

Table I.

Resting-to-Spiking & Spiking-to-Resting Bifurcations

Using the DST strategy, we can design a neuron that integrates, resonates, or does one or the other, depending on its settings. Such reconfigurability can be realized by adding an inhibitory or excitatory state variable that opposes the membrane potential’s change, activating or inactivating as the membrane potential increases [28]. Depending on the variable’s speed and sensitivity the neuron could integrate, resonate, or switch between types [29]. In this paper, we focus on the saddle-node bifurcation, designing a neuron that integrates rather than one that resonates.

III. Neuron Design

In this section, we present a method to design and to implement a silicon neuron, using DSD. We show how to move from the dimensionless ordinary differential equation (ODE) that describes the desired bifurcation to one in terms of currents. Finally, we show how this ODE can be implemented in circuits with logarithmically related voltages (V ∝ log(I)).

A. Saddle-Node Bifurcation

The saddle-node bifurcation is simpler than the Androv–Hopf one, requiring only a single state variable (plus a reset) to realize spiking. We choose this simpler type because we are not exploring subthreshold oscillations or other effects of resonance with this chip.

The canonical saddle-node bifurcation uses quadratic positive feedback [17, 21]:

$$\begin{array}{l}\tau \stackrel{.}{x}=r-r_{\text{th}}+\frac{1}{2}{(x-x_{\text{i}})}^2\\ =r-\frac{1}{2}+\frac{1}{2}{(x-1)}^2\\ =-x+r+\frac{x^2}{2}\end{array}$$ (2)

where r and x are the neuron’s dimensionless input current and membrane potential, respectively. τ is its membrane time constant, r_th = 1/2 is its threshold input, and x_i = 1 is the inflection point, above which x accelerates (i.e., spiking occurs). The −x term corresponds to a leak conductance, a current proportional to membrane potential. We use the slightly more complex cubic system:

$$\tau \stackrel{.}{x}=-x+r+\frac{x^3}{3}$$ (3)

with x_i = 1 and r_th = 2/3. Using cubic positive feedback has two advantages over quadratic feedback: its circuit implementation is more flexible and its spike acceleration is sharper, better approximating biological spike-generating sodium currents [16, 30].

The saddle-node bifurcation occurs as r increases, moving from resting to spiking. For small r, Equation 3 has two equilibrium points, one stable (near r) and one unstable (higher): Starting at x = 0, the system will settle at the stable equilibrium (Fig. 1). As r increases, the stable and unstable equilibrium points increase and decrease, respectively. At r = r_th, the two equilibrium points collide, annihilating each other—a saddle-node bifurcation. Once this bifurcation occurs, x increases without bound, until it reaches x_MAX (≫ 1), at which point a spike is declared and the neuron reset.

Fig. 1.

Measured silicon neuron membrane traces (x, normalized) rise like a resistor-capacitor circuit, with a positive feedback spike for several step-input current levels (r=0.48, 0.57, 0.69, 0.82, 0.98, and 1.2). Below a threshold input, the neuron reaches a steady state at which the input and positive feedback are insufficient to overpower the leak. Above threshold, larger inputs enable the positive feedback to overcome the leak more quickly, resulting in a shorter time to spike. Inset The neuron’s phase plot shows ẋ versus x (black), fit with a cubic (gray). The neuron has two fixed points (circles) when its input is small, r < 2/3, one stable (filled) and one unstable (open). As r increases above 2/3, the fixed points merge and destroy each other, undergoing a saddle-node bifurcation, the transition from resting to spiking. Phase plot traces filtered by a 5 ms halfwidth gaussian.

To visualize the dynamics of the spike, we use a DST workhorse, the phase plot (see [17, 21]). Phase plots show the relationships among states and dynamics of the system. For our one-dimensional neuron, we plot ẋ versus x, revealing how the neuron’s membrane changes depending on its current state (Fig. 1 inset).

B. Circuit Synthesis

To implement the neuron circuit, we compute the polynomial expressions by using currents to represent our variables of interest. In the subthreshold regime, a (metal-oxide semiconductor) transistor’s (gate–source) voltage is logarithmically related to its (drain–source) current. Therefore, currents can be multiplied simply by adding voltages. Furthermore, since we store the circuit’s state on capacitors, as voltage, we need to compute the derivative of the logarithm.

The process to convert the neuron ODE into a circuit requires three steps. First, we transform the ODE into a current-mode description by replacing each dimensionless variable with a ratio of currents. Second, based on a current’s time derivative, we compute the capacitor voltage’s time derivative (CV̇ = ΣI_i(t)). Third, we design a subcircuit to implement each current term, I_i(t).

First, we transform Equation 3 by replacing each dimensionless variable with a ratio of currents, $x=\sqrt{3}\frac{I_x}{{\text{I}}_{\text{C}}},r=\sqrt{3}\frac{I_r}{{\text{I}}_{\text{C}}}$, where I_C is constant, yielding:

$$\begin{array}{l}\tau \sqrt{3}\frac{{\stackrel{.}{I}}_x}{{\text{I}}_{\text{C}}}=-\sqrt{3}\frac{I_x}{{\text{I}}_{\text{C}}}+\sqrt{3}\frac{I_r}{{\text{I}}_{\text{C}}}+\sqrt{3}{\left(\frac{I_x}{{\text{I}}_{\text{C}}}\right)}^3\\ \iff \tau {\stackrel{.}{I}}_x=-I_x+I_r+\frac{{I_x}^3}{{{\text{I}}_{\text{C}}}^2}\end{array}$$ (4)

To find a description in terms of a capacitor’s voltage, we find the relation between İ_x and V̇_x, where V_x is the gate voltage (referenced below the positive voltage supply, V_DD) of the transistor whose current is I_x. Since we tune the PMOS transistors to be in the subthreshold regime:

$$\begin{array}{l}{I}_x={\text{I}}_0{e}^{\kappa V_x/{\text{U}}_{\text{t}}}\\ \Rightarrow {\stackrel{.}{I}}_x=\frac{\kappa }{{\text{U}}_{\text{t}}}{\text{I}}_0{e}^{\kappa V_x/{\text{U}}_{\text{t}}}{\stackrel{.}{V}}_x\\ =\frac{\kappa }{{\text{U}}_{\text{t}}}{I}_x{\stackrel{.}{V}}_x\end{array}$$ (5)

where I₀ and κ are transistor parameters, and U_t is the thermal voltage. Substituting Equation 5 into Equation 4, we find:

$$\begin{array}{l}\tau \frac{\kappa }{{\text{U}}_{\text{t}}}{I}_x{\stackrel{.}{V}}_x=-I_x+I_r+\frac{{I_x}^3}{{{\text{I}}_{\text{C}}}^2}\\ \frac{{\text{C}}_{\text{x}}{\text{U}}_{\text{t}}}{\kappa {\text{I}}_{\text{L}}}\frac{\kappa }{{\text{U}}_{\text{t}}}{I}_x{\stackrel{.}{V}}_x=-I_x+I_r+\frac{{I_x}^3}{{{\text{I}}_{\text{C}}}^2}\\ \iff {\text{C}}_{\text{x}}{\stackrel{.}{V}}_x=-{\text{I}}_{\text{L}}+\frac{{\text{I}}_{\text{L}}{I}_r}{I_x}+\frac{{I_x}^2}{{\text{I}}_{\text{pth}}}\end{array}$$ (6)

where $\tau \equiv \frac{{\text{C}}_{\text{x}}{\text{U}}_{\text{t}}}{\kappa {\text{I}}_{\text{L}}}$ (see [31]), and we define ${\text{I}}_{\text{pth}}=\frac{{{\text{I}}_{\text{C}}}^2}{{\text{I}}_{\text{L}}}$.²

To realize the circuit we require three currents to drive the capacitor (Fig. 2): one current decreases the capacitor voltage (towards V_DD) and two increase it (towards GND). The first current term (I_L) corresponds to x’s decay towards zero; M_L accomplishes this decay.

Fig. 2.

The neuron circuit comprises a capacitor C_x, driven by three currents: an input (M_r), a leak (M_L), and positive feedback (M_F1–5). When the input and positive feedback currents drive V_x low enough, REQ transitions from low to high, signaling a spike.

The second term corresponds to r, realized by driving V_x towards GND. It equals the product of the input (I_r) and leak currents (I_L), divided by the membrane current (I_x). We generate this current using the translinear principle for subthreshold transistors [32, 33]. In short, we set M_r’s gate to V_L + V_r to generate I_LI_r. Connecting its source and bulk to V_x realizes division by I_x, yielding $\frac{{\text{I}}_{\text{L}}{I}_r}{I_x}$.

The third term corresponds to the cubic (positive) feedback, x³/3, driving V_x towards GND. It equals the membrane current squared divided by a constant current (I_pth). Again, we use the translinear principle, mirroring I_x (M_F2,3) to a differential pair (M_F4,5) and shorting one side’s gate to the mirror, which realizes the square. The bias voltage on the other side of the pair sets I_pth, which sets the current–voltage range over which the neuron operates. Alternatively, we could implement quadratic feedback by removing M_F4,5, but we would have less control, as our operating range would be set by transistor sizing alone.

The base circuit requires eight transistors and one capacitor (Fig. 2). When the input and positive feedback currents drive V_x low enough, M_x and M_F1 behave like an inverter [34], generating a digital request, REQ, which transitions from low to high, signaling a spike. After a neuron spikes, it is reset.

The neuron’s reset drives x to x_RES by driving V_x towards V_DD. In the simplest implementation, the reset briefly sets V_L = 0; M_L overcomes the positive feedback and resets V_x. The duration of the reset pulse (t_r) sets x_RES. A long reset pulse, sets V_x = V_DD, corresponding to x_RES = 0; a shorter reset pulse, sets V_x < V_DD, corresponding to x_RES > 0. In practice, we do not use M_L, but use another circuit that provides better control over t_r (see Fig. 7).

Fig. 7.

To implement adapting and bursting the neuron circuit is augmented with two ion-channel population circuits, realizing g_k (M_k) and r_ca (M_ca), and a reset circuit (M_res).

Biasing the neuron circuit requires us to set each current such that ratios of currents realize the dimensionless variables in Equation 3. From Equation 6, we see that we only need to set three currents: I_L, I_pth, and I_r. First, we set I_L to obtain the desired τ. Next, we set I_pth to obtain the desired threshold, which defines the sub-spike-threshold range (V_pth = 0.8 V for all data in this paper). In general, as V_pth increases the neuron uses greater power, but the signals sent off-chip are easier to measure. Finally, we set I_r to achieve a specified r, using $I_r=\frac{r\sqrt{{\text{I}}_{\text{pth}}{\text{I}}_{\text{L}}}}{\sqrt{3}}$.

The Neuron chip was fabricated through MOSIS in 1P5M 0.25 μm CMOS process, consuming 10 mm² of area. It has a 16 by 16 array of microcircuits. Each microcircuit contains four neurons (77 by 14 μm each) and one interneuron (not used here). Each neuron has 21 STDP circuits (not used here). The Neuron Chip uses the address-event representation (AER) to transmit spikes off chip and to receive spike input [35, 36] in addition to an analog scanner that allows us to observe the state of one neuron at a time. The chip consumes on the order of 1–5 mW with all neurons and interneurons spiking at average rates up to 40 Hz.³ All data figures in this work are recorded from a single neuron on this chip. For a complete description of the Neuron chip, circuit layout, and test board, see [31].

IV. Dynamical Systems Analysis

In this section, we analyze and characterize the neuron’s frequency-current relation. First, we use Equation 3 to obtain both exact and approximate solutions to the neuron’s period as a function of input current in the monostable regime. Then, we use these results to fit measured data from a silicon neuron. Next, we show that we can configure the neuron in the bistable regime in which it expresses spike-frequency hysteresis.

A. Frequency-Current Relation

As r surpasses r_th, the neuron moves from the resting state to the spiking state (reset to x_res = 0). Once the neuron enters the spiking state, its frequency increases as r increases above r_th. We view this relationship in terms of the neuron’s phase plot (Fig. 1 inset). Increasing r drives the phase plot up, increasing ẋ for all x values. If ẋ lies just above zero, x increases slowly near the inflection point, resulting in a long period, T, and a low spike frequency, f. Increasing ẋ decreases the time x spends near its inflection, increasing the spike frequency.

We calculate T by summing the time intervals the neuron takes to increase from x to x + Δx for constant values of r and x_res, equivalent to integrating $\frac{1}{\stackrel{.}{x}}$ from Equation 3 with respect to x from x_res to ∞:

$$\begin{array}{l}T(r,x_{\text{res}})=\tau {\int }_{x_{\text{res}}}^{\infty }\frac{dx}{-x+r+\frac{x^3}{3}}\\ =\tau \sum _{i=1}^3\frac{log(x_{\text{res}}-p_i)}{-p_i^2+1}\end{array}$$ (7)

where p_i is the ith root of the neuron’s characteristic polynomial: p³/3 − p + r. Though analytically tractable this exact solution is sufficiently complicated to preclude us from gaining much insight into neuron behavior, so we choose not to evaluate it further.

To gain intuition, we simplify Equation 7 in the regime where r ≫ x. We ignore x and replace r with r − r_th, which preserves the bifurcation point. Also, to simplify the integral, we set x_res = 0, yielding:

$$\begin{array}{l}T(r,0)\approx \tau {\int }_0^{\infty }\frac{dx}{r-r_{\text{th}}+\frac{x^3}{3}}\\ =\frac{2\pi \tau }{3^{7/6}{(r-r_{\text{th}})}^{2/3}}\end{array}$$ (8)

We see that for large r, f(r, 0) = 1/T(r, 0) increases as r^2/3.

To characterize the neuron’s frequency-current relationship, we drove the neuron by stepping r from zero to a range of values (input currents) and measured the neuron’s time to spike, the inverse of which corresponds to f.⁴ We step r up by stepping V_r down towards GND (transistor M_r’s gate bias V_r + V_L; see Fig. 2), and measure f over a range of V_r values.

We fit f versus r to Equation 7 (Fig. 3). We found that f was within 5% of the predicted value for all r values (τ = 27.1 ms). We calibrated I_r’s dependence on V_r (I_r = I₀e^κV_r/U_t) using a property of the monostable saddle-node bifurcation: The neuron spikes when $r>r_{\text{th}}=\frac{2}{3}$ and near the bifurcation $f^2\propto r-\frac{2}{3}$ [21]. Therefore, we find the smallest five values of I_r that result in the neuron spiking and fit the frequency squared to find r’s value as a function of I_r (Fig. 3 inset). This procedure yielded I₀ and the value of I_r that corresponds to $r=\frac{2}{3}$.⁵

Fig. 3.

The silicon neuron responds sublinearly to current above a threshold (dots). See text for fit equation. Inset f² is fit (gray line) versus the input to find and normalize to the threshold r = 2/3.

B. Frequency Bistability

We verified that our saddle-node-bifurcation neuron is capable of expressing bistability (Fig. 4). We put the neuron in the bistable regime by setting x_res ≈ 1.7. We drove the neuron with a below-threshold input current, r = 0.36. The neuron did not spike; its membrane settled to a constant level. Next, we increased r to 0.70, causing the neuron to spike repeatedly at 36 Hz. Then, we returned the input to the previous level 0.36, but because the neuron’s membrane potential x was never pulled below it’s unstable point (about 1.57 for r = 0.36), it continued spiking at a reduced rate of 22 Hz.

Fig. 4.

The neuron expresses frequency bistability when reset to 1.7. Initially, when the input is low, r = 0.36, the neuron is silent, but when it increases to 0.70 then, drops back to 0.36, the neuron spikes at 22 Hz. Inset The neuron trajectory (black) follows the fits for r = 0.36, 0.70 (gray). When it is reset above the unstable point (open circle) for r = 0.36, the neuron spikes; otherwise it sits at the stable point (filled circle). Phase plot traces filtered by a 5 ms halfwidth gaussian.

V. Square-Wave Bursting

In this and the following two sections, we apply the dynamical systems design approach to design neurons capable of bursting and adaptation by adding model voltage-gated ion channels. We chose types of bursting and adaptation that are commonly found in computational models as well as observed in biology [21]. We implement these dynamics with channels that increment their activity only during a spike (high-threshold variety) and decay thereafter, and limit ourselves to adding at most one excitatory and one inhibitory channel population to the neuron.

To augment the neuron, we follow the DSD procedure introduced in Sections II and III: We determine the bifurcation(s) and equation(s) that implement the desired dynamics and implements them in circuits. In the case of reconfiguring the neuron, we modify and augment Equation 3, rather than starting from a canonical equation.

Square-wave bursting (SWB) is characterized by a silent phase with low membrane potential followed by a high-frequency spiking phase with high membrane potential (i.e., x_res > 1) (Fig. 5). During the high phase, sodium positive feedback remains active, causing repetitive spiking (Fig. 5 inset). Spiking ends when an inhibitory potassium conductance grows strong enough to overcome the positive feedback, which pulls the membrane low, removing the positive feedback and terminating the burst until the potassium conductance decays. We use DSD to endow our neuron with the appropriate bifurcations to realize SWB.

Fig. 5.

In square-wave bursting, as g_k decays the burst begins, x spikes rapidly until g_k overcomes the positive feedback. Inset The neuron rests at its stable point (closed circle), which becomes destabilized when the ẋ versus x curve rises as g_k decays, starting a burst (arrows). During the burst, the ẋ versus x curve drops as g_k rises, eventually pushing the unstable point (open circle) above x_res, which terminates the burst. Phase plot and g_k traces filtered by a 5 ms halfwidth gaussian.

A. Design

SWB requires two bifurcations, one from resting to spiking and one from spiking to resting. For its resting-to-spiking bifurcation, SWB employs a bistable saddle, setting its reset above the saddle’s unstable equilibrium (as in Section IV-B). For its spiking-to-resting bifurcation, SWB employs a homoclinic bifurcation, moving its unstable point up to intersect the (spiking) limit cycle; an inhibitory conductance (g_k), which increments after each spike, achieves this. When the unstable point crosses the limit cycle, spiking ceases and x drops to the stable point. In a dynamical-systems context SWB is referred to as fold-homoclinc bursting [37]; a bistable saddle is also known as a fold bifurcation.

g_k is situated in parallel with the neuron’s leak, augmenting Equation 3:

$$\tau \stackrel{.}{x}=-x(1+g_{\text{k}})+r+\frac{x^3}{3}$$ (9)

As g_k increases, the bifurcation point, $r_{\text{th}}=\frac{2}{3}{(1+g_{\text{k}})}^{3/2}$, increases, reducing r − r_th and hence ẋ. We model g_k after the M-type potassium (MK) channel [38]. An MK channel population has a slow decay and high activation threshold. Its high threshold ensures that the MK population is only activated during spikes and decays during interspike intervals. Its slow decay enables MK channels to integrate across spikes, increasing their conductance in proportion to spike frequency.

We model g_k as a first-order ODE with a spike response described by:

$${\tau }_{\text{k}}{\stackrel{.}{g}}_{\text{k}}=-g_{\text{k}}+g_{\text{max}}{p}_{\text{k}}(t)$$ (10)

where p_k(t) equals one for a brief duration (t_k) after the neuron spikes, resulting in an increase in g_k by Δg_k = g_maxt_m/τ_k (for g_k ≪ g_max).

B. Circuit

Once we know the dynamics and equations we want to implement, we need to generate circuit implementations for the channel population (Equation 10) and connect it to the neuron circuit (Equation 9). We use the same approach presented in Section III-B: We replace each variable with a ratio of currents ( $g_{\text{k}}=\frac{I_{\text{k}}}{{\text{I}}_{\text{L}}}$, where I_k = I₀e^κV_k/U_t) and use the translinear principle to construct appropriate subcircuits. The resulting circuit equations are:

$$\begin{array}{l}{\text{C}}_{\text{x}}{\stackrel{.}{V}}_x=-{\text{I}}_{\text{L}}-I_{\text{k}}+\frac{{\text{I}}_{\text{L}}{I}_r}{I_x}+\frac{{I_x}^2}{{\text{I}}_{\text{pth}}}\\ {\text{C}}_{\text{k}}{\stackrel{.}{V}}_{\text{k}}=-{\text{I}}_{\text{LK}}+\frac{{\text{I}}_{\text{Lk}}{\text{I}}_{\text{kmax}}}{I_{\text{k}}}{p}_{\text{k}}(t)\end{array}$$ (11)

where I_Lk determines g_k’s decay constant: ${\tau }_{\text{k}}\equiv \frac{{\text{C}}_{\text{k}}{\text{U}}_{\text{t}}}{\kappa {\text{I}}_{\text{Lk}}}$. g_k’s first-order dynamics are realized in the same manner as the neuron circuit with the addition of a series transistor to gate the input by p_k(t), which is provided by a pulse-extender circuit (Fig. 6). SWB is realized by placing the pulse extender and low-pass filter in a feedback loop around the positive-feedback neuron (Fig. 7). To bias g_k, we set τ_k with I_Lk, and we set g_max with I_kmax relative to I_L. For example, if g_max is 10, we set I_kmax to 10 times I_L.

Fig. 6.

The ion-channel population circuit consists of two modules, one implements the pulse-like spike response, p(t) (M_p1,2 and C_p), and the other implements the first-order dynamics, V_ch (M_ch1–3 and C_ch). V_ch generates the output current, I_ch, when it is applied to the gate of an output transistor M_out.

C. Analysis and Characterization

To understand the mechanics of SWB, we recall the bistable neuron without an MK conductance. If x_RES > 1, the sodium overpowers the leak conductance, and therefore even if we lower r spiking continues. The high reset realizes bistability in the spike rate: For r near the bifurcation, the neuron can be active or silent. Similarly, for g_k near the bifurcation, the neuron can be active or silent.

To characterize SWB, we set x_RES = 2.35 and drove the neuron with r = 0.9, observing bursting with three spikes per burst. We calculate the values to which g_k must decay and grow to initiate and terminate the burst, respectively. To initiate the burst, g_k must decay enough such that $r>r_{\text{th}}=\frac{2}{3}{(1+g_{\text{k}})}^{3/2}$, which yields $g_{\text{k}}<{\left(\frac{3}{2}r\right)}^{2/3}-1=0.22$. To terminate the burst, g_k must grow enough such that x_RES equals x’s unstable equilibrium. We find this equilibrium by setting ẋ = 0 (Equation 9) and solving for g_k given x = x_RES, which yields $g_{\text{k}}=\frac{3r+x_{\text{RES}}^2}{3x_{\text{RES}}}-1=1.22$. To analyze SWB, we again use a phase plot.

The SWB neuron’s phase plot considers the relationship between x and g_k (Fig. 8). For g_k below 0.22, x has no (positive) equilibria points (it has only a stable spiking limit cycle). For g_k above 0.22, x has two equilibria points, one stable and one unstable (as well as the stable spiking limit cycle). However for g_k greater than 1.22, the unstable equilibrium enters the spiking limit cycle, destabilizing it. When its limit cycle becomes unstable the neuron can still spike if it is kicked into the limit cycle’s region of phase space, but only once, then the neuron is reset and descends to the stable equilibrium.

Fig. 8.

In square-wave bursting, x and g_k follow a trajectory (black) in which x moves towards either a stable equilibrium or a spiking limit cycle. Initially for low g_k (below 0.22), x enters the spiking limit cycle (light gray shading). As g_k increases (between 0.22 and 1.22), x remains in its spiking limit cycle, even though a stable point and an unstable point have appeared (solid and dashed lines). Once g_k exceeds 1.22, the limit cycle becomes unstable (dark gray shading); x drops to its only stable point, until g_k decays below 0.22, repeating the cycle. Traces filtered by a 5 ms halfwidth gaussian; dots are 5 ms apart.

From this phase-space perspective, we see that for small g_k, after a silent phase, x enters the spiking limit cycle. As g_k increases, the spiking limit cycle remains stable despite the creation of the two other equilibria; so in the absence of perturbation, the neuron continues spiking. Only when g_k exceeds 1.22 does the limit cycle become unstable, resulting in one last spike, ending the burst. During the silent phase, as g_k decays, x follows its calculated (not fit) stable equilibrium.

VI. Spike-Frequency Adaptation

Spike-frequency adaptation (SFA) reduces a neuron’s sensitivity to sustained excitatory input, lowering its spike frequency over time (Fig. 9). For example, if an adapting neuron receives a potent input current step, it will fire several rapid spikes, but each subsequent period will be longer than the one before, until the neuron reaches a steady-state frequency. Like SWB, SFA is realized by a potassium conductance that builds up from one spike to another. Unlike SWB, however, the neuron is reset below its unstable point, eliminating bistability.

Fig. 9.

In spike-frequency adaptation, as g_k (dark gray) increases x’s (light gray) spike frequency decreases. Inset g_k decreases frequency by decreasing ẋ (black) towards zero, slowing spiking. Fits (gray) are a guide for the eye. Phase plot and g_k traces filtered by 10 and 5 ms halfwidth gaussians, respectively.

A. Design

We realize SFA by pushing the neuron progressively closer to the saddle-node bifurcation responsible for its transition from resting to spiking. For a fixed input current r, the bifurcation occurs at $g_{\text{kth}}={\left(\frac{3}{2}r\right)}^{2/3}-1$. As g_k approaches this value, ẋ decreases, lowering the neuron’s frequency (Fig. 9 inset).

B. Circuit

SFA’s circuit is identical to the one used in SWB (Fig. 7), described by Equation 11. The one difference is that we set the reset circuit to deliver a longer reset pulse, resulting in x_res = 0, below the unstable point.

C. Analysis and Characterization

Once the circuit is implemented, we analyze and characterize its behavior, focusing on SFA’s response to steps to a range of r values. We drove the adapting neuron with five r values (1.0, 2.0, 3.7, 6.7, and 11.8) and observed f and g_k. We consider f instead of x, since g_k and f directly depend on each other, whereas x influences g_k only through f. For each r value, we allow the neuron’s frequency to reach steady state.

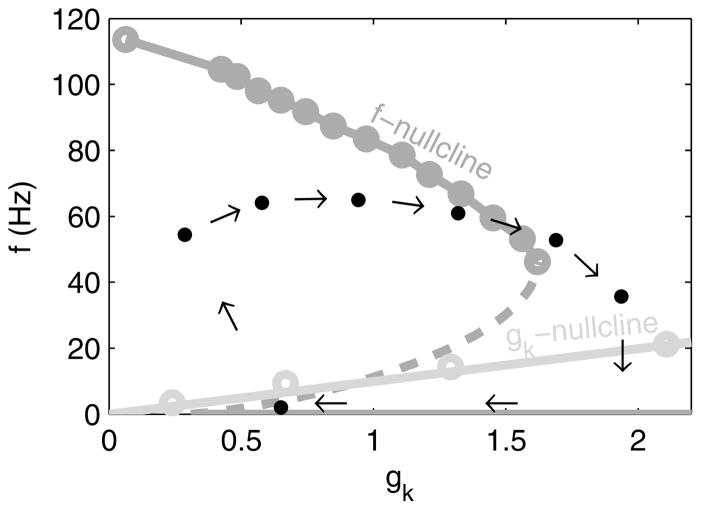
To visualize the dynamics, we again use a phase plot, showing the f-g_k trajectory (Fig. 10). In addition, we plot a nullcline for each variable. The f-nullcline is the curve where f is in equilibrium for a given value of $g_{\text{k}}(\frac{df(g_{\text{k}})}{dt}=0)$. Similarly, the g_k-nullcline is the curve where g_k is in equilibrium for a given value of $f(\frac{dg(f)}{dt}=0)$. Nullclines provide insight into the dynamics of the system; from any given point on the phase plot, f and g_k always move along their respective axes towards their respective nullclines. Eventually, f and g_k arrive at the intersection of their nullclines, an equilibrium point. This equilibrium is stable: If we perturb the system, it returns.

Fig. 10.

In spike-frequency adaptation, f starts high but decreases as g_k increases (arrows), following the f-nullcline (light gray) until it crosses the g_k nullcline, reaching a stable equilibrium. Each dot corresponds to one interspike interval’s instantaneous f and mean g_k. g_k values filtered by a 5 ms halfwidth gaussian.

To find the neuron’s f-nullcline, we calculate T in the same manner as Section IV, by integrating $\frac{1}{\stackrel{.}{x}}$ from Equation 9 with respect to x, from x_res(= 0) to ∞:

$$\begin{array}{l}T(r,x_{\text{res}},g_{\text{k}})=\tau {\int }_{x_{\text{res}}}^{\infty }\frac{dx}{-x(1+g_{\text{k}})+r+\frac{x^3}{x}}\\ =\tau \sum _{i=1}^3\frac{log(x_{\text{res}}-p_i)}{-p_i^2+1+g_{\text{k}}}\end{array}$$ (12)

where p_i is the ith root of the neuron’s characteristic polynomial: p³/3 − p(1 + g_k) + r. f(r, x_res, g_k) = 1/T corresponds to the f nullclines (Fig. 10). These nullclines assume g_k is constant; because we set g_k to be slow (τ_k = 190 ms, fitted), it is approximately constant over a neuron’s interspike interval.

To find the neuron’s g_k-nullcline with respect to f, we calculate g_k’s steady-state conductance, g_k∞(f) by equating its decay over one period to its growth, Δg_k:

$$\begin{array}{l}{g}_{\text{k}\infty }(f)=\frac{1}{e^{1/(f{\tau }_{\text{k}})}-1}\mathrm{\Delta }{g}_{\text{k}}\\ \approx f{\tau }_{\text{k}}\mathrm{\Delta }{g}_{\text{k}}\end{array}$$ (13)

which is a good approximation (within 8%) for f τ_k > 1 (Fig. 10). This linear relationship enables us to obtain Δg_k(= 0.60) from the g_k-nullcline’s slope.

VII. Parabolic Bursting

Parabolic bursting (PB) is characterized by a quiescent phase followed by a bursting phase in which the spike frequency rises and falls like a parabola (Fig. 11). After the quiescent phase, each interspike interval becomes shorter until a peak frequency is reached, after which each interspike interval becomes longer until the burst terminates, resulting in another quiescent phase. This smooth frequency increase and decrease contrasts with SWB’s abrupt frequency changes, which arise from bistability in the membrane potential. Reseting its membrane potential to zero after a spike eliminates this source of bistability and calls for a different mechanism, which directly produces bistability in spike frequency. The membrane potential’s bifurcations remain monostable—also known as circle bifurcations—hence PB is referred to as circle-circle bursting [37].

Fig. 11.

In parabolic bursting, as g_k (dark gray) decays the burst begins, x (light) spikes faster then slower until the burst ends. Inset g_k shifts the conceptual f(r_ca) curve. For medium g_k (middle curve), two stable points coexist (filled circles), one at a high frequency and one at a low, with an unstable point in between (open circle). For low g_k (top curve), the low stable point collides with the unstable point, leaving only the high stable point, initiating spiking. For high g_k (bottom curve), the high stable point collides with the unstable point, leaving only the low stable point, terminating spiking. g_k filtered by a 5 ms halfwidth gaussian.

A. Design

We realize frequency bistability by introducing positive feedback in the form of an excitatory current, r_ca, which models a calcium channel (CC) population:

$$\tau \stackrel{.}{x}=-x(1+g_{\text{k}})+r+r_{\text{ca}}+\frac{x^3}{3}$$ (14)

Each time the neuron spikes, r_ca increments, but decays slowly, increasing the drive to the neuron and making it spike more frequently. This linear frequency-to-r_ca curve (see below) intersects the neuron’s compressive current-to-frequency curve in three places, producing two stable points separated by an unstable one (Fig. 11 Inset). This situation pertains to intermediate g_k values that shift the neuron’s current-to-frequency curve to the right a moderate amount. For lower g_k values, the lower stable point disappears (transition from resting to spiking); for higher g_k values, the higher stable point disappears (transition from spiking to resting).

As the CC population has a high threshold, only activating during spikes, we model r_ca in the same manner as g_k:

$${\tau }_{\text{ca}}{\stackrel{.}{r}}_{\text{ca}}=-r_{\text{ca}}+r_{max}{p}_{\text{ca}}(t)$$ (15)

where p_ca(t) equals one for a period (t_ca) after the neuron spikes, resulting in an increase in r_ca by Δr_ca = r_maxt_ca/τ_ca (for r_ca ≪ r_max). We tune CC to have a decay slow enough to enable it to integrate across spikes. In that case, Equation 13 applies, yielding a linear frequency relationship r_ca∞ = fτ_caΔr_ca for r_ca’s steady-state value. Note that this design assumes that both r_ca and g_k approach values proportional to f, requiring both to decay on a time scale slower than the membrane and spike dynamics. We measured τ_k = 190 ms and τ_ca = 53 ms, compared to a typical intraburst spike interval of 17ms.

B. Circuit

Except for the addition of ion-channel population circuit for $r_{\text{ca}}=\sqrt{3}\frac{I_{\text{ca}}}{{\text{I}}_{\text{C}}}$, PB’s circuit (Fig. 7) is identical to SFA’s:

$$\begin{array}{l}{\text{C}}_{\text{x}}{\stackrel{.}{V}}_x=-{\text{I}}_{\text{L}}-I_{\text{k}}+\frac{{\text{I}}_{\text{L}}(I_r+I_{\text{ca}})}{I_x}+\frac{{I_x}^2}{{\text{I}}_{\text{pth}}}\\ {\text{C}}_{\text{ca}}{\stackrel{.}{V}}_{\text{ca}}=-{\text{I}}_{\text{Lca}}+\frac{{\text{I}}_{\text{Lca}}{\text{I}}_{\text{rmax}}}{I_{\text{ca}}}{p}_{\text{ca}}(t)\end{array}$$ (16)

where ${\tau }_{\text{ca}}\equiv \frac{{\text{C}}_{\text{ca}}{\text{U}}_{\text{t}}}{\kappa {\text{I}}_{\text{Lca}}}$ and g_k’s equation is omitted (See Equation 11). Notice that I_ca and I_r are in parallel. We realize p_ca(t) by putting a transistor in series with the input transistor ( $\frac{{\text{I}}_{\text{Lca}}{\text{I}}_{\text{rmax}}}{I_{\text{ca}}}$), turned on for period t_ca after each spike (Fig. 7). To bias r_ca, we set τ_ca with I_Lca, and we set I_rmax in the same manner we set I_r in Section III-B.

C. Analysis and Characterization

To understand PB, we again employ a two-dimensional phase plot with two nullclines, for f and g_k (Fig. 12).⁶ Whereas the g_k nullcline is identical to the one for SFA, the f nullcline has three branches, which trace the loci of f’s three fixed points as g_k varies (Fig. 11 Inset). As g_k increases, the upper stable point drops (in frequency), the lower stable point remains at zero, and the unstable point rises. These three branches coexist over an intermediate range of g_k values (bistable region) whose lower and upper limits correspond to the values of g_k at which resting-to-spiking and spiking-to-resting transitions occur, respectively. We determine the lower limit the same way we did for SWB’s transition to spiking, yielding $g_{\text{k}}<{\left(\frac{3}{2}r\right)}^{2/3}-1=0.31$ for r = 1.0. We determine the upper limit by finding when the two curves in Fig. 11 Inset are tangential, which does not yield a closed-form solution.

Fig. 12.

In parabolic bursting, f and g_k follow a trajectory (black) in which both move towards stable portions of their respective nullclines (dark and light gray). Each dot corresponds to one interspike interval’s instantaneous f and mean g_k. g_k values filtered by a 5 ms halfwidth gaussian.

Although we also cannot obtain the f-nullcline analytically, we can characterize it experimentally by varying Δg_k. Reducing Δg_k increases the g_k-nullcline’s slope, causing it to intersect the f-nullcline’s upper stable branch, and the neuron to fire at the corresponding frequency. Thus, we can trace this branch by sweeping Δg_k until the neuron starts bursting. We estimate the middle branch by extrapolating between this point and the calculated lower limit. The resulting nullcline is consistent with the measured bursting limit cycle (Fig. 12).

Once we have obtained the nullcline, we track a burst through its phase space (Fig. 12). A burst initiates when g_k decays below its lower limit, causing f to move towards its nullcline’s upper branch. This trajectory crosses the g_k nullcline, causing g_k to move to the right. Eventually, this upward and rightward trajectory crosses the f nullcline. The burst terminates when g_k exceeds its upper limit, causing f to move towards its nullcline’s lower branch. The trajectory crosses the g_k nullcline once again, causing g_k to move to the left, initiating a new burst.

VIII. Discussion

We presented DSD, an approach to design silicon neurons at the appropriate level of abstraction, epitomized by simple but complete. This approach uses dynamical systems theory to develop equations that describe model neurons. Our work offers a solution to selecting an appropriate level of abstraction, a fundamental challenge in neuromorphic design.

DSD strikes a balance between biologically-detailed top-down and technologically-simple bottom-up approaches, taking strengths from each one. DSD allows the designer to match biological neurons’ dynamics, thereby reproducing much of their computing power. Further, it allows the designer to reproduce these dynamics while maintaining circuit simplicity and density, keeping the system away from the Valley of Death.

We provided a method to transform DSD-derived equations into subthreshold log-domain (current-mode) circuits, an efficient implementation technique. We demonstrated this technique by designing compact neuron circuits that realize regular spiking, square-ware bursting, spike-frequency adaptation, and parabolic bursting. The 1,024 excitatory neurons on the chip presented in this work express a spike-frequency coefficient of variation (CV) between 18 and 25 percent, depending on their settings, whereas we have previously designed neurons with similar behaviors but with greater transistors counts expressing variations close to 100 percent [11], validating the simple but complete axiom.

DSD will remain a viable design strategy as technology advances due to its flexibility. Agnostic to current, voltage, or any physical quantity, DSD simply prescribes the behavior of the system. Such flexibility is crucial to enable the use of whatever circuit medium is available to scale artificial neurons towards the integration density and energy efficiency of neurobiology.

Appendix A.

Transistor Sizes and Capacitor Values

Transistor	Width/Length (μm/μm)	Transistor	Width/Length (μm/μm)
ML, p2, ch3, k	0.7/4.7	Mp1	1.0/1.6
Mr, ca	1.4/2.0	Mch1	1.2/4.7
Mx, out	1.4/3.2	Mch2	1.7/2.5
MF1–3, F5	0.6/2.4	Mres	0.6/1.4
MF4	0.6/2.2
Capacitor	Value (fF)	Capacitor	Value (fF)
Cx	900	Cp	60
Cch	840

Biographies

John V. Arthur received the B.S.E. degree (summa cum laude) in electrical engineering from Arizona State University, Tempe, and the Ph.D. degree in bioengineering from the University of Pennsylvania, Philadelphia, in 2000 and 2006, respectively.

He was a Post-Doctoral Scholar in bioengineering at Stanford University, Stanford, CA, where he worked on the SyNAPSE project. In addition, he was the lead analog and neuron designer for the Neurogrid project, which aims to build a desktop supercomputer for neuroscientists, allowing them to model complex cortical systems of up to 10⁶ neurons at a fraction of the cost of a general purpose supercomputer.

He is currently a research staff member at IBM Almaden Research Center, San Jose, CA. His research interests include dynamical systems design, neuromorphic learning systems, silicon olfactory recognition, generation of neural rhythms, and asynchronous interchip communication.

Kwabena A. Boahen Kwabena A. Boahen is an Associate Professor in the Bioengineering Department at Stanford University. He is a bioengineer who is using silicon integrated circuits to emulate the way neurons compute, linking the seemingly disparate fields of electronics and computer science with neurobiology and medicine. His contributions to the field of neuromorphic engineering include a silicon retina that could be used to give the blind sight and a self-organizing chip that emulates the way the developing brain wires itself up. His scholarship is widely recognized, with over seventy publications to his name, including a cover story in the May 2005 issue of Scientific American. He has received several distinguished honors, including a Fellowship from the Packard Foundation (1999), a CAREER award from the National Science Foundation (2001), a Young Investigator Award from the Office of Naval Research (2002), and the National Institutes of Health Directors Pioneer Award (2006). Professor Boahens BS and MSE degrees are in Electrical and Computer Engineering, from the Johns Hopkins University, Baltimore MD (both earned in 1989), where he made Tau Beta Kappa. His PhD degree is in Computation and Neural Systems, from the California Institute of Technology, Pasadena CA (1997), where he held a Sloan Fellowship for Theoretical Neurobiology. From 1997 to 2005, he was on the faculty of the University of Pennsylvania, Philadelphia PA, where he held the first Skirkanich Term Junior Chair.