An AIMD study of the CPD dimer repair mechanism in water: reaction free energy surface and mechanistic implications

Abstract

In a series of two papers we report the detailed mechanism of cyclobutane pyrimidine dimer repair in aqueous solvent using ab initio simulations. Umbrella sampling is used to determine the free energy surface for dimer splitting. The two dimensional free energy surface for splitting of the C5-C5′ and C6-C6′ bonds on the anion surface is reported. The splitting of the C5-C5′ and C6-C6′ bonds occurs on a picosecond timescale. The transition state along the splitting coordinate in the anion state coincides with a maximum in the free energy along the same coordinate on the neutral surface. The implication is that back electron transfer occurring before the anion reaches the transition state leads to re-formation of the cyclobutane dimer, while back electron transfer after transit through the transition state, leads to successful repair. Based on our calculations for CPD splitting in water, we propose a framework for understanding how various factors, such as solvent polarity, can control repair efficiency. This framework explains why back electron transfer leads predominantly to unsuccessful repair in some situations, and successful repair in others. A key observation is that the same free energy surfaces that control dimer splitting also govern how the back electron transfer rate changes during the splitting process. Configurational changes of the dimer along the splitting coordinate are also documented.

1 Introduction

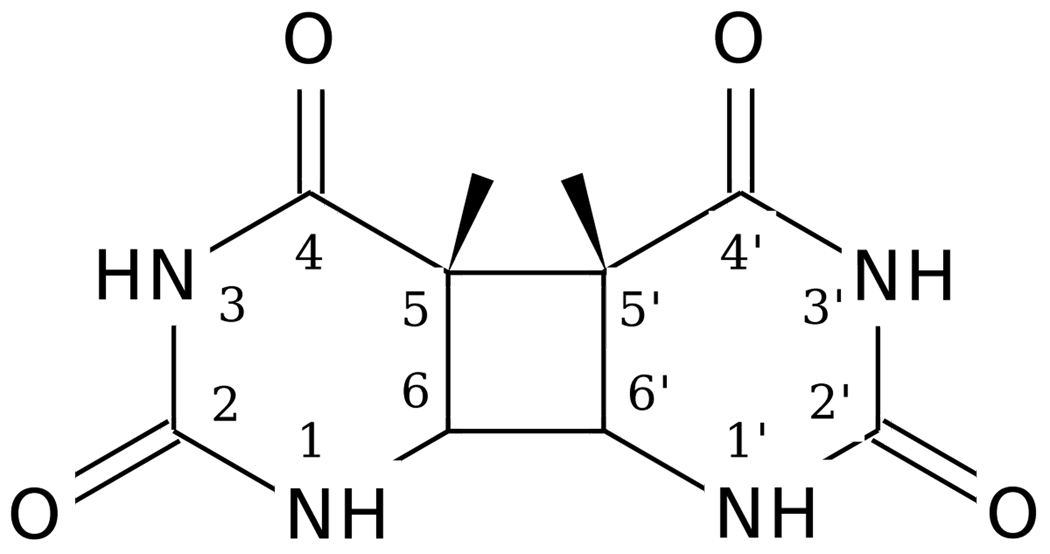
Exposure to far UV radiation induces DNA damage mainly in the form of cyclobutane pyrimidine dimers (CPDs).^1–3 The thymine CPD is shown in Fig. 1. This is the most prevalent mechanism for UV-induced mutations,⁴ and has been implicated as a first step in the generation of tumors.^{5, 6} Cyclobutane dimer lesions can be repaired by the enzyme photolyase, in which absorption of a blue light photon initiates a sequence of photochemical events leading to the injection of an electron at the site of a CPD lesion in DNA. The electron catalyzes the repair of the cyclobutane dimer, splitting the CPD into the original pyrimidine units, and is subsequently recaptured by photolyase. DNA photolyase is not found universally in all organisms: it is not present in placental mammals, but it is found in other organisms, such as archea, bacteria, and some vertebrates.

Figure 1.

Thymine cyclobutane dimer.

Interest in the mechanism of CPD lesion repair is intense because of the health benefits of preventing or reversing events leading to mutations. Mice that have been genetically modified to express photolyase exhibit greatly increased resistance to skin cancer.⁶ There have been many studies of the action of DNA photolyase,^{1, 7} and the electron injection mechanism has recently been directly observed using ultrafast laser spectroscopy.⁸ There have also been many studies of model compounds, usually a CPD moiety linked to an electron donor in which dimer splitting is initiated by photo-induced electron transfer to the cyclobutane dimer.^9–11 Several theoretical studies of photolyase and the dimer splitting reaction^12–14 have also been reported. While significant progress has been made on both the experimental and theoretical fronts, our understanding of the repair mechanism is still far from complete. Ultimately, what is desired is an understanding of the remarkable efficiency of lesion repair catalyzed by DNA photolyase.

Ab initio simulations of the cis,syn-thymine cyclobutane dimer splitting in aqueous solvent are reported in this paper. The motion of both the CPD unit and the solvent are governed by a potential surface calculated using electronic density functional theory. Umbrella sampling has been used to elucidate the free energy surface for dimer splitting. The important role of water has previously been identified in quantum chemical cluster calculations.¹⁴ These calculations only included up to three waters near the CPD unit, too few to build a realistic picture of dimer splitting in solvent but enough to identify the importance of solvent. Dimer splitting within a DNA oligomer has previously been theoretically investigated using QM/MM techniques.¹³ No water molecules were treated quantum mechanically in that study, so issues like charge transfer between dimer and solvent were not addressed. Recently Masson et al.¹⁵ have reported QM/MM simulations of the thymine dimer in the active site of DNA photolyase. In this study, a glutamic acid and the thymine dimer were treated quantum mechanically and proton transfer was found to occur between the carboxylic acid of the glutamic acid and one of the carbonyl oxygens of the dimer. Kawabata and co-workers have performed gas phase ab initio MD simulations of the thymine dimer with both Hartree Fock and B3LYP levels of theory. They find that the C5-C5′ bond breaks spontaneously within the first 100 f s but do not run their simulations long enough to determine the timescales over which the C6-C6′ bond breaks in the gas phase.¹⁶ Our results confirm the crucial role of water, including a significant degree of charge transfer between the CPD and neighboring water molecules, not reported in any previous theoretical treatments because the models used in these studies could not describe charge delocalization on to the solvent.^12–15 Furthermore, water motions also emerge as a critical part of the reaction coordinate, facilitating the splitting process.

Splitting of CPD radical ions has been experimentally studied using a series of model compounds, or within the active site of photolyase. The results of our work are most relevant to the model compound literature, which has been reviewed on several occasions.^{2, 17–19} Model compound studies involve a CPD which is either tethered to a chromophore that donates an electron upon photoexcitation, or in solution with a sufficient concentration of electron-donating chromophores, or simple CPDs exposed to a source of electrons such as ionizing radiation. Model compounds offer an opportunity to investigate the basic reactions without the complexity of the enzymatic environment. Some of the earliest work on model compounds found that CPD anions did not split at liquid nitrogen temperature.⁹ Later studies found that dimer splitting was facile at 77K.^{20, 21} Model compound experiments in which an indole-based chromophore was tethered to the CPD have tended to exhibit increased dimer splitting efficiency in non-polar solvents,^{22, 23} leading to the conclusion that the back electron transfer which competes with splitting was in the inverted Marcus regime. Three recent works by Song et al. observed the opposite trend with respect to solvent polarity using indole-based chromophores with longer tethers,^{10, 11, 24} and suggested that the length of the tether may account for the opposite trend. Flavin-based chromophores have tended to induce more efficient dimer splitting with increasing solvent polarity.^{2, 19} In this work we use our ground state calculations to provide a framework for understanding the molecular mechanisms by which back electron transfer and bond splitting compete and hence affect the quantum yields of repair in different solvent environments.

Experiments have suggested various time scales for the splitting of CPD anions in solution. Yeh and Falvey found that splitting of the thymine dimer, triggered by electron transfer from N,N-dimethylanaline in aqueous solution following a nanosecond laser pulse, was slow enough to follow spectroscopically on the millisecond time scale.²⁵ Other studies have observed much faster rates of dimer splitting.²¹ A recent study in which dimer splitting was induced using electrons from ionizing radiation found that solvated electrons were consumed at essentially the same rate as dimers were split, and gave an upper limit of 35ns for the splitting time scale.²⁶ Hopefully, progress in the theoretical description of dimer anion splitting will provide clues that will help reconcile these various reports.

In this paper we report our results on the molecular mechanisms involved in the repair of the cyclobutane thymine dimer in water, treating the electronic degrees of freedom for all the thymine dimer atoms and the surrounding water molecules. We begin in section 2 by reviewing the computational methods used in our calculations. In section 3 we illustrate the 1D profiles for splitting of the C5-C5′ and C6-C6′ bonds, in addition to the 2D free energy surface, showing the remarkable acceleration in splitting achieved compared to the large activation barrier for splitting the neutral dimer. We also estimate the splitting rate of the C6-C6′ bond from our umbrella sampling simulations using classical transition state theory. The fate of the dimer after back electron transfer once it has returned to the neutral surface is explored in section 4. In section 5 we advance a simple model using our ground state calculations that illustrates the mechanism by which environmental factors such as solvent polarity affect the extent of competition between the splitting process and back electron transfer. Finally we end with conclusions of our work in section 6. Configurational changes of the dimer during the splitting process are documented in the Supporting Information.

2 Molecular dynamics, umbrella sampling, andWHAM

2.1 Electronic structure methods for ab initio simulation

Ab initio molecular dynamics simulations of the thymine CPD were conducted using Quickstep which is part of the CP2K package.^{27, 28} In these calculations, ab initio Born-Oppenheimer molecular dynamics is used for propagation of the classical nuclei. The electronic orbitals are converged to the Born-Oppenheimer surface at every step in the molecular dynamics simulation. The wave function was optimized using an orbital transformation method²⁹ in conjunction with the DIIS scheme,^{30, 31} as described in Ref.28. The convergence criterion for optimization of the wave function was set to 10⁻⁶. Using the Gaussian and plane waves (GPW) method, the wave function was expanded in the Gaussian DZVP basis set. An auxiliary basis set of plane waves was used to expand the electron density up to a plane wave cutoff of 300Ry. We used the Becke-Lee-Yang-Parr gradient correction^{32, 33} to the local density approximation and Goddecker-Tetter-Hutter (GTH) pseudopotentials.³⁴ In all anion simulations the local spin density approximation (LSD) is used for the exchange-correlation energy.

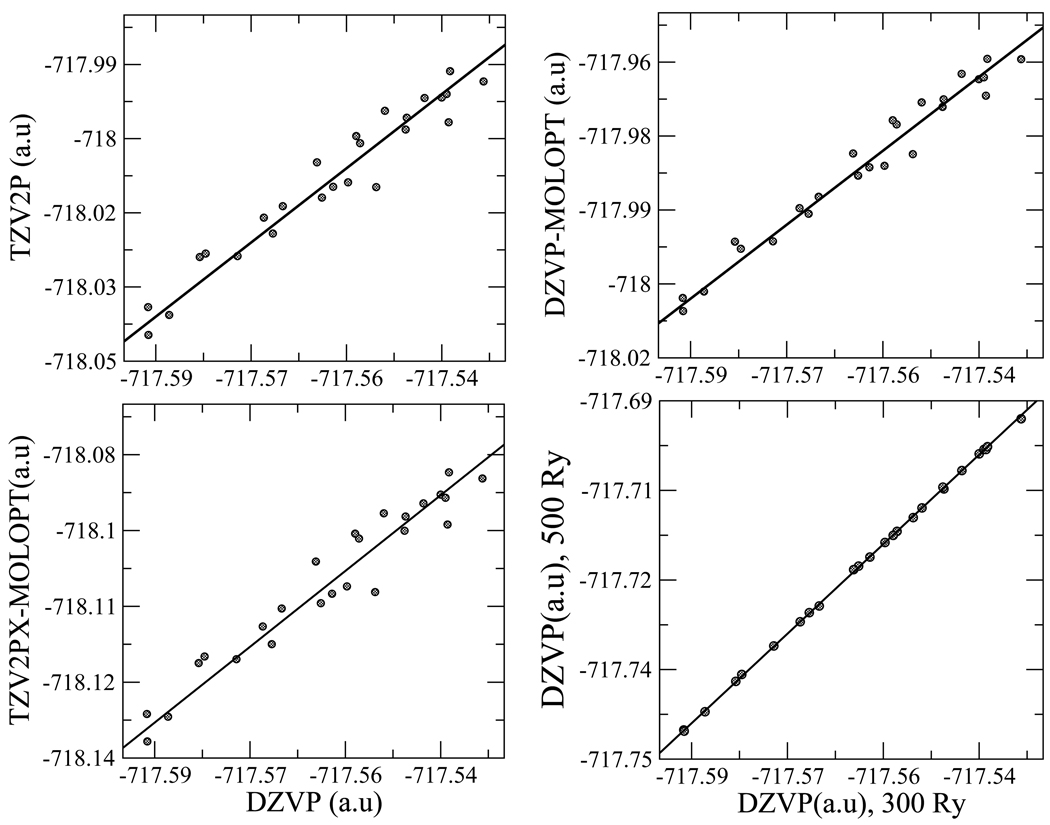
Shown in the top left panel of Fig. 2, is a comparison of DZVP and TZV2P basis set energies in a box size of 9.8Å including all the 32 waters which is the system we use in our simulations below. The TZV2P basis set is too costly for use in the umbrella sampling calculations reported below, but we were able to compare double and triple zeta basis sets at isolated configurations picked at various points across the splitting of the C5-C5′ bond. In the top right panel and bottom left panel of Fig. 2 we show a comparison of DZVP and DZVP-MOLOPT, and DZVP and TZV2PX-MOLOPT basis set (molecularly optimized) energies respectively, for the same set of configurations. The molecularly optimized basis sets include diffuse functions with small exponents for all primitive functions and have been shown to outperform basis sets of similar or slightly larger size³⁵ but are also too costly to employ in the calculation of free energy surfaces, which require extensive sampling. The slope of the solid black line in all the panels is very close to 1 (see figure caption), but the scatter from the line in Fig. 2 indicates the DZVP calculations are not fully converged with respect to basis set. The RMSD of the DZVP and TZV2P energy data sets is 3.76 × 10⁻³a.u while that of the DZVP and DZVP-MOLOPT energy data sets is 2.77 × 10⁻³a.u. The RMSD between the DZVP and TZV2PX-MOLOPT basis set was 3.91 × 10⁻³a.u. These are of the magnitude of typical errors that are inherent in this DFT method compared to more rigorous electronic structure methods.^{36, 37} As seen in the bottom right panel of Fig. 2, increasing the plane wave cut-off from 300Ry to 500Ry had almost no effect on the energy differences.

Figure 2.

Comparison of DZVP, TZV2P, DZVP-MOLOPT and TZV2PX-MOLOPT energies in a box of length 9.8Å with 32 waters. The solid line in all the panels indicates a linear fit with slope of 1.00064(top left), 1.00059(top right), 1.00076(bottom left) and 1.00022(bottom right). Shown in the bottom right panel is a comparison of DZVP energies using 300Ry and 500Ry for the plane wave cutoff.

Errors due to finite box size effects is always a concern in ab initio MD simulations. Repeating all our umbrella sampling calculations for larger box sizes is computationally intractable. In order to test the sensitivity of some of our results to smaller box sizes, we have repeated some our non-equilibrium calculations reported in our companion paper,³⁸ for a box of side length 12.35Å including a hydration pocket of 64 waters. The results indicate that the splitting times of the C5-C5′ and C6-C6′ bond, the signatures for non-equilibrium effects and role of solvent in the splitting process, are present in both small and larger system sizes. Details of these effects in the splitting process are reported in our companion paper.³⁸

2.2 Computational Methods

A time step of 0.5 fs was used in all simulations. The system consists of the thymine dimer solvated by 32 waters in a cubic periodic box of side length 9.8Å. The umbrella sampling simulations were performed within the NVT ensemble using the Nosé thermostat^{39, 40} with a time constant of 0.2ps. The system temperature was maintained at 300K in the simulations. Several powerful methods have been developed for determining free energies from simulations. Some of the most popular techniques are umbrella sampling,⁴¹ Jarzynski’s identity based on non-equilibrium sampling,⁴² adaptive force bias,^{43, 44} and more recently metadynamics.⁴⁵ The weighted histogram analysis method^{46, 47} (WHAM) greatly improves the accuracy and efficiency of combining distributions from umbrella sampling,^{48, 49} and this combination was our choice for determining the reaction free energy surface for dimer splitting.

Umbrella sampling allows the system to sample regions that are otherwise explored infrequently in the microcanonical or canonical ensemble by constraining the system along a specific reaction coordinate η(r^N), where r^N denotes the Cartesian coordinates of all particles in the system. A biasing harmonic potential W_i(η(r^N)) = k(η(r^N) − η_i)² confines the system in a specific window i. The unbiased probability distribution for the ith window ${\rho }_i^u(\eta )$ for the reaction coordinate η is expressed in terms of the biased probability ${\rho }_i^b(\eta )$ which is accumulated under the influence of the window potential W_i(η) obtained from our simulations as,

$${\rho }_i^u(\eta )=\text{exp}(\beta [W_i(\eta )-C_i]){\rho }_i^b(\eta )$$ (1)

The constants C_i could be determined by matching ${\rho }_i^b(\eta )$ at the boundary between adjacent windows as in the original formulation of umbrella sampling by Torrie and Valleau,⁴¹ but are more efficiently and accurately determined in the WHAM method^{46, 48, 49} by writing the total probability distribution ρ(η) as a weighted sum of contributions from each of the windows,

$$\rho (\eta )=C{\displaystyle \sum _{i=1}^{N_w}}{w}_i(\eta ){\rho }_i^u(\eta ),$$ (2)

where C with no subscripts is an overall normalization constant and N_w is the number of windows used. The weights w_i(η), are normalized such that

$${\displaystyle \sum _{i=1}^{N_w}}{w}_i(\eta )=1,$$ (3)

and are chosen in such a manner that the total error in ρ(η) is minimized at each value of η.^{46, 48, 49} In our analysis, a convergence criterion of 10⁻¹² was used for determining the constants C_i.

Previous work^{12–14, 50, 51} and our own preliminary studies suggest that the C5-C5′ and C6-C6′ bond lengths are essential reaction coordinates. We have found that a detailed and complete mechanism of splitting must explicitly involve additional reaction coordinates to understand the crucial role of the surrounding solvent. Including an additional solvent reaction coordinate modifies the splitting rate of the C5-C5′ bond. However, it does not affect the qualitative conclusions presented in this paper, and the two-dimensional free energy surface with respect to the C5-C5′ and C6-C6′ bond lengths presented in this work, is a useful starting point. Details of the role of solvent in the splitting process are discussed in a companion paper.³⁸ As will be shown later, the initial reaction path is mainly along the C5-C5′ coordinate, while the later stages of the splitting reaction involve more motion along the C6-C6′ distance. The reaction coordinate η(r^N) was first chosen to be the C5-C5′ distance to explore the initial cleavage of the C5-C5′ bond on the anion surface. 20 windows were placed to constrain the C5-C5′ distance between the range of 1.6–2.7Å.⁵² For the cleavage of the second bond on the anion surface, the C6-C6′ bond length was subsequently chosen as the reaction coordinate. 33 windows were placed to constrain the C6-C6′ distance between the range of 1.6–3.0Å.⁵³ We also conducted umbrella sampling simulations for the neutral surface along the C5-C5′ coordinate to estimate the extent of kinetic trapping in this state. 19 windows were placed to constrain the C5-C5′ distance within the range of 1.6–2.75Å⁵⁴ in these simulations. The force constant k for the harmonic potentials in all the windows for the anion system was 448.175 kcal mol⁻¹Å⁻² while that of the neutral system was 559.788 kcal mol⁻¹Å⁻². These force constants ensured that in each of the windows, the system sampled a region in which the reaction free energy surface varied by an amount comparable to k_BT. The combination of k and window placement gave good overlap between the distributions. Even though just one reaction coordinate was constrained during any of the umbrella sampling runs, we could still extract a two- (or, in principle, n-) dimensional free energy surface by accumulating probability distributions along several degrees of freedom within each umbrella sampling window. Thus, we are able to construct a two-dimensional free energy surface in the reaction variables C5-C5′ and C6-C6′.

Each window was equilibrated for 1ps. In order to gauge the sensitivity of the free energy curves to the simulation length, the curves for the anion system were first constructed from ~ 4–5ps umbrella sampling trajectories and then compared with an aggregate trajectory consisting of an additional trajectory of equal length or greater for each window. The good agreement between the free energy curves constructed from the short and longer umbrella sampling trajectories suggest convergence with respect to simulation length. The umbrella sampling windows between point 1 and point 2 labeled in Fig. 4, were run for an additional ~ 4–5ps. For the neutral system, the free energy curve along the C5-C5′ bond was constructed from umbrella sampling trajectories most of which were ~ 6–8ps in length. Longer sampling times are computationally prohibitive. However, a comparison of the splitting dynamics predicted from the equilibrium free energy curves obtained from the umbrella sampling simulations with non-equilibrium trajectories, indicate that our umbrella sampling simulations adequately predict the timescales and mechanisms associated with splitting of both the C5-C5′ and C6-C6′ bonds. An analysis of our non-equilibrium trajectories of the splitting of the C5-C5′ and C6-C6′ bonds, is the subject of our companion paper.³⁸

Figure 4.

Free energy surface for lengthening the C6-C6′ bond of the thymine CPD anion in water. The solid curve was obtained from ~ 4–5ps trajectories in each umbrella sampling window, the dashed curve from trajectories at least double in length.

3 Free energy surfaces

In this section we present results from the umbrella sampling free energy calculations. In order to demonstrate the remarkable acceleration of the dimer splitting kinetics which is caused by the injection of an electron, we conducted umbrella sampling simulations on both the anion and neutral thymine dimer systems. For the neutral surface, we limited umbrella sampling runs to the part of the C5-C5′ coordinate where the C6-C6′ bond did not split, which was sufficient to demonstrate the enormous activation energy needed for bond breaking on the neutral surface. We first lay out the overall topography of our free energy surfaces along the C5-C5′ and C6-C6′ coordinates for the anion surface and then use TST to estimate the splitting time of the C6-C6′ bond.

3.1 Anion: C5-C5′ and C6-C6′

Both experimental⁸ and theoretical^13–15 studies have established that adding an electron to the thymine dimer results in the cleavage of both bonds. The present work provides information about the free energy surface for the process of bond breaking in aqueous solution. This surface determines the reaction path and whether the process is concerted or not. Shown in Fig. 3 is the free energy curve associated with the breakage of the C5-C5′ bond. There is in fact a small barrier of 0.6 kcal mol⁻¹ for the cleavage of this bond. However, this barrier is so small, roughly k_BT at room temperature, that the time scale for escape over the barrier would be comparable to relaxation in the reactant well (left hand corner of Figs. 3 and 5) and transition state theory is not meaningful in this situation. Durbeej and Eriksson⁵⁵ conducted gas phase optimizations of the thymine dimer using DFT and found the breakage of the C5-C5′ bond to be barrierless. However Voityuk et al.,¹² who conducted gas phase optimizations of the thymine dimer in continuum solvents at the AM1 level of theory, found significant barriers for the breakage of the C5-C5′ bond. The small barrier shown in Fig. 3 for the splitting of the C5-C5′ bond and the 2D surface in Fig. 5, suggest that the system will rapidly move to the local free energy minimum where the first bond is partially cleaved on addition of an electron. In our companion paper,³⁸ we will demonstrate that multidimensional or non-equilibrium effects can change the underlying mechanism and timescale associated with splitting of the C5-C5′ bond although the overall timescale for splitting of both bonds occurs within several picoseconds.

Figure 3.

Free energy surface for lengthening the C5-C5′ bond of the thymine CPD anion in water. The solid curve was obtained from ~ 4–5ps trajectories in each umbrella sampling window, the dashed curve from trajectories at least double in length.

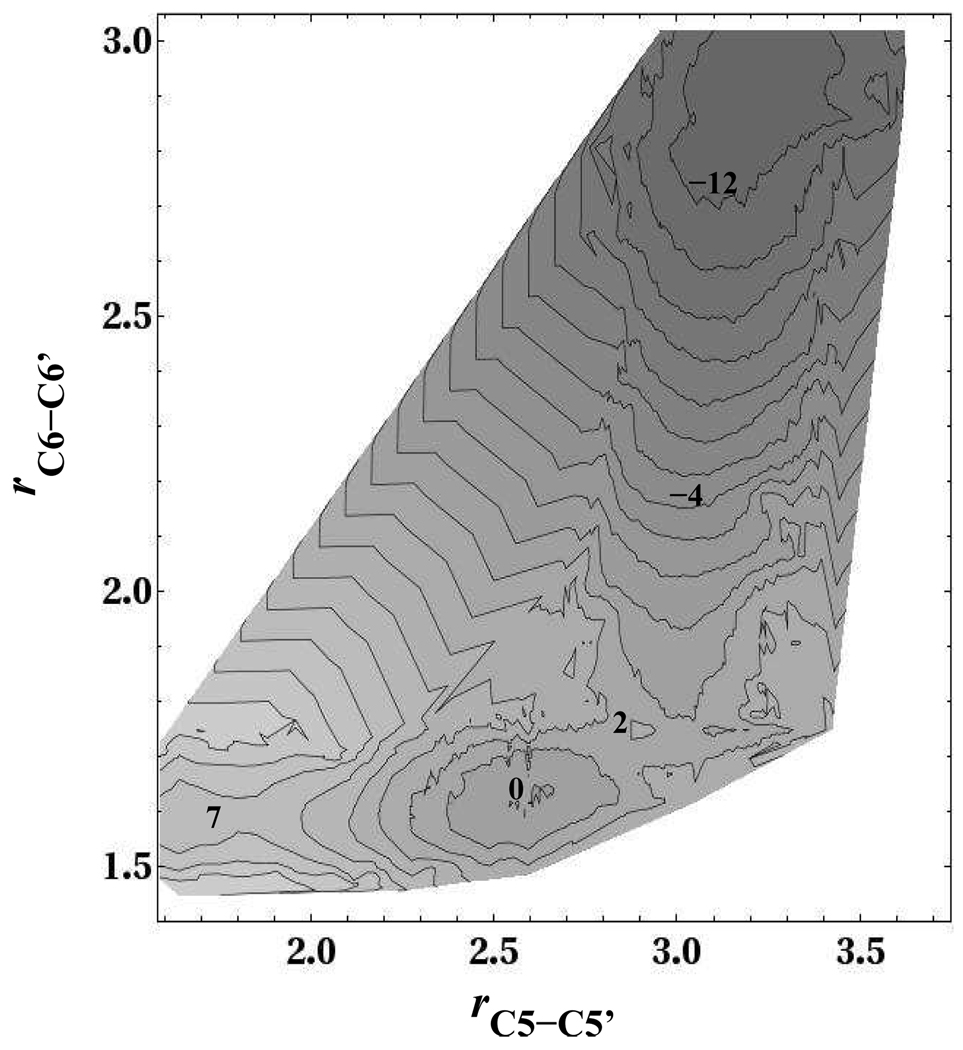
Figure 5.

Overall reaction free energy surface for thymine CPD anion repair (kcal mol⁻¹). The free energy well in which the C5-C5′ bond is broken and the C6-C6′ bond is intact (r_C5−C5′ = 2.57Å, r_C6−C6′ = 1.61Å) is assigned as the zero of energy. The energy value on several contours is labeled.

We now turn our attention to the rate-limiting part of the bond splitting process that involves the cleavage of the C6-C6′ bond. The free energy curve along the C6-C6′ coordinate (Fig. 4) shows a small barrier of 1.5 kcal mol⁻¹, followed by a release of 14.6 kcal mol⁻¹ after passage over the barrier. In Fig. 4 we have labeled four points for future reference: Point 1 is the partially cleaved free energy minimum where the C5-C5′ bond is broken while the C6-C6′ bond is intact. Point 2 is the transition state for C6-C6′ bond splitting. Point 3 is intermediate between the transition state and cleaved products. Finally, at point 4 both bonds are cleaved. If our system were at high dilution and not in a periodically replicated simulation cell, the two thymine bases would eventually diffuse from each other after splitting, beyond point 4 in Fig. 4. Our barrier height of 1.5 kcal mol⁻¹ is in excellent agreement with Masson et al.’s^{13, 15} upper bound estimate of the barrier of 2.5 kcal mol⁻¹ that was found for both self-repair in DNA and photolyase protein environments. The overall reaction free energy starting at the partially cleaved local minimum (from point 1 to point 4 in Fig. 4) is 13.1 kcal mol⁻¹. The conformational changes during splitting of the thymine CPD anion is better described by a two-dimensional free energy in the C5-C5′ and C6-C6′ distances (Fig. 5). This surface was obtained by accumulating histograms in the C6-C6′ distance while the C5-C5′ distance was constrained by umbrella sampling, and then accumulating histograms in the C5-C5′ distance while the C6-C6′ distance was constrained by umbrella sampling (Fig. 4). The two data sets were aligned by setting the bottom of the free energy well in which the C5-C5′ bond is broken and the C6-C6′ bond is intact (r_C5−C5′ = 2.57Å, r_C6−C6′ = 1.61Å), which is shared by the two data sets, to the same arbitrary value, zero. Fig. 5 reveals that during the splitting of the C5-C5′ bond the C6-C6′ bond is intact, although there is a minor opening of the C6-C6′ bond. During this stage of the repair the C5-C5′ bond length widens from 1.60Å to 2.57Å. After cleavage of the C5-C5′ bond, further lengthening of the C5-C5′ bond by 0.35Å and somewhat smaller, but still significant lengthening of the C6-C6′ bond by 0.14Å is required to reach the transition state for cleavage of the C6-C6′ bond. After passage through this transition state, the reaction proceeds mostly by major lengthening of the C6-C6′ bond by 1.2Å and minor lengthening of the C5-C5′ bond by about 0.2Å which completely cleaves both bonds. The difference in average potential energy between points 1 and 4 of Fig. 4 is 12.6±2.0 kcal mol⁻¹. Since the overall splitting free energy is 13.1 kcal mol⁻¹, this indicates that entropic contributions are small.

Our free energy curves indicate that the total free energy of splitting starting from the equilibrium configuration of the unsplit neutral dimer is −19.8 kcal mol⁻¹. This is in fairly good agreement with the splitting energy of −21 kcal mol⁻¹ reported by Wiest and co-workers¹⁴ for a uracil anion cluster with 3 waters at the B3LYP level of theory, although the splitting mechanism is different and specific for their fragment system. They find a barrier of 1.1 kcal mol⁻¹ for the cleavage of the C5-C5′ bond while the splitting of the C6-C6′ bond is found to be barrierless. The calculations of Wiest et al. do not incorporate thermal effects as they perform geometry optimizations of their uracil dimer with 3 waters. The only available experimental data to our knowledge on the free energy of splitting of pyrimidine dimer anions is by Falvey and co-workers⁵⁶ who report a free energy of splitting of −20 kcal mol⁻¹, with which our value of −19.8 kcal mol⁻¹ is in good agreement.

3.2 Estimates of k_split

From our free energy surfaces, we can estimate k_split for the bond breaking process. The rate-determining step is the cleavage of the C6-C6′ bond. The probability that reactants thermalized in the partially cleaved state will sample the transition state can be calculated using the data in Fig. 4. The transition state theory rate for cleavage of the C6-C6 bond is evaluated from the following expression,

$$k_{\mathit{\text{split}}}=\frac{\langle |v|\rangle }{2}P(|{\mathbf{r}}_{C6}-{\mathbf{r}}_{C6\prime }{|}_{\mathit{\text{TST}}})=2.0\times {10}^{12}{s}^{-1},\frac{1}{k_{\mathit{\text{split}}}}=0.5\mathit{\text{ps}}$$ (4)

The effective mass used for determining the velocity 〈|v|〉 was 6a.u, the reduced mass for a pair of carbon atoms. Calculating the transition state theory rate from a 2D model using our free energy surface in Fig. 5 barely affected k_split. Our TST estimate of 0.5ps is rigorously a lower bound to the splitting time. These results are consistent with recent theoretical studies that demonstrate the ultra-fast nature of CPD splitting within a DNA duplex and in photolyase.^{13, 15} They are also consistent with a recent pulse radiolysis study in which the products of CPD anion splitting in water appeared at the same rate at which hydrated electrons were consumed.²⁶ This experiment provides an upper bound to the rate of splitting. The time scale for reaction of $e_{\mathit{\text{aq}}}^{-}$ with thymine CPD was 35ns, so the splitting time had to be negligible compared to this time scale. In this same work, using B1B95 DFT gas phase calculations of the thymine dimer with the phosphate backbone, Chatgilialoglu et al.²⁶ estimated a barrier of 3.2kcal mol⁻¹ for splitting the C6-C6′ bond. Assuming a negligible temperature dependence of the back electron transfer, Song and co-workers¹¹ determined the temperature dependent splitting efficiency of model compounds where the CPD is tethered to an indole and predicted an activation barrier for splitting of 0.45kcal mol⁻¹ in equal glycerol/water mixtures as the solvent. These experimental results corroborate our theoretical predictions of the splitting rate.

Kao et al. tracked the dynamics of thymine dimer repair in photolyase using femtosecond spectroscopy.⁸ They observed electron donation from the FADH^−* to the dimer on a time scale of 170ps when the data is fit to a stretched exponential, or 60 and 335ps time scales when the data is fit to a double exponential. The FADH· intermediate was directly monitored, and its decay following return of the electron after dimer splitting occurred on a stretched exponential time scale of 560ps. Since the dimer splitting efficiency was close to 100%, 560ps is an upper bound to the inverse dimer splitting rate. If dimer splitting was the rate-determining step for the 560ps process, this would either indicate that we underestimated the activation energy for dimer splitting by 4.2kcal mol⁻¹, or that the activation free energy for dimer splitting is somewhat higher when the enzyme is in the active site of photolyase. Alternatively the actual dimer splitting may not be the rate-determining step for electron return to the excited FADH· co-factor. This is possible in a scenario where the splitting of the C5-C5′ and C6-C6′ bonds occurs on a fast timescale, after which the electron resides on the dimer with both C5-C5′ and C6-C6′ bonds split awaiting back ET. It is worth noting that several gas-phase studies have shown that an error of 2–3kcal mol⁻¹ would not be surprising in the energetics obtained from DFT calculations.^{36, 37} The accuracy of our calculations could also be affected by the finite box size. It should also be noted that the splitting of CPD anion occurs in the vicinity of the electron donor in the enzymatic system as well as in model compounds. At this point we cannot rule out the possibility that these differences could affect the splitting process.

3.3 Neutral

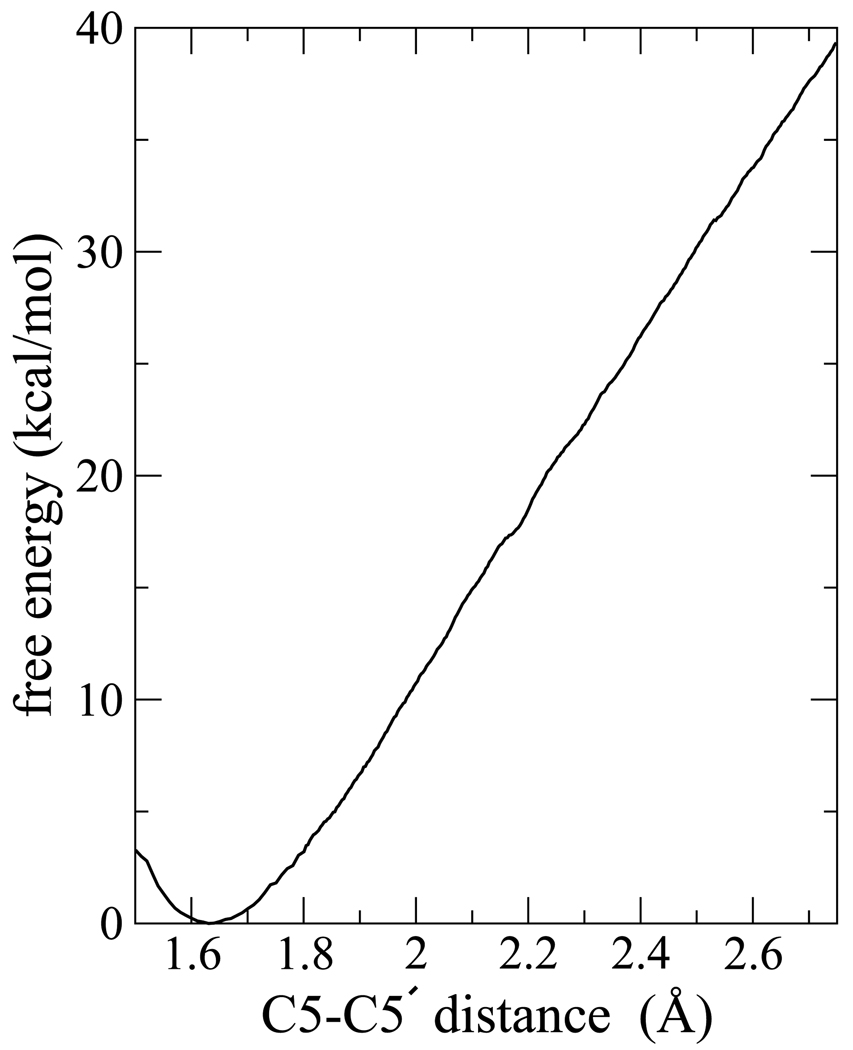
Shown in Fig. 6 is the free energy curve along the C5-C5′ coordinate for the neutral thymine dimer, confined to the region where the C6-C6′ bond remained intact. We did not extend our umbrella sampling calculations for the neutral dimer to include the C6-C6′ bond coordinate, so the full reaction path and splitting barrier was not obtained, as it was for the anion. However, the data in Fig. 6 shows that a lower limit for the barrier is approximately 39 kcal mol⁻¹. From the simulation of the neutral dimer and split neutral fragments, we also determined that the difference in average potential energy between the split neutral products (both C5-C5′ and C6-C6′ split) and unsplit neutral reactants (both C5-C5′ and C6-C6′ uncleaved) is approximately −23.3±3.0 kcal mol⁻¹ showing that the splitting reaction is exothermic on the neutral surface, and by roughly the same amount as splitting on the anion surface. At room temperature, the minimum barrier of 39 kcal mol⁻¹ will not be overcome by thermal fluctuations and the system would be kinetically trapped in this state, as observed experimentally. Without repair, the cyclobutane dimer remains within the DNA and would ultimately prevent DNA replication and lead to mutations and possibly cell death.⁸

Figure 6.

Free energy surface for lengthening the C5-C5′ bond in neutral thymine dimer.

Recently there has been an interest in understanding the mechanisms by which UV radiation leads to the thymine dimer photoproducts. Experiments have shown that thymine dimers are formed within 1ps after photoexcitation.⁵⁷ Dimer formation is the inverse of the reaction we study. Therefore, we can exploit experimental and theoretical results pertaining to dimer formation to test some of our findings. On the neutral ground state surface, the thymine bases must surmount a large activation barrier to form the CPD dimers. Unfortunately, there have been no theoretical studies to our knowledge reported on the splitting or dimerization of neutral thymines in solvent. However, we can compare our relative energetics to recent work by Robb and coworkers⁵⁸ who have performed high level gas phase CASSCF and CASPT2 calculations to determine the dimerization barrier of thymine bases on the ground state and first singlet excited state. Robb et al. report a barrier of approximately 41kcal mol⁻¹ to reach the TST in the direction of splitting starting from the closed dimer. This compares well with our lower limit of 39kcal mol⁻¹. They also report that the split thymine neutral products (in their case the reactants for a dimerization process) is 19kcal mol⁻¹ more stable than the unsplit reactants (in their case the products for dimerization) which is in good agreement with our predicted value of the potential energy difference of approximately 23kcal mol⁻¹. Our results are also consistent with experimental estimates of −19kcal mol⁻¹ for the enthalpy of splitting of neutral dimethyl thymine dimers (DMTD) using photothermal techniques.⁵⁶ Diogo and co-workers report a splitting enthalpy of −26kcal mol⁻¹ of a derivative pyrimidine photodimer.⁵⁹

4 Back electron transfer (BET) from anion dimer

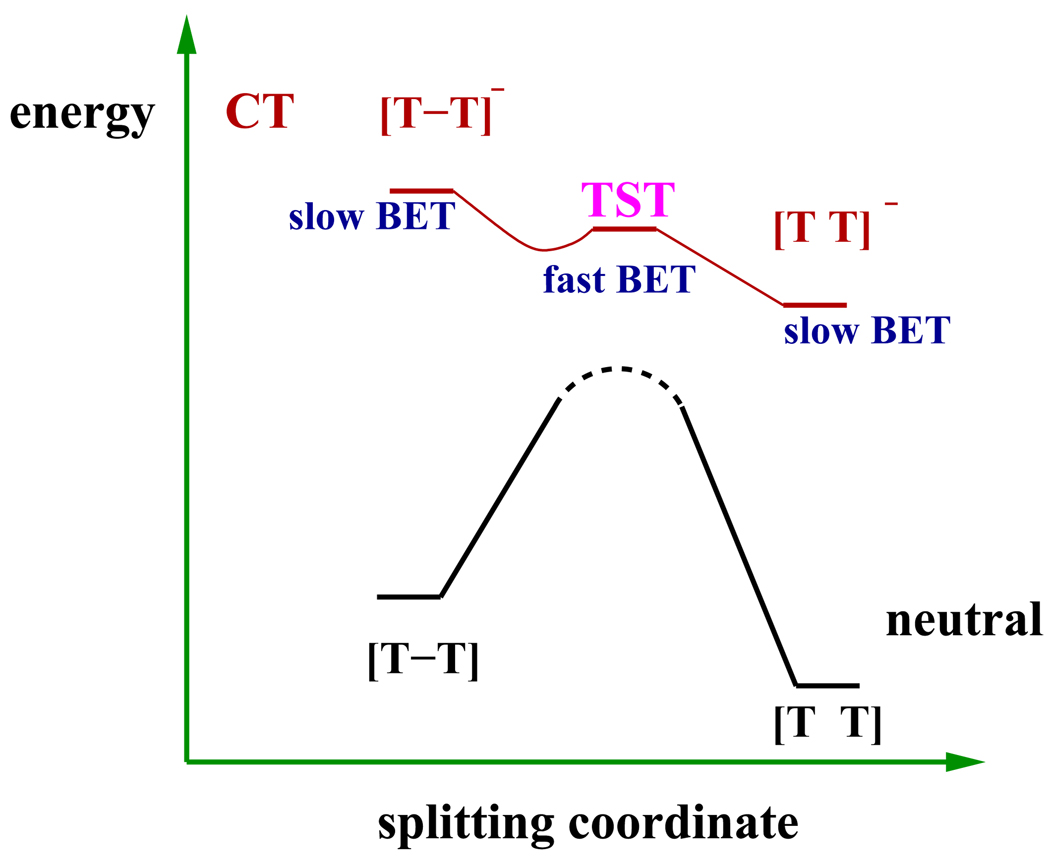
An important aspect of the repair mechanism as it has been examined in experiments to date⁸ is the back electron transfer (BET) process from the anion dimer to the electron donor. While detailed modeling and understanding of the BET process is beyond the scope of this work, we address aspects of BET that we believe play a crucial role in the repair process. BET is essential for the completion of biological repair insofar as the split anion is not yet a healed DNA segment (see Fig. 10 below). Where and when the BET occurs during the splitting process can either result in ring reclosure (no repair) or completion of splitting on the neutral surface. The fate of the complex following BET, failed or successful repair, will depend on the spatial arrangement of the complex at the instant of BET.

Figure 10.

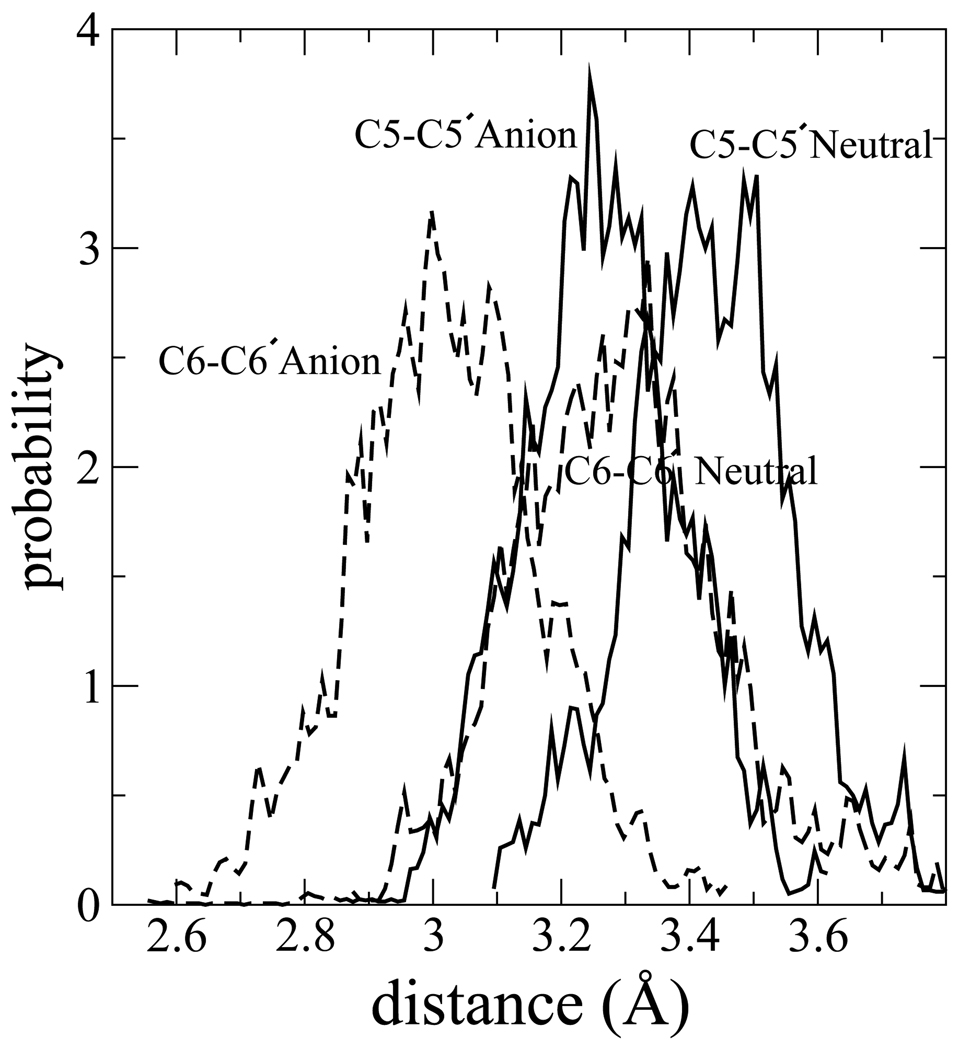
Distribution of C5-C5′ (solid) and C6-C6′ (dashed curves) distances before and after back ET on anion and neutral surfaces. In each case, the distribution on the neutral surface lies at larger distances compared to the anion.

In the absence of an explicit donor cation to re-accept the electron, we model the back ET process simply as a vertical detachment of the electron from the anion placing the system on the neutral surface. This assumption neglects the bias of initial conditions for the system following electron transfer in favor of fluctuations needed to bring the system to the transition state for electron transfer. These assumptions do not allow us to determine the rate of back ET to a particular donor, but do allow us to address some important issues regarding the role of back ET in DNA repair. Assuming that the back ET can occur on the same timescale as splitting or faster, we can determine how far along the dimer splitting reaction coordinate the system must be before back ET leads to successful ring opening, and not reclosure of the CPD dimer. Conceivably, this point may be quite different from the dimer splitting transition state. However the results presented below indicate that the point where back ET generally leads to an equal number of ring opening and ring closure events is rather close to the dimer anion transition state, lying slightly before the transition state is reached from the reactant side on the anion surface.

We selected 653 statistically independent configurations from our umbrella sampling windows at various points before and after the transition state. All 653 configurations obtained from sampling the dimer anion were propagated with energy conserving dynamics on the neutral surface for 120fs which was sufficient time to distinguish eventual ring closing from successful repair. Fig. 7 shows that once back ET takes place, ring closure or splitting of the C5-C5′ and C6-C6′ bonds is complete within 80fs. The population that undergoes ring closure after back ET quickly equilibrates into the deep well of the neutral free energy profile in the left hand corner of Fig. 6. Similarly, for the population that undergoes splitting after back ET, both the C5-C5′ and C6-C6′ bonds rapidly move toward the split products indicating that a one-dimensional downhill free energy profile beyond the free energy maximum on the neutral surface is sufficient for describing the evolution of the system after back ET has occurred.

Figure 7.

Dynamics of a) C5-C5′ or b) C6-C6′ bond length after back ET leading to either ring closure (gray curves) or ring splitting (black curves)

The location of the circles in Fig. 8 indicates the sampling of initial C5-C5′ and C6-C6′ bond distances among the 653 trajectories that were propagated on the neutral surface to model back electron transfer (BET). The initial conditions for trajectories that were propagated on the neutral surface are shown in Fig. 8 relative to the same free energy surface shown in Fig. 5. The open white circles represent initial points that lead to ring splitting while the solid circles represent points that led to ring closure. Although there is some overlap in the distribution of white and black circles along the C5-C5′ and C6-C6′ coordinates, there is a critical region, roughly 0.2Å before the dimer anion splitting transition state, where the quantum yield for successful repair shifts from near zero to almost unity. The bifurcation between trajectories leading to ring re-formation and splitting in Fig. 8 implies a free energy maximum along splitting coordinates of the neutral surface in this region, but not necessarily a transition state. The initial conditions in Fig. 8 are sampled near the minimum free energy path of the anion surface, not the neutral. Therefore the free energy maximum implied by the circles in Fig. 8 is not necessarily a saddle point on the neutral surface, and is not a transition state for the splitting reaction on the neutral surface.

Figure 8.

Overall free energy surface with open white circles for trajectories that split after back ET and solid black circles for trajectories that close after back ET.

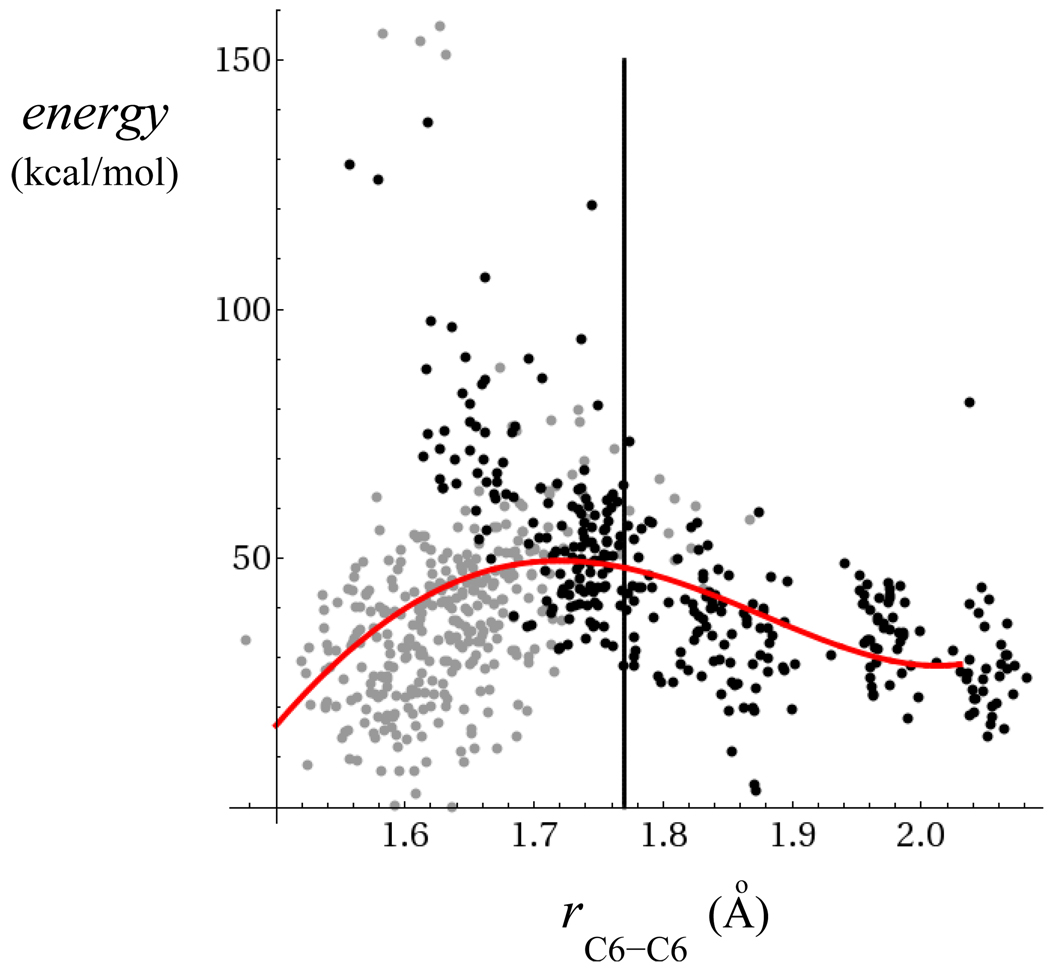
Fig. 9 furnishes further evidence that a free energy maximum on the neutral surface along the C6-C6′ bond is quite close to that on the anion surface. Fig. 9 is a scatter plot of the potential energies (the potential energies have been uniformly shifted relative to their minimum value) on the neutral surface at time t = 0 after back ET has occurred as a function of C6-C6′ bond distances shown for both ring splitting and ring closure trajectories. Fig. 9 shows that average potential energy on the neutral surface has a maximum slightly before the anion surface TST, the latter indicated with a vertical solid line in Fig. 8. The maximum of the neutral surface potential energies lies close to where trajectories shift from mostly reclosing to mostly splitting, suggesting that the energy maximum is also a free energy maximum, entropic effects are minor, and that Fig. 9 is an approximate cut through the neutral free energy surface in the vicinity of the anion splitting reaction path. Both Figs. 8 and 9 indicate that many of the trajectories that begin on one side of the free energy maximum on the neutral surface, equilibrate into minima on the opposite side of the maximum. This indicates that there could be other coordinates coupled to the dynamical evolution of the trajectories once BET occurs, possibly describing collisions with the surrounding solvent.

Figure 9.

Potential energies on the neutral surface at time t = 0 after BET for splitting trajectories (solid grey circles) and trajectories undergoing ring closure (solid black circles). The vertical solid line is the position of the TST on the anion surface. The solid red line is a 4th order polynomial fit through the data that highlights the overall trend.

Our results suggest that once the CPD anion reaches its product well where both bonds are split, BET from this region will never result in dimer reformation. However, BET from the split product well is needed to complete the repair process. The split anion system has a distribution of bond lengths distinct from the neutral base pair, even when splitting is initially achieved and before the fragments have a chance to separate in solution. In Fig. 10 we show the equilibrium distances of the broken C5-C5′ and C6-C6′ bonds on the anion and neutral surface. The results indicate that the equilibrium broken C5-C5′ and C6-C6′ distances are longer on the neutral surface than on the anion surface. Configurational adjustment, especially in the C6-C6′ distance, will take place after back ET while the base pairs are still adjacent in solution. The geometry re-arrangement that we observe once the electron is vertically detached from the anion surface to the neutral surface is consistent with observations made by Adamowicz and co-workers⁶⁰ who have conducted geometry optimizations of uracil monomers with several waters on both anion and neutral surfaces. Adomowicz et al. show that there does not exist a stable neutral geometry at the minimum energy point on the anion surface. Hence when the system is optimized on the neutral surface, starting from the minimum on the anion surface, reorganization occurs in the structure.

5 A framework for understanding the competition between bond splitting and charge recombination

As indicated earlier, there have been a number of experiments on model compounds containing a photoinduced electron donor tethered to a CPD unit, that have shed light on the role of the solvent environment in the repair process. The splitting efficiency (quantum yield) in model compounds is generally far below that achieved by the enzyme photolyase. For model compounds in which electron transfer to the CPD results in a zwitterionic charge transfer (CT) state and the tether is short, there is a clear experimental trend in which greater splitting efficiency is associated with decreased solvent polarity.^{23, 24} This trend has been explained^{10, 11, 22–24} by attributing splitting inefficiency to short-circuiting of the process by premature back electron transfer (BET) in the Marcus inverted regime. Polar solvents stabilize the zwitterionic CT state, the reactant for BET, more than the product. Hence increased solvent polarity means smaller driving force and, in the inverted regime, more rapid BET that could short-circuit the repair. However, this is not a complete explanation. While early BET can short-circuit repair, BET at the proper stage of the reaction is required to complete a successful repair. A mechanism that explains why BET could occur at the proper moment for repair in some situations, most notably in the enzyme photolyase,⁸ and not in others has not been addressed previously in the literature. Our computational studies suggest a qualitative framework which can rationalize the strong dependence of splitting efficiency on solvent properties, and possibly why repair is so efficient in photolyase.

The free energy surfaces obtained from ab initio MD simulations indicate that the splitting of the C5-C5′ and C6-C6′ bonds of the CPD anion is complete within several picoseconds in water. We now consider the general properties of the anion and neutral free energy surfaces. Our studies, and previous theoretical and experimental works,^{14, 51, 56} have found that the overall splitting free energy is similar on the anion and neutral surface. The main difference is the markedly reduced free energy barrier for splitting of the anion. Results presented in section 3 indicate that in water the activation free energy for splitting of the neutral is at least 39kcal mol⁻¹, much larger than the splitting barrier of the anion, and close to the value obtained in gas phase calculations.⁵⁸ We also showed that the transition state for dimer splitting on the anion free energy surface lines up with a free energy maximum along the splitting coordinate on the neutral surface. This maximum divides trajectories that lead to dimer reformation following BET from trajectories that lead to successful repair. These properties along the splitting coordinate are depicted in the schematic shown in Fig. 11 which illustrates the energetic changes along a combined splitting coordinate of the C5-C5′ and C6-C6′ bonds. Fig. 11 immediately demonstrates that the driving force for BET is minimized near the transition state region of the CPD anion. In the subsequent discussion, we will develop a qualitative framework that explains observed trends when the donor and acceptor, before electron transfer, are neutral, such as in many model compound studies. After forward electron transfer, the donor is a cation and together with the dimer anion, forms a zwitterionic charge transfer (CT) state. We believe the model provides a useful framework for understanding other situations, such as when the electron-donating group is anionic and therefore the CT state also contains a single negative charge. If the framework proposed here is useful, then the widely varying dimer splitting rates and quantum yields will eventually be organized in terms of the relative placements of the two free energy surfaces shown in Fig. 11, and the implications for back electron transfer during the splitting process, which are developed in this section.

Figure 11.

Schematic showing placement of a neutral ground state and CT state energetics with respect to the dimer splitting coordinate. The dashed black line on the neutral state indicates, as per our calculations, a free energy maximum in close vicinity of the anion TST.

The CT state, reached by forward electron transfer from a photoexcited electron donor, lies above the neutral state and BET is generally thought to occur in the inverted Marcus regime, as shown in Fig. 12a where BET near the transition state for splitting is depicted as nearly barrierless. In Fig. 12a, the splitting of the C5-C5′ and C6-C6′ bond is encapsulated into a combined splitting coordinate q which tracks progress from reactants to products in the two-dimensional surface of Fig. 5, or a higher dimensional surface if local water motions closely tied to the BET reaction coordinate (see companion paper) are included. The role of coordinates orthogonal to the reaction coordinate, principally but not exclusively solvent polarization fluctuations, is captured by a collective coordinate X which is assumed to be harmonic. The neutral state is located at X = 0, while the equilibrium solvent polarization in a zwitterionic CT state is non-zero. Motion along X may represent relaxation after forward ET, or a fluctuation leading to the transition state for BET. In constructing this model we tacitly assume that the presence of a donor cation or donor radical species will not qualitatively change the splitting energetics. As drawn in Fig. 12a, we assume that the coordinates q and X are weakly coupled. Our data presented in section 4 indicate that a maximum of the neutral surface is quite close to the anion transition state. This feature is reflected in Figs. 11 and 12a. The maximum on the neutral surface with respect to q continues from this point at roughly the same value of X, reflecting the assumed weak coupling of X and q in Fig. 12a. However, this assumption can certainly be relaxed and it is quite possible that the relative positions of the anion and neutral TST’s will change in different physical systems. As the CPD splits (motion along the white line in Fig. 12a), BET is driven by a solvent polarization fluctuation along the X coordinate that brings the CT reactants to a point where they are in resonance with the neutral products (solid red line).

Figure 12.

a) Schematic showing placement of a neutral ground state and CT(CPD anion + donor cation) state free energy surfaces, light and dark surfaces, respectively, with respect to the dimer splitting and solvent polarization coordinates. The white curve within the CT surface, is the minimum free energy path from dimer to split products on the CT surface. The red curve above the white curve is the intersection between the anion and neutral surfaces. b) Decreasing solvent polarity will raise a zwitterionic CT state surface, as shown in the panel a), and generally increase the activation energy for BET, which is the energetic difference between the red and white curves. c) In a polar solvent the zwitterionic CT surface is lowered, and the activation for BET decreases.

If, as shown in Figs. 11 and 12a, similar overall reaction free energy but larger splitting barrier on the neutral dimer surface compared to the anion are generic features, then it also must be a generic feature that the free energy difference between CT and neutral surface grows as one moves along the reaction coordinate in either direction away from the transition state. Consequently, moving away from the dimer splitting transition state, the reaction free energy for BET becomes more negative and the activation energy for BET increases. The BET rate is a maximum in the dimer splitting transition state region. In order to achieve higher splitting efficiency, the system must rapidly move through the transition state region and/or ensure that the magnitude of BET in this region is slow enough so that it does not compete with splitting. The fact that the main difference between CT and neutral free energy surfaces is the larger splitting barrier in the neutral state, implies that the region of fastest BET occurs near the transition state where the white and red curves in Fig. 12 are close to each other. As mentioned earlier, the position of the TST on the anion surface is quite close to the position of a free energy maximum along the splitting coordinate on the neutral surface. This suggests that once the system passes the splitting barrier on the CT surface without short-circuiting BET in this region, subsequent BET from the product region of the anion surface will take the system to the product region of the neutral surface.

The scheme of Fig. 12a implies that potential short-circuiting of the dimer repair principally occurs via BET near the transition state, and the rate of BET at this point is strongly modulated by the solvent (compare Figs. 12b and 12c). Polar solvents (Fig. 12c) will lower the CT state, decrease the driving force for BET, and in the inverted region increase the degree of short-circuiting of dimer repair. Rapid splitting of the C5-C5′ and C6-C6′ bonds on the picosecond timescale and a sufficiently non-polar environment (Fig. 12b) will suppress short-circuiting through BET until the system reaches the split product well on the CT state. At this point, BET from the charge transfer state to states of similar energy within the dense vibrational manifold of the ground state will likely occur on a somewhat slower, perhaps nanosecond time scale typical of radiationless processes in molecules of this size.^61–63 We showed in the previous section that BET beyond the transition state region on the anion surface, leads to repair and further lengthening of the C5-C5′ and C6-C6′ bonds. To our knowledge, Savéant was the first to consider how the rate of electron transfer could be modulated during a bond-breaking process, and his study served as the inspiration for our model.⁶⁴ We have discussed the effect of solvent polarity in terms of the effect on the relative position of the reactant and produce free energy surfaces, which is the dominant effect because the BET rate depends exponentially on activation energy. When influenced by dynamic solvent effects,⁶⁵ the increased polarity is associated with smaller longitudinal relaxation time and faster BET rates, further increasing the likelihood of short-circuiting of the repair in polar solvent.

In this section, we have discussed the role of solvent polarity on the BET rate through the relative placement of the CT and neutral free energy surfaces. Besides modulating the activation barrier for BET, the solvent can influence the quantum yield in other ways. These effects can be incorporated within our framework presented in this section. In our companion paper,³⁸ we show that the solvent plays an important role in the splitting of the C5-C5′ and C6-C6′ bonds. Our framework predicts that non-polar solvents slow down charge-recombination throughout the splitting process as shown in the Supporting Information, and could in principle lead to a very high splitting efficiency. However, the activation barrier for splitting of the C6-C6′ bond, must also be taken into account in different environments. For example, a larger activation barrier for splitting the C6-C6′ bond, would increase the time spent in the partially cleaved state (point 1 in Fig. 4) and could increase the fraction of BET leading the ring re-closure. Another important aspect that should be considered in greater detail, are the non-equilibrium initial conditions of the solvent polarization coordinate X following forward ET.⁶³ In our discussion above, we have tacitly assumed that the relaxation of X on the CT state after forward ET, occurs on a faster timescale than the splitting process. However, this may not be true in general. If the initial distribution begins to the left of the solid white line in Fig. 12 as one might expect for a zwitterionic CT state, then a slower non-equilibrium relaxation rate of X, for example in a more viscous media, could effectively bypass the region of maximum BET by equilibrating to the solid white line in Fig. 12 after the system has moved beyond the splitting TST where BET then leads to ring opening.

As indicated earlier, there have also been experiments conducted on model compounds²⁴ with longer tethers and flavin electron donors that show an increase in quantum yields of repair in solvents with higher polarity. The behavior of longer spacer model compounds might be altered by enhanced conformational flexibility²⁴ compared to the short spacer compounds. The difference in energy between the CT and neutral surfaces illustrated in Fig. 12 will be affected by the distance between the electron donor and acceptor, which will in turn affect the driving force for BET. Thus, the framework we propose in this section should be considered as an initial model that will require further parametrization, refinement and possibly the addition of other coordinates beyond q and X to describe systems such as the long-tether model compounds. More detailed calculations like the ones we have done in this work, in different solvents and in the active site of the protein, will also be needed to determine the extent to which the framework we propose in this work can rationalize a rather large body of experimental results.

6 Conclusions

Our ab initio MD simulations of the cyclobutane thymine dimer surrounded by 32 waters show that the splitting of the C5-C5′ and C6-C6′ bond is complete within several picoseconds. The umbrella sampling simulations generates a free energy surface in two important reaction coordinates, the C5-C5′ and C6-C6′ bonds lengths, which provides the broad outlines for the reaction mechanism. This surface quantifies how the minimum free energy path evolves from principally along the C5-C5′ distance early in the reaction to along the C6-C6′ distance as the second bond is cleaved. There is a local minimum where the C5-C5′ bond is partially cleaved and the C6-C6′ bond is intact followed by a rather small 1.5kcal mol⁻¹ transition state. Using TST theory we predict that the splitting time of the C6-C6′ bond in water to be ~ 0.5ps. The return of the electron from the anion dimer to the donor cation should be considered as a critical part in the biological repair of the dimer in the active site of the protein. Our work shows that back ET can result in either ring closure, where the C5-C5′ and C6-C6′ bonds reform, hence aborting repair, or ring splitting, where the C5-C5′ and C6-C6′ bonds undergo further lengthening. There exists a free energy maximum on the neutral surface quite close to the TST position on the anion surface. Hence if back ET occurs after the transition state on the anion surface, then the quantum yield of splitting will be close to unity. The 2D-free energy surface in Fig. 5 suggests that the splitting process is asynchronous concerted, although we will demonstrate in our companion paper,³⁸ that multidimensional and non-equilibrium effects can give the splitting process some stepwise character although this does not change the overall splitting times of the C5-C5′ and C6-C6′ bonds significantly.

While our results are consistent with other theoretical works in the literature on similar systems,¹³ inadequate basis sets, finite box size effects and errors in energetics could affect the splitting timescales. Furthermore, as indicated earlier, all theoretical calculations of this system are anionic systems, while most of the experiments that involve the donation of an electron to the dimer, are neutral systems overall. If the donor and acceptor are in close proximity, the splitting dynamics might be affected. This will require detailed calculations using ab initio MD methods of the dimer splitting in different solvents and an explicit treatment of both the forward and backward electron transfer processes, which is beyond the scope of the current study.

Numerous experiments have been performed on the repair dynamics of the thymine dimer using model compounds where the CPD unit is tethered to an electron donor that can be photoexcited.^{10, 11, 22–24} Additionally, the repair of the CPD anion has also been monitored spectroscopically in the active site of photolyase⁸ using the flavin moiety as a probe. A recent work by Stanley and co-workers⁷ uses electronic absorption spectroscopy to monitor the formation of the repair photoproducts. They attributed the change in the absorption signal over time to the splitting of the CPD anion, but the assignment of this process to other dynamical processes such as back electron transfer or solvation, is also possible. Hence these experiments do not provide a direct measurement of the evolution of the thymine anion species and the splitting timescales. Our theoretical calculations can compare directly with experiments by Carrell and co-workers²⁶ where splitting of the thymine dimer in water with no attached electron donor group was induced by ionizing radiation. Their results provide an upper bound to the splitting time of 35ns, limited by the time resolution of their method, for the splitting of the C5-C5′ and C6-C6′ bonds.

Using a simple model that takes advantage of generic thermodynamic properties along the splitting coordinate on both the anion and neutral surfaces, we have shown that the back ET rate in the Marcus inverted region will first increase, pass through a maximum, and then later decrease during the splitting process. The precise placement of the CT and neutral surfaces with respect to each other, as shown in Fig. 12 and the activation barrier of splitting on the CT state, will either enhance or suppress short-circuiting via BET and hence control the splitting efficiency. The central idea of the framework proposed here is that widely varying dimer splitting rates and quantum yields can be organized by considering the relative placements of the CT and neutral free energy surfaces in different experimental situations. Anion dimer splitting rates are determined by the activation barrier of one of the surfaces. The relative placement of these surfaces affects the back electron transfer rate during the splitting process, and hence have direct bearing on the observed quantum yields of repair. Our generic model helps provide a framework for understanding why the quantum yields of repair of short-spaced tethers increase with non-polar environments. The ultimate utility of the framework proposed here will be determined by whether other experiments can also be rationalized in terms of the relative placement of free energy surfaces for the electron transfer pair. More work is needed in this area to understand for example, why the trends in quantum yields of repair are reversed for longer-spaced tethers.