Abstract
The “canonical” generalized Born (GB) formula [C. Still, A. Tempczyk, R. C. Hawley, and T. Hendrickson, J. Am. Chem. Soc. 112, 6127 (1990)] is known to provide accurate estimates for total electrostatic solvation energies ΔGel of biomolecules if the corresponding effective Born radii are accurate. Here we show that even if the effective Born radii are perfectly accurate, the canonical formula still exhibits significant number of gross errors (errors larger than 2kBT relative to numerical Poisson equation reference) in pairwise interactions between individual atomic charges. Analysis of exact analytical solutions of the Poisson equation (PE) for several idealized nonspherical geometries reveals two distinct spatial modes of the PE solution; these modes are also found in realistic biomolecular shapes. The canonical GB Green function misses one of two modes seen in the exact PE solution, which explains the observed gross errors. To address the problem and reduce gross errors of the GB formalism, we have used exact PE solutions for idealized nonspherical geometries to suggest an alternative analytical Green function to replace the canonical GB formula. The proposed functional form is mathematically nearly as simple as the original, but depends not only on the effective Born radii but also on their gradients, which allows for better representation of details of nonspherical molecular shapes. In particular, the proposed functional form captures both modes of the PE solution seen in nonspherical geometries. Tests on realistic biomolecular structures ranging from small peptides to medium size proteins show that the proposed functional form reduces gross pairwise errors in all cases, with the amount of reduction varying from more than an order of magnitude for small structures to a factor of 2 for the largest ones.
INTRODUCTION
We begin this section by describing the existing “canonical” generalized Born formalism in the context of the implicit solvation framework and specifically the Poisson model. This will be followed by a discussion of some of its known accuracy problems. The section is concluded by a brief outline of the rest of this work.
The so-called implicit solvation framework1, 2, 3, 4, 5, 6, 7, 8 is a popular approximation for estimating molecular energy in realistic aqueous environment. Within the framework, solute and solvent are treated at different level of detail: the solute atoms are retained “as is,” while the discrete solvent molecules (and mobile ionic species) are replaced by a continuum with the dielectric and “nonelectrostatic” properties of water. While the implicit solvation framework is just an approximation to the more traditional, explicit solvent representation in which both the solvent and the solute are treated on the same footing, the approximation is widely used due to several critical advantages over the explicit water representations. These advantages include, among others, computational efficiency and effective ways to estimate free energies. Within the implicit solvation framework, the total energy of a solvated molecule is decomposed as W=Evac+ΔGsolv , where Evac represents the molecule's potential energy in vacuum (gas-phase), and ΔGsolv is defined as the free energy of transferring the molecule from vacuum into solvent, i.e., solvation free energy. Accurate estimation of the solvation effects encapsulated in the ΔGsolv term in the above equation is difficult. A hierarchy of approximations has to be made9 to obtain a practical representation for ΔGsolv. For example, the following decomposition is often assumed:
| (1) |
where ΔGnonpolar is the free energy of solvating the molecule from which all charges have been removed (i.e., partial charges of every atom are set to zero), and ΔGel is the free energy of first removing all charges in the vacuum, and then adding them back in the presence of a continuum solvent environment. Here we focus on ΔGel, that is presently the most computationally intensive part in practical application of Eq. 1. Accuracy of ΔGel estimates is of paramount concern since the underlying long-range interactions are critical to function and stability of many classes of biological and chemical structures.
The canonical generalized Born model
At the level of the linear response, continuum dielectric approximation, ΔGel can be obtained from solutions of the Poisson (PE) (or Poisson–Boltzmann if mobile ions are also considered) equation. For arbitrary molecular shapes, this approach typically relies on numerical computations that limit its applicability to problems where speed and computational facility are critical, such as molecular dynamics (MD). In this respect, the so-called generalized Born (GB) model6, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33 is an approximation relative to the PE treatment which provides a good balance between accuracy and speed, and is currently the most widely used model of implicit solvation in molecular dynamics. The key idea of the GB model is approximation of the electrostatic solvation free energy of a given charge distribution {qi} of partial atomic charges within the solute via some simple analytical function F(ri,rj) of atomic coordinates ΔGel =1∕2∑ijF(ri,rj)qiqj. The very existence of such a universal and simple function for arbitrary biomolecular shapes is completely nontrivial. The idea of “generalization” of the single-ion Born formula to approximate electrostatic solvation energy of small molecules has had a long history,34 but it was not until 1990 that a reasonably accurate, yet amazingly simple (and thus robust and efficient) form of the reaction field Green function F(ri,rj) in Eq. 2 was proposed by Still et al.:11
| (2) |
where rij is the distance between atomic charges i and j, εout and εin are the dielectric constants of the solvent and the solute, respectively, and γ is a constant, see below. At the moment, this specific form of F(ri,rj) with γ = 1/4 is the most common form of Eq. 2 used in practice—we will be referring to it as the canonical GB. Slight variations such as the use of γ = 1/2 or γ = 1/10 have also been explored, but apparently were not found to deliver better accuracy than the original on a wide class of biomolecules to warrant universal acceptance. The key input parameters in the GB formula are the so-called effective Born radii of the interacting atoms, Ri and Rj, which represent each atom's degree of burial within the solute; these have to be estimated for every atom. Generally, the more accurate are the effective radii the more accurate is the resulting ΔGel; a multitude of approximations is available to estimate Ri based on input molecular configuration. These different approximations are essentially just different flavors of the same canonical GB model based on the same functional form of Eq. 2 by Still et al. The existing flavors differ greatly in accuracy and speed, with the usual trade-offs between them. One such flavor is unique in a sense that it is based directly on the definition of the effective Born radius, and uses no further approximations on top of the approximations already present in the PE of continuum solvent electrostatics.35 Namely, the effective Born radius of an atom is defined by inverting the Born equation36 for a corresponding spherical ion of radius Ri having the same electrostatic solvation energy as the self-energy of atom i in the molecule,
| (3) |
Perfect radii correspond to in the above equation computed directly by PE. Since the Poisson equation formalism is more fundamental than the GB, the resulting perfect radii represent a useful accuracy limit for the effective radii. At the time the concept of perfect effective radii was introduced, the limit was far ahead of what fast, practical routines for computing effective Born radii could deliver based on approximations for in Eq. 3. When substituted into Eq. 2, the perfect radii invariably delivered more accurate estimates of the electrostatic free energies than did fast practical GB flavors. The push to close the accuracy gap between the GB and PE has lead to dramatic improvements in the accuracy of the GB model, which in turn promoted the model's usage in a wide range of molecular modeling applications, from protein folding37, 38, 39, 40, 41, 42, 43, 44 to applications directly relevant to structure-based drug discovery.45, 46 For some types of simulations, e.g., constant pH molecular dynamics, models based on implicit solvation such as the GB appear to be the only ones currently available in practice.47, 48, 49
Known accuracy limitations of the canonical GB
Despite its documented successes, there is a clear sense in the modeling community that the canonical GB approximation is still a much less faithful representation of reality than the standard numerical PE (PB) implicit solvation treatment,50 let alone the more fundamental explicit solvation framework.27, 50, 51, 52 For example, it appears that the GB does not have the right balance between intrasolute and solvent–solute charge–charge interactions, resulting in over-stabilization of salt bridges;52, 53, 54 erroneous salt bridges appear to be a generic property of various GB flavors.51 And while some of the discrepancies (relative to the explicit solvent results) are already present at the continuum solvent (PE) level, the rest come directly from the approximations of the PE→GB step.55 Thus, there still exists room for meaningful improvement within the PB→GB approximation. Since the latest generation of effective Born radii are able to approximate the perfect radii very closely,20, 56 it is unlikely that appreciable improvements in accuracy can still originate from improving the accuracy of the best available routines that compute the effective radii (making these approximations computationally efficient is another story). The above considerations have led us to conclude that in order to improve the accuracy of the GB formalism one must substantially improve the part of the GB formalism that remained unchanged since its modern form was introduced by Still et al.—the “canonical” heuristic Eq. 2.
The rest of this work is organized as follows. We begin by revealing and discussing gross pairwise errors inherent in the canonical GB formula. To understand physical origins of these errors, we consider exact analytical solutions of the PE for decidedly nonspherical geometries. These show that while the canonical GB correctly describes one of the two spatial modes of these solutions, the other is completely missed. Analysis of these solutions suggest a simple analytical approximation for the Green function to replace Eq. 2. We then present extensive testing of the resulting model on a variety of realistic biomolecular shapes, from small peptides to proteins and DNA. Methodological details, including description of test structures, calculation of the PE reference energies and the effective Born radii, and also the derivations of the exact analytical PE solutions for idealized nonspherical geometries are presented in Sec. 5.
GROSS ERRORS OF THE CANONICAL GB GREEN FUNCTION
It is well known that if effective radii Ris, and hence the self-terms are somehow estimated for each of the N atoms in the molecule, then the generalized Born formalism immediately provides an extremely simple and computationally effective way to estimate all of the remaining N(N − 1)/2 cross terms and thus the total solvation energy,
| (4) |
The ability of estimate all of the cross terms of the reaction field Green function from the knowledge of only the self-terms, is perhaps, the most nontrivial, yet not fully appreciated aspect of the model. However, given how complex realistic biomolecular shapes may be, one cannot expect that a single simple function F(ri,rj) can deliver uniformly accurate estimate for all possible molecular geometries even if the effective radii are perfect. Inaccuracies are inevitable. To the best of our knowledge, the extent and origin of these inaccuracies for realistic biomolecular shapes have not been studied. As we shall see, errors in translate directly into errors in physical pairwise charge–charge interactions which can obviously affect dynamics of the system. Our illustrative test case for the canonical GB model is a 247-atom β-hairpin peptide structure that has been used extensively in testing of the GB and other implicit solvation models.53 At first, it appears that, given accurate effective radii, the canonical GB can be quite accurate. When the perfect radii are used, that is when all the self-terms in Eq. 2 are computed exactly, the error in ΔGel is less than 0.5%, or 2 out of −590 kcal∕mol—the total solvation energy of this structure as estimated by numerical PE. Such a small inaccuracy is within the error margin of numerical Poisson solvers57 for a structure of this size. However, a very different picture emerges, Fig. 1, if individual cross terms computed with the use of the canonical GB model are compared with the corresponding terms obtained via the numerical PE reference, see Sec. 5.
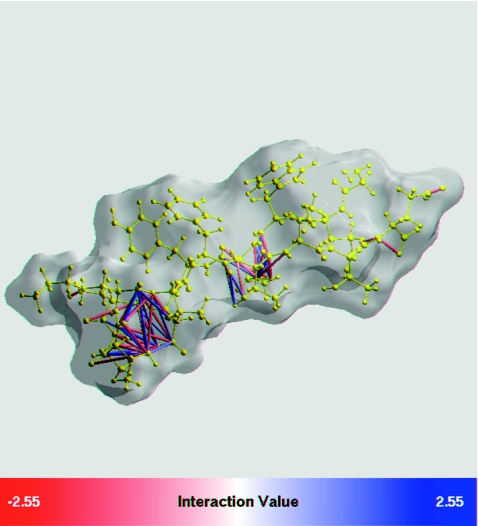
Figure 1.
Gross pairwise errors of the canonical GB model, Eq. 2, relative to numerical PE reference, in a β-hairpin peptide from protein G. Perfect (numerical PE) effective Born radii are used. Each pair of atomic charges i and j with error in charge–charge interaction Wij larger than 2kBT (error in larger than 2kBT) is shown by either a red atom–atom link (underestimation) or a blue link (overestimation). There is a total of 50 such pairs in this structure. Intensity of the color corresponds to the magnitude of the error. The peptide backbone is yellow. Molecular surface is light gray. The graphics is by GEM package.58, 59
Namely, the GB pairwise exhibit gross errors—errors larger than 2kBT or ∼1.2 kcal∕mol—for 50 pairs of atoms in the structure. Note that an error of 2kBT in translates into the same 2kBT error in the total pairwise interaction energy between the two atoms since the vacuum part of the energy is estimated outside of the GB or PE, and so the difference between the GB and the PE comes solely from the solvation part. Most of the pairs in gross error seen in Fig. 1 are comprised of atoms not connected by a chemical bond. Obviously, even a single charge–charge interaction in gross error may lead to significant under- or over-sampling of salt bridges in MD simulations, which in turn can alter the thermodynamics of the system. Indeed, the lowest free energy state of the beta-hairpin observed in GB-based simulations of Ref. 53 was quite different from the “correct” one observed in the explicit solvent simulations; nonnative salt bridges formed at the core of the peptide, in place of correct hydrophobic contacts.
As we shall see later, the gross pairwise errors seen in Fig. 1, and the fact that the errors are of both signs, are a generic feature of Still's equation, not limited to the specific test structure shown in Fig. 1. Physical origins of these errors will be discussed later in this work. A useful feature of Still's Eq. 2 is that for many, if not most, realistic biomolecular shapes these over- and under-estimations of individual values nearly cancel in the summation, yielding a very reasonable estimates of the total ΔGel. However, this cancellation masks a crucial weakness of the canonical model—gross errors in pairwise interactions, present even when the effective radii are computed with perfect accuracy. Since efforts to improve the canonical GB model almost invariably used the total ΔGel as the key accuracy metric,57 it is perhaps not so surprising that the pairwise gross errors are still present in the model.
CONSTRUCTION OF AN ALTERNATIVE GB GREEN FUNCTION
We have become convinced that slight modifications to the existing functional form of the canonical GB equation 2 are not going to bear fruit in terms of reducing the gross pairwise errors significantly. For example, an attempt made in this work to further optimize parameter γ in by minimizing the gross pairwise errors in all of the test molecules used in this study returned the “canonical” γ = 1/4. Several functional forms similar to Eq. 2 but with somewhat different asymptotic were explored earlier, however without much follow-up success.35 Later in this work we will see that the canonical GB formula essentially misses “half” of the correct physics of relatively short range interactions for realistic biomolecular shapes. A systematic new approach to find a replacement to Eq. 2 is needed, one that goes beyond the “underlying” geometry of Eq. 2—the sphere. We should point out that the gross errors of the canonical GB discussed above have nothing to do with the known, but correctable,60, 61 deficiency of Still's equation with respect to finite values of εout. Efforts to re-derive the GB model starting from exact solutions of the PE for a sphere have lead to an equation (ALPB) similar in complexity to Eq. 2. The ALPB equation corrects a systematic bias of the canonical GB that stems from its wrong dependence on the internal and external dielectrics.60, 61 However, this improvement address a very different deficiency of the canonical GB, the one that is not present in the conductor limit εout → ∞ where the ALPB and GB models coincide. To make that distinction clear, all of the calculations reported here (including Fig. 1) are performed in the εin = 1, εout → ∞ limit.
The Ψ ansatz
In what follows, we will seek a more accurate analytical Green function to replace Eq. 2. Without loss of generality, we will represent the sought after reaction field Green function in terms of a dimensionless quantity Ψ, defined as
| (5) |
| (6) |
where the nonequivalence between self- and cross-terms is now explicit and consistent with our current definition of and Eq. 4 for ΔGel. Obviously, without any restriction on Ψ, the above ansatz is as general as using no ansatz at all. However, representing the solution in terms of Ψ has the following advantage: deviations of Ψ from unity should reflect deviations of the molecular shape from a perfect sphere (in which case60 Ψ ≡ 1), giving us clues as to how Ψ function should be constructed if one wants to go beyond the perfect sphere model.
Exact solutions for idealized nonspherical geometries
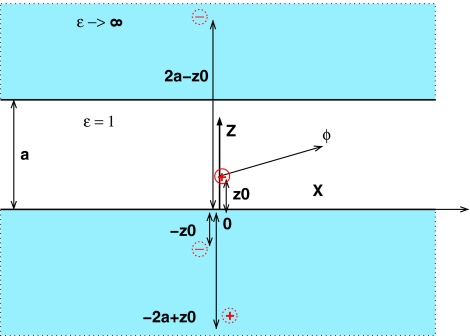
To find a different, more accurate form of the pairwise Green function to be used in the GB formalism, we need to analyze analytical solutions of the PE equations for boundary conditions that are decidedly different from a single dielectric sphere (surrounded by high dielectric solvent). Such solutions exist for only a handful of geometries, and not all of them are very useful to us here, either because of little relevance to realistic biomolecular shapes or due to mathematical complexity of the solutions. The two cases that we find most useful are shown in Fig. 2, the corresponding solutions of the Poisson equation are worked out in Sec. 5.
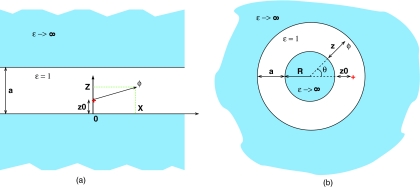
Figure 2.
Two geometries other than the perfect sphere used here to derive alternative forms of the analytical reaction field Green function F(ri,rj) in the GB formalism. (a) Parallel plates. The source charge is at (0, z0), and the potential ϕ is determined at (x, z). (b) Concentric spheres. The source charge is at (0, z0) and the potential is determined at (θ, z). The enclosed space is assumed to be the low dielectric medium (solute, εin = 1), while the outside space (solvent) is treated in the conductor limit εout → ∞. Geometric parameters are shown in the figures. Due to cylindrical and spherical symmetries, respectively, the potential is independent of the third coordinate.
The parallel plates geometry, Fig. 2 (a), is sought to mimic the two distinct positional “modes” in which a pair of atoms can be found in nonspherical geometries of realistic molecules such as that in Fig. 1: the longitudinal and the transverse. The longitudinal “mode” is along the “long” dimension of the molecule, and the transverse one is along its “short” dimension. The corresponding directions are represented by the x and z axes, respectively, in Fig. 2 (a). The concentric spheres geometry is intended to mimic biomolecules with deep solvent-filled regions, e.g., enzymatic clefts. In this geometry, the transverse mode corresponds to moving along the radius perpendicular to the surfaces, and the longitudinal mode is along the azimuthal coordinate θ, Fig 2 (b).
Exact solutions for the potential φ(r) satisfying the Poisson equation for a point source charge placed anywhere in the solute space as defined by geometries in Fig. 2 are given by infinite series, see Sec. 5. Apart from a few special symmetric cases where exact summation can be performed, we represent the solution as partial sums over k ≫ 1 terms to achieve numerical convergence. Since we will ultimately be looking for a new analytical reaction field Green function F(ri,rj) in the form of Eq. 5, we express these solutions in terms of the same dimensionless quantity Ψ introduced in Eq. 5,
| (7) |
| (8) |
where are the exact electrostatic solvation energies obtained from the exact φ(r) within the PE formalism, see Sec. 5.
Examination of each of the exact solutions in terms of Ψ reveals qualitatively different behavior depending on the mutual position of charges, Fig. 3, that is whether we consider the longitudinal or transverse mode of the PE solution (we use the familiar terminology—mode—to denote what strictly speaking is a projection of the unique PE solution onto the given spatial direction). For each geometry, the form of the longitudinal mode, ΨL, is similar to the familiar Still's function of the canonical GB, Ψ ⩽ 1, while the transverse ΨT mode is radically different, Ψ ⩾ 1. Thus, the canonical GB formula can at best capture only “half” of the correct physics in these nonspherical test geometries. Later we will see that PE solutions for realistic biomolecular shapes contain the same two modes, which explains why the canonical GB formula exhibits gross pairwise errors: the latter completely misses the transverse mode Ψ ⩾ 1. To address the problem we will have to find a better form of the GB equation that will contain both of these two modes.
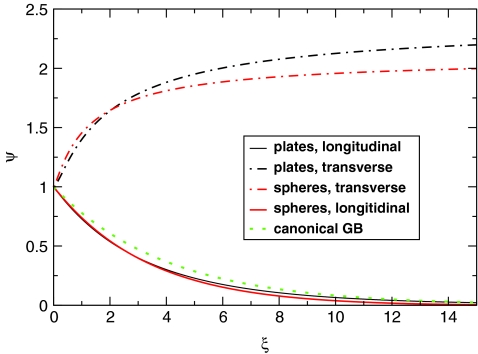
Figure 3.
Two modes of the exact solution of the PE equation for the nonspherical geometries of Fig. 2 expressed as a function of . The source charge qi is always at the midpoint of the interior: at (x = 0, z0 = a/2) for the plates, and at (θ = 0, z0 = a/2) for the spheres. In the longitudinal mode, the test charge qj moves along the positive z direction, the other coordinate being fixed at x = 0 or θ = 0, respectively. In the transverse mode, the z coordinate of the test charge is kept constant, z = z0 = a/2, while x (or θ for the spheres) increases. The solutions are expressed via dimensionless Ψ variable defined in Eq. 7. Note that Ψ = 1 corresponds to the exact solution for a perfect sphere, while Ψ = exp ( − 0.25ξ) (dashed green line) is the canonical GB.
Construction of Ψ function for nonspherical geometries
One way to find an analytical form of Ψ consistent with the existence of the two modes in Fig. 3 would be to find accurate, closed-form approximations to the corresponding exact infinite series solutions. Unfortunately, we did not find it possible. We thus pursue an alternative strategy: find a simple function that interpolates between the two modes, consistent with their asymptotic behavior. To proceed, we need to decide what parameters such function should depend upon. Within the canonical (sphere-based) GB these variables are charge–charge distance rij and effective Born radii for each atom, Ri and Rj. Due to high spherical symmetry, these three variables are enough to uniquely determine the exact Green function for the perfect sphere case (in the conductor limit). In other words, each pair of charges can be mapped onto a local sphere containing the charges.60 This is true even if the actual molecular geometry is not spherical: the canonical GB formula treats the charges as if they were inside a sphere. For finite εout the situation is qualitatively similar, but one also needs to know the molecule's effective electrostatic size,60, 61A. However, once the spherical symmetry is broken, more variables will clearly be required if one hopes to incorporate into the Green function signatures of the more complicated geometry. Here we follow the same strategy that is so successful in the canonical GB case: use local variables such as charge–charge distance and effective radii.60, 61 The strategy is also justified by the fact that highly accurate, fast and robust routines now exist that compute the effective radii and the effective electrostatic size A.61 For our purposes, the latter is just a convenient metric of the over-all size of the structure which also reflects possible uneven distribution of mass in it, see Sec. 5 for a brief description of the analytical procedure. We then take the next logical step in complexity of Ψ and make it explicitly depend on gradients of the effective Born radii ∇Ri, ∇Rj. The idea here is that the gradients will carry an additional, more subtle information about the local molecular geometry around charges i and j.
To proceed, and to derive a reasonably simple expression for Ψ, and hence the reaction field Green function to replace the canonical GB, we will make several simplifying assumptions. First, we assume the following separation of variables: the two modes in Fig. 3 are described by functions ΨL and ΨT that depend only on (rij, Ri, Rj). We further assume that a smooth interpolation between the modes is controlled by some function S(μ) of a single “order parameter” μ that determines, for a given pair of charges, whether the pair belongs to the transverse or the longitudinal mode of the PE solution, Fig. 3. This parameter must have a more subtle dependence on molecular geometry than can be provided by Ri, Rj alone; we assume that it also depends on ∇Ri, ∇Rj, and the electrostatic size A. To be specific, we require that
In addition, we need the μ(rij, Ri, Rj, ∇Ri, ∇Ri, A) function to be at least twice differentiable with respect to its arguments. Obviously, there is no unique μ that satisfies the above criteria; after testing several functional forms we used Occam's razor argument to single out the following expression:
| (9) |
which also has the two additional properties: (1) μij = μji (note that ) and (2) μ → 0 when rij → 0. One can verify that μij = 0 for any two charges inside a perfect sphere in the conductor limit. Most importantly, the “order parameter” μ can be used to distinguish between the two modes of the exact PE solution, transverse Ψ > 1, and longitudinal Ψ < 1, for the two nonspherical geometries analyzed so far. For these idealized geometries the correlation between the sign of μ(i, j) and the mode to which the pair of charges (qi, qj) belongs to is nearly perfect, Fig. 4.
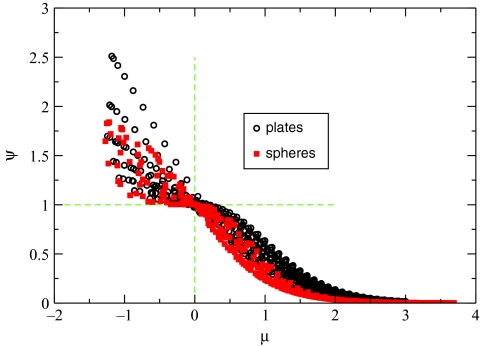
Figure 4.
Correlation between the order parameter μ from Eq. 9 and modes of the exact solution of the PE equation for nonspherical geometries shown in Fig. 2. The values of μij and Ψ are computed for a set of locations of the source qi and test charges qj inside the low dielectric solute space. Locations of qi are (x = 0, z = z0) for the plates geometry or (θ = 0, z = z0) for the concentric spheres, where z0 uniformly spans the interval a/10 < z0 < 0.9a. Locations of qj span the same set of points along the z axis, and vary from x = 0.1a to x = 5a for the plates (from θ = 0 to θ = π for the concentric spheres) in the longitudinal direction. Here a is the structure size, see Fig. 2. All quantities are computed (numerically) exactly.
The same qualitative correlation holds (results not shown) for an ellipsoid structure constructed from a large number of atomic spheres, although the near perfect correlation μ < 0 ⇔ Ψ > 1, and μ > 0 ⇔ Ψ < 1 becomes somewhat blurred, most likely due to the fact that the dielectric boundary has a fine grain structure due to the use of finite size atomic spheres.
We now have the key ingredient, μ(rij, Ri, Rj, ∇Ri, ∇Ri, A) of Eq. 9, needed to construct the full function Ψ that can describe both modes of the PE solution seen in Fig. 3. We require that Ψ(μ = 0) = 1 (perfect sphere case), and that μ < 0 and μ > 0 yield the transverse and longitudinal modes, respectively, Fig. 3. Also note that in the case of perfect Ri, Rj, one always expects Ψ → 1 when rij → 0. To see why, consider a pair of identical “atoms” carrying equal and opposite charges qi and qj. Now let the distance between them tend to zero. Obviously, the total electrostatic solvation energy of the resulting net neutral system tends to zero, , from which it follows that . This limiting behavior is automatically satisfied by Eq. 5 when Ψ → 1 and rij → 0 due to the definition of the perfect effective Born radius. To further narrow down the search for a suitable Ψ, we use several properties of the exact Ψ in the parallel plates case, see Sec. 5 for derivation details. For the longitudinal mode (along the x axis) the following asymptotic holds at z = z0 = a/2 for small : ΨL ∼ 1 + 1/2(3Z(3)/(ln 4)3 − 2)ξ ≈ 1 − 0.323ξ, where Z(n) is Riemann zeta function. As is evident from Fig. 3, the transverse mode has a similar in magnitude, but opposite in sign, derivative ∂Ψ/∂ξ at zero, so we can expect the following asymptotic for it: ΨT ∼ 1 + 0.323ξ for small ξ. While the exact slope is likely to be somewhat different from that of the longitudinal mode, we do not pursue its derivation here as it is very unlikely to remain unchanged for realistic biomolecular shapes. However, the order of magnitude of the parameters that will control the asymptotic behavior of the solution is now clear. Again, we use Occam's razor argument to propose what we believe is close to the simplest differentiable function Ψ(μ, rij, Ri, Rj) = (S1(μ)ΨT(ξ) + S2(μ)ΨL(ξ)) that satisfies all of the above,
| (10) |
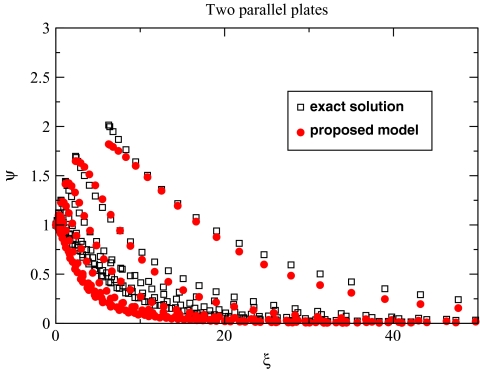
where, as before, . Here γL and γT parameters describe the steepness of the longitudinal and transverse modes, respectively. In general, γL and γT do not have to be exactly equal to each other, although based on Fig. 3 and the asymptotic discussed above it is reasonable to assume γL ≈ γT < 1. As seen from Fig. 5, Eq. 10 used along with Eq. 9 provides a reasonable approximation for the exact PE solution for the parallel plates, similar agreement is found for the concentric spheres (results not shown).
Figure 5.
Numerically exact solution of the PE equation for the parallel plates is compared with that of the proposed analytical model defined by Eqs. 10 (γL = γT = 0.323) and 9. Each point corresponds to the Ψ value computed for a pair of charges inside the low dielectric region between the plates; the charges are uniformly distributed as described in the caption of Fig. 4.
At this point, we are ready to assess the performance of the new model defined by Eqs. 10, 9 on realistic biomolecular shapes.
Realistic molecular shapes
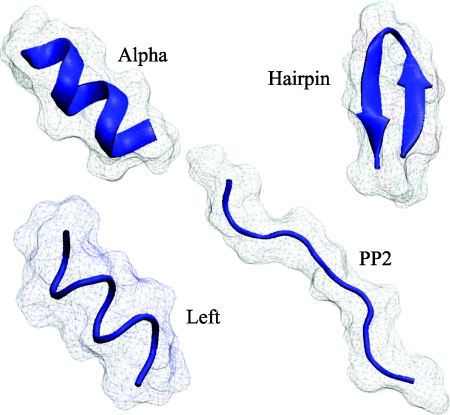
The first critical question is whether the two qualitatively different modes of the solution of the PE equation—the longitudinal Ψ < 1 and the transverse Ψ > 1 modes identified for nonspherical, but idealized dielectric boundaries—also exist in realistic biomolecular shapes. To address this question, and to further develop the new model, we have analyzed exact PE pairwise solvation energies, , in four very different conformational states of a 10-residue polyalanine peptide, Fig. 6. These states represent different common structural classes found in proteins, including both compact and extended (unfolded) conformations; the structures were used previously in the analysis of GB model performance.50
Figure 6.
The four conformational states of alanine decapeptide (ala10) used for parameter fitting and testing of the new model. The secondary structure (blue trace) and the molecular surface (gray) are shown. The polyproline (pp2) conformation represents an unfolded state of the peptide, while the three other conformations correspond to three distinct Ramachandran regions of the folded space: alpha helix, left-handed alpha helix, and beta-hairpin. Each state is represented by a number of structurally similar, but not identical snapshots (one set of snapshots is shown). The snapshots are courtesy of Daniel Roe, see Sec. 5 and Ref. 50 for details of how they were generated.
The immediate observation is that both modes of the numerically exact PE solution are also found in the case of realistic molecular boundaries, Fig. 7.
Figure 7.
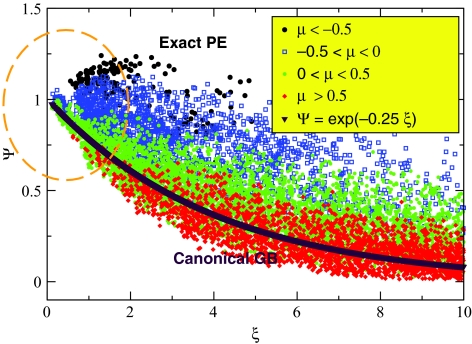
Numerically exact solution of the PE equation, expressed as Ψ(ξ) via Eq. 7, for all pairs of atoms in the four conformations of alanine decapeptide shown in Fig. 6. Each point in the plot corresponds to the Ψ value computed for a pair of charges in one of the structures; results from all four conformations are combined here into one plot. The Ψ values are color coded according to the corresponding values of μ in Eq. 9, see the insert. The region of small ξ corresponding to the strongest charge–charge interactions is highlighted by an orange contour line. The canonical GB formula Ψ = exp ( − 0.25ξ) is also shown for reference (purple line).
Moreover, in the region of small charge–charge distances (small ξ) where the interactions are strongest and thus most important, both modes are equally represented. The origin of a whole class of gross errors in the canonical GB model now becomes transparent: Still's Eq. 2 represents only one mode, Ψ < 1, of the correct PE solution. The formula should perform well for distant pairs, ξ ≫ 1, but is bound to entirely miss the transverse mode Ψ > 1 that represents “half” of the most critical region ξ ∼ 1. The second observation from Fig. 7 is that the “order parameter” μ, Eq. 9, performs reasonably well at identifying which mode a pair of charges belongs to: positive values of μ correspond mostly to the Ψ < 1 mode, while the Ψ > 1 mode is mostly presented by points with μ < 0. The correlation is most pronounced for small values of ξ that matter most because these correspond to the largest absolute values of the pairwise interaction terms. However, as expected, the correlation is not nearly as perfect as seen for the idealized parallel plates case, Fig. 4. This should not be surprising given that we are now dealing with realistic molecular shapes, dielectric boundary being defined by the complex molecular (Lee–Richards) surface. In particular, we find that even for an “ideal sphere” constructed from a large number of individual atoms, μ = 0 no longer holds exactly. Also, one cannot expect that the exact same value of γL = γT = 0.323 in Eq. 10 derived as a specific asymptotic for parallel plates will be optimal for realistic shapes. Thus, we propose the following slightly more general expression to replace Eq. 10 for realistic biomolecules:
| (11) |
where μ0 and γ0 are now adjustable parameters. Following the insight from the analysis of the idealized shapes, we explicitly restrict ourselves to solutions with one and the same γL = γT = γ0 for both modes. We optimize the parameter values for the four ala10 structures in Fig. 6 based on the following criterion: the optimal set (γ0, μ0) minimizes the combined number of gross pairwise errors (errors in greater that 2kBT) in all four ala10 conformations, subject to additional constraints that ensure that the electrostatic part of solvation free energy closely approximates the numerical PE reference. Since it is relative energy between various conformation states that is most important, these four additional constraints are
| (12) |
| (13) |
| (14) |
| (15) |
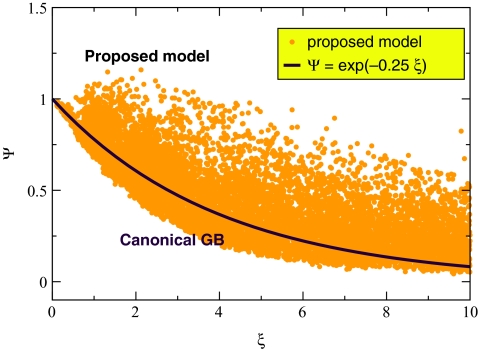
where and denote ΔGel computed by the proposed model and the numerical PE, respectively, for conformation C of the ala10 peptide. At this point we are going to make an important departure from our strategy of using perfect effective Born radii for testing of the approximate models. Instead, from now on we will be using the so-called “R6” radii: these are based on integrating r−6 over the proper (molecular) volume of the solute. At least for small proteins, the R6 prescription was shown56 to be as accurate as perfect radii in computing ΔGel via canonical GB. The R6 flavor has a solid theoretical basis,62 and, what is most critical for us, it can lead to practical, analytical routines for fast estimation of the effective radii.63 Since we are developing the current theory with an eye toward its use in molecular dynamics, the latter property is critical. We have performed an exhaustive search for the optimal values of (γ0, μ0) via the above procedure in the intervals 0 < γ0 < 1 and 0 < μ0 < 1 with steps of 0.01 and 0.05 for γ0 and μ0, respectively. The following pair (γ0 = 0.5, μ0 = 0.6) was found to be optimal: all of the results presented throughout the rest of this work will be based on these values of (γ0, μ0) (the second best pair is (γ0 = 0.5, μ0 = 0.55; its over-all performance is similar). Initial testing of the proposed Eq. 11 with the optimal γ0 = 0.5 and μ0 = 0.6 shows that if used in the general ansatz of Eq. 5, it does reproduce the correct PE behavior in terms of the existence of the two modes, Ψ < 1 and Ψ > 1, Fig. 8, which is in contrast to the canonical GB, Fig. 7.
Figure 8.
The proposed approximate analytical solution of the PE equation, Eqs. 11, 9, for all pairs of atoms in the four conformations of alanine decapeptide shown in Fig. 6. Each point in the plot corresponds to the Ψ value computed for a pair of charges in one of the structures; results from all four structures are combined here into one plot. The canonical GB formula Ψ = exp ( − 0.25ξ) is also shown for reference (purple line).
Accuracy of the proposed model
The reduction of gross errors through the inclusion of both of the modes of the PE solution into the proposed pairwise Green function [Eqs. 9, 11] is illustrated in Fig. 9 for the same four ala10 conformations as discussed above. The most dramatic consequence of the complete omission of the transverse mode by the canonical GB is gross errors in strong charge–charge interactions seen in the lower left quadrant and upper right quadrant of the graph. It is in the latter region of large and positive where strong salt bridges are expected. The uniform use of Ψ < 1 in Eq. 5 would result in an overestimation of the true reaction field Green function, and thus too large positive values of for pairs of opposite charges that happen to be on the transverse mode Ψ > 1. The proposed formalism brings down 1 or 2 kcal∕mol relative to the canonical GB, thus moving the corresponding charge–charge interactions outside of the “gross error” zone, Fig. 9. Thus, to the extent that salt bridge over-stabilization seen in MD simulations is caused by PE → GB errors, the proposed model may be expected to mitigate the problem.
Figure 9.
Errors in pairwise solvation (charge–charge interaction) cross terms compared between the canonical GB and the proposed model based on Eqs. 5, 9, 11. The error in is computed relative to numerical PE as error. The two red dashed lines at ±2kBT indicate the gross error threshold.
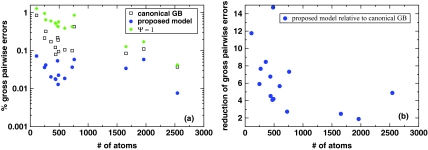
Further analysis of the effect of the proposed approximation on gross errors in pairwise electrostatic energy is presented in Fig. 10, where a comparison with the canonical GB is made for a variety of biomolecular structures. In all of the 16 structures tested, with sizes ranging from the small decapeptide ala10 to medium size proteins, the proposed model reduces the gross pairwise errors as compared to the canonical GB model. The improvement, estimated as the relative reduction in the number of charge pairs showing gross errors, ranges from a factor of 2 to a factor of more than 10, depending on the structure.
Figure 10.
(a) Relative numbers of gross pairwise errors in the canonical GB and the proposed model, Eqs. 9, 11. The test structures range from alanine decapeptide (∼100 atoms) to myoglobin (∼2500 atoms). For reference, gross errors of the Ψ = 1 model of Ref. 62 are also shown. (b) The relative reduction in the number of gross pairwise errors in the proposed model relative to the canonical GB.
It is also worth mentioning that the proposed model tends to reduce errors across the entire range, with the “reduction factor” being larger for larger errors. For example, for the four ala10 conformational states combined, the number of errors in larger than 3kBT is reduced by a factor of 50, compared to 11 for errors larger than 2kBT and a factor of 2 for errors larger than kBT. We note that errors less than kBT relative to numerical PE are not very meaningful given that the PE itself is just another approximation to reality (though more fundamental than the GB).
Next, we explore the performance of the proposed model in predicting relative changes in ΔGel between compact and extended states of ala10 peptide as well as of a small protein, protein-A, Table 1.
Table 1.
Error in relative ΔGel between conformational states C1 and C2 of various realistic structures as specified below. The error, in kcal∕mol, is computed as error. A set of snapshots representing the four conformations of ala10 used in this analysis is different from the one used for finding optimal values of (γ0, μ0).
| Conformations C1, C2 | Alpha, pp2 | Left, pp2 | Hairpin, pp2 | Alpha, hairpin | Protein-A: folded, unfolded |
|---|---|---|---|---|---|
| Error, Ψ = 1 | 5.0 | 8.1 | 3.3 | 1.2 | 37.8 |
| Error, canonical GB | 1.7 | 1.8 | 2.7 | −0.16 | 2.8 |
| Error, proposed model | −0.1 | 0.07 | 0.5 | −0.17 | 0.7 |
The proposed model shows no bias toward compact or extended structures, relative to the numerical PE treatment. With respect to absolute values of ΔGel, the proposed model performs as well as the canonical GB model for all but the three largest structures in our test set: the relative (to numerical PE) RMS errors are 1.4% and 1.6%, respectively, over this subset. On average, canonical GB model slightly underestimates, and the proposed model slightly overestimates ΔGel relative to numerical PE. The relative accuracy of ΔGel varies between structures in both the canonical GB and the proposed models. For example, for the four conformations of ala10 (∼100 atoms), the RMS errors are 1.9% and 0.6% for the canonical GB and the proposed model, respectively. For the B-form DNA (760 atoms), the relative errors in ΔGel are −0.8% and +0.3%, respectively for the canonical GB and the proposed model. For the three largest proteins in our test, ∼2000 atoms each, the RMS relative errors are 0.6% and 3%. However, given small numbers of structures in each of the above subgroups, the corresponding RMS values may not represent true statistical trends. Detailed investigation of performance of the models as a function of system size would require much larger numbers of structures in each size group—an investigation that is beyond the scope of this work that focuses on general principles.
Plausible origins of the remaining errors in the proposed model
Several structures of our test set lie in the narrow range of sizes around 450 atoms, Fig. 10, and so some conclusions related to variability of the model's accuracy within this narrow group can be made. The largest difference in the number of gross errors for proteins of this size is seen between structures 1cmr and 1dmc: 60 and 17 pairs in gross error, respectively. The large variation may seem odd given that these two small proteins are very similar similar in size, 472 and 440 atoms, respectively. They are also similar in their over-all shape: both are globular proteins with aspect ratios close to 1. However, a closer look reveals that 1cmr contains a deep internal solvent pocket, completely disconnected from the solvent space, while no similar pockets are found in 1dmc. We find that most of the 60 gross pairwise errors in 1cmr occur for pairs of atoms “across” the isolated solvent pocket from each other. Given that the largest deviations of the R6 effective radii from the PE reference are known to occur in the vicinity of such isolated, deeply buried solvent pockets,56 the presence of a relatively large number of gross errors still remaining in 1cmr may not be surprising. To test the hypothesis further, we recomputed the gross errors in both structures, but now using a slightly larger solvent probe radius (1.8 Å vs original 1.4 Å) in all of the calculations, including the PE reference. With this slightly larger probe, the isolated solvent pocket is no longer present in 1cmr; and, consistent with our logic, the gross errors are reduced three-fold to 21 pairs. The number is now close to what is found in 1dmc: 17, which has not changed upon the increase of the solvent probe radius. Note that the relatively high number of gross errors in 1cmr does not contradict the fact that the exact concentric spheres solution is approximated well by the proposed model. In testing of the model against the PE solution for the ideal concentric spheres geometry we used the exact (perfect) effective Born radii estimated directly from that exact solution. Moreover, the exact analytical solution assumed that the inner sphere was kept at the same potential as the solvent, see Sec. 5, in contrast to how a typical numerical PE solver would treat a disconnected solvent pocket. Whether or not an effort should be made in the future to reduce the type of gross pairwise errors associated with deep, isolated solvent pockets locked inside biomolecules may be a matter of debate. One can argue against such an effort in the context of numerical PE reference only. Indeed, it is unclear if such pockets are filled with water in realistic structures; even if they are, this water is likely to be highly structured, with properties very much different from that of bulk solvent.
We also explore to what extent the remaining gross errors may be due to the use of the practical, but still not exactly perfect R6 effective Born radii. Not unexpectedly, the use of the perfect (PE based) instead of the R6 effective radii in the canonical GB formalism results in only a very modest reduction of the number of pairs in gross error: averaged over all of the test structures, the reduction is 1.4, which for the most test structures is many times smaller that the corresponding reduction due to the use of the proposed formalism based on the R6 radii, Fig. 10 (b). This is most likely because the R6 radii are not too far from perfect.56 However, when the perfect radii are used in the new formalism, the average reduction in the number of pairwise gross errors—20—is considerably larger than in Fig. 10 (b) based on the R6 radii. For many structures, the reduction is at least twice as large as seen in the R6 case. However, that number varies considerably between structures. For the ala10 structures the reduction is 160, while for the B-DNA it is the same as obtained with the new formalism based on the R6. It appears that the use of perfect radii and the use of the new formalism act almost independently of each other, each reducing gross errors of a certain kind. For example, in the B-DNA, no error reduction due to the perfect radii alone (within the canonical GB) is seen, and consequently the observed 8-fold reduction due to the combination of both approaches is the same as within the new formalism alone. In contrast, in ala10, a modest (1.4) further reduction of gross error due to the use of the perfect radii decreases the number of pairs in gross error by a few, but that small change leads to the dramatic relative reduction of error because so few are already left within the new formalism. An example that is more representative of what appears to be the general trend is the beta-hairpin. Within the canonical GB and R6 radii, the total number of pairs in gross error is 60. The number is reduced to 50 via the use of the perfect radii alone, Fig. 1. The proposed formalism further reduces the number to 11 when the R6 radii are used, and to 4 with the perfect radii.
The Ψ = 1 model
We conclude our analysis by touching upon an interesting suggestion made in Ref. 62 where it was proposed, based on simplicity and efficiency arguments, that the simplest form of Ψ = 1 could be used instead of the canonical GB's Ψ = exp ( − 0.25ξ). Unfortunately, our results (Fig. 10, Table 1) show that the accuracy of this very appealing Ψ = 1 model—exact for a perfect sphere—is many times worse than that of even the canonical GB when applied to realistic biomolecular shapes. Apparently, in making realistic molecular shapes into perfect spheres, Occam's razor may sometimes cut off too much. The canonical GB formula Ψ < 1 is a better, though still far from perfect, solution than the Ψ = 1 perfect sphere model. This is because in realistic molecules many pairs of charges exist for which more of the electric field lines between the charges go through the high dielectric region than would be the case in a purely spherical geometry; the corresponding charge–charge interactions are thus weaker than they would be in an ideal sphere. The use of in the canonical GB partially accounts for that effect, see, e.g., Fig. 7. However, while the correction to Ψ = 1 provided by the canonical GB model is quite accurate asymptotically at large charge–charge separations where essentially only the longitudinal Ψ < 1 mode remains, it completely misses the transverse Ψ > 1 mode of the correct solution. The defect is most pronounced at short charge–charge distances where the mishandling of a whole class of strong interactions leads to appreciable loss of accuracy. Further deterioration of accuracy within the canonical GB stems from the need to balance out the total solvation energy by using a slightly smaller γ value than would be needed to best describe the longitudinal mode alone. The alternative formula presented in this work addresses these problems by treating both modes consistently on the same footing.
CONCLUSIONS
In many areas of molecular modeling, and especially in molecular dynamics simulations, the GB approximation is arguably the most widely used practical model based on the implicit solvation framework. Over the past two decades, the accuracy of the GB approximation has improved dramatically through efforts of many research groups. However, a wide gap still exists between the accuracy of the GB and explicit solvent representation. While some of it is due to fundamental assumptions made in the continuum → discrete step, a substantial part of the accuracy gap still comes from the approximate nature of the GB relative to the fundamental level of description at the continuum level—the PE. In this work we show that the key equation of the current GB approximation—the simple and effective formula due to Still et al. that remained unchanged since it was introduced 20 years ago—needs to be replaced in order to move the GB approach to the next level of accuracy. Analysis of exact solutions of the Poisson equation for idealized, but decidedly nonspherical dielectric boundaries suggested a simple analytical alternative to the “canonical GB” formula.
The work contains three key results:
- Even if the effective Born radii Ri, Rj are perfectly accurate, e.g., obtained via the numerically exact PE, solvation cross-terms computed via the “canonical” (Still's) GB equation
contain gross errors (errors larger than 2kBT relative to numerical PE reference). These gross errors in translate into errors of the same magnitude in pairwise charge–charge interactions Wij that affect energy landscape and ultimately dynamics of the system. The gross errors are found for up to 1% of the total number of atomic pairs for realistic structures. This means that even in very small structures such as a 16-residue β-hairpin, interaction between tens of atomic pairs, potentially forming salt bridges, may be in gross error. The errors contain both under- and over-estimations, which tend to cancel each other to yield deceptively accurate total electrostatic solvation energy, . The gross errors cannot be reduced by merely optimizing the value of γ in the canonical formula. To go beyond the canonical GB, we explored exact analytical solutions of the Poisson equation for two idealized, but decidedly nonspherical geometries. These were chosen to have relevance to biomolecular shapes. We found that the exact Green function of the Poisson problem for these nonspherical boundaries exhibits two spatial modes: a longitudinal mode that goes along the “long” dimension of the “molecule,” and a transverse mode which runs along its “short” dimension. The canonical GB Green function completely misses the transverse mode. Importantly, the same two modes are also seen in realistic biomolecular shapes, although the modes are not as distinct as in the idealized cases. The idealized solutions suggested a specific form for the alternative analytical Green function to replace the canonical GB formula. The proposed functional form is mathematically nearly as simple as the original, but depends not only on the effective Born radii but also on their gradients, which allows for better representation of details of nonspherical molecular shapes. In particular, the proposed functional form captures both of the modes of the PE solution seen in nonspherical geometries.
Tests on realistic biomolecular structures ranging from small peptides to medium size proteins show that the new proposed functional form reduces gross pairwise errors in all cases, with the amount of reduction varying from more than an order of magnitude for small structures to a factor of two for the largest ones. That magnitude of improvement is far beyond what can be achieved through the use of perfect effective radii alone within the canonical GB model; however, as with the canonical model, the use of more accurate effective radii within the proposed formalism helps reduce the gross errors further.
The proposed model is ready to be implemented and tested in molecular dynamics simulations. A question that remains is whether there is still room for meaningful improvement of the model relative to the PE, which is itself just an approximation to reality.
METHODOLOGICAL DETAILS
Structures
The snapshots representing the four conformational states of alanine decapeptide (called “ala10” here) were kindly provided by Daniel Roe. A detailed description of the Ala10 structures, their generation, and the methods used to compute ΔGel for these structures can be found in Ref. 50. Briefly, the trajectories of the four conformations of Ala10 were obtained from replica-exchange molecular dynamics simulations using TIP3P as solvent model. During the simulation, each structure was held in the corresponding region (α-helix, left-handed helix, hairpin or pp2-polyproline) of the (ϕ, ψ) space by weak harmonic constraints. Thus, there exist some structural variations between individual snapshots belonging to the same structure type.
In addition to the ala10 snapshots described above, the following protein structures were used for testing: (PDB ID) 1bdd, 1vii, 1az6, 1bh4, 1bku, 1brv, 1byy, 1cmr, 1dmc, 2lzt, 2mb5, 2trx. These proteins were employed previously in the context of GB model testing.64 To this set we added a canonical B-DNA (PDB 2bna) and a β-hairpin (residues 41–56 from PDB 2gb1). The three helix bundle 1bdd protein was represented by two conformations: the native folded (F) and an unfolded, fully extended conformation (U) that was prepared via an implicit solvent MD simulation at T = 450K described in Ref. 22. The structures in PQR format are available from the supplementary material.65
The Poisson equation reference
Here we briefly outline the PE formalism in a form tailored to the specific purpose of the current work. Within the linear response, continuum solvent framework, and in the absence of mobile ions, the electrostatic potential φ(r) produced by an arbitrary charge distribution ρ(r) is given exactly by the Poisson equation,
| (16) |
Here, ε(r) represents the position-dependent dielectric constant which equals that of bulk solvent far away from the molecule, and is expected to decrease fairly rapidly across the solute∕solvent boundary. The charge density ρ(r) is given by a set of “fixed” atomic charges qi at positions ri inside the dielectric boundary, ρ(r)=∑iqiδ(r−ri). A common simplification also used here is to assume an abrupt dielectric boundary, in which case ε(r) takes only two values: εin inside the dielectric boundary and εout outside—the so called two-dielectric model. Analytical solutions of the PE for arbitrary ρ(r) are available only for a handful of highly symmetric geometries, such as the sphere.66 Numerical methods exist for solving the PE for essentially any realistic dielectric boundary.2, 3, 67, 68, 69 Once the potential φ(r) is obtained, the electrostatic part of the solvation free energy is given by70
| (17) |
where φ(ri)|vac is the electrostatic potential computed for the same charge distribution in the absence of the dielectric boundary, e.g., in vacuum or more generally in uniform dielectric of molecular interior, εin. In this work the total ΔGel and its pairwise components , Eq. 17, obtained via the PE formalism are always used as reference in calculation of errors in analytical approximations to the PE.
Reference PE energies, perfect effective radii, and effective size
To compute the perfect effective Born radius of each atom, the charge–charge pairwise solvation energy for each pair of atoms, and the total electrostatic solvation energy of a given structure, a Poisson problem is set up and solved separately for each atom. In the process, the dielectric boundary of the full molecule is present, but only the charge of that particular atom is nonzero (all other charges are set to zero). Unless otherwise stated, the van der Waals radii of Bondi or mbondi2 (for ala10 test case only) and a solvent probe radius of 1.4 Å are used to define the molecular surface, which is taken as the dielectric boundary. The solute dielectric εin = 1, and we used εout = 1000 for the solvent to mimic the conductor limit. The accumulation of the PE solutions for all charges gives the necessary Green function from which the full Poisson solvation energy, the perfect effective Born radii, and the pairwise solvation energies are obtained. Software package PEP developed by P. Beroza3 is used to set up and solve these Poisson problems. The finest grid spacing used in all calculations is 0.07 Å, decreasing from 4 Å in eight steps of focusing on the atom in question. The reaction field Green function F(ri,rj) is obtained by subtracting the Coulomb part qiqj/(εinrij) from the total Green function. For each structure, the reaction field Green function is computed for all atom–atom pairs—this is the pairwise electrostatic solvation energy matrix used as reference throughout this work. Its diagonal (self) elements yield the perfect effective Born radii through Eq. 3. The matrices are available from the supplementary material.65
The effective electrostatic size is conveniently approximated via the simplest of expressions derived in Ref. 61: , where Iab are structure's moments of inertia around its center of mass , and M its “geometric mass” M = ∑imi; here , ai being intrinsic radius of atom i.
The R6 radii and their gradients
The inverse of the “R6” effective Born radius of atom i is computed numerically using the surface formulation outlined by Mongan et al.,56 and implemented as “NSR6” method in Ref. 63. After a triangulation of the surface, Ri is approximated by
| (18) |
where the summation is performed over the surface triangles. For each surface triangle k, ck represents the position of its center, Sk its area, and is a unit vector orthogonal to the triangle k pointing toward the inside of the solute. The surface triangulation was carried out by MSMS package71 using a probe radius of 1.4 and triangle density of 16 per Å2 for all the structures except 2mb5 and 2lzt for which a lower density of 8 per Å2 was used. A small constant correction (offset, B = 0.028) to the inverse radii in the above equation was used as suggested in Ref. 56. The gradients were always estimated by numerical differentiation of the R6 radii (even when the radii themselves were PE-based). To this end, for each atom of interest located at (x, y, z) six “ghost atoms” were created positioned at (x ± h, y, z), (x, y ± h, z), (x, y, z ± h), h = 0.01 Å. The R6 effective radii of the original atom and those of the six “ghost atoms” were then computed via Eq. 18. To avoid divergences due to abrupt changes in molecular surface upon infinitesimal changes of the atomic positions, we used one and the same triangulated molecular surface for the above calculations, i.e., the surface did not change with the introduction of the “ghost atom.” We chose the outlined procedure because it is absolutely straightforward. However, we suggest that efficient practical implementations of the R6 gradients should be based either on analytical approximations such as AR6 of Ref. 63 or on direct surface integration of the gradient of the above integral (e.g., first take the derivative under the integral, then integrate). Generally speaking, implementation of Eqs. 5, 9, 11 does not have to rely of the R6: any reasonably accurate approximation for the effective radii should work.
Parallel plates solution
The exact solution of the PE equation for the parallel plates configuration is given by an infinite series of image charges, the first three of which are illustrated in Fig. 11. The sum of the unit image charge contributions gives the reaction field part of the Green function,
| (19) |
Figure 11.
First three charges of the infinite system of image charges that provide the exact solution of the PE equation for the parallel plates geometry. A unit positive source charge is located at (z = z0, x = 0), and the first three images, also unit charges, are at ( − z0, 0), ( − 2a + z0, 0), and (2a − z0, 0). The potential is calculated at (z, x).
Note that terms in () have to be summed together to ensure convergence. In practice, a partial sum of F(ri,rj)plates is used; convergence is improved by summing first k terms exactly, and using an integral approximations for the remainder of the infinite series, such as
| (20) |
and similar ones for the other terms. To compute the partial sums we use k = 100 in all of the calculations reported here, except for the exact estimates outlined below.
We use the definition of Ψ, Eq. 5, to compute exact value of . The expressions simplify because ∂Ri/∂x = 0 by translational symmetry of the problem.
We proceed by calculating via term by term differentiation of Eq. 19. The following known expressions
are used, where Z (n) is Riemann zeta function. Also, at z = z0 = a/2, F(ri,rj)plates can be calculated exactly: F(ri,rj)plates(z=z0=a∕2)=−ln4∕a, which yields for the effective Born radius R(z=z0=a∕2)=−1∕F(ri,rj)plates(z=z0=a∕2)=a∕ln4. This leads to
| (21) |
Integrating Eq. 21 we find that for small x, . Also, const=1 since Ψ(0) = 1. Now recall that ξ = x2/(RiRj) to arrive at Ψ ∼ 1 − 0.323ξ.
Concentric spheres solution
The image charge solution of this problem is worked out in detail in Ref. 72; here we list the key result. The solution is given by two infinite sets of image charges, one inside the inner sphere and the other outside the outer sphere in the solvent space, see Fig 12.
Figure 12.
First four charges of the infinite system of image charges that provide the exact solution of the PE equation for the concentric spheres geometry. A unit positive source charge is located at (z = z0, θ = 0). Positions and magnitudes of the image charges are specified in text. The origin of the z axis is at the surface of the inner sphere. The potential ϕ is calculated at (z, θ).
The image charges of magnitude S and T located at positions X and Y are
inner:
outer:
outer:
inner:
where p = 0, 1, 2… The reaction field Green function is then,
ACKNOWLEDGMENTS
The authors thank Igor Tolokh for reading the article and making helpful suggestions. Financial support from the National Institutes of Health (NIH) (R01 GM076121) is acknowledged.
References
- Cramer C. J. and Truhlar D. G., Chem. Rev. 99, 2161 (1999). 10.1021/cr960149m [DOI] [PubMed] [Google Scholar]
- Honig B. and Nicholls A., Science 268, 1144 (1995). 10.1126/science.7761829 [DOI] [PubMed] [Google Scholar]
- Beroza P. and Case D. A., Methods Enzymol. 295, 170 (1998). 10.1016/S0076-6879(98)95040-6 [DOI] [PubMed] [Google Scholar]
- Madura J. D., Davis M. E., Gilson M. K., Wade R. C., Luty B. A., and McCammon J. A., Rev. Comput. Chem. 5, 229 (1994). 10.1002/SERIES6143 [DOI] [Google Scholar]
- Gilson M. K., Curr. Opin. Struct. Biol. 5, 216 (1995). 10.1016/0959-440X(95)80079-4 [DOI] [PubMed] [Google Scholar]
- Scarsi M., Apostolakis J., and Caflisch A., J. Phys. Chem. A 101, 8098 (1997). 10.1021/jp9714227 [DOI] [Google Scholar]
- Luo R., David L., and Gilson M. K., J. Comput. Chem. 23, 1244 (2002). 10.1002/jcc.10120 [DOI] [PubMed] [Google Scholar]
- Simonson T., Rep. Prog. Phys. 66, 737 (2003). 10.1088/0034-4885/66/5/202 [DOI] [Google Scholar]
- Onufriev A., Annu. Rep. Comp. Chem. 4, 125 (2008). 10.1016/S1574-1400(08)00007-8 [DOI] [Google Scholar]
- Constanciel R. and Contreras R., Theor. Chim. Acta 65, 1 (1984). 10.1007/BF02427575 [DOI] [Google Scholar]
- Still W. C., Tempczyk A., Hawley R. C., and Hendrickson T., J. Am. Chem. Soc. 112, 6127 (1990). 10.1021/ja00172a038 [DOI] [Google Scholar]
- Onufriev A., Bashford D., and Case D., J. Phys. Chem. B 104, 3712 (2000). 10.1021/jp994072s [DOI] [Google Scholar]
- Dominy B. N. and Brooks C. L., J. Phys. Chem. B 103, 3765 (1999). 10.1021/jp984440c [DOI] [Google Scholar]
- Bashford D. and Case D., Annu. Rev. Phys. Chem. 51, 129 (2000). 10.1146/annurev.physchem.51.1.129 [DOI] [PubMed] [Google Scholar]
- Calimet N., Schaefer M., and Simonson T., Proteins: Struct., Funct., Genet. 45, 144 (2001). 10.1002/prot.1134 [DOI] [PubMed] [Google Scholar]
- Hawkins G. D., Cramer C. J., and Truhlar D. G., Chem. Phys. Lett. 246, 122 (1995). 10.1016/0009-2614(95)01082-K [DOI] [Google Scholar]
- Hawkins G. D., Cramer C. J., and Truhlar D. G., J. Phys. Chem. 100, 19824 (1996). 10.1021/jp961710n [DOI] [Google Scholar]
- Schaefer M. and Karplus M., J. Phys. Chem. 100, 1578 (1996). 10.1021/jp9521621 [DOI] [Google Scholar]
- Feig M., Im W., and Brooks C. L., J. Chem. Phys. 120, 903 (2004). 10.1063/1.1631258 [DOI] [PubMed] [Google Scholar]
- Lee M. S., Salsbury J. F. R., and C. L.BrooksIII, J. Chem. Phys. 116, 10606 (2002). 10.1063/1.1480013 [DOI] [Google Scholar]
- Lee M. S., Feig M., Salsbury F. R., and Brooks C. L., J. Comput. Chem. 24, 1348 (2003). 10.1002/jcc.10272 [DOI] [PubMed] [Google Scholar]
- Onufriev A., Bashford D., and Case D. A., Proteins 55, 383 (2004). 10.1002/prot.20033 [DOI] [PubMed] [Google Scholar]
- Srinivasan J., Trevathan M., Beroza P., and Case D., Theor. Chem. Acc. 101, 426 (1999). 10.1007/s002140050460 [DOI] [Google Scholar]
- Tsui V. and Case D., J. Am. Chem. Soc. 122, 2489 (2000). 10.1021/ja9939385 [DOI] [Google Scholar]
- Wang T. and Wade R., Proteins 50, 158 (2003). 10.1002/prot.10248 [DOI] [PubMed] [Google Scholar]
- Gallicchio E. and Levy R. M., J. Comput. Chem. 25, 479 (2004). 10.1002/jcc.10400 [DOI] [PubMed] [Google Scholar]
- Nymeyer H. and García A. E., Proc. Natl. Acad. Sci. U.S.A. 100, 13934 (2003). 10.1073/pnas.2232868100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh A., Rapp C. S., and Friesner R. A., J. Phys. Chem. B 102, 10983 (1998). 10.1021/jp982533o [DOI] [Google Scholar]
- Im W., Lee M. S., and Brooks C. L., J. Comput. Chem. 24, 1691 (2003). 10.1002/jcc.10321 [DOI] [PubMed] [Google Scholar]
- Haberthür U. and Caflisch A., J. Comput. Chem. 29, 701 (2008). 10.1002/jcc.20832 [DOI] [PubMed] [Google Scholar]
- Grant J. A., Pickup B. T., Sykes M. J., Kitchen C. A., and Nicholls A., Phys. Chem. Chem. Phys. 9, 4913 (2007). 10.1039/b707574j [DOI] [PubMed] [Google Scholar]
- Tjong H. and Zhou H. X., J. Phys. Chem. B 111, 3055 (2007). 10.1021/jp066284c [DOI] [PubMed] [Google Scholar]
- Labute P., J. Comput. Chem. 29, 1693 (2008). 10.1002/jcc.20933 [DOI] [PubMed] [Google Scholar]
- Hoijtink G. J., Boer de E, Van Der Meij P. H., and Weijland W., Recl. Trav. Chim. Pays-Bas 75, 487 (1956). 10.1002/recl.19560750502 [DOI] [Google Scholar]
- Onufriev A., Case D. A., and Bashford D., J. Comput. Chem. 23, 1297 (2002). 10.1002/jcc.10126 [DOI] [PubMed] [Google Scholar]
- Born M., Z. Phys. 1, 45 (1920). 10.1007/BF01881023 [DOI] [Google Scholar]
- Simmerling C., Strockbine B., and Roitberg A. E., J. Am. Chem. Soc. 124, 11258 (2002). 10.1021/ja0273851 [DOI] [PubMed] [Google Scholar]
- Chen J., Im W., and Brooks C. L., J. Am. Chem. Soc. 128, 3728 (2006). 10.1021/ja057216r [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jang S., Kim E., and Pak Y., J. Chem. Phys. 128, 105102 (2008). 10.1063/1.2837655 [DOI] [PubMed] [Google Scholar]
- Zagrovic B., Snow C. D., Shirts M. R., and Pande V. S., J. Mol. Biol. 323, 927 (2002). 10.1016/S0022-2836(02)00997-X [DOI] [PubMed] [Google Scholar]
- Jang S., Kim E., Shin S., and Pak Y., J. Am. Chem. Soc. 125, 14841 (2003). 10.1021/ja034701i [DOI] [PubMed] [Google Scholar]
- Lei H. and Duan Y., J. Phys. Chem. B 111, 5458 (2007). 10.1021/jp0704867 [DOI] [PubMed] [Google Scholar]
- Pitera J. W. and Swope W., Proc. Natl. Acad. Sci. U.S.A. 100, 7587 (2003). 10.1073/pnas.1330954100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jagielska A. and Scheraga H. A., J. Comput. Chem. 28, 1068 (2007). 10.1002/jcc.20631 [DOI] [PubMed] [Google Scholar]
- Hornak V., Okur A., Rizzo R. C., and Simmerling C., Proc. Natl. Acad. Sci. U.S.A. 103, 915 (2006). 10.1073/pnas.0508452103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amaro R. E., Cheng X., Ivanov I., Xu D., and Mccammon A. J., J. Am. Chem. Soc. 131, 4702 (2009). 10.1021/ja8085643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M. S., Salsbury F. R., and Brooks C. L., Proteins 56, 738 (2004). 10.1002/prot.20128 [DOI] [PubMed] [Google Scholar]
- Mongan J., Case D. A., and McCammon J. A., J. Comput. Chem. 25, 2038 (2004). 10.1002/jcc.20139 [DOI] [PubMed] [Google Scholar]
- Khandogin J. and Brooks C. L., Proc. Natl. Acad. Sci. U.S.A. 104, 16880 (2007). 10.1073/pnas.0703832104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roe D. R., Okur A., Wickstrom L., Hornak V., and Simmerling C., J. Phys. Chem. B 111, 1846 (2007). 10.1021/jp066831u [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou R., Proteins 53, 148 (2003). 10.1002/prot.10483 [DOI] [PubMed] [Google Scholar]
- Geney R., Layten M., Gomperts R., Hornak V., and Simmerling C., J. Chem. Theory Comput. 2, 115 (2006). 10.1021/ct050183l [DOI] [PubMed] [Google Scholar]
- Zhou R. and Berne B. J., Proc. Natl. Acad. Sci. U.S.A. 99, 12777 (2002). 10.1073/pnas.142430099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okur A., Wickstrom L., and Simmerling C., J. Chem. Theory Comput. 4, 488 (2008). 10.1021/ct7002308 [DOI] [PubMed] [Google Scholar]
- Zhou R., Krilov G., and Berne B. J., J. Phys. Chem. B 108, 7528 (2004). 10.1021/jp037812c [DOI] [Google Scholar]
- Mongan J., Svrcek-Seiler W. A., and Onufriev A., J. Chem. Phys. 127, 185101 (2007). 10.1063/1.2783847 [DOI] [PubMed] [Google Scholar]
- Feig M., Onufriev A., Lee M. S., Im W., Case D. A., and Brooks C. L., J. Comput. Chem. 25, 265 (2004). 10.1002/jcc.10378 [DOI] [PubMed] [Google Scholar]
- Fenley A. T., Gordon J. C., and Onufriev A., J. Chem. Phys. 129, 075101 (2008). 10.1063/1.2956497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon J. C., Fenley A. T., and Onufriev A., J. Chem. Phys. 129, 075102 (2008). 10.1063/1.2956499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigalov G., Scheffel P., and Onufriev A., J. Chem. Phys. 122, 094511 (2005). 10.1063/1.1857811 [DOI] [PubMed] [Google Scholar]
- Sigalov G., Fenley A., and Onufriev A., J. Chem. Phys. 124, 124902 (2006). 10.1063/1.2177251 [DOI] [PubMed] [Google Scholar]
- Grycuk T., J. Chem. Phys. 119, 4817 (2003). 10.1063/1.1595641 [DOI] [Google Scholar]
- Aguilar B., Shadrach R., and Onufriev A. V., J. Chem. Theory Comput. 6, 3613 (2010). 10.1021/ct100392h [DOI] [Google Scholar]
- Mongan J., Simmerling C., McCammon J., Case D., and Onufriev A., J. Chem. Theory Comput. 3, 156 (2007). 10.1021/ct600085e [DOI] [PMC free article] [PubMed] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.3578686 for the structure files and the corresponding PE charge-charge interaction matrices.
- Kirkwood J. G., J. Chem. Phys. 2, 351 (1934). 10.1063/1.1749489 [DOI] [Google Scholar]
- Baker N. A., Sept D., Joseph S., Holst M. J., and McCammon J. A., Proc. Natl. Acad. Sci. U.S.A. 98, 10037 (2001). 10.1073/pnas.181342398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocchia W., Alexov E., and Honig B., J. Phys. Chem. B 105, 6507 (2001). 10.1021/jp010454y [DOI] [Google Scholar]
- Nicholls A. and Honig B., J. Comput. Chem. 12, 435 (1991). 10.1002/jcc.540120405 [DOI] [Google Scholar]
- Jackson J. D., Classical Electrodynamics (Wiley, New York, 1975). [Google Scholar]
- Sanner M. F., Olson A. J., and Spehner J. C., Biopolymers 38, 305 (1996). [DOI] [PubMed] [Google Scholar]
- Dick B., Am. J. Phys. 41, 1289 (1978). 10.1119/1.1987548 [DOI] [Google Scholar]