Broad disorder and the allosteric mechanism of myosin II regulation by phosphorylation

Abstract

Double electron electron resonance EPR methods was used to measure the effects of the allosteric modulators, phosphorylation, and ATP, on the distances and distance distributions between the two regulatory light chain of myosin (RLC). Three different states of smooth muscle myosin (SMM) were studied: monomers, the short-tailed subfragment heavy meromyosin, and SMM filaments. We reconstituted myosin with nine single cysteine spin-labeled RLC. For all mutants we found a broad distribution of distances that could not be explained by spin-label rotamer diversity. For SMM and heavy meromyosin, several sites showed two heterogeneous populations in the unphosphorylated samples, whereas only one was observed after phosphorylation. The data were consistent with the presence of two coexisting heterogeneous populations of structures in the unphosphorylated samples. The two populations were attributed to an on and off state by comparing data from unphosphorylated and phosphorylated samples. Models of these two states were generated using a rigid body docking approach derived from EM [Wendt T, Taylor D, Trybus KM, Taylor K (2001) Proc Natl Acad Sci USA 98:4361–4366] (PNAS, 2001, 98:4361–4366), but our data revealed a new feature of the off-state, which is heterogeneity in the orientation of the two RLC. Our average off-state structure was very similar to the Wendt model reveal a new feature of the off state, which is heterogeneity in the orientations of the two RLC. As found previously in the EM study, our on-state structure was completely different from the off-state structure. The heads are splayed out and there is even more heterogeneity in the orientations of the two RLC.

Myosin II is a motor protein that can transduce chemical energy from ATP hydrolysis into mechanical work. This process involves cyclic interactions between actin in thin and myosin in thick filaments causing relative filament sliding. Smooth muscle myosin (SMM), which contains two heads, each with a motor domain (MD) and regulatory domain (RD), connected by a long coiled-coil tail domain is an example of a large multisubunit protein that is allosterically regulated by phosphorylation (for review, see ref. 1). Phosphorylation of a single serine on each regulatory light chain (RLC), which are about 100 Å distant from the active sites, is sufficient to transform the protein from a state in which the ATPase activity is weakly actin-activated to one in which it is strongly actin-activated by controlling the rate of Pi release (2). Because phosphorylation modulates the rate of ADP release (3) and also alters the attitude of the lever arm domain with respect to the MD (4), it is likely that phosphorylation modulates strain between the two heads (5).

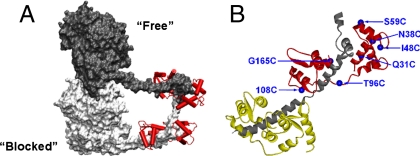
The structural basis for the allosteric regulation has been a topic of intense study. It is a difficult problem because regulation by phosphorylation requires the presence of both head domains. Cryogenic EM studies of double-headed constructs (6–9) have incorporated data from crystallographic atomic resolution structures, which are limited to single head domains, to produce several pseudoatomic models. These static structures of the inhibited state all reveal that one head binds to the other through the MDs. The “blocked” head has its actin-binding interface sterically occupied by the MD of the “free” head (Fig. 1A). The model suggests that the binding of the blocked head to actin is inhibited as well as the ATPase activity of the free head because its converter domain cannot rotate to release Pi from the active site. Interactions of portions of the heads with the proximal region of the tail (called S2) may also be important (6, 10). Here the heads point “down,” essentially lying on top of S2 (7). This implies that the head-tail junction is highly flexible, because the heads-down conformation must convert to a heads-up conformation to support actin interaction and relative filament sliding once myosin is activated by phosphorylation.

Fig. 1.

Myosin structure. (A) Cartoon model of the off state of SMM from EM data (9) showing MD–MD interactions—the actin-binding site on the heavy chain of one head (in light gray) is blocked by an interaction with the converter domain of the free head (dark gray) (9). The RLCs are shown in red attached to the RDs (lever arms) but the essential light chain (ELC) is not shown for clarity. (B) Ribbon model of RD. ELC (yellow), the truncated HC (in gray) and RLC (red), with the mutated sites highlighted (blue text and spheres). Sites 15, 23, and 31 are not shown for clarity.

We are interested in the distribution of conformational states of myosin II, specifically the role of such distribution in the allosteric mechanism. It is now clear that allosteric processes can be described by a redistribution in the fractional contributions of preexisting structurally distinct populations or substates, which dynamically interchange also in the absence of the allosteric ligand (for reviews, see refs. 11 and 12). In our case the allosteric effectors are nucleotide binding to the active site and phosphorylation of the RLC. This conformational selection model predicts that unphosphorylated (uP) myosin exists as an ensemble of conformations that includes the conformations present after phosphorylation. Understanding the structural basis of the myosin II allosteric mechanism has been slowed by the same stumbling blocks found for other proteins, that is the difficulty in characterizing the structures of the predicted multiple conformations (or conformational substates) in dynamic equilibrium.

To address this problem, we have examined the conformational space of SMM and its role in the allosteric mechanism by measuring the effects of allosteric modulators on the distances and distance distributions between the two RLCs, one on each head. This region of the protein is where the phosphorylation occurs, and is immediately adjacent to the aforementioned flexible head-tail junction. We have measured these parameters between several spin-labeled sites on the RLC using pulsed EPR [double electron electron resonance (DEER)], which is sensitive in the 20–70 Å range. This method is advantageous for several reasons. Many different constructs can be compared, in our case full-length monomeric versus filamentous SMM, and the monomeric heavy meromyosin (HMM). Also, several states can be examined such as the presence or absence of phosphorylation and ATP. Our results suggest that the mechanism of phosphorylation may be only to direct stochastic, large-scale conformational fluctuations that are ingrained in the structure of SMM.

The fact that cryo-EM and EPR are suited to draw complementary pictures of the same process provides great opportunities in coming to an understanding of regulation. Toward this end, the average distances obtained by EPR were used as constraints in a modeling strategy proposed here. We have generated two models, which likely represent the inhibited (off) and activated (on) states. Our model of the inhibited state is remarkably consistent with the cryo-EM models with an additional unexpected finding of wide conformational heterogeneity under all conditions and states studied. Our model of the activated state shows a dramatic change in the attitude of the two heads, again with wide conformational heterogeneity under all conditions and states studied.

Results

Experimental Approach and Data Analysis.

We reconstituted SMM or HMM with nine single cysteine RLC mutants labeled with the spin-label (1-oxyl-2,2,5,5-tetramethyl-∆3-pyrroline-3-methyl) methanethiosulfonate (MTSSL): Q15, A23, Q31, N38, I48, S59, T96, C108, and G165 (Fig. 1B). Table S1 shows that, as expected from prior studies, there is minimal effect of reconstitution with selected labeled mutant RLC (> 70% labeling) on the phosphorylation-dependent regulation of the actin-activated ATPase. Prior data from other studies for other mutated sites used here are summarized. Importantly, the ATPase in the uP state remains inhibited. For EPR experiments, two different states of SMM were studied, monomeric and filamentous at high and low ionic strengths respectively. To examine low ionic strength conditions without filament formation, we also studied HMM, which contains both heads but lacks the C-terminal approximately 2/3 of the tail that is required for filament assembly. We studied the effects of two allosteric effectors, phosphorylation of the RLC and ATP binding to the active site.

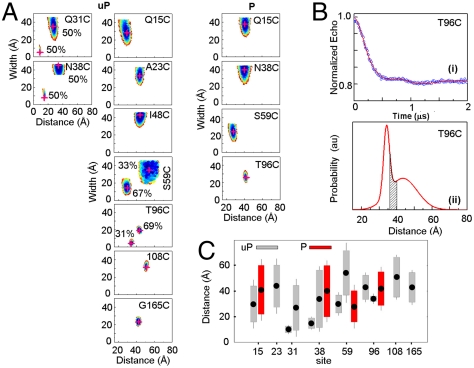
A combination of conventional EPR (for distances < 20 Å) and pulsed DEER [20–70 Å (13, 14)] techniques were used to measure inter-RLC spin-spin distances and distance distributions. Spectral data found in the figures are summarized in Table S2. Figs. S1–S3 show the time evolution of the echo decay for each corresponding contour in Figs. 2 and 3. To quantify distance distributions, EPR signals were fitted by a dipolar evolution expected for a certain Gaussian distance distribution. The number of Gaussians, their average distance (r_ave), width (full width at half maximum, Δ), and amplitude were varied to achieve the best fit (lowest χ²). The effects of evolution time and background subtraction are illustrated in Fig. S4. Fits to 2 and 3 Gaussians were always tried and improvement in χ² was evaluated by an F-test. The quality of the fit, its uniqueness, and associated errors are described by the χ² surface on the width versus distance plots seen in Figs. 2 and 3. The surface was created by randomly sampling the distance, width, and amplitude and plotting the quality of fit for all solutions that are within 1 standard deviation of the best fit (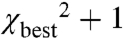; 67% confidence level). Narrower contours indicate better defined distance distributions. Wider contours indicate less unique solutions, any parameters that lie within the contours yield similar EPR signals to those observed experimentally. Note that all the contours in Figs. 2 and 3 are more elongated along the y axis than the x axis. This means that the uniqueness of the average distance is high but the uniqueness of the width of the distance distribution is less so. The errors on each of the measured parameters, r_ave and Δ, are the width of the contours (Table S2).

Fig. 2.

EPR data for SMM monomers. (A) Contour plots of average distance and distance distribution width for uP (Left) and P (Right) SMM monomers in 0.5 M KCl, 0.1 mM EGTA, 10 mM 3-(N-morpholino)propanesulfonic acid (MOPS), pH 7.5. The contours depict associated χ² error surface, the goodness of fit as a function of the fitting parameters [color coded from blue (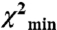) to red (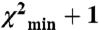)] to denote 67% confidence limit. Best fit position is highlighted by a red “+.” For sites 31, 38, 59, and 96 two Gaussian populations are plotted separately, fractional contributions are indicated. (B) DEER signal time evolution of the echo (Upper, circles), best fits (Upper, solid line) corresponding to the Gaussian distance distribution in the Lower panel for site 96. Gray area is the range of interspin distances predicted by MMCM. (C) Summary of phosphorylation effects on distances and distance distributions. Filled points show the average distance, r_ave. Lengths of open and hashed bars represent the y-axis value of the magenta cross in (B) for uP and P myosin, respectively. The error on the distances is represented by the visible length of whiskers attached to the bars. For sites 31, 38, 59, and 96 the two Gaussian populations are plotted separately.

Fig. 3.

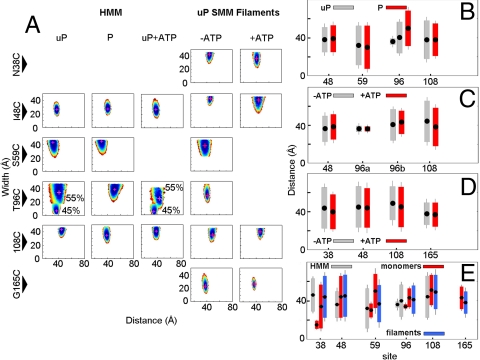
EPR data for HMM and myosin filaments. (A) Average distance and width of distribution contours for uP HMM, P HMM, and uP HMM + ATP. (B) Comparison of RLC–RLC distances and distributions in P versus uP HMM (+ATP where applicable) summarized from data in panel A. (C) Effect of ATP in uP HMM. For site 96, two Gaussians are shown as “a” and “b”. (D) Effect of ATP in uP SMM filaments. (E) Comparison of distance distributions for HMM (open), SMM monomers (stippled), and SMM filaments (hashed). All samples are uP and in absence of ATP. For sites 38, 59, and 96 two Gaussian populations are plotted separately. For (b–e), average distances are denoted by filled points, bars depict the width of distribution.

EPR Data for SMM Monomers.

Fig. 2A shows the contour plots of distance versus width of the distance distribution for SMM in the monomeric state. Fig. 2B shows the time evolution of the echo decay and corresponding Gaussian distance distribution for T96C. The shaded region shows the expected distance distribution due solely to rotamer diversity and spin-label flexibility (see below).

The effect of phosphorylation for four sites is shown in Fig. 2A and these data are summarized in Fig. 2C. In each case, phosphorylation had a large effect. For N38, S59, and T96, two populations were observed in the uP state. Upon phosphorylation of N38, S59, and T96 two populations could no longer be justified. The population characterized by narrower distance distribution vanished leaving the broader population. For uP N38, the shorter distance was measured by conventional EPR and the longer by DEER. These data are each combined on the same contour plot in Fig. 2A. Upon phosphorylation of N38 the shorter distance population resulting in broadening of conventional EPR vanished but a longer distance of approximately 40 Å was observable by DEER (Fig. 2A). Q15 was also responsive to phosphorylation, but one population was sufficient to fit the data in the uP state. The average distance increased by 11 Å from 30 ± 5 to 41 ± 5 Å. For 108, 48, and 165, only a single, long distance population was observed in the uP state and therefore phosphorylation was not examined for these sites.

EPR Data for HMM and SMM Filaments at Low Ionic Strength.

To investigate the effect of ionic strength we compared SMM monomers (high ionic strength; Fig. 2) with two other states, filamentous SMM at low ionic strength and HMM (Fig. 3), which cannot form filaments at low ionic strength. For HMM the data were similar to monomers except that S59 could no longer be described by 2 populations in the uP state. The distance best matched the distance with the larger fractional contribution in SMM monomers. T96 remained best described by two distances, but both the distance and width were appreciably less unique. As we found for SMM monomers, phosphorylation eliminated the contour with the smaller fractional contribution. We also examined the effect of the allosteric modulator ATP on the uP state, which is the condition used for the EM studies (Fig. 3 A and C). In HMM the width of the 55% population for T96C decreased significantly and the distance for site 108 decreased by approximately 6 Å but for the latter site in filaments the change was only 3 Å. For sites 48 and 165 we have directly compared KCl versus KAc in the buffers and found no changes (< 2 Å) in the average distance and distance width (< 1 Å). These experiments were motivated by the common avoidance of KCL (although, see ref. 7) and preference for KAc in EM studies.

The data for full-length uP SMM at low ionic strength (Fig. 3A) was also largely unaffected by the addition of ATP (Fig. 3D). Under the conditions of EPR data acquisition (20–60 mg/mL), the SMM is filamentous and the addition of ATP did not cause any detectable filament disassembly to the soluble 10S conformer. There was essentially no protein in the supernatant after sedimenting the filaments. This was expected because the protein is far above the critical concentration for filament assembly. The most notable difference between filaments and other states is that all mutants were best described as single populations in the uP state. For sites 38, 59, and 96, which were described by two populations in the SMM monomers, were a single population in the filaments. The distances observed in the filaments however matched reasonably well with one of the distances observed in SMM monomers and HMM. For the other sites, the pattern was less clear, but ATP did not significantly change the distances or the distributions (Fig. 3D). Further studies with filaments are required. The data for all SMM monomers, HMM, and filaments are summarized in Fig. 3E.

Spin-Label Rotamer Diversity Is not Sufficient to Explain the Broad Distance Distributions.

All the distance distributions in Figs. 2 and 3 are very wide. The distances measured by EPR are between the unpaired electrons in the nitroxide rings of the spin labels. In our case the N–O bond is about 8.5 Å from the Cα and is separated by five single bonds about which the ring is potentially free to rotate. This results in flexibility of the spin label, and uncertainty of its position due to rotamer diversity. To evaluate whether the wide distance distributions were due solely to rotamer diversity and spin-label flexibility, we performed molecular modeling using Metropolis Monte Carlo minimization (MMCM) (15, 16), which can find the lowest energy rotamer (i.e., the most probable conformation) within the constraints of a local structure. Using the coordinates from the Wendt model, the most probable rotamer conformations for MTSSL on the RLC were found for each of the labeled sites (Table S2 and Fig. S1) This generated the modeled distances (r_ave) and widths (Δ) at each site. Note that the modeled widths are much smaller than the observed widths for all positions studied except one. This suggests that the broad widths of the experimental distance distributions cannot be explained simply by rotamer diversity of the spin label. The broad widths are consistent with broad conformational heterogeneity of the protein structures.

Discussion

Interpretation of EPR Results.

The comparison of unphosphorylated and phosphorylated (P) samples, suggested a hypothesis that the allosteric effect of phosphorylation is to bias or redistribute preexisting structurally distinct populations or substates, which dynamically interchange also in the absence of phosphorylation. This idea is consistent with a conformational selection mechanism of allostery (11, 12).

The key findings that led to this idea was that in four sites (31, 38, 59, and 96 in SMM monomers), even with the broad distributions, the EPR methods were capable of resolving two populations in the uP samples. Interestingly, the relative fractions of these populations (approximately 1/2 - 1/1) are very similar to two conformations, loosely defined as off and on, of scallop myosin II (regulated by Ca²⁺) in the absence of Ca²⁺ and nucleotide. Kinetics suggests that Ca²⁺ is an allosteric effector of the equilibrium between the conformations (17). The phosphorylation-induced change in the EPR data from two populations to one could be due to (i) a loss of a population, (ii) an increased distance distribution, and/or (iii) a too small difference between the average distances.

Based upon the above, we tested the hypothesis that one of the populations corresponds to the distances expected from the EM off state and the other corresponds to the activated state for which there is no model. Generally we attributed populations with smaller distribution of distances, as expected for a docked head, to the off state. Therefore, for example, for S59 we attributed the 30 Å distance with 14 Å distribution to the off state, and the 50 Å distance with 35 Å distribution as the on state. Similarly, for T96 we attributed the 43 Å distance to the on state and the 34 Å distance as the off state, based upon the consistent pattern for monomers and HMM. For Q31, the shorter distance was attributed to the off state because its distribution was much smaller than the longer distance, five versus 35 Å. Q15 was an exception in that only one population was observed in the uP sample, which showed a clear change in distance from 30 to 41 Å upon phosphorylation. But again, the distribution of distances in the P sample was broader than the uP, consistent with the other sites. Table S2 shows the attributions of all populations to an on or off state.

Superficially, the above interpretation of the data seems to be contradicted by the sites that showed a single Gaussian population in the uP samples. At first glance, one might insist that these samples too should have shown two populations, if the on and off structures coexist. However, the observation of one or two Gaussians depends on the difference between the average distances, and on the relative widths and fractions of the populations. The rule of thumb is that average distances have to be separated by more than the combined half-widths of each population for two Gaussians to be justified. Otherwise one Gaussian describes the data adequately. Accordingly, we hypothesize that these samples contained two populations in the uP samples but they were not resolved by EPR due to small differences in the distances. The HMM data for 108 and 48 support this interpretation because there was little change in distances or distributions upon phosphorylation. Also, the data for A23, 48, and 108 in the uP monomers show a relatively broad distribution, much broader than the populations we attribute to the off state in Table S2, Therefore, the distances were assigned to both the off and on states. Please, note that the reorientation of an object with respect to another object can leave some distances unchanged whereas distances between the other points change dramatically; e.g., distances between sites close to the axis of rotation are less sensitive to reorientation (see Materials and Methods).

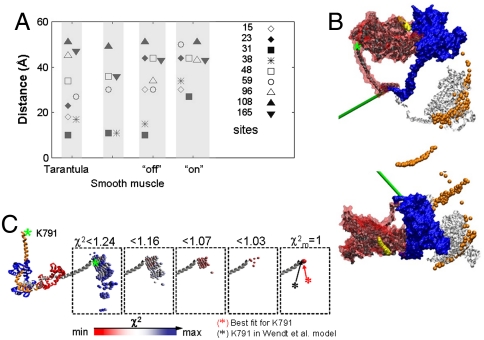
The interpretation of the EPR data is shown in Fig. 4A. The predicted RLC–RLC distances from two published off-state models are in agreement with the data that we attributed to the off state. This strongly supports our interpretation. As expected the distances we attribute to the on state, however, diverge from the off-state models.

Fig. 4.

Modeling results. (A) Comparison of RLC–RLC distances. Distances measured by EPR in the monomers were attributed to off and on states. RLC–RLC distances shown are for the off and on models derived from rigid body docking. The corresponding distances from smooth muscle [Wendt et al., (9)] and tarantula [Alamo et al., (6)] off-state models are shown. Note that for some sites there is little difference between off and on states. (B) (Enlargement of Fig. 4B appears in Fig. S5.) Comparison of modeled structures using EPR constraints versus EM model from Wendt et al. (9). Free head of Wendt model (9) is blue and blocked head is red. Light chains have been omitted for clarity. The dark gray and white ribbons depict our attributed off- and on-state blocked head positions, respectively, both at 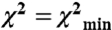. Note the close similarity of our off-state with the EM model. The ribbons show the MD in the original Wendt “bent” configuration for clarity, but our data do not stipulate this. Our data stipulate the position of the lever arm only. The on model is generated by a complex rotation and a twist that can be approximated by 110° rotation about the axis depicted in green. The yellow and orange balls show the positions of the top of the MD (residue 560) for all solutions for which 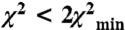for the off and on models respectively, again assuming that the MD adopts the blocked conformation. Green asterisk shows position of K791 of HC. The model on the top was rotated by 90° to generate orthogonal view of the model, bottom. (C) The relationship between the χ² threshold (red minimum and blue maximum) for the position of K791 at the N-terminus of HC lever arm helix in off-state EPR model (colored balls) for the blocked head helix (gray) and its RLC (red) relative to a fixed free head (orange, HC; blue, RLC) of Wendt model.

Molecular Modeling of RD Positions.

To visually evaluate the above hypothesis and to fully appreciate the magnitude in variability of the inter-RLC geometry we used the EPR data as constraints to generate an off- and on-state model using a rigid body docking approach. To be consistent, we chose to model only the SMM monomer data for which a more complete dataset was collected. Importantly, the two models used the same number of constraints. Fig. 4B compares our off-state model to the model of Wendt et al. (9). Enlargement of this figure appears in Fig. S5. Using the free head of the Wendt model (blue) as a reference position, it can be seen that our off-state model of the blocked head (dark gray ribbons; 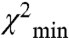) compares well to that of the Wendt model (red surface). The dark gray MD is shown in the blocked conformation for visualization purposes only. Of course we do not know the conformation of the MD relative to the lever arm, only the relative orientations of the two lever arms. This is true also for the white ribbon structure, which shows our on-state model. Our attributed on-state structure is completely different from our off-state model. The two heads are now splayed apart and the blocked head no longer makes the contacts with the free head as it did in the off-state structure. The rotation is complex consisting of tilt and twist angles but it can be approximated by a rotation of 110° ± 20° around an axis denoted in green in Fig. 4B (Fig. S5). There are other positions that are also likely—the orange balls in Fig. 4B show the positions of the top of the MD (residue 560) for all solutions for which 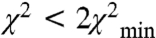. The range of the distance distributions for the off-state structure can be best seen in Fig. 4C, which shows the positions of K791 at the end of the long heavy chain (HC) lever arm helix as the χ² threshold is varied. The best solution at the essentially overlaps the Wendt et al. model (9). As the χ² increases more solutions are found corresponding to the positions of the colored balls. The fact that our attributed off-state modeled structure is so similar to the Wendt model supports our hypothesis stated above.

The fact that others have observed a similar splayed out conformation (18) supports our initial attribution of the populations to the on state. The broad distribution of the population observed experimentally and ascribed to the on state is consistent with the increased motional freedom of noninteracting heads. This suggests that distance measurements by DEER are a powerful method to measure the distributions of various populations in the same sample.

Meaning of Broad Distance Distributions.

One of our most significant findings is that broad conformational heterogeneity was observed under all conditions. Spin-label rotamer diversity was not sufficient to account for these broad distance distributions. Therefore, the broad widths of the distance distributions represent heterogeneity in the orientations of the two RLCs (Fig. S6). Part of this heterogeneity is due to motion of one head with respect to the other, but differences in the magnitudes of the widths among the probed sites suggest some site-specific contributions from backbone conformational heterogeneity. For the heads moving as rigid bodies the magnitudes of the distance distributions observed at different sites would be proportional to the distance from a pivot point. This was not observed, thus the variation in the distributions between the sites has to originate from a heterogeneity of the backbone. Incidentally, the fact that some sites exhibit wide and others exhibit narrow distance distributions argues against the attribution of th ebroad distributions to global unfolding of the protein.

We cannot estimate the timescale of the fluctuations giving rise to the heterogeneity. The protein motions are trapped during sample freezing, which takes at least a few milliseconds. Fast (submillisecond) motions would be averaged, it is the longer-lived conformations that are trapped. Thus, the heterogeneity can be referred to as “static” on the ms timescale. This is consistent with other studies where the motions correlated to allosteric effects are on the ms timescale (11, 12).

Implications.

Our interpretation of the EPR data and our subsequent modeling results reinforce each other and strongly suggest that an off-state structure similar to the Wendt model can coexist with an on-state structure in uP myosin. Interestingly, our data are consistent with a lack of the off-state structure in the P samples, suggesting that the protein preparations are allosterically competent and that phosphorylation is a powerful allosteric stabilizer of the on state. For the uP samples, the distribution of the two states was affected by the different experimental conditions and protein states. For example, we observed both the on and off states in uP SMM at high ionic strength (Fig. 2) even though it is known that such conditions promote destabilization of the off state (19). Similarly in uP HMM at low ionic strength without ATP, contributions from both the on and off states were observed. ATP did not detectably bias the populations toward the off state (Fig. 3C). We predicted that ATP would stabilize the off state because it is known to have nucleotide trapped at the active sites (20) and RLC phosphorylation primarily increases the rate of Pi release from acto-SMM (2).

We are not sure whether these data in general speak to the question of the structural requirements for inhibition of the ATPase. It is unlikely that uP myosin in general always contains large fractions of the on-state. For technical reasons (high protein concentration, frozen sample) we cannot measure the ATPase under the conditions of the EPR experiments, although we have shown that the samples have normal regulatory ATPase activity under standard ATPase assay conditions. This leaves open the possibility that under EPR conditions uP myosin is turned on to some extent. This would explain the existence of the on-state structure in the uP samples.

Our off-state structure showed conformational heterogeneity as evidenced by the broad widths of the distance distributions as discussed above. Such large movements in the RLC region are expected to propagate to the MDs. This raises the interesting question as to whether or not the MD–MD interactions seen in the Wendt model remain intact for all members of the heterogeneous off-state population, but our data does not apply to this question. Our prior studies of SMM head dynamics (21) suggest that the heads are free to rotate, the rotational correlation time estimated from the saturation transfer-EPR and phosphorescence anisotropy was approximately 4 μs in monomeric myosin (both the RLC domain and the MD). Such a fast motion would suggest that even if there is an interaction between the heads in the monomers it must be short-lived as the heads are free to move as separate bodies. Interestingly, our parallel work in the filaments showed slow motion of the RLC domain (441 μs correlation time) that was little affected by phosphorylation. The cone angle of the motion however was increased by phosphorylation from 24° to 36°, consistent with the general increase in distance distributions measured here.

Conformational Heterogeneity may Explain Prior RLC–RLC Photocross-Linking Data.

A method that has likely detected the variability of interhead geometry is UV-induced photocross-linking (22, 23) between the two RLC using benzophenone-labeled RLC mutants. Modeling including conformational heterogeneity shows that cross-links can be made by benzophenone attached to positions 15, 23, and 108 but not to positions 59 and 134, consistent with the observed cross-linking pattern. In the P state no cross-linking was observed for any site, consistent with our EPR data. An interhead cross-linking that cannot be explained by the Wendt model, even with heterogeneity, is from Cys108 to . In the context of the parallel RLC arrangement (as in Wendt), this cross-link would occur only if the junction between the two RDs was more flexible than accounted for in our modeling. The antiparallel RLC arrangement originally proposed by Wahlstrom et al. (23) is not consistent with our EPR distances.

Other Studies Revealing Conformational Heterogeneity.

Many EM studies of SMM and HMM, by replica shadowing (24) and negative stain (7), show a wide variety of head geometries present in 10S myosin and HMM. Heads appear folded back toward the rod, extended in a “Y” or splay out in a “T” conformation. Interestingly, phosphorylation did not induce a new conformation but rather shifted slightly the relative population of the classes. This is reminiscent of our findings in that phosphorylation caused changes in populations of distances for a subset of the positions studied. Stafford et al. (25) also observed multiple conformations by EM. The conformations were in rapid equilibrium in solution because ultracentrifugation did not resolve distinct sedimentation coefficients expected for different EM classes. The relative populations observed by EM depend on the sample preparation (7) suggesting that the energy barrier between these conformers is small. The energy barrier between the two conformers was estimated to be less than 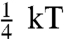in both the P and uP states as visualized by atomic force microscopy (AFM) (26). Such a low barrier would easily allow conformational transitions at ambient temperatures. Thus the heads are likely to be in dynamic equilibrium between various populations.

A recent FRET study (27) of intra-RLC distances, as opposed to inter-RLC like ours, showed evidence for two structural states (open and closed) of the RLC N-terminal domain. Phosphorylation partially shifted the distribution toward the open state. Interestingly, broad bimodal intra-RLC distance distributions were observed in both the uP and P states at ambient temperature in solution. The relevance of this intra-RLC conformational heterogeneity to our data is not clear because (i) the FRET study was done with S1, which is not regulated by phosphorylation, (ii) another study from the same laboratory (28) showed that solvent accessibility and dynamics of EPR probes on the RLC N-terminal domain behave in an opposite manner in S1 (used in ref. 27) versus HMM (used here), and (iii) a large structural transition in the N-terminal domain from disordered to ordered helix was found in HMM (without ATP), but not in S1 (27). Yet another study has shown that fluorophores on the RLC N-terminal domain sense changes in solvent exposure upon ATP binding and phosphorylation but only in regulated constructs HMM but not S1 (29). Therefore it is likely that backbone conformational heterogeneity in the N-terminal domain contributes to the heterogeneity in the RLC–RLC distances, consistent with the variation of the distance distribution widths measured here.

Conclusion

We have measured seven RLC–RLC distances and distance distributions in two states of SMM, monomers and filaments, and in HMM, two more sites were measured in monomers only. We conclude that two heterogeneous populations exist. One is very similar to the model of Wendt et al. (9), at least with regard to the RLC–RLC distances. This suggests that the structure observed by Wendt et al. is stable in the absence of a charged bilayer (9) or in the absence of potentially stabilizing interactions with the thick filament backbone (6). The second population, modeled by rigid body rotation, does not have interacting heads and is characterized by broader distance distributions as might be expected from noninteracting heads. Our findings are consistent with the idea that phosphorylation acts in an allosteric manner by biasing preexisting populations of structures with each population having broad conformational heterogeneity. One of the populations of structures present after phosphorylation also exists prior to phosphorylation, suggesting that the conformational requirements for phosphorylation-induced structural changes are ingrained in the structure. Our data are consistent with the presence of many protein conformations that can interconvert on the millisecond timescale.

These findings concur with modern understandings of the mechanisms of allosteric regulation in many systems. One aspect of the conformational selection is that protein dynamics may be evolutionarily conserved for allosterically regulated proteins.

Materials and Methods

Methods for protein preparations, spin-labeling, phosphorylation, ATPase assays, EPR spectroscopy, and data analysis have been previously described. Specific details are in SI Text.

Molecular Modeling of Spin-Label Conformations.

The conformational space available to MTSSL on the cryo-EM structure of a chicken gizzard SMM fragment in the uP state [Protein Data Bank (PDB) ID code 1I84, (9)] was determined using MMCM algorithms (15, 16). The structure of the RLC was homology built (Modeller) using the smooth RLC sequence and skeletal RLC (PDB ID code 2MYS) aligned to the Ca²⁺-trace of the RLC in 1I84. The positions of residues 15 and 23 that are not visualized in 1I84, were estimated by overlaying residues 25–69 from the recent structure of scallop RLC (PDB ID code 3JTD), which has the N-terminus resolved to residue 14 and smooth muscle side-chains were rebuilt by homology. Native residues were mutated to spin-labeled cysteines using scripts written in-house for Visual Molecular Dynamics, after which approximately 2,000 minimized structures where generated (chain U and V in 1I84) to exhaustively sample the spin-label conformational space. For each chain, the 300 conformations with the lowest energy were examined by calculating all possible combinations of low energy rotamers on two chains. The most favorable interspin distances and distribution widths were calculated using a Boltzmann distribution for the total energies of the conformers (16). A pseudo molecule consisting of the position of the nitroxide oxygen was constructed for the best spin-label rotamers. For the RLC, a single conformer was found at each site. In summary, the results of the MMCM calculations, which represent the behavior of the spin-label on the 1I84 structure are approximated conservatively by a square box centered at 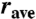with the width (Δ) corresponding to the range of the possible distances, see Table S2.

Molecular Modeling of RDs.

The relative positions of the RDs were modeled using the observed distances, which are the magnitude of a vector joining the two spin labels, with our rigid body docking approach based on a ReDCat (30). One of the heads was kept fixed and the other head, after being firstly randomly positioned, was moved through translations/rotations: three Cartesian coordinates and three Eulerian angles. Residues 870 of the two heavy chains were kept within 10 Å of each other to account of the common point of origin of the heads at the head-tail junction. For each transformation, the position of the mobile head was scored using a sum of deviations of the calculated distances between corresponding sites and the observed value weighted by measured distance distributions (Figs. S1–S3). The distance populations were then assigned (see Discussion). Q15, G165 were not used in the model building, to avoid errors due to necessity to extrapolate N- and C-termini of existing X-ray structures (31). The solutions that resulted in steric clash of the heads approximated by a set of 12 spheres were rejected. The optimization of transformation parameters that had the lowest penalty score (χ²) was performed via Monte-Carlo/Simplex strategy. A database was generated prior to the simulation, containing the array of all the possible positions of the investigated space. This matrix was created with 10° and 5 Å steps for rotation and translation respectively, thus significantly decreasing computational time. We confirmed that six distance restraints are sufficient to determine the correct docking of monomers, using band3 dimer (PDB ID code 1HYN) as a test case (Fig. S7).