Structure of even/odd trinucleotide repeat sequences modulates persistence of non-B conformations and conversion to duplex

Abstract

Expansion of trinucleotide repeats (TNR) has been implicated in the emergence of neurodegenerative diseases. Formation of non-B conformations such as hairpins by these repeat sequences during DNA replication and/or repair has been proposed as a contributing factor to expansion. In this work we employed a combination of fluorescence, chemical probing, optical melting, and gel shift assays to characterize the structure of a series of (CTG)_n sequences and the kinetic parameters describing their interaction with a complementary sequence. Our structure-based experiments using chemical probing reveal that sequences containing an even or odd number of CTG repeats adopt stem-loop hairpins that differ from one another by the absence or presence of a stem overhang. Furthermore, we find that this structural difference dictates the rate at which the TNR hairpins convert to duplex with a complementary CAG sequence. Indeed, the rate constant describing conversion to (CAG)₁₀/(CTG)_n duplex is slower for sequences containing an even number of CTG repeats than for sequences containing an odd number of repeats. Thus, when both the CAG and CTG hairpins have an even number of the repeats they display a longer lifetime relative to when the CTG hairpin has an odd number of repeats. The difference in lifetimes observed for these TNR hairpins has implications towards their persistence during DNA replication or repair events and could influence their predisposition towards expansion. Taken together these results contribute to our understanding of trinucleotide repeats and the factors that regulate persistence of hairpins in these repetitive sequences and conversion to canonical duplex.

The expansion of trinucleotide repeat (TNR)¹ sequences has been implicated in an array of neurodegenerative disorders (1-4). The length of these repeat polymorphisms predicts whether an individual will be healthy or will be afflicted by disease. The number of TNR repeats falls into one of three categories: (1) a small number of repeats in which case the individual will be healthy and the repeat tract will be stably transmitted to offspring; (2) an intermediate or pre-mutation number of repeats in which case individuals typically do not present symptoms of the disease, but are capable of transmitting an expanded TNR tract to their offspring, or; (3) a large number of repeats in which case the individual will develop the disorder. Notably, from the disease state the number of repeats can expand further in subsequent generations. As a result, a distinct trait of TNR disorders is the phenomenon of anticipation, in which the offspring of individuals that are afflicted by the disorder will have TNR tracts that are expanded further (5). As an example, in Huntington’s disease (HD) which is caused by the expansion of a (CAG)_n/(CTG)_n TNR sequence, healthy individuals have 5-35 repeats, individuals with 36-39 repeats are in the pre-mutation range, and individuals with 40 or more repeats will develop the disorder (6).

While the molecular basis for TNR disorders is known to be expansion of the repetitive DNA sequence, the mechanism of the expansion is not fully understood. However, a common element of TNR sequences that are prone to expansion is their ability to adopt non-B DNA conformations such as triplexes, quadruplexes, and hairpins (7-15). For example, (CAG)_n and (CTG)_n sequences have been shown to form hairpins both in vitro (16) and in vivo (17). Additionally, TNR sequences have been observed to form slipped-strand structures where the repetitive nature of the sequence allows the complementary strands to slip out of register and fold into hairpins (18-20). The propensity to form such non-B DNA structures has been shown to increase with length of the TNR sequence (21). Indeed, formation and persistence of non-B conformations have been proposed as contributing factors in the prevailing models for expansion, which involve polymerase non-processivity caused by slippage of the nascent strand during DNA synthesis or aberrant repair events following DNA damage (1, 3, 4, 22, 23).

Given the proposed importance of non-B conformations and repeat length in expansion, in this work we define the structural properties of TNR sequences of varying length and delineate the role of structure in modulating the persistence of non-B TNR hairpins. Specifically, using a (CAG)₁₀ sequence we examined the role of the length of the complementary (CTG)_n sequence (when n = 6-14) in influencing the structure and lifetime of the TNR DNA. Surprisingly, using sequences that correspond to the healthy allele in HD, we find that incremental changes of one repeat unit affect the structure and persistence of the non-B conformations. While all the sequences adopt hairpin structures with a loop size of four nucleobases, hairpins with an even number of repeats have blunt-ended stems whereas those with an odd number of repeats have one repeat overhanging the stem. Importantly, we also find that the presence of an overhanging repeat decreases the lifetime of the non-B conformations by facilitating conversion to (CAG)₁₀/(CTG)_n duplex. Understanding structure-based reactivity and lifetime of even and odd-repeat hairpins can provide insight into how TNR sequences expand, and thus, shed light on the molecular mechanism of several diseases.

EXPERIMENTAL PROCEDURES

Synthesis and Purification of Oligonucleotides

Oligonucleotides were synthesized using standard phosphoramidite chemistry (24). All phosphoramidites, including 5′ fluorescein (FL) and 3′-(E)-N-(3-(dihydroxymethoxy)propyl)-4-((4-(dimethylamino)phenyl)diazenyl) benzamide (DCL) were purchased from Glen Research. Oligonucleotides were purified using a Dynamax Microsorb C18 reverse phase HPLC column (10 × 250 mm) as described previously (25). Quantification was performed at 90 °C using ε₂₆₀ values estimated for single-stranded DNA (26).

Fluorescence Measurements

The (CTG)_n oligonucleotides were prepared in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0 at a concentration of 3 μM. In order to obtain the thermodynamically-favored DNA conformations, oligonucleotides were incubated for 5 min at 90 °C and cooled to room temperature. The FL-(CAG)₁₀-DCL oligonucleotide was prepared in the same fashion with all sample manipulations performed in the dark. The FL-(CAG)₁₀-DCL and (CTG)_n oligonucleotides were chilled on ice for 1 h prior to mixing in a 1:1 ratio for a final sample (25 μL) that contained 1.5 μM FL-(CAG)₁₀-DCL and 1.5 μM (CTG)_n in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0. After mixing the samples were subjected to the following temperature cycle on a MX4000 Real-Time PCR instrument (Stratagene): 10 °C for 10 min, 10 °C to 90 °C at 1 °C/min, 5 min at 90 °C, and 90 °C to 10 °C at 1 °C/min. Over the course of this temperature cycle the samples were excited at 492 nm and the emission was monitored at 520 nm. The melting temperature (T_m) of FL-(CAG)₁₀-DCL was taken as the maximum in the first derivative of the fluorescence profile. The experiments were performed in triplicate.

Characterization of Oligonucleotides Using the Chemical Probe DEPC

Oligonucleotides were 5′-[³²P] end-labeled using T4 polynucleotide kinase according to the manufacturer’s protocol. Radiolabeled oligonucleotide was supplemented with the unlabeled version to obtain a final DNA concentration of 5 μM in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0. The oligonucleotides were incubated for 5 min at 90 °C and slowly cooled to room temperature. The DNA samples were incubated with 4% diethyl pyrocarbonate (DEPC, v/v) for 30 min at 37 °C with vortexing at the start of the reaction and halfway through incubation. Following incubation with DEPC, the samples were dried under vacuum, treated with 10% piperidine (v/v) for 60 min at 90 °C, and again dried under vacuum. Samples were resuspended in denaturing loading buffer (80% formamide, 0.1 mM EDTA, 0.1% xylene cyanol, and 0.1% bromophenol blue), electrophoresed through an 18% denaturing PAGE gel, and visualized using phosphorimagery. Control samples were prepared similarly but excluded DEPC and/or piperidine treatment. To obtain values of percent cleavage the amount of strand cleavage at a given nucleotide was determined relative to total intensity in the lane. Prior to analysis each lane was corrected for background using the rolling disk lane background correction in Quantity One™ software. Experiments were performed in triplicate.

Optical Melting Analysis

Melting temperatures for the structures adopted by each oligonucleotide were obtained using a Beckman Coulter DU800 UV-visible spectrophotometer equipped with a Peltier thermoelectric device. Oligonucleotides were diluted to 325 μL in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0 such that at 90 °C they would have an absorbance at 260 nm of 1.0 ± 0.1. Prior to optical analysis samples were incubated for 5 min at 90 °C and slowly cooled to room temperature. The samples were then heated at a rate of 1 °C/min from 25 to 90 °C while monitoring absorbance at 260 nm, held at 90 °C for 5 min, and returned to the starting temperature at a rate of 1 °C/min. The T_m was taken as the maximum in the first derivative plot of the absorbance profile generated during heating from 25 to 90 °C. Experiments were performed in triplicate.

In order to extract van’t Hoff enthalpies (ΔH_VH) from the data obtained by optical melting analysis, the melting curves were baseline adjusted and fit to a sigmoidal equation (27). The van’t Hoff enthalpies were then calculated from the following equation as reported by Breslauer (27) where α represents the fraction of oligonucleotide present in the hairpin conformation:

$$\Delta {\text{H}}_{\text{VH}}=4{{\text{RT}}_{\text{m}}}^2{\left(\frac{\partial \alpha }{\partial \text{T}}\right)}_{\text{T}={\text{T}}_{\text{m}}}$$

Determination of Rate Constants for Hairpin to Duplex Conversion

The (CAG)₁₀ strand was 5′-[³²P] end-labeled. Radiolabeled DNA was supplemented with unlabeled DNA to obtain the desired concentrations. The (CAG)₁₀ or (CTG)_n hairpins were obtained by incubating the appropriate oligonucleotide at 90 °C for 5 min followed by slow cooling to room temperature. Prior to mixing, each hairpin was incubated at 37 °C for 30 min; the hairpins were then combined and incubated at 37 °C. Experiments were performed under pseudo first-order conditions using (CAG)₁₀ and (CTG)_n (n = 10 or 11) in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0 in a 10 μL total sample volume. DNA concentrations were 0.04 μM for (CAG)₁₀ and 0.4 μM for (CTG)₁₀ or (CTG)₁₁. The longest time point was mixed first. After the desired incubation time, 5 μL of non-denaturing loading buffer (15% Ficoll, 0.25% xylene cyanol, and 0.25% bromophenol blue) were added, and the sample was immediately loaded onto a 12% non-denaturing PAGE gel and electrophoresed at 50 V at 4 °C. Mixing of the remaining samples was timed such that there was a 15 min delay between the loading of each sample. After the final sample was loaded onto the gel, electrophoresis at 50 V proceeded for 6 h at 4 °C. Products were visualized using phosphorimagery. The amount of duplex product was quantified and plotted as a function of time. The data were fitted in either Origin or Kaleidagraph to a monoexponential curve using the following equation, D = H₀(1-e^−k’t), where D is percentage of duplex at time t (in sec), H₀ is percentage of hairpin at t = 0 which was set to 100% during data fitting (28) and k’ is the observed rate. The reported second-order rate constant was obtained by dividing k’ by the concentration of the sequence that was in excess. Half-lives were obtained using the equation t_1/2 = 1/(kH₀), where k is the second-order rate constant and H₀ is the concentration of the (CTG)_n hairpin at t = 0. Experiments were performed in triplicate.

RESULTS

Reactivity of a (CAG)₁₀ Fluorescent Probe in Presence of (CTG)_n Sequences of Variable Length.

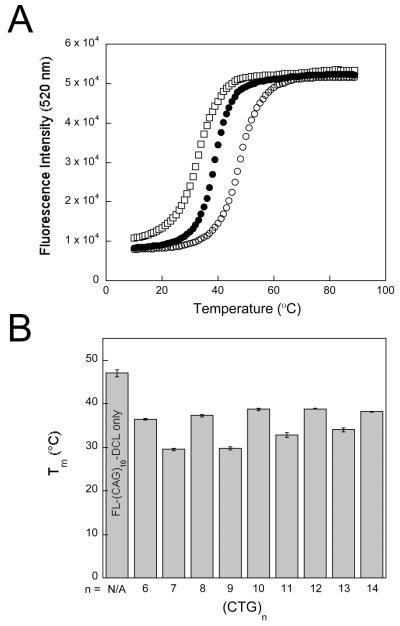
We have previously described a fluorescence-based strategy to assess the propensity of a CAG hairpin to convert to duplex in the presence of a complementary CTG hairpin (25). The fluorescent probe, FL-(CAG)₁₀-DCL, is a (CAG)₁₀ oligonucleotide with fluorescein covalently attached at the 5′-end and a dabcyl quencher at the 3′-end. When the probe is in a hairpin conformation the fluorophore and quencher are in close proximity and fluorescence quenching occurs (Figure 1). In contrast, when the probe is unstructured or is part of a CAG/CTG duplex the fluorophore and quencher are spatially separated and fluorescence is observed. Using this fluorescent probe we reported previously the mechanism by which the (CAG)₁₀ and (CTG)₁₀ hairpins convert to (CAG)₁₀/(CTG)₁₀ duplex (25). The goal of the work described here was to determine how length of the CTG sequence modulates reactivity with the FL-(CAG)₁₀-DCL hairpin. The fluorescence profile of FL-(CAG)₁₀-DCL was obtained by monitoring fluorescence intensity as a function of temperature. As a control, the fluorescence profile of FL-(CAG)₁₀-DCL in the absence of other DNA is shown in Figure 2A (open circles). While at low temperatures the fluorescence is quenched, as the temperature is increased from 10 to 90 °C there is an increase in fluorescence intensity. This increase is consistent with FL-(CAG)₁₀-DCL forming a hairpin at low temperatures which melts as the temperature is raised; a melting temperature (T_m) of 47.0 ± 0.8 °C for FL-(CAG)₁₀-DCL is obtained from this fluorescence profile.

Figure 1.

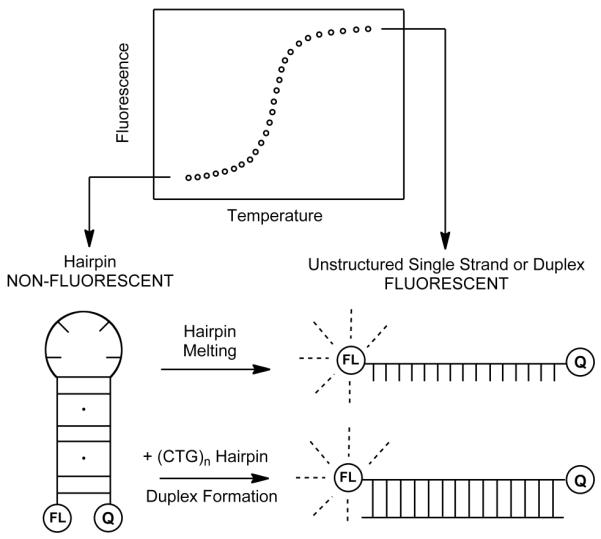
Overview of the fluorescence quenching experiment showing schematic representations of the non-fluorescent and fluorescent conformations of the FL-(CAG)₁₀-DCL probe.

Figure 2.

(A) Fluorescence intensity at 520 nm of 1.5 μM FL-(CAG)₁₀-DCL alone (open circles), 1.5 μ M FL-(CAG)₁₀-DCL in the presence of 1.5 μM (CTG)₁₀ (closed circles), and 1.5 μ M FL-(CAG)₁₀-DCL in the presence of 1.5 μM (CTG)₁₁ (open squares). (B) Melting temperature of FL-(CAG)₁₀-DCL in presence of (CTG)_n sequences. All samples were prepared in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0.

The fluorescent probe was then combined with an equimolar amount of (CTG)_n where n = 6-14. Notably, this series of CTG sequences contains 5 even-repeat sequences (n = 6, 8, 10, 12, 14) and 4 odd-repeat sequences (n = 7, 9, 11, 13). As seen in Figure 2A, addition of an equimolar amount of (CTG)₁₀ results in a shift of the transition in the fluorescence profile to a lower temperature (38.7 ± 0.2°C; closed circles). Addition of (CTG)₁₁ (open squares) shifts the transition lower still (32.8 ± 0.5°C). A pattern emerges when comparing the fluorescence profiles of the FL-(CAG)₁₀-DCL probe in the presence of the series of (CTG)_n sequences (Figure 2B). The transition temperature is higher for the even-repeat (CTG)_n sequences than for the odd-repeat sequences. In an attempt to reveal the source of this behavior we next examined the structure adopted by the series of even-repeat and odd-repeat CTG sequences.

Structural Characterization of Even-Repeat and Odd-Repeat (CTG)_n Sequences.

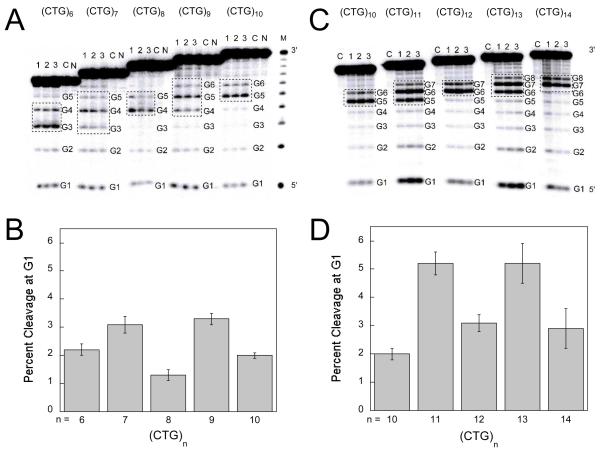
In order to evaluate the structure adopted by the family of CTG sequences, (CTG)_6-14 were reacted with the chemical probe diethyl pyrocarbonate (DEPC). DEPC is known to modify adenines and guanines (29, 30). Furthermore, the level of reactivity of a nucleobase towards DEPC reflects the extent of solvent accessibility, and as a result, adenines and guanines in loops, bulges or overhangs are more reactive than those in canonical base pairs (31, 32). For the CTG sequences used in this work the differential reactivity of unpaired guanines was used to reveal loops, bulges, and overhangs and also to distinguish them from guanines in well-matched base pairs. We have previously characterized (CTG)₁₀ based on its reactivity towards DEPC (25). The selective modification of two centrally-located guanines (G5 and G6) indicates that the sequence adopts a hairpin conformation with a loop of four nucleobases and a blunt-ended stem with no overhangs (Figure 3A). It is of note that the reactivity at G6 is reduced in comparison to G5, thus, we propose that G5 is in the loop while G6 is part of the loop-closing base pair with C5.

Figure 3.

Schematic representation of the proposed structures for (A) (CTG)₁₀ and (B) (CTG)₁₁ sequences.

When examining the reactivity towards DEPC for the rest of the (CTG)_n sequences there are two patterns that emerge (Figure 4). The first pattern is that there are two reactive guanines in the loop region of even-repeat sequences and three reactive guanines in the loop region of odd-repeat sequences (Figure 4A and 4C, dashed boxes). The second pattern is the oscillation in the level of reactivity of G1, which is the terminal 5′-G; G1 is significantly more reactive towards DEPC in odd-repeat sequences than in even-repeat sequences (Figure 4B and 4D). These reactivity patterns are likely due to the presence of a mixture of hairpins that have either 5′ or 3′ overhangs as in the proposed structures for (CTG)₁₁ (Figure 3B).

Figure 4.

(A) Autoradiogram showing DEPC chemical probe reactivity profiles of (CTG)₆ through (CTG)₁₀. Each group contains two control lanes (N is DNA only and C is DNA treated with piperidine) and three replicates (lanes 1, 2, and 3) corresponding to reaction of the DNA with DEPC and piperidine. Conditions were 5 μM DNA in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0. (B) Percent cleavage at G1 for (CTG)_6-10. Error represents the standard deviation obtained for the three replicates. (C) Autoradiogram showing DEPC chemical probe reactivity profiles of (CTG)₁₀ through (CTG)₁₄. Each group contains one control lane C which is piperidine-treated DNA and three replicates (lanes 1, 2, and 3) corresponding to reaction with DEPC and piperidine. (D) Percent cleavage at G1 for (CTG)_10-14. Error represents the standard deviation obtained for the three replicates.

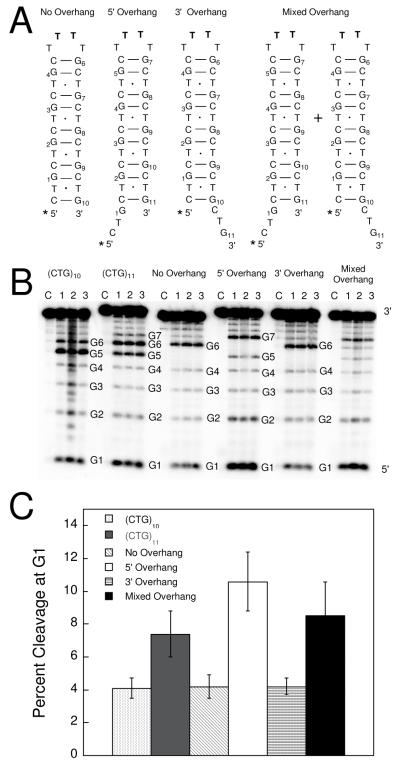
To determine whether the oscillating patterns of reactivity towards DEPC observed for the (CTG)_n sequences correspond to these proposed structures we synthesized a series of standards that mimic the blunt-ended and overhanging stem regions proposed for (CTG)₁₀ and (CTG)₁₁, respectively (Figure 5A). By replacing the two apical nucleobases in the loop of the CTG hairpins with 5′-TT-3′, the DNA hairpins can be locked into distinct conformations. First, in the case of (CTG)₁₀ a blunt-ended hairpin (No Overhang) is created. For (CTG)₁₁, substitution of these apical nucleobases creates hairpins with one CTG repeat overhanging the 5′ end (5′ Overhang), or one repeat overhanging the 3′ end (3′ Overhang). These standards were subjected to chemical probing with DEPC and the results obtained were compared to those for (CTG)₁₀ and (CTG)₁₁.

Figure 5.

(A) Schematic representations of the standards No Overhang, 5′ Overhang, 3′ Overhang, and Mixed Overhang. The asterisk indicates the location of the 5′-[³²P]-radiolabel. (B) DEPC chemical probe reactivity profiles for standard sequences at 5 μM. Each group contains one control lane (C) which is piperidine-treated DNA and three replicates (lanes 1, 2, and 3) corresponding to reaction with DEPC and piperidine. All samples were prepared in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0. (C) Percent cleavage at G1. Error represents the standard deviation obtained for the three replicates.

The reactivity of G1 in 5′ Overhang is the most intense of all the sequences, indicative of a hairpin conformation with a CTG repeat overhanging the 5′ end (Figure 5B and 5C). On the other hand, 3′ Overhang displayed reactivity towards DEPC that is comparable to the blunt-ended hairpin No Overhang; this lack of reactivity at G1 is consistent with the absence of a 5′ overhang. Lastly, an equimolar mixture of 5′ Overhang and 3′ Overhang (Mixed Overhang) shows a percent cleavage at G1 that is comparable to that of (CTG)₁₁ (Figure 5C), suggesting that a combination of 5′ and 3′ overhang-containing structures are the most likely conformations adopted by (CTG)₁₁.

Enthalpy of Melting of Even-Repeat and Odd-Repeat (CTG)_n Hairpins.

Analysis by optical melting offers further information about the series of (CTG)_n hairpins by providing melting temperatures and thermodynamic parameters describing the transition from the structured to unstructured state. Optical melting profiles were obtained for the (CTG)_n hairpins in which the absorbance of the DNA was monitored as a function of temperature (Supporting Information). As shown in Table 1 there is a general increase in the T_m across the series of hairpins from n = 6 to 14. To understand the thermodynamic impact of additional CTG repeats we extracted the model-dependent van’t Hoff enthalpy (ΔH_VH) from the optical melting profiles. As seen in Table 1, ΔH_VH increases across the series of hairpins. Instead of increasing linearly with the number of repeats an apparent stepping is observed (Figure 6). Starting with the hairpins (CTG)₆ and (CTG)₇, both show similar enthalpies of melting. Likewise, (CTG)₈ and (CTG)₉ have similar enthalpies of melting with the ΔH_VH being larger relative to (CTG)₆ and (CTG)₇. (CTG)₁₀, (CTG)₁₁, (CTG)₁₂ and (CTG)₁₃ display similar enthalpies of melting at the next ‘step’. Finally, (CTG)₁₄ displays the largest enthalpy of melting in this series of hairpins.

Table 1.

Hairpin melting temperatures and van’t Hoff enthalpies of melting^a

Strand	Tm (°C)	ΔHVH (kcal/mol)
(CTG)6	54.3 ± 0.8	38 ± 1
(CTG)7	54.6 ± 0.8	40 ± 2
(CTG)8	56.0 ± 0.2	46 ± 1
(CTG)9	55.5 ± 0.8	48 ± 2
(CTG)10	56.4 ± 0.3	56 ± 2
(CTG)11	56.3 ± 0.2	56 ± 5
(CTG)12	57.5 ± 0.3	57 ± 2
(CTG)13	58.3 ± 0.1	56 ± 1
(CTG)14	57.2 ± 0.1	65 ± 4
No Overhang	56.3 ± 0.1	82 ± 7
5′ Overhang	55.3 ± 0.2	66 ± 2
3′ Overhang	54.6 ± 0.1	64 ± 1

^aError represents standard deviation derived from three experiments.

Figure 6.

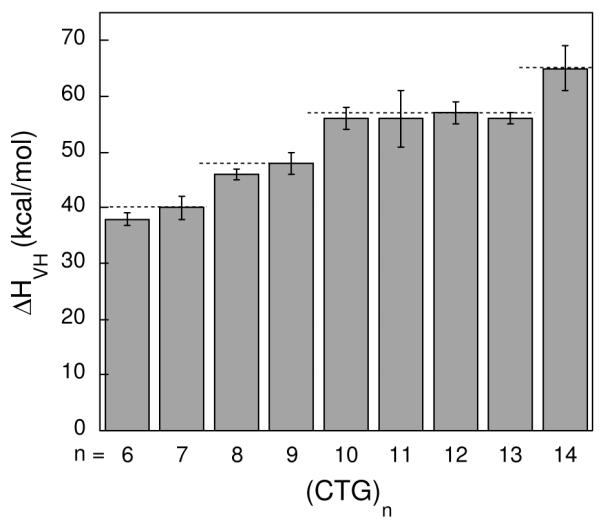
Enthalpies of melting for (CTG)_n sequences derived from optical melting data by van’t Hoff analysis.

Rate of Hairpin to Duplex Conversion for (CAG)₁₀ and (CTG)_n Hairpins.

We have previously shown that (CAG)₁₀ and (CTG)₁₀ hairpins can convert to (CAG)₁₀/(CTG)₁₀ duplex (25). In order to quantitatively describe the (CAG)₁₀ and (CTG)_n hairpins converting to (CAG)₁₀/(CTG)_n duplex we determined the rate constant for this process. These kinetic experiments were performed under pseudo-first order conditions in which radiolabeled 5′-³²P-(CAG)₁₀ hairpin was combined with a ten-fold excess of (CTG)₁₀, which was used to represent the even-repeat hairpins, or (CTG)₁₁ which was used to represent the odd-repeat hairpins. After incubation of 5′-³²P-(CAG)₁₀ and (CTG)_n at 37 °C for a defined period of time the hairpin and duplex species were separated by non-denaturing PAGE. The amount of duplex product was quantitated, plotted as a function of time, and the data were fitted to a monoexponential curve in order to obtain the rate constant for duplex formation.

Using 0.04 μM (CAG)₁₀ and 0.4 μM (CTG)₁₁ a rate constant of 4,625 ± 728 M⁻¹s⁻¹ was obtained for the hairpin to duplex conversion (Figure 7A and B). When comparable experiments were performed using 0.04 μM (CAG)₁₀ and 0.4 μM (CTG)₁₀ the rate was determined to be 1,085 ± 214 M⁻¹s⁻¹ (Figure 7C and D), 4-fold slower than duplex conversion for (CAG)₁₀ and (CTG)₁₁. Thus, conversion to duplex for (CAG)₁₀ in presence of the odd-repeat hairpin (CTG)₁₁ occurs faster than in presence of the even-repeat hairpin (CTG)₁₀. Based on these rates, the upper-limit for the half-life of the (CTG)₁₁ hairpin is 9 ± 1 min and 40 ± 8 min for the (CTG)₁₀ hairpin.

Figure 7.

(A) Autoradiogram revealing conversion of (CAG)₁₀ and (CTG)₁₁ hairpins to (CAG)₁₀/(CTG)₁₁ duplex and (B) plot of percent duplex as a function of time showing the fit to a monoexponential curve. (C) Autoradiogram revealing conversion of (CAG)₁₀ and (CTG)₁₀ hairpins to (CAG)₁₀/(CTG)₁₀ duplex and (D) plot of percent duplex as a function of time showing the fit to a monoexponential curve. Experiments were carried out at 37 °C in 20 mM sodium phosphate, 10 mM NaCl, pH 7.0.

DISCUSSION

(CTG)_n Repeat Number Modulates Reactivity with (CAG)₁₀ Complement.

We have previously described the mechanism of hairpin to duplex conversion for the TNR hairpins (CAG)₁₀ and (CTG)₁₀ (25). In fact, we identified two distinct interactions that mediate conversion to duplex by the TNR hairpins. These are kissing interactions, which result from base pairing by the complementary nucleobases in the loop of the CAG and CTG hairpins, and cruciform interactions, which occur between the terminal nucleobases of the hairpin stems. In this previous report we focused on characterizing sequences containing 10 repeat units and we sought here to expand our knowledge regarding the effect of repeat sequence length of the complementary (CTG)_n sequence on the (CAG)₁₀ hairpin.

Beginning with our fluorescence-based assay, we characterized the thermal stability of the FL-(CAG)₁₀-DCL hairpin probe in the presence of the family of (CTG)_n sequences. We observed an oscillating pattern in the thermal stability of the probe in presence of even repeat sequences versus odd-repeat sequences. The CAG hairpin probe melts at a lower temperature in presence of a CTG hairpin containing an odd number of repeats as compared to an even number of repeats. This pattern revealed a higher degree of reactivity of the odd-repeat CTG sequences with the complementary (CAG)₁₀ hairpin and we hypothesized that differences in structure between even and odd-repeat sequences were the cause of the oscillating pattern observed by fluorescence.

Chemical Probes Reveal a Constant Loop Size for the (CTG)_n Hairpins and an Overhanging Repeat in the Odd-Repeat Hairpins.

In order to characterize the structure(s) adopted by these sequences in solution, we conducted chemical probing experiments with DEPC. Interestingly, the oscillating pattern observed in the fluorescence profiles for the even and odd-repeat sequences is echoed in the DEPC reactivity of the family of (CTG)_n sequences. Notably, even-repeat sequences show two reactive guanines in the loop region and low reactivity at G1 whereas odd-repeat sequences show three reactive guanines in the loop region and high reactivity at G1.

There are two scenarios that could explain these observed DEPC reactivity patterns. First, the size of the loop might be alternating between the even and odd-repeat hairpins. For instance, even-repeat hairpins could have a loop of 4 nucleobases while odd-repeat hairpins could have a loop of 7 nucleobases. If this were the case the stem of both the even and odd-repeat hairpins would be blunt ended and there would be no overhanging bases.

Based on NMR studies using (CTG)_n sequences where n = 4-10, Chi and Lam concluded that loop size alternates between 3 and 4 nucleobases for odd and even-repeat sequences, respectively (33). However, in order to suppress the formation of homoduplex at the relatively high DNA concentrations required for NMR the repeat hairpins also included a well-matched and non-repetitive stem extension of 4 base pairs. While this stem extension provides a kinetic advantage to the formation of an intramolecular hairpin over an intermolecular homoduplex, it also prevents overhangs since this extension forms the end of the stem. Thus, we cannot compare our results directly to those obtained by Chi and Lam.

Further support for loop size alternating between 3 and 4 nucleobases for odd and even-repeat sequences came from Mariappan and co-coworkers who used NMR to examine the conformation adopted by (CTG)₅ and (CTG)₆ (34). They reported that (CTG)₅ forms a 3 nucleobase loop while (CTG)₆ forms a 4 nucleobase loop. The stem of both hairpins is blunt ended. Additionally, based on cleavage of the DNA by single-strand specific nucleases Amrane and co-workers proposed that the loop size alternates between 3 and 4 nucleobases for (CTG)₁₅ and (CTG)₁₆; notably, features such as 5′ bulges and 3′ overhangs were also proposed (35).

If the odd-repeat hairpins had smaller loops than the even-repeat hairpins we would expect a trend opposite to that seen in Figure 4A and 4C, with even-repeat hairpins having more reactive guanines in the loop region. In contrast, we observe that the even-repeat hairpins have two reactive guanines while the odd-repeat hairpins have three. While it may be tempting to suggest, based on the number of guanines in the loop region that are modified by DEPC, that the odd-repeat hairpins have a larger loop than even-repeat hairpins this conclusion is not consistent with the reactivity observed in the stem region.

A second scenario that can explain the DEPC pattern observed for the family of (CTG)_n hairpins would be for the loop size to remain constant rather than alternate between even and odd-repeat hairpins. If the loop size remains the same across the family of (CTG)_n hairpins, it would be most likely comprised of 4 nucleobases. In order to accommodate this constant loop size, one CTG repeat would overhang the 5′ or 3′ end of the odd-repeat hairpins. Since the same type of nucleobases (C, T, G) would be present in either a 5′ or 3′ overhang neither is expected to form preferentially. In fact, a mixture of both species of overhangs is likely. It is noteworthy that if the loop size alternates between even and odd-repeat hairpins, the reactivity towards DEPC would represent the reactivity of a single DNA conformation, whereas if the loop size was constant across the series the reactivity pattern would represent a superimposition of those generated by two species in solution.

If there are no overhangs present and the hairpins have blunt ends we would expect a similar amount of modification of G1 across the series of hairpins. If odd-repeat hairpins have a mixture of 5′ and 3′ overhangs we would expect the species with the 5′-overhang to be more reactive towards DEPC at G1 than the even-repeat hairpins. Indeed, we observe more reactivity at G1 in the case of the odd-repeat hairpins (Figure 4B and 4D).

The results we obtained for modification of the (CTG)_n (n = 6-14) hairpins by DEPC are consistent with this series of hairpins maintaining the same loop size. We came to this conclusion by examining the DEPC reactivity patterns in both the loop and stem regions of the hairpins. Therefore, we propose that both the even-repeat and odd-repeat hairpins have a loop of 4 nucleobases and that the stem is blunt-ended when there is an even number of CTG repeats and one repeat overhanging the stem in odd-repeat hairpins. It is noteworthy that our proposed structure for (CTG)₆ is consistent with that reported by Mariappan and co-coworkers based on NMR characterization of the same sequence (34).

If all the hairpins have the same size loop, why is the number of reactive guanines in the loop region not the same across the series? Examination of the two structures proposed for (CTG)₁₁ depicted in Figure 3B provides the rationale: the 5′ and 3′ overhang species have different guanines in the loop and loop-closing base pair. In the (CTG)₁₁ hairpin with a 5′ overhang, G6 is in the loop and G7 is in the loop-closing base pair. For the (CTG)₁₁ hairpin with a 3′ overhang, G5 is in the loop and G6 is in the loop-closing base pair. When the DEPC reactivity patterns of these two hairpins are overlaid, one would expect to see three reactive guanines: G5, G6, and G7. Moreover, the extent of reactivity for each guanine will depend on its position in the two hairpins. G6 is expected to have the highest reactivity, as it is either in the loop or is part of a loop-closing base pair, G5 would have less reactivity towards DEPC than G6 because it is either in the loop or in the stem and, lastly, G7 will be the least reactive towards DEPC since it is either in the loop-closing base pair or the stem. Indeed, consistent with the predicted structures for (CTG)₁₁ the observed level of reactivity towards DEPC is G6 > G5 > G7.

To confirm these predictions we constructed a series of standards that, due to substitution of various nucleobases in the loop, adopt locked structures differing only in presence or absence of 5′ and 3′ overhangs. Several predictions can be made about the expected reactivity of these standards towards DEPC. First, the No Overhang hairpin has a blunt end and, therefore, reactivity of guanines in the stem should mimic those in the (CTG)₁₀ stem. In contrast, the 5′ Overhang and 3′ Overhang hairpins were designed to mimic the proposed (CTG)₁₁ structures that either have a 5′ or 3′ repeat overhanging the stem, respectively. Therefore, the 5′ Overhang standard should display more reactivity at G1 than (CTG)₁₁ because (CTG)₁₁ is predicted to have half as many G1 nucleobases in a 5′ overhang as compared to the 5′ Overhang standard. The 3′ Overhang standard has only a 3′ overhang, and not a 5′ overhang, and should not have heightened reactivity at G1 relative to (CTG)₁₁. The Mixed Overhang sample is an equimolar mixture of the 5′ and 3′ Overhang hairpin standards and, therefore, if the proposed (CTG)₁₁ structures are correct the reactivity profile at G1 for Mixed Overhang should resemble that observed for (CTG)₁₁.

Indeed, the observed reactivity of these standards towards DEPC is consistent with our proposed (CTG)₁₁ structures and confirms that (CTG)₁₁ adopts two distinct structures with a 4 nucleobase loop and either a 5′ or 3′ overhang. The use of these standards supports our conclusions that loop size is constant across the series of (CTG)_n hairpins (n = 6-14) and that it is the absence or presence of an overhang that varies in the even and odd-repeat hairpins.

Enthalpy of Melting Supports a Constant Loop Size in Even-Repeat and Odd-Repeat Hairpins.

Van’t Hoff analysis of thermal melting data revealed that (CTG)₆ and (CTG)₇ have a similar ΔH_VH. Our proposed structures for these (CTG)_even and (CTG)_odd hairpins have the same loop size and the same number of well-matched and mismatched base pairs in their stems. Assuming that the base stacking contributed by the nucleobases in the overhang is minimal we would predict they would have a similar ΔH_VH. Similarly, based on our proposed structures we would predict that (CTG)₈ and (CTG)₉ have similar enthalpies of melting with ΔH_VH being greater than that observed when n = 6 or 7 due to the base stacking and hydrogen bonding interactions of three additional base pairs in the stem. At the next ‘step’ in ΔH_VH we observe (CTG)₁₀, (CTG)₁₁, (CTG)₁₂ and (CTG)₁₃. Notably, a plateau in ΔH has been reported previously for TNR hairpins (35). However, we observe that ΔH_VH of (CTG)₁₄ is larger than that observed for (CTG)₁₀, (CTG)₁₁, (CTG)₁₂ and (CTG)₁₃. It should be noted that van’t Hoff analysis assumes a two-state transition, where the hairpin proceeds directly from the structured to the unstructured state. If intermediates populate this transition ΔH_VH will be an underestimation of ΔH (27). Using calorimetric methods, which provide values of ΔH that are independent of the nature of the melting transition (ΔH_cal), it was observed that when there are 12 or more CTG repeats ΔH_VH ≠ ΔH_cal (35). Thus, the ΔH_VH we obtained for sequences containing 12, 13, and 14 CTG repeats is likely an underestimate of ΔH and does not reflect a true plateau.

With an understanding of the structure and thermodynamics of the (CTG)_n sequences, the oscillating pattern of fluorescence transitions observed for even and odd-repeat sequences can be rationalized. The transitions observed in the presence of the odd-repeat hairpins are at lower temperatures than those for the even-repeat hairpins (Figure 2B). The transition temperature refx2lects FL-(CAG)₁₀-DCL melting as a result of conversion to duplex to form FL-(CAG)₁₀-DCL/(CTG)_n. While the FL-(CAG)₁₀-DCL/(CTG)_n duplexes formed with even and odd-repeat CTG sequences are expected to have the same thermodynamic stability the fluorescence data suggest that odd-repeat hairpins, which have one repeat overhanging the stem, convert more readily to duplex than the even-repeat hairpins that lack these overhangs. Thus, we determined the rate constant describing the hairpin to duplex conversion for even and odd-repeat hairpins.

Kinetic Experiments Reveal that Structural Differences Alter the Rate of Hairpin to Duplex Conversion.

We reported previously that the complementary (CAG)₁₀ and (CTG)₁₀ hairpins can convert to duplex via two independent mechanisms: kissing or cruciform interactions in which the hairpins interact by the loop or stem regions, respectively (25). Furthermore, we have shown that kissing and cruciform interactions contribute equally to the rate of duplex formation by (CAG)₁₀ and (CTG)₁₀. In this work, our kinetic data reveal that hairpin to duplex conversion occurs faster for the (CAG)₁₀ hairpin in presence of the odd-repeat hairpin (CTG)₁₁ than in the presence of (CTG)₁₀. In fact, we find that the rate of formation of (CAG)₁₀/(CTG)₁₁ duplex is 4-fold faster than formation of (CAG)₁₀/(CTG)₁₀ duplex. These results indicate that, when present together, the lifetimes of the (CAG)₁₀ and (CTG)₁₀ hairpins are longer than the lifetimes of (CAG)₁₀ and (CTG)₁₁. We postulate that the unpaired nucleobases of the overhanging repeat on either the 3′ or 5′ end of the (CTG)₁₁ hairpin facilitate cruciform interactions and are responsible for the faster conversion to duplex and shorter lifetimes of the (CAG)₁₀ and (CTG)₁₁ hairpins.

Taken together the results obtained by chemical probing with DEPC, optical melting analysis, and kinetic analysis by non-denaturing PAGE indicate that the structural differences in the series of (CTG)_n modulate their ability to form (CAG)₁₀/(CTG)_n duplex and that these differences are responsible for the oscillating even/odd patterns seen in our fluorescence experiments using the probe FL-(CAG)₁₀-DCL.

Lifetime of Hairpins as a Contributing Factor to TNR Expansion.

It has been proposed that the presence of hairpins formed by TNR sequences induces expansion. If hairpin formation were to occur during DNA replication, slippage of polymerase during DNA synthesis could promote expansion. Additionally, during the gap-filling step of long-patch base excision repair (LP-BER), formation of a structured hairpin flap could inhibit cleavage by the flap endonuclease FEN1 and lead to expansion (3). We can therefore envision that lifetime of these hairpins during replication and/or repair may dictate whether or not expansion occurs.

In this work we have shown that the lifetime of (CTG)_n TNR hairpins is modulated by whether the number of repeats is even or odd. Indeed, we have shown that when n = 10 the lifetime of the hairpin is significantly longer than when n = 11. Thus, the lifetime of hairpins formed during replication or from the single-stranded flap generated in LP-BER may be controlled by the number of repeats in the hairpin.

It is of note that an oscillating pattern in the behavior of even and odd-repeat TNR sequences was also reported by Darlow and Leach, who evaluated the size of viral plaques in bacteria infected with phage containing an even or odd number of CAG/CTG repeats (36). The repeats were embedded in a palindromic sequence which is capable of forming a hairpin. Using bacteriophages that contained 1-5 CAG/CTG repeats, plaque size was smaller for bacteria infected with phages containing an even number of repeats than for those containing an odd number of repeats (36). Earlier work from the same laboratory (37) demonstrated a correlation between plaque size, phage infectivity, and palindromic hairpin stability; phages containing more stable hairpins are less infective and yield smaller plaques. Thus, Darlow and Leach postulated that since phages containing even-repeat sequences yield smaller plaques, even-repeat sequences form more stable hairpins than odd-repeat hairpins.

While admittedly quite different systems, our results can shed light on the viral infectivities observed for phage DNA containing an even or odd number of TNR repeats. In the phage system used by Darlow and Leach the even-repeat hairpins may have longer lifetimes than the odd-repeat hairpins. When considering DNA constrained in a circular phage genome, as opposed to the unconstrained oligonucleotides used in the work described here, cruciform interactions, as opposed to kissing interactions, are the likely mechanism for hairpin to duplex conversion since the terminal stem bases of the complementary strands can interact and unzip the hairpins to convert to duplex. While overhangs are not possible in circular DNA, the structure of the even versus odd repeats may still modulate conversion to duplex.

Our findings pose an interesting question regarding TNR expansion: Is expansion more likely in alleles that contain an even number of repeats than in alleles that have an odd number of repeats? Clinical data gathered to examine the phenomenon of anticipation in HD patients displays no noticeable oscillation in expansion propensity between an even or odd number of repeats. Offspring of HD patients possess TNR regions that are dependent on the total number of repeats in the parental allele regardless of whether the parental allele had an even or odd number of repeats (38). This observation suggests that in vivo, the structural differences in sequences containing an even or odd number of repeats are not as clearly differentiated as the ones studied in this work. However it is noteworthy that our studies characterized sequence lengths that would be found in healthy individuals; repeat tracts of these lengths are not prone to expansion. Interestingly, our findings suggest that even though sequences of this length are not prone to expansion the ability for hairpins to form and persist in repeat lengths that are considered healthy may not be uniform across the entire regime.