Consistent Sulcal Parcellation of Longitudinal Cortical Surfaces

Abstract

Automated accurate and consistent sulcal parcellation of longitudinal cortical surfaces is of great importance in studying longitudinal morphological and functional changes of human brains, since longitudinal cortical changes are normally very subtle, especially in aging brains. However, applying the existing methods (which were typically developed for cortical sulcal parcellation of a single cortical surface) independently to longitudinal cortical surfaces might generate longitudinally-inconsistent results. To overcome this limitation, this paper presents a novel energy function based method for accurate and consistent sulcal parcellation of longitudinal cortical surfaces. Specifically, both spatial and temporal smoothness are imposed in the energy function to obtain consistent longitudinal sulcal parcellation results. The energy function is efficiently minimized by a graph cuts method. The proposed method has been successfully applied to sulcal parcellation of both real and simulated longitudinal inner cortical surfaces of human brain MR images. Both qualitative and quantitative evaluation results demonstrate the validity of the proposed method.

1. Introduction

The human cerebral cortex is a highly folded and complex anatomical structure, composed of sulci (the valleys of the cortical surface representation) and gyri (the ridges of the cortical surface representation). Major cortical sulci and gyri, which are common across different subjects and relatively stable in contrast to the extremely variable minor sulci and gyri (Ono et al., 1990), have been extensively adopted for assisting spatial normalization of human brain MR images (Thompson and Toga, 1996; Davatzikos, 1997; Collins et al., 1998; Vaillant and Davatzikos, 1999; Hellier and Barillot, 2003; Van Essen, 2005; Auzias et al., 2009; Perrot et al., 2009; Joshi et al., 2010; Zhong and Qiu, 2010), analyzing the variability of healthy human brains (Mangin et al., 2004a,b; Fillard et al., 2007; Durrleman et al., 2007; Sun et al., 2007; Lohmann et al., 2008; Im et al., 2010; Mangin et al., 2010), studying the cross-sectional and longitudinal changes of brain aging (Kochunov et al., 2005; Rettmann et al., 2006; Liu et al., 2010), and identifying the difference between normal and diseased brains (Ashburner et al., 2003). Since manually labeling sulcal structures is extremely time-consuming, tedious, error-prone and subject to inter-rater variation, a wide variety of automated or semi-automated methods have been proposed for extraction of sulci (Le Goualher et al., 1999; Lohmann and von Cramon, 2000; Rivière et al., 2002; Rettmann et al., 2002; Yang and Kruggel, 2008; Li et al., 2009) or sulcal fundi curves (Lohmann, 1998; Khaneja et al., 1998; Bartesaghi and Sapiro, 2001; Tao et al., 2002; Cachia et al., 2003a,b; Lui et al., 2006; Kao et al., 2007; Tu et al., 2007; Shi et al., 2008; Shi et al., 2009; Shattuck, 2009; Li et al., 2010a; Seong et al., 2010).

In addition, automatic sulcal parcellation of cortical surfaces is of great importance in structural and functional mapping of human brains. Several methods have been proposed for sulcal segmentation or parcellation on cortical surfaces, including the watershed segmentation method based on the geodesic sulcal depth map (Rettmann et al., 2002), the watershed-like region growing method based on both the sulcal depth and the mean curvature map (Yang and Kruggel, 2008), and the surface principal direction flow field tracking method (Li et al., 2009). For example, in the method by Li et al. (Li et al. 2009), the cortical surface is first partitioned as a set of sulcal regions using the hidden Markov random field model and the Expectation-Maximization method (Zhang et al., 2001) based on the maximum principal curvature, and then the principal direction flow field tracking procedure is performed on the diffused principal direction field, which is obtained by propagating the reliable and informative principal directions to cortical regions with unreliable and noisy principal directions, to parcellate the cortical surface into a set of corresponding sulcal basins. However, most existing sulcal segmentation or parcellation methods were designed for working on a single cortical surface (Lohmann and von Cramon 2000; Rettmann et al., 2002; Yang and Kruggel, 2008; Li et al., 2009). For studying longitudinal changes of cortical surfaces, it requires accurate cortical surface parcellation, since longitudinal changes are normally very subtle, especially in normal aging and Alzheimer's disease (AD). Therefore, applying these methods independently to the cortical surface of each time-point image of the same subject in a longitudinal study might generate longitudinally-inconsistent results. To overcome this limitation, in this paper, we propose a new method for accurate and consistent sulcal parcellation of longitudinal cortical surfaces of human brain MR images. In our method, consistent cortical sulcal parcellation is formulated as an energy minimization problem, in which both spatial and temporal smoothness is imposed to the longitudinal sulcal parcellation results. Then, the energy function is efficiently minimized by a graph cuts method (Boykov and Kolmogorov 2004; Kolmogorov and Zabih 2004), which can guarantee to achieve a strong local minimum for certain energy functions. Our proposed method has been successfully applied to both real and simulated longitudinal inner cortical surfaces of human brain MR images. Both qualitative and quantitative evaluation results demonstrate the validity of our proposed method.

Specifically, compared to the existing sulcal segmentation or parcellation methods (Lohmann and von Cramon 2000; Rettmann et al., 2002; Yang and Kruggel, 2008; Li et al., 2009), the advantage of our proposed method is summarized as follows. First, our proposed method is general, since it can work on both single cortical surface and longitudinal cortical surfaces, whereas the existing watershed method or the flow tracking based method is not straightforward to be extended to the longitudinal cortical surfaces. Second, in our proposed method, a clear energy function is formulated for the sulcal parcellation problem, and the energy function is efficiently minimized by a graph cuts method, whereas no clear energy function is generally defined in the existing watershed method or the flow tracking based method. Third, a spatial smoothness term and a temporal smoothness term are included in our energy function to conveniently control the smoothness and consistency of the segmented sulcal boundaries, whereas it is not easy to do this in the existing watershed method or the flow tracking based method. Finally, our method is very flexible to incorporate other cortical attributes such as fiber density (Zhang et al., 2010).

2. Method

Given the reconstructed topologically-correct and geometrically-accurate cortical surfaces at successive time points of the same subject, we aim to consistently parcellate these longitudinal cortical surfaces into a set of sulcal regions (which are the buried cortical regions surrounding the sulcal space on cortical surfaces (Rettmann et al., 2002; Yang and Kruggel, 2008; Li et al., 2009)), and the corresponding sulcal basins (which are the cortical regions bounded by the adjacent gyral crest lines on cortical surfaces (Lohmann and von Cramon 2000; Rettmann et al., 2002; Li et al., 2009)). Figure 1 shows a two-dimensional (2D) schematic illustration of sulcal regions and sulcal basins. As we can see from Figure 1, sulcal regions are relatively easy to be identified in contrast to sulcal basins. Therefore, in our proposed method, sulcal regions are first consistently extracted from the longitudinal cortical surfaces. And then, based on the segmentation results of sulcal regions, the longitudinal cortical surfaces are further consistently parcellated as a set of the corresponding sulcal basins. Both sulcal region and sulcal basin segmentations are formulated as an energy minimization problem, and a graph cuts method (Boykov and Kolmogorov 2004; Kolmogorov and Zabih 2004) is used to efficiently solve the energy minimization problem. In subsequent sections, each segmentation step will be explained in detail.

Figure 1.

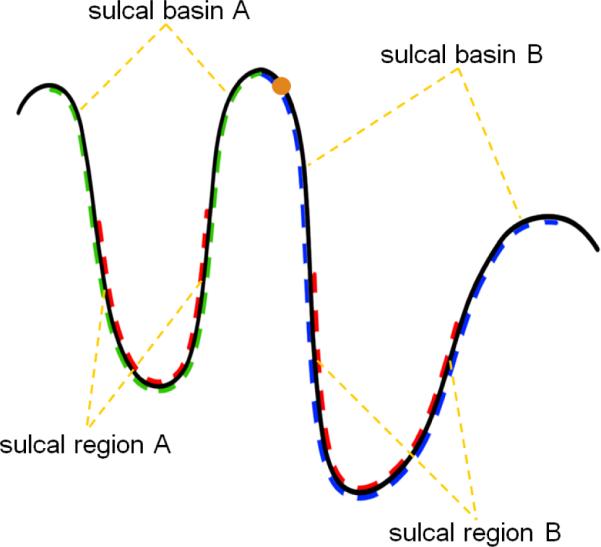
A 2D schematic illustration of sulcal regions and sulcal basins. The red dash curves indicate two sulcal regions. The blue and green dash curves represent the two adjacent sulcal basins. The orange point indicates a point belonging to sulcal basin B.

2.1 Problem formulation

Both consistent sulcal region and sulcal basin segmentations on longitudinal cortical surfaces can be considered as a discrete labeling problem. For sulcal region segmentation, the problem is to assign a label indicating sulcal or gyral region to each vertex. For sulcal basin segmentation, the problem is changed to assign a label indicating a sulcal basin to each vertex in gyral regions. Meanwhile, both the spatial and temporal contextual information of adjacent vertices are taken into account when performing the labeling. Therefore, the general energy function of sulcal region or sulcal basin segmentation can be formulated as:

$$E=E_d+{\lambda }_{\mathrm{s}}{E}_s+{\lambda }_{\mathrm{t}}{E}_t$$ (1)

where E_d is the data term, and E_s and E_t are spatial and temporal smoothness terms, respectively. λ_s and λ_t are the weighting parameters for the spatial and temporal smoothness terms, respectively.

Specifically, the data term represents the sum of the set of data costs on all vertices:

$$E_d=\sum _x{D}_x\left(l_x\right)$$ (2)

where D_x (l_x) indicates the cost of labeling a vertex x as l_x, which denotes a possible label and will be clarified in the next sections.

The spatial smoothness term represents the sum of the cost of labeling a pair of spatial neighboring vertices in a cortical surface. It is used to impose the spatial smoothness on the segmentation results as defined below:

$$E_s=\sum _{\{x,y\}∊N_s}{V}_{x,y}^s(l_x,l_y)$$ (3)

where N_s represents the set of the spatial neighboring vertex pairs in the cortical surface. $V_{x,y}^s(l_x,l_y)$ indicates the cost of labeling a pair of spatial neighboring vertices x and y as l_x and l_y. In this paper, the one-ring neighborhood in the triangular surface mesh is adopted to define the spatial neighboring vertex pairs. Note that the distribution of vertices in the triangular meshes of our cortical surfaces is relatively uniform, therefore, all spatial neighboring vertex pairs are treated equally without considering triangular edge lengths in the paper. However, if the distribution of vertices is not uniform at all, one may have to treat each spatial neighboring vertex pair differently by considering triangular edge lengths

The temporal smoothness term represents the sum of the cost of labeling a pair of temporal neighboring vertices in the cortical surfaces of two successive time points. And, it is used to impose temporal smoothness as defined below:

$$E_t=\sum _{\{x,y\}∊N_t}{V}_{x,y}^t(l_x,l_y)$$ (4)

where N_t represents the set of the temporal neighboring vertex pairs between two successive longitudinal cortical surfaces. $V_{x,y}^t(l_x,l_y)$ indicates the cost of labeling a pair of temporal neighboring vertices x and y as l_x and l_y. In this paper, we focus on the aging brains. Since the longitudinal cortical change for the aging brains within a short time (such as 6 months) is generally very subtle, especially for the inner cortical surface (the interface between whiter matter and gray matter), the temporal neighbors are defined as the closest vertices along the normal directions of the current vertex in the two neighboring cortical surfaces immediately before and after the current time point. Note that the closest vertices are searched along both the inward-oriented and outward-oriented normal directions. It should be noted that when λ_t is set as 0, which means no temporal smoothness is imposed, the above energy function can be used for sulcal parcellation on a single cortical surface.

The definitions of the data term, the spatial smoothness term, and temporal smoothness term are quite different for sulcal region and sulcal basin segmentations, which will be detailed in Sections 2.2 and 2.3, respectively.

2.2 Consistent sulcal region segmentation

Before introducing the detailed terms in the above energy function, the attributes on cortical surfaces used for sulcal parcellation in this paper are first listed as follows: (1) the maximum principal curvature c(·), which is the principal curvature with the larger magnitude in the two principal curvatures at each vertex of the cortical surface, (2) the maximum principal direction p(·), which is the direction corresponding to the maximum principal curvature, and (3) the normal direction n(·). Note that the normal direction does not have a unique direction, since the opposite direction of a normal direction is also a normal direction. In the paper, we always adopt the outward-oriented normal direction to define energy terms. The maximum principal curvature and the maximum principal direction measure the maximum strength and its corresponding direction of the normal direction variation, respectively. All attributes on the cortical surfaces used for sulcal parcellation in this paper are computed using the method in Rusinkiewicz (2004).

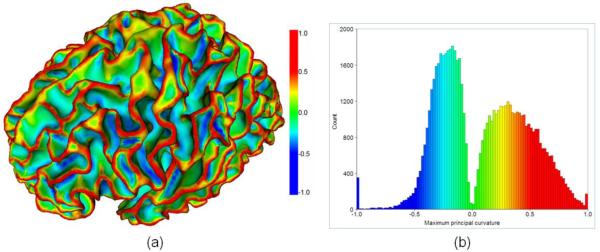
To distinguish sulcal and gyral regions, we adopt the maximum principal curvatures which are the large negative values at sulcal bottoms and the large positive values at gyral crests. It has been shown that the maximum principal curvature is more discriminative than the mean curvature for distinguishing sulcal and gyral regions (Li et al., 2009). Figure 2(a) shows an example of the maximum principal curvature map on a cortical surface. And, Figure 2(b) shows the histogram of the maximum principal curvatures of the cortical surface shown in Figure 2(a). The distributions of the maximum principal curvatures in the sulcal and the gyral regions can be modeled as the two respective Gaussian functions (Li et al., 2009). In principle, when labeling a vertex x as a certain region l_x (i.e., sulcal or gyral region) which it belongs to, the cost D_x(l_x) should be small. Therefore, for sulcal region segmentation, D_x (l_x) is defined as:

$$D_x\left(l_x\right)=1.0-\text{exp}(-{(c\left(x\right)-m_{l_x})}^2∕2{\theta }_{l_x}^2)$$ (5)

where l_x ε{0, 1} indicates sulcal or gyral region, respectively. m_lx and θ_lx and standard deviation of the maximum principal curvature c(·) in the region l_x. Thresholding the maximum principal curvature map using zero value is adopted to obtain the initial sulcal and gyral region segmentation results and to estimate the parameters m and θ for the sulcal and gyral regions, respectively.

Figure 2.

(a) An example of the maximum principal curvature on an inner cortical surface; The color bar is on the right. (b) The histogram of the maximum principal curvatures for the cortical surface shown in (a); Color coding is the same as in (a).

The spatial smoothness term $V_{x,y}^s(l_x,l_y)$ is defined as:

$$V_{x,y}^s(l_x,l_y)=1-\delta \left(\mid l_x-l_y\mid \right)$$ (6)

where δ is the Dirac delta function. This setting is used to penalize the cost of the discontinuous labeling for spatial neighboring vertex pairs.

The temporal smoothness term $V_{x,y}^t(l_x,l_y)$ is defined as:

$$V_{x,y}^t(l_x,l_y)=0.5\times (1+(\mathbf{n}\left(x\right)\cdot \mathbf{n}\left(y\right)))\times (1-\delta \left(\mid l_x-l_y\mid \right)$$ (7)

The central idea behind this definition is explained as follows. Currently, the temporal neighboring vertices are determined by the closest vertex pairs along the normal directions. However, the defined temporal neighboring vertices might contain incorrect anatomical correspondence, especially for the vertices around gyral crests as shown in Figure 3. For example, given a vertex around the gyral crest of the current time-point cortical surface, i.e., the orange point in Figure 3, its closest vertex in the next time-point cortical surface as determined by the above method might be in an adjacent yet different sulcal basin. Therefore, in order to alleviate the influence from incorrect temporal vertex correspondences, we should reduce the cost of the discontinuous labeling for these incorrect temporal neighboring vertex pairs. Since the vertices in adjacent yet different sulcal basins generally have quite different normal directions, we accordingly force the cost of the discontinuous labeling for a pair of temporal neighboring vertices with dissimilar normal directions to be small. As a result, this setting can be used to adaptively penalize the cost of the discontinuous labeling.

Figure 3.

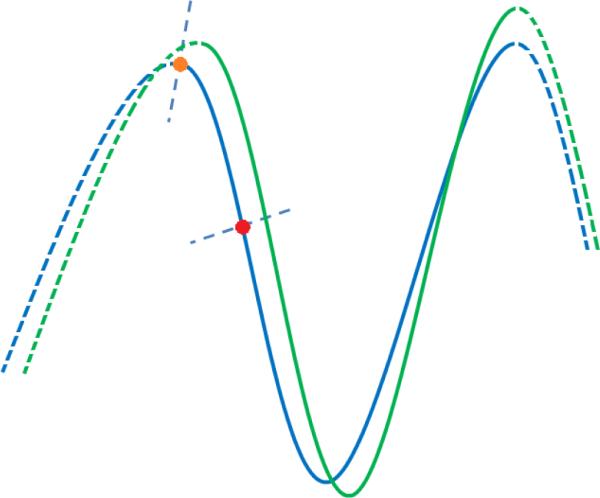
A 2D schematic illustration on how to define temporal correspondence for the vertices on the cortical surface. The blue and green curves are the two cortical surfaces at successive time points. The dash and solid curves indicate different sulcal basins. The orange and red points are the two vertices, with their normal directions indicated by the blue dash lines, along which the closest vertices in the other cortical surface are defined as the temporal correspondences. As we can see, for the point around the gyral crest such as the orange point, its temporal correspondence defined by our method might not be correct. To deal with this issue, we adaptively penalize the cost of the discontinuous labeling for temporal correspondences based on the similarity of their normal directions.

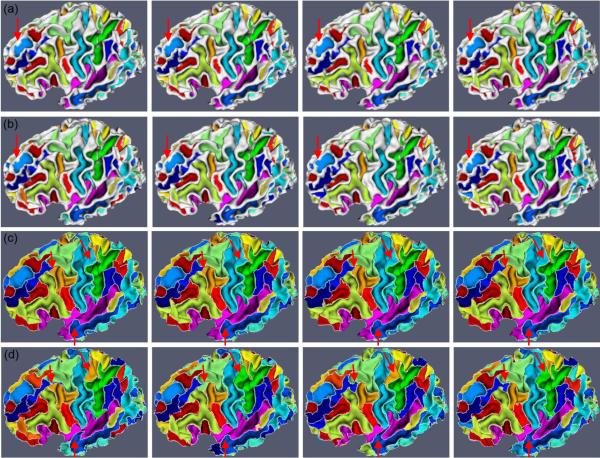
To efficiently solve the above energy minimization problem, we adopt the alpha-expansion graph cuts method (Boykov and Kolmogorov, 2004; Kolmogorov and Zabih, 2004) for consistent sulcal region segmentation. In the graph cuts method, for the purpose of consistent sulcal region segmentation, longitudinal cortical surfaces are represented as an undirected weighted graph G = (V,E), where V is the set of nodes, including all vertices on the longitudinal cortical surfaces and the terminals represented by two labels corresponding to the sulcal and gyral regions. E = E_N⋃E_T is the collection of edges, where E_N is the edges formed by spatial and temporal neighboring vertices, called n-links, and E_T is the edges formed by vertices to terminals, called t-links. In the above constructed graph, D_x(·) describes the edge weight of t-links, and $V_{x,y}^s(\cdot )$ and $V_{x,y}^t(\cdot )$ describe the edge weights of n-links. A cut is a set of edges by removing which the linked nodes are divided as disjoint sets, and meanwhile each node connects to only one terminal corresponding to its label indicating sulcal or gyral region. The cost of a cut is the sum of the weights on the edge set. For more details of the graph cuts method, please refer to Boykov and Kolmogorov (2004) and Kolmogorov and Zabih (2004). After sulcal region segmentation, we perform connective component analysis to label each connective sulcal region as a unique value (Li et al., 2009), which will be further used for sulcal basin segmentation as described below. Figure 4 (a) shows the consistent longitudinal cortical sulcal region segmentation results on a subject with 4 successive time points. As we can see, the longitudinal cortical sulcal region segmentation results are visually reasonable and consistent.

Figure 4.

An example of sulcal parcellation results on longitudinal cortical surfaces of a subject with 4 successive time points. Figures (a) and (b) show the sulcal region segmentation results by our proposed method and the flow tracking method (Li et al., 2009), respectively. Figures (c) and (d) show the corresponding sulcal basin parcellation results by our proposed method and the flow tracking method (Li et al., 2009), respectively. White curves in Figures (c) and (d) indicate the boundaries of parcellated sulcal basins. Red arrows indicate the selected locations where our results are much more consistent than those by the flow tracking method.

2.3 Consistent sulcal basin segmentation

With consistent sulcal region segmentation, which provides the source locations of sulcal basins, we further consistently parcellate the longitudinal cortical surfaces into sulcal basins. Assuming that we have N isolated sulcal regions in each cortical surface and each sulcal region has a corresponding sulcal basin, we aim to assign a sulcal basin label to each vertex on the gyral regions. One intuitive way is to assign the sulcal basin label based on the closest geodesic distance on the cortical surface to the N sulcal regions; however, due to the non-symmetric structures of gyri, the generated boundaries of sulcal basins by this way might not follow the gyral crests. For example, in Figure 1, the geodesic distance from the orange point in sulcal basin B to sulcal region B might be larger than the geodesic distance to sulcal region A. Therefore, the orange point in sulcal basin B will be incorrectly grouped into sulcal basin A. To deal with this problem, for sulcal basin segmentation, the data term is defined based on the weighted geodesic distances (Li et al., 2010a) from the segmented sulcal regions as:

$$D_x\left(l_x\right)=1.0-\text{exp}(-\beta \cdot g_{r_x}\left(x\right))$$ (8)

where g_rx(x) is the weighed geodesic distance between vertex x and sulcal region r_x, which corresponds to the sulcal basin l_x ε{0, …, N -1}. β is a non-negative weighting parameter. Generally, larger value of β makes the data term more sensitive to the weighted geodesic distance g_rx(x). Note that, when β is set as 0, the data term will become 0, thus the spatial and temporal smoothness terms will completely dominate the energy function. In this paper, β is set as 0.2 experimentally, which is found to achieve reasonable results. The weighted geodesic distance g_rx(x) is computed using the fast marching method on the triangular surface mesh (Kimmel and Sethian, 1998). In general, the fast marching method is a numerical approach for solving Eikonal equation (Kimmel and Sethian, 1998):

$$\mid \nabla T\left(x\right)\mid F\left(x\right)=1,x∊S$$ (9)

which describes the evolution of closed curves on a surface as a function of arrival time T(x) with marching speed F(x) at a point x on the curve and with the constraint that x is on the surface S. The weighted geodesic distance from source points can be computed by solving the Eikonal equation on the surface. The marching speed F(x) at vertex x is defined as:

$$F\left(x\right)=\text{exp}(-\mid c\left(x\right)\mid )$$ (10)

The central idea behind this setting is that: Given a sulcal region, if a vertex in gyral regions is not in the sulcal basin corresponding to the current sulcal region, the geodesic path from the vertex to the current sulcal region will pass through gyral crests, where the marching speeds are designed as small values. Therefore, the weighted geodesic distance between the vertex and the current sulcal region will be large. As a result, the cost of labeling a vertex as the sulcal basin to which it does not belong will be large. Otherwise, the geodesic path from the vertex to the current sulcal region will not pass through gyral crests, thus the weighted geodesic distance will be small. As a result, the cost of labeling a vertex as the sulcal basin to which it belongs will be small. In each cortical surface, from each of the N segmented sulcal regions, in which geodesic distances are set as 0, the fast marching method (Kimmel and Sethian, 1998) is conducted to calculate, for each vertex on gyral regions, the weighted geodesic distance away from the current sulcal region. Therefore, each vertex on gyral regions has N weighed geodesic distances from N sulcal regions in a cortical surface.

The spatial smoothness term $V_{x,y}^s(l_x,l_y)$ is defined as:

$$V_{x,y}^s(l_x,l_y)=w(x,y)\times (1-\delta \left(\mid l_x-l_y\mid \right))$$ (11)

$$w(x,y)=0.5\times (1+\mathbf{p}\left(x\right)\cdot \mathbf{p}\left(y\right))\times (\text{exp}(-c\left(x\right))+\text{exp}(-c\left(y\right)))∕2$$ (12)

where w(x, y) represents the weight between the two spatial neighboring vertices. Note that the maximum principal direction p(·) is not unique at each vertex, since the opposite direction of p(·) can also be considered as the maximum principal direction, therefore, the maximum principal direction p(·) has been forced to point towards the decreasing direction of the maximum principal curvature c(·) using the method in Li et al. (2009). The basic idea for the above setting is that the two spatial neighboring vertices belonging to the two adjacent yet different sulcal basins generally meet at gyral crests, where the maximum principal curvatures are the large positive values and the maximum principal directions point away from each other (Li et al., 2009). Therefore, with the above setting, the cost of discontinuous labeling of sulcal basins is set as a small value for a pair of spatial neighboring vertices belonging to two adjacent yet different sulcal basins.

The temporal smoothness term is defined the same as the one used for sulcal region segmentation. The central idea is to force the cost of discontinuous labeling for a pair of temporal neighboring vertices with dissimilar normal directions to be small, since they are most likely incorrect temporal correspondences.

The alpha-expansion graph cuts method (Boykov and Kolmogorov, 2004; Kolmogorov and Zabih, 2004) is adopted here again to efficiently solve the above energy minimization problem for consistent sulcal basin segmentation. Similarly, in the graph cuts method, for the purpose of consistent sulcal basin segmentation, the longitudinal cortical surfaces are represented as an undirected weighted graph G = (V,E), where V is the nodes, including all vertices on gyral regions of the longitudinal cortical surfaces and the terminals represented by the set of discrete labels corresponding to the set of sulcal basins. And E is the collection of edges, which is defined in the similar way for consistent sulcal region segmentation. Although searching for the global optimum of multiple-label energy functions is NP-hard, the graph cuts can guarantee to achieve a strong local minimum efficiently for certain energy functions. The sulcal basin segmentation generates a complete parcellation of cortical surfaces ((Lohmann and von Cramon 2000; Rettmann et al., 2002; Li et al., 2009), where each vertex has a unique sulcal basin label. The boundaries of sulcal basins can be considered as gyral crest lines (Lohmann and von Cramon 2000; Rettmann et al., 2002; Stylianou and Farin, 2004; Li et al., 2009) and the junctions of gyral crest lines correspond to the 3-hing or 4-hing gyral patterns (Li et al., 2010b). Figure 4 (c) shows the longitudinal sulcal basin segmentation results on a subject with 4 successive time points by our proposed method. As we can see, the longitudinal cortical sulcal basin segmentation results by our proposed method are visually reasonable and consistent.

3. Results

In this section, a set of experiments on both real and simulated data are carried out to evaluate our proposed sulcal parcellation method on the longitudinal inner cortical surfaces of human brain MR images. The topologically-correct and geometrically-accurate longitudinal inner cortical surfaces used in all experiments are generated as follows: (1) rigid registration of the follow-up images onto the baseline image space using FLIRT (Jenkinson and Smith, 2001) in Oxford FSL tools, (2) skull stripping of the baseline images using BET (Smith, 2002) in Oxford FSL tools, (3) removing cerebellums and brain stems of the baseline images using in-house tools, (4) masking the brains of the follow-up scans using the brain masks of their corresponding baseline images, (5) correction of intensity nonuniformity of the longitudinal images using N3 (Sled et al., 1998), (6) simultaneous and consistent tissue segmentation of the longitudinal images using CLASSIC (Xue et al., 2006) which iteratively performs joint segmentation of longitudinal images and refinement of longitudinal deformations using a 4D elastic warping (Shen and Davatzikos 2002, 2004), and (7) topology correction of the white matter volumes and reconstruction of the inner cortical surfaces of the longitudinal images using BrainSuite (Shattuck and Leahy, 2002). It should be noted that our proposed method is not limited to work on the cortical surfaces generated by BrainSuite (Shattuck and Leahy, 2002), and it can also work on the cortical surfaces reconstructed by other methods (Mangin et al., 1995; Xu et al., 1998; Dale et al., 1999; MacDonald et al., 2000; Han et al., 2004; Van Essen et al., 2005; Kim et al., 2005; Liu et al., 2008). Currently, all the parameters in the energy functions are set experimentally. Specifically, for consistent sulcal region segmentation, the parameters λ_s and λ_t are set as 0.5 and 0.5, respectively. And, for consistent sulcal basin segmentation, the parameters λ_s and λ_t are set as 0.8 and 0.8, respectively. The above parameter settings are kept unchanged throughout the whole paper. With the above parameter setting, reasonable sulcal parcellation results on longitudinal cortical surfaces have been achieved as will be reported below. As for the optimal setting of these parameters, we will investigate in the future.

3.1 Results on real longitudinal cortical surfaces

3.1.1 Visual inspection

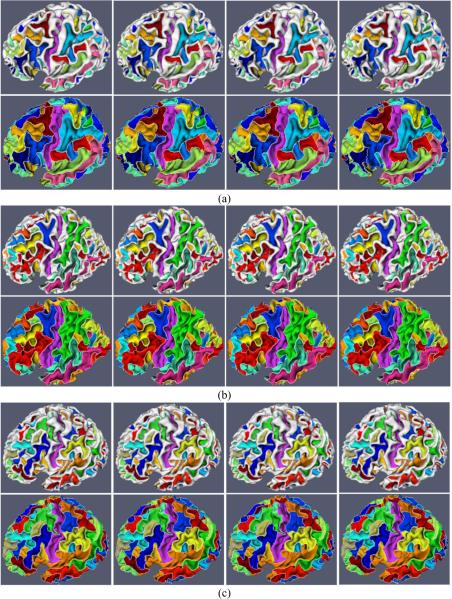
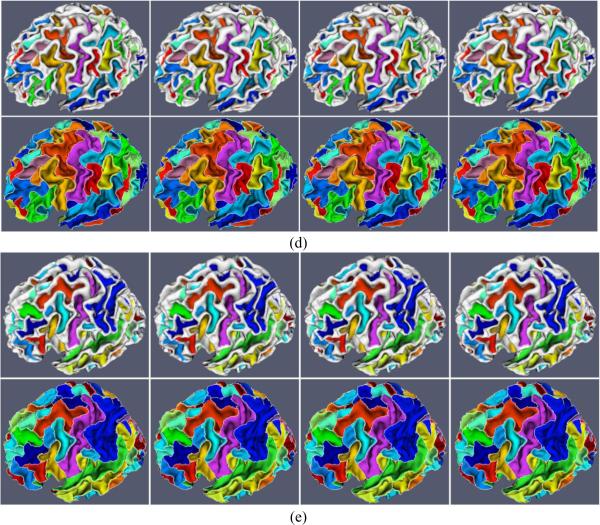
Our proposed method is applied to 10 normal healthy subjects, in which each subject has been scanned 4 times with the interval of 6 months. Figures 4 (a) and (c) show an example of consistent sulcal parcellation results on longitudinal cortical surfaces of a subject with four time points. In this figure, we also compare our cortical sulcal parcellation results with the results (Figures 4 (b) and (d)) from the flow tracking method (Li et al., 2009), which was developed for sulcal parcellation on a single cortical surface. As we can see, the longitudinal cortical sulcal parcellation results with our proposed method are more consistent and reasonable, since both spatial and temporal smoothness are imposed in our proposed method. Figure 5 shows the consistent sulcal parcellation results on longitudinal cortical surfaces of 5 more subjects, randomly selected from the 10 subjects. It is obvious that all of the longitudinal cortical surfaces are consistently segmented into anatomically-meaningful sulcal regions and sulcal basins by our proposed method. For example, the extracted central sulcal regions and sulcal basins, represented by purple colors in Figure 5, are quite visually reasonable. Currently, we have not reached the stage of automatic recognition of these segmented sulcal regions and sulcal basins yet. Thus, each sulcal region and sulcal basin in each subject is randomly assigned a color in Figure 5; therefore, anatomically corresponding sulcal regions and sulcal basins in different subjects generally have different colors, except for the colors of central sulcal regions and basins that are interactively assigned by the expert for visualization purpose.

Figure 5.

Consistent sulcal region and sulcal basin segmentation results on longitudinal cortical surfaces of 5 subjects (Figures (a), (b), (c), (d) and (e)), each with 4 successive time points. For each subject, the top row shows the sulcal region segmentation results, and the bottom row shows the corresponding sulcal basin segmentation results, in which white curves represent the boundaries of segmented sulcal basins. Each sulcal region and its corresponding sulcal basin are labeled with the same color in each subject. However, the anatomically corresponding sulcal regions and sulcal basins in different subjects may have different colors, because the colors are currently assigned randomly, except for the colors of central sulcal regions and sulcal basins that are interactively identified by the expert for visualization purpose.

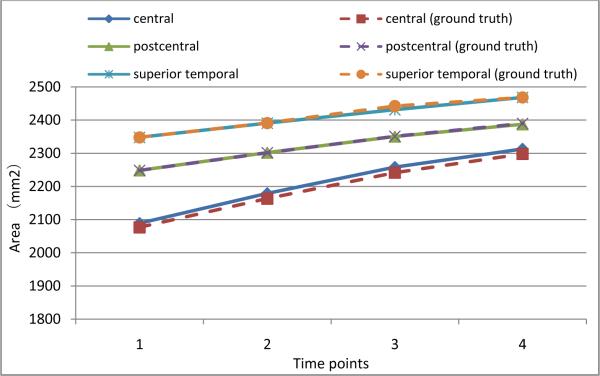
3.1.2 Quantitative evaluation

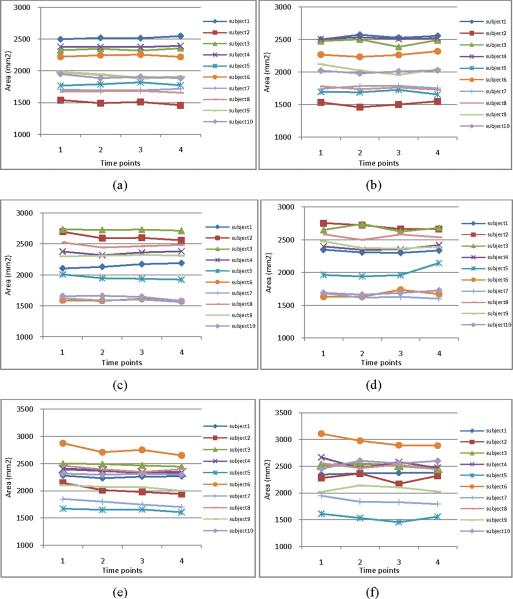
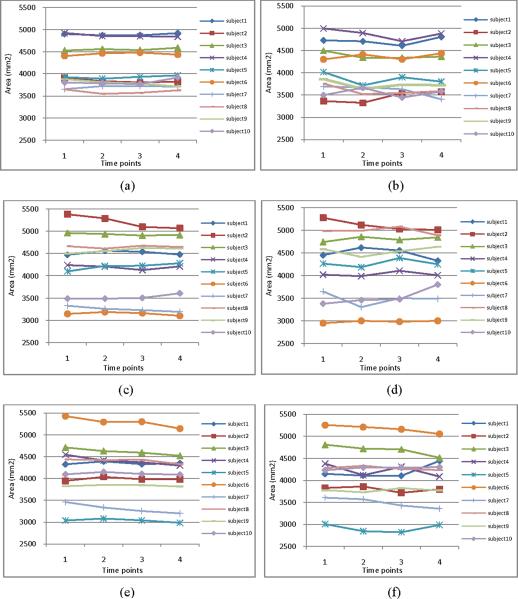
In order to quantitatively evaluate the consistency of the longitudinal sulcal parcellation results, we calculate the areas of left central, postcentral, and superior temporal sulcal regions and sulcal basins on 10 subjects along 4 time points. Figure 6 and Figure 7 show the areas of the segmented sulcal regions and sulcal basins, respectively. For example, Figures 6(a), 6(c) and 6(e) (and Figures 7(a), 7(c) and 7(e)) show the results of left central, postcentral, and superior temporal sulcal regions (and sulcal basins) obtained by our proposed method, respectively, while Figures 6(b), 6(d) and 6(f) (and Figures 7(b), 7(d) and 7(f)) show the results of left central, post-central, and superior temporal sulcal regions (and sulcal basins) obtained by the flow tracking method (Li, et al., 2009), respectively. Since the longitudinal change of inner cortical surfaces within 6 months for the normal aging brains is generally very subtle, it is expected that the estimated cortical surface areas should change smoothly along time. As we can see from both Figure 6 and Figure 7, the results obtained by our proposed method are much smoother than those obtained by the flow tracking method (Li, et al., 2009).

Figure 6.

The cortical surface areas of left central (a–b), post-central (c–d), and superior temporal (e–f) sulcal regions on the 10 subjects along their respective 4 time points. Figures (a), (c) and (e) show the segmentation results by our proposed method, while Figures (b), (d) and (f) show the segmentation results by the flow tracking method (Li et al., 2009). As we can see, the sulcal region segmentation results by our proposed method are much smoother than those by the flow tracking method (Li et al., 2009).

Figure 7.

The cortical surface areas of left central (a–b), post-central (c–d), and superior temporal (e–f) sulcal basins on the 10 subjects along their respective 4 time points. Figures (a), (c) and (e) show the segmentation results by our proposed method. Figures (b), (d) and (f) show the segmentation results by the flow tracking method (Li et al., 2009). As we can see, the sulcal basin segmentation results by our proposed method are much smoother than those by the flow tracking method (Li et al., 2009).

We also define a distance measurement to quantitatively evaluate the performance of the consistency of sulcal parcellation results. Denoting the boundaries of parcellated sulcal basins in the two cortical surfaces at successive time points as S₁ and S₂, their distance measurement can be defined as:

$$d=0.5\times (\frac{1}{n}\sum _{i∊S_1}\underset{j∊S_2}{\text{min}}\mid S_1\left(i\right)-S_2\left(j\right)\mid +\frac{1}{m}\sum _{i∊S_2}\underset{j∊S_1}{\text{min}}\mid S_2\left(i\right)-S_1\left(j\right)\mid )$$ (13)

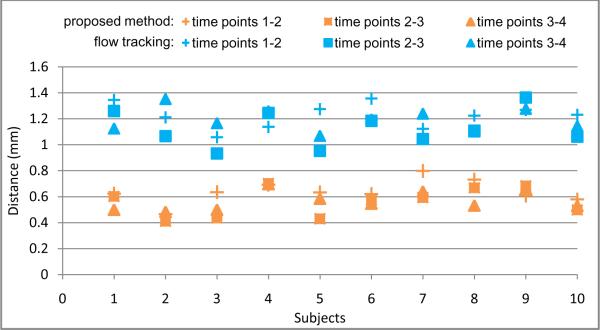
where n and m are the total numbers of points in S₁ and S₂, respectively. Figure 8 shows the overall distance measurement between each pair of two successive time points (i.e., 1–2, 2–3 and 3–4 time points) for each of 10 subjects. Since the longitudinal change of the inner cortical surfaces within 6 month for the normal aging brain is generally very subtle, a small distance measurement is expected. As we can see from Figure 8, the distance measurement from our proposed method is consistently smaller than that by the flow tracking method (Li et al., 2009). This result further demonstrates the consistency of our proposed longitudinal cortical sulcal parcellation method.

Figure 8.

The distance measurement between boundaries of parcellated sulcal basins at each pair of successive time points on the whole cortical surfaces of 10 subjects, by our proposed method and the flow tracking method (Li et al., 2009), respectively.

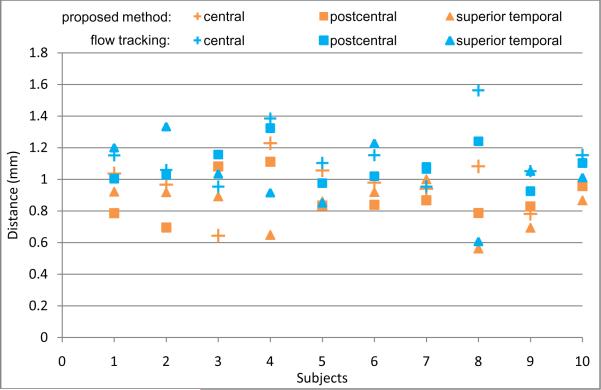
To further validate the accuracy of our proposed method, we have an expert manually label the left central, postcentral, and superior temporal sulcal basins for the cortical surface of the first time-point image of each subject and then calculate the above distance measurements between the automatically and manually labeled boundaries of sulcal basins. Figure 9 shows the distance measurement results on the 10 subjects, with comparison to the flow tracking method (Li et al., 2009). Overall, the average distance error is around 0.9 mm for all three major sulci by our proposed method, compared to the average distance error of around 1.1 mm by the flow tracking method (Li et al., 2009), which renders the relative accuracy of our proposed method.

Figure 9.

The comparison of the automated segmentation results (by our proposed method and the flow tracking method (Li et al., 2009)) with the manual segmentation results, on left central, postcentral, and superior temporal sulcal basins of each of 10 subjects.

3.2 Results on simulated longitudinal cortical surfaces

3.2.1 Robustness

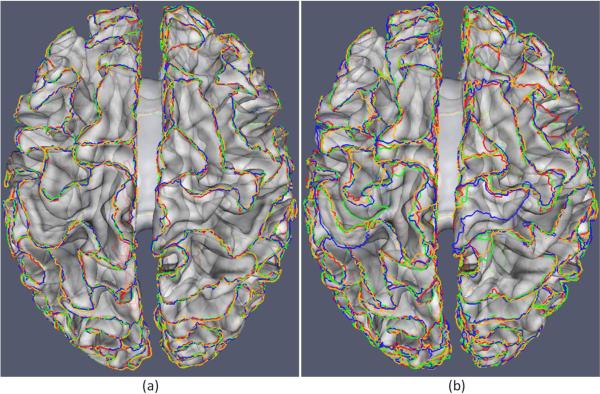
To evaluate the robustness of our proposed method, we employ the simulated brain MR images with different noise levels obtained from the BrainWeb website (Cocosco et al., 1997). We generated four simulated images with 1 mm slice thickness, 20% intensity non-uniformity, and 18×217×181 image size. The noise levels of the four images are set as 3%, 5%, 7% and 9%, respectively, and we refer them as scans 1, 2, 3 and 4 of the subject, respectively. The average distance measurements of the parcellated sulcal basin boundaries on the whole cortical surfaces by our proposed method, between scans 1–2, scans 2–3, and scans 3–4, are 0.59mm, 0.60mm, and 0.65mm, respectively. And, the corresponding average distance measurements by the flow tracking method (Li et al., 2009) are 1.22mm, 1.29mm, and 1.53mm, respectively. Since there is no longitudinal change in the simulated longitudinal data, it is expected that the average distance measurement between each pair of successive time points be close to zero. Figure 10 gives a visual comparison result of parcellated sulcal basin boundaries between our proposed method and the flow tracking method. All the parcellated sulcal basin boundaries are overlaid on the cortical surface of the first time point (the first scan), where the opacity is set to be 0.5 for better visual inspection. It can be observed that the results by our proposed method are more consistent, thus more robust to noise.

Figure 10.

A comparison of the parcellated sulcal basin boundaries of the simulated longitudinal data, achieved by our proposed method and the flow tracking method. The red, green, blue, and yellow curves represent the automatically-extracted boundaries of sulcal basins for the four simulated longitudinal images with the respective noise levels of 3%, 5%, 7% and 9%. (a) The results by our proposed method; (b) The results by the flow tracking method (Li et al., 2009). The opacity of the cortical surface is set to be 0.5 for better visual inspection. It can be observed that the results by our proposed method are more consistent, thus more robust to noise.

To further validate our proposed method, we simulate the whole brain atrophy on 10 subjects using the technique proposed in Karacali and Davatzikos (2006). Specifically, for the first time-point image of each subject (which is used as a baseline image), we generate three different deformation fields to simulate three different degrees of atrophy, i.e., 0.2, 0.4, and 0.6 mm (Karacali and Davatzikos, 2006). Then, with these deformation fields, we can warp the original cortical surface of each subject to obtain three simulated cortical surfaces. Since the generated deformation fields are smooth and topology-preserving (Karacali and Davatzikos, 2006), the warped cortical surfaces are still topology-correct. As a result, we have four topology-correct cortical surfaces (including the baseline cortical surface and three simulated cortical surfaces with different atrophies) for each subject, which can be considered as simulated longitudinal cortical surfaces. Finally, we apply our proposed method and the flow tracking method to separately perform sulcal parcellation on these 10 sets of simulated longitudinal cortical surfaces. Figure 11 shows an example of the cortical sulcal parcellation results on the simulated longitudinal cortical surfaces of a subject, using our proposed method and the flow tracking method, respectively. Specifically, Figures 11 (a) and (c) show the sulcal region segmentation results by our proposed method and the flow tracking method, respectively, while Figures 11 (d) and (e) show the sulcal basin segmentation results by our proposed method and the flow tracking method, respectively. For convenience of visual inspection of folding changes in the simulated longitudinal cortical surfaces, Figure 11 (b) shows a zooming view of a selected sulcal region segmentation result in Figure 11 (a). It can be observed that sulci become wider and gyri become narrower in the simulated longitudinal cortical surfaces, consistent to the overall changing trend of cortical folding in aging brains. In Figure 11, red arrows are also placed to indicate the selected locations where the results by our proposed method are much more consistent than those by the flow tracking method. This experimental result shows that our method can better perform sulcal parcellation for the aging brains with different atrophies.

Figure 11.

An example of sulcal parcellation results on the simulated longitudinal cortical surfaces of a subject with 4 successive time points. Figures (a) and (c) show the sulcal region segmentation results by our proposed method and the flow tracking method (Li et al., 2009), respectively. Figures (d) and (e) show the sulcal basin segmentation results by our proposed method and the flow tracking method (Li et al., 2009), respectively. Figure (b) shows a zoomed view of the bounded cortical regions in the red dash rectangles of Figure (a), from which we can see that sulci become wider and gyri become narrower, consistent to the overall changing trend of cortical folding in the aging brains. White curves in Figures (d) and (e) indicate the boundaries of sulcal basins. Red arrows indicate the selected locations where the results by our proposed method are much more consistent.

3.2.2 Accuracy

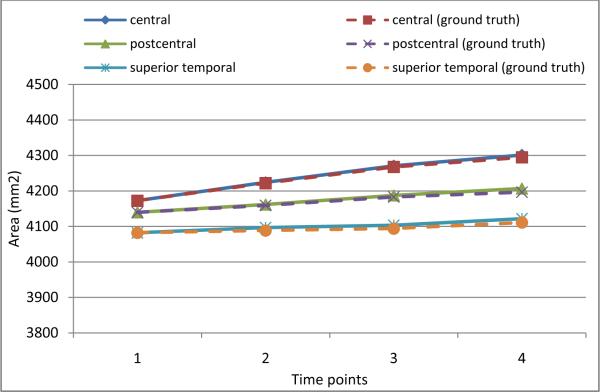
With the simulated longitudinal cortical surfaces described above, we know exactly the ground truth of vertex correspondence across different time points. To evaluate how accurate the parcellated sulci can follow the longitudinal change of the cortical surfaces, we calculate the cortical surface areas on three major sulci, including the left central, postcentral, and superior temporal sulcal regions and sulcal basins, and compare them with the ground truths. Figures 12 and 13 show the surface area comparison results on the three sulcal regions and sulcal basins, respectively. As we can see, the surface areas of parcellated sulci can follow the ground truth very well by our proposed method, indicating its ability in capturing longitudinal change of cortical surfaces. Note that the surface areas of the three sulcal basins and regions increase with the degrees of simulated atrophy, since the sulci become wider with increase of brain atrophy in the simulated cortical surfaces.

Figure 12.

The accuracy of average surface area measurements of left central, postcentral, and superior temporal sulcal regions on simulated cortical surfaces of 10 subjects by our proposed method.

Figure 13.

The accuracy of average surface area measurements of left central, postcentral, and superior temporal sulcal basins on simulated cortical surfaces of 10 subjects by our proposed method.

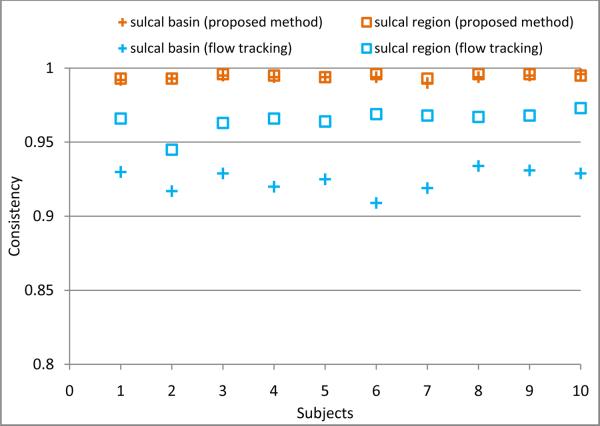
In order to further quantitatively evaluate the sulcal parcellation results, we calculate the consistency measurement of the cortical sulcal parcellation results r as follows:

$$r=\frac{1}{n}\sum _x(1-\frac{n_c\left(x\right)}{N-1})$$ (14)

where n_c(x) is the accumulated times of label changes between each pair of successive time points at vertex x, and n is the total vertex number in a cortical surface. And, N = 4 is the total number of time points for each subject. Ideally, the consistency measurement should be close to 1.0 for the longitudinal cortical sulcal parcellation. Figure 14 shows the consistency measurement of cortical sulcal parcellation results by our proposed method and the flow tracking method on 10 subjects with simulated longitudinal atrophy. We can see that our proposed method is more longitudinally consistent than the flow tracking method (Li et al., 2009).

Figure 14.

The comparison of the consistency measurement of cortical sulcal parcellation results between our proposed method and the flow tracking method (Li et al., 2009) on the 10 subjects with simulated longitudinal atrophy.

4. Discussion and Conclusion

We have presented a novel energy-function based method for consistent sulcal parcellation of longitudinal cortical surfaces of human brain MR images. Our proposed method has been applied to both real and simulated longitudinal brain images, and achieves promising results. However, it should be noted that the proposed method is mainly developed for working on the adult brain images with subtle longitudinal morphological changes. Therefore, the method might not work well on other longitudinal brain images, such as the developmental brains, where the longitudinal cortical changes might be dramatically and thus more sophisticated method is needed for establishing temporal correspondences.

There are still some other limitations in our proposed method. First, the longitudinal cortical surfaces are currently reconstructed independently from the longitudinal images using BrainSuite (Shattuck and Leahy, 2002), although the longitudinal images were simultaneously and consistently segmented by CLASSIC (Xue et al., 2006). Therefore, the reconstructed longitudinal cortical surfaces at different time points might not be very consistent, and can generally have different triangular mesh configuration. Also, the temporal corresponding vertices between cortical surfaces of different time points are currently determined by the closest vertex pairs along the normal directions, which might generate incorrect anatomical correspondences. In the future, we will investigate methods for consistent reconstruction of longitudinal cortical surfaces and obtaining more accurate temporal vertex correspondences, thus further improving our longitudinal cortical sulcal parcellation results (although we have designed strategies to alleviate the influence of these incorrect temporal vertex correspondences in our current proposed method).

Second, several parameters in our energy function are currently set experimentally, which cannot guarantee the optimal solution, although our results are reasonable and better than the method under comparison (Li et al., 2009). The optimization of these parameters will be investigated in the future.

Third, we have not reached the stage of automatically recognizing or naming the parcellated sulci (Lohmann and von Cramon 2000; Rivière et al., 2002; Behnke et al., 2003; Yang and Kruggel, 2009; Perrot et al., 2009). In the future, we will develop methods for automatic recognition of the segmented sulcal regions and sulcal basins. One potential problem is that some sulci might be inherently connected together (Ono et al., 1990; Rettmann et al., 2005; Yang and Kruggel, 2009), i.e., the superior-frontal sulcus and the precentral sulcus. In this situation, the connected sulcal regions or basins will be partitioned as a single sulcal region or basin no matter what method (the proposed method or the existing sulci extraction method) is used (Rettmann et al., 2002; Yang and Kruggel, 2008; Li et al., 2009). Therefore, before recognizing sulci, one has to explicitly interrupt the connected sulci either by semi-automatic method (Rettmann et al., 2005) or automatic method (Yang and Kruggel, 2009). Since only major sulci are relatively consistent across individuals, we will focus on recognition of these major sulci. With the extracted and recognized major sulci, one can analyze the longitudinal change of a specific sulcus and its variability in a population of human brains. The recognized sulci could also help spatial normalization of human brain MR image by first matching the corresponding sulci across individuals and then matching other cortical regions progressively. In fact, the recognition of sulci could also benefit from the spatial normalization result, therefore, the sulci recognition and spatial normalization could be performed jointly (Perrot et al., 2009) to improve the accuracy of both procedures.

Besides, our future work will also include the further validation of our proposed method using more longitudinal data, and the analysis of longitudinal attribute changes of the parcellated sulci for the aging and disease progression applications, i.e., using cortical thickness, gray matter density, cortical area, and cortical folding.