Dynamics of epileptiform activity in mouse hippocampal slices

Abstract

Increase of the extracellular K⁺ concentration mediates seizure-like synchronized activities in vitro and was proposed to be one of the main factors underlying epileptogenesis in some types of seizures in vivo. While underlying biophysical mechanisms clearly involve cell depolarization and overall increase in excitability, it remains unknown what qualitative changes of the spatio-temporal network dynamics occur after extracellular K⁺ increase. In this study, we used multi-electrode recordings from mouse hippocampal slices to explore changes of the network activity during progressive increase of the extracellular K⁺ concentration. Our analysis revealed complex spatio-temporal evolution of epileptiform activity and demonstrated a sequence of state transitions from relatively simple network bursts into complex bursting, with multiple synchronized events within each burst. We describe these transitions as qualitative changes of the state attractors, constructed from experimental data, mediated by elevation of extracellular K⁺ concentration.

Introduction

Epileptic seizures represent a dramatic shift in normal physiological activity toward hyperexcitability and synchronization of neuronal firing. This synchrony is reflected in large-amplitude EEG patterns with characteristic temporal profiles and complex spatial distribution. While specific forms of epileptic activity may be manifested by different spatio-temporal profiles, one common EEG pattern found in patients with Lennox–Gastaut syndrome [1], and resembling paroxysmal oscillations observed in experiments with anesthetized and non-anesthetized animals [2], consists of slow spike-wave (SW) or polyspike-wave (PSW) complexes and runs of rapid EEG “spikes” (10–25/s). The occurrence of SW complexes in the depths of monkey cortex without a reflection at the cortical surface [3] and observation of seizures with SW/PSW complexes in completely isolated cortical slabs in vivo [4] suggest that generation of focal SW seizures depends on the basic neuronal circuitry involving excitatory neurons and inhibitory interneurons.

While multiple and still unknown factors may promote epileptogenesis leading to SW/PSW seizures, it is well established that the extracellular potassium concentration ([K⁺]_o) increases during epileptogenesis [5]. Whether deficiencies of the K⁺ regulatory system are a primary mechanism of such seizures, or increase of K⁺ is a result of high neuronal activity during seizures, is still actively debated (for review see, for example, [6]). Nevertheless, recent studies on the pathophysiology of tissue from epileptic human patients [7–9] and animal epilepsy models [10–12] revealed aberrations in [K⁺]_o regulation, suggesting possible involvement of [K⁺]_o elevation as a triggering factor of seizures. Elevation of [K⁺]_o was found to lead to characteristic activity patterns, including episodes of fast runs (tonic phase) and slow bursting (clonic phase resembling SW/PSW EEG patterns) [13–15] and therefore provides a generic approach to study epileptiform activities.

Progressive elevation of [K⁺]_o depolarizes reversal potential of the ionic currents permeable for K⁺ ions and may also affect the maximal conductance of some depolarizing currents such as the hyperpolarization-activated depolarizing current (I _h) [16] and the persistent sodium current (I _Na(p)) [17], thus increasing excitability. Computer modeling revealed that increase of [K⁺]_o leads to a sequence of state transitions (bifurcations) between silent, tonic spiking and bursting states of a cortical pyramidal neuron [18]. Furthermore, it revealed an existing bistability between tonic spiking and bursting states of a neuron for a range of [K⁺]_o [19, 20], which may lead to complex state transitions resembling those occurring during a SW seizure [20–22].

In this study, we used a combination of in vitro electrophysiology and dynamical system analysis to explore the transition from normal activity to paroxysmal firing in the hippocampal slice exposed to artificial cerebrospinal fluid (ACSF) solution with elevated potassium concentration. Progressive diffusion of potassium ions into the neuronal tissue after increase of ACSF potassium concentration mimics progressive [K⁺]_o increase and leads to a sequence of state transitions between different spatio-temporal activity patterns.

Methods

Preparation of hippocampal slices

Acute hippocampal slices were prepared from wild-type (P10-P20 days old) mice (The Jackson Laboratory, Bar Harbor, ME). Mice were anesthetized and decapitated according to UC Riverside IACUC approved protocols. The brain was rapidly removed and slices (300 μm) were cut using a Leica 1200 vibrotome in low Ca ice-cold ACSF, followed by recovery in normal ACSF for 1 h at 32°C.

Multi electrode array recordings

Multi electrode array (MEA) recordings were performed using 32 channels arrays from (ALA Scientific Instruments Inc.). Hippocampal slices were prepared as described above and placed on the array so that CA1 or CA3 areas covered most of the recording electrodes. Exact placements were photographed for further analysis. All MEA recordings were done at 32°C. Data were acquired and preliminarily analyzed by MC Rack tools (Multi Channel Systems) and exported to PClamp10 (Molecular Devices) and MatLab (The MathWorks, Inc.) for final analysis and plotting.

Solutions

Brain slices were continuously perfused by gravitational flow at a 5 ml/min rate at room temperature (20–22°C). The standard bath solution (ACSF) contained (mM): NaCl 125; KCl 2.5; NaHCO₃ 25; NaH₂PO₄ 1.25; MgCl₂ 1; CaCl₂ 2; d-glucose 25; Sucrose 10; pH 7.4 maintained by continuous oxygenation with 95% O₂ and 5% CO₂ gas mixture, osmomolarity 290. The standard pipette solution contained (mM): K-gluconate 130 (Tokyo Chem. Ind. Co., LTD; Mg-ATP 1.2 (Alexis #480-021-G005); GTP 0.3 (Roche); EGTA 3; HEPES 10; phosphocreatine 10; creatine phospokinase type I 0.1 mg/ml (Sigma #c3755-3.5KU) buffered to pH 7.4 with KOH, osmomolarity 310. The standard dissecting solution contained (mM): NaCl 87; KCl 2.5; NaHCO₃ 25; NaH₂PO₄ 1.25; MgCl₂ 4; CaCl₂ 0.5; d-glucose 10; Sucrose 75; pH 7.4 oxygenated with 95% O₂ and 5% CO₂ gas mixture. All chemicals were from Fisher Scientific Inc. unless otherwise specified.

Spectrogram

Time–frequency spectrograms were obtained on the data from individual channels. A 100% Hanning taper was used before using the fast Fourier transform (FFT). This taper was applied to moving window segments to reduce bias in the estimation of both power and phase [23]. The sliding window was 256 ms long with a non-overlapping time steps of 128 ms. Power from the spectrogram was obtained by taking the absolute value of the complex number returned from FFT for each time step and frequency.

PCA

Principal component analysis (PCA) was performed by obtaining singular value decomposition on the mean subtracted data segments from all 32 channels. PCA analysis provided weights of the channels for each component. The weights were then multiplied by the original data to obtain the time course of activity of each component. The variance contributed for each component was computed and the cumulative variance was plotted. PCA analysis was done on a representative dataset which showed high signal to noise ratio.

Data analysis of bursting dynamics

We studied qualitative dynamical changes during the development and evolution of the bursts. To capture spatial distribution of neuronal activity with a single variable, we computed a standard deviation of data distribution measured from all electrodes at each sample time. Standard deviation SD(t) contained less noise than the data from individual channels and better captured events of neuronal activity that occurred at various locations of the hippocampus. High-frequency noise components of SD(t) were filtered out by an eighth order Butterworth low-pass filter with 50 Hz frequency cutoff. The trajectories representing bursting activity were plotted as a projection on the plane of variable SD(t) and a slow variable U(t) that was obtained from SD(t), using low-pass filtering and integration of SD(t) with a leakage:

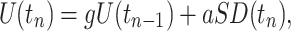where g = 0.98 and a = 0.05. If the value of g was set closer to 1, then the dynamics of U(t) became slower. The value of a controls the scale of U(t). The construction of the slow variable in the present case had several advantages over the time delay embedding method typically used for unfolding trajectories from data analysis of attractor properties in a phase space. First, the bursting activity contains several distinct time scales, which makes it difficult to select a proper time delay to show all properties of the attractor with a single image. Second, the use of integration for the slow variable significantly reduces the level of noise in comparison with a time delay approach.

Results

Multi-electrode array recordings in hippocampus

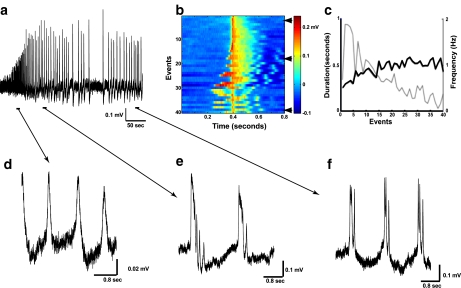
In this study, we recorded simultaneous extracellular activity from CA regions of the mouse hippocampus. We utilized a 32 recording channel array (ALA Scientific Instruments Inc.) to gain insight into spatio-temporal resolution of the hippocampal epileptiform development. Figure 1a illustrates initiation of network synchronization in response to rising [K⁺]_o from 2.5 mM (normal ACSF) to 10 mM. Bath application of high KCl led to an increase in multiunit activity, followed about 2 min later by appearance of the synchronized network events with progressively increasing amplitude and frequency. This initial phase of oscillations lasted for about 30 to 60 s, after which oscillations reached maximum amplitude. Frequency changes followed a more complex pattern and are summarized in Fig. 3 below. Temporal dynamics of all epileptiform events are summarized in Fig. 1b. The initial phase of oscillations was characterized by burst events at lower amplitude, higher frequency and usually consisted of one intraevent peak (Fig. 1d). As time progressed, amplitude of network bursting increased, frequency decreased, and multiple intraevent peaks appeared. At the end of the initial phase, epileptiform reached steady state, which can be characterized by largest amplitude, lowest frequency, longest interevent intervals and biggest area of the event (Fig. 1e). From that point, the pattern of epileptiform development reversed, showing slow decrease in amplitude, interevent intervals and the area of the event (Fig. 1f). A later phase exhibited fewer intraevent peaks, which, together with decreased event area, reflected a lesser degree of synchronization. Time dependence of the frequency of burst events was inverse to the event duration (Fig. 1c). Duration and frequency of the event can be defined by the set of synaptic and intrinsic properties of the cell and reflects the degree of network synchronization.

Fig. 1.

Extracellular field potential (LFP) recordings show large amplitude network events following application of high KCl. a Representative LFP trace (1 channel of MEA) shows development of synchronized network oscillations upon application of high (10 mM) KCl. The first 2 min of recording following high KCl application are not shown. Arrows indicate time intervals expanded in panels d–f. b Temporal structure of all burst events from a. Each row shows one event. The events are ordered chronologically from top to bottom and aligned by the peak of the amplitude. c Frequency and duration of the burst events from the entire course of recording. Duration of the events was computed by identifying contiguous time periods which had activity higher than sum of the mean and 50% of standard deviation, where mean and standard deviation were obtained from the 800 ms window that included burst and baseline activity. d Magnification from a shows network bursts with single spike at the beginning of epileptiform development. e Magnification from a shows network bursts at the maximum activity of the oscillations. f Magnification from a shows network bursts with multiple intraevent peaks at the end of the run

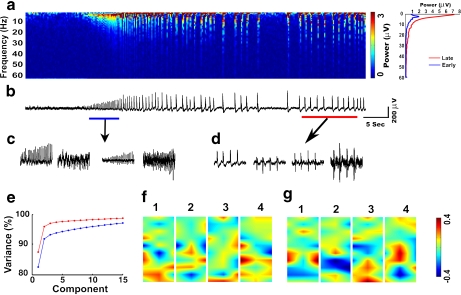
Fig. 3.

Power spectrum and principal component analysis of network oscillations. a Time–frequency spectrogram based on Fourier transform for the entire period of activity from one recording channel. The plot on the right shows the averaged power spectrum during the early and late phases of the oscillations. b LFP recording that was used to compute spectrogram in a. Blue and red lines indicate the periods selected for principal component analysis (PCA), as initial and later phases correspondingly. High KCl was applied at the start of the recording shown. c, d Projections of the 32-channel data sets to the first four PCA components. e The cumulative increase of variance. Blue and red lines indicate initial and later phases of the oscillations. f, g Spatial distribution of the PCA weights for the first four components for initial (f) and later (g) phases of the oscillations. Each color-scaled image indicates the interpolated PCA weights on the electrode grid

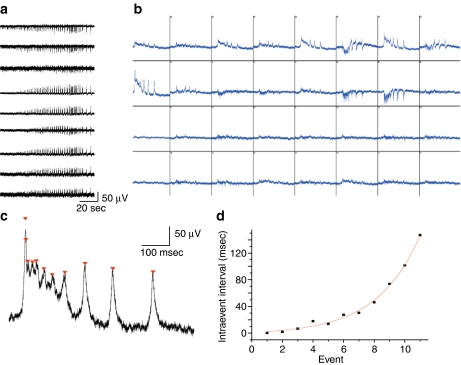
Figure 2a shows initiation of the network synchronization recorded on a few selected channels of the same slice. Events can be categorized as positive or negative, as well as bidirectional, which is defined by the current direction (sinks vs. sources) at each particular electrode. Figure 2b shows isolated network events recorded on all 32 channels near the maximum activity. The amplitude of the event varied across channels and reflected distance from the site of origin and the relative strength of this origin, as well as the relative orientation of cell bodies. When a recording electrode was close enough to an active cell, single action potentials could be resolved (e.g., see channels 11, 23, 27; Fig. 2b). Those spikes were recorded from a few nearby cells, as the amplitude of spikes varied significantly. Analysis of the internal structure of each event revealed a dynamically changing number of intraevent peaks (Figs. 1d, e, f and 2c). Furthermore, analysis of the intraevent peaks intervals (each intraevent peak capped and shown on Fig. 2c) showed gradual increase until event termination (Fig. 2d). Length of those intraevent intervals was perfectly fit with a single exponential (Fig. 2d).

Fig. 2.

Multi-electrode array (MEA) recordings reveal complex distribution of activity patterns across electrodes. a Representative example of 9 MEA channels (out of 32 channels total) recorded simultaneously show spatio-temporal evolution of the network dynamics upon application of high (10 mM) KCl. b Example of a single synchronized network event occurring at the steady-state phase of the oscillations. All 32 channels are shown (display resolution 1 s/500 V) on a short time scale. Channels are numbered successively from the upper left to the lower right. c Close up of single event channel 9 from b, notice exponential increase in the length of intraevent peak intervals, closed triangles cap each intraevent peak. d Single exponential fit of the intraevent intervals from c

Power spectrum and principal component analysis

The spectrogram analysis of the MEA data revealed complex evolution of epileptiform activity in frequency space (Fig. 3a). During the initial phase (marked by a blue line in Fig. 3b), the spectrogram showed an increase of power (over baseline) in frequencies between approximately 2 Hz on the lower end and around 15 Hz on the upper end of the frequency range. The increase of activity in the lower frequency range during the initial phase temporally overlapped across multiple burst events, leading to poor temporal localization of individual bursts in the frequency domain. In contrast, during the later phase (red line in Fig. 3b), individual bursts are easily identified by power increase for the entire range up to approximately 40 Hz (right panel, Fig. 3a). During later phase oscillations, the bursting became irregular, with the inter-burst spectrogram resembling that prior to the onset of bursting. These changes in the spectrogram reflect the complex evolution of the nature of the burst events from initial to later stages of epileptiform activity. PCA was applied to the time segments from initial and later phases of epileptiform activity. The first four principal components from both time segments are shown in Fig. 3c and d. These four components contributed about 95% of the variance. The cumulative change in variance with addition of each new component was less for the initial phase compared to the later phase (Fig. 3e), which likely reflected a lower degree of synchrony. More complex activity patterns required more components to describe variance during the initial phase of the seizure. The spatial distribution of the PCA weights revealed significant changes between initial and later phases (Fig. 3f and g). Furthermore, the spatial distribution of the first principal component for the initial and later phases showed inversion in polarity (Fig. 3f and g, component 1).

Epileptiform waveform distribution

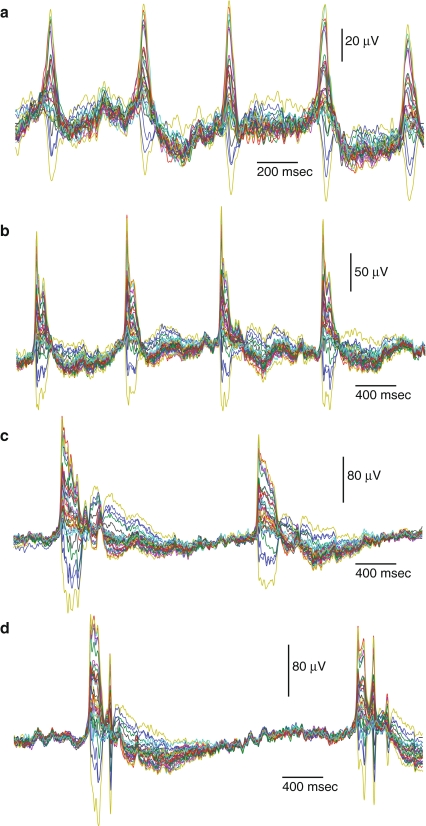
Waveforms plotted for the four different time intervals of typical bursting activity measured in all 32 channels are shown in Fig. 4. Depending on the location of the electrode relative to the origin, different channels show different amplitudes and signs of the LFP during each network burst event. The bursts that occurred up to 20 s after the beginning of paroxysmal oscillations had only one peak and exhibited rather uniform spatio-temporal noise distribution between bursts (Fig. 4a). As development continued, these bursts grew in amplitude and duration; after about 40 s of activity, they developed a fine structure of peaks on the top of each burst event (Fig. 4b). This part of the waveform was reflected in the spectrogram as a high frequency component, which was more prominent in the later phase of oscillations (Fig. 1d, e, f). Note that the duration of the inter-burst intervals increased from early to later phases of the oscillations (compare Fig. 4a and d), while the variance between channels gradually reduced during each inter-burst interval, reaching its minimum right before the next burst onset. Both reduced dispersion before each burst event and increased bursting amplitude indicate a higher degree of synchronization of bursting activity among the measured network sites. Continuous development of this synchrony led to longer inter-event intervals of almost homogeneous activity and more complex structure of the bursts with multiple peaks. These types of bursts are shown in Fig. 4c and d, corresponding to the activity at 65 and 148 s of the epileptiform development (see Fig. 1d and f).

Fig. 4.

Waveform distributions of data in multi-channel recordings for selected typical burst events from recordings shown in Fig. 1a. a High-frequency bursting at the beginning of epileptiform development (see Fig. 1d). b High-amplitude bursts at the end of the initial phase of epileptiform development. c Low frequency bursting near the peak at the maximum activity of the oscillations (see Fig. 1e). Note different voltage scale. d Long multi-peak burst events at the end of the run corresponding to Fig. 1f

Qualitative dynamical analysis of the epileptiform development

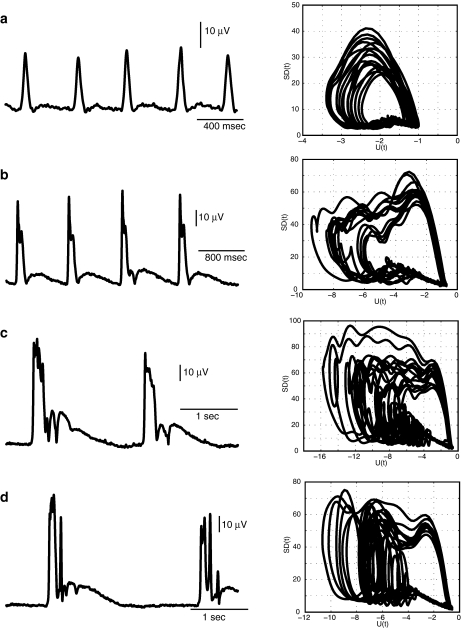
We next analyzed spatio-temporal development of the network bursting activity using dynamics of the standard deviation, SD(t), of LFP signals across multiple channels. Our analysis revealed several transitions between qualitatively different network states during epileptiform evolution (Fig. 5). This evolution was described in terms of a few simple attractors, constructed using SD(t) and a slow variable U(t) (see Section 2). Qualitative changes in the shape of trajectories occurred both during and after the burst (Fig. 5). At the beginning of the epileptiform development, oscillations had the form of a relatively simple attractor. When the trajectory passed through a slow phase between network bursts, it formed almost horizontal motions along the slow variable U(t) near a critical region at the lower right corner of the attractor. It exhibited fast spike of activity during the burst event, and then jumped out of the critical region towards high values of SD(t). Later, the trajectory returned back to the slow motion region (Fig. 5a). As the synchronization of the network developed, the amplitude and duration of such simple bursts increased, leading to the ripple formation on the top of each burst (Fig. 5b). These ripples appeared in the attractor as oscillations at the top area during the fast motion phase (Fig. 5b, right panel). As duration and amplitude were approaching the maximum levels during the later phases of the oscillations, some modulation appeared right after the burst. This modulation caused the formation of additional loops in the attractor trajectories right before the return to the quiet state of SD(t) at the lower right corner of the attractor (Fig. 5c). Comparison of the attractor shapes presented in Fig. 5b and c revealed that the modulation of the after-burst activity builds up gradually in the region of the slow motions. The modulation developed after each burst of network spikes, which appeared on the attractor as large amplitude loops at the left side of the attractor (Fig. 5d). These loops were formed in the region where after-burst modulation occurred (compare Fig. 5c and d, note different scales).

Fig. 5.

Characteristic state attractors during different epochs of epileptiform activity. Waveforms of standard deviation SD(t) computed for data sets shown in Fig. 4 (left panels) and attractors plotted as a projection on variable plane (SD(t), U(t)) for each type of oscillations (right panels)

Discussion

Using a combination of multi-electrode recordings from mouse hippocampal slice and data analysis based on dynamical systems theory, we found that increase of the extracellular K⁺ concentration leads to appearance of epileptiform activity in a form of synchronized network events with progressively increasing amplitude and frequency. Time evolution of epileptiform activity was represented by a sequence of transitions between characteristic network states. These states were characterized by different degrees of synchronization across populations of neurons and were qualitatively described by different state attractors.

Previously, using computer simulations of a detailed compartmental model of pyramidal neurons, we showed that increase of [K⁺]_o leads to transition from silent neuron state to tonic spiking and then to bursting, followed by depolarization block for very high levels of [K⁺]_o [18, 19, 21, 24, 25]. Similar observations were reported in other computational studies [26, 27]. When [K⁺]_o was allowed to change freely (rather than being a control parameter of the model), its dynamics led to complex periodic transitions between tonic spiking and bursting states [19, 20] resembling tonic and clonic activity during epileptic seizures [13–15]. Slower dynamics of sodium and chloride concentrations can lead to termination of paroxysmal activity, followed by a postictal depression state (Krishnan and Bazhenov, submitted). The slice preparation used in this study provides an intermediate case between fully controlled and freely changing [K⁺]_o. Indeed, a practically infinite K⁺ source/sink in the form of the perfused ACSF tightly controlled the average level of [K⁺]_o which would be impossible in vivo. Still, the various buffering mechanisms provide some degree of separation between in-depth [K⁺]_o and its bath concentration, therefore allowing [K⁺]_o to fluctuate as a result of network activity [14].

Progressive evolution of the spatio-temporal patterns of network bursting reported in our study is likely linked to progressive change of the effective [K⁺]_o in slice. Indeed, increase of the bath concentration of K⁺ should lead to delayed elevation of [K⁺]_o in the depth of the tissue. The time constant of [K⁺]_o increase would depend both on K⁺ diffusion and capacitance of the K⁺ regulatory mechanisms, such as glial buffering, compensating changes of external K⁺. These mechanisms ensure relatively slow increase of the average [K⁺]_o in the slice depth and allowed observance of a sequence of state transitions following bath application of high KCl.

Initial increase of the average [K⁺]_o level from baseline depolarized membrane resting potentials and led to increase of spontaneous activity, which at some point in time became synchronized in the form of population (network) burst events. Further, [K⁺]_o increase led to elevation of firing and network bursts with several network spikes, which repeated at progressively decreasing frequency within a burst. The state attractor representing each burst event also changed, reflecting multiple fast transitions during each network event. The shapes of these attractors and dynamical changes of the trajectories’ development found in this study are rather typical for systems with bursting instabilities. Similar observations were reported previously in the Belousov–Zhabotinsky chemical reaction [28, 29], dynamics of laser systems [30, 31], models of neurobiological networks [32] and other systems.

Our study suggests that the early single peak network events (Fig. 1d) can occur for relatively mild levels of [K⁺]_o elevation when individual cell dynamics is dominated by tonic spiking [18]. Potassium diffusion and saturation of [K⁺]_o regulatory mechanisms lead to progressive elevation of effective [K⁺]_o level in the depth of the tissue, triggering network bursts with multiple spikes (Fig. 1e, f). Appearance of multiple spikes per network burst event at higher levels of [K⁺]_o can be explained by either the bursting pattern of individual neurons under conditions of elevated [K⁺]_o (then a typical cell produces at least one action potential per each network spike) or by effects of inhibition synchronizing individual action potentials within several groups/events (then each cell only makes one action potential per burst and different cells fire at different times). Our preliminary data of whole-cell and juxta-cellular recordings, as well as extracellular recordings [19] and computational modeling [18], strongly suggest that at least some neurons may switch to the bursting mode after sufficient [K⁺]_o elevation, producing several action potentials per network event, with each action potential locked to a specific network spike.

Sharp increase in frequencies from 4–12 Hz was observed during the initial phase of the epileptiform activity in the spectrogram. Similar increase in this frequency range has been shown in rats during seizure [33]. Furthermore, during a later phase, each burst event was represented by a response across the entire spectrum, with power decaying slowly even for very high frequencies. Thus, high frequency activity co-occurred with low frequency oscillations. Similar effects of cross frequency coupling between gamma frequency (40–55 Hz) oscillations and lower frequency (15–30 Hz) dynamics were also seen in EEG during seizure [34].

The cumulative variance described by the first N principal components vs. number of components N grew slower for the initial phase of the seizure compared to the later period, suggesting more complex spatio-temporal patterns during the earlier phase of epileptiform activity. This difference could arise due to the lower synchronization during the initial phase compared to the later phase. This is consistent with the qualitative dynamical system analysis in this paper and previous experimental studies [35]. The spatial distribution of the first PCA component (which accounts for more than 80% of variance in both cases) switched polarity between the initial and the late phase of the seizure, suggesting a switch in the nature of its contribution to the burst activity from the same spatial sources. Such changes in polarity may arise from interaction of coupled oscillators [36].

We found a complex spatio-temporal distribution of network activities during burst events and relatively synchronized temporal profiles across different electrodes between bursts. The first reflects complex distribution of sinks and sources of currents generated during each population burst, and can be traced to cell anatomy (e.g., difference between electrodes located near the cellular somas vs. those located near dendrites) and difference between hippocampal regions (e.g., CA1 and CA3) included in our multi-electrode recordings. The random low-amplitude fluctuations between bursts which were synchronized across all channels possibly reflected a common drive related to the perfusion system or external noise. Furthermore, analysis of time events across multiple electrodes suggests that each burst event was usually initiated in the CA3 region and propagated to other areas of the hippocampus; multiple overlapping sources appeared at high levels of [K⁺]_o.

In conclusion, our study suggests that the complex network dynamics underlying the transition between normal physiological network activity and seizure-like events can be described as a sequence of relatively simple attractors with attractor dynamics mediated by synaptic interactions and intrinsic cell dynamics and transitions between attractors mediated by elevation of the average level of [K⁺]_o. Understanding the exact nature of these transitions would not only allow us to provide a low-dimensional description of these complex network events, but also to propose interventions that may prevent evolution of the pathological epileptic activity.