Sequential Population Pharmacokinetic Modeling of Lopinavir and Ritonavir in Healthy Volunteers and Assessment of Different Dosing Strategies^,

Abstract

Nonlinear mixed-effects modeling was applied to explore the relationship between lopinavir and ritonavir concentrations over 72 h following drug cessation and also to assess other lopinavir and ritonavir dosing strategies compared to the standard 400-mg–100-mg twice-daily dose. Data from 16 healthy volunteers were included. Possible covariates influencing lopinavir and ritonavir pharmacokinetics were also assessed. Data were modeled first separately and then together by using individually predicted ritonavir pharmacokinetic parameters in the final lopinavir model. The model was evaluated by means of a visual predictive check and external validation. A maximum-effect model in which ritonavir inhibited the elimination of lopinavir best described the relationship between ritonavir concentrations and lopinavir clearance (CL/F). A ritonavir concentration of 0.06 mg/liter was associated with a 50% maximum inhibition of the lopinavir CL/F. The population prediction of the lopinavir CL/F in the absence of ritonavir was 21.6 liters/h (relative standard error, 14.0%), and the apparent volume of distribution and absorption rate constant were 55.3 liters (relative standard error, 10.2%) and 0.57 h⁻¹ (relative standard error, 0.39%), respectively. Overall, 92% and 94% of the observed concentrations were encompassed by the 95% prediction intervals for lopinavir and ritonavir, respectively, which is indicative of an adequate model. Predictions of concentrations from an external data set (HIV infected) (n = 12) satisfied predictive performance criteria. Simulated lopinavir exposures at lopinavir-ritonavir doses of 200 mg-150 mg and 200 mg-50 mg twice daily were 38% and 65% lower, respectively, than that of the standard dose. The model allows a better understanding of the interaction between lopinavir and ritonavir and may allow a better prediction of lopinavir concentrations and assessments of different dosing strategies.

INTRODUCTION

Coformulated lopinavir-ritonavir (Kaletra; Abbott Laboratories, Chicago, IL) has demonstrated durable treatment efficacy in HIV-infected treatment-naïve and -experienced patients (12). It is approved for use at doses of 400 mg-100 mg twice daily and additionally at 800 mg-200 mg once daily for treatment-naïve patients in Europe and the United States (1, 2). Initially, lopinavir-ritonavir was available as soft-gel capsules, which required refrigerated storage and administration with food. However, a tablet formulation has been developed, with a diminished food effect, reduced variability compared to that of soft-gel capsules, and increased heat stability, therefore no longer needing refrigeration (9). Furthermore, data suggest a trend toward an increased bioavailability of the tablets (9).

Hill et al. recently performed a systematic review of 17 dose-ranging pharmacokinetic studies involving ritonavir-boosted protease inhibitors in order to assess the effects of ritonavir on different protease inhibitors and vice versa. Lopinavir concentrations were significantly increased in the presence of ritonavir and were correlated with the ritonavir dose (i.e., higher ritonavir doses produce higher lopinavir concentrations) (8). Moreover, ritonavir plasma concentrations were reduced in the presence of lopinavir; for example, ritonavir exposure was 50% lower with coadministration with lopinavir (400 mg-100 mg twice daily) than with coadministration with saquinavir (1,000 mg-100 mg twice daily) (14). Following a previously reported meta-analysis of 5 lopinavir-ritonavir pharmacokinetic studies, a dose of 200 mg-150 mg twice daily (1 lopinavir-ritonavir tablet plus 1 ritonavir tablet) was determined to exhibit exposures and minimum concentrations similar to those of the standard 400-mg–100-mg twice-daily dose based on geometric mean ratios (GMRs) and 95% confidence intervals (CIs) (8). As suggested previously by Hill and coworkers, it may be possible to reduce the lopinavir dose but compensate for this with a slightly higher ritonavir dose (200 mg and 150 mg twice daily, respectively), thus reducing medication costs (8). However, such a strategy may be suitable only for a select group of patients (e.g., treatment-naïve and virologically suppressed patients). Different dosing strategies could be explored by means of population pharmacokinetic modeling and simulation. This requires an understanding of the parameters that govern absorption, distribution, and drug elimination and also the variability of these parameters. Due to the dependence of lopinavir on ritonavir concentrations, a model that incorporates this relationship would be advantageous and may provide a better description of lopinavir pharmacokinetics and variability.

The aims of this analysis were first to develop and validate a population pharmacokinetic model that integrates the relationship between lopinavir and ritonavir over 72 h following drug cessation and second to assess other lopinavir-ritonavir doses compared to the standard 400-mg–100-mg twice-daily dose.

MATERIALS AND METHODS

Study participants, blood sampling, and drug analysis.

Data were taken from a previously reported study with healthy volunteers (4). All individuals were recruited and assessed at St. Stephen's Centre, Chelsea and Westminster Foundation Trust (London, United Kingdom). The study received approval from the Riverside Research Ethics Committee and the Medicines and Healthcare Products Regulatory Agency (London, United Kingdom). All volunteers provided written informed consent, and the study was conducted in accordance with the Declaration of Helsinki. Study details were discussed in detail previously (4). Healthy volunteers (n = 16; 6 female, 3 Hispanic, and 2 black individuals) were administered 400-mg–100-mg lopinavir-ritonavir tablets twice daily to steady state, and on the morning of pharmacokinetic sampling, drug intake was observed directly and timed. The evening dose was omitted, and blood was drawn predose (0 h) and at 0.5, 1, 2, 3, 4, 6, 8, 10, 12, 16, 20, 24, 30, 36, 48, 60, and 72 h postdose. Plasma lopinavir and ritonavir concentrations were quantified by a fully validated high-performance liquid chromatography-tandem mass spectrometry method (6), with lower limits of quantification (LLQs) of 0.005 and 0.002 mg/liter for lopinavir and ritonavir, respectively.

Data analysis.

Nonlinear mixed-effects modeling was applied by using NONMEM (version VI 2.0, level 1.1, double precision; ICON Development Solutions, Ellicott City, MD) (3) with first-order conditional estimation with interaction (FOCE-I). The model fit was assessed by statistical and graphical methods. The minimal objective function value (OFV) (equal to a −2-log likelihood) was used as a goodness-of-fit diagnostic, with a decrease of 3.84 points corresponding to a statistically significant difference between nested models (P = 0.05, χ² distribution, and 1 degree of freedom). Graphical diagnostics were performed with Microsoft Office Excel 2007 for Windows (Microsoft Corporation, Redmond, WA). Standard errors of the parameter estimates were determined with the COVARIANCE option of NONMEM, and individual Bayesian parameter and concentration estimates were determined with the POSTHOC option. The model-building process was in 3 stages: (i) a separate model was developed for lopinavir, (ii) a separate model was developed for ritonavir, and, finally, (iii) a combined model was developed, incorporating the influence of ritonavir concentrations on lopinavir clearance.

Lopinavir and ritonavir structural model.

To determine the best structural model, one- and two-compartment models with first- or zero-order absorption without and with lag time were considered. Proportional, additive, and combined proportional-additive error models were evaluated to describe the residual variability.

Interindividual variability (IIV) was described by an exponential model, an example of which is shown below for the apparent oral clearance (CL/F):

$$\text{CL}/F_i={\theta }_1\times \exp \left({\eta }_i\right)$$ (1)

where CL/F_i is the lopinavir CL/F of the ith individual, θ₁ is the population parameter estimate, and η_i is the IIV assumed to have a mean of zero and a variance of ω².

The first concentration within the sampling window that fell below the LLQ of the assay was included as the LLQ/2 (i.e., 0.0025 mg/liter and 0.0010 mg/liter for lopinavir and ritonavir, respectively). All other samples below the LLQ were discarded.

Lopinavir and ritonavir covariate analysis.

Once a baseline model was established, the following covariates were explored: the ritonavir (for the lopinavir model) or lopinavir (for the ritonavir model) area under the curve to the first sample below the LLQ (AUC), sex, ethnicity, body weight, body mass index (BMI), and age. For continuous variables (e.g., body weight), plots of covariates versus individual predicted pharmacokinetic parameters were performed to determine possible relationships. Continuous variables were introduced into the model by linear functions. For dichotomous variables, here defined as X (such as male/female sex), the following equation was applied, using CL/F as an example:

$$\text{TVCL}={\theta }_1\times {\theta }_2^x$$ (2)

where TVCL is the typical value of the lopinavir CL/F in the population for a male (denoted by X = 0, and thus equal to θ₁) and θ₂ is the relative difference in the CL/F for a female (X = 1).

Each covariate was introduced separately and retained only if inclusion in the model produced a statistically significant decrease in the OFV of at least 3.84 points (P ≤ 0.05), was biologically plausible, and reduced variability (by at least 10%). A backwards elimination step was carried out once all relevant covariates were incorporated, and covariates were retained if their removal from the model produced a significant increase in the OFV (>6.63 points) (P ≤ 0.01, χ² distribution, and 1 degree of freedom). Lopinavir and ritonavir AUCs were determined from the concentration-time data using noncompartmental methods (WinNonlin 5.2; Pharsight Corporation, Mountain View, CA).

Combined lopinavir-ritonavir pharmacokinetic model.

Once the separate models incorporating all significant covariates for lopinavir and ritonavir were determined, a number of models were evaluated to incorporate the influence of ritonavir concentrations at each time point on lopinavir clearance (rather than using the ritonavir AUC). Ritonavir concentrations were calculated from the individual posterior parameter estimates obtained from the final fit of the ritonavir model. Lopinavir and ritonavir were expressed as a set of differential equations using the $DES function and ADVAN9 in NONMEM. The models explored to describe the inhibition of lopinavir clearance by ritonavir are outlined below.

Competitive inhibition models.

Assuming competitive inhibition of lopinavir clearance by ritonavir, the following equation was used:

$$\text{CL}/F_{\text{LPV}}=\text{CL}0/F_{\text{LPV}}/\left(1+C_{\text{RTV}}/K_i\right)$$ (3)

where CL/F_LPV is the lopinavir clearance, CL0/F_LPV is the lopinavir clearance in the absence of ritonavir, C_RTV is the concentration of ritonavir, and K_i is the ritonavir inhibition constant (initial estimate of 0.0288 mg/liter, converted from 0.04 μmol/liter [7]).

Assuming competitive inhibition of lopinavir clearance by ritonavir and an estimation of the first-pass effect, the following equations were used:

$${\text{CL}}_{\text{INT}}=\text{CL}0/F_{\text{LPV}}/\left(1+C_{\text{RTV}}/K_i\right)$$ (4)

$$\text{CL}/F_{\text{LPV}}={\text{CL}}_{I\text{NT}}\times QR/\left(QR+{\text{CL}}_{\text{INT}}\right)$$ (5)

where CL_INT is the lopinavir intrinsic clearance and QR is the median liver blood flow (90 liters/h) multiplied by the blood-to-plasma ratio of lopinavir (0.44 [10]).

Direct-response models.

Assuming a direct relationship between ritonavir concentrations and lopinavir clearance, the following equation was used:

$$\text{CL}/F_{\text{LPV}}=\text{CL}0/F_{\text{LPV}}\times I\left(t\right)$$ (6)

where CL/F_LPV is the lopinavir clearance, CL0/F_LPV is the lopinavir clearance in the absence of ritonavir, and I is the inhibition of lopinavir by ritonavir, which can be modeled as a linear (equation 7) or a maximum-effect (equation 8) function, as outlined below:

$$I=1-\left(\text{SLOPE}\times C_{\text{RTV}}\right)$$ (7)

$$I=1-\left[\left(I_{\text{MAX}}\times C_{\text{RTV}}\right)/\left({\text{IC}}_{50}+C_{\text{RTV}}\right)\right]$$ (8)

where SLOPE is the parameter associated with the negative relationship between C_RTV and CL0/F_LPV, I_MAX is the maximum inhibitory effect of ritonavir on CL/F_LPV, and IC₅₀ is the C_RTV producing 50% of the I_MAX.

Indirect-response models.

Indirect-effect models, unlike direct-effect models, have a delay in equilibrium between the plasma concentration and effect or outcome, and this outcome is governed by various inhibitory and/or stimulatory factors. In this case, we assume a delay in equilibrium between C_RTV and the inhibition of CL/F_LPV governed by the stimulation of a loss of enzyme. The rate of change of the enzyme responsible for lopinavir metabolism (ENZ) is outlined below:

$$d\text{ENZ}/dt=k_{\text{IN}}-k_{\text{OUT}}\times S\left(t\right)$$ (9)

where k_IN represents the enzyme turnover rate, k_OUT represents the fractional turnover, and S(t) represents the stimulation of enzyme degradation, which can be modeled as a linear or maximum-effect function, as shown above for the direct-response models (equations 7 and 8).

Model validation.

To perform a visual predictive check, 1,000 patients were simulated by using the fixed and random effects defined by the final models with the SIMULATION SUBPROBLEMS option of NONMEM. From the simulated data, 95% prediction intervals (P2.5 to P97.5) for lopinavir and ritonavir were constructed, and observed data from the original data set were superimposed for comparison.

Concentration-time data from a cohort of HIV-infected patients (n = 12; 4 female and 2 black patients) not included in the model building process were used to further validate the model. Drug concentrations were obtained predose (0 h) and at 1, 2, 4, 6, 9, and 12 h postdose following the administration of lopinavir-ritonavir tablets (400 mg-100 mg twice daily; 1 profile per patient; 84 concentrations) as part of a standardized routine therapeutic drug monitoring protocol used for all outpatients, approved by the Ethics Committee of the Goethe University Hospital Frankfurt am Main (Frankfurt, Germany). Lopinavir and ritonavir final model estimates were used to provide individual predictions of the concentration-time data and were then compared to the measured data by calculating the mean relative prediction error (%MPE) as a measure of bias and the root mean squared relative prediction error (%RMSE) as a measure of precision. An adequate predictive performance is defined as a %RMSE of <15% and an %MPE not significantly different from zero (13). A comparison between the measured AUC_0–12, the maximum concentration (C_max), and the trough concentration (C_trough) (defined as the concentration at 12 h postdose) and those calculated from predicted concentrations was also performed for lopinavir.

Simulation of different lopinavir-ritonavir doses.

Ten simulations of the original data set (containing data from 16 individuals) were performed by using the fixed and random effects of the final models at lopinavir-ritonavir doses of 200 mg-50 mg, 200 mg-150 mg, 400 mg-200 mg, and 400 mg-100 mg, all twice daily. The lopinavir AUC_0–12 was calculated (WinNonlin v. 5.2) and compared to the lopinavir AUC_0–12 at the standard dose of 400 mg-100 mg twice daily via means of GMRs and 95% CIs (AUC_0–12 values were considered significantly different if the CI did not contain 1).

RESULTS

Patients.

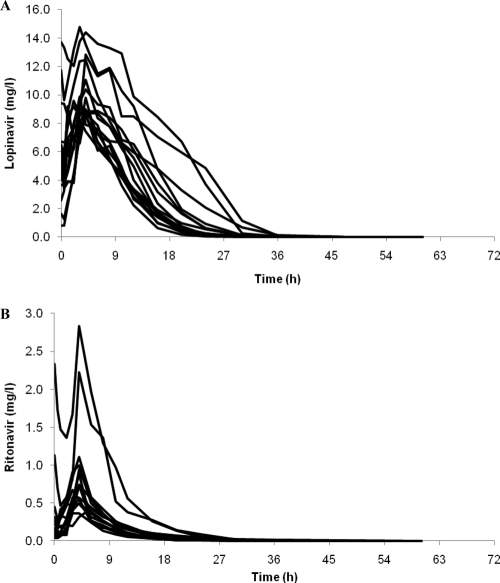
The median age, body weight, BMI, lopinavir AUC, and ritonavir AUC were 42 years (range, 25 to 55 years), 85 kg (53 to 115 kg), 24 kg/m² (20 to 32 kg/m²), 107.14 mg · h/liter (77.92 to 257.18 mg · h/liter), and 4.57 mg · h/liter (2.53 to 21.93 mg · h/liter), respectively. Concentrations of lopinavir and ritonavir included in the model ranged between 0.0025 and 14.76 mg/liter and between 0.0010 and 2.84 mg/liter, respectively (minimum values set as LLQ/2) (Fig. 1). In total, 36/288 matched lopinavir and ritonavir samples below the LLQ were discarded at a combination of time points, including 36, 48, 60, and 72 h postdose.

Fig. 1.

Concentration-time curves of lopinavir (A) and ritonavir (B) over 72 h following cessation of treatment with lopinavir-ritonavir (400-mg–100-mg twice-daily) tablets (n = 16).

Lopinavir pharmacokinetic and covariate models.

A one-compartment model with first-order absorption and a combined proportional-additive error model best described the data (ADVAN2 TRANS2). A one-compartment model with zero-order absorption or a two-compartment model did not improve the fit. The IIV was included for the apparent oral clearance (CL/F), apparent volume of distribution (V/F), and absorption rate constant (k_a). The incorporation of an absorption lag time also improved the fit.

Of the covariates explored, only the ritonavir AUC was significantly associated with the lopinavir CL/F. Based on graphical plots, the linear, power, and exponential relationships between the lopinavir CL/F and ritonavir AUC were assessed. A power relationship provided the best description of the data. The association between the ritonavir AUC and the lopinavir CL/F was described as follows:

$$\text{CL}/F_i={\theta }_1\times {\left({\text{RTV}}_i/4.57\right)}^{{\theta }_2}$$ (10)

where CL/F_i is the lopinavir CL/F of the ith individual; θ₁ is the population parameter estimate; RTV_i is the ritonavir AUC of the ith individual; 4.57 is the median ritonavir AUC of all individuals, expressed as mg · h/liter; and θ₂ is the factor associated with the effect of the ritonavir AUC on the lopinavir CL/F.

Parameter estimates for the basic and covariate lopinavir models are summarized in Table 1.

Table 1.

Parameter estimates and standard errors obtained for lopinavir from the basic and covariate models^b

Parameter	Value for modela
	Basic		Covariate
	Estimate	RSE (%)	Estimate	RSE (%)
CL/F (liters/h)	4.1	8.0	4.5	5.3
V/F (liters)	14.9	9.5	15.9	8.7
ka (h−1)	0.26	6.9	0.26	6.4
Lag time (h)	1.7	2.5	0.7	7.9
IIV CL/F (%)	23.1	35.4	9.2	37.2
IIV V/F (%)	28.2	49.1	23.1	54.2
IIV ka (%)	29.2	42.3	26.8	43.7
Residual error
Proportional (%)	42.9	14.4	40.0	11.8
Additive (mg/liter)	0.002	23.3	0.002	51.6
Factor associated with effect of RTV AUC on CL/Fc			−0.398	11.8

^aRSE = (SE_estimate/estimate) × 100.

^bCL/F, apparent oral clearance; V/F, apparent volume of distribution; k_a, absorption rate constant; RSE, relative standard error; IIV, interindividual variability; SE, standard error; RTV, ritonavir; AUC, area under the concentration-time curve.

^cCovariate not included in the basic model.

Ritonavir pharmacokinetic and covariate model.

Similarly to lopinavir, ritonavir data were best described by a one-compartment model with first-order absorption and a combined proportional-additive error model. The IIV of CL/F, V/F, and k_a values improved the fit, as did the addition of the absorption lag time. To provide a better characterization of absorption, sequential first- and zero-order absorptions were assessed and found to significantly improve the model by the addition of parameter D1 (duration of the zero-order process, in this case a zero-order absorption).

The inclusion of the lopinavir AUC on the CL/F was the only significant covariate and was best described by a linear model:

$$\text{CL}/F_i={\theta }_1+{\theta }_2\times \left({\text{LPV}}_i-107.14\right)$$ (11)

where CL/F_i is the ritonavir CL/F of the ith individual; θ₁ is the population parameter estimate; LPV_i is the lopinavir AUC of the ith individual; 107.14 is the median lopinavir AUC of all individuals, expressed as mg · h/liter; and θ₂ is the factor associated with the effect of the lopinavir AUC on the ritonavir CL/F.

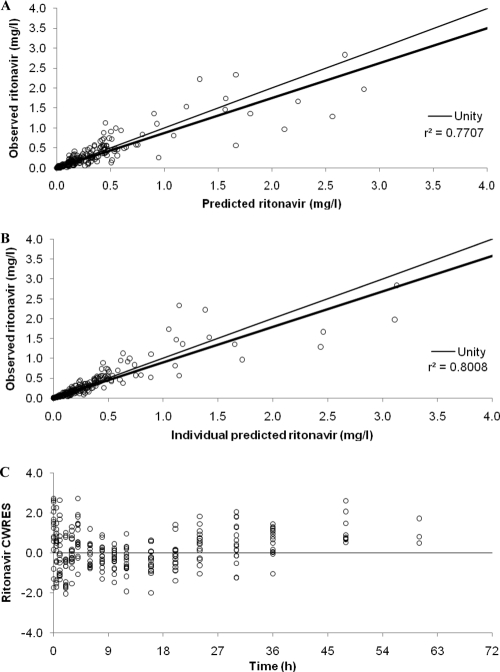
Parameter estimates for the basic and final ritonavir models are summarized in Table 2, and goodness-of-fit diagnostic plots for the final model are shown in Fig. 2.

Table 2.

Parameter estimates and standard errors obtained for ritonavir from the basic and final population pharmacokinetic models^b

Parameter	Value for modela
	Basic		Final
	Estimate	RSE (%)	Estimate	RSE (%)
CL/F (liters/h)	23.3	15.2	29.3	5.5
V/F (liters)	13.3	17.4	13.7	17.4
ka (h−1)	0.184	6.1	0.184	6.2
Lag time (h)	0.298	49.0	0.273	51.3
D1 (h)	2.97	6.2	2.94	6.3
IIV CL/F (%)	61.2	52.0	17.3	47.5
IIV V/F (%)	109	47.5	106	44.1
IIV ka (%)	25.5	45.5	25.1	47.6
Residual error
Proportional (%)	33.9	15.5	33.8	15.4
Additive (mg/liter)	0.001	37.4	0.001	37.1
Factor associated with effect of LPV AUC on CL/Fc			−0.171	6.3

^aRSE = (SE_estimate/estimate) × 100.

^bCL/F, apparent oral clearance; V/F, apparent volume of distribution; k_a, absorption rate constant; D1, duration of zero-order input; RSE, relative standard error; IIV, interindividual variability; SE, standard error; LPV, lopinavir; AUC, area under the concentration-time curve.

^cCovariate not included in the basic model.

Fig. 2.

Goodness-of-fit plots for the final ritonavir pharmacokinetic model illustrating population predictions of ritonavir versus observed concentrations (A), individual predictions of ritonavir versus observed concentrations (B), and conditional weighted residuals (CWRES) versus time postdose (C). The fine line is the line of unity, and the bold line is the line of regression.

Sequential combined lopinavir-ritonavir model.

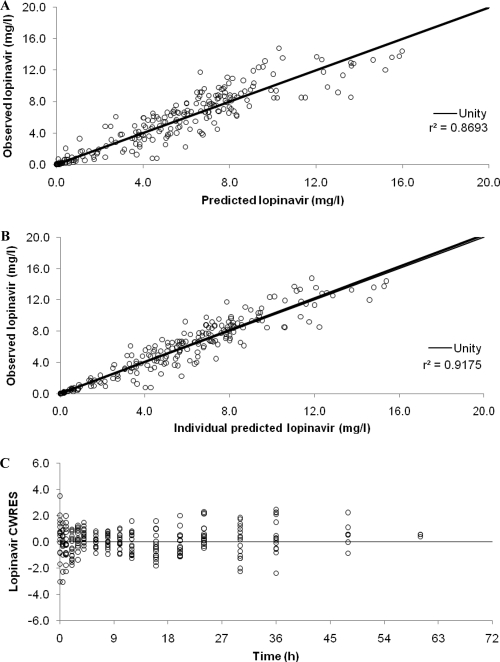
The competitive inhibition model, with the IIV used on the V/F, produced a significantly better fit to the data than did the lopinavir model incorporating the ritonavir AUC as a covariate (ΔOFV, −191.9); however, the parameters were highly correlated. The addition of IIV to the k_a and an absorption lag time further improved the fit (ΔOFV of −214.6 compared to the covariate model) but failed to fully converge and did not output standard error estimates, potentially due to the level of correlation between parameters. A manipulation of the initial starting estimates did, however, produce full convergence (ΔOFV of −205.8 compared to the covariate model). Competitive inhibition with first-pass effects produced a similar drop in the OFV but would not run unless an absorption lag time was added. The addition of the IIV to the V/F was significant, but again, parameter estimates were highly correlated (typically between CL0/F_LPV, K_i, and V/F); furthermore, the inclusion of IIV for k_a was significant but failed to produce standard errors. The direct-response model with a linear function did not greatly improve the fit of the data compared to the other models described above (ΔOFV of −14.7 compared to the covariate model), and the inclusion of additional parameters was problematic. The direct-response model with a maximum-effect function produced the best description of the data, had the lowest IIV and OFV values (ΔOFV of −224.4 compared to the covariate model), and had good diagnostic and individual plots. The addition of IIV to k_a failed to produce standard error estimates and was therefore not included. Final estimates for fixed and random effects for lopinavir are summarized in Table 3, and diagnostic plots are shown in Fig. 3. Indirect-response models would not converge.

Table 3.

Lopinavir parameter estimates and standard errors obtained from the final population pharmacokinetic model using a direct-response model with a maximum-effect function^a

Parameter	Estimate	RSE (%)	IIV (%)	RSE of IIV (%)
CL0/F (liters/h)	21.6	14.0	10.7	36.4
IMAX	0.929	0.95
IC50 (mg/liter)	0.057	21.8
V/F (liters)	55.3	10.2	18.5	41.9
ka (h−1)	0.572	0.39
Lag time (h)	0.371	3.5
Residual error
Proportional (%)	25.6	18.3
Additive (mg/liter)	0.004	33.7

^aRSE = (SE_estimate/estimate) × 100. CL0/F, apparent oral clearance of lopinavir in the absence of ritonavir; I_MAX, maximum inhibitory effect of ritonavir on the lopinavir CL/F; IC₅₀, ritonavir concentration associated with half the maximal inhibition of the lopinavir CL/F; V/F, apparent volume of distribution; k_a, absorption rate constant; RSE, relative standard error; IIV, interindividual variability; SE, standard error.

Fig. 3.

Goodness-of-fit plots for the final lopinavir pharmacokinetic model illustrating population predictions of lopinavir versus observed concentrations (A), individual predictions of lopinavir versus observed concentrations (B), and conditional weighted residuals (CWRES) versus time postdose (C). The fine line is the line of unity, and the bold line is the line of regression.

Model validation.

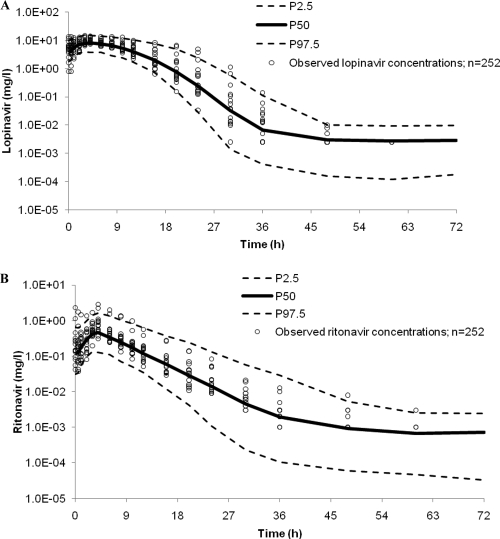
A 95% prediction interval over 72 h was generated for ritonavir from 1,000 simulated pharmacokinetic profiles using the fixed and random effects of the final ritonavir model (Fig. 4). Of the 252 observed ritonavir concentrations, 94% were within the prediction interval. A total of 16/252 concentration-time points were above P97.5, accounting for all but one of the points outside the prediction interval, most of which were around the C_max and could be attributed mainly to two individuals in particular, whose concentrations peaked much higher than those of the rest of the population (Fig. 4). When removed from the model, final parameter estimates were not influenced, and therefore, these individuals were retained. Overall, the final ritonavir model provided an adequate fit to the data.

Fig. 4.

Ninety-five-percent prediction intervals (P2.5 to P97.5) for lopinavir (A) and ritonavir (B) (400 and 100 mg twice daily, respectively) determined from 1,000 simulations. Observed data were superimposed (n = 252).

The generation of a 95% prediction interval for lopinavir was a 2-step process. First, the 1,000 simulated ritonavir concentration-time profiles were used to estimate population-predicted ritonavir pharmacokinetic parameters. The ritonavir pharmacokinetic parameters were then fed into the lopinavir model, and a simulation of 1,000 lopinavir concentration-time profiles was performed by using the fixed and random effects of the final lopinavir model ($SIMULATION). Individual predictions of ritonavir pharmacokinetic parameters could not be used, as the initial analysis was performed with a sequential rather than a simultaneous approach and so did not include the correlation between lopinavir and ritonavir CL/F values. Of the observed lopinavir concentrations, 3% lay below P2.5 and 5% were above P97.5, suggesting a good description of the data (Fig. 4).

External validation.

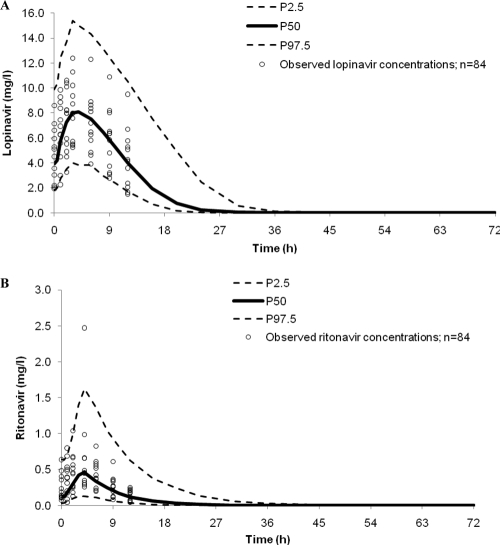
The median age, body weight, and BMI of the validation data set (n = 12) were 40 years (range, 30 to 56 years), 74 kg (34 to 89 kg), and 21 kg/m² (15 to 30 kg/m²), respectively. Baseline CD4 cell counts and viral loads ranged between 18 and 364 cells/mm³ and 399 to 523,000 copies/ml, respectively. There were no statistically significant differences in lopinavir or ritonavir AUC_0–12, C_max, or C_trough values between the validation cohort and the healthy volunteers used for the model (P ≥ 0.180 for all comparisons by Mann-Whitney U test), with the exception of the lopinavir C_max, which was lower for HIV patients (P = 0.042 by Mann-Whitney U test). The predictive performance of the ritonavir model was acceptable, providing precise (%RMSE, 14.2%) and unbiased (%MPE, −2.8% [95% CI, −12.8, 10.1]) predictions. The lopinavir model also produced precise (%RMSE, 10.0%) and unbiased (%MPE, −0.4% [95% CI, −2.6, 1.8]) predictions of lopinavir concentrations. The lopinavir AUC_0–12, C_max, and C_trough were determined by using the predicted concentrations (WinNonlin v. 5.2), and upon comparison with the observed values, the model provided both precise and unbiased predictions (%RMSE of 0.4% and %MPE of 5.5% [95% CI, −3.3, 4.0] for AUC_0–12, %RMSE of −2.3% and %MPE of 6.9% [95% CI, −6.6, 2.0] for C_max, and %RMSE of 0.4% and %MPE of 10.3% [95% CI, −6.4, 7.3] for C_trough). The measured lopinavir and ritonavir concentrations (n = 84) from the external validation data set were superimposed on the 95% prediction intervals; 3/84 (4%) lopinavir concentrations were below P2.5, and none were above P97.5. Of the ritonavir concentrations, 1% and 4% were below P2.5 and above P97.5, respectively (Fig. 5).

Fig. 5.

Ninety-five-percent prediction intervals (P2.5 to P97.5) for lopinavir (A) and ritonavir (B) (400 and 100 mg twice daily, respectively) determined from 1,000 simulations, with observed data from HIV-infected patients superimposed (n = 84).

Simulation of different lopinavir-ritonavir doses.

The calculated lopinavir AUC_0–12 values from simulated concentrations of lopinavir-ritonavir at 400 mg-200 mg twice daily were significantly higher than those from the simulated 400-mg–100-mg twice-daily dose (GMR, 1.418; 95% CI, 1.415 to 1.420) and were significantly lower following a dose of 200 mg-50 mg twice daily (GMR, 0.349; 95% CI, 0.349 to 0.350). Furthermore, lopinavir-ritonavir at 200 mg-150 mg twice daily produced 38% lower lopinavir AUC_0–12 values than did lopinavir-ritonavir at 400 mg-100 mg twice daily (GMR, 0.616; 95% CI, 0.616 to 0.617). A similar scenario was observed for lopinavir C_max and C_trough values (Table 4).

Table 4.

Lopinavir pharmacokinetic parameters derived from simulations of different lopinavir-ritonavir doses compared with the standard dose^a

Parameter	GMR (95% CI) for regimen:
	B/A	C/A	D/A
AUC0–12	0.349 (0.349–0.350)	0.616 (0.616–0.617)	1.418 (1.415–1.420)
Cmax	0.375 (0.373–0.378)	0.597 (0.595–0.598)	1.352 (1.344–1.355)
Ctrough	0.270 (0.266–0.272)	0.688 (0.685–0.692)	1.685 (1.671–1.700)

^aLopinavir pharmacokinetic parameters were derived from simulations of different lopinavir-ritonavir doses (200 mg-50 mg, 200 mg-150 mg, and 400 mg-200 mg twice daily) in comparison with the standard dose of 400 mg-100 mg twice daily. Regimen A, 400 mg-100 mg; regimen B, 200 mg-50 mg; regimen C, 200 mg-150 mg; regimen D, 400 mg-200 mg. AUC_0–12, area under the concentration-time curve at 0 to 12 h postdose; C_max, maximum concentration; C_trough, trough concentration, i.e., concentration at 12 h postdose; GMR, geometric mean ratio; CI, confidence interval.

DISCUSSION

A model has been developed and validated to describe ritonavir-boosted lopinavir pharmacokinetics in healthy individuals over 72 h following drug cessation and incorporated the influence of ritonavir concentrations at each time point on the lopinavir CL/F. A direct-effect model best described the relationship between ritonavir and the inhibition of the lopinavir CL/F. A ritonavir concentration of 0.06 mg/liter was associated with a 50% reduction in the lopinavir clearance. Simulations of lopinavir-ritonavir doses at 200 mg-50 mg and 200 mg-150 mg twice daily generated significantly lower lopinavir exposures compared to simulated doses of 400 mg-100 mg twice daily and 400 mg-200 mg twice daily.

Molto and colleagues also used a direct-response model with a maximum-effect function to describe the relationship between lopinavir and ritonavir (11). Our analysis overall produced similar results, but a few differences should be noted. The V/F values for both drugs were lower in the present analysis (55.3 liters versus 91.6 liters for lopinavir and 13.7 liters versus 54.7 liters for ritonavir), as was the IC₅₀ (0.057 mg/liter versus 0.36 mg/liter). However, the variability of the ritonavir V/F was considerable for both analyses (106% versus 81%). Furthermore, in the present study lopinavir and ritonavir both required a lag time for the best description of the concentrations, and ritonavir also needed a double-absorption model to account for its absorption. Potentially, these differences could be attributed to the present study utilizing the tablet formulation, whereas Molto et al. used data for soft-gel capsules (11). Also, our study was conducted with healthy volunteers and not patients, although no substantial differences in lopinavir pharmacokinetics between healthy volunteers and HIV patients have been observed (1, 2). Furthermore, sampling times were different between the two analyses. It is worth noting that for the present analysis the estimate of the lopinavir V/F changed substantially in the final model compared to the basic lopinavir model. Potentially, this could be explained by flip-flop kinetics; however, this is not the case here, as the lopinavir elimination and absorption rate constants are similar for the basic model. The differences in V/F values can be explained by the elimination rate constant continuously changing as the degree of inhibition changes, as a result of the changing ritonavir concentration, even in the presence of the ritonavir AUC as a covariate. This gives rise to an erroneous estimate of the V/F, and only after correctly accounting for the changing inhibition is the V/F better estimated.

To further assess the validity of the model with respect to HIV-infected patients, an external validation was performed. Overall, the predictive performances of the lopinavir and ritonavir models were good, with concentrations and pharmacokinetic parameters being predicted reasonably well within the predefined predictive performance limits. Additionally, the lopinavir C_max was significantly lower for the HIV patients (validation set) than for the healthy volunteers (model-building set); however, the prediction of the lopinavir AUC_0–12, C_max, and C_trough satisfied the predictive performance criteria. We acknowledge that the sample size of the validation data set was low (n = 12), but compared to the number of patients included in the model (n = 16), this is considered adequate.

There is an interaction between the model fits for ritonavir and lopinavir. In the case of lopinavir the effect of ritonavir is handled in a sequential manner for simplicity. The effect of lopinavir on ritonavir could potentially feed back to affect both models. However, the lopinavir AUC used in the ritonavir model was obtained by the trapezoidal rule and not from the lopinavir fit; this should minimize any feedback. It is important to note that the present model assumes only the inhibition of the lopinavir CL/F by ritonavir and does not take into consideration any direct influence that lopinavir may have on ritonavir concentrations. Although ritonavir is given in combination with protease inhibitors in order to boost concentrations, it is important to note that protease inhibitors themselves can impact ritonavir pharmacokinetics, as it is not only an inhibitor of CYP3A4 but also a substrate. For example, increases in ritonavir plasma concentrations in the presence of atazanavir by approximately 70% compared to those with ritonavir alone (15) and between 39% and 69% also in combination with saquinavir (5) have been observed. Furthermore, exposure and maximum concentrations were reduced by 14% and 17%, respectively, when given with darunavir (800 mg-100 mg once daily) (15) and between 70% and 90% in the presence of different tipranavir doses (2a). One study previously documented approximately 50% lower ritonavir concentrations with lopinavir (14), and another study observed significantly lower ritonavir concentrations in the presence of lopinavir (400 mg-100 mg twice daily) than in the presence of atazanavir (300 mg-100 mg once daily). In addition, the ritonavir AUC_0-24 and C_max were only 26% and 43% higher, respectively, when given once daily with lopinavir than with atazanavir despite doubling the daily dose (lopinavir-ritonavir at 800 mg-200 mg once daily versus atazanavir-ritonavir at 300 mg-100 mg once daily) (4). Potentially, lopinavir is inducing ritonavir clearance. Although this was not taken into consideration, the model for ritonavir still provided a reasonable fit to the data, and the lopinavir AUC was included as a covariate. The complicated two-way interaction between lopinavir and ritonavir would require a much more complex model than that described here, which would possibly need to incorporate further information obtained from in vitro studies. The main focus of this analysis was not to model the influence of lopinavir on ritonavir pharmacokinetics but to describe the dramatic changes in lopinavir concentrations and the CL/F throughout the 72 h following drug cessation and the dependence of these changes on ritonavir concentrations; this has been successfully accomplished. Furthermore, this model does not include any influence that ritonavir may have on the lopinavir CL/F as a result of an inhibition of P-glycoprotein-mediated efflux transport or any other transporters. Despite this, the model provides a good description of the data and is underscored by the validation process.

A previously reported meta-analysis of 5 lopinavir-ritonavir pharmacokinetic studies showed that a dose of lopinavir-ritonavir of 200 mg-150 mg twice daily generated exposures similar to those of the standard 400-mg–100-mg twice-daily dose based on the GMR (95% CI). (8) That analysis utilized a bootstrap analysis to simulate ratios of AUCs between the two doses rather than concentrations (8). In the present analysis, the model was used to simulate concentration-time profiles of lopinavir-ritonavir at 200 mg-150 mg twice daily, from which lopinavir AUC_0–12 values were calculated and compared to the simulated lopinavir AUC_0–12 at the standard dose (400 mg-100 mg twice daily). The lopinavir AUC_0–12 values were 38% lower than those obtained following dosing at 400 mg-100 mg twice daily, and this reached significance (confidence intervals did not cross 1). However, the ratio calculated previously by Hill et al. showed approximately 15% lower lopinavir AUCs for a dose of 200 mg-150 mg than for a dose of 400 mg-100 mg twice daily and did not reach significance. Conversely, the differences in GMRs between our model and that of Hill et al. for doses of 200 mg-50 mg and 400 mg-200 mg were not as great, although they were potentially overestimated by the model for lower doses and underestimated for higher doses (0.35 versus 0.54 and 1.42 versus 1.59, respectively). The differences observed in GMRs between the two investigations may be inherent to the types of analyses performed. It would not be advisable to use modeling and simulation uncritically as a surrogate for clinical studies, but it may help inform future studies and provide an insight into whether this form of dose optimization is possible. Lopinavir-ritonavir at 200 mg-150 mg twice daily may be suitable for some patients (e.g., treatment-naïve individuals); however, it is important to stress that both analyses take into account only pharmacokinetic data, and the effect of the alternate lopinavir-ritonavir dose on viral suppression would require investigation. Furthermore, whether an increase in the ritonavir dose from 200 mg daily to 300 mg daily would be an attractive option to patients, given its toxicity profile, also remains to be seen.

In conclusion, lopinavir and ritonavir pharmacokinetics have been modeled sequentially, and a maximum-effect model best described the relationship between ritonavir concentrations and the inhibition of the lopinavir CL/F. Although the analysis was performed with healthy volunteers, the validation process showed that it is also applicable to HIV-infected patients. The model helps give a better understanding of the interaction between lopinavir and ritonavir, may allow a better prediction of lopinavir concentrations, and may aid in the design of dose optimization studies.