Bias in Hotelling Observer Performance Computed from Finite Data

Abstract

An observer performing a detection task analyzes an image and produces a single number, a test statistic, for that image. This test statistic represents the observers “confidence” that a signal (e.g., a tumor) is present. The linear observer that maximizes the test-statistic SNR is known as the Hotelling observer. Generally, computation of the Hotelling SNR, or Hotelling trace, requires the inverse of a large covariance matrix. Recent developments have resulted in methods for the estimation and inversion of these large covariance matrices with relatively small numbers of images. The estimation and inversion of these matrices is made possible by a covariance-matrix decomposition that splits the full covariance matrix into an average detector-noise component and a background-variability component. Because the average detector-noise component is often diagonal and/or easily estimated, a full-rank, invertible covariance matrix can be produced with few images. We have studied the bias of estimates of the Hotelling trace using this decomposition for high-detector-noise and low-detector-noise situations. In extremely low-noise situations, this covariance decomposition may result in a significant bias. We will present a theoretical evaluation of the Hotelling-trace bias, as well as extensive simulation studies.

1. INTRODUCTION

To objectively measure the quality of images produced by a medical imaging system, one must take into account the task (or tasks) to be performed using the images, the observer performing the task (or tasks), the statistics of the ensemble of object being imaged, and the properties of the imaging system itself. A common task in medical imaging is the detection of an abnormality such as a tumor. Receiver operating characteristic (ROC) analysis is often used to assess the performance of observers detecting signals. The best possible ROC curve is obtained when the observer uses the likelihood ratio to make decision – the so-called Bayesian ideal observer. This observer provides an upper bound on the area under the ROC curve (AUC) for all other observers performing the signal-detection task. As such, the AUC of the Bayesian ideal observer could be used as a figure of merit for the performance of the imaging system on the given detection task. However, computation of the likelihood ratio requires full knowledge of the probability density functions of the image data and can be computationally expensive. An alternative figure of merit is the performance of the Hotelling observer as measured by the signal-to-noise ratio (SNR). The performance of the Hotelling observer is optimal among all linear observers in terms of SNR. Since linear test statistics tend to have Gaussian distributions, the relationship between the SNR and the AUC of the Hotelling observer is monotonic. To the extent that these Gaussian assumptions are valid, the Hotelling observer also maximizes the AUC among linear observers.

The Hotelling observer requires only knowledge of the first- and second-order statistics of the image data, i.e., the mean data vector and the covariance matrix for the data under both the signal-present and signal-absent hypotheses. In simulation studies, the mean and covariance of the image data are often known exactly and the only computational difficulty is in inverting the usually large covariance matrix. For more complicated simulated systems or real-world systems, the mean and covariance of the image data must be estimated from samples. In addition to the problem of inverting a large matrix, we must now acquire a good estimate of the covariance matrix. There are methods for estimating and inverting the covariance matrix based on a decomposition of the covariance into a system noise component and a background-variability component. There are also data-reduction methods for easing the computational burden based on channelized Hotelling observers. In this paper we will present some theoretical and simulation-study results on the bias that can be expected from these methods as a function of the contribution to the covariance matrix from the system noise.

2. THE HOTELLING OBSERVER

We represent the imaging process by the equation,

$$\mathit{g}=\mathscr{H}f(\mathit{r})+\mathit{n},$$ (1)

where g is the image data, f(r) is the object being imaged as a function of position r, n is the detector noise, and ℋ represents the continuous-to-discrete imaging system. Bold-faced symbols denote vectors. In this paper, we consider random detector noise n and random objects being imaged f(r). We do not consider random imaging system ℋ. Under the signal-present hypothesis (H₁), the data vector g has a mean value of g̅₁ and covariance matrix K₁. Similarly, under the signal-absent hypothesis (H₀), the mean data vector is given by g̅₀ and the covariance matrix is denoted by K₀. The mean signal in the data is the vector Δg̅ = g̅₁ − g̅₀. The average covariance matrix is given by $K=\frac{1}{2}{K}_1+\frac{1}{2}{K}_0$. With this notation, the SNR of the Hotelling observer is given by,

$${\text{SNR}}^2=\mathrm{\Delta }{\overline{\mathit{g}}}^{†}{K}^{-1}\mathrm{\Delta }\overline{\mathit{g}}.$$ (2)

This SNR is the figure of merit we wish to estimate.

Under the weak-signal hypothesis (i.e., small Δg̅) K₀ and K₁ are equal and therefore equal to K. The covariance matrix K can be decomposed into two terms,

$$K={\overline{K}}_{\mathit{n}}+K_{\overline{\mathit{g}}}.$$ (3)

The matrix K̅_n is computed by first determining the covariance of the vector n for a fixed object f(r) and then averaging over objects. The term K_g̅ is the covariance of the noise-free image data ℋf(r) and is due only to the randomness in the object f(r). The weak-signal hypothesis is not necessary for this decomposition although it does simplify the exposition.

2.1. An eigenanalysis

Consider a decomposition as in Eqn. 3 where we insert a parameter ε to control the relative importance of the average noise covariance K̅_n term, i.e.,

$$K=\epsilon {\overline{K}}_{\mathit{n}}+K_{\overline{\mathit{g}}}.$$ (4)

The expressions for the SNR given in Eqn. 2 may be modified to isolate the dependence on ε

$${\text{SNR}}^2={\left[{\overline{K}}_{\mathit{n}}^{-1/2}\mathrm{\Delta }\overline{\mathit{g}}\right]}^{†}{[\epsilon I+{\overline{K}}_{\mathit{n}}^{-1/2}{K}_{\overline{\mathit{g}}}{\overline{K}}_{\mathit{n}}^{-1/2}]}^{-1}\left[{\overline{K}}_{\mathit{n}}^{-1/2}\mathrm{\Delta }\overline{\mathit{g}}\right].$$ (5)

We define eigenvectors and eigenvalues by,

$$\left[{\overline{K}}_{\mathit{n}}^{-1/2}{K}_{\overline{\mathit{g}}}{\overline{K}}_{\mathit{n}}^{-1/2}\right]{\mathit{u}}_m={\lambda }_m{\mathit{u}}_m$$ (6)

and note that the λ_m are all real and non-negative since they are eigenvalues of a symmetric, non-negative definite matrix. We define signal components x_m as

$$x_m={\left[{\overline{K}}_{\mathit{n}}^{-1/2}\mathrm{\Delta }\overline{\mathit{g}}\right]}^{†}{\mathit{u}}_m.$$ (7)

Now, the Hotelling SNR is given by

$${\text{SNR}}^2={\displaystyle \sum _{m=1}^M\frac{x_m^2}{\epsilon +{\lambda }_m}}$$ (8)

where M is the total number of pixels in the image-data vector g. We define a low-noise imaging system as one for which ε << min(λ_m). Conversely, a high-noise system is one for which ε >> max (λ_m). This formalism applies whether K_g̅ is the exact background covariance matrix or an estimate of it from samples. This formalism also applies if the data vector g is replaced by a channelized data vector υ.

2.2. Known background covariance

When the background covariance matrix K_g̅ is known exactly, we can analyze both the high- and low-noise situations by studying Eqn. 8. We see that in the high-noise limit, the SNR (not the SNR²) is well approximated by the equation

$$\text{log}(\text{SNR})=\frac{1}{2}\text{log}\left[{\displaystyle \sum _{m=1}^M{x}_m^2}\right]-\frac{1}{2}\text{log}(\epsilon ).$$ (9)

Thus, on a log-log scale, a plot of SNR versus ε is linear with slope −0.5 and y-intercept of$\frac{1}{2}\text{log}\left[{\displaystyle {\sum }_{m=1}^M{x}_m^2}\right]$. We also note that this plot will approach this asymptote from below.

In the low-noise limit, the SNR approaches a constant value given by,

$${\displaystyle \sum _{m=1}^M\frac{x_m^2}{{\lambda }_m}.}$$ (10)

The behavior of SNR between the high- and low-noise limits depends on the distributions of the eigenvalues λ_m. All we can state for certain is that the SNR is decreasing as ε increases.

2.3. Estimated background covariance

It is often the case that the background covariance matrix K_g̅ must be estimated from samples and the average noise covariance term K̅_n may be known or also estimated from samples. For simplicity, we will consider the case where K̅_n is known and full rank. In this case, we do not need a full-rank estimate of K_g̅ to compute the inverse of the matrix K = K̅_n + K_g̅. This fact is useful because we would need on the order of M samples to obtain a full-rank estimate of K_g̅. Let us examine the low-noise limit when the estimate of K_g̅ is not full rank. The expression for our estimate of SNR is given by,

$${\widehat{\text{SNR}}}^2={\displaystyle \sum _{m=1}^M\frac{{\widehat{x}}_m^2}{\epsilon +{\widehat{\lambda }}_m},}$$ (11)

where hats denote destimates resulting from the replacement of K_g̅ with the low-rank estimate K̂_g̅. At least one of the λ̂_m values will be 0 because the matrix is not full rank. As a result, the plot of log(SNR) versus log(ε) will not approach a constant as ε gets small but will instead approach the line

$$\text{log}(\widehat{\text{SNR}})=\frac{1}{2}{\displaystyle \sum _{m=R+1}^M{\widehat{x}}_m^2-\frac{1}{2}\text{log}(\epsilon ),}$$ (12)

where R is the rank of our estimate K̂_g̅. In the high-noise limit, the result will be similar to Eqn. 9 except with hats on the appropriate quantities.

Due to the linear dependence of log$(\widehat{\text{SNR}})$ on log(ε) in the low-noise situation, where the exact log(SNR) is approaching a constant, estimates of SNR using the decomposition may exhibit a large positive bias. This bias has been seen experimentally in fluorescence-enhanced optical imaging.¹ Overall the plot of log$(\widehat{\text{SNR}})$ versus log(ε) will be linear at both extremes with slope −0.5 but with different intercepts. The region between low noise and high noise will exhibit a smooth transition between these two asymptotes. As the rank of the estimated K̂_g̅ increases, the difference in the y-intercepts between the two asymptotes also increases and the transition region broadens. When the estimate of K̂_g̅ becomes full rank, log$(\widehat{\text{SNR}})$ approaches a constant for small ε as in the known K_g̅ situation. In general for the low-noise situation, as we increase the number of samples used to estimate K_g̅ we expect log$(\widehat{\text{SNR}})$ to decrease toward the true value of log(SNR).

3. THE CHANNELIZED HOTELLING OBSERVER

To avoid the difficulties with estimating and inverting large covariance matrices, researchers often employ a channelized form of the Hotelling observer. This channelized Hotelling observer (CHO) first reduces the dimension of the data vector via a linear transformation υ = T_g, where T is the L × M matrix of channels, and υ is the channel-output vector. The matrix T is chosen such that L << M. The SNR for the CHO is given by,

$${\text{SNR}}_{\text{CHO}}^2=\mathrm{\Delta }{\overline{\mathit{\upsilon }}}^{†}{K}_{\mathit{\upsilon }}^{-1}\mathrm{\Delta }\overline{\mathit{\upsilon }},$$ (13)

where Δυ̅ = TΔg̅ is the difference in the means of the channel-output vector under the two hypotheses, and K_υ = TKT^† is the covariance matrix for the channel outputs. The channel matrix T can be chosen to mimic the average performance of human observers.^{2, 3} We will focus on choices of T designed to approximate the performance of the full Hotelling observer.⁴ Thus, we desire that SNR_CHO = SNR.

Using the covariance decomposition shown in Eqn. 4, we can write the channel covariance matrix as,

$$K_{\mathit{\upsilon }}=\epsilon T{\overline{K}}_{\mathit{n}}{T}^{†}+{\mathit{\text{TK}}}_{\overline{\mathit{g}}}{T}^{†}=\epsilon {\overline{K}}_{\mathit{\eta }}+K_{\overline{\mathit{\upsilon }}}.$$ (14)

In this case, the second term in Eqn. 14 is easy to estimate but there still may be problems at low noise. The low-noise regime for CHO is defined by the condition that ε is much smaller than the minimum eigenvalue of the matrix ${\overline{K}}_{\mathit{\eta }}^{-1/2}{K}_{\overline{\mathit{\upsilon }}}{\overline{K}}_{\mathit{\eta }}^{-1/2}$. It is likely that this minimum eigenvalue is larger than the minimum eigenvalue of ${\overline{K}}_{\mathit{n}}^{-1/2}{K}_{\overline{\mathit{g}}}{\overline{K}}_{\mathit{n}}^{-1/2}$ which defines the low-noise regime for the Hotelling observer. As ε goes to 0, the plot of log(SNR_CHO) versus log(ε) will asymptote on its constant value sooner than the corresponding plot of log(SNR) versus log(ε). As a result, in the low-noise regime, there may be a negative bias for estimates of the Hotelling SNR. This bias will be reduced as the number of channels L is increased.

4. RESULTS

To illustrate the difficulties of estimating Hotelling SNR in the low-noise regime, we performed a simulation study. We simulated one-dimensional, noise-free image data g of length M = 64. The image data were generated by a discrete convolution of Gaussian white noise with a smoothing filter to simulate variable background texture. A constant background was added to ensure that all elements of g are positive. A total of 5000 sample images g were employed to produce an accurate estimate of the background covariance term K_g̅. The noise covariance term K̅_n was set to a diagonal matrix with diagonal elements given by the mean of the noise-free image data g. Thus, when ε = 1, the detector noise component had a variance equal to the mean of the image data as in the case of Poisson detector noise.

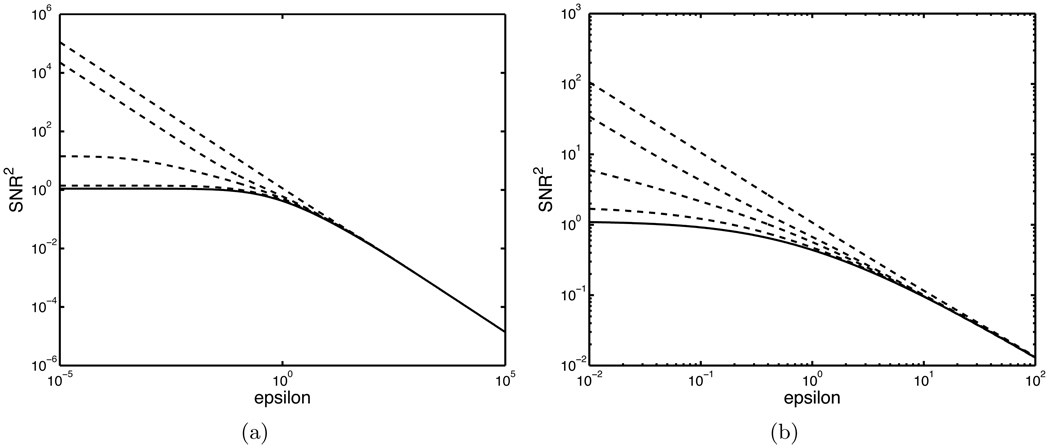
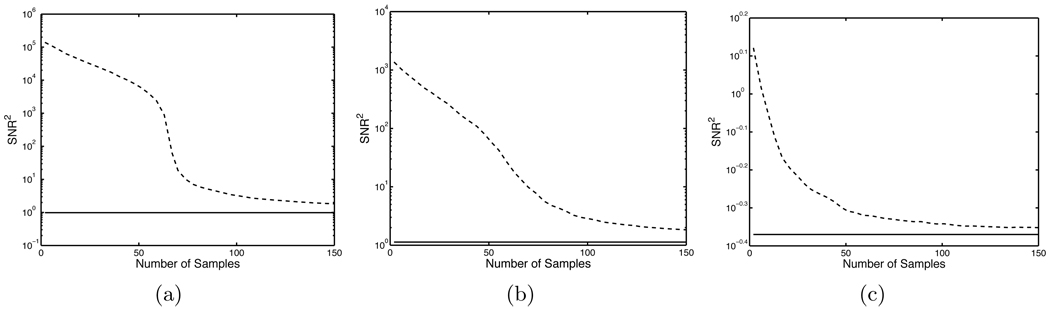
In the first study, we computed estimates of the Hotelling observer SNR using estimates of the background covariance term K_g̅ with varying numbers of samples. Figure 1 shows the plot of the estimated SNR² as a function of the noise level ε. The solid curve is the actual Hotelling observer performance as a function of ε. The dashed curves show the estimates ${\widehat{\text{SNR}}}^2$ produced using, from top to bottom, 4, 32, 70, and 200 samples. We see that in the low-noise regime, when the number of samples is less than the dimension of the image data g, our estimate of the Hotelling SNR using the covariance decomposition exhibits a large positive bias. This bias is reduced as we increase the number of samples. As predicted, when the number of samples is greater than the dimension of the image data (e.g., the case when the number of samples is 70), the estimate of Hotelling SNR approaches a constant. To further study this transition region, we plot the estimate of Hotelling SNR as a function of the number of samples for ε = 1 × 10⁻⁵, 1 × 10⁻³ and 1 in Fig. 2. In Fig. 2(a), we clearly see that a transition occurs when the number of samples is equation to 64, the dimension of g.

Figure 1.

Plots illustrating the difficulties of estimating Hotelling SNR in the low-noise regime. For both (a) and (b), the solid line is the true Hotelling SNR; the dashed lines are estimates of SNR produced using 4, 32, 70, and 200 samples. As the number of samples increases, the estimate of SNR approaches the true value of the SNR. Plot (b) is a zoomed-in version of plot (a) showing the region around ε = 1.

Figure 2.

The behavior of the estimated SNR as a function of the number of samples used to estimate the background covariance term. The value of ε was set to (a) 1 × 10⁻⁵, (b) 1 × 10⁻³ and (c) 1. When ε is small, we see a transition when the number of samples equals 64, the dimension of the image data g. The solid lines represent the actual Hotelling observer performance.

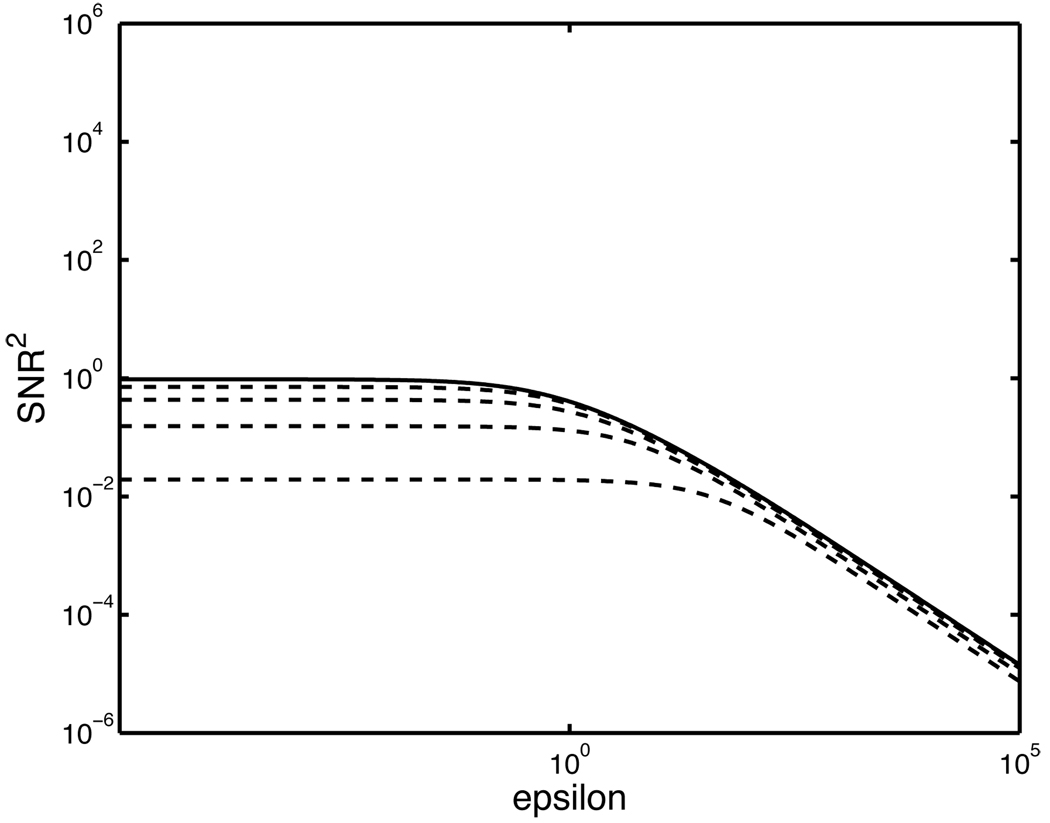
In the second study, we used the same images but used the channelized Hotelling observer with Hermite-Gaussian channels to estimate the performance of the Hotelling observer. The Hermite-Gauss channels are the one-dimensional analog to the Laguerre-Gauss channels often used in image-quality assessment.⁴ Figure 3 shows the estimates of the Hotelling SNR using the channelized observer as a function of noise level and for varying numbers of channels. The true Hotelling SNR is the solid curve; the dashed curves are the estimates for 2, 4, 8, and 16 channels. The estimate of SNR approaches the true value of SNR as the number of channels increases. In the low-noise regime, there is a large negative bias when the channelized Hotelling observer is used with too few channels.

Figure 3.

A plot illustrating the difficulties of estimating Hotelling SNR in the low-noise regime using the channelized Hotelling observer. The solid line is the true Hotelling SNR. The dashed lines are estimates of SNR produced using 2, 4, 8, and 16 channels. As the number of channels increases, the estimate of SNR approaches the true value of the SNR.

5. DISCUSSION AND CONCLUSIONS

In summary, in the low-noise regime, there is a positive bias in the Hotelling SNR estimate when the object covariance matrix is computed from a few samples. There may be a negative bias in the low-noise regime when the channelized Hotelling observer is used to estimate the Hotelling SNR. The location of the low-noise regime is determined by the minimum eigenvalues of the matrix given in Eqn. 6. For a large matrix, this minimum eigenvalue may be very small and the low-noise regime may correspond to an unphysical situation. For analytical calculations, where the background covariance matrix is replaced with an operator, there may be no low-noise regime at all. Finally, for small object-covariance matrices, which occur with channelized Hotelling observer, the low-noise regime may occur in simulations and/or experiments.

The original motivation for this work was a Hotelling SNR calculation for a fluorescence-enhanced optical imaging system.¹ The authors of that study generated noise-free sample images to estimate K_g̅ and assumed 5% Gaussian noise for K̅_n. They found that, using the covariance decomposition used in Eqn. 3, the estimate of the Hotelling SNR dropped substantially as the number of samples used to estimate K_g̅ increased (as in Fig. 2). We believe that this occurred because they were in the low-noise regime for this imaging system. Their solution was to increase the number of samples until the estimated Hotelling SNR stabilized.