Localization of spontaneous magnetoencephalographic activity of neonates and fetuses using independent component and Hilbert phase analysis

Abstract

The fetal magnetoencephalogram (fMEG) is measured in the presence of large interference from maternal and fetal magnetocardiograms (mMCG and fMCG). These cardiac interferences can be attenuated by orthogonal projection (OP) technique of the corresponding spatial vectors. However, the OP technique redistributes the fMEG signal among the channels and also leaves some cardiac residuals (partially attenuated mMCG and fMCG) due to loss of stationarity in the signal. In this paper, we propose a novel way to extract and localize the neonatal and fetal spontaneous brain activity by using independent component analysis (ICA) technique. In this approach, we perform ICA on a small subset of sensors for 1-min duration. The independent components obtained are further investigated for the presence of discontinuous patterns as identified by the Hilbert phase analysis and are used as decision criteria for localizing the spontaneous brain activity. In order to locate the region of highest spontaneous brain activity content, this analysis is performed on the sensor subsets, which are traversed across the entire sensor space. The region of the spontaneous brain activity as identified by the proposed approach correlated well with the neonatal and fetal head location. In addition, the burst duration and the inter-burst interval computed for the identified discontinuous brain patterns are in agreement with the reported values.

I. Introduction

An in-utero assessment of fetal brain development can offer clinicians important information regarding the presence, severity and persistence of prenatal neurological disorders. However, the sheer inaccessibility of the fetal brain has been a limitation in this investigation process. With the advent of Superconducting Quantum Interference device (SQUID) technology, Magnetoencephalography (MEG), a magnetic homologue of Electroencephalography (EEG) was established over the last decades to record human brain activity. This technique is non-invasive and records the magnetic fields corresponding to the electric currents generated by neurons in the brain. Based on the MEG technology, a first-of-a-kind device named SARA (SQUID Array for Reproductive Assessment) was designed and installed in the department of OB/GYN at the University of Arkansas for Medical Sciences (UAMS) specifically to study the functional fetal brain development [1. 2].

The fetal MEG (fMEG) is measured in the presence of environmental noise, near-field biological signals (maternal magnetocardiogram (mMCG), fetal magnetocardiogram (fMCG)), motion artifacts and other interferences. The mMCG and fMCG are usually the dominant interfering signals and are attenuated by a signal space projection technique [3], which assumes the signals are stationary. However, when the signals or non-stationary because of reasons such as fetal movement, maternal movement, this approach redistributes the fMEG signal among sensors [4], even to sensors distant from the fetal head location where the fMEG signal should not be present. In addition to redistribution, cardiac residuals (partially attenuated mMCG and fMCG signals) are also left in the fMEG data as a result of the loss of stationarity.

In this paper, we propose a novel way to extract and localize the spontaneous brain activity in neonates and fetuses using independent component analysis (ICA) [5]. Several research groups have used ICA to successfully separate fetal Electrocardiogram [6] and fetal Magnetocardiogram [7] signals from maternal cardiac interference. In our approach, ICA has been performed in the data corresponding to sensors of a small subset (approximately the size of fetal head) for 1-min duration. The independent components (ICs) obtained are further investigated for the presence of discontinuous brain patterns based on the Hilbert phase (HP) analysis [8]. The ICs identified as discontinuous brain patterns are populated in the sensors around the centroid of the sensor subset. In order to localize the region of the highest spontaneous brain activity content, the sensor subset is traversed across the entire sensor space. This is done in order to account for scenarios of change in fetal head location during the recording. The proposed approach was first tested in two neonatal datasets wherein there was no maternal cardiac interference, low movement artifact, and a prior knowledge of the neonatal brain location. Then it was further extended to test its feasibility in fetal datasets and the results were correlated with the fetal head location based on the ultrasound assessment. The HP analysis was further used to detect the burst-duration and the inter-burst interval for ICs identified as discontinuous patterns.

II. Methods

A. Data Acquisition

Two neonatal recordings, each of 3-min duration and two fetal recordings of 6 and 30 min duration, all sampled at 312.5 Hz were analyzed for the current study. The neonatal MEG recordings were performed at gestational age corresponding to 39 and 40 weeks and the two fetal recordings were performed at 32 and 36 weeks of gestation. The study was approved by the local Institutional Review Board and for additional details about the data collection, see [1, 2].

B. Localization of spontaneous brain activity based on ICA and HP analysis

1) Independent component Analysis (ICA)

Assuming an n-dimensional vector x of observables generated by a mixture of n independent sources s, we can formulate the system as

$$x=\mathit{As}$$ (1)

The mixture matrix containing the elements a_ij will be denoted by A or more realistically to account for the additive noise N from unknown sources.

$$x=\mathit{As}+\mathit{N}$$ (2)

ICA uses the observed signals denoted by x to estimate A and s with the assumptions of independence and a non-Gaussian distribution [7]. Once the matrix A has been estimated, the inverse W can be computed to obtain the independent components

$$\mathit{s}=\mathit{Wx}$$ (3)

In this study, the FastICA approach developed by Hyvarinen and Oja [7] is used.

2) Hilbert phase (HP) metrics

For a signal x(t), the Hilbert transform h(t) is defined by the following convolution integral:

$$h(t)=\frac{1}{\pi }\text{P}.\text{V}.\underset{-\infty }{\overset{\infty }{\int }}\frac{x(\tau )}{t-\tau }d\tau$$ (4)

where P.V. denotes Cauchy’s Principal value. The signal together with its Hilbert transform can be represented as a complex analytic signal a(t) = x(t)+ i h(t), where $\text{i}=\sqrt{-1}$ Using the complex signal a(t), the Hilbert phase is defined as φ(t) = a tan{h(t)/x(t)} and thus the Hilbert transform allows one to study the instantaneous phase of the signal. The Hilbert phase exhibits slips when the magnitude of their successive phase differences |φ(t_i+1) − φ(t_i)| exceed π. The time difference between the successive Hilbert phase slips (Δτ) is characteristic of a system [9]. In the case of periodic signals, Δτ defines the signal’s periodicity and standard deviation of Δτ, σ(Δτ) is zero in such cases. A histogram of Δτ sheds light on the spectral content of the signal [10]. Recently, it has been shown that the standard deviation of the inter-slip intervals normalized by the total number of slips, ρ = (Δτ)/total number of slips, is capable of localizing the spontaneous brain activity in neonates and fetuses [9. 11] and will be used in this work to delineate the independent components reflecting spontaneous brain activity.

3) Localization of the spontaneous brain activity

The step-by-step procedure involved in the localization of the spontaneous brain activity is described below, also presented as a block diagram in Figure 1.

Fig. 1.

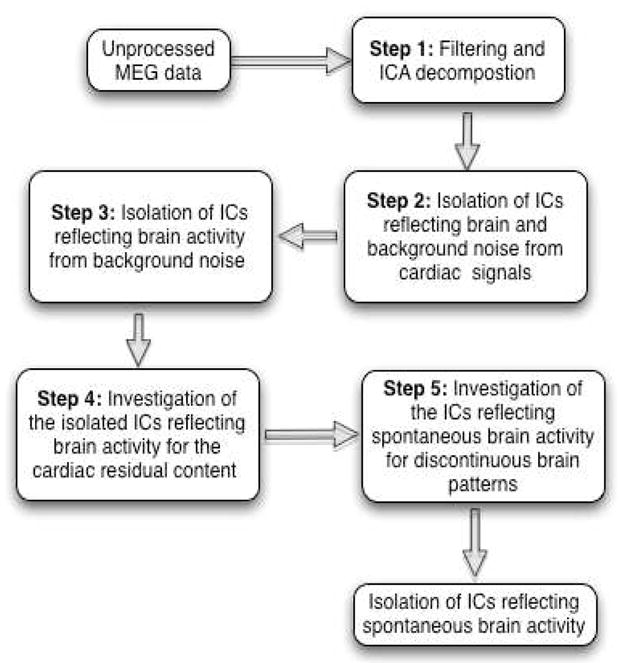
Block diagram of the steps involved in localizing spontaneous brain activity.

As mention before, the unprocessed MEG data corresponding to the sensors of a small subset of radius 5 cm (encompassing ≥ 8 sensors) for 1-min duration are chosen and subjected to the following steps for the localization of spontaneous brain activity.

Step 1: Filtering and ICA decomposition

The data corresponding to the chosen subset of sensors are band-pass filtered between 0.5 and 25 Hz using a Butterworth filter with zero phase distortion to limit the frequency content of the data to that of the spontaneous brain data. The filtered data are then subjected to ICA decomposition. Figure 2 shows an example of the chosen sensor subset for the ICA decomposition. For each decomposition, an arbitrary choice of N-3 ICs are retrieved, where N is the total number of sensors in each sensor subset. The reason for this arbitrary choice is based on the observation that the brain signals show up with in N-3 ICs.

Fig. 2.

SARA sensor coordinates with a highlighted sensor subset for ICA processing.

Step 2: Isolation of ICs reflecting brain and background noise from cardiac signals

Each IC is full-wave rectified (FWR) to enhance the high frequency activity in the signal. The HP metrics is computed for the FWR ICs and the ones reflecting the cardiac signals will have a high HP metrics. In the current work, an arbitrary threshold < 0.26 is used to separate the spontaneous brain and background noise signals from the interfering cardiac signals.

In our calculations, the FWR procedure encompasses a two-step process involving the difference between the successive time points of the data, which is an equivalent to applying high-pass filter to the data, and followed by the computation of its absolute value.

Step 3: Isolation of ICs reflecting brain activity from background noise

Among the ICs identified as brain signal and background noise, the signal to noise ratio (SNR) of the ICs based on the HP metrics [11] is used as discrimination factor in separating the brain signal and the background noise. The HP metrics gives information about the spectral content of the signal and the higher its value, the better the SNR of the signal under investigation. In the current work, an arbitrary threshold of > 10 is used to separate the brain signal from the background noise.

Step 4: Investigation of the isolated ICs reflecting brain activity for the cardiac residual content

Even in the 1-min window chosen, the stationarity of the data is sometimes lost due to fetal movement. As a result, the orthogonality constraint which is the basic assumption of ICA cannot be achieved and this leaves partially attenuated cardiac signals (cardiac residuals) in the brain components. In order to investigate the cardiac residual content of the detected ICs, a spectral estimation with a resolution of 1Hz is carried out. A typical spectral estimation of a brain signal will reveal a 1/f behavior and this is used as discrimination factor in eliminating brain signal with traces of cardiac residuals from residual free brain signals. To accomplish this, a spectral ratio (SR) is defined for each local max of the estimated spectrum as follows:

$$\text{SR}=\frac{\text{Power}\text{at}\text{the}\text{local}max}{\text{Power}\text{at}\text{the}\text{immediate}\text{neighbors}\text{to}\text{the}\text{local}max}$$ (5)

In the current work, SR is monitored with an arbitrary threshold of < 0.68 in order to delineate the brain signal from brain signal data contaminated with traces of cardiac residuals. In cases of the brain signals with cardiac residuals, SR will have a higher value, which is observed as a sharp spike in power spectrum at the frequency of the heart rate such as 2.5 Hz, 5 Hz or its harmonics.

Step 5: Investigation of the ICs reflecting spontaneous brain activity for discontinuous brain patterns

The ICs passing the above mentioned steps could possibly reflect spontaneous brain activity. However, the discontinuous brain patterns observed as Tracé Alternant (TA) or Trace Discontinue (TD) in neonates and fetuses would be the final decision criteria in labeling a particular IC reflecting spontaneous brain activity.

The discontinuous patterns are observed as burst of activity interleaved by relative quiescence, namely, the inter-burst interval (IBI). The neurologists typically score discontinuous patterns in 15-sec duration in neonates and 30-sec duration in fetus (in order to account for the longer inter-burst interval).

For this purpose, the HP metrics is computed for shorter windows of 2-sec with 1-sec overlap in neonates and 4-sec with 2-sec overlap in fetuses. The standard deviation of the HP metrics of > 8 is used as the final discriminating factor in the identification of ICs that best reflect the spontaneous brain activity.

The ICs reflecting the spontaneous brain activity are then populated in the sensors around the centroid of the sensor subset and this procedure is repeated by moving to the next sensor subset. On traversing the entire sensor space for the first 1-min duration of the data, this procedure is repeated for rest of the data in the similar way.

III. RESULTS AND DISCUSSION

Figure 3 represents the localization of neonatal spontaneous brain activity. The neonates are placed in a cradle near the lower half of SARA sensors. The localized region, as identified by the proposed approach, correlates well with the neonatal head location. Figure 4 represents the localization of fetal spontaneous brain activity. The localized region identified as the highest spontaneous brain activity content correlates well with the fetal head location as identified by the ultrasound assessment (shown as white dot in Figure 4(a, b)). The discontinuous patterns detected by the algorithm in the ICs with the highest SNR in neonates and fetuses were also confirmed by the neurophysiologists by visual inspection. In addition, the burst duration (BD) and IBI computed by the HP approach [8] for the discontinuous patterns are well within the range of the reported values [12].

Fig. 3.

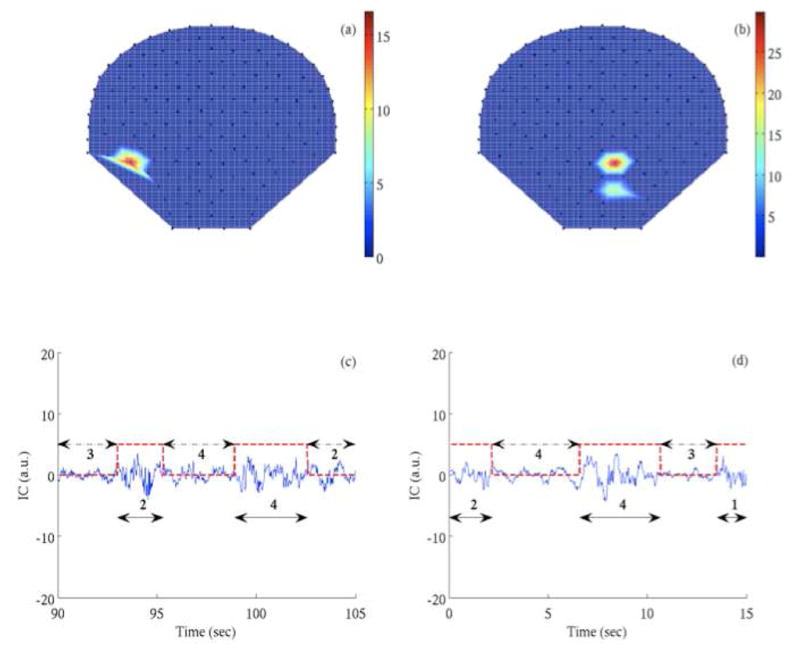
Localization of neonatal spontaneous brain activity. (a, b) Iso-potential map of HP metrics indicating the sensor region of spontaneous brain activity. (c, d) The discontinuous pattern observed in the IC corresponding to the highest HP metrics reflecting the spontaneous brain activity. The amplitude of the IC is in arbitrary units (a.u.).

Fig. 4.

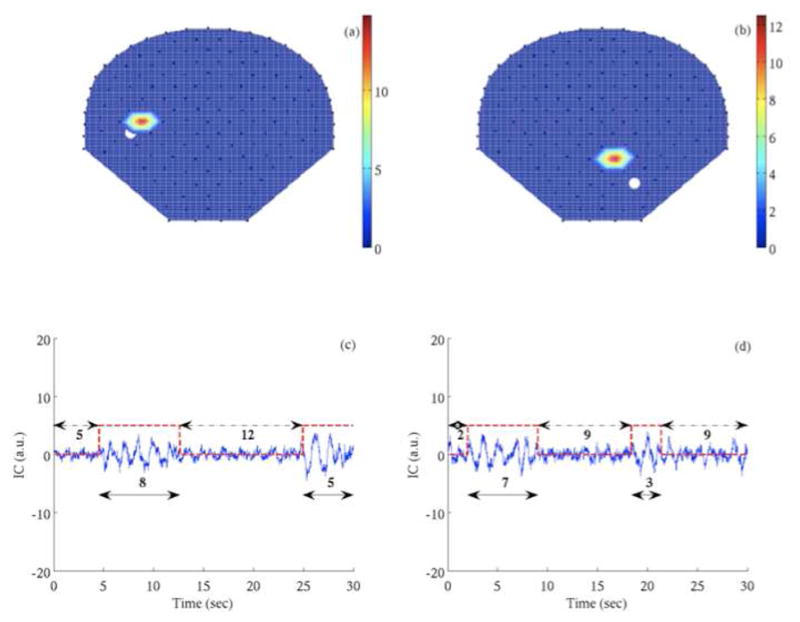
Localization of fetal spontaneous brain activity. (a, b) Iso-potential map of HP metrics indicating the sensor region of spontaneous brain activity. (c, d) The discontinuous pattern observed in the IC corresponding to the highest HP metrics reflecting the spontaneous brain activity. The white dot in (a) and (b) represent the fetal head location as marked from ultrasound assessment. The amplitude of the IC is in arbitrary units (a.u.).

The proposed approach employs an inherent search process in which the data corresponding to a small group of sensors are analyzed for the signatures of discontinuous brain patterns. This enables the approach to locate the regions of highest spontaneous brain activity content even in scenarios of change in fetal head position during the recording, which is very much possible during the early trimester. In addition, the proposed approach works on the independent component and hence will not suffer from any re-projection issues as with other methods [3].

However, as any blind source separation technique works on the very fact that the signal source is stationary and the proposed approach is no exception. Investigation of data corresponding to 1-min duration carried out in the proposed approach, is actually a step towards the establishment of the stationarity in our data to enable the ICA to better separate the signals corresponding to different sources. However, there could be scenarios wherein the fetus could be in motion during the 1-min period that is being investigated and in such scenarios, the fetal movement as detected by actogram [13] will be in monitored in parallel to discard those segments from the analysis.

IV. Conclusion

A novel approach based on ICA and HP analysis for the localization of spontaneous brain activity of neonates and fetuses has been presented. The region of the spontaneous brain activity identified by this approach correlated well with the neonatal and fetal head location. The BD and the IBI computed for the discontinuous patterns identified in spontaneous brain data of neonates and fetuses are well within the range of the reported values. In future work, the different arbitrary thresholds employed for the detection of spontaneous brain data will be standardized based on receiver operating characteristics curve and the proposed approach will be applied to a large population of low-risk fetal datasets to investigate the variation of BD and IBI and in effect understand the neurological maturation of the fetus.