In complex biology, prior knowledge is power

Abstract

Complexity is the grand challenge for science and engineering in the 21^st century. We suggest that biology is a discipline that is uniquely situated to tackle complexity, through a diverse array of technologies for characterizing molecular structure, interactions and function. A major difficulty in the analysis of complex biological systems is dealing with the low signal-to-noise inherent to nearly all large-scale biological data sets. We discuss powerful bioinformatic concepts for boosting signal-to-noise through external knowledge incorporated in processing units we call Filters and Integrators. These concepts are illustrated in four landmark studies that have provided model implementations of Filters, Integrators, or both.

Introduction

Complexity distinguishes a system that has many parts in an intricate arrangement that gives rise to seemingly inexplicable or emergent behaviors. For example, a radio captures an electromagnetic signal and converts it through electronic circuitry into sound that we hear. To most, the radio is a black box with an input (electromagnetic waves) and an output (sound waves). However, understanding the inner workings of this box requires going head-to-head with the challenges of complexity. What are the component parts of the system and how are these parts interconnected? How do these connections influence functions and dynamic system outputs? In biology, ultimately one would like to create models that predict the emergent behaviors of complex entities— and even re-engineer these behaviors to humankind’s benefit.

To decipher complexity, biologists have developed an impressive array of technologies— next-generation sequencing, tandem mass spectrometry, cell-based screening, and so on— which are capable of generating millions of molecular measurements in a single run. This enormous amount of data, however, is typically accompanied by a fundamental problem— an incredibly low rate of signal-to-noise. For example, the millions of single nucleotide variants (SNVs) found in a typical genome-wide association study or by the International Cancer Genome Consortium (Hudson et al., 2010) make it extremely difficult to identify which particular SNVs are the true causes of disease. Due to the overwhelming number of measurements, such analyses either lack power to detect the true signal or must admit an unacceptable quantity of noise.

Fortunately, biologists have two major weapons with which signal-to-noise may be improved. First is what we know about complexity, which can and should be used as strong prior assumptions when analyzing biological data. Known principles of complexity such as modularity, hierarchical organization, evolution, and inheritance (Hartwell et al., 1999) all provide important insights into how biological systems are constructed and how they function. Second is the availability of data in many complementary layers— including the genome, transcriptome, proteome, metabolome, and interactome. A recent wave of new bioinformatic methods has demonstrated how both weapons— strong prior assumptions related to complexity and systematic accumulation of complementary data— can be used together or separately to exact substantial increases in signal-to-noise.

In what follows, we summarize these developments within a general paradigm for signal detection in biology. Central to this paradigm are processing units we call Filters and Integrators, which draw on prior biological assumptions and hierarchical data to reduce noise and to boost statistical power. To illustrate these ideas in context, we review four landmark studies that have provided model implementations of Filters and Integrators.

The signal detection paradigm

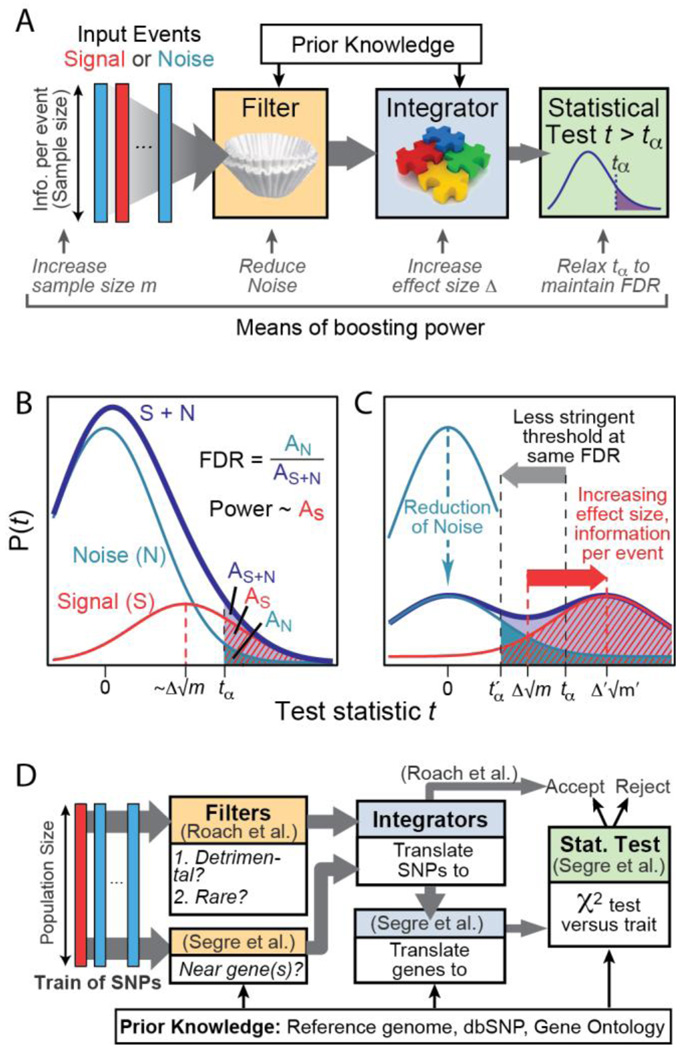
Imagine a biological data set as a stream of information flowing into a hypothetical signal detection device (Figure 1A). The information flow is quantized into atomic units or events, representing measurements for entities such as genes or proteins, protein interactions, SNVs, pathways, cells, or individuals. Each event contains a certain amount of information, ranging from a single measurement (e.g., strength of protein interaction) to thousands (e.g., a SNV state or gene expression value over a population of patients). Some events represent true biological signals, with the definition of ‘signal’ depending exquisitely on the type of results the experimentalist is looking for (e.g., a SNV causing disease or a true protein interaction, many examples are given later). The remaining events are noise, which can be due to errors that are technical in nature (uncontrollable variation in different instrument readings collected from the same sample) or biological in nature (uncontrollable variation in different samples collected from the same biological condition). An event may also be considered part of noise even if it is biological and reproducible, simply because it encodes aspects of phenotype irrelevant to the current studies.

Figure 1. Boosting signal-to-noise in biological data using prior knowledge.

(A) Signal detection paradigm in which an input data stream is routed through a series of filtering and integration units, ending in a statistical test which makes accept or reject decisions. Symbols: m, information per event or sample size; Δ, effect size; t_α, threshold test value; FDR, False Discovery Rate. (B) Probability distribution P(t) of the test statistic t over the entire data stream of signal plus noise [purple]. This distribution is factored into a red signal and a blue noise component. FDR and power are visualized in terms of the areas under these curves to the right of a decision threshold t_α. (C) Effect of varying parameters on the signal, noise, and signal plus noise probability distributions. The power is increased by more than six-fold compared to panel B, at an identical FDR. Colors are shown as in panel B. (D) A specific implementation for disease gene mapping as described in Segre et al. (2010) and Roach et al. (2010). The input signal is a stream of SNPs with each SNP observed across a population of individuals. This input is filtered to remove SNPs based on multiple criteria, and multiple SNPs are integrated into genes and/or pathways.

Since we do not know exactly which events are signal, the device scores each event and accepts those for which the score exceeds a decision threshold (Figure 1A). It is precisely this decision that becomes problematic in many large-scale biological studies, in which one either mistakenly rejects a large proportion of the true signal (low statistical power) or must tolerate a high proportion of accepted events that are noise (high False Discovery Rate or FDR).

Boosting signal with Filters and Integrators

To increase signal-to-noise, a pivotal trend in bioinformatics has been to augment the signal detection process with complementary data sets and with prior knowledge about the nature of signal. The vast majority of these approaches fall into either of two categories that we call Filters and Integrators (Table 1). Filters attempt to cull some events from the information flow immediately and reject them as noise. For example, a detection system for differential expression might reject certain genes immediately if their expression levels fail to exceed a background value in any condition. Integrators, on the other hand, transform the information flow by aggregating individual events into larger units to yield a fundamentally new type of information. For example, genes might be aggregated into clusters of similar expression or of related function, in which the median level of the clusters— not their individual genes— are propagated as the ‘events’ on which final accept / reject decisions are made (Park et al., 2007). Importantly, the combining of Filters or Integrators results in a new device which itself can be recombined with other signal detection systems in a modular fashion.

Table 1.

Seven ways to boost power with knowledge

Power Boost	Example Use in Filters or Integrators
Sequences & structures	Filtering GWAS to focus on SNVs close to gene coding regions (Segre et al., 2010). Integrating information about multiple SNVs that fall near the same gene (Segre et al., 2010).
Molecular function (Gene sets)	Integrating individual signals from functionally related genes (Chasman, 2008; Wang et al., 2010).
Molecular networks (Interactions)	Projecting data on networks to identify novel pathways enriched for differentially-expressed genes or candidate SNVs (Ideker et al., 2002). Filters can prioritize gene candidates by their network proximity to known disease genes (Lage et al., 2007) or via signaling pathways that connect gene knockouts to their downstream effects (Suthram et al., 2008; Zhu et al., 2008).
Multiple layers of data	Filtering based on multiple layers of data can retain true signals which are reflected coherently across data sets and filter out noise which usually cancels out (Lee et al., 2004).
Evolutionary conservation	Evolutionary filters retain information that is preserved across multiple species and therefore likely represents functionally relevant signal (Erwin and Davidson, 2009; McGary et al., 2010).
Inherent modularity	Inherent biological modules identified by clustering or eigenvalue decomposition can be used to integrate the stream of information on individual biological entities to a new stream of information about modules (Zhu et al., 2008).
Focusing phenotype by 'Asking the right question'	Phenotypes of interest are often confounded by miscellaneous factors such as age, gender, race, or geographic location. Subtracting away these factors represents a powerful filter that reduces information irrelevant to the analysis (Segre et al., 2010).

Both Filters and Integrators influence statistical power and FDR, but by fundamentally different means. Filters reduce the fraction of noise passing through the system and, as a consequence, the FDR. Alternatively, FDR can be held constant as filters are added by relaxing the decision threshold, resulting in higher statistical power (Figure 1B,C). By comparison, Integrators combine a train of weak signals into fewer stronger events, leading to an increase in ‘effect size’ and thus a direct increase in statistical power. These methods compliment the more classical means of boosting power by increasing the amount of information per event (also called the sample size, Figure 1A).

In each of the following examples, boosting power with a combination of Filters and Integrators has been critical to the success of a landmark genome-scale analysis project.

Example 1: Pathway-level integration of genome-wide association studies

Genome-wide association studies (GWAS) seek to identify polymorphisms, such as SNVs, that cause a disease or other phenotypic trait of interest. Despite the success of this strategy in mapping SNVs underlying many diseases, the identified loci typically explain only a small proportion of the heritable variation. For such diseases, one likely explanation is that the genetic contribution is distributed over many functionally-related loci with large collective impact, but with only modest individual effects which do not reach genome-wide significance in single-SNV tests (Wang et al., 2010; Yang et al., 2010).

Based on this hypothesis, Segre et al. (2010) investigated the collective impact of mitochondrial gene variation in type II diabetes. They described a method called MAGENTA that performs a meta-analysis of many different GWAS to achieve larger sample sizes than any single study, thereby increasing statistical power. MAGENTA also includes both filtering and integration steps (Figure 1D). First, a Filter is applied so that SNVs that fall far from genes are removed. Next an Integrator is applied to transform SNVs to genes, such that each gene is assigned a score equal to the most significant p-value of association among its SNVs. Gene scores are further corrected for confounding factors such as gene size, number of SNVs per kilobase, and genetic linkage. Finally, a second Integrator combines the scores across sets of genes assigned to the same biochemical function or pathway, resulting in a single pathway-level p-value of association.

Simulation studies using MAGENTA suggest a potentially large boost in power to detect disease associations (Supplemental Figure 1A). For example, the method has 50% power to detect enrichment for a pathway containing 100 genes of which 10 genes have weak association to the trait of interest. This performance is compared to only 10% power to detect any of the 10 genes at the single SNV level. At this increased power, MAGENTA did not identify any mitochondrial pathways as functionally associated with type II diabetes, suggesting that mitochondria have overall low genetic contribution to diabetes susceptibility overall– a surprise given the conventional wisdom about the disease. On the other hand, in an independent analysis of genes influencing cholesterol, MAGENTA identified pathways related to lipid and fatty acid metabolism which, troublingly, had been missed by classical GWAS.

Example 2: Mapping disease genes in complete genomes

Sequencing and analysis of individual human genomes is one of the most exciting emerging areas of biology, made possible by the rapid advances in next-generation sequencing (Metzker, 2010). As complete genome sequencing becomes pervasive, one of the most important challenges will be to determine how such sequences should best be analyzed to map disease genes. The signal filtering and integration paradigm provides an excellent framework for developing methods in this arena. As a landmark example, Roach et al. (2010) described a filtering methodology for disease genes based on the complete genomic sequences of a nuclear family of four. This approach was used to identify just three candidate mutant genes, one of which encoded the Miller syndrome, a rare recessive Mendelian disorder for which both offspring, but neither parent, were affected.

To begin the analysis, the four genome sequences were processed to identify approximately 3.7 million SNVs across the family. SNVs were then directed through a series of filters (Figure 1D). In the first, SNVs were rejected if they were unlikely to influence a gene-coding region annotated in the human genome reference map (http://genome.ucsc.edu/), leaving approximately 1% of SNVs which led to mis-sense or nonsense mutations or fell precisely onto splice junctions. A second filter removed SNVs that were common in the human population and thus were unlikely to cause a rare Mendelian disorder. Like the first one, this filter yielded an approximate 100-fold decrease in the number of candidates. A third filter was designed to check inheritance patterns, which can be gleaned only from a family of related genomes. SNVs were removed which had a non-Mendelian pattern of inheritance (result of DNA sequencing errors) or did not segregate as expected for a recessive disease gene, in which each affected child must inherit recessive alleles from both parents. This filter yielded another 4 to 5-fold decrease in candidate SNVs versus using only a single parental genome. Finally, an Integrator was used to translate all remaining SNVs into their corresponding genes.

Using the entire system of filters and integrators under a compound heterozygote recessive model, a total of three genes were identified as candidates. One of these (DHODH) was concurrently shown to be the cause of Miller syndrome. In this way, the family genome sequencing approach used the principles of Mendelian genetics (prior knowledge) to correct approximately 70% of the sequencing errors and reduce enormously the search space for disease traits (corresponding to an increase in statistical power from 0.15% to 33%, Supplemental Figure 1B).

Example 3: Assembly of global protein signaling networks

Another area in which filtering and integration are turning out to be key is assembly of protein networks. An excellent example of network assembly is provided by the recent work of Breitkreutz et al. (2010), in which mass spectrometric analysis was used to report a high quality network of 1844 interactions centered on yeast kinases and phosphatases. Central to the task of network assembly was a signal detection system for quality control and interpretation of the raw data. The data consisted of a stream of more than 38,000 proteins that had been co-immunoprecipitated with a different kinase or phosphatase used as bait. Bait proteins can interact both specifically and non-specifically with a wide variety of peptides, and the non-specific interactions comprise a major source of noise. To remove non-specific interactions the authors introduced a method called Significance Analysis of INTeractome (SAINT), in which each putative interacting protein is assigned a likelihood of true interaction based on its number of peptide identifications (representing an increased amount of information per event or sample size, Supplementary Figure 2A). After filtering, the remaining protein interactors are funneled to an Integrator stage in which they are clustered into modules based on their overall pattern of interactions (Table 1).

The resulting modular interaction network reveals an unprecedented level of cross-talk between kinase and phosphatase units during cell signaling. In this network, kinases and phosphatases are not mere cascades of proteins ordered in a linear fashion. Rather, they are more akin to the neurons of a vast neural network, in which each kinase integrates signals from myriad others, enabling the network to sense cell states, compute functions of these states, and drive an appropriate cellular response. It is likely that evolution tunes this network, such that some interactions dominate and others are minimized in a species-specific fashion. This might help explain two paradoxical effects seen pervasively in both signaling and regulation: (1) The same network across species can be used to control very different phenotypes (McGary et al., 2010); and (2) Very different networks across species can be used to execute near identical responses (Erwin and Davidson, 2009).

Example 4: Filtering gene regulatory networks using prior knowledge

One of the grand challenges of biology is to decipher the networks of transcription factors and other regulatory components that drive gene expression, phenotypic traits, and complex behaviors (Bonneau et al., 2007). Towards this goal, probabilistic frameworks such as Bayesian networks have been extensively applied to learn gene regulatory relationships from mRNA expression data gathered over multiple time points and/or experimental conditions (Friedman, 2004). However, due to a limited sample size, large space of possible networks, and probabilistic equivalence of many alternative models, these approaches are often unable to find the underlying causal gene relationships.

Recently, Zhu et al. (2008) showed that supplementing gene expression profiles with complementary information on genotypes may help to overcome some of these problems. These authors sought to assemble a gene regulatory network for the yeast Saccharomyces cerevisiae using previously-published mRNA expression profiles gathered for 112 yeast segregants. Rather than assemble a Bayesian network from expression data alone, the data were first supplemented with the genotypes of each segregant. The combined data set was then analyzed to identify expression quantitative trait loci (eQTL)— genetic loci for which different mutant alleles associate with differences in expression for genes at the same locus (cis-eQTL) or for genes located elsewhere in the genome (trans-eQTL). The eQTLs were then used as a filter to prioritize some gene relations and demote others. Any candidate cause-effect relations in which the effect gene is near an eQTL were removed, since the cis-eQTL already explains the gene expression changes at that locus. Conversely, cause-effect relations that were supported by trans-eQTLs and passed a formal causality test were prioritized. As indicated by previous simulation studies (Zhu et al., 2007), supplementing gene expression profiles with genetic information significantly enhanced the power to identify bona fide causal gene relationships. Further improvement was achieved by introducing a second filter which prioritized cause-effect relations that correspond to measured physical interactions, including data from the many genome-wide chromatin immunoprecipitation experiments published for yeast which document physical interactions between transcription factors and gene promoters.

Summary

Biology is expanding enormously in its ability to decipher complex systems. This ability derives from the expanded power to incorporate diverse and complementary data types and to inject prior understanding of biological principles. Signal detection systems such as those discussed here— along with their Filters, Integrators, and other components— are leading to fundamental new biological discoveries and models, some of which will ultimately transform our understanding of healthcare. It is also likely that many of the strategies, technologies and computational tools developed for healthcare can be applied to problems of complexity inherent in other scientific domains, including energy, agriculture and the environment. Healthcare and energy will attract significant societal resources moving forward— and hence offer unique opportunities to push the development and application of approaches for attacking complexity.

Supplementary Material

01

Supplemental Figure 1. Effects of Filters and Integrators on statistical power. (A) Power curve for the pathway-based genome-wide association study described in Example 1, adapted from Segre et al. (2010). Under the assumption that the disease is linked to a set of genes in a common causal pathway, the curve shows the power to identify this pathway as a function of the percentage of genes that have been correctly annotated with pathway information. (B) Related power curve adapted from Roach et al. (2010), as described in Example 2. The power to identify the single correct SNP through complete genome sequencing of families is shown as a function of family size (1 to 4 individuals).

Supplemental Figure 2. Instances of the signal processing paradigm for Examples 3 and 4. The framework of Figure 1A is implemented for (A) the SAINT method (Breitkreutz et al., 2010) or (B) the Bayesian network reconstruction method (Zhu et al., 2008).