Aromaticity in cyanuric acid

Abstract

This study analyzes the aromatic nature of cyanuric acid (hexahydrotriazine) and some of its derivatives, in terms of aromatic stabilization energy (ASE) and electronic behavior. The simplest molecule (C₃N₃O₃H₃) is the most aromatic item out of the entire set, but some of the others also display aromatic character. The structure of all the rings is analyzed considering their molecular orbitals as well as studying the inductive effect.

Introduction

Is isocyanuric acid aromatic? A number of premises need to be scrutinized here. Zabardasti [1] claims the molecule is aromatic, whereas Korkin [2] suggests the HCNO monomer spontaneously trimerizes in order to reach a more stable configuration, a feature which if proved correct would indicate that aromaticity is an indication of stabilization energy. The substituted NO₂ derivative in particular has been extensively studied. Korkin [3] discovered that it manifests strong stabilization energy and likewise Tarko [4] revealed it has descriptors of aromaticity and one of their targets is this same hexahydrotriazine derivative. Molecular structure and electronic behavior (charge distribution) of cyanuric acid has also been the focus of X-ray and neutron difraction studies [5–7]. In this context, the important point is that the planarity of the molecule and its electronic delocalization has been achieved, both of which are important characteristics for evaluating aromaticity.

Theoretical calculations of these molecules have been carried out for the purpose of studying an array of topics. The marked capability of cyanuric acid for generating hydrogen bonds has been analyzed in terms of nanostructures [8] and intrinsic capability [9]. Furthermore analogs containing sulfur atoms instead of oxygen atoms in the carbonyl groups have also been theoretically studied and compared with cyanuric acid [10, 11]. Hydrogen bonded supramolecular clusters [12] of cyanuric acid and melamine in particular have been the focus of several studies because these clusters display interesting electrical [13] and material [14] behavior. Besides, some adducts to a metallic complex have been prepared [15], showing promising characteristics in terms of their supramolecular chemistry for the development of new materials.

Another particularity of cyanuric acid, also derived from this characteristic of facile hydrogen bond formation is the formation of Hamilton complexes [16–18]. These kinds of complexes result from the interaction of a substrate containing electron donor ends with terminal hydrogen atoms, which have the capacity to easily interact with negative charge densities. This feature offers several possibilities for preparing novel compounds with applications in different fields, for example biochemistry, synthesis or in the pharmaceutical industry, as in the case of barbituric acid [16–18].

The goal of the present manuscript is to evaluate from different points of view, the intrinsic electronic characteristics that we foresee helping to explain the possible aromatic character of these compounds. The evaluation was carried out by applying the HOMA method [19, 20] and the ASE [21] approximation, employing isodesmic reactions [22–24].

Methods

All structures were optimized in the gas phase using the Jaguar 4.0 package [25]. A pure DFT method which included Becke’s gradient correction [26] for exchange and Perdew-Wang’s for correlation [27] was used for the energy evaluations. All calculations were performed applying the 6-31G** basis set. Frequency calculations were carried out at the same level of theory in order to confirm that the optimized structures were at the minimum of the potential surface. These frequencies were then used to evaluate the zero-point vibrational energy, the thermal vibrational corrections to the enthalpy and the total enthalpy values, calculated at 273°K. The bond lengths of the optimized structures were incorporated into the harmonic oscillator model of aromaticity (HOMA) method [19, 20] used to study aromaticity.

Results and discussion

In almost all cases, the molecules in this study resemble the general structure depicted in Fig. 1.

Fig. 1.

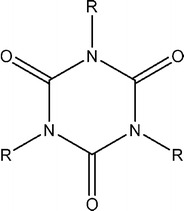
General structure of the compounds in this study

The calculation of the tautomer of compound (5) that corresponds to the structure shown in Fig. 2 is also included.

Fig. 2.

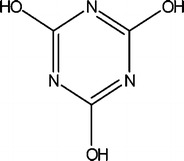
Tautomer of compound (5)

It is a known fact that in the majority of cases, the keto form of any species manifesting keto-enolic tautomerism is more stable that its corresponding enol form [28]. This phenomenon is due to the fact that a stronger bond exists between carbon and oxygen than the bond between carbon-carbon (considering π bonds). However, the presence of non bonding electrons in heteroatoms close to carbonyl groups, in this case causes a cyclic delocalization, resulting in an aromatic system (4n + 2), n = 1. Surprisingly, the calculation of both tautomers gives a total energy difference of 28.87 kJ mol⁻¹, with the keto form taking the lead. This result contradicts the previous premise concerning aromatics because the enol form shows the typical delocalization of an aromatic compound, in contrast to the keto form which does not; thus we return to the initial question. Does cyanuric acid present aromatic behavior in its keto form? The answer will be deduced with reference to the results from HOMA and ASE.

The ASE results come from the evaluation of the isodesmic reactions based on cyanic acid (NCOH) and its interaction with several simple molecules; the set of reactions is as follows:

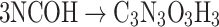1

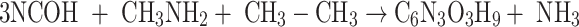2

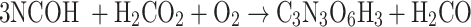3

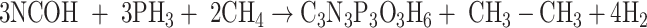4

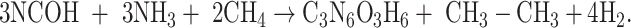5

The isodesmic reaction (1) yields unsubstituted cyanuric acid, the CH₃- derivative is obtained by a means reaction (2), whereas OH-, PH₂ and NH₂ derivatives are the result of reactions (3), (4), and (5) respectively.

The important component is the energy results. The ASE values relating to these isodesmic reactions are shown in Table 1.

Table 1.

ASE values from the isodesmic reactions

Molecule	ASE
HydOH	92.87 kJ/mol
HydCH3	119.23 kJ/mol
HydH	135.56 kJ/mol
HydPH	82.20 kJ/mol
HydNH2	53.97 kJ/mol

The greatest stabilization energy corresponds to unsubstituted cyanuric acid (HydH); therefore the inductive effect has little importance in this kind of molecule.

The HOMA results are shown in Table 2. Several factors emerging from these results should be noted. First, the most aromatic species in this set is the enol form of cyanuric acid (5b), with the next strongest value corresponding to the keto form of the same derivative. Likewise, this result suggests that the enol form will turn out to be the most stable isomer. However, the energy results indicate the contrary, and as outlined above the explanation for this phenomenon arises from the existence of a zwitterionic species which converts from 5 to become 5b, based on the proton mobility of both species [29]. On the other hand, the same zwitterionic species is also described as having a canonical structure as in 5, presented in Scheme 1.

Table 2.

Direct HOMA for the compounds being considered. For comparison purposes benzene HOMA is 0.999

Molecule	HOMA
HydCH3 (1)	0.710
HydOH (2)	0.691
HydN2 (3)	0.6
HydPH2 (4)	0.612
HydH (5)	0.7373
Hydrol (5b)	0.998

Scheme 1.

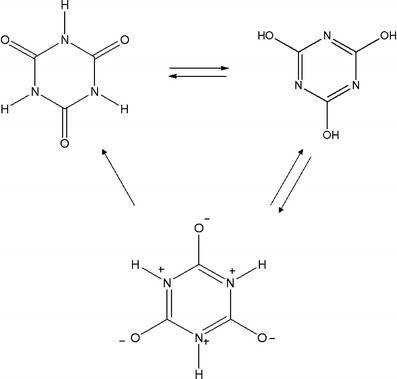
Contributing structures in cyanuric acid

These results can be compared to those for a different molecule that has little resemblance to cyanuric acid, in order to evaluate the suitability of the HOMA method for the present study. This molecule is 1,2,5-Trihydroxybenzene, commonly known as Phloroglucinol (see Fig. 3). With respect to this species, it has the same three OH substituents, but in this case it is expected to be very difficult to detect the phenomenon of tautomerism because the hydrogen atoms which leave the hydroxyl groups converting to the keto form should unite with the free carbon atoms on the ring, resulting in a severe distortion. The HOMA results for the enol and keto forms of this species are 0.9995 and 0.357 respectively. The difference between these two cases is larger than those in the case of cyanuric acid because this last is constituted from nitrogen atoms with dangling bonds which favor the keto-enolic equilibrium. Thus our comparison is useful in this context to validate the use of the HOMA method.

Fig. 3.

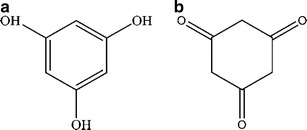
Phloroglucinol (a) enol form (b) keto form

The cyanuric acid molecule presents two zones of electronic flow; the first one is the typical delocalization zone in the ring, generated by the movement of the three electronic pairs inherent in the C = N bond. This flow has a current which resembles that of a classical aromatic ring. The second zone is that generated by the electrons associated with the three oxygen atoms in the carbonyl groups. Thus, two contributions to the stabilization of the molecule exist, relating to these two sets of electrons that will be analyzed with reference to the molecular orbitals analysis.

A diagram of molecular orbital (MO) interaction is shown in Fig. 4. There are several factors that should be noted here. First, cyanuric acid seems to represent a very strange case of aromaticity because of its particular MO arrangement. Several aromatic compounds manifest the set of six delocalized electrons in one single MO (HOMO) and a two-fold degenerate set (HOMO-1) which causes the resonant interaction, generating the aromatic cloud. The cyanuric acid molecule belongs to the D₃h symmetry group, therefore the sets that contain the six electrons of the resonant group belong to the e’ and a₂” irreducible representations. However, the energy of the three orbitals is practically the same, so that we have a strange case of an accidental triple degenerated set. This set keeps the electrons that participate in the aromatic flow at the center of the molecule, indeed this set is very curious because it is not common to find that all the MO’s manifest the same energy and neither is it common to find this set representing the HOMO-1 group. This degeneracy was confirmed with calculations up to MP4 level [30–32].

Fig. 4.

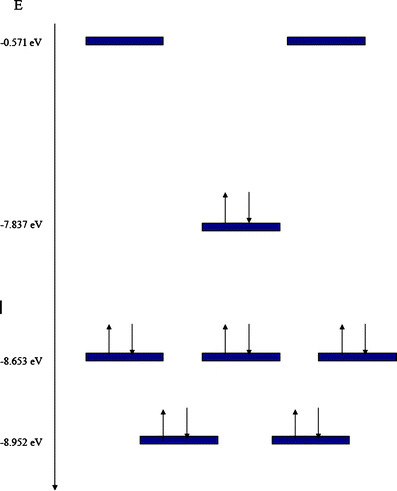
Interaction MO diagram showing both sets of electronic interaction for compound 5

Besides, although it might be expected that the HOMO would participate in aromaticity, at first sight this is not the case, because it seems that all “central” aromaticity is found in the HOMO-1 group. However it is also important to analyze the set formed by HOMO and HOMO-2. This set is a degenerated set that belongs to the e” irreducible representation that occupies almost the same region as the HOMO, therefore, it seems to be a classical set of three orbitals, separated by 1.115 eV depicting an aromatic set. However the set of the HOMO-1 orbitals is localized at the middle of the scheme. Both sets are shown in Fig. 5.

Fig. 5.

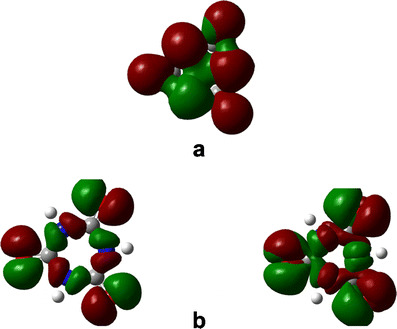
(a) Accidental triple degenerated set corresponding to HOMO-1. (b) Classic aromaticity set formed by HOMO and HOMO-2

The conclusion to all this is that we have two aromatic sets (double aromaticity [33, 34]); HOMO-1 represents one set, and HOMO, HOMO-2 the other one, and there is interaction between them. These two sets do not occupy the same space, although there is some overlap. This means that there must be competition between them and that they should thus shield each other. In other words, the contribution of each set is reduced with a concomitant decline in aromaticity. Thus, the molecule should have a very weak aromatic character concurring with the result obtained when aromaticity indexes are used. Applying this framework we can reveal the inductive effect due to the different substituents, but a drastic change is not expected because the strong interaction of molecular orbitals causes the molecule to imitate the same electronic behavior.

In Scheme 1, we put forward the equilibrium presented by cyanuric acid. The scheme is relatively simple in the case where the substituents are hydrogen atoms; however it can become very complicated in cases where compounds of this kind contain other types of substituents. Firstly; other substituents may not have the same mobility as hydrogen, therefore, it is to be expected that they will remain in their position on the nitrogen atom, secondly; it is a known fact that certain substituents have inductive effects, strongly affecting the electronic behavior of the aromatic ring.

The zwitterionic form continues to be aromatic and display interesting electronic properties. In order to evaluate the aromaticity of this family, the HOMA method is once again applied, however in this case we are using the theory designed by Krygowski [19] in order to develop an equation with specific characteristics, permitting a comparison to be made between the different aromaticity values for these substances. The keto form of the cyanuric acid (molecule 5 in the last table) has the most geometrically regular structure of any of the molecules in this study, therefore, we consider this species to represent the ideal model and establish that this is the most aromatic example out of the entire family. Thus the parameters of this molecule are applied to the Krygowski scheme, in the following way.

Krygowski’s general equation is presented as:

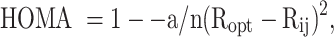6

where α corresponds to an empirical constant that helps take into account the length and angles of a particular ring and is evaluated in terms of

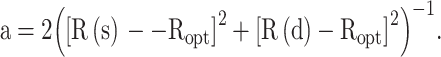7

By taking (6) and (7), an equation was developed for the purpose of evaluating the changes in cyanuric acid and its derivatives. Considering the calculated measurements of cyanuric acid itself as a pattern for evaluating α, substituting R(s) = 1.465 (the length of a single bond N-C as is described in the same work by Krygowski), R(d) = 1.269 (the length of a double bond between N and C as described by Krygowski) and Ropt = 1.387 in Eq. 7 yields a value of 99.96 for α. All these parameters were included in Eq. 6 and the relative HOMA aromaticity (named “internal” HOMA) for all species are presented in Table 3.

Table 3.

“Internal” HOMA for the compounds included in this study

Molecules	HOMA
HydCH3	0.999
HydOH	0.977
HydNH2	0.962
HydPH2	0.967
HydH	1.000
HydCOOH	0.912
HydCN	0.927
HydNO2	0.995

The order is the same as that in Table 2, but this time the molecules with substituents, which extract electronic charge from the ring (-COOH, -CN and –NO₂) have also been included. It should be noted that in the case of HydNO2, the value of aromaticity is increased, almost to the level of the reference molecule (HydH). This phenomenon is due to the presence of high electronic density in the substituent, which strongly reinforces the electronic flow on the periphery of the ring, in strong contrast to classic aromatic molecules.

Conclusions

Cyanuric acid and several derivatives were calculated in order to study their possible aromatic character. All species are aromatic in the enol form, but the keto form is more stable than the enol one. Therefore the aromaticity of all species in keto form was analyzed using ASE and HOMA methods. Surprisingly, both methods yield aromatic character, albeit not strong. The explanation is thus found in the frontier molecular orbitals analysis, where it is possible to identify two aromatic systems for cyanuric acid in keto form but it seems these systems are opposed, thus tending to decrease the overall aromatic character. As a result these molecules are only slightly aromatic.