Abstract
One of the critical steps in the development of an analytical technique is to confirm that its experimental response correlates with predictions derived from the theoretical framework on which it is based. This validates the technique quantitatively, and, in the case of a biosensor, facilitates a correlation of the sensor’s output signal to the concentration of the analyte being tested. Herein we report studies demonstrating that the quantitative response of Arrayed Imaging Reflectometry (AIR), a highly sensitive label-free biosensing method, is a predictable function of probe and analyte properties. We first incorporated a standard one-site Langmuir binding model describing probe-analyte interactions at the surface into the theoretical model for thickness-dependent reflectance in AIR. This established a hypothetical correlation between analyte concentration and the AIR response. Spectroscopic ellipsometry, surface plasmon resonance (SPR) and AIR were then used to validate this model for two biomedically important proteins, fibroblast growth factor-2 (FGF-2) and vascular endothelial growth factor (VEGF). While our studies demonstrated that the 1:1 one-site Langmuir model accurately described the observed response of macro spot AIR arrays, either a two-site Langmuir model or a Sips isotherm better described the behavior of AIR microarrays. These studies confirmed the quantitative performance of AIR across a range of probe-analyte affinities. Furthermore, the methodology developed here can be extended to other label-free biosensing platforms, thus facilitating a more accurate and quantitative interpretation of the sensor response.
Keywords: Label-free, biosensor, Langmuir binding isotherm, Sips isotherm, surface plasmon resonance, spectroscopic ellipsometry, arrayed imaging reflectometry
INTRODUCTION
The detection and quantitation of biomolecules is important in expanding our understanding of fundamental biology, and for clinical applications such as disease diagnosis and prognosis. Detection of biomolecules has traditionally been carried out using either fluorescently labeled targets1,2 or direct or sandwich immunoassays where the secondary antibody is conjugated to a fluorophore, enzyme or other reporter molecule.3,4,5 Although these techniques have been useful in research and diagnosis, the cost and complexity of such assays, along with their semi-quantitative nature due to the presence of the labels, have been widely recognized as inherent shortcomings.6,7 Moreover, the label itself may alter probe-analyte interactions.8 Hence, much research is currently focused on developing label-free detection methods and has resulted in the invention of biosensors transducing signals through plasmonic,9,10 optical,11,12,13,14,15 electrical16,17 or mechanical means.18,19,20
These signal transduction methods provide a measure of the occupancy of the surface- or solid-phase bound probe molecules by solution-phase analytes. Several studies have reported the quantitative interpretation of the sensor response by converting the surface occupancy to the surface concentration (mass per area) of the bound molecules. For example, in ellipsometry, the measured layer thickness can be converted to surface concentration either by simple multiplication (if the density of active probe molecules is known) or by using de Feijter’s formula, which provides surface mass density as a function of the measured thickness and the rate of change of the refractive index with the change in solution concentration of the analyte.21,22 A correlation of 1 pm thickness change to approximately 1 pg/mm2 surface density has been proposed for other related optical interference techniques.12,23 For surface plasmon resonance (SPR) spectroscopy, one can either use full numerical simulations of Maxwell’s equations24 or a simple calibration of the instrument’s response sensitivity25 (the resonance angle shift per unit change in bulk refractive index) to convert the SPR signal to the adsorbate surface concentration. A similar treatment has been used for SPR microscopy, wherein the reflectivity of a particular spot is converted to surface coverage based on an instrument calibration curve relating the change in reflectivity to the change in bulk refractive index.26 The course of translating the presence of biomolecules into the sensor response has two aspects: (i) the sensor itself responds to the change in the surface coverage, and (ii) the dependence of this surface coverage on the solution analyte concentration is in turn governed by the probe-analyte interactions occurring at the surface. Therefore, in order to ascertain how a sensor responds to different concentrations of analytes, a thorough understanding of the biomolecular interactions at the surface is a basic requisite. The ability to correlate sensor response to solution analyte concentration facilitates an accurate and quantitative understanding of the sensor performance and the physical and biomolecular factors affecting it.
We have previously reported the initial development of Arrayed Imaging Reflectometry (AIR) as a highly sensitive label-free biosensing technique. AIR relies on the creation and analyte binding-based destruction of a near-zero reflectance condition on a silicon chip.27,28 In brief, a substrate consisting of probe molecules immobilized on a thin layer of silicon dioxide on a planar silicon chip is designed to have near-zero reflectance for a fixed wavelength (632.8 nm), polarization (s-polarized) and angle of incidence (70.7°) of light. This low reflectance is highly sensitive to the thickness of the layers that comprise the substrate. The binding of analyte molecules to the immobilized probes causes a change in the thickness of the surface layer, and hence an increase in the reflectance of the system, which can then be measured using a simple optical apparatus. Spatially separated probe spots of approximately 100 μm in diameter can be easily resolved, and the technique is therefore useful for multiplexed detection.29,30
In our prior work, we calculated the dependence of the AIR sensor chip reflectance on the silicon dioxide layer thickness and showed it to be in agreement with experiments.28 In order to fully validate AIR in the context of probe-analyte binding, it was necessary to next extend the quantitative model by incorporating the solution analyte concentration as an independent variable. With this motivation, the main aim of this work was to first understand and model the probe-analyte interactions (antibody and protein in this case, respectively) occurring at the sensor surface. We could then incorporate these results into a model that correlates the surface coverage and thus the solution analyte concentration directly to the response from the AIR biosensor. Herein we report the full development of this model, and cross-correlation of AIR reflectivity measurements with thickness values obtained by spectroscopic ellipsometry and dissociation constants measured by surface plasmon resonance.
EXPERIMENTAL SECTION
AIR chip preparation, image acquisition, and image analysis were carried out using protocols similar to those previously described.30,29 Detailed protocols and sources of materials may be found in the Supplementary Information.
Theoretical Framework
The biosensing structure used in this work consists of a silicon substrate followed by a layer of thermal oxide, a probe layer (comprising the linking chemistry and the immobilized antibody), and a target layer accounting for the binding of the protein of interest. The reflectance of this structure was simulated using a standard characteristic matrix method, as reported previously.28 It was determined from this simulation that for 632.8 nm wavelength and for s-polarized light striking the substrate at an angle of incidence of 70.7°, the minimum reflectance condition occurs at a total layer thickness of 1420 Å (including the oxide and the probe layer). This differs slightly from the optimum thickness reported previously,28 resulting from differences in the index of refraction of the silicon substrates used, owing to different suppliers. The characteristic matrix method enabled us to model the increase in the reflectance of the sensor as a function of the protein thickness bound on top of the probe layer.
Protein-antibody interactions on the chip surface were initially modeled using both a 1:1 one-site Langmuir binding isotherm31,32 and a two-site Langmuir isotherm.33,34,35 The 1:1 model is generally viewed as applicable for protein-antibody interactions in which the antibody is immobilized, since although each antibody molecule provides two binding sites they can be treated as independent and equivalent.36,37 The 1:1 one-site Langmuir isotherm and the two-site Langmuir isotherm is described by
| (1a) |
and
| (1b) |
respectively. Here, Γ is the fractional surface coverage, C is the concentration of the protein in solution, KD is the dissociation constant for a protein-antibody pair, Θ1 is the fraction of binding sites having a dissociation constant KD1 and Θ2 is the fraction of binding sites having a dissociation constant KD2. The two-site Langmuir isotherm thus assumes two different types of binding sites on the surface. Since the sensor response depends on the thickness of the protein layer, fractional coverage is given by
| (2a) |
where t is the thickness of the protein layer at a given solution concentration, and tmax is the maximum thickness of the protein layer under a complete surface coverage condition. The fractions of the two different types of binding sites in the two-site Langmuir model can be expressed in terms of thickness as
| (2b) |
and
| (2c) |
where tmax1 is the thicknesses of the protein layer when the Θ1 fraction of binding sites is saturated and tmax2 is the thicknesses of the protein layer when the Θ2 fraction of binding sites is saturated. It should be noted that tmax1 + tmax2 = tmax.
Combining equations 1a and 2a or 1b and 2b results in
| (3a) |
and
| (3b) |
respectively, which express the measured thickness as a function of the solution protein concentration, maximum thickness, and dissociation constant(s). KD values for the protein-antibody interactions were determined using SPR and tmax values were determined by spectroscopic ellipsometry. For the 1:1 Langmuir model, the experimentally obtained KD and tmax values were sufficient to model the sensor response as a function of analyte concentration. For the two-site Langmuir model, KD1 was held constant at the dissociation constant obtained by SPR, while KD2, tmax1 and tmax2 were varied (with the constraint tmax1 + tmax2 = tmax) to obtain a best fit to experimental AIR data using a least squares method.
The thicknesses of the protein layer for different solution concentrations of the protein were then included in the AIR thickness based simulations to calculate the corresponding change in reflectance as a function of protein concentration. Thus, combining the characteristic matrix method for calculating the change in the reflectance (or response) of the AIR sensor as a function of protein thickness and one of the Langmuir models for correlating the protein layer thickness to the solution protein concentration yielded a direct correlation between the response of the AIR sensor and the solution protein concentration.
In order to facilitate a comparison with experimental data, the sensor response was normalized between 0 to 1 using
| (4) |
where R is the reflectance at a given protein concentration, Rmin is the minimum reflectance corresponding to the antibody-terminated chip treated with buffer alone, and Rmax is the maximum reflectance obtained for a saturating protein concentration or for 100% surface coverage (t = tmax).
RESULTS AND DISCUSSION
AIR reports changes in reflectivity as a function of material deposited on the surface of an antireflective chip. To verify that this behaves in a predictable fashion as a function of solution protein concentration in the context of antibody-protein binding, it was important to relate the experimentally obtained reflectance values to independently measured thicknesses and affinities. The direct relationship obtained between the chip reflectance and the solution protein concentration was tested by studying the binding of two model proteins, fibroblast growth factor-2 (FGF-2) and vascular endothelial growth factor (VEGF), to their corresponding monoclonal antibodies immobilized on an AIR chip. Both FGF-2 and VEGF play important roles in many normal and altered physiological processes, including angiogenesis, wound healing, bone growth, cancer development and retinopathy.38,39,40,41,42,43 The levels of these proteins in various body fluids (particularly serum, saliva or wound fluid) have been shown to be indicators of disease/healing stage and disease recurrence.44,45,46 Therefore, in addition to their value as representative proteins for testing the sensor, sensitive and quantitative detection of these growth factors from biological fluids is of critical importance to the field of clinical diagnostics. Because the commercially obtained antibody-protein pairs displayed substantially different affinities in these two cases (vide infra), they also provided an opportunity to examine sensor performance and model congruence as a function of capture molecule (antibody in this case) affinity.
Our overall strategy proceeded as follows: the solution protein concentration was used to calculate the thickness build-up of the protein layer, which could then be converted into sensor reflectance. Initial efforts centered on using a 1:1 one-site Langmuir binding model to determine the fractional surface coverage of the total available binding sites in a spot containing an antibody probe, for a given protein concentration based on the affinity of interaction for the protein-antibody pair. The fractional surface coverage could then be converted into a thickness if the thickness of the protein layer at 100% surface coverage was known. The reflectance of the antibody spot was then calculated based on the change in thickness induced by protein binding. In addition to the one-site Langmuir model, two-site Langmuir and Sips isotherms were also explored to explain experimental observations and provide additional insight into the biomolecular interactions occurring at the surface.
Determination of Protein-Antibody Interaction Affinity
Surface plasmon resonance experiments were carried out to determine the binding affinity (expressed as the dissociation constant, KD) for the interaction of FGF-2 and VEGF with their respective monoclonal antibodies. The FGF-2 sensorgrams were obtained in duplicate, and each was globally fit to a 1:1 Langmuir binding model which resulted in a dissociation constant (KD) of 1.6 ± 0.1 nM and rates of association (ka) and dissociation (kd) of (2.8 ± 0.5) × 107 M−1s−1 and 0.044 ± 0.004 s−1, respectively. Preliminary measurements of the VEGF - anti-VEGF interaction suggested that the affinity constants were outside the dynamic range of the instrument,47 and hence an SPR-based solution affinity assay48,49 was used to accurately determine the interaction affinity. A KD of 97.1 ± 24.5 pM was obtained by fitting the data to a ligand depletion model (Supporting Information S7 and S8, Figures S2 and S3).
Determination of tmax
The tmax was determined experimentally by measuring the thickness change induced by protein binding at concentrations of 10 μg/mL and 1 μg/mL (corresponding to molar concentrations of 575 nM and 57.5 nM for FGF-2 and 250 nM and 25 nM for VEGF) using spectroscopic ellipsometry. These concentrations were chosen because the preliminary simulations using the measured KD values suggested that the protein-antibody interaction signal saturates around 1 μg/mL (i.e., 57.5 nM and 25 nM for FGF-2 and VEGF, respectively). Since the measured thicknesses at the two concentrations tested were not significantly different, this confirmed that the signal saturates at 1 μg/ml (see Supporting Information Figure S1), and this was used as the highest concentration for all subsequent experiments.
Model
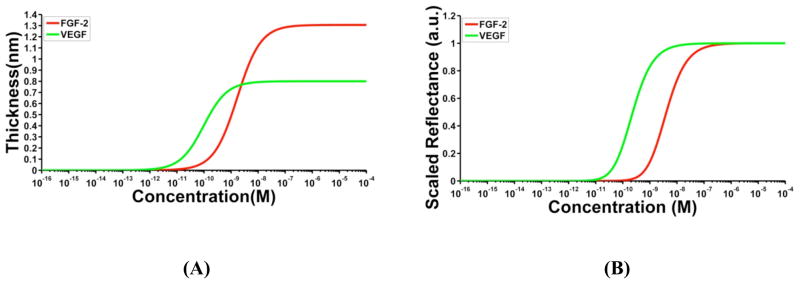
Having experimentally determined the KD and tmax values for both FGF-2 and VEGF, a 1:1 one-site Langmuir binding curve was simulated using equation 3a. Figure 1A shows the sigmoidal variation of the thickness of FGF-2 and VEGF protein layers with their respective solution concentrations. We observe that the dissociation constant corresponds to the protein concentration at which the thickness of the protein layer is half of its maximum value, in accordance with the expected behavior for a one-site Langmuir binding isotherm. The difference in the tmax of the two proteins can be seen as the different saturating values for the y-axis, and the difference in the interaction affinities is evident as a shift in the one-site Langmuir curve along the x-axis. Next, an AIR response curve was simulated by incorporating the one-site Langmuir curve into the AIR thickness-based model, and the results are shown in Figure 1B for both the proteins. The different tmax values for FGF-2 and VEGF result in different saturation reflectance changes on the AIR setup. We normalized the simulated signals plotted in Figure 1B with respect to the Rmax of each protein individually (See Supporting Information, Figure S4 for the variation of unscaled raw reflectance values as a function of protein concentration).
Figure 1.
Simulated binding curves. (A) One-site Langmuir curves depicting the 1:1 binding interaction of FGF-2 (red) and VEGF (green) with their respective antibodies simulated using equation 3a. The maximum thicknesses (tmax) for FGF-2 and VEGF used in the simulations were determined using spectroscopic ellipsometry to be 1.3 nm and 0.8 nm, respectively. Dissociation constants of 1.6 nM and 100 pM, as determined by SPR, were used in the simulations for FGF-2 and VEGF, respectively. (B) AIR response curves for FGF-2 and VEGF were simulated by incorporating the 1:1 Langmuir model into the AIR thickness-dependent reflectance model. Raw reflectance values from the simulation were scaled between 0 and 1.
The predicted AIR response curve for the protein-antibody interactions is sigmoidal in nature. Unlike a Langmuir isotherm, the KD now corresponds to the protein concentration at which the scaled reflectance value is 25% of its maximum. This is expected because of the non-linear nature of the AIR response with thickness.28 While this non-linear response confers the technique its high sensitivity to very small thickness changes, it also mandates that the scaled reflectance versus concentration curve cannot be directly interpreted as a one-site Langmuir curve. It can also be seen that the scaled AIR response curve is dependent only on the interaction affinity between the probe and the target analyte and not on the saturation thickness tmax. This implies that any variations in the surface density of the probe, which can be due to different types of capture molecules or surface attachment chemistries, will not have a significant effect on the scaled AIR response as long as the affinity of the probe-analyte interaction remains unchanged.
Thickness Measurements
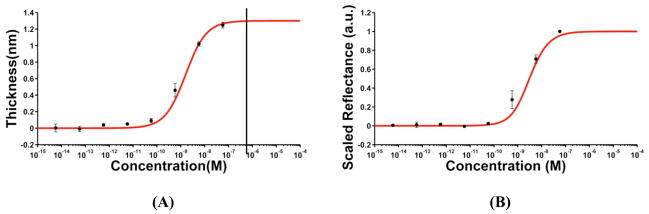
Thickness changes for different concentrations of FGF-2 obtained from spectroscopic ellipsometry were consistent with the presence of a single-affinity binding site on the surface. Thus, we utilized a one-site Langmuir model, the simplest isotherm that describes protein-antibody interactions, to fit the data. Figure 2A shows the thickness changes overlaid on the plot depicting the one-site Langmuir model with a KD of 1.6 nM. This model makes several assumptions for the protein-antibody binding interactions: (i) it assumes that all the surface-attached antibody binding sites are equivalent and equally accessible by the protein molecules, and (ii) that the binding event occurring at one site is not affected by the neighboring sites. It is important to note that these assumptions are not strictly fulfilled in our system owing to the random orientations of the antibody binding sites on the surface along with the steric factors associated with the protein-antibody interactions on a two dimensional surface (discussed further below). Nevertheless, we see that the experimental data closely follow the one-site Langmuir curve. The small deviations at some of the lower concentrations can be attributed to the difference involved in the KD measured using SPR and the actual KD on the chip surface. For SPR experiments, anti-human FGF-2 was covalently attached to a carboxymethyldextran (CMD) modified gold chip (CM5). The dextran layer provides a three-dimensional, flexible matrix for antibody immobilization.50 In contrast, the antibody on an AIR chip is covalently attached to a flat surface, likely causing slight changes in antibody-protein binding kinetics.
Figure 2.
Comparison of ellipsometric (A) and AIR binding data (B) for FGF-2 using a one-site Langmuir isotherm. In both graphs, the red trace represents the theoretically modeled curves, while the black points correspond to the average ellipsometric thickness measurements of the FGF-2 layer at different concentrations in (A) and to the scaled reflectance values measured by AIR in (B). Error bars represent the standard deviation of the respective measurements from the mean value for three replicate experiments. The black line in (A) indicates the highest protein concentration (10 μg/mL or 575 nM) used to verify saturation thickness (Supporting Information Figure S1).
Figure 2A suggests that, in spite of the random orientations, the surface presents a relatively uniform binding affinity. The fact that the effect of any steric hindrances is not easily observed can be attributed to the methodology followed for the determination of tmax, or the maximum surface coverage for the protein. This thickness measurement takes into account the low accessibility of some of the surface-bound binding sites and the effect of steric factors associated with the binding events occurring at neighboring sites on the surface, thus, facilitating a close agreement between the experimental measurements and the model.
The high affinity of the anti-VEGF antibody, combined with the large size of the macro spots (~6 mm) caused significant depletion of VEGF in the target volume at low concentrations (data not shown). Ellipsometric measurements, therefore, were not feasible at any but the highest VEGF concentrations of 10 μg/mL and 1 μg/mL (250 nM and 25 nM, respectively). These measurements were used only to determine the tmax for this protein (Supporting Information Figure S1).
Reflectance Measurements for AIR Response
FGF-2 Macro spots
Intensity values for the anti-FGF-2 macro spots subjected to different concentrations of FGF-2 were analyzed as described in the methods section, and the obtained reflectance values were scaled between 0 and 1. Since the thickness measurements obtained from the macro spots closely followed a one-site Langmuir (Figure 2A), we expected the corresponding AIR response to follow the same model. Figure 2B shows an overlay of the measured AIR reflectance values on the simulated AIR response obtained by considering the one-site Langmuir binding isotherm. We observe that the experimental measurements closely follow the model as expected. Thus, for FGF-2 in macro spots, thickness measurements from ellipsometry, one-site binding behavior using an SPR-derived binding constant, and AIR reflectance data all cross-correlate well. As mentioned earlier, the target depletion effect observed in the case of VEGF macroarrays, owing to a combination of high affinity between the antibody-protein pair and large spot size, made it unfeasible to acquire reliable AIR reflectance data from the anti-VEGF macro-spotted chips.
Microarrays
Our initial experiments used macro spots because they provided a platform to directly compare ellipsometric measurements with AIR reflectance data, and provided insight on the applicability of our model to represent protein-antibody interactions on the surface. We next studied the AIR response for antibody microarrays, as microarrays are a more versatile and widely used platform, and are essential for high throughput applications of the sensor. Intensity values from anti-FGF-2 and anti-VEGF microarrays exposed to different concentrations of their respective proteins were analyzed as described in the methods section. The obtained reflectance values were scaled and overlaid on the simulated AIR response to a one-site binding model.
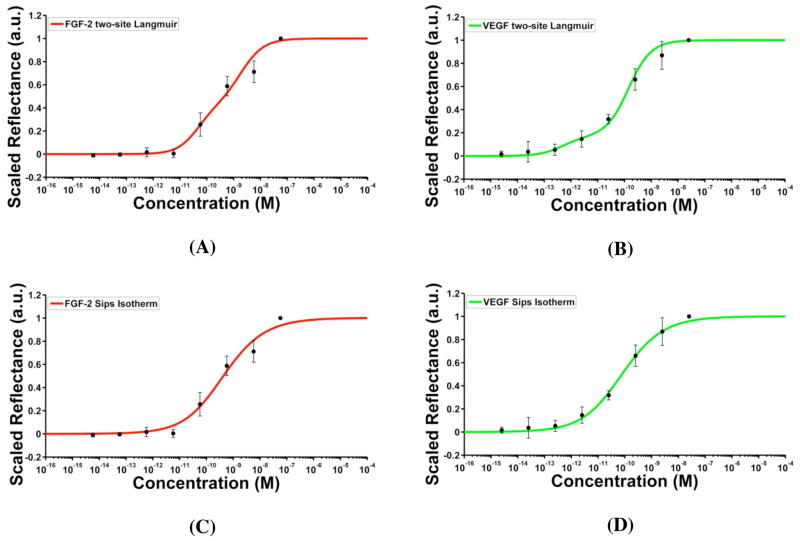
As expected, the reflectance measurements for both FGF-2 and VEGF largely followed the predicted sigmoidal behavior. However, there was a noticeable deviation between the model and experimental observations at concentrations below 575 pM for FGF-2 and below 25 pM for VEGF (Supporting Information Figure S8). The higher than expected signal at these concentrations suggested the presence of a population of binding sites with affinities stronger than the measured KD. To test this possibility, we fit the data to a two-site Langmuir model, for which one of the two dissociation constants was kept constant at the value obtained from SPR and the second dissociation constant was allowed to vary. The relative fractions of the two types of sites represented by tmax1 and tmax2 were allowed to vary with the constraint that tmax1 + tmax2 = tmax. The fits, obtained by a least-squares method, are shown in Figure 3A and B for FGF-2 and VEGF, respectively. For FGF-2 microarrays, the simulated model corresponds to ~40% of binding sites with a KD of 1.6 nM, and the remaining with a KD of 27.2 pM. In the case of VEGF, the best fit was obtained for ~71% of the binding sites with a KD of 100 pM and the remaining sites with a KD of 0.36 pM. It is evident from the close agreement between the data and the simulated response that a two-site Langmuir better represents the binding interactions on the AIR microarray chip surface than the one-site Langmuir binding.
Figure 3.
AIR response curves based on the two site Langmuir fits to FGF-2 (A) and VEGF microarrays (B), and Sips isotherm fits to FGF-2 (C) and VEGF (D). Red and green traces correspond to the simulated curves and the black points represent experimental scaled reflectance measurements. Error bars correspond to the standard deviation of the scaled reflectance values from the mean for three replicate experiments.
An alternative model that accounts for binding site heterogeneity on the surface is the Sips isotherm. Rather than positing a highly constrained set of affinities (such as the two-site Langmuir), the Sips isotherm assumes a Gaussian-like distribution of affinities centered about an average affinity constant.51,52 The isotherm is given by
| (6) |
where a is the heterogeneity index that determines the width of the distribution and KDa is the average dissociation constant. The case of a = 1 represents a homogeneous distribution, and the Sips isotherm reduces to a one-site Langmuir model. A value of a < 1 corresponds to a heterogeneous distribution of binding site affinities. Fitting the reflectance data obtained from the anti-FGF-2 and anti-VEGF microarrays to an AIR model based on the Sips isotherm results in the plots shown in Figure 3C and 3D. From the fits to equation 6, values of a and KDa were obtained for FGF-2 (0.52 and 122.2 pM) and VEGF (0.53 and 27.2 pM).
The results of different isotherms used to model the AIR response are compared in Table 1. Consistent with the fits already discussed, in the case of microarrays, AIR reflectance models based on either the two-site Langmuir or a Sips isotherm fit the experimental data with higher fidelity than a model based on a one-site Langmuir isotherm. However, how does one determine which model (two-site Langmuir or Sips) provides a better representation of the actual physical processes taking place on the surface of the chip? In our surface attachment chemistry, the antibodies are immobilized via a non-directed amine-aldehyde coupling reaction, potentially resulting in multiple antibody orientations. One could readily imagine that the changes in conformation and accessibility of binding sites caused by this method of immobilization could give rise to either a discrete set or a range of closely spaced antibody affinities.52
Table 1.
Comparison of the different models used to study protein-antibody interactions on the surface via AIR.
| Protein | Array Format | One-site Langmuir | Two-site Langmuir | Sips Isotherm |
|---|---|---|---|---|
| FGF-2 | Macro spots |
KD = 1.6 nMb tmax = 1.3 nmc R2 = 0.98d |
NSd |
KDa = 1.6 nMb tmax = 1.3 nmc a = 1 R2 = 0.98 |
|
| ||||
| FGF-2 | Microarrays |
KD = 1.6 nMb tmax = 1.3 nmc R2 = 0.82 |
KD1 = 1.6 nMb KD2 = 27.2 pM tmax1 = 0.51 nm tmax2 = 0.79 nm R2 = 0.98 |
KDa = 122.2 pM tmax = 1.3 nmc a = 0.52 R2 = 0.98 |
|
| ||||
| VEGF | Microarrays |
KD = 100 pMb tmax = 0.8 nmc R2 = 0.97e |
KD1 = 100 pMb KD2 = 0.36 pM tmax1 = 0.57 nm tmax2 = 0.23 nm R2 = 0.99e |
KDa = 27.2 pM tmax = 0.8 nmc a = 0.53 R2 = 0.99 |
Determined by SPR.
Measured by spectroscopic ellipsometry for saturating concentrations of the protein. tmax = tmax1+ tmax2 was fixed at 1.3 nm for FGF-2 and 0.8 nm for VEGF, as measured by ellipsometry.
NS (Not Significant); for FGF-2 macro spot data a two-site based Langmuir model was fit and an F-test was utilized to statistically compare the two models.53 The analysis resulted in a P value of 0.0680; for a 99% confidence interval this indicates that there is not a significant difference between the one-site and the two-site-based Langmuir fits.
Similarly, an F-test was utilized to compare the one-site and two-site Langmuir fits for the VEGF microarray data. A P value of 0.0036 was obtained and at a 99 % confidence interval this indicated that the two-site based model was statistically better than the one-site model.
In order to understand the significance of the heterogeneity indices obtained from the Sips-based fit, we estimated the distributions of the affinities predicted by the isotherm (Supporting Information, Eq. S4). The widths of the distributions of affinities obtained from the a values for the two proteins (Supporting Information Figure S9) suggest that the obtained fits correspond to a highly heterogeneous population of binding sites, with affinities ranging over four orders of magnitude. While one cannot a priori rule out such a broad distribution of affinities, it seems less plausible than the physical picture represented by the two-site Langmuir model. This is particularly compelling when one considers macro spot results for FGF-2, which closely followed a one-site Langmuir model. In order to further verify this observation, we also fit our FGF-2 macro spots data to a two-site Langmuir and Sips-based AIR reflectance curve (Supporting Information Figure S10). Statistical analysis suggested that the two-site fit was not significantly different from the one-site fit (Table 1). For a Sips isotherm, the best fit with the KD fixed was obtained for an a value of 1 (R2 = 0.98), consistent with a homogeneous population of binding sites on the surface.
An interesting observation in this study is the difference in the behavior of the same antibody when immobilized in a macro spot versus microarray format. Anti-FGF-2 binding sites in the macro spots appeared to present a uniform affinity towards the protein in solution, whereas they presented a binary (or even more heterogeneous) distribution in the microarrays. It should be noted that the spot size changes almost 60-fold in going from macro spots to microarrayed spots, resulting in ~3600 fold change in the spot surface area. The spotting volumes used for the two methods are very different, with 30 μL in a macro spot and ~ 1 nL in a micro spot. Although the spotting concentrations used are similar, different rates of evaporation can cause differential increases in the concentration of the spotted solutions. Thus, the dynamics of the immobilization process can be very different in the two cases, and can result in different surface densities of the immobilized molecules, as has been shown for amine-mediated DNA immobilization.54 It is also known that increased density of the immobilized probe molecules on a surface can affect the affinity constant for probe-analyte interactions by, in most cases, increasing the affinity by slowing the dissociation rates.55,56,57 We hypothesize that the above-mentioned factors all contribute to the difference in the antibody behavior observed in the two instances. Different surface densities of the antibodies can result in altered saturation thickness (tmax) values for the proteins and affect the absolute reflectance values observed with our sensor, but the process of normalization to the saturation reflectance Rmax corrects for such changes, and hence the model itself is unaltered.
CONCLUSIONS
We have developed and validated a theoretical and experimental framework that correlates the response of AIR with the solution protein concentration by combining appropriate probe-analyte binding isotherms with the AIR thickness-based model for reflectivity. We used SPR measurements and spectroscopic ellipsometry to demonstrate that the interaction of FGF-2 with anti-FGF-2 on our sensor surface in a macro spot format follows a one-site Langmuir isotherm. The AIR measurements obtained in this format are also in agreement with the corresponding response model. For a microarrayed format, we showed that AIR signals from two different proteins, VEGF and FGF-2, closely followed a model corresponding to a two-site Langmuir binding isotherm. These data together suggest that, although a nonselective immobilization method (imine formation) was used for antibody deposition, binding is well represented by a discrete set of affinities. We also observed that the affinity of at least one population of binding sites present on our chip surface is consistent with that measured using SPR as a reference technique. The response of AIR microarrays is also well modeled by a Sips isotherm, although this model requires a highly heterogeneous distribution of affinities to provide a good fit. Further studies examining the relationship of antibody immobilization chemistry (including oriented vs. non-oriented methods) with sensor performance and model correspondence may be useful. Of critical importance, this study demonstrates that the performance of AIR is a highly predictable function of the size and binding properties of the biomolecular partners (antibody and protein) used in the experiment, and therefore provides confidence that high-quality analytical data can be obtained from the technique.
Supplementary Material
Acknowledgments
We thank Dr. Prakash B. Palde and Leslie O. Ofori for assistance with the surface plasmon resonance experiments. This work was supported by the University of Rochester Human Immunology Center (NIH R24-AL054953).
Footnotes
SUPPORTING INFORMATION AVAILABLE
Abbreviations used, materials, experimental procedures for chip preparation, maximum thickness change (tmax) measurements for FGF-2 and VEGF (Figure S1), replicate SPR kinetics data for FGF-2 and anti-FGF-2 binding interaction (Figure S2), ligand depletion model (Eq.S1), theoretical model depicting the variation of raw reflectance values with the concentration of protein (Figure S3), AIR chip images for FGF-2 macroarrays, (Figure S4, S5 and S6), and Sips isotherm to describe the protein-antibody binding interactions on the surface. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Miller JC, Zhou H, Kwekel J, Cavallo R, Burke J, Butler EB, Teh BS, Haab BB. Proteomics. 2003;3:56–63. doi: 10.1002/pmic.200390009. [DOI] [PubMed] [Google Scholar]
- 2.MacBeath G. Nat Genet (Suppl) 2002;32:526–532. doi: 10.1038/ng1037. [DOI] [PubMed] [Google Scholar]
- 3.Engvall E, Perlman P. Immunochemistry. 1971;8:871–874. doi: 10.1016/0019-2791(71)90454-x. [DOI] [PubMed] [Google Scholar]
- 4.Palma RD, Reekmans G, Liu C, Wirix-Speetjens R, Laureyn W, Nilsson O, Lagae L. Anal Chem. 2007;79:8669–8677. doi: 10.1021/ac070821n. [DOI] [PubMed] [Google Scholar]
- 5.Alefantis T, Grewal P, Ashton J, Khan AS, Valdes JJ, Del Vecchio VG. Mol Cell Probes. 2004;18:379–382. doi: 10.1016/j.mcp.2004.06.003. [DOI] [PubMed] [Google Scholar]
- 6.Qavi AJ, Washburn AL, Byeon JY, Bailey RC. Anal Bioanal Chem. 2009;394:121–135. doi: 10.1007/s00216-009-2637-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ray S, Mehta G, Srivastava S. Proteomics. 2010;10:731–748. doi: 10.1002/pmic.200900458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sun YS, Landry JP, Fei YY, Zhu XD. Langmuir. 2008;24:13399–13405. doi: 10.1021/la802097z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Homola J, Yee SS, Gauglitz G. Sens Actuators, B. 1999;54:3–15. [Google Scholar]
- 10.Haes AJ, Van Duyne RP. J Am Chem Soc. 2002;124:10596–10604. doi: 10.1021/ja020393x. [DOI] [PubMed] [Google Scholar]
- 11.Bornhop DJ, Latham JC, Kussrow A, Markov DA, Jones RD, Sorensen HS. Science. 2007;317:1732–1736. doi: 10.1126/science.1146559. [DOI] [PubMed] [Google Scholar]
- 12.Piehler J, Brecht A, Gauglitz G. Anal Chem. 1996;68:139–143. doi: 10.1021/ac9504878. [DOI] [PubMed] [Google Scholar]
- 13.Arnold S, Shopova SI, Holler S. Opt Express. 2010;18:281–287. doi: 10.1364/OE.18.000281. [DOI] [PubMed] [Google Scholar]
- 14.Wang ZH, Jin G. Anal Chem. 2003;75:6119–6123. doi: 10.1021/ac0347258. [DOI] [PubMed] [Google Scholar]
- 15.Ozkumur E, Needham JW, Bergstein DA, Gonzalez R, Cabodi M, Gershoni JM, Goldberg BB, Unlu MS. Proc Natl Acad Sci. 2008;105:7988–7992. doi: 10.1073/pnas.0711421105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zheng G, Patolsky F, Cui Y, Wang WU, Lieber CM. Nat Biotechnol. 2005;23:1294–1301. doi: 10.1038/nbt1138. [DOI] [PubMed] [Google Scholar]
- 17.Kim JP, Lee BY, Lee J, Hong S, Sim SJ. Biosens Bioelectron. 2009;24:3372–3378. doi: 10.1016/j.bios.2009.04.048. [DOI] [PubMed] [Google Scholar]
- 18.Godber B, Thompson KSJ, Rehak M, Uludag Y, Kelling S, Sleptsov A, Frogley M, Wiehler K, Whalen C, Cooper MA. Clin Chem. 2005;51:1962–1972. doi: 10.1373/clinchem.2005.053249. [DOI] [PubMed] [Google Scholar]
- 19.Carrascosa LG, Moreno M, Alvarez M, Lechuga LM. Trends Anal Chem. 2006;25:196–206. [Google Scholar]
- 20.Liu Y, Zhang W, Yu X, Zhang H, Zhao R, Shangguan D, Li Y, Shen B, Liu G. Sens Actuators, B. 2004;99:416–424. [Google Scholar]
- 21.De Feijter JA, Benjamin J, Veer FA. Biopolymers. 1978;17:1759–1772. [Google Scholar]
- 22.Arwin H. Thin Solid Films. 2000;377:48–56. [Google Scholar]
- 23.Ozkumur E, Yalcin A, Cretich M, Lopez CA, Bergstein DA, Goldberg BB, Chiari M, Unlu MS. Biosens Bioelectron. 2009;25:167–172. doi: 10.1016/j.bios.2009.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stenberg E, Persson B, Roos H, Urbaniczky C. J Colloid Interface Sci. 1991:143, 513. [Google Scholar]
- 25.Jung LS, Campbell CT, Chinowsky TM, Mar MN, Yee SS. Langmuir. 1998;14:5636–5648. [Google Scholar]
- 26.Shumaker-Parry JS, Campbell CT. Anal Chem. 2004;76:907–917. doi: 10.1021/ac034962a. [DOI] [PubMed] [Google Scholar]
- 27.Lu J, Strohsahl CM, Miller BL, Rothberg LJ. Anal Chem. 2004;76:4416–4420. doi: 10.1021/ac0499165. [DOI] [PubMed] [Google Scholar]
- 28.Mace CR, Striemer CC, Miller BL. Anal Chem. 2006;78:5578–5583. doi: 10.1021/ac060473+. [DOI] [PubMed] [Google Scholar]
- 29.Mace CR, Striemer CC, Miller BL. Biosens Bioelectron. 2008;24:334–337. doi: 10.1016/j.bios.2008.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mace CR, Topham DJ, Mosmann TR, Quataert S, Treanor J, Miller BL. Talanta. 2011;83:1000–1005. doi: 10.1016/j.talanta.2010.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Langmuir I. J Am Chem Soc. 1916;38:2221–2295. [Google Scholar]
- 32.Duschl C. In: Biomolecular Sensors. Gizeli E, Lowe CR, editors. Taylor and Francis; London: 2002. pp. 87–120. [Google Scholar]
- 33.Tetin SY, Hazlett TL. Methods. 2000;20:341–361. doi: 10.1006/meth.1999.0927. [DOI] [PubMed] [Google Scholar]
- 34.Johnson CP, Jensen IE, Prakasam A, Vijayendran R, Leckband D. Bioconjugate Chem. 2003;14:974–978. doi: 10.1021/bc034063t. [DOI] [PubMed] [Google Scholar]
- 35.Ahmed SR, Lutes AT, Barbari TA. J Membrane Science. 2006;282:311–321. [Google Scholar]
- 36.Adamczyk M, Moore JA, Yu Z. Methods. 2000;20:319–328. doi: 10.1006/meth.1999.0925. [DOI] [PubMed] [Google Scholar]
- 37.Karlsson R, Larsson A. In: Methods in Molecular Biology. Lo BKC, editor. Vol. 248. Humana Press Inc; Totowa, NJ: 2003. pp. 389–415. [DOI] [PubMed] [Google Scholar]
- 38.Montesano R, Vassalli JD, Baird A, Guillemin R, Orci L. Proc Natl Acad Sci. 1986;83:7297–7301. doi: 10.1073/pnas.83.19.7297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cronauer MV, Hittmair A, Eder IE, Hobisch A, Culig Z, Ramoner R, Zhang J, Bartsch G, Reissigl A, Radmayr C, Thurnher M, Klocker H. Prostate. 1997;31:223–233. doi: 10.1002/(sici)1097-0045(19970601)31:4<223::aid-pros3>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 40.Barrientos S, Stojadinovic O, Golinko MS, Brem H, Tomic-Canic M. Wound Repair Regen. 2008;16:585–601. doi: 10.1111/j.1524-475X.2008.00410.x. [DOI] [PubMed] [Google Scholar]
- 41.Shivakumar S, Prabhakar BT, Jayashree K, Rajan MGR, Salimath BP. J Cancer Res Clin Oncol. 2009;135:627–636. doi: 10.1007/s00432-008-0497-9. [DOI] [PubMed] [Google Scholar]
- 42.Ferrara N. J Mol Med. 1999;77:527–543. doi: 10.1007/s001099900019. [DOI] [PubMed] [Google Scholar]
- 43.Stadelman WK, Digenis AG, Tobin GR. Am J Surg. 1998;176(Suppl A):26S–38S. doi: 10.1016/s0002-9610(98)00183-4. [DOI] [PubMed] [Google Scholar]
- 44.Shariat SF, Karam JA, Jochen W, Roehrborn CG, Montorsi F, Margulis V, Saad F, Slawin KM, Karakiewicz PI. Clin Cancer Res. 2008;14:3785–3791. doi: 10.1158/1078-0432.CCR-07-4969. [DOI] [PubMed] [Google Scholar]
- 45.Brooks MN, Wang J, Li Y, Zhang R, Elashoff D, Wong DT. Mol Med Report. 2008;1:375–378. [PMC free article] [PubMed] [Google Scholar]
- 46.Brozovic S, Vucicevic-Boras V, Mravak-Stipetic M, Jukic S, Kleinheinz J, Lukac J. Oral Pathol Med. 2002;31:106–108. doi: 10.1034/j.1600-0714.2002.310208.x. [DOI] [PubMed] [Google Scholar]
- 47.Biacore X Instrument Handbook. Biacore AB; Uppsala, Sweden: 2001. [Google Scholar]
- 48.Karlssson R. Anal Biochem. 1994;221:142–151. doi: 10.1006/abio.1994.1390. [DOI] [PubMed] [Google Scholar]
- 49.Cochran S, Li C, Fairweather JK, Kett WC, Coombe DR, Ferro V. J Med Chem. 2003;46:4601–4608. doi: 10.1021/jm030180y. [DOI] [PubMed] [Google Scholar]
- 50.Myszka DG. Curr Opin Biotechnol. 1997;8:50–57. doi: 10.1016/s0958-1669(97)80157-7. [DOI] [PubMed] [Google Scholar]
- 51.Sips RJ. Chem Phys. 1948;16:490–495. [Google Scholar]
- 52.Vijayendran RA, Leckband DE. Anal Chem. 2001;73:471–480. doi: 10.1021/ac000523p. [DOI] [PubMed] [Google Scholar]
- 53.Motulsky HJ, Christopoulos A. Fitting models to biological data using linear and nonlinear regression. A practical guide to curve fitting. GraphPad Software Inc; San Diego, CA: 2003. [Google Scholar]
- 54.Gong P, Harbers GM, Grainger DW. Anal Chem. 2006;78:2342–2351. doi: 10.1021/ac051812m. [DOI] [PubMed] [Google Scholar]
- 55.Nygren H, Czerkinsky C, Stenberg M. J Immunol Methods. 1985;85:87–95. doi: 10.1016/0022-1759(85)90276-5. [DOI] [PubMed] [Google Scholar]
- 56.Kanda V, Kariuki JK, Harrison DJ, McDermott MT. Anal Chem. 2004;76:7257–7262. doi: 10.1021/ac049318q. [DOI] [PubMed] [Google Scholar]
- 57.Giraudi G, Rosso I, Baggiani C, Giovannoli C. Analytica Chimica Acta. 1999;381:133–146. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.