Using luminosity data as a proxy for economic statistics

Abstract

A pervasive issue in social and environmental research has been how to improve the quality of socioeconomic data in developing countries. Given the shortcomings of standard sources, the present study examines luminosity (measures of nighttime lights visible from space) as a proxy for standard measures of output (gross domestic product). We compare output and luminosity at the country level and at the 1° latitude × 1° longitude grid-cell level for the period 1992–2008. We find that luminosity has informational value for countries with low-quality statistical systems, particularly for those countries with no recent population or economic censuses.

One of the central issues in social and environmental research has been how to improve the quality of socioeconomic data in developing countries. Many countries of tropical Africa, particularly those war-torn countries, have no reliable censuses of population and only rudimentary economic statistics. The poor quality of the data has hindered attempts to understand economic growth, poverty, health status, and environmental quality in these countries. The lack of good regional data has been even more daunting for researchers working at the subnational level, for example in the geographically based economic data (G-Econ) project at Yale University, which has undertaken the construction of geophysically based data on gross output for grid cells measuring 1° latitude × 1° longitude (1).

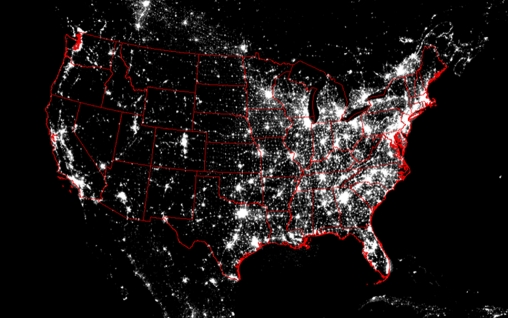
Because of the shortcomings of standard statistical sources, we undertook to examine approaches that could supplement or substitute for existing measures of regional output, income, and other economic and demographic variables. The obvious place to look was nighttime luminosity. There is a large literature on luminosity and its use as a proxy for population, output, and poverty. The intuitive notion is that luminosity might serve as a useful proxy because it is objectively measured, is highly correlated with output, and is available since 1992 for all world land areas except for high latitudes. Fig. 1 shows a striking image of nighttime stable lights for North America, and it is immediately obvious that high-income regions have higher luminosity. The question is whether these data can be usefully exploited for measuring output.

Fig. 1.

Nighttime lights of North America. Nighttime stable lights for year 2006 in arc 30-s resolution are shown. The projected coordinate system of US contiguous Albers equal area conic projection is used and the image is generated with ArcGIS 9.3.

The distinct advantage of nighttime lights is that they are a unique dataset related to human activities that is available for most of the globe at a very high resolution. We find that with careful processing it may provide useful information on economic activity for countries or regions with poor-quality data systems or no data. This conclusion is based on comparing standard output and luminosity measures in a statistical framework for both time-series and cross-sectional approaches for the period 1992–2008.

Use of Luminosity as a Proxy for Socioeconomic Indicators

Data on nighttime lights have been used to study regional socioeconomic systems in developing countries. Previous studies have used nighttime image data as a proxy for socioeconomic development of particular geographic areas (2–8). Elvidge et al. (ref. 2, p. 51) concluded, “Nighttime lights provide a useful proxy for development and have great potential for recording humanity's presence on the earth's surface and for measuring important variables such as annual growth for development.” In the past decade, researchers have undertaken a series of studies to support this conclusion. An earlier study by Elvidge et al. focused on the correlation between luminosity and gross domestic product (GDP) at the country level and found a strong correlation (R² = 0.97) between illuminated area and GDP (both expressed in logarithms) for 21 countries (3). Sutton and Costanza (4) found a high correlation between luminosity and GDP per square kilometer at the national level.

More recently, studies have used nighttime lights to predict income per capita at the subnational level. Ebener et al. show that lit area and percentage of frequency of lighting can predict GDP per capita at the national and subnational levels. They write that, when climate and agriculture are considered, the model yields better results in predicting GDP (5). Later Sutton et al. (6) improved Ebener's model by adding estimated urban population at the state level to solve the problem of saturation in traditional luminosity image and applied the new model to four countries: China, India, Turkey, and the United States. The variable “urban population” of each state of a country was estimated by using a log-log linear relationship between the size of urban areas and population. Then they used the estimated urban population as a predictor for GDP values for subnational administrative units and concluded that “spatial disaggregation of estimates dramatically improves aggregate national estimates” of GDP (ref. 6, p. 12).

One of the advantages of the nighttime lights data is that they are available at a very high spatial resolution. For instance, they have been used to construct the Human Footprint and Human Influence Index (9) for a 30 arc-second grid (∼1 km × 1 km at the equator). An important question is whether lights data can be used to improve measures of economic activity at national or subnational levels. In our application, we examine the proxy value added of nighttime lights for 1° latitude × 1° longitude grid cells, where the output data come from the geographically based economic data (G-Econ) dataset. The advantage of using the G-Econ data is that they are available for the period 1990–2005 and provide output estimates globally at a much smaller scale than standard economic accounts. For example, G-Econ data generate the grid cell output for 3,500 observations for Russia, 1,100 for China, and 800 for Brazil. We can therefore use the gridded data as a test to determine the relative merits of disaggregated economic data (based on population and business censuses) and luminosity data.

To date, virtually all studies have used the nighttime luminosity data without comparing them with other measures. A recent National Research Council report emphasized the need to use statistical approaches to proxy construction (10). However, few studies have undertaken a formal statistical analysis comparing luminosity with traditional output measures; the pioneering study by Henderson, Storeygard, and Weil (7) using an error-measurement approach is an important exception. We first describe the construction of the data, then describe the statistical model, and then present our results.

Description of the Luminosity Data

The primary nighttime image data used in the literature were gathered by US Department of Defense satellites starting in the mid-1960s to determine the extent of worldwide cloud cover. The data were later declassified and made publicly available as the Defense Meteorological Satellite Program Operational Linescan System (DMSP-OLS). The raw data can be acquired in two spatial resolution modes. The full resolution data, also referred to as “fine” data, have nominal spatial resolution of 0.5 km. The “smoothed” data are an average of 5 × 5 blocks of fine data and have a nominal spatial resolution of 2.7 km (11). The data that we obtained from the National Oceanic and Atmospheric Administration–National Geophysical Data Center are constructed using the smoothed spatial resolution mode, at a resolution of 30 arc-seconds, covering 180° W to 180° E longitude and 75° N to 65° S latitude (12).

Creation of a nighttime luminosity dataset is an undertaking of monumental difficulty. The raw data are processed on an empirical basis to correct for various optical and atmospheric distortions (see ref. 13 for a comprehensive description and ref. 14 for a description of the most recent version). Examination of the data indicates the presence of atmospheric disturbances such as water vapor, scanning errors, errors in mapping of the earth's topography, and blooming or overglow across pixels.

There are different versions of the data; three of particular importance are the “raw,” the “stable lights,” and the “calibrated” versions. The stable lights version removes ephemeral events such as fires and background noise. The calibrated version is currently available only for 2006 and has the advantage of not being saturated (top-coded) at the highest intensities. We performed the analyses here primarily with the stable lights version, but did sensitivity checks using other measures and found only small quantitative differences (we report on these below). This paper, therefore, reports primarily the results based on the stable lights data.

The annual stable lights data are presented as digital numbers (DN) from 0 to 63. The current datasets are DN proportional to radiance. To calculate aggregate luminosity for a 1° longitude × 1° latitude grid cell, we summed the DN values over all pixels in the grid cell. A complete grid cell thus contains 120 × 120 pixels. This procedure yielded 40,570 grid cells with data for 17 years, with overlaps of 12 satellite years. The current version of stable lights is not intercalibrated across time or satellites. We have corrected for differences across satellites and years by using panel regression estimation with fixed effects for time and satellites.

We then merged our grid cell luminosity data with G-Econ 3.4 data (available at gecon.yale.edu). Because the G-Econ data do not cross country borders, we divided luminosity values for cells containing a national border according to the shares of total cell population in each subcell.

We used all available cells from merging the G-Econ 3.4 data and DMSP-OLS time-series (version 4) data in the time-series analysis. At the country level, we used GDP purchasing power parity (PPP) values at constant 2005 international US dollars from the World Bank from 1992 to 2008. We aggregated luminosities for all grid cells in a country to obtain that country's luminosity for the corresponding year.

Although luminosity may additionally serve as a proxy at more disaggregated scales where no socioeconomic data are available, the main concern with such a high-resolution proxy is reliability. We can use estimates of the errors within and across satellites to provide a lower-bound estimate of the measurement error in using luminosity as an output proxy (SI Appendix, discussion in part V and Tables S2a and S2b). Regressions using data for 1° × 1° grid cells of the logarithm of luminosity in the same cell and year across different satellites have SEs in the range of 0.28–0.59 (SI Appendix, Table S2a). Similar errors are found for year-to-year variations of individual satellites and the same grid cell. If we use 0.5° × 0.5° grid cells, we find that the logarithmic SEs are slightly larger than those at the 1° × 1° scale. For both 1° × 1°and 0.5° × 0.5° grid cells, the current data on luminosity are likely to produce estimates of an output-luminosity proxy with an error of measurement of output of at least 25% (SI Appendix). This measurement error for lights is at present the minimum possible error when using luminosity data as a proxy variable.

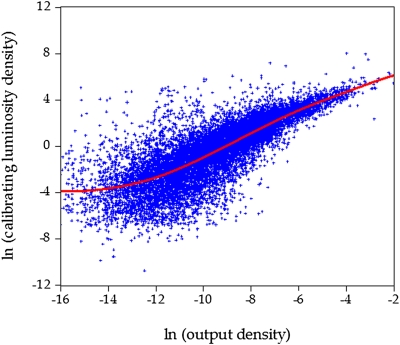
Fig. 2 is a scatter plot of log luminosity density and log output density for all grid cells for 2006 (n = 12,393). “Log” always refers to natural logarithms. A positive correlation is evident at high output densities, but the correlation is low at low output densities. Additionally, the relationship is extremely noisy. (Plots for the United States and Africa are shown in SI Appendix, Figs. S1 and S2.)

Fig. 2.

Gross cell product (GCP) and luminosity data, all cells. Shown are the scatter plot of log calibrated luminosity for 2006 and log of gross cell product for all 1° × 1° grid cells. Output density is gross cell product (PPP in billions in 2005 international dollars) per square kilometer. Luminosity density per square kilometer is the radiance calibrated luminosity for 2006. All grid cells (n = 12,393) are included. The solid line is the kernel estimator using an Epanechnikov kernel and 100 grid points per kernel.

Model

Analytical Background.

Our ultimate purpose is to determine whether luminosity contains useful information for constructing economic data at either the national or the subnational level. The most natural place to hope for value added is in countries with poor conventional data and those with few or no data at a subnational scale.

We can describe the issue intuitively. Suppose you are hiking and want to determine your exact location. You have a contour map from which you make one estimate. Additionally, you have a GPS device that provides another estimate. You know that each of the estimates is measured with error. The question is how to combine the two estimates to determine the best-guess location. From a statistical point of view, the issue is straightforward if you know the measurement error for each estimate as well as the distance scales.

The problem examined here is similar in that we have two different techniques for estimating country or grid-cell output. If we can determine the measurement error for each technique and the measurement scales, we can determine the best-combined estimate. The specific parameter we are testing for is the relative weights on the conventional output measure and on luminosity.

The basic assumption is that we have measures on luminosity and standard output for each grid cell and country and that these are measured with error. The variable y is the log of true output, m is the log of nighttime luminosity, an asterisk denotes the true value, and ε and ξ are the measurement errors for standard output and luminosity, respectively. In addition, we assume a structural relationship between luminosity and true output, with a coefficient of β and error u. We measure each variable in country or grid cell i averaged over year t. For this exposition, we remove means from all variables:

Eqs. 1 and 2 are the error processes for output and luminosity, respectively. Eq. 3 is the data-generating process for luminosity as a function of true output. We want to construct a luminosity-output proxy from these relationships. Following some statistical derivations described in SI Appendix to deal with biases from errors in measurement of luminosity and output, we then estimate a luminosity-output proxy as follows by inverting Eq. 3,

where 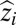is the log of our luminosity-output proxy and 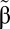is the consistently estimated coefficient in Eq. 3, taking into account measurement error (see SI Appendix for a more detailed discussion).

We classified countries into five “grades” (k = A, B, C, D, E) according to the quality of their statistical systems, as described in ref. 15 and below. Next, we construct a synthetic measure of output by taking weighted averages of conventional measures of output and our luminosity-output proxy,

where

Our purpose is to find the optimal weights on luminosity (θ*) and standard output (1 − θ*), where the optimal weights are ones that minimize the mean squared error for the difference between the synthetic measure and true output, 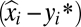. SI Appendix shows that a consistent estimator for 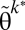is

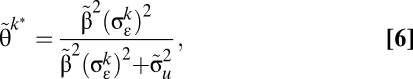The expression for the optimal weight makes intuitive sense as we can see for each of the three terms: The weight on the luminosity-output proxy is 0 (θ* = 0), and that on measured output is 1, when 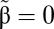(that is, when luminosity is unrelated to true output), or when 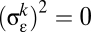(when there is no measurement error in output), or when 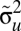is indefinitely large (when the relationship between luminosity and output is extremely noisy).

The present study provides consistent estimates of these weights. It is well established that weighting estimates for proxies need to be treated in a statistical manner (10). Estimating the errors of the weights through bootstrap and Monte Carlo methods is an important further project to determine the error bounds on the estimates.

Estimating Errors in Conventionally Measured Output and Luminosity.

The previous section showed that the statistical model for deriving the optimal weights on conventional GDP measures and luminosity is underidentified and requires estimates of the two error variances as well as of the coefficient in the luminosity equation. We discuss each of these terms. The first two are relatively simple, but the third is difficult to estimate.

Errors in measurement of nighttime lights.

The error variance of the luminosity equation Eq. 2 can be estimated using data both from different satellites and from different years of the same satellite, as well as directly from estimates of Eq. 3. The estimates are straightforward, and we therefore describe them verbally. Satellites differ in their optical quality, which may also degrade over time. In addition, there is sampling variation because of physical factors. In our final estimates, we use the error variance obtained from regression results of Eq. 3, assuming that the error terms in the structural equation are primarily caused by errors in measuring luminosity. (SI Appendix, Table S5 presents a suite of equations used to estimate Eq. 3 for grid cells.)

Estimating the structural coefficient in the luminosity equation.

Estimates of the coefficient β in Eq. 3 are a second ingredient in the estimation of the optimal weights on the two measures. Our procedure used an errors-in-variables correction to calculate an unbiased estimate of β (SI Appendix, Table S5).

Errors in output measurement.

The most difficult parameters to determine are the errors of standard GDP measures for different countries. National statistical offices typically do not provide error estimates on GDP. Depending on the country and the time period, many errors arise in measuring national output because of conceptual differences, data sources, index construction, and sectoral definitions such as how to treat home production. For our purposes, we define the “ideal” measure of output as one corresponding to the concept outlined in the United Nations System of National Accounts (16).

We can distinguish two different kinds of errors. The first are time-series errors. Statistical agencies generally keep the conceptual basis of their output estimates as well as the data sources invariant over time (at least for short periods); errors arise primarily from errors in the source data or errors in aggregation. Moreover, because there are two or three alternative methods of constructing national output (e.g., income and expenditure), we can examine the statistical discrepancy between them to arrive at a first estimate of the measurement error.

The second kinds of measurement error are cross-sectional level or density errors. These would apply to comparisons of output per unit area in a common currency across countries or regions. Cross-sectional errors have a multitude of sources including data errors, differences in concepts, and price measurement errors, as well as errors in measuring appropriate exchange rates across different currencies. Moreover, there are no identities that provide alternative estimates of the kind that produce the statistical discrepancy in time-series measures. We therefore expect the cross-sectional errors to be larger than the time-series errors.

In addition, because we examine both country output data and grid cell output data, we consider errors in both of these geographical levels as well as in time-series and density estimates (Table 1). In our estimates of measurement errors, we rely on the country grading system defined by the Penn World Table (PWT) and other authors (15, 17). The authors of the PWT assigned countries subjective quality grades from A to D on the basis of several criteria. We add grade E for those countries with essentially no statistical systems or countries that are missing from the PWT and other standard sources. Table 2 reports the number of countries and cells by grade, and SI Appendix, Table S4 provides a complete grade sheet for all countries. A full description of the technique used to estimate measurement errors is available in SI Appendix and in documents cited therein.

Table 1.

Estimates of errors of national and gridded GDP data used in estimates of combined measures of output

	Estimates for country output		Estimates for grid-cell output
Country grade	1-y growth rate, %	Output level, %	1-y growth rate, %	Output level, %
A	0.6	10	1.2	20
B	0.8	15	1.6	30
C	3.0	20	4.0	40
D	5.0	30	5.0	60
E	6.0	50	8.0	100

Country grades are from the Penn World Table and ref. 17. Estimated errors by authors are described in SI Appendix. Generally, A countries have highest-quality systems, C countries are middle-income countries, and grade E countries have little or no operative statistical systems and often have not had population censuses for at least a decade. A list of countries by grade is provided in SI Appendix.

Table 1 shows our estimates of the output-measurement errors for different countries and concepts that we use in our empirical estimates in the next section. The estimates for country time-series and cross-sectional (density) errors are based on a variety of studies. For countries, the cross-sectional error estimates are largely consistent with the PWT grades, and the growth error estimates are largely drawn from results reported by Johnson et al. (17). The assumption for grid cells is based on the change for the G-Econ data between revisions. We also note that the errors for the E countries are particularly uncertain, because they are not found in other studies.

Results

For formal tests of the optimal weights on luminosity and conventionally measured output, we conducted two sets of estimates. The first set is for the growth of output from 1992 to 2008, and the second uses output density measured as constant-price output per unit area. We look at both country data and grid cell data. The sample sizes are large for all estimates except the time-series country concepts, and the sample size for countries is small for E countries (Table 2). For density estimates using all grid cells in all countries in all years, the sample size is 353,843 observations.

Table 2.

Distribution of countries and cells without missing values by grade

Grade level	No. countries	No. cells	Representative country
A	16	2,839	Australia, Canada, United States
B	13	881	Argentina, South Korea, Spain
C	103	6,630	Bangladesh, Egypt, Mexico, Russia
D	29	924	Algeria, Cambodia, Democratic Republic of Congo, Libya
E	9	285	Iraq, Myanmar, North Korea, West Bank and Gaza
Total	170	11,559

The list of countries by grade is provided in SI Appendix. Cells are defined as the 1° × 1° grid cell. The sample of cells (used in the growth rate analysis) includes all available observations after merging the G-Econ dataset (3.4) and DMSP-OLS Nighttime Stable Lights Time Series (Version 4) and taking the logarithm of both variables.

Our ultimate goal is to see how much luminosity can contribute in constructing the true GDP measures. We do this by estimating the weight θ^k in Eq. 6. We report θ^k estimates for countries and grid cells for both the 17-y growth rates and the output density. We also run a separate analysis for observations with low-density GDP, because many of the low-quality statistical systems are also in low-output-density regions. For countries, we defined low-density observations as those where log 2000 GDP per unit area is <11.5 and belongs to C, D, or E country grades. For grid cells, we defined low-density observations as those where output density is <$8,100/km² in 2000. Low-density cells contributed in 2000 ∼2.7% of global output, 12.3% of global population, and 73.5% of global land total.

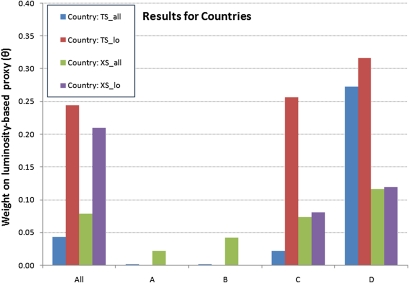
Figs. 3 and 4 show the estimated weights on luminosity (θ^k) for countries and grid cells, respectively. Detailed estimates are presented in SI Appendix, Tables S6 and S7. The main results are as follows. First, for the time-series estimates, the luminosity signal adds considerable information for D countries, with a weight of ∼30%. However, the value added by luminosity is very small, <3%, for A, B, and C countries. We do not report E country results because the sample size is too small.

Fig. 3.

Summary estimates of the value of θ or the weight on luminosity for countries of different grades. Shown is the estimated optimal weight (θ) for the both 17-y growth rate (TS) and cross-sectional data (XS) for countries. Blue and green bars indicate the values of θ for all countries, and red and purple bars indicate estimates for low-GDP density countries only. The sample size for the E countries is too small to be statistically reliable.

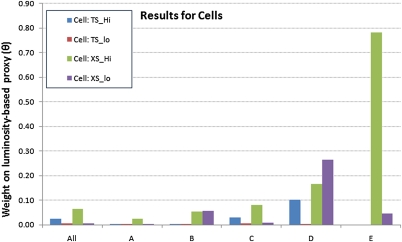
Fig. 4.

Summary estimates of the value of θ or the weight on luminosity for cells of different grades. See Fig. 3 for description. Note that the sample size for cells is generally large (Table 2). There are no observations for high-density E countries.

Second, the cross-sectional (output density) estimates, shown in green and purple bars in Figs. 3 and 4, are consistent across both countries and grid cells. For A through D countries, luminosity has a small value added: The weights on luminosity range from 1.0% to 12.0%. By contrast, luminosity adds substantial value in the E countries, with a weight of 25% for all cells.

A third result concerns the relative contribution of luminosity for grid cells and countries. We originally expected that luminosity would be more useful for grid-cell output measures because of the low quality of regional economic data in most countries. This turns out not to be the case. Generally, the information content of luminosity is approximately the same for grid cell data and for country data.

A fourth result concerns low-output-density observations. We had expected that luminosity would be most valuable for low-density observations. This hypothesis was generally not confirmed. For the time series for countries, low-density regions have slightly higher weights on the luminosity-output proxy than all regions. However, for grid-cell time series, there was little difference in the optimal weight between low-density and high-density regions. Surprisingly, for cross-sectional estimates for grid cells, the weights on luminosity are uniformly lower, and often markedly lower, for the low-density cells than for the high-density cells, except for D countries. Part of the reason is that luminosity data derived from stable lights are zero for many low-density cells. Of the 6,841 low-density cells with positive output, 36% have zero recorded stable lights luminosity. The difficulty is that the low level of anthropogenic lights in these regions cannot be distinguished from the background noise. Because improving estimates of output in just these cells is one of the important objectives of using luminosity as a proxy, this finding is a major hurdle for this approach.

We examined several other sensitivity tests and specifications. As an alternative to the global data, we examined output and luminosity data for US states (SI Appendix, Table S9). This test is useful because US states provide the most accurate cross-sectional data constructed with a uniform and high-quality methodology. They are less accurate than the US national data but in our judgment are better for comparative purposes than any other set of regional data. We obtained real annual GDP by state from the US Bureau of Economic Analysis and aggregated luminosity to the state boundaries. We assumed that states are the equivalent of grade B countries. Using the standard approach in Eq. 6, we calculate that the optimal weight on luminosity is <1% for the growth rate and <7% for the density measure. This result reinforces the finding that for countries with high-quality data systems, luminosity has a small proxy value for estimating economic output.

Additionally, we examined three other measures of nighttime lights. One set was the averaged raw light data. The raw light data have the advantage of containing nonzero values for most cells, but an analysis shows that the noise in the raw lights data leads to less precise estimates than those for stable lights. Additionally, we used the series with calibrated lights for 2006 for the density analysis. The results were virtually identical to the results based on stable lights (SI Appendix, Table S10).

A third alternative measure was the intercalibrated data. Elvidge et al. (18) generated equations for intercalibrating the annual nighttime light time series. However, these equations apply to the “avg_lights_x_pct” products and not to stable lights, and they generate many cells with negative values for lights. We nevertheless tested the series applying the intercalibrations to the stable lights series. We found the coefficients are generally less precise, but the basic results for the weights on luminosity are very close to our preferred estimates. Given these difficulties, we did not pursue the intercalibrated data (see SI Appendix for a further discussion).

We also we investigated an alternative statistical approach to correct for errors in measurement of output. The present study relies on classical errors in variable corrections to derive a consistent estimate of β in Eq. 3. In addition, for the cell analysis, we used an instrumental variables (IV) approach in adjusting gross cell output error, using as instruments a suite of exogenous cell variables such as climate, proximity to ports, and population density. The results differ very little from the correction using classical measurement error except in the case of the cross-sectional output of grade E countries (SI Appendix, Table S8). Because the results of the IV approach are very similar to those of the standard approach, we do not pursue this approach further.

We note additionally that these findings may overestimate the value of luminosity for regions where stable lights are set at zero. About 22% of cells with positive output (2,478/10,882) are recorded as having zero stable lights. These cells are therefore omitted from the estimates. The luminosity-output proxies are therefore available only for cells with positive stable lights. The zero-lights cells are only a small fraction of global output, but they are ones that tend to have the lowest-quality economic data. More than half of the grade E grid cells are recorded as having a value of zero for stable lights (in effect, truncating the lower tail of the lights distribution). Because we use logarithmic regressions, we must omit the zero-value observations. Therefore, the results based on stable lights probably overestimate the potential contribution of luminosity as a proxy for economic output.

Summary and Conclusions

This study proposed a method and then implemented it for the question of whether nighttime luminosity measures could be used to improve estimates of output at the regional level. The tests are particularly aimed at countries and subnational regions with low-quality data systems.

We find that luminosity is likely to add value as a proxy for output for countries with the poorest statistical systems, those that receive a D or an E grade, but has very limited value added for A, B, and C countries. This is true at the national level and at subnational levels where data are available. The reason for the low value added of luminosity in high-grade countries is that the luminosity data have high measurement error and the measurement errors in the standard economic data are relatively small. We further determined that luminosity data do not allow reliable estimates of low-output-density regions largely because the level of stable lights is too low to be distinguished from the background lights and is set at zero. We conclude luminosity data may be a useful supplement to current economic indicators in countries and regions with very poor quality or missing data.