B cells within germinal centers migrate preferentially from dark to light zone

Abstract

One of the main questions in the field of imaging immune cell migration in living tissues is whether cells fulfill their functionality via random or nonrandom migration processes. For some applications, this issue has remained controversial even after publication of various imaging studies. A prime example is B-cell migration in germinal centers (GCs) where somatic hypermutation and clonal selection of B cells are thought to occur within morphologically distinct regions termed dark zone (DZ) and light zone (LZ). Here, we reanalyze a previously published dataset on GC B-cell migration, applying a sensitive analysis technique to detect directed migration and using a procedure to correct for a number of artifacts that frequently occur in time-lapse imaging experiments. Although B cells roughly perform a persistent random walk, we present evidence that they have a small preference (of on average about 0.2−0.3 μm min⁻¹) to migrate from DZ to LZ, which is consistent with classical views of the GC reaction. This preference is most pronounced among a large subset of almost half of the B-cell population migrating along relatively straight tracks. Using a computational model to generate long-lasting B-cell tracks based on the experimental motility data (including the small directional preference), we predict a time course to travel from DZ to LZ of a few hours. This is consistent with experimental observations, and we show that at the observed cellular motility such a time course cannot be explained without the small preferential migration from DZ to LZ.

Thanks to the application of two-photon microscopy to living lymphoid tissues, an exciting glimpse of how the migration of various types of immune cells takes place was recently obtained (1–5). One of the central questions in this field is whether migration is best described as a (persistent) random walk or whether directed or confined migration is involved, because this is important for our understanding of how cells manage to carry out their functions. Examples of persistent random walk include the migration of T cells, B cells, and plasma cells in lymph nodes (2, 6–8) and of effector T cells migrating in tumors (9), whereas nonrandom migration has for instance been discovered in antigen-engaged B cells moving toward the T zone boundary early in a B-cell response (10), CD8⁺ T cells being attracted toward “licensed” dendritic cells (11–14), neutrophil movement in skin (15, 16), and during thymocyte maturation (17, 18).

In some applications, it is controversial whether migration is best described as random or not, and a prime example is B-cell migration in germinal centers (GCs). At these sites, B lymphocytes mature by somatic hypermutation and clonal selection of the mutants that produce antibody of high affinity. These two processes are thought to occur in morphologically distinct regions termed dark zone (DZ) and light zone (LZ), but in the literature competing views exist on the functional meaning of DZ and LZ, as well as on the expected migration behavior of antigen-specific B cells within and between the zones. In a classical view, B lymphocytes proliferate mainly in the DZ and subsequently travel toward the LZ where they are selected on the basis of their affinity to antigen (19). Interactions with follicular dendritic cells (FDCs) that retain antigen in the form of immune complexes and with follicular T helper cells are considered to be essential in the selection process. From an optimality argument, it was postulated that the B cells that survive might travel back to the DZ and that their cycle of proliferation in the DZ and selection in the LZ then continues, a model termed “cyclic reentry” (20). However, although cells were observed to move from the DZ to the LZ over a period of hours using labeling studies (19), the actual cellular migration patterns could not be directly assessed at the time.

In 2007, three GC imaging studies were published by different groups (21–23) and although it was pointed out that B cells roughly migrate according to a persistent random walk (23), cells were found to occasionally cross the border between DZ and LZ bidirectionally, and this was considered to be consistent with the classical view (21, 23). However, in one of these imaging studies, a more detailed vector analysis was performed on the migration of B cells as a function of the location in space (22). It was concluded that B cells prefer to recirculate within the zone in which they already reside and only infrequently cross the border. As a result, the authors challenged the classical view and instead proposed a competing hypothesis termed “intrazonal recirculation,” in which proliferation and selection occur in both the DZ and the LZ, i.e., the zones would be functionally independent (22, 24, 25).

Following up on the GC two-photon imaging studies, Figge et al. (26) considered various computational models of B-cell migration within GCs to assist in the interpretation of those experimental data. They searched for models that were consistent with both the experimentally observed GC morphology and the observed migration behavior in imaging experiments. By their analysis, they demonstrated that the presence of weak, transient chemotaxis of proliferating B cells from DZ toward LZ and of selected B cells from LZ toward DZ was consistent with these two observations. Indeed, such directed migration could easily be hidden in the experimental cell migration data because the standard technique used to detect it, i.e., deducing it from the shape of the so-called mean displacement plot, is not very sensitive (27). The results of Figge et al. (26) are at odds with the observation of Hauser et al. (22) that B cells preferably recirculate within the LZ or within the DZ. Therefore, it was suggested that the observed suppression of transzone migration was due to statistical fluctuations and needs to be reconsidered (26). Adding to this controversy is the fact that the Hauser group reanalyzed their own data and found that activated B cells exhibit directed migration, whereas naive B cells probably do not.* However, the question of where the activated GC B cells could be going was not addressed, so at present it remains unclear how this finding can be reconciled with their original intrazonal recirculation hypothesis. In a more recent study, GC B cells were imaged over a prolonged time period of 6 h, and by photoactivation of either DZ or LZ B cells it could be shown that in this time period ∼50% of DZ cells end up in the LZ, whereas ∼15% of the LZ cells reach the DZ (28). Although these findings are perfectly consistent with both the classical view and cyclic rentry, they do not show which short-term migration process is responsible for the observed long-term cellular distribution pattern. For example, 50% of the DZ cells ending up in the LZ after 6 h could be explained by random migration of cells in the DZ and a retainment of the cells that cross the DZ–LZ border in the LZ. Alternatively, it could be that there is a (previously nondetected) directed migration component guiding DZ cells toward the LZ.

A complicating factor in the analysis of cell migration data from two-photon imaging is the presence of a number of experimental and tracking artifacts in such data. We recently gave an overview of currently known artifacts and proposed how it can be avoided that they affect the interpretation of results (27). Especially when there is a role for small effects (such as weak chemotaxis predicted by Figge et al., ref. 26), it is important to properly deal with potential artifacts. In this paper, we reanalyze in vivo B-cell migration datasets published by Allen et al. (21), including a correction of known artifacts, and find evidence for weak directed migration from DZ to LZ as proposed by Figge et al. (26). Furthermore, we develop a computational model of cell migration that incorporates the experimentally measured data on speeds and migration angles, and we show that compared with random migration, the observed directed migration has a strong impact on arrival time in the LZ.

Results

Approximating the Orientation of the GC.

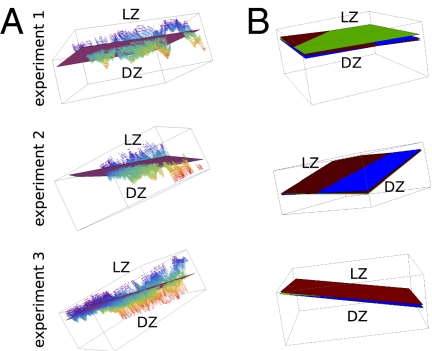
We reanalyzed a dataset previously published by Allen et al. (21) in which in vivo time-lapse imaging of GCs was performed. In that study, a relatively thick volume was visualized (about 100 μm), and the microscope was oriented toward the center of the lymph node such that the LZ–DZ axis is pointing away from the microscope. LZ FDCs were visualized by labeling them with immune complexes containing the fluorescent protein phycoerythrin. The migration of B cells expressing green fluorescent protein was monitored over time and we wanted to quantify their migration directions relative to the orientation of the GC. Therefore, we set out to estimate the GC orientation as being perpendicular to the orientation of the interface region between DZ and LZ. We used a segmentation threshold based on visual inspection to assign voxels as belonging to FDCs or not and then used a hole-filling algorithm to fill up the spaces between the FDC voxels within the LZ (Methods). The result of this procedure is an estimate of all of the voxels that make up the LZ, and therefore it also provides an approximation of the whereabouts of the border between LZ and DZ. Although the LZ–DZ border tends to be quite irregular (Fig. 1A), approximating its orientation as a plane should give a good description of the direction of chemokine gradients (i.e., perpendicular to the estimated plane) that have been proposed to exist between DZ and LZ (26, 29). Thus, we fitted a plane through the estimated LZ–DZ border (Fig. 1A) and used this plane in our analysis of B-cell migration below. Because the FDC network is relatively dynamic over time (8), this could potentially mean that the orientation of the estimated LZ–DZ border plane could also vary with time. Thus, we estimated the border plane at three time points (first, middle, and final time point of imaging), which demonstrated that the changes in the orientation of the GC in the course of the experiment were minimal (Fig. 1B). Nevertheless, we took the small changes in LZ–DZ border plane orientation into account by using the estimates from the three time points as well as the interpolation of these estimated planes for all time points in between in our further analysis.

Fig. 1.

Estimating a plane through the interface region between DZ and LZ for each experiment separately. (A) Voxels forming the DZ–LZ interface are plotted as individual dots along with the plane fitted through these data. Dots are color coded by their depth in 3D space (z coordinate). (B) Comparison of the DZ–LZ border planes estimated at the first (in brown), middle (in green), and final (in blue) time point of imaging for each experiment. Planes are oriented such that all are visible.

B Cells Preferentially Move from DZ Toward LZ.

Cellular position data from time-lapse imaging experiments come with a variety of artifacts that stem from both the experimental procedure itself and from the (automated) tracking performed after the raw data are acquired. We recently proposed how such artifacts could be repaired or circumvented (27), and we applied this approach to the B-cell migration data within GCs. Thus, we excluded track parts from the analysis that were close to the image volume borders, because they frequently contain tracking errors (i.e., it would lead to motion that appears to be parallel to the image volume borders). This is especially important for our purpose because we want to quantify the migration directions of B cells, and consistently incorrect migration directions would lead to incorrect results. We also corrected for small tissue drift that occurs during the experiments by using changes observed in the FDC network over time to correct the tracked B-cell positions (Methods). Finally, we noted that the speed components in the axial (z) direction were about 25% higher than those in the lateral (x and y) directions. This could be due to an imprecise calibration of the axial dimension (27), and to correct for this we multiplied the z coordinates of all cells by a factor of about 0.8. Note that leaving out this final correction would not affect our main conclusion (see below).

Next, we used the corrected 3D cell coordinates over time to quantify how the cells moved relative to the orientation of the GC and whether this depends on the distance from the estimated plane separating LZ and DZ. In our calculations, instead of first calculating an average per cell and then calculating an average of the averages (“cell-based” analysis), we let each movement step of a cell contribute separately to the end result (“step-based” analysis). In this manner we avoid the shape of the imaged space affecting our calculations (27). Furthermore, it allows for a straightforward quantification of cell movement as a function of the distance from the estimated DZ–LZ separation plane.

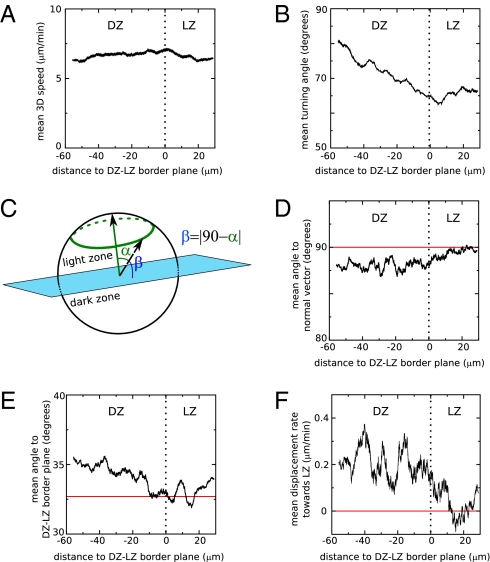
We first quantified the 3D speeds and turning angles of cells as a function of the distance to the DZ–LZ border. This analysis demonstrated that there are no clear differences in speeds among cells residing in LZ and DZ (P = 0.08, Mann–Whitney test; Fig. 2A). However, it confirms that cells move more persistently (have lower turning angles, P = 0.0005, Mann–Whitney test; Fig. 2B) in the LZ than in the DZ (as found in the original study of Allen et al., ref. 21). We next studied the migration direction of cells relative to the orientation of the estimated DZ–LZ border to determine whether B-cell migration is completely random or whether we can detect more intricate patterns of movement using a sensitive method of analysis. We calculated both the angle with a vector perpendicular to the plane pointing toward the LZ, i.e., the normal vector (this can vary between 0° and 180°), and the angle with the plane itself (due to the absolute value involved in its calculation, this can vary between 0° and 90°; Fig. 2C). For a migration process that is random (no preferential migration direction) the mean of these angles is expected to be ∼90° and ∼32.7°, respectively (27). Consistent deviations from these expectations would point to a nonrandom migration process. For B cells in the DZ of GCs, we do find such a consistent deviation (a smaller than 90° mean angle to the normal vector, and a bigger than 32.7° mean angle to the DZ–LZ border plane) (Fig. 2 D and E). Thus, cells within the DZ do not migrate entirely randomly, but have a small preference to migrate toward the LZ, and in the LZ the behavior approaches random migration. However, because the data do not extend so far into the LZ, the migration behavior in the LZ cannot be accurately established in the current dataset. The conclusion that there is preferential migration from DZ to LZ is supported by an analysis of the mean displacements of the B cells in the direction perpendicular to the DZ–LZ border plane (Fig. 2F): B cells in the DZ displace on average about 0.2 μm min⁻¹ toward the LZ, which significantly differs from the 0 μm min⁻¹ displacement rate that is expected for random migration (P = 0.008, Mann–Whitney test). Note that the conclusion that B cells migrate preferentially from DZ to LZ is not affected by our rescaling of the z axis: Without rescaling the preferential migration would be even stronger because the estimated DZ–LZ interface plane is approximately orthogonal to the z axis.

Fig. 2.

B cells within germinal centers preferentially move from DZ to LZ. A plane was fitted to the interface region between DZ and LZ, and various measures of cell migration were plotted as a function of the shortest distance to the estimated plane. All values represent running averages of movement steps. Plotted are the mean 3D speed (A), the mean turning angle (B), the mean angle to the normal vector that defines the DZ–LZ border plane and that points toward the LZ (D), the mean angle to the estimated DZ–LZ border plane (E), and the mean displacement rate toward the LZ (F). The relationship between the angles measured in D and in E is further explained by the drawing in C.

Preferential Movement Is Overrepresented Within a Large Subset of Straight-Moving B Cells.

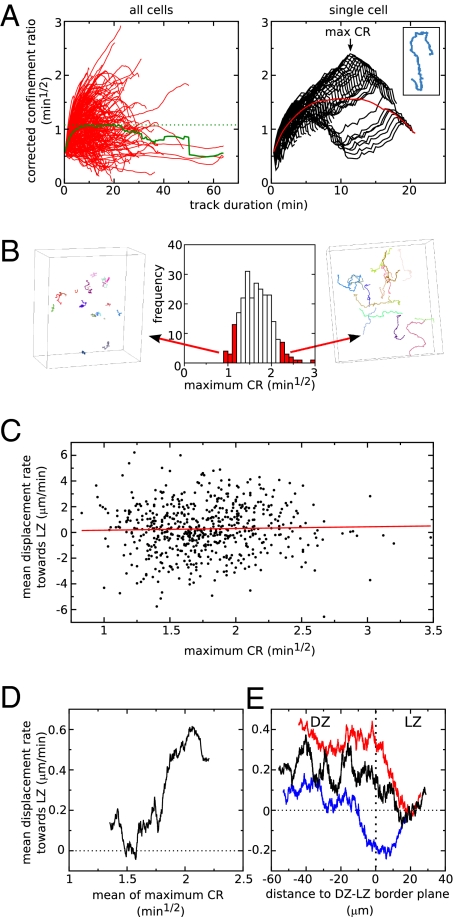
From the above analysis it can be roughly predicted that over a period of 1 h, the B cells in the DZ would be getting ∼10–15 μm closer to the LZ if they would all exhibit a similar migration tendency from LZ to DZ. However, it seems unlikely that they would indeed form a single population in terms of their migration because only a fraction of the DZ cells has been observed to move into the LZ in a few hours in long-term imaging experiments (28). Furthermore, Allen et al. (21) previously noted that the few cells that crossed the boundary between DZ and LZ tended to move along relatively straight paths, so it could be that these few cells are actually causing the observed pattern. Alternatively, it could be that a large fraction of the cells display directed migration from DZ to LZ. To investigate whether the pattern is caused by a (large or small) subpopulation of B cells, we next applied a cell-based analysis by calculating a measure for the straightness of each track using the “corrected” confinement ratio (CR) (Methods and ref. 27). Although the CR is expected to approach a constant mean value for long durations, on a per-cell basis it varies greatly with the duration of the track (Fig. 3A, Left). For example, a cell could first attain a high CR value by moving in a straight manner from DZ to LZ, but for longer durations the value could decline again if the cell subsequently remains at about the same spot within the LZ. To make sure that we do not miss such a cell in our classification of straight tracks, we need to search for cells having straight track parts rather than only cells having an overall straight track. Therefore, as a measure of the straightness of a cell's path, we used the maximum of the CR values coming from every possible observed duration for that cell (example in Fig. 3A, Right). Visual inspection confirms that this procedure indeed classifies cells on the basis of the straightness of their path (Fig. 3B).

Fig. 3.

Preferential migration from DZ to LZ is overrepresented within a large subset of straight moving cells. (A) The corrected confinement ratio (CR) as a function of track duration. (Left) The red lines represent the different tracks in an experiment, and the green line gives the average behavior of all cells. (Right) Demonstration of how the maximum CR is calculated for the example track shown in the Inset. Each black line represents the CR for one particular part of the track, and the maximum of all these lines is the maximum CR (denoted by arrow). The red line represents the average CR for this particular cell (i.e., this is one of the red lines on the Left. (B) The frequency distribution of maximum CR values for all cells in one experiment and the corresponding tracks for two subselections of the cells. (C and D) Mean displacement rate toward the LZ in the straightest part of the track as a function of the maximum CR value of the cell. In C, each dot represents one cell (red line represents a linear regression), whereas in D, running averages of 200 cells are presented. (E) The mean displacement rate toward the LZ as a function of the distance to the DZ–LZ border plane for a subpopulation with relatively straight tracks (red line, cells with max CR values above 1.75 min^1/2) and for one with relatively condensed tracks (blue line, cells with max CR values below 1.75 min^1/2). For comparison, the behavior of the entire B-cell population is plotted in black (same as Fig. 2F). Lines are running averages of 3,000 movement steps. The horizontal dotted line in D and in E gives the expected mean value for the displacement rate toward LZ in a randomly migrating population.

We next studied whether the preferential movement toward the LZ was overrepresented among straight tracks. The mean displacement rate toward the LZ (measured within the straightest part of the track) appears to be highly variable among cell tracks with different straightness (Fig. 3C). However, on average the cells with the straightest track parts (with a maximum CR approximately above 1.75 min^1/2) tend to be the cells that most preferentially move toward the LZ (Fig. 3D). On the basis of this maximum CR value, we split the B-cell population in two parts (high versus low maximum CR) and studied the mean displacement rates toward the LZ as a function of the distance to the DZ–LZ border plane among the two populations. Indeed, the pattern of preferential movement from DZ to LZ is strongest within the population with straight tracks and is nearly absent in the population with more condensed tracks (Fig. 3E). This indicates that the directed migration toward the LZ occurs mostly within a large subpopulation of all B cells having relatively straight tracks. In particular, these straight-moving B cells (having a maximum CR bigger than 1.75 min^1/2) make up 48.2% of the B-cell population, and 58.5% of these straight-moving cells have a positive displacement rate toward the LZ (i.e., the subpopulation of cells that have both a high maximum CR and are moving toward the LZ comprises 28.2% of the total B-cell population).

Time Required to Migrate from DZ to LZ.

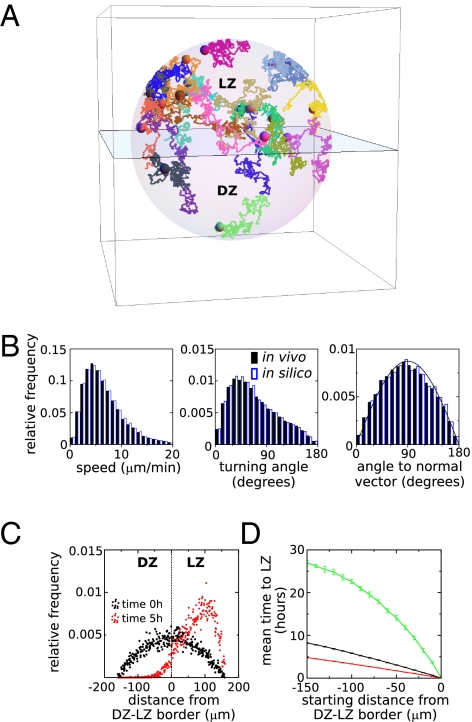
Although our analysis of B-cell migration shows that there is preferential migration from DZ to LZ, it is unclear whether the preference is sufficiently strong to make a difference on top of the random component of migration that at first sight seems to be more pronounced. To address this issue, we constructed a model of B-cell migration that was able to generate realistic, long-lasting tracks by directly using the movement steps observed in the experimental data (example in Fig. 4A). In the model, cell paths consist of a random sequence of steps sampled from the data, while taking into account that the cells have an approximately correct persistence (Methods). By this procedure we can indeed simulate cells traveling at similar speeds and migration angles as B cells within GCs (Fig. 4B). Cell movement was simulated within a 3D sphere of radius 160 μm representing a complete GC consisting of a DZ and a LZ separated by a plane in the middle. During a simulation, we required that all simulated cells stayed within the GC, and we did not incorporate cell division and cell death because we wanted to estimate the effect of preferential migration alone. Furthermore, because the behavior in the DZ differs from that in the LZ (Fig. 2), the experimental data were split into two parts: One part coming from cells traveling within the DZ and one from movement steps made within the LZ. Depending on whether the simulated B-cell resided in the LZ or DZ, one of these respective parts of the data was used.

Fig. 4.

Modeling shows that directed B-cell migration from DZ to LZ strongly affects the time to reach the LZ. (A) Example of 20 in silico cells migrating in a simulated GC. The plane represents the border separating LZ and DZ. (B) Comparison of the experimentally measured and simulated distributions of speed, turning angle, and angle to the vector normal to the DZ–LZ border pointing toward the LZ. Note that the latter distribution deviates only slightly from the distribution expected for random migration (denoted by the solid line). (C) The spatial distribution of simulated cells in 10 simulations at the beginning and at the end of a 5-h simulation. Each dot represents the relative frequency of cells within distance bins of 10 μm wide in a single simulation of 1,000 cells. (D) The mean time to reach the LZ when starting at various depths within the DZ of the simulated GC. Simulations are either based on all DZ migration data (green and black line) or on the DZ migration data of B cells with straight tracks (maximum confinement ratio 1.75 min^1/2, red line). Simulations either incorporate the directed migration as observed experimentally (black and red line) or are based on random migration with similar speeds and turning angles as in the experimental data (green line). Error bars denote SD of the mean.

To investigate the impact of preferential migration from DZ to LZ, we first initialized our simulations by placing B cells randomly in the GC, and we asked whether the spatial distribution would change over the time course of a few hours. After 5 h of simulation, nearly all of the B cells resided in the LZ (Fig. 4C), indicating that the directed component of migration does have a strong impact on the migration of B cells. Next, we used our simulations to predict how much time it takes on average to reach the LZ when starting from various depths in the DZ. We compared this to the time it would take in simulations of random migration, in which cells travel at similar speed and persistence but do not migrate preferentially toward the LZ. The mean time to reach the LZ was approximately three times lower in directed than random simulations (Fig. 4D). As expected, within the subset of cells traveling along relatively straight tracks, it takes even less time to reach the LZ (on average about 5 h at the farthest distance). In conclusion, although the preference to migrate from DZ to LZ is small, it has a strong impact on B-cell migration because it greatly decreases the time to reach the LZ compared with random migration.

Discussion

From a reanalysis of the Allen et al. (21) dataset on B-cell migration within GCs, we discovered that B cells have a small preference to migrate from DZ to LZ, and that this preference is strongest among a large subset of cells moving relatively straight (comprising almost half of the total B-cell population). This suggests that these cells are following a chemotactic gradient emanating from the LZ. It is likely that the chemokine CXCL13 has a role in this attraction because this ligand is known to be present at higher levels in the LZ than in the DZ (29). Furthermore, B cells that are deficient for CXCR5 (a chemokine receptor recognizing CXCL13) were absent from the LZ and they accumulated in the DZ (29).

Our results are consistent with the classical view on the GC reaction in which B cells are attracted toward the LZ after having proliferated within the DZ (19). Furthermore, the fact that B-cell migration is roughly random with only a minor directed migration component is consistent with the prediction by Figge et al. (26) that only weak chemotaxis can explain both the observed B-cell migration data and maintenance of the DZ during a GC reaction. However, our results are at odds with the intrazonal circulation model of Hauser et al. (22) who reported that migration close to the DZ–LZ border was predominantly parallel to that border. Although a similar vector analysis was used in that study (see their figure 5F), that analysis was 2D and based on a relatively thin slice of the GC (∼40 μm) so the estimation of the DZ–LZ border orientation may have been suboptimal. Moreover, a quantification of the migration vectors combined with a comparison with the behavior expected for random migration was not performed. Finally, when the Hauser group reanalyzed their own imaging data they reported that activated B cells perform directed migration with unknown preferred direction* and we expect that this is the same directed migration from DZ to LZ that our analysis has revealed.

According to the cyclic reentry hypothesis, selected B cells in the LZ should return to the DZ, and it has been suggested that the cells become responsive to the chemokine CXCL12 that is more abundant in the DZ than in the LZ (26, 29). In that case, one may also expect to find a directed migration component from LZ to DZ in experimental migration data. Why did we not find evidence for such directed migration from LZ to DZ? One explanation is that the dataset did not extend sufficiently deep into the LZ. Alternatively, it could be that, contrary to the directed migration from DZ to LZ that occurs in a large subset of the B cells, only few B cells become selected and are subsequently attracted toward the DZ. Within a large population of randomly migrating cells, it would be difficult or even impossible to detect just a few cells with divergent migration behavior. If this scenario were true, it would only become possible to detect directed migration from LZ to DZ if the subpopulation of recently selected B cells can be distinguished via independent information (for example, via a fluorescent reporter of signaling; see also ref. 26).

Recently, in a long-term imaging study, Victora et al. (28) showed that about 50% of the DZ cells reach the LZ in a period of 4–6 h. This is consistent with our finding that preferred migration from DZ to LZ is overrepresented in a subpopulation consisting of approximately half of the B cells (Fig. 3), and with the prediction from our simulations that it takes this subpopulation several hours to migrate into the LZ (Fig. 4D). This time course is also consistent with 5-bromo-2′-deoxyuridine (BrdU) pulse labeling studies of GC B cells (21, 30): A large fraction of recently divided G1 phase cells, which resided primarily in the DZ 5 h after BrdU labeling, were found to have moved to the LZ 12 h after labeling. Combining these data with our cell migration analysis, this suggests that DZ cells that recently divided migrate to the LZ in a time course of on average about 5 h, due to the small directed migration component. A persistent random walk without preferential migration from DZ to LZ is unable to explain the BrdU labeling data and the long-term imaging data, because at the measured motility it would take up to a day for B cells to travel from DZ to LZ (Fig. 4D). Thus, although the preferred migration from DZ to LZ is small (with a directed component toward the LZ of on average ∼0.2–0.3 μm min⁻¹), our simulations of long-lasting B-cell tracks show that this strongly affects the time it takes to reach the LZ compared with persistent random migration. As a result, a large percentage of the cells would end up in the LZ in just a few hours if there were no processes counteracting the accumulation in the LZ. Such opposing processes are likely to include proliferation occurring mainly (but not exclusively) (21, 22) in the DZ as well as cells disappearing from the LZ through apoptosis, return to the DZ, or exit from the GC.

The small yet very relevant directed migration component from DZ to LZ was not picked up in the original GC imaging studies by a conventional mean displacement analysis (21, 23), although these studies did note a small tendency for cell tracks to cross the DZ–LZ interface region more frequently from DZ to LZ than vice versa. This suggests that the conventional displacement analysis is not sufficiently sensitive to pick up small directed migration components, which may be due to the large variance of (square) displacement measurements in persistent random walks (31) as well as to the spatial dependence of GC-directed migration that our results suggest. Furthermore, the mean displacement analysis relies on data from long-lasting tracks and, depending on the size of the z dimension of the image volume, these are biased to cells that do not displace much because fast-displacing cells are more likely to have moved out of the image volume (27, 32). As a result, directed migration may look like random or confined migration in a displacement plot (note that the latter effect probably has a limited role in the dataset studied here because of the relatively thick image volume, i.e., about 100 μm). Hence, previously published studies that have reported migration processes as roughly random on the basis of a displacement plot, e.g., for T cells infiltrating in tumors (9) or plasma cells migrating toward the medulla in lymph nodes (7), might contain small directed migration components that at first sight seem irrelevant yet have a big effect when studied on a longer time scale. Our approach could also be applied to settings where directed migration is already known to occur, for instance in the case of CD8⁺ T cells that are attracted toward licensed dendritic cells (11–14), because quantification of directed migration helps to clarify how cells manage to carry out their functions in a timely manner.

Methods

Estimation of the DZ–LZ Border.

The 3D images of the FDC network were used to obtain an estimate of the border region between LZ and DZ. After application of a Gaussian filter to smoothen the images, a segmentation threshold was chosen on the basis of visual inspection of the images. To further remove noise and to define the LZ as a continuous region rather than as isolated patches of FDC, we performed a series of dilation and erosion operations. Specifically, these operations were performed using a neighborhood consisting of all voxels that were at a distance of at most three positions away from the center voxel. Consecutively, four dilation operations were followed by four erosion operations (to fill up holes between FDCs), and then two erosion operations were followed by two dilation operations (to remove isolated patches). By this procedure (implemented in the C programming language), each voxel is assigned to either the LZ or the DZ. We subsequently fitted a plane (using the software package R; available at http://www.r-project.org/) through all LZ voxels that were at the border of the two zones (colored dots in Fig. 1A) by minimizing the sum of the shortest distances between each border voxel and the plane. DZ–LZ border planes at intermediate time points were estimated by linearly interpolating all parameters defining the plane, i.e., by gradually morphing one estimated plane into the next estimated plane.

Cell Migration Analysis.

The B-cell coordinates from the imaging data of ref. 21 were corrected for known artifacts using customized Perl scripts (27). First, each movement step whose starting coordinate was within a 5-μm distance from one of the borders of the image volume was discarded. Second, the z coordinates of each recorded position was multiplied by a factor of about 0.8 per experiment to correct for imprecision in the axial dimension. Third, tissue drift was corrected for by using the images of the relatively static FDC network at the initial, middle, and final time points of imaging. We did not succeed in identifying fluorescent objects that were obviously static yet appeared to move due to tissue drift. Therefore, we focused on estimating the tissue drift that occurred in the direction perpendicular to the DZ–LZ border plane (the direction of interest for our study). This was achieved by fitting planes to the image data at the middle and final time points according to the procedure described above, except that the orientation of the fitted planes was now fixed to the orientation found at the initial time point (i.e., the fitted planes were only allowed to translate and not to rotate). The drift at all time points in between was estimated by linear interpolation. The B-cell coordinates were subsequently corrected by subtracting the estimated drift. Note that the tissue drift estimated by this procedure appeared to be minor in this dataset (∼1 μm, ∼2 μm, and ∼7 μm per hour in experiments 1, 2, and 3, respectively).

After artifact correction, we calculated for each recorded movement step (using customized Perl scripts) (i) the speed, (ii) the turning angle (i.e., the angle between subsequent movement steps), (iii) the shortest distance to the fitted DZ–LZ border plane, (iv) the angle to normal vector (i.e., the angle between the migration direction of a cell and a normal vector to the DZ–LZ border plane pointing toward the LZ), (v) the angle between the migration direction of a cell and the DZ–LZ border plane, and (vi) the displacement rate toward the LZ (i.e., the length of the projection of the movement step onto the normal vector pointing toward the LZ). For statistical analysis, we used only movement steps that were 5 min apart, i.e., sufficiently far apart to consider them as independent measurements (due to persistent movement at short time intervals, movement steps up to several minutes cannot be considered independent). Two-tailed Mann–Whitney tests (using the software package R) were performed on this subset of movement steps to test whether DZ migration differs from a persistent random walk and whether speed and turning angles differ between DZ and LZ.

To objectively select a subpopulation of cells moving along relatively straight trajectories, we used the corrected confinement ratio as a basis (27). Briefly, the “correction” is done by multiplying the confinement ratio (i.e., the ratio of the displacement from first and last position of a cell track and the total path length of the track) by the square root of the duration of the analyzed track. This procedure removes the dependency on track duration of the confinement ratio and thus enables a fair comparison of tracks. On top of this, for each track we searched for the maximum value of the corrected confinement ratio when considering all possible parts of the track (Fig. 3A, Right and explanation in Results).

Model of Cell Migration.

In our computer simulations (coded in the C programming language) we generated long-lasting B-cell tracks within a sphere of radius 160 μm, representing a GC consisting of two hemispheres (DZ and LZ) separated by a plane (the DZ–LZ border). B-cell motion was described as a series of discrete 3D steps (similar to the approaches in Beauchemin et al., ref. 33 and Figge et al., ref. 26) taken directly from the experimentally observed distributions of speed, turning angle, and angle to normal vector. After merging the data from the three imaging experiments, they were split into two categories (DZ steps or LZ steps), depending on whether the inital position was in the DZ or in the LZ. For simulations of directed migration, pairs of observed speed and angle to normal vector were maintained. For simulations of random migration, the speed and turning angle distributions were kept the same, but the steps were modified such that the direction of migration was taken from a sine distribution [i.e., the distribution expected for random migration (27, 34)] rather than from the experimentally observed distribution of angles to the normal vector.

In silico B cells were initialized either randomly throughout the GC or within the DZ at a particular distance away from the DZ–LZ border. The inital movement step was chosen at random from the possible speed/angle-to-normal-vector combinations observed among the DZ or LZ steps (depending on where the cell was located). For each combination, the possible movement steps are described by a circle in 3D space, and the cell was moved to a random position on that circle. Subsequently, movement steps were again chosen from the speed/angle-to-normal-vector combinations among either the DZ or LZ steps. However, steps were accepted with a probability that ensured a correct turning angle distribution (otherwise the procedure would result in a random turning angle distribution, i.e., cells would move at a persistence not exceeding that of a single step). Specifically, the turning angle distributions from all DZ and all LZ steps were discretized into 18 bins of 10° wide, and the proportions p_i for each bin were recorded (where i represents the turning angle bin number varying from 0 to 18). Each proportion p_i was then weighted by the factor 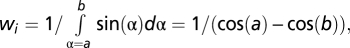where a and b are the lower and upper limits for each turning angle bin. As acceptance probability for the chosen movement step, we used the normalized and weighted proportion 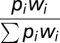because this ensured that sampling of movement steps occurred in an order that correctly recapitulated the turning angle distribution (Fig. 4B). In case a movement step was rejected (either because of the above procedure or because it would lead to a B-cell moving out of the simulated GC), another movement step was chosen until one was accepted.