Estimating the reproductive numbers for the 2008–2009 cholera outbreaks in Zimbabwe

Abstract

Cholera remains an important global cause of morbidity and mortality, capable of causing periodic epidemic disease. Beginning in August 2008, a major cholera epidemic occurred in Zimbabwe, with 98,585 reported cases and 4,287 deaths. The dynamics of such outbreaks, particularly in nonestuarine regions, are not well understood. We explored the utility of mathematical models in understanding transmission dynamics of cholera and in assessing the magnitude of interventions necessary to control epidemic disease. Weekly data on reported cholera cases were obtained from the Zimbabwe Ministry of Health and Child Welfare (MoHCW) for the period from November 13, 2008 to July 31, 2009. A mathematical model was formulated and fitted to cumulative cholera cases to estimate the basic reproductive numbers R₀ and the partial reproductive numbers from all 10 provinces for the 2008–2009 Zimbabwe cholera epidemic. Estimated basic reproductive numbers were highly heterogeneous, ranging from a low value of just above unity to 2.72. Partial reproductive numbers were also highly heterogeneous, suggesting that the transmission routes varied by province; human-to-human transmission accounted for 41–95% of all transmission. Our models suggest that the underlying patterns of cholera transmission varied widely from province to province, with a corresponding variation in the amenability of outbreaks in different provinces to control measures such as immunization. These data underscore the heterogeneity of cholera transmission dynamics, potentially linked to differences in environment, socio-economic conditions, and cultural practices. The lack of traditional estuarine reservoirs combined with these estimates of R₀ suggest that mass vaccination against cholera deployed strategically in Zimbabwe and surrounding regions could prevent future cholera epidemics and eventually eliminate cholera from the region.

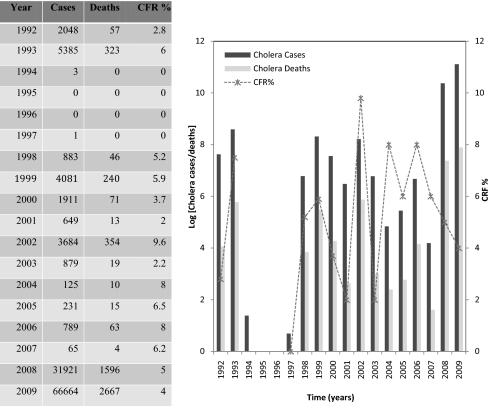
The 2008–2009 cholera outbreak in Zimbabwe was the worst African cholera epidemic in the last 15 y. In addition to the large number of cases, the outbreak was characterized by its high case fatality ratio (CFR) and extensive spread. The outbreak began in August 2008 and swept across the whole country by December 2008, and by the end of July 2009 there were 98,585 reported cases and 4,287 deaths. Zimbabwe has experienced sporadic outbreaks of cholera since the introduction of seventh pandemic El Tor strains in the 1970s. These outbreaks have increased in frequency and severity since the early 1990s and have become increasingly difficult to control as a result of deterioration of the health system and its associated infrastructure, related to the national economic crisis. Zimbabwe had cholera outbreaks in 1992 and 1993 with 2,048 and 5,385 reported cases, respectively (1): Outbreaks were linked to influx of refugees from Mozambique (a cholera endemic area) and drought (2, 3). There were no cholera outbreaks recorded from 1994 to 1997; however, since 1998, a period that coincides with the start of the economic crisis in the country, cholera has been reported every year (4) (Fig. 1).

Fig. 1.

Cholera cases and deaths in Zimbabwe from 1992 to 2009 (4). The y axis for the graph is logged.

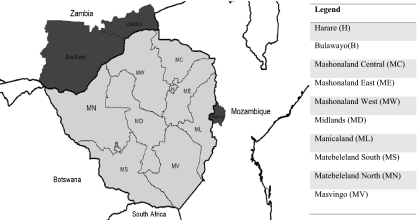
Cholera outbreaks in Zimbabwe occurred previously in communities that border endemic regions, particularly in the provinces of Manicaland and Mashonaland East on the border with Mozambique and also in Kariba (in Mashonaland West province) on the border with Zambia (5) (Fig. 2). Cholera cases in early 2008 were first noted during a small outbreak in Mashonaland East, Mashonaland Central, Mashonaland West, Harare, and Manicaland between January and April 2008. The disease resurfaced in mid-August from St. Mary's and Zengeza wards of Chitungwiza (5, 6). Between September and October 2008, cholera cases were reported in Mashonaland West, Mashonaland East, and Harare provinces and a full cholera epidemic wave that swept across the country emerged between November 1 and 15, affecting 9 of the 10 provinces, with disease reported from all 10 provinces by the end of December 2008 (6). The Zimbabwe Minister of Health and Child Welfare declared a state of emergency on December 3, 2008 and launched an appeal for international humanitarian aid (7, 8). WHO then set up a Cholera Command and Control Centre in Harare to coordinate international groups that were distributing medication and helping in the treatment of water in the country (9).

Fig. 2.

Map of Zimbabwe, provinces, and neighboring countries. The darker-colored regions show one of the cholera-affected districts (Manica) in Mozambique in 2006 (26) and some of the cholera-affected provinces (Southern and Lusaka) in Zambia in 2010 (27) that are on the border with Zimbabwe.

A good understanding of the transmission dynamics and ecology of cholera in emergent epidemic regions like Zimbabwe can help to improve the control of future epidemics. Mathematical models provide a quantitative and potentially valuable tool for this purpose. Although multiple models for cholera have been created, most of the earlier models focused on endemic cholera and interactions between environmental variables and disease occurrence, building on data from areas (such as Bangladesh) where there is close contact between infected populations and the estuarine (or riverine) environment. Zimbabwe, as a land-locked country in the middle of Africa, presents a very different setting for cholera, presaging the future of cholera epidemics in a rapidly urbanizing world. We present here a model, fitted to the Zimbabwe data, that provides insights into the nature of the epidemic in Zimbabwe and, on a broader scale, to control of cholera at a global level. More specifically, we used Zimbabwe data to derive estimates of the basic reproductive number (R₀) of cholera on a regional basis, building on a modified version of the cholera model initially proposed by our group (10). The epidemic threshold R₀ provides information for the occurrence of an epidemic. If R₀ < 1, then the pathogen introduced into a wholly susceptible population will eventually die out, and when R₀ > 1, endemicity is possible. It also defines the average time it takes for an epidemic to complete one generation and the larger it is, the shorter the generation and the more explosive epidemic transmission will be.

Methods

Codeço (11) extended the Capasso and Paveri-Fontana cholera model (12) with an additional equation for the susceptible individuals in the host population and explored the role of the aquatic reservoir in the persistence of endemic cholera. Hartley et al. (10) modified this model on the basis of laboratory findings that passage of Vibrio cholerae O1 Inaba El Tor through the gastrointestinal tract results in a short lived, hyperinfectious state of the bacterium that decays in a matter of hours in a state of lower infectiousness (13). Further, it was shown that incorporating the hyperinfectious state in a cholera model provides a much better fit with the observed epidemic pattern of cholera. Other mathematical studies on modeling cholera dynamics include refs. 14–16.

In the current study we simplify a model with fast and slow environmental transmission (10). Environment-to-human transmission is defined as a “slow” transmission process with a high infectious dose, resulting from drinking contaminated water from water bodies such as rivers, dams, wells, and ponds. V. cholerae present in these locations may represent “reservoir” microorganisms, which have been in the environment for extended periods of time; alternatively, they may represent V. cholerae from human waste, which has been in the environment for a sufficiently long period (anywhere from 5 to 18 h) to no longer be hyperinfectious. In contrast, human-to-human transmission is assumed to be a very “fast” transmission process with a lower infectious dose that encompasses infection in settings such as households, market places, and funeral feasts as a result of immediate water or food contamination by hyperinfectious vibrios from freshly passed human stool. The results in ref. 10 provide the basis for the critical importance of the fast human-to-human versus the slower environment-to-human transmission in the explosive nature of cholera epidemics. These simplifications result in a model with very similar dynamics, including the model's ability to describe the explosive cholera outbreaks (17).

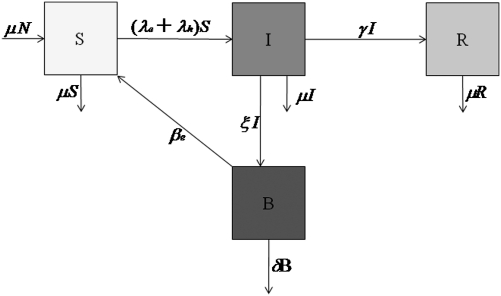
The cholera model classifies the human population, denoted by N, into susceptibles S, infected I, and recovered R. Individuals are born and die at an average rate μ. The concentration of vibrios in contaminated water is denoted by B. Susceptible individuals acquire cholera infection either by ingesting environmental vibrios from contaminated aquatic reservoirs or through human-to-human transmission resulting from the ingestion of hyperinfectious vibrios (18) at rates

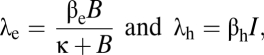respectively, with the subscripts e and h denoting environment-to-human and human-to-human transmissions. Here, κ is the concentration of vibrios in contaminated water in the environment, and β_e and β_h are rates of ingesting vibrios from the contaminated environment and through human-to-human interaction, respectively. Infected individuals progress at a rate γ into the recovered class. Cholera-infected individuals contribute to V. cholerae in the aquatic environment at rate ξ and vibrios have a net death rate δ in the environment. The model flow diagram is presented in Fig. 3. The differential equations describing the cholera model are given in SI Methods.

Fig. 3.

Model flow diagram.

To estimate the basic reproductive numbers for the cholera outbreak in the 10 provinces and the whole country (Zimbabwe), we used the weekly data on numbers of cholera cases reported to the Zimbabwe Ministry of Health and Child Welfare (MoHCW) for the period from November 13, 2008 to July 31, 2009. This is the period with a complete cholera dataset for all of the provinces in Zimbabwe and marks the onset of a countrywide epidemic. We also used other demographic and epidemiological parameter values for cholera in literature given in Table S1. We obtained this dataset from the Epidemiology and Disease Control department in the Ministry of Health and Child Welfare. Despite that the cholera outbreak in Zimbabwe is one of the worst cholera outbreaks in Africa to date, this dataset has not yet been fully analyzed.

The discussion in ref. 10 indicates that parameters β_e and β_h (rates of Vibrio ingestion) are sensitive and vary from place to place. Thus, in the fitting we estimate β_e and β_h to match the reported infections in each province and for the whole country with other parameter values fixed as given in Table 1. Cholera data are fit using the built-in MATLAB (Mathworks, Version 7.10.0.499, R2010a) least-squares fitting routine lsqcurvefit in the optimization tool box. The 95% confidence intervals are calculated from the covariance matrix at the solution using the MATLAB function nlparci.

Table 1.

Population sizes (28), cholera cases, and deaths reported to the MoHCW from November 2008 to July 2009

	Population size	Total infected	Attack rate/10,000	Total deaths	CFR %
Harare	2,012,784	19,577	97	655	3.35
Bulawayo	718,278	445	6	18	4.04
Mashonaland Central	1,056,666	1,039	98	297	2.86
Mashonaland East	1,196,772	6,526	55	453	6.94
Mashonaland West	1,300,012	22,751	175	945	4.15
Midlands	1,554,058	7,156	46	331	4.63
Manicaland	1,665,451	13,673	82	667	4.88
Matebeleland South	693,230	5,257	76	159	3.02
Matebeleland North	748,317	1,166	16	71	6.09
Masvingo	1,401,672	11,644	83	691	5.93
Zimbabwe	12,347,240	98,585	80	4,287	4.35

The advantage of using cumulative over weekly number of new infections is that the former somewhat smoothes out known reporting delays on weekends and holidays (19, 20). For estimating R₀ for the cholera outbreak, we use the set of data points maximizing the basic reproductive number at the beginning of the outbreak i.e., β_e and β_h. The mathematical properties of the cholera model including graphical illustrations (Figs. S1 and S2) are given in SI Methods.

Results

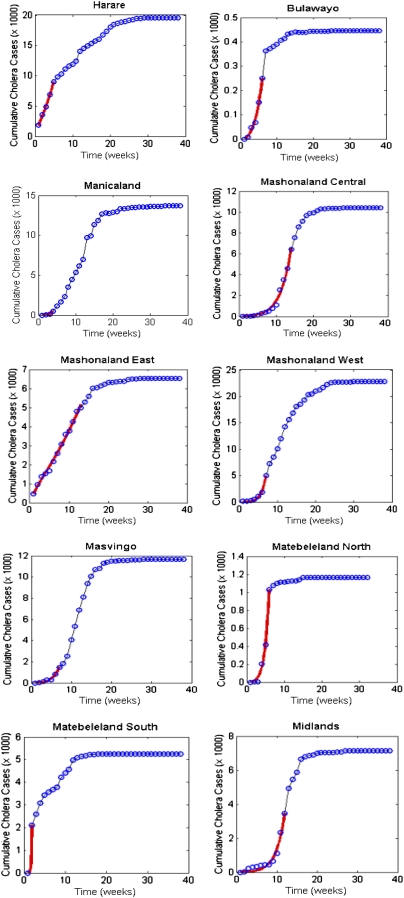
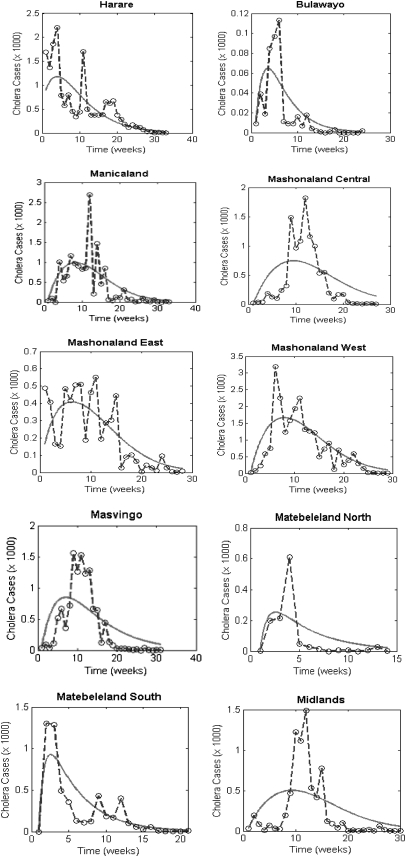
The obtained estimates for β_e and β_h and in Table S2 and the corresponding values of R_e, R_h, and R₀ for the 10 provinces and the whole country are given in Table 2. The plots for the data fitting of the cumulative cholera cases are shown in Fig. 4 for the provinces and for the whole country (Fig. S3) and we also show fitting of weekly reported cholera cases in Fig. 5 for the provinces and in Fig. S4 for the whole country.

Table 2.

Estimates of R_e, R_h, and R₀

	Re	95% CI	% R0	Rh	95% CI	% R0	R0	95% CI
Harare	0.9	(0.57–1.24)	59.4	0.62	(0.57–0.72)	40.6	1.52	(1.14–1.96)
Bulawayo	0.14	(0.071–0.22)	10.6	1.22	(1.05–1.39)	89.4	1.36	(1.12–1.61)
Mashonaland Central	0.2	(0.11–0.29)	14.3	1.18	(1.11–1.25)	85.7	1.38	(1.21–1.54)
Mashonaland East	0.45	(0.31–0.58)	40.4	0.66	(0.58–0.74)	59.6	1.11	(0.90–1.32)
Mashonaland West	0.32	(0.01–0.62)	16.9	1.54	(1.33–1.76)	83.1	1.87	(1.34–2.38)
Midlands	0.077	(0.012–0.14)	5.5	1.31	(1.21–1.41)	94.5	1.39	(1.23–1.56)
Manicaland	0.2	(0.099–0.29)	9.5	1.87	(1.68–2.05)	90.5	2.06	(1.78–2.34)
Matebeleland South	1.44	(0.68–2.2)	52.9	1.28	(0.52–2.04)	47.1	2.72	(1.19–4.24)
Matebeleland North	0.14	(0.036–0.24)	8	1.58	(1.4–1.76)	92	1.72	(1.44–1.99)
Masvingo	0.25	(0.047–0.46)	15.8	1.36	(1.15–1.56)	84.2	1.61	(1.20–2.03)
Zimbabwe	0.2	(0.15–0.25)	17.3	0.95	(0.93–0.98)	82.7	1.15	(1.08–1.23)

Fig. 4.

Cholera model fitting for the cumulative cholera cases where the solid red line represents the model fit and the circles mark the reported data for the cumulative number of cholera cases in the provinces using parameter values in Table S1 and population sizes in Table 1.

Fig. 5.

Cholera model fitting for the cholera cases. The solid line represents the model fit, and the dashed line and the circles mark the reported data for cholera cases in the provinces using parameter values in Table S1 and population sizes in Table 1.

The basic reproductive number provides useful guidelines for the prevention and control strategies for cholera epidemics in Zimbabwe, for example, considering the use of vaccination to reduce susceptibility to cholera infection. On the basis of ref. 21, the vaccination program has to achieve a minimum coverage of

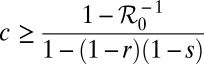to contain a cholera epidemic, where r is the fraction of the vaccinated population who are completely immunized (i.e., with zero susceptibility), and s is the proportional reduction of the susceptibility for those partially immunized. For r = 0 and s = 78% (22) we note that the vaccination coverage required to contain the epidemic in Table 3 ranges from ∼13% to 82%.

Table 3.

Estimates of minimum vaccination coverage

	Vaccination coverage threshold, c %
Harare	44
Bulawayo	34
Mashonaland Central	35
Mashonaland East	13
Mashonaland West	59
Midlands	36
Manicaland	66
Matebeleland South	81
Matebeleland North	53
Masvingo	49
Zimbabwe	17

To explore the effects of other forms of unreported cholera infection such as asymptomatic colonization on the estimate of R₀, we assumed that the current data represent a certain percentage of reported cases in the clinical spectrum of cholera infection and fitted the model to Zimbabwe data. Sensitivity analysis was carried out to assess the effects of varying the percentage of reported cases in the clinical spectrum of cholera infection on the basic reproductive number. The results show that incorporating other forms of unreported cholera infection into the model changed the R₀ estimate by <5% (Fig. S5).

Discussion

An estimate of the basic reproductive number in emergent cholera epidemic regions like Zimbabwe conveys important information about the prospects for effective control of future cholera outbreaks and for designing targeted surveillance programs. The indirect transmission routes, the potential for amplification in an environmental reservoir, and the potentially long timescales of environmental paths make the estimation of the numerical value of R₀ for cholera a difficult task. Classification of cholera transmission routes into defined contacts as in the cholera model, a useful simplification of cholera models, facilitates quantification of transmission dynamics and estimation of R₀. In general, even for diseases with clearly defined contacts, contact rates are difficult or impossible to estimate in the field especially for diseases transmitted directly through close contact or through multiple routes of infection (23). Thus, some methods for estimating R₀ use reported data from the epidemic at the invasion or the endemic phase.

These quantities of R₀ > 1 obtained for the 10 provinces and the whole country (Table 2) imply that future epidemics are highly likely, after population immunity has waned, unless effective control measures are put in place. They also suggest that cholera epidemics could be prevented by mass vaccination with a cholera vaccine that achieved moderate uptake. These estimates suggest that environment-to-human and human-to-human modes of transmission both contributed in initiating and sustaining cholera outbreaks across the provinces in Zimbabwe independently, with the latter mode of transmission contributing more (Table 2). The lack of a large estuarine system or other possible long-term ecological reservoirs for cholera suggests that cholera could be eliminated from the region if vaccination were sustained. Considering that the provinces (8 rural and 2 urban) in the country are very distinct in so many ways including sources of water supply, rainfall distribution, and population densities, it would be difficult for one mode of transmission to influence the spread of the epidemic in all of the provinces.

The challenge in controlling the cholera epidemic in Zimbabwe was abetted by the economic collapse in the country that left clinics and hospitals unable to acquire and stock even basic medicines and materials to provide health care, with most clinics in the rural areas closed. The basic oral rehydration salts (salt, sugar, and clean water), credited for preventing 40 million deaths since they were formally endorsed by WHO, were even beyond the means of many Zimbabweans as they could not afford to purchase sugar and salt as a result of the economic crisis (5, 24).

Epidemiological reports on cholera in Zimbabwe suggest that contamination of drinking water sources and funeral feasts were major factors in initiating the epidemic. For example, the MoHCW and WHO (6) outbreak investigation revealed that the probable index case in Norton town (in Zimbabwe) died on November 18 and the first nine cases to present around November 21 and 22 had attended the funeral. In Zimbabwe and Africa in general, funeral feasts associated with the culture of eating together with fingers from the same bowl and an obligation to shake hands in comforting the bereaved have been a major cause of cholera spread during an outbreak. We also note in Fig. 5 that the data for weekly reported cases show very explosive epidemic peaks during the course of the epidemic and these may have been the result of large outbreaks associated with contaminated water sources; explosive outbreaks associated with contamination of drinking water amount to a kind of superspreading. The town (Norton) also had water and sanitation problems, with burst sewers, unprotected wells, and only one tanker and one borehole available to the population of 44,000.

The results in Table 3 suggest that a vaccine with 78% efficacy was sufficient to contain an epidemic in the provinces at different vaccination coverage rates. However, we note that our evaluation of vaccination coverage estimates is based on direct vaccine protection: need for coverage would potentially be further reduced if herd protection of cholera vaccines was taken into account (25). Preemptive vaccination in regions at risk for cholera would represent the ideal approach, with the potential for drastically reducing or eliminating subsequent cholera transmission. Unfortunately, preemptive vaccination requires a degree of prescience that is seldom present and assumes a functioning public health system, which is often not present immediately before onset of an epidemic. In practical terms, this lack results in vaccination after onset of an epidemic (reactive vaccination): Although not an ideal approach, our data underscore the importance of including vaccination as an important component of an overall response to epidemic cholera. We recognize, however, that due to the collapse of the economy, a broken health system, and the severe shortage of primary care facilities (5), such vaccination coverage may not have been feasible in Zimbabwe either before or after onset of the epidemic.

The study has some limitations. The estimate of the basic reproductive number is based on available data and this estimate could possibly change depending on the quality of the data from the start of the epidemic. We note that we had no data on weekly reported cholera cases for the early affected provinces (Harare, Mashonaland East, and Mashonaland West) till mid-November but the outbreaks in these provinces began between September and October 2008. This lack of data for weekly and/or daily reported cholera cases for this period was due to possible logistic problems (human resource and material shortages at the province and the district level and communications problems) (6) affecting the surveillance system at the onset of the epidemic. The lack of complete datasets from the onset of the epidemic in provinces may affect our results. Nevertheless, our estimates of the basic reproductive numbers in the provinces and for the whole country are the first significant step in quantifying the magnitude of the cholera outbreaks in Zimbabwe and are a platform to help public health officials scale intervention strategies if such an outbreak befalls the country again.

Cholera has the potential to spread widely and to cause many deaths; thus a well coordinated timely and effective response to outbreaks is paramount. In the ongoing emerging and reemerging cholera outbreaks in poor resource settings, the building of reasonable mathematical models for cholera will help us understand the spread and control of the disease, identify the mechanisms influencing transmission dynamics, and assist (potentially in real time) in making forecasts and public health policy decisions. Thus, it is our view that similar methods can be used to forecast the spread of cholera and scaling intervention strategies not only in Zimbabwe but also in other regions with endemic and epidemic cholera.