Quantifying Water-Mediated Protein–Ligand Interactions in a Glutamate Receptor: A DFT Study

Abstract

It is becoming increasingly clear that careful treatment of water molecules in ligand–protein interactions is required in many cases if the correct binding pose is to be identified in molecular docking. Water can form complex bridging networks and can play a critical role in dictating the binding mode of ligands. A particularly striking example of this can be found in the ionotropic glutamate receptors. Despite possessing similar chemical moieties, crystal structures of glutamate and α-amino-3-hydroxy-5-methyl-4-isoxazole-propionic acid (AMPA) in complex with the ligand-binding core of the GluA2 ionotropic glutamate receptor revealed, contrary to all expectation, two distinct modes of binding. The difference appears to be related to the position of water molecules within the binding pocket. However, it is unclear exactly what governs the preference for water molecules to occupy a particular site in any one binding mode. In this work we use density functional theory (DFT) calculations to investigate the interaction energies and polarization effects of the various components of the binding pocket. Our results show (i) the energetics of a key water molecule are more favorable for the site found in the glutamate-bound mode compared to the alternative site observed in the AMPA-bound mode, (ii) polarization effects are important for glutamate but less so for AMPA, (iii) ligand–system interaction energies alone can predict the correct binding mode for glutamate, but for AMPA alternative modes of binding have similar interaction energies, and (iv) the internal energy is a significant factor for AMPA but not for glutamate. We discuss the results within the broader context of rational drug-design.

1. Introduction

Water constitutes the cellular environment where biomolecules interact. Specifically it plays a crucial role in mediating interactions between ligands and macromolecular receptors. Water is also important for protein folding and stability, and it is also known to actively participate in many catalytic processes in the cell. As such its importance has been increasingly recognized through protein–protein and protein–ligand interaction studies with respect to rational drug design.(1) However, despite the wealth of structural information, the precise role of water molecules in mediating receptor–ligand interactions remains unclear.(2)

In the context of drug design, one key problem is knowing whether a certain water molecule will be readily displaceable by functional groups designed to replace it. This issue has been the focus of recent computational studies.³⁻⁵ While pure molecular dynamics studies focused on identifying and characterizing the interactions between the protein, ligand, and conserved water molecules,(6) free energy^3,7 calculations were used to further elucidate the functions of these water molecules and probe their apparent stabilizing role in the protein binding site. A measure of the free energy is ultimately what is required in order to assess the stability of water molecules within binding sites. However, obtaining sufficient accuracy of these calculations, especially for charged systems (which encompasses most biological systems),^8,9 is particularly challenging and an area of intense investigation.(10) One factor in these calculations is the underlying simplicity of the force-field which may or may not account for interactions at the necessary level required. Even with these simplified models, the calculations are still time-consuming enough to be prohibitive at the level of virtual screening. Nevertheless they do form the underlying physical basis of many scoring functions employed in virtual high-throughput screening methods, and consequently, it is of great interest to improve them as much as possible.

Many binding pockets have a complex network of water molecules and in some instances this has already been exploited to give increased drug potency, for example, in the case of HIV-1 protease where cyclic urea derivatives were designed to displace a conserved water molecule.(11) Related to the problem of displaceable water molecules is the concept that water molecules can be considered as part of the drug rather than part of the protein. This can lead to the situation where similar compounds that might be expected to adopt the same binding pose on the basis of their chemical structure, actually adopt different poses within the binding pocket. A good example of this can be found in structures of the ionotropic glutamate receptors which are an important set of potential drug targets within the central nervous system.

The ionotropic glutamate receptors (iGluRs) can be classified, both in terms of sequence similarity and pharmacology, into three major subclasses: (S)-2-amino-3-(3-hydroxy-5-methyl-4-isoxazolyl) propionic acid (AMPA; GluA1–4), N-methyl-d-aspartic acid (NMDA; GluN1–3)) and kainic acid (GluK1–5) receptors.(12) These receptors are activated by glutamate, the major excitatory neurotransmitter in the vertebrate central nervous system (CNS).(13) iGluRs play key roles in various physiological processes, in particular synaptic plasticity, which is thought to be essential in memory and learning.(14) Furthermore, they have been associated with abnormal neuronal activity leading to a wide range of neurodegenerative diseases such as Alzheimer’s, Parkinson’s, Huntington’s chorea, amyotrophic lateral sclerosis (ALS), epilepsy, and ischemic stroke.¹⁴⁻¹⁸ Thus, pharmacological intervention at these neuronal receptors is a valuable therapeutic strategy.

Recently, the structure of a full-length tetrameric GluA2 construct was solved to a resolution of 3.6 Å.(19) However, because working with the full-length protein is difficult, it has in the past been more common to perform structure work with the soluble domains; the ligand-binding core domain(20) and the N-terminal domain.²¹⁻²³ Currently there are over 75 crystal structures for the GluA2 ligand binding domain.²⁴⁻⁴⁶ These X-ray structures provide a wealth of information about the interactions of agonists, antagonists, and allosteric modulators particularly with respect to the glutamate receptor subunit GluA2. Many of these structures are of sufficient resolution to have reasonable confidence in the positions of water molecules within the binding pocket. These observations have been supported by multiple crystal structures along with data from molecular dynamics simulations.^6,47,48

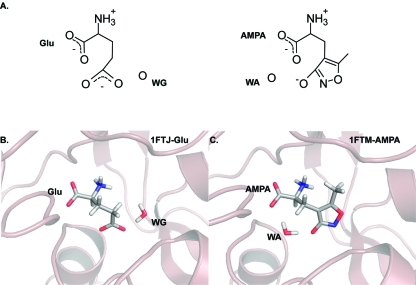
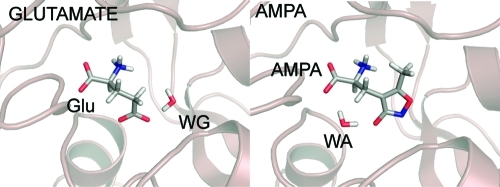
Prior to the crystal structures and on the basis of pharmacophoric models, it was thought that glutamate and AMPA would adopt similar poses within the binding pocket. However, crystal structures revealed that AMPA adopts a slightly different binding-mode with a water molecule assuming a position that would normally be occupied by the γ-carboxyl group of glutamate (Figure 1).(24) It has also been reported that docking studies that did not take into account the crystallographic waters failed to obtain the correct poses.(49) This unexpected difference in binding mode raises some interesting questions: (i) What is the underlying cause for the difference? (ii) Can the differences in the position of water molecules and binding pose of the ligand be rationalized in terms of interaction energies? (iii) Does glutamate cause polarization effects that AMPA does not? (iv) Can the correct binding mode be predicted by energetic (enthalpic) considerations alone?

Figure 1.

(A) Chemical structures of glutamate and AMPA. The 3-oxyanion oxygen and nitrogen from the ring of AMPA were thought to mimic the γ-carboxylate of the glutamate. Cartoons of glutamate from the 1FTJ structure (B) and AMPA from the 1FTM structure (C) bound to GluA2 along with the water molecules that act as surrogate ligands. WG occupies the site occupied by the ring nitrogen of AMPA. WA sits in the site occupied by left-most (in this view) carboxylate oxygen of glutamate.

In order to address these questions we use a quantum mechanical level treatment to accurately calculate interaction energies of both glutamate and AMPA in the two different binding modes. Ab initio calculations have been used previously in order to account for subtype specificity between GluA1 and GluA3 where the difference in the binding pocket was a phenylalanine instead of a tyrosine.(50) Here we use density functional theory (DFT) to calculate the interaction energies of components of the GluA2 binding site with AMPA and glutamate. The calculations demonstrate that interaction energies alone are able to discriminate between the “correct” binding mode for glutamate but not for AMPA. We also show that the interaction energy of a water found in the glutamate-bound crystal structure (1FTJ) is more favorable than its counterpart at a different position in the AMPA-bound crystal (WA in Figure 2B). We find that polarization effects are stronger in glutamate than in AMPA and that the difference in strain energy between alternative conformations of glutamate is very small but is over 2 kcal mol^–1 for the alternative conformation of AMPA.

Figure 2.

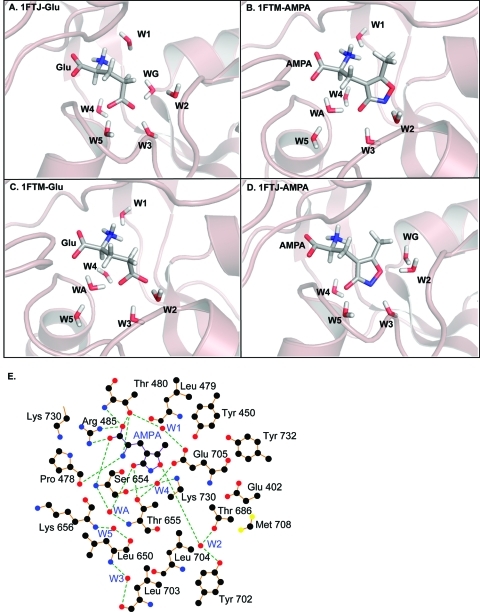
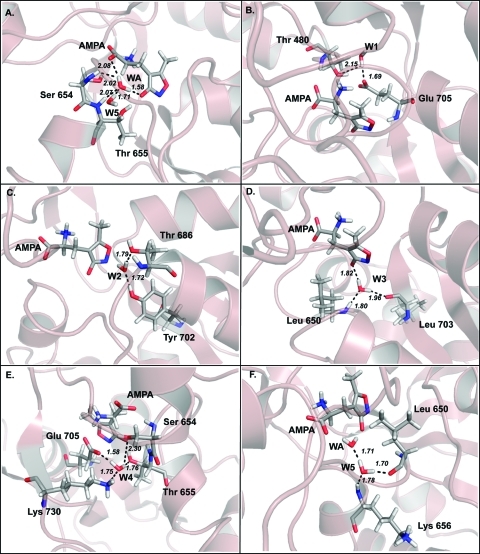
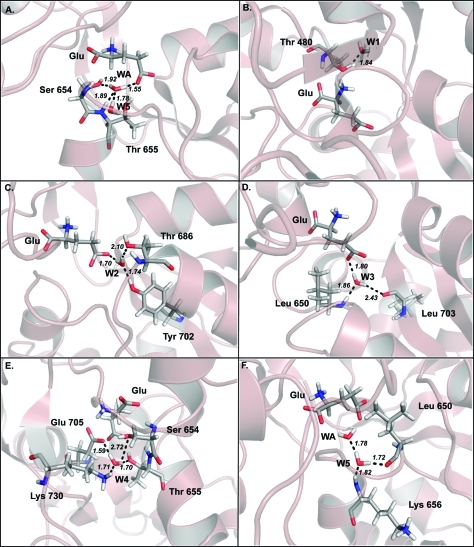
Cartoon illustrating the four model systems. (A) Glutamate in 1FTJ structure. (B) AMPA in the 1FTM structure. (C) Glutamate in the 1FTM structure. (D) AMPA in the 1FTJ structure. (E) Schematic diagram indicating the atoms of the system (taken in this case from the 1FTM with AMPA bound). Green lines indicate hydrogen bonds. Not all atoms are shown for the sake of clarity. All atoms from residues 649 to 656 are present in the calculations but not all make direct contacts with the ligand. Only the atoms Cα, C and O from Gly 648 are present in the calculations but also omitted here for clarity as are all hydrogen atoms. Figure drawn with ligplot.(77)

2. Methods

The model-systems have been assembled using the high-resolution crystallographic structures of the GluA2 ligand binding core bound with glutamate and AMPA available at the Protein Data Bank with PDB Code 1FTJ (resolution 1.9 Å) and 1FTM (resolution 1.7 Å), respectively. Since the crystal structures were composed of 3 protomers (chains A, B, and C), only one monomer (i.e., chain A) was selected as the starting geometry for a molecular mechanics energy minimization. This choice was based on previous work done on GluA2 protomers.(51) In total, four model systems were prepared (Figure 2): two “wildtype” where the ligand (glutamate or AMPA) is in the pose observed crystallographically which we refer to as 1FTJ-Glu and 1FTM-AMPA and two where the ligand is in the alternative pose (Figure 2). For glutamate in the 1FTM structure this was achieved by converting AMPA to glutamate (by matching equivalent torsion angles, deleting atoms and converting the isoxazole nitrogen to an oxygen). For AMPA in the 1FTJ structure, AMPA was fitted to the C, Cα, Cβ, Cγ and Cδ atoms of glutamate such that the amide of AMPA fitted onto the side-chain carboxylate of glutamate. Missing side-chains of the protein were completed with the WHAT IF web interface at http://swift.cmbi.kun.nl/whatif/. All the water molecules reported in the crystal structure were included in the simulations. The system was then solvated using a box of TIP3P(52) water molecules. Counterions were added to neutralize the system and water molecules were randomly replaced with cations and anions to make a 150 mM solution. The system was then minimized using the steepest descent algorithm, until it converged with a force tolerance of 100 kJ mol^–1 nm^–1. GROMACS version 3.3.1(53) was used in these calculation utilizing the all atom OPLS-AA force field.^54,55 This energy minimized structure was then chosen as the representative structure to assemble the quantum mechanical (QM) model.

The QM models were assembled by considering the specific ligand of interest, with water molecules within 5 Å from the ligand and all amino acids within a distance of 10 Å from the ligand and water molecules. In the end 23 interacting residues from the GluA2 receptor were chosen that included Glu402, Tyr450, Pro478 - Thr480, Arg485, Gly648 - Lys656, Thr686, Tyr702 - Glu705, Met708, Lys730, Tyr732 (Figure 2E shows a schematic summary of the resulting QM system). Our rationale for this selection protocol was to ensure that we had the residues of the protein interacting with the ligand (and observed waters) in a system that was computationally feasible.

The numbering employed here is according to the mature sequence as employed by Armstrong and Gouaux (2000) for ease of comparison.(24) It is important to note that residues Arg485, Thr480 and Pro478 from Domain 1 and Ser654, Thr655 and Glu705 from Domain 2 directly interact with both ligands. The side-chain of each residue was shortened to keep only those hydrogen-bonded interactions with the ligand or adjacent residues. Additionally, each peptide bond was replaced with a Cα-H bond to reduce the size of the QM model system.

The final QM models consisted of 357 atoms for 1FTJ-Glu and 1FTM-Glu, 358 atoms for 1FTJ-AMPA and 361 atoms for 1FTM-AMPA. As such each model has 23 residues, the ligand and 6 water molecules, except 1FTJ-AMPA, which only maintained 5 water molecules within 5 Å from the ligand after the energy minimization step.

Prior to the calculation of single point interaction energies with density functional theory, each structure was initially optimized using the ab initio Restricted Hartree–Fock (RHF) method(56) with the 3-21G split valence basis set.⁵⁷⁻⁵⁹ To take into account the partially constraining effect of the protein environment on the active-site geometry, the side-chains were geometry optimized while the backbone was “frozen”. Also, for contiguous amino acidic residues we froze the positions of atoms involved in the peptide bond.

The RHF/3-21G geometry provided structural parameters that were then used as the input in a subsequent theoretical refinement step with the inclusion of electron correlation effects to obtain more reliable energy. These single point density functional theory calculations were carried out with the Gaussian 03(60) program. Both the B3LYP^61,62 and the MPW1B95^63,64 functionals were used. Ideally one would have used this level of theory to have also performed the optimizations, but these calculations are simply too prohibitive at the present time. Nevertheless, this combined approach should provide a means to compare the different possible modes of interaction.

Interaction energies were calculated for a series of fragments (Table 2) that form the major components of the binding pocket (waters, protein, and ligands). The interaction energies for any two fragments can systematically be corrected for by the basis set superposition error (BSSE) using the function counterpoise method of Boys and Bernardi.(65) As such, the interaction energies can be described as in eq 1

Table 2. Fragment Interaction Energies of Water Molecules and Ligand in Each QM System^a.

	kcal mol–1
fragment	Ws	L	P	LP	WsL	WsP	WsLP
1FTJ-GLU
W1	0.09	1.98	–57.13	–13.18	2.10	12.26	–3.65
W2	–1.90	–3.22	3.56	–34.21	–7.04	–0.67	–29.05
W3	0.42	4.43	–61.78	–29.15	4.65	–52.58	–23.18
W4	0.11	5.27	–83.72	–22.52	5.34	–38.83	–21.79
W5	–0.12	–9.43	–52.17	–15.27	–8.62	5.14	–14.87
WG	–4.00	–13.28	–45.08	–3.10	–19.37	–15.19	–7.87
L						–380.13
1FTJ-AMPA
W1
W2	–0.37	–3.79	–24.21	–26.85	–3.41	–30.48	–30.47
W3	–0.50	–9.42	–6.16	–12.72	–8.84	13.35	–18.01
W4	0.24	5.65	–47.94	–25.44	5.73	–12.32	–24.56
W5	0.50	–10.33	–61.64	–16.48	–9.02	24.28	–14.87
WG	0.93	–5.80	–11.21	–13.35	–3.89	–81.47	–9.75
L						–329.53
1FTM-AMPA
W1	0.41	–1.43	2.09	–4.69	0.03	–20.95	4.21
W2	0.27	–2.28	–0.27	–37.59	–1.36	–24.21	–37.21
W3	1.69	–13.68	–9.27	–18.05	–9.74	10.59	–14.65
W4	0.07	4.04	–49.34	–20.69	4.69	–26.70	–19.55
W5	–2.17	–3.56	–4.90	–5.92	–11.23	–12.12	–11.76
WA	0.30	–11.85	0.60	–5.58	–15.70	18.39	–6.26
L						–327.93
1FTM-GLU
W1	–0.85	1.49	–10.07	–8.36	0.55	–10.95	–1.26
W2	0.77	–2.64	–20.55	–21.54	–1.15	–20.34	–20.40
W3	1.59	–10.60	–7.82	–13.62	–7.08	–30.77	–10.70
W4	–0.83	2.68	–53.96	–22.96	2.82	–51.65	–23.68
W5	–2.54	–3.00	–5.30	–5.60	–11.00	–7.11	–12.03
WA	–0.05	–11.54	2.11	–3.62	–16.21	4.13	–5.59
L						–304.81

^aFragments are defined as follows: WX; water molecules where X is 1-5 or A or G as described in Figure 2. Ws; all other water molecules (e.g. for the W1-Ws cell for 1FTJ-Glu, Ws would mean W2, W3, W4, W5, and WG), L; ligand (AMPA or Glu), P; protein, LP; ligand and protein, WsL; water molecules and ligand, WsP; water molecules and protein, WsLP; water molecules and ligand and protein.

3. Results

3.1. Basis Set Choice

We began by first assessing the influence of different levels of theory on the interaction energies. We selected two water molecules (WG and W5) from the 1FTJ-Glu system (see Figure 2A), and calculated the interaction energies with the MPW1B95 and B3LYP methods (Table 1) on unoptimized systems. The MPW1B95(63) meta-hybrid method was first used in conjunction with three different basis sets. These included the more mathematically complete 6-31G* and 6-31G** basis sets^66,67 as well as the locally dense basis set (LDBS)(68) approach, where the model-system can be partitioned into two very different regions, which are assigned basis sets of different accuracy. Specifically, the atoms directly involved in the formation of hydrogen bonds (including the ligand and water molecules) were described by the 6-31G* basis set. The 3-21G⁵⁷⁻⁵⁹ basis set was chosen for all remaining atoms. We find that the basis set superimposition error (BSSE) was the smallest at the MPW1B95/6-31G** level of theory with comparable interaction energy values for each water molecule (Table 1). The B3LYP/6-31G** level of theory was also investigated and in this context the BSSE is larger than the MPW1B95/6-31G** level of theory. However, although reportedly less accurate in its description of hydrogen-bond interactions than MPW1B95(63) it still offers a good compromise between computational expedience and reliability of the values for BSSE. Thus we pursued B3LYP/6-31G** for the series of calculations for all fragments as detailed in Table 2.

Table 1. Interaction Energies with Counterpoise Correction and Basis Set Superposition Error (BSSE) for Two Specific Water Molecules (WG and W5) in the Binding Site of 1FTJ-Glu System at Four Different Levels of Theory.

	MPWB1K/gena		MPWB1K/6-31 g*		MPWB1K/6-31 g**		B3LYP/6-31 g**
water	ΔECP (kcal mol–1)	BSSE	ΔECP (kcal mol–1)	BSSE	ΔECP (kcal mol–1)	BSSE	ΔECP (kcal mol–1)	BSSE
WG	–14.81	8.39	–15.71	7.70	–15.91	7.61	–12.29	9.26
W5	–12.76	7.72	–13.68	7.22	–13.89	7.16	–9.49	8.74

^agen refers to the locally dense basis set (LDBS) approach.

3.2. Ligand–Protein Interaction Energies

Analysis of the ligand to protein+water interaction energies (L-WsP cells, Table 2) reveals that glutamate is much more favorable in its crystallographically observed mode compared to AMPA in its crystal structure (1FTM-AMPA). Comparing glutamate in alternative binding poses, we find that the L-WsP interaction energy for 1FTJ-Glu is more favorable than 1FTM-Glu by 75.32 kcal mol^–1. However, the situation is not simply reversed for AMPA; in this instance the energies of interaction between AMPA and protein are similar in both modes of binding. The L-WsP interaction energy for 1FTM-AMPA (−327.93 kcal mol^–1) is slightly less favorable than for 1FTJ-AMPA (−329.53 kcal mol^–1). Thus glutamate clearly has a strong preference for a binding mode, but AMPA it would seem is energetically capable of adopting a “glutamate-binding” pose. We then proceeded to examine the origin of this in more detail by examining the interaction energies of water molecules within the binding pocket.

3.3. Water–System Interaction Energies

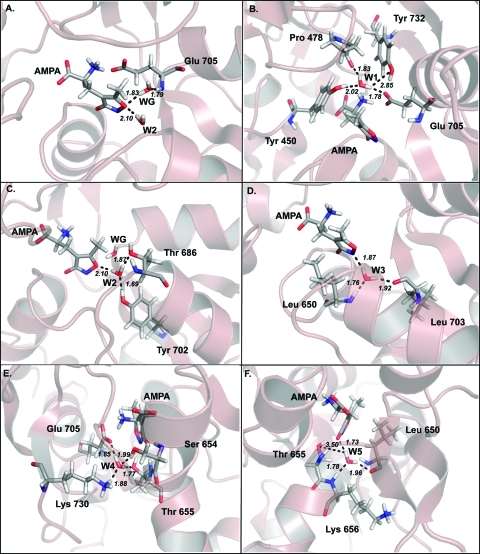
Figures 3–4 describe the water interactions in the four models. We first discuss what we refer to above as the “pharmacophoric water”, which is the water that appears to act as a surrogate part of the ligand in either the glutamate (WG, see Figure 2, panels A and D) or AMPA (WA, see Figure 2, panels B and C) complexes. Before an in depth analysis, one might expect that the interaction energy of WG or WA would be more favorable in the poses adopted in the crystal. However, the interaction energy of the pharmacophoric water with the remainder of the system (WA-WsLP and WG-WsLP cells in Table 2) presents a different perspective of what is observed in the crystal structures. We find that regardless of the ligand bound WA appears to be iso-energetic with a 0.67 kcal mol^–1 difference between the glutamate bound (−5.59 kcal mol^–1) mode and the AMPA bound (−6.26 kcal mol^–1) mode. In the 1FTJ-based models, WG appears to also be iso-energetic albeit with a slight preference of 1.88 kcal mol^–1 for the AMPA bound (−9.75 kcal mol^–1) mode than the glutamate bound (−7.87 kcal mol^–1) mode. One might expect these to be exactly isoenergetic, but the optimizations are done in the presence of ligands and thus there will be some small effects on the final positions of the protein atoms dictated by the ligand. In the 1FTJ-based models, WG forms hydrogen bonds (Figures 3A and 5A) with the backbone NH group of Glu705, the water W2 and an oxygen atom from the ligand (one of the carboxylate oxygens for Glu, and the ring oxygen for AMPA). In the 1FTM-based models, WA forms hydrogen bonds (Figures 5A and 6A) with the OH group of Ser 654, the backbone NH of Thr 655, W5 and two oxygen atoms from the ligand in each case.

Figure 3.

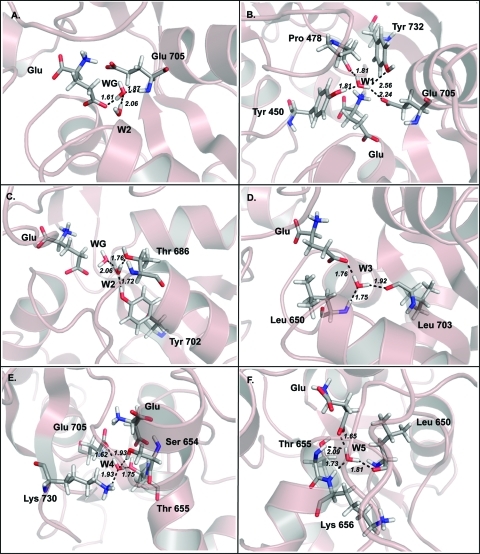
Hydrogen bond interactions for individual water molecules for the 1FTJ-Glu model system (A) WG, (B) W1, (C) W2, (D) W3, (E) W4, and (F) W5.

Figure 4.

Hydrogen bond interactions for individual water molecules for the 1FTJ-AMPA model system (A) WG, (B) W1, (C) W2, (D) W3, (E) W4, and (F) W5.

Figure 5.

Hydrogen bond interactions for individual water molecules for the 1FTM-AMPA model system (A) WA, (B) W1, (C) W2, (D) W3, (E) W4, and (F) W5.

Figure 6.

Hydrogen bond interactions for individual water molecules for the 1FTM-Glu model system (A) WA, (B) W1, (C) W2, (D) W3, (E) W4, and (F) W5.

The detailed breakdown of how this water interacts with the various components of the binding pocket (the WG or WA rows in Table 2) shows that the overall interaction energy (WG/WA-WsLP) does not arise from the contribution of the ligand solely but instead appears to be related to the whole environment of the system in which each ligand is bound. Table 2 also demonstrates that the fragments are clearly nonadditive in nature. WG appears to have favorable interaction energies with all fragments. However, the interaction of WA with protein alone appears to be nonfavorable.

W1 was found to have the least favorable interaction energies in all and indeed in none of the models does W1 make a hydrogen bond with the ligand. W2 is most energertically favorable in the 1FTM-AMPA system. W2 makes contacts with Tyr 702 and Thr 688 in all models. The pattern of interaction energies relates directly to the number and geometry of the hydrogen bonds formed. W3 makes hydrogen bonds with Leu 650 and Leu 730 in all four models (Figures 3–4D), and a third hydrogen bond to the ligand. The interaction energy (Table 2) is most favorable in the 1FTJ-Glu mode and is a result of an optimal arrangement of both ligand and protein.

W4 was found to maintain comparable interaction energies across the models and could be associated with the fact that it forms a tetrahedral association with mostly charged side-chain of the residues; Glu 705, Lys 730, Ser 654, and Thr 655 in all four models. This water does not form any direct interaction with the ligands and occupies a well-defined site apparently serving a structural role, presumably helping to define the shape of the binding pocket.

W5 is another water molecule that occupies a well-defined site and is also a well conserved water molecule, found in the majority of published high-resolution ligand-bound iGluR structures. In the 1FTJ derived models (Figures 3F and 5F) W5 makes four direct hydrogen bonds to the ligand, Leu 650, Thr 655, and Lys 656 and has an identical interaction energy of −14.87 kcal mol^–1 regardless if glutamate or AMPA is bound. In the 1FTM derived models W5 can also be considered iso-energetic with a 0.27 kcal mol^–1 between the glutamate bound (−11.76 kcal mol^–1) mode and the AMPA bound (−12.03 kcal mol^–1) mode. It does not make any direct hydrogen bond with the ligand but instead makes a hydrogen bond with WA. W5 makes three further hydrogen bonds with Leu 650 and Lys 656 in 1FTM-AMPA (Figure 5F) and with the backbone carbonyl of Leu 650, backbone NH of Lys 656 and backbone NH of Gly 653 in 1FTM-Glu.

3.4. Polarization

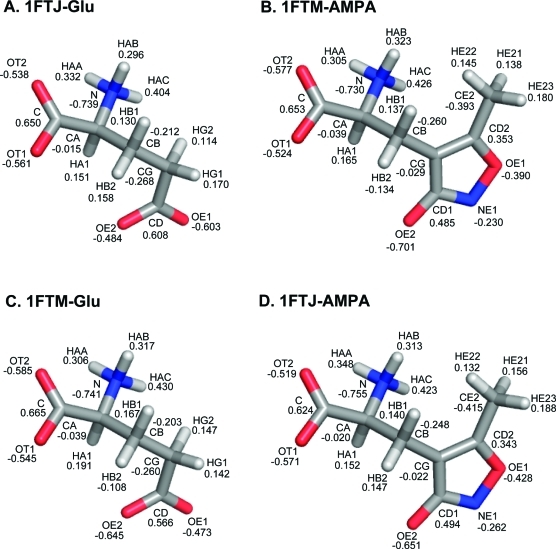
A method commonly employed to calculate partial charges for compounds that are not already parametrized in modern force-fields is to use the restricted electrostatic potential (RESP) fitting method.(69) We performed RESP calculations on the ligands within the four models in order to assess to what extent polarization from the environment in the different binding modes might be a factor. The results are shown for the four models in Figure 7. The calculations show that there is reasonable agreement at the amino and carboxylic acid groups in all four systems (which is to be expected). The greatest variation is observed at the OE1 and OE2 atoms of Glu, which have an asymmetric charge distribution, presumably reflecting the local environment in each case (WG or WA). In contrast there is much less variation observed at the OE2 (or OE1) atoms of AMPA in 1FTM or 1FTJ.

Figure 7.

Comparison of the resulting partial charge on atoms using the RESP(69) method (A) Glutamate in 1FTJ structure. (B) AMPA in the 1FTM structure. (C) Glutamate in the 1FTM structure. (D) AMPA in the 1FTJ structure.

3.5. Internal Energies

We also examined the internal energies of the different fragments as isolated fragments in the gas phase. Differences between the internal gas-phase energies for the water molecules were all under 0.25 kcal mol^–1. The results for the ligands suggest that gas-phase internal energy of glutamate is raised by 13.35 kcal mol^–1 when placed in the AMPA-binding mode (1FTM-Glu system). Similarly, when AMPA is positioned in the glutamate binding mode, the internal energy of AMPA rises by 8.19 kcal mol^–1. When using the polarizable continuum model (PCM) of solvent,(70) the internal energy for glutamate in the 1FTM derived system is only 0.15 kcal mol^–1 higher than the glutamate conformation observed crystallographically in 1FTJ. However, AMPA in 1FTJ is still 2.06 kcal mol^–1 more unfavorable compared to AMPA in 1FTM, suggesting that internal strain is a considerable factor in dictating the binding mode of AMPA, but is not a contributing factor to the glutamate mode of binding.

4. Discussion

The crystallographically determined binding pose of AMPA was rather contrary to expectation. Prior to structural knowledge it was anticipated that the 3-oxyanion and ring nitrogen of AMPA would superimpose on the γ-carboxylate oxygens of glutamate. Instead a water molecule occupies the position of one of the carboxylate oxygen atoms (WA in Figure 2B). Similarly, the position of the ring nitrogen in the GluA2-glutamate complex (1FTJ) is also occupied by a water molecule (WG in Figure 2A). In this sense we can consider this water molecule as part of the ligand in each case. However it is not clear why this water molecule should preferentially occupy different sites with respect to these ligands and hence why the resulting binding pose for AMPA differs from glutamate. Previous docking studies have shown that consideration of this water molecule is essential to retrieve the correct binding pose for AMPA and that omission of this water molecule leads to a docking pose that overlays with the glutamate-GluA2 complex.(49) In the context of drug-design, there has been a lot of work aimed at determining whether water molecules in a binding site can be displaced by modifications to existing ligands. Indeed (RS)-2-amino-3-(3-carboxy-5-methyl-4-isoxazolyl) propoionic acid (ACPA), an analogue of AMPA where the 3-oxyanion moiety is replaced by a carboxylic acid, interacts directly with the side-chain OH of Thr 655.(31) ACPA has both a lower IC₅₀ (IC₅₀ = 20 nM compared to 79 nM for AMPA)(71) and lower EC₅₀ (EC₅₀ = 0.74 μM(31) compared to 3.5 μM for AMPA(72)). The improvement may be more modest than expected as ACPA loses an additional water interaction that AMPA makes, the overlay is not quite perfect and there are small differences in the binding pose and the conformation of binding pocket residues.

In this study we wanted to examine to what extent the observed differences in binding orientation between AMPA and glutamate could be attributed to stabilization effects of water molecules and how the water molecules interact with the protein and/or ligand. Because polarization effects may be critical to this analysis, we used ab initio calculations to calculate the interaction energies between the various components of the binding site.

Our calculations show that a simple interaction energy calculation between the ligand and the rest of the system is sufficient to be able to predict the correct mode of binding for glutamate, but not for AMPA. Clearly, entropic effects, which are neglected in these calculations, must play a more dominant role in the case of AMPA.

Table 2 shows that the “pharmacophoric water” (WG/WA) has no energetic preference for the ligand (glutamate or AMPA) it was crystallized with. The interaction energies in each case are essentially iso-energetic pointing to the possibility that the binding mode must be due to more than the presence of the ligand alone. One contributing factor is polarization effects which do not appear to be pairwise additive for these systems. One notable example is the clearly defined W5 site which influences the binding of the ligand.(48) Although the interaction energies are iso-energetic for W5-WsLP, the breakdown across each subtype is different in each case. The results here suggest that consideration of the binding pocket in the absence of ligand(s) may not always give the correct answer without taking into consideration the significant effects from polarization. This is a particularly important aspect in the context of drug design as there is increasing interest in being able to predict how readily water molecules in the active site are displaced.(5)

Docking programs often have an energetic term that accounts for the internal or strain energy of the ligand and indeed this can be a contributing factor to the binding pose. The most useful measure of this strain energy though is the comparison between binding modes and in solvent. Our calculations showed that the differences in internal energy for the glutamate conformations using the PCM solvent model are very small (0.15 kcal mol^–1). Previous calculations of glutamate in solution suggest that the energy difference between two minima for glutamate in solution may be as small as 0.1 kcal mol^–1 and that the conformation in the crystal structure is intermediate between these two minima.(73) Thus internal strain is not likely to be a factor for dictating the pose that glutamate adopts. On the other hand, the results for AMPA suggest that internal strain could be a contributing factor. Recently, Keith et al.(74) demonstrated via the use of ab initio calculations, in conjunction with a solvent model, that bioactive (as observed by X-ray crystallography) conformations of ligands are very close to conformations expected in solution, suggesting that the best docking poses would impose little conformational strain energy on the ligand (less than 0.5 kcal mol^–1 in two-thirds of the cases examined). The strain for AMPA in the 1FTJ is above this level (at 2.06 kcal mol^–1). Together, the results support the notion that scoring functions must incorporate terms other than interaction energies in an accurate fashion if they are to be useful.(75)

The results from the RESP calculations suggest that polarization effects can be quite significant in the case of glutamate but less so for AMPA. The charge assignments in the region of the molecule where the environment is the same in the four systems (the amino and carboxyl groups) are in good agreement with each other suggesting that the differences observed for the glutamate side-chain group are genuine and system dependent. The RESP method is one of the standard methods for calculating charges for ligands in force fields for which parameters are not already available. These calculations are usually performed in the gas phase. The variation in these charges shown in Figure 7 demonstrates that this may potentially be a source of error if simple point charges are used to evaluate electrostatic contributions in molecular mechanics or docking approaches. Large, conformationally dependent variation in charge assignment for glutamate has been observed before; Odai et al reported the variation in Mulliken charges for four distinct conformations of glutamate in solution.(73) More systematic work is clearly required in this area to assess how significant these effects are in general.

We also should reiterate that we selected the B3LYP/6-31G** level of theory as the best compromise between accuracy and computational time. Although we found that basis set superimposition error (BSSE) was the smallest at the MPW1B95/6-31G** level (Table 1), it is beyond our current resource to operate at that level.

5. Conclusion

We have shown here how various components of the binding site of GluA2 contrive to dictate the binding mode for glutamate and AMPA. Our calculations highlight that for glutamate there is very little internal strain energy for the different binding modes and that it could readily adopt any one of those conformations. The water, W5, which could be considered part of the ligand or part of the protein, appears to be energetically favorable regardless of the ligand present (and indeed appears slightly more favorable when AMPA is bound). Although simple interaction energies of ligands and waters could partly account for the observed glutamate binding mode, they do not appear to account for the crystallographically observed binding mode of AMPA. Although there is more internal strain energy of AMPA in the 1FTJ-AMPA system, the overall interaction energy of AMPA with the system is more favorabale (than in 1FTM). Thus, there must be other factors, which control the pose of AMPA; most likely an entropic contribution, which is not considered here. Calculations for entropic calculations are beyond the scope of the current approach (optimizations would be needed for every fragment), but is something that could be performed in future studies as computational power increases. Although interaction energies can go some way to providing insight into what factors are controlling binding, they do not provide a complete picture.

There are many reasons why compounds may adopt different binding modes within a receptor, ultimately dictated by the free energy of binding, but with many different contributions. The problem of computing that free energy is complex because often the difference in energy that dictates different binding poses is a very small difference between very large numbers. Thus we must strive to be as accurate as possible if we are to make progress on this front. An accurate consideration of the role of waters within the binding pocket is going to be critical. Our results suggest that for establishing trends, treatment at the B3LYP/6-31G** level is sufficient, but that absolute values are in general much lower than that reported for MPWB95/6-31G** for two test cases.

Finally, the results also indicate that polarization effects could mean that initial partial charge assignments based on gas-phase calculations may lead to problems. More work is required to assess those effects in detail. Having said that, there is much work in progress in developing polarizable models for molecular mechanics,(76) so there is good reason to be optimistic on that front.

Supporting Information Available

Tables of the basis set superimposition errors for the interaction energies for all water molecules in the four studied systems is available. This material is available free of charge via the Internet at http://pubs.acs.org.