Input and Output Compensation for the Cochlear Traveling Wave Delay in Wide-Band ABR Recordings: Implications for Small Acoustic Tumor Detection

Abstract

Background

The Stacked ABR (auditory brainstem response) attempts at the output of the auditory periphery to compensate for the temporal dispersion of neural activation caused by the cochlear traveling wave in response to click stimulation. Compensation can also be made at the input by using a chirp stimulus. It has been demonstrated that the Stacked ABR is sensitive to small tumors that are often missed by standard ABR latency measures.

Purpose

Because a chirp stimulus requires only a single data acquisition run whereas the Stacked ABR requires six, we try to evaluate some indirect evidence justifying the use of a chirp for small tumor detection.

Research Design

We compared the sensitivity and specificity of different Stacked ABRs formed by aligning the derived-band ABRs according to (1) the individual’s peak latencies, (2) the group mean latencies, and (3) the modeled latencies used to develop a chirp.

Results

For tumor detection with a chosen sensitivity of 95%, a relatively high specificity of 85% may be achieved with a chirp.

Conclusion

It appears worthwhile to explore the actual use of a chirp because significantly shorter test and analysis times might be possible.

The traveling wave that is set up in the cochlea by a brief, broadband stimulus, like for instance a click, takes a significant amount of time to reach from the base to the apical end of the cochlea. This phenomenon was originally described in details from the characteristics of single auditory nerve fiber responses to click stimuli in the cat by Kiang et al (1965). Indirect observations of the traveling wave delay from compound auditory responses were made by Teas et al (1962), who introduced the high-pass masking technique. Teas et al (1962) measured the socalled derived or narrow-band auditory compound action potentials (ACAPs) in guinea pigs in response to click stimuli under successive high-pass masking and were able to describe some characteristics of the click-evoked traveling wave. Evans and Elberling (1982) applied the same technique to recordings in the cat and compared the derived ACAP with single fiber responses recorded under the same conditions. Based on these results, Evans and Elberling (1982) were able to confirm the underlying assumptions of the applied high-pass masking technique. In humans, the high-pass masking technique was first applied to the ACAP by Elberling (1974) and Eggermont (1976), and later to the auditory brain stem response (ABR) by Don and Eggermont (1978), and Parker and Thornton (1978).

In the cited references the described high-pass masking experiments were able to demonstrate derived-band responses from specific frequency regions along the cochlear partition. The derived-band responses had latencies that were increasingly longer the lower the center frequency of the narrow band. Thus, the results characterize the cochlea traveling wave in the different species (e.g., guinea pig, cat, and human) and allow for specific calculations of the corresponding average traveling wave delay and velocity (e.g., Eggermont, 1976; Donaldson and Ruth, 1993).

In addition to the high-pass masking technique and the resulting derived-band responses, tone-burst responses, either ACAPs or ABRs, reflect the effect of the traveling wave in that the lower the stimulus frequency the longer the latency of the frequency-specific response (e.g., Gorga et al, 1988). Characteristics of the traveling wave can also be evaluated in a cochlear model (e.g., de Boer, 1980), in combination with specific mapping parameters for different species (e.g., Greenwood, 1990).

Thus, from many different sources, estimates of the traveling wave in different species may be obtained. However, even within the same species, the estimates vary considerably. For instance, estimates of the difference in traveling wave delay between the 8000 Hz and 500 Hz locations in the human cochlea, obtained from (1) a cochlear model, (2) tone-burst ABRs, (3) narrow-band ACAPs, and (4) narrow-band ABRs, may vary over a range from 2.7 to 5.1 msec (Elberling et al, 2007, fig. 1).

The delay introduced by the traveling wave has the consequence that the individual areas along the cochlear partition, the corresponding hair cells, and nerve fibers of the auditory nerve will not be stimulated simultaneously by brief, broadband stimuli (e.g., clicks or other transient sounds). Due to the temporal dispersion (or smearing) the synchronization between the nerve fibers is decreased. This, in turn, results in a reduction of the amplitude of the corresponding compound neural response (ACAP or ABR). In the clinic, this means longer test time, because, especially at lower stimulus levels, the recording time must be adapted to the amplitude of the compound auditory response: the lower the amplitude the longer the test time to achieve a given signal-to-noise ratio of the neural response recorded via signal averaging.

There seem to be two different ways to compensate for the cochlear traveling wave delay: (1) input compensation and (2) output compensation. Input compensation counteracts the temporal dispersion by means of a specific brief stimulus, a chirp, in which the higher stimulus frequencies are delayed relative to the lower frequencies. The introduced delay between the high and low frequencies is based on a chosen model of the traveling wave. A chirp stimulus attempts to compensate for the traveling wave delay by aligning the arrival time of each frequency component of the stimulus to its place of maximum excitation along the cochlear partition. This compensation strategy will make the brief stimulus more efficient by achieving higher temporal synchronization of excitation between the neural elements that contribute to the compound response. Several papers describe the basic considerations, the design, and the testing of chirp stimuli for human ABR applications (e.g., Lütkenhöner et al, 1990; Dau et al, 2000; Wegner and Dau, 2002; and Fobel and Dau, 2004). Similar descriptions for the human auditory steady-state response (ASSR) have recently been made by Cebulla et al (2007) and Elberling et al (2007). In the referenced articles, different traveling wave models have been applied. However, the generated chirps are all significantly more efficient than the corresponding click stimuli, and chirp ABRs and chirp ASSRs are recorded with amplitudes that are about two to three times larger than those recorded using the click. Thus by using a chirp stimulus instead of a click, the necessary recording time can be reduced significantly. The results obtained in groups of normal-hearing individuals show that chirps based on different models of the traveling wave are not equally efficient (e.g.,Fobel and Dau, 2004;Elberling et al, 2007).Therefore it is unclear whether a chirp based on one specific model will prove sufficient for clinical use or whether and how a chirp could be individualized to embrace the variations in cochlear characteristics encountered across a normal-hearing population.

Output compensation of the traveling wave delay for the ABR was developed by Don et al (1994) and can be explained as follows: First, by means of successive high-pass masking, the click-ABR is decomposed into location-specific or frequency-specific components (i.e., the derived- or narrow-band ABRs). Next, the derived-band ABRs are temporally aligned by time shifting each derived-band response in accordance with its observed latency. Third, the time-shifted derived-band ABRs are added together to produce the “Stacked” ABR. In general, the Stacked ABR is significantly larger than the corresponding unmasked click-ABR that demonstrates that compensation for cochlear traveling wave delay greatly affects the amplitude of the ABR. Contrary to input compensation by means of a chirp stimulus, output compensation by the Stacked ABR method is independent of a model of the traveling wave, because the observed, individual derived-band response latencies are used for the compensation instead of a model. The recording of the Stacked ABR is, however, very time-consuming because both the unmasked and five high-pass masked ABRs need to be recorded with a reasonably high waveform definition.

Input compensation with a chirp stimulus and output compensation with the Stacked ABR technique are based on the same fundamental concept, that is, compensation of the traveling wave delay to increase the temporal synchronization of the activity from the contributing neural elements. However, compensation with a chirp uses an average traveling wave delay (via a model) and applies the compensation to the input stimulus waveform. In contrast to this, the Stacked ABR uses a traveling wave delay that is obtained from the derived-band recordings in the individual subject and applies the compensation to the recorded output waveforms.

In conclusion, both input compensation of the traveling wave delay (chirp stimulus) and output compensation (Stacked ABR) have demonstrated that appropriate compensation schemes increase the amplitude of early electrophysiological responses (ACAP, ABR, and ASSR) by increasing the temporal synchronization between the contributing neural elements.

There are two major purposes of this study. The first purpose is to compare the benefit of traveling wave compensation using the Stacked ABR based on (1) individual latency data (standard), (2) mean gender-specific latency data and (3) chirp model latencies (or model-based latencies) data. In the latter, the latencies derived from the chirp model (see Eq. [1] later and Elberling et al, 2007) are used in aligning the responses to form the Stacked ABR.

For the compensation of the traveling wave delay the Stacked ABR can be regarded as an “optimal” reference because compensation is carried out using the observed latency value for each derived-band ABR in each individual test subject. The Stacked ABR may represent the maximal, individual benefit (increase in response amplitude) that can be obtained and therefore what optimally can be expected from the use of a chirp stimulus (see, however, the caveats mentioned in the discussion section below). The data presented in this article come from Don, Kwong, Tanaka (2005). In that study, the responses to clicks alone and to the clicks in the five high-pass masking noise conditions were obtained from 39 normal-hearing and 23 Meniere’s disease patients to evaluate the presence of cochlear hydrops. For the present paper, we formed the derived-band ABRs and constructed the Stacked ABRs from this group of 39 normal-hearing subjects.

The second purpose of the present communication is to evaluate tumor detection efficiency (i.e., sensitivity and specificity) under the application of different latency compensating methods (individual, means, and model based). In clinical studies, Don et al (1997) and Don, Kwong, Tanaka, et al (2005), it was demonstrated that the Stacked ABR technique is particularly useful for the detection of small, intracanalicular acoustic tumors by comparing the amplitude of the Stacked ABR in the tumor patients to reference values from the above mentioned group of normal-hearing test subjects. Since the recording procedure for the Stacked ABR is time-consuming and the construction of the Stacked ABR is complex, it would be interesting to investigate whether the procedure could be further automated or could be substituted with an input compensation method by using a chirp.

For the general application of the Stacked ABR procedure and especially for the detection of small tumors, the results will generate an estimate of what optimally may be expected from substituting the standard Stacked ABR method with a method that uses model-based latencies, or with a chirp-ABR recording method. However, we felt that because of the large time commitment of resources and the rarity of small tumors, a full study with actual tumor patients and this newly developed chirp is not warranted without some suggestion that the measure would perform with acceptable sensitivity and specificity. Thus, we compared the sensitivity and specificity of standard Stacked ABRs formed by aligning the derived-band ABRs according to the individual’s peak latencies with Stacked ABRs formed according to the group mean latencies and latencies resulting from modeling a chirp stimulus based on these mean values. It is important to note that the measures described in this paper are technically still the result of an output compensation method as derived-band ABRs were aligned according to either the individual’s peaks, the mean for the NTNH (nontumor normal hearing) group, or the modeled peak latencies used in constructing a chirp (Elberling et al, 2007).

METHODS

Data Recorded from Previous Studies

Details can be found in Don, Kwong, Tanaka, et al (2005) but are summarized below.

Subjects

This investigation received institutional review board (IRB) approval. Prior to testing, the purpose and procedure of the study were orally presented by the experimenter. The experimenter then answered any questions the subject had regarding his or her participation. Finally, each subject read and signed an IRB-approved informed consent form.

Nontumor Normal Hearing (NTNH). For all subjects, otoscopic examinations were performed to identify existing conditions that would preclude audiometric and ABR testing. The control group was 39 (20 females and 19 males) NTNH subjects in good general health and reported normal otologic and neurological status. The left ear was tested in the NTNH group. The criteria for normal hearing were defined as pure-tone thresholds of 10 dB HL or better for frequencies between 0.5 to 4 kHz; 15 dB HL or better for 6 and 8 kHz. This was the same control group used in a previous study (Don, Kwong, Tanaka, 2005) that only studied the high-pass masked responses and not the derived-band ABRs or the Stacked ABRs.

Small Acoustic Tumor (SAT). The test population for this study was restricted to patients recruited from the House Clinic who had (1) clinical complaints related to hearing or balance; (2) a Gd-DTPA (Gadolinium-DiethyleneTriaminePentaacetic Acid [MRI contrast agent])–enhanced MRI (magnetic resonance imaging) indicating the presence of a tumor; (3) and a tumor that was either undetected by the standard interaural wave V delay (IT5) ABR measure irrespective of its size or 1.0 cm or smaller irrespective of the IT5 results. The first restriction is important because individuals without symptoms normally would not be clinically evaluated. A total of 17 small-tumor patients were tested. Of the 17 patients, 12 had positive standard IT5 ABR (71% detection) resulting in a missed rate of 29%. These results are consistent with many published studies. The tumor was surgically confirmed in all cases except for two patients who elected not to have surgery. However, MRI evaluations resulted in diagnosis of acoustic tumors. These patients had been recruited for studies subsequent to the work published earlier by Don, Kwong, Tanaka, et al (2005) and not specifically for this current study because the chirp stimulus discussed in this study had not been developed and was not available. For all of these 17 patients, the mean clinical pure-tone threshold averages (average threshold for 0.5, 1. 2, and 3 kHz) was 28.5 dB, and for 5 of these 17 patients it was 18 dB or less. Because hearing loss will reduce the Stacked ABR, we briefly review its impact later in the discussion section of our paper.

Stimuli

The stimuli were rarefaction clicks produced by applying to an ER-2 insert phone 100 µsec voltage pulses that were generated, filtered, and amplified by an Ariel DSP-16 board. The clicks were presented 22 msec apart (≈ 45 clicks/sec) at 60 dB above the average perceptual detection threshold for a group of 19 normal-hearing subjects (i.e., 60 dB nHL [dB re normal hearing level]) corresponding to 82 dB p-p.e. SPL (dB peak-peak equivalent sound pressure level) measured in a 2 cc coupler (Brüel & Kjær 4152).¹

Ipsilateral pink-noise masking was used to obtain the derived-band ABRs used in forming the Stacked ABR. The noise was produced by a General Radio Noise Generator (Type 1310) and presented at a level sufficient to mask the ABR to the clicks. The average required level of the noise to mask the click ABR was 81 dB SPL RMS (root mean square) measured in a 2 cc coupler. There were six stimulus conditions: clicks presented alone (unmasked condition) and clicks presented with ipsilateral pink noise high-pass filtered at 8, 4, 2, 1, and 0.5 kHz. The slope of the high-pass filtered masking noise was 96 dB/octave and was achieved by cascading both channels of a Krohn-Hite (Model 3343) dual filter, each with a 48 dB/octave slope.

ABR Recordings

Subjects were placed in a reclining chair in a double-walled sound-treated room (IAC). ABRs were recorded differentially between electrodes applied to the vertex (Cz) and the ipsilateral mastoid (M1 or M2); the electrode at the contralateral mastoid was used as ground. The EEG (electroencephalogram) was band-pass filtered from 0.1 to 3.0 kHz using filter slopes of 12 dB/octave. ABRs were obtained using noise estimation techniques (Elberling and Don, 1984) and weighted averaging techniques (Elberling and Wahlgreen, 1985; Don and Elberling, 1994). These techniques reduced the destructive effects of episodic physiological background noise variation on the ABR average by weighting the average toward those blocks of sweeps with low estimated background noise. Data collection for a run was terminated when the estimated residual background noise in the average reached 20 nV (RMS) or less. Thus, all recordings had approximately the same low residual background noise levels. In addition, by making sure that the residual noise in all our ABR averages was low, we can be confident that the responses we measured represent mostly neural activity and not unaveraged physiological noise.

Forming and Measuring the Amplitudes of the Stacked ABRs

The derived ABR technique consists of recording ABRs first to broadband clicks presented alone and then to a series of simultaneous ipsilateral presentations of the clicks and high-pass pink noise with varying cutoff frequencies as described above. By subtracting the response for one run from the previous one, a derived or narrow-band response is formed. This method for generating a series of five derived ABRs has been presented before in a number of studies (Don and Eggermont, 1978; Parker and Thornton, 1978; Don et al, 1997; Don, Kwong, Tanaka, et al, 2005) and is based on the high-pass masking technique.

The derived-band responses represent octave-wide synchronous activity with a theoretical center frequency (CF) equal to the geometric mean of the high-pass cutoff frequencies used to form the derived ABR. The theoretical CFs of the five derived ABRs are: 11.3, 5.7, 2.8, 1.4, and .7 kHz.

Table 1 shows the average peak latencies for the nontumor normal-hearing group (N = 39) used in a previous study (Don, Kwong, Tanaka, 2005). These mean values were fitted by Elberling et al (2007) to a power function describing the traveling wave delay. However, the mean value corresponding to the highest band center-frequency, that is, 11.3 kHz, was excluded from the curve fitting, since this data point was regarded to be invalid because the level of activation is much lower in this frequency region given the ear’s sensitivity curve and the falling spectrum of the click above 8–9 kHz (Don et al, 1979). Before the power function was generated, a total of 4.96 msec was subtracted from each latency value, that is, 4.10 msec for the ABR wave I–V delay in normal-hearing subjects (Elberling and Parbo, 1987) and 0.86 msec for the acoustical delay in the ER-2 sound tube. The final power function is as follows:

$$\tau =0.0920·{\mathrm{f}}^{-0.4356}$$ (1)

where:

• τ is the traveling wave delay in sec

• f is the frequency in Hz

Table 1.

Observed Latencies (mean and SD) for the NTNH Group for Each of the Five Derived Octave Bands Indicated by the Center Frequency (CF)

Derived-band CF (kHz)	11.3	5.7	2.8	1.4	0.7
Observed latencies
Mean (ms)	7.06	7.15	7.78	8.75	10.44
SD (msec)	0.27	0.35	0.39	0.54	0.86
Modeled latencies (msec)	(1.58)	2.13	2.90	3.92	5.30
Modeled latencies (msec) +4.96	(6.54)	7.09	7.86	8.88	10.26

Note: The modeled derived band latencies (Elberling et al, 2007) and the modeled latencies +4.96 msec are also shown. The parentheses around the modeled latencies for the 11.3 kHz band indicate that the observed mean latency for this band was not used to generate the modeled power function.

The latencies of the fitted power function at the octave band center frequencies were also shown in Table 1 together with the addition of 4.96 msec, which was subtracted prior to the curve fitting.

This description of the traveling wave delay was subsequently used to construct a chirp, which was evaluated in an ASSR experiment in a group of normal-hearing test subjects (Elberling et al, 2007). The chirp stimulus was developed after we collected our Stacked ABR data in tumor patients. At this time we did not have the resources nor the justifications to pursue a new study with the chirp in tumor patients given the expense, time, and involvement of patients. Our intent was to determine if the results of our analyses presented here can provide some justification for committing the time and resources to pursuing studies using the chirp stimulus. Furthermore, publishing these analyses would give us the additional benefit of outside peer review of our work.

For each individual in both the NTNH and SAT populations, the standard Stacked ABR was obtained by (1) temporally aligning the derived-band ABR waveforms so that the peak latencies of wave V in each derived band coincided, and (2) adding together these aligned derived-band ABR waveforms to form the Stacked ABR. Arbitrarily, the wave V peaks of the derived-band ABRs were aligned to the wave V peak latency for the selected 5.7 kHz CF derived band. By temporally aligning the peak activity initiated from each segment of the cochlea, we synchronized the total activity and minimized much of the temporal smearing (or cancellation) that occurred in the standard click ABR. The Stacked ABR amplitude was the peak-to-trough measure of wave V in the Stacked ABR. Thus, compared to standard ABR amplitude measures, the amplitude of the Stacked ABR wave V reflected more directly the total amount of activity initiated across the cochlea in response to click stimulation. The Kolmogorov-Smirnov test of normality was performed on the data of various ABR amplitude measures investigated in this study. The results indicated that none of the data distributions could be significantly distinguished from a Gaussian distribution described by the observed mean and standard deviation. Thus, it was assumed that all the data reported here were normally distributed, justifying the use of normal parametric statistics in the analyses.

In this study we compared the NTNH group and the SAT group, as well as the standard Stacked ABR (using individual derived-band latencies) and two other Stacked ABRs formed in the following ways: (1) For each subject, the five derived-band responses were aligned using the mean peak latencies for the NTNH group (Table 1); (2) For each subject, the five derived band responses were aligned using the modeled latency values obtained from the power function given above (Eq. [1]).

RESULTS

In the following presentation of the data, we have typically plotted the Stacked ABR values in terms of a cumulative distribution curve. These graphs simply plot on the abscissa (x-axis) the measured value and on the ordinate (y-axis) the percentage of that test population that achieved that value or less. This graphic form is useful in determining very quickly the approximate sensitivity or specificity percentages for given measured value (e.g., Stacked ABR amplitude).

Comparing the Gain in Synchronization of the Compensation Methods

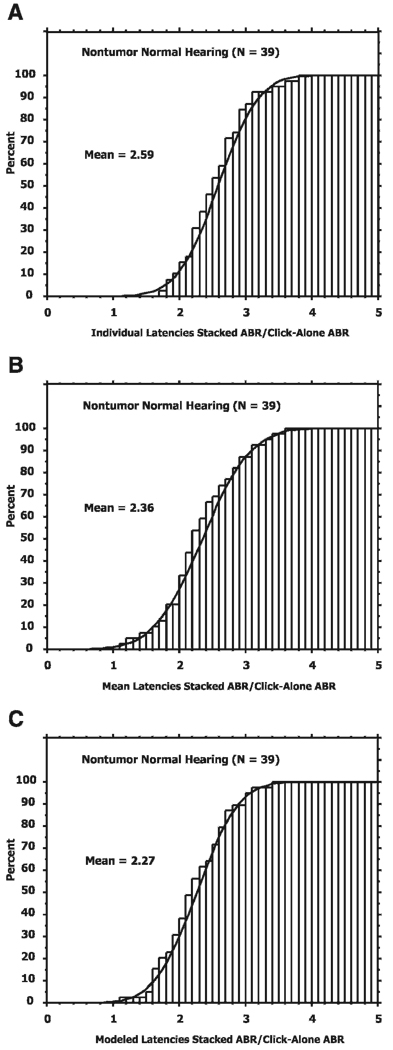
For each of the above methods of compensating for the cochlear temporal dispersion, a Stacked ABR is formed and the wave V amplitude (peak to succeeding trough) of the Stacked ABR measured. We then divide the Stacked ABR amplitude by the amplitude of wave V in the response to clicks presented alone (i.e., the standard click evoked ABR). This ratio reflects the gain in amplitude achieved by the attempt to synchronize the neural activity and compensate for the temporal dispersion in the cochlea. Figure 1 shows the cumulative distributions of this amplitude ratio for each of the compensation methods for the NTNH population. As seen in Table 2, the mean ratios for the females were slightly larger than for the males. However, the differences were not statistically significant. Thus, Figure 1 shows the distribution of these amplitude ratios for both males and females pooled together.

Figure 1.

Cumulative distributions for the NTNH individuals of the ratio of the Stacked ABR amplitude to the click-alone ABR amplitude for each of the latency compensation methods: (A) individual latencies, (B) mean latencies, and (C) modeled latencies.

Table 2.

Amplitude Ratios of the Stacked ABR to the Click-Alone ABR, for the NTNH Group of Females and Males and the Three Different Stacked ABR Methods

	Amplitude Ratio individual latencies	Amplitude Ratio mean latencies	Amplitude Ratio modeled latencies
Females	2.83	2.65	2.18
Males	2.58	2.27	1.83

As expected, it can be seen that the highest ratio is for the Stacked ABR that uses the individual peak latencies (Figure 1A) followed by the mean latencies (Figure 1B) and then the modeled latencies (Figure 1C). In general, compensating for the cochlear temporal dispersion using the Stacked ABR technique will increase the amplitude by a factor of two to three over that of the standard click evoked ABR depending on the compensation method and the gender.

Standard Stacked ABR

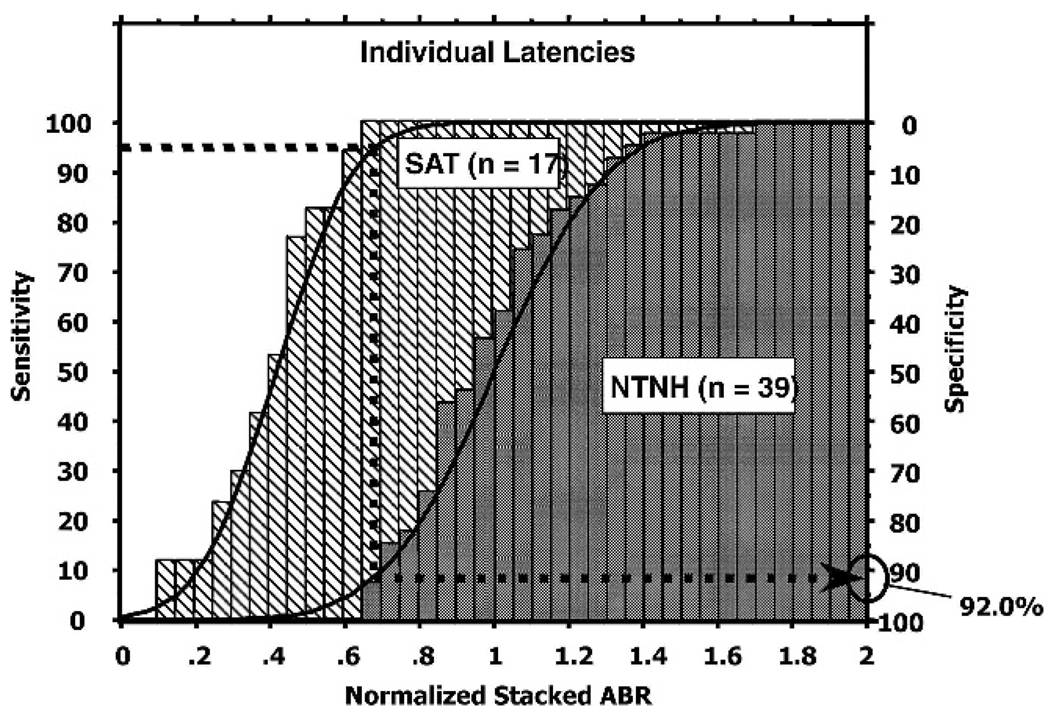
Figure 2 shows the cumulative distributions of the wave V Stacked ABR normalized amplitudes for both the NTNH (gray histograms) and SAT (hatched histograms) populations. Basically the normalized value is equal to the subject’s Stacked ABR amplitude divided by the mean Stacked ABR amplitude for his or her gender. Thus, a subject with a normalized value of 1 has a Stacked ABR amplitude that is equal to the mean for his or her gender. For the amplitude normalization calculation, the mean values used were 1069 nV for the females and 957 nV for the males. We chose 95% as our criterion sensitivity. First, as an estimate of the specificity for the 95% sensitivity criterion, a horizontal line (dashed) from the 95% point on the sensitivity (left) axis is drawn to the cumulative distribution curve for the SAT population. At the point of intersection with this curve, a vertical (dashed) line is drawn toward the horizontal x-axis until it intersects with the cumulative distribution curve for the NTNH population. This line would intersect the x-axis at a normalized value of 0.67 indicating that 95% of the small tumor cases had Stacked ABR values of about 715 nV and 640 nV or less for the females and males respectively. To estimate the specificity of a Stacked ABR of a normalized value of 0.67, another horizontal dashed line is projected to the specificity axis from the point of intersection of this vertical line and the cumulative distribution curve for the NTNH population. This horizontal line intersects the specificity axis at 92.0%.² Thus, for these data, using a criterion value of 715 nV for females and 640 nV for males, we can detect 95% of the small tumor cases with 92.0% specificity relative to the NTNH population using the standard Stacked ABR based on the individual peak latencies described by Don et al (1997; Don, Kwong, Tanaka, et al, 2005).

Figure 2.

Cumulative distributions and histograms of the normalized Stacked ABR wave V amplitude for the NTNH (gray) and SAT (hatched) populations based on the individual’s derived band wave V peak latencies. 95% sensitivity yields 92.0% specificity.

Stacked ABR Using NTNH Mean Latency Values

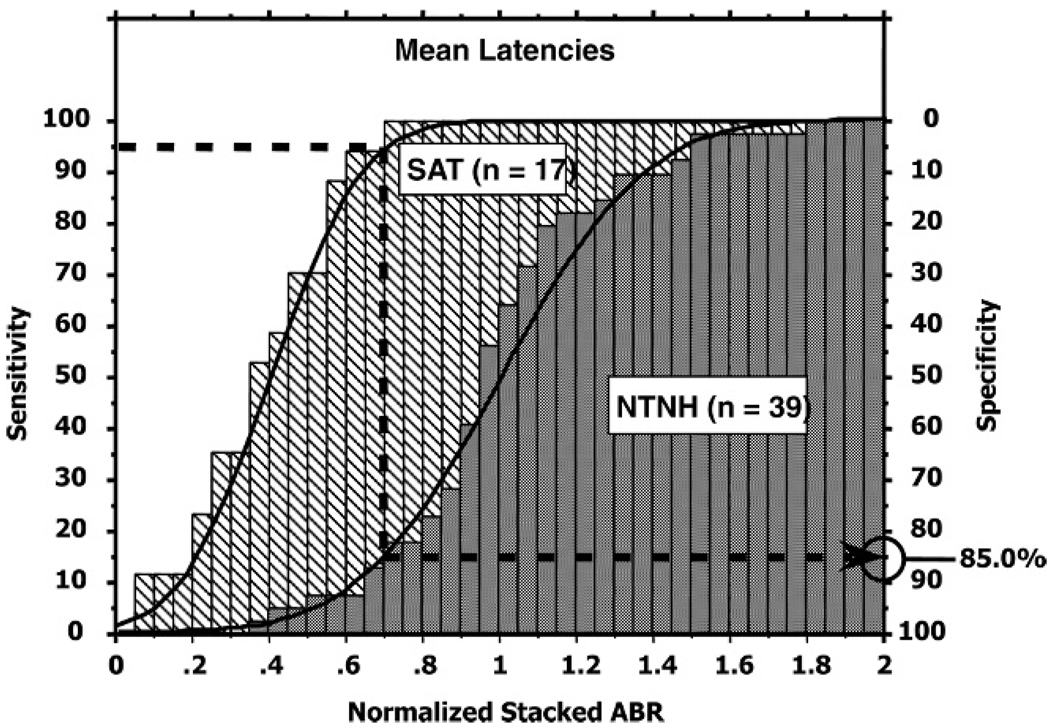
In this analysis, we formed the Stacked ABR using the mean latency values shown in Table 1 instead of the individual’s derived-band peak latencies. In Figure 3, the cumulative distributions of the Stacked ABR amplitudes based on the mean latencies are plotted for both the NTNH and SAT populations. For the amplitude normalization calculation, the mean values used were 1014 nV for the females and 840 nV for the males. To compare these results to the standard Stacked ABRs based on the individual’s derived-band latencies shown in Figure 2, we again chose the 95% sensitivity criterion. To estimate the specificity, we use the same procedure described for Figure 2 and find that for this 95% sensitivity criterion, a Stacked ABR normalized amplitude of about 0.70 is required and that the specificity has dropped to 85.0% in comparison to the 92.0% achieved by using the individual’s peak latency value. As expected, using the mean instead of the individual’s latency values results in lower Stacked ABR amplitudes as evidenced by the lower Stacked ABR amplitude of 705 nV and 584 nV for females and males, respectively, needed for the 95% sensitivity criterion. The drop in specificity suggests that the two distributions have moved closer.

Figure 3.

Cumulative distributions and histograms of the normalized Stacked ABR wave V amplitude for the NTNH (gray) and SAT (hatched) populations based on the mean derived band wave V peak latencies of the NTNH group. 95% sensitivity yields 85.0% specificity.

Stacked ABRs Using Modeled Latencies

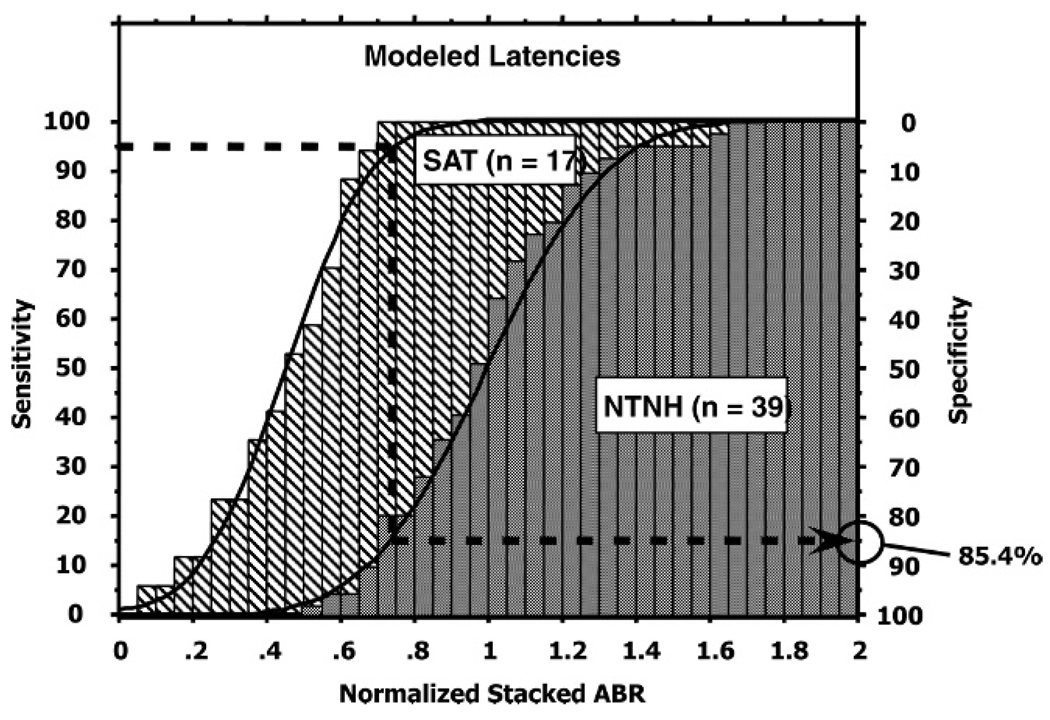
As described by Elberling et al (2007), the mean derived-band latencies shown in Table 1 were used to construct a power-function equation (Eq. [1]) describing the cochlear traveling wave delay. From this equation, a chirp stimulus designed to compensate for the estimated cochlear traveling wave delay was developed. As discussed earlier, such a chirp stimulus would compensate for the cochlear traveling wave delay at the input to the cochlea rather than at the output as is the case with the Stacked ABR. To get a general idea of the potential of such a chirp stimulus, we performed one more output compensation analysis shown in Figure 4. Instead of using the individual’s derived-band latencies (Fig. 2) or the mean latencies of the NTNH group (Fig. 3), we used the modeled latencies based on Equation (1) for the theoretical CF of the five derived bands as shown in Table 1. For the amplitude normalization calculation, the mean values used were 932 nV for the females and 827 nV for the males. Again, for comparison, we chose the 95% sensitivity criterion to evaluate these results. It can seen that for the 95% sensitivity criterion, a Stacked ABR normalized amplitude of about 0.73 is required corresponding to Stacked ABR amplitudes of 680 nV and 604 nV for females and males, respectively. These values result in an estimated specificity of about 85.4%. In comparison to the results shown in Figures 2 and 3, this suggests that using the modeled latencies separates the two populations to about the same extent as that of the mean latencies (Figure 3) and about 7% less than that obtained using the individual’s latency values.

Figure 4.

Cumulative distributions and histograms of the normalized Stacked ABR wave V amplitude for the NTNH (gray) and SAT (hatched) populations based on the modeled derived band wave V peak latencies of the NTNH group (Elberling et al, 2007). 95% sensitivity yields 85.4% specificity.

DISCUSSION

As detailed in the introduction, the Stacked ABR is an attempt to compensate at the output for the temporal dispersion of neural activation caused by the cochlear mechanics in response to click stimulation. It has been shown that the Stacked ABR is sensitive to small tumors that are often missed by the standard ABR latency measures (Don et al, 1997; Don, Kwong, Tanaka, et al, 2005). While the Stacked ABR has been shown to overcome the standard ABR’s lack of sensitivity to small tumors, it is not intended to serve as a sole test for acoustic tumors as the MRI scan with Gd-DTPA is the definitive test. As detailed by Don, Kwong, Tanaka, et al (2005), the main potential role is for screening because of its lower cost, wider availability, and better patient comfort. It is hypothesized that because the Stacked ABR is composed of neural activity that has been artificially synchronized across the cochlea, it is sensitive to small disturbances by a small tumor either in the degree of synchronization and/or in the number of elements involved. However, a drawback of this standard Stacked ABR method is the need to record and process six data acquisition runs. Additionally, the Stacked ABR method requires careful attention to electrophysiological recording practices and patient comfort because amplitude measures are sensitive to such issues. A possible remedy for this is to use a method for input compensation for the cochlear temporal dispersion. Such a method is achieved by using a chirp stimulus that presents low frequencies before the high frequencies in a temporal order that is essentially the inverse to the time of cochlear activation, thus synchronizing the neural activity across the cochlea. ABR and ASSR studies using chirps do show two to three times larger responses than those obtained with clicks alone (Dau et al, 2000; Fobel and Dau, 2004; Elberling et al, 2007). An advantage of the chirp is that only a single run is needed. We tried to explore in this paper the potential of a chirp stimulus for detecting small acoustic tumors. The chirp stimulus of interest was proposed and evaluated for ASSR recordings by Elberling et al (2007). As mentioned in the introduction, we felt that because of the large time commitment of resources and the rarity of small tumors, a full study with actual tumor patients and this newly developed chirp was not warranted without some suggestion that the measure would perform with acceptable sensitivity and specificity. Thus, we compared the sensitivity and specificity of standard Stacked ABRs formed by aligning the derived-band ABRs according to the individual’s peak latencies with Stacked ABRs formed according to the group mean latencies and latencies resulting from modeling a chirp stimulus based on these mean values. It is important to note that the measures described in this paper are technically still the result of an output compensation method as derived-band ABRs were aligned according to either the individual’s peaks, the mean for the NTNH group, or the modeled peak latencies used in constructing a chirp (Elberling et al, 2007). Although no actual chirp was used and, therefore, no input compensation method directly compared, we assume that the modeled latencies would reflect the approximate temporal activation in the cochlea by such a chirp. Under this assumption, some insights into the potential value of the chirp stimulus for detecting small tumors are provided.

The first insight is the gain factor of the response amplitude for the various compensation methods. First, by measuring the ratio of the Stacked ABR wave V amplitude to the click alone wave V amplitude (Figure 1), we obtain this gain factor. These ratios range from two to three. The highest ratio (largest gain) and, therefore, the largest Stacked ABRs are obtained for the derived band ABRs aligned according to the individual’s peak latencies, followed by those based on the NTNH mean latencies and then those based on the modeled latencies. While these measures describe the effect of the compensation methods on the amplitude of the Stacked ABR in the NTNH population, we cannot easily predict their value in detecting small tumors as the compensation methods might have similar effects on the SAT population. As described above, chirp stimuli seem to provide gain factors of the same order of magnitude as found here for the Stacked ABRs—both with the ABR (Fobel and Dau, 2004) and the ASSR (Elberling et al, 2007).

The second and final insight is provided by comparisons of the sensitivity and specificity of these compensation methods. Our comparisons between the NTNH and SAT populations suggest that for a high detection sensitivity of 95%, a relatively high specificity of 85% was achieved using Stacked ABRs based on the modeled latencies. This specificity was only about 7% less than that achieved by the standard Stacked ABR (92%). Thus, for tumor detection it would be worthwhile to explore the use of a chirp because much can be gained in terms of test and analysis time as well as simplicity of data processing with possibly a small sacrifice in terms of specificity.

A few caveats related to our current results are that (1) we are still using the derived band responses to form a Stacked ABR, (2) we are compensating for the cochlear traveling delay across narrow frequency bands, and (3) like the Stacked ABR, sensitivity and specificity of the chirp will also be affected by hearing loss. In the first caveat, using derived bands may enhance the results because these responses are somewhat free from the upward spread of activation that would occur with a chirp that starts with the low frequencies. In the second caveat, based on the work of Stürzebecher et al (2006), compensation for the cochlear traveling delay across narrow frequency bands (about 500 Hz wide) produces frequency-specific responses with higher signal-to-noise ratios than those obtained without such compensation. Thus, while in contrast to the standard Stacked ABR the chirp does not compensate for the individual cochlear delay because it uses an average traveling wave, there is the possibility that it still may provide better synchronization overall and larger response amplitudes than the standard Stacked ABR. In the third caveat, hearing loss often accompanies the presence of the tumor and contributes to the sensitivity of the Stacked ABR to the small tumors. As discussed by Don, Kwong, Tanaka, et al (2005), hearing loss will reduce the Stacked ABR further and thereby increase the likelihood of an abnormally low Stacked ABR amplitude and improve the detection of any tumor that is present. Thus, hearing loss will improve the Stacked ABR sensitivity, and sensitivity was the main problem in using ABRs for tumor detection. However, the hearing loss will decrease the specificity (i.e., higher false positives) of the test measure. Clinically, false positives are less of a problem. A more complete discussion of this issue can be found in Don, Kwong, Tanaka, et al (2005). The issue of hearing loss will also apply to the chirp methodology.

However, the real issue in the context of tumor detection is not so much which method gives the maximal activation or largest amplitudes but, rather, whether one method provides greater separation of the distributions of amplitudes. It is the separation of the distributions of amplitude values that will determine the sensitivity and specificity of the measure. Based on our results and assumptions, there is good impetus to pursue a study of using the chirp for small tumor detection as it may provide acceptable sensitivity and specificity with minimal test time.

Abbreviations

ABR

auditory brainstem response

ACAP

auditory compound action potential

ASSR

auditory steady-state response

CF

center frequency

dB nHL

dB re normal hearing level

dB p-p.e SPL

dB peak-peak equivalent sound pressure level

Gd-DTPA

Gadolinium-Diethylene-TriaminePentaacetic Acid (MRI contrast agent)

IRB

institutional review board

IT5

interaural wave V delay

MRI

magnetic resonance imaging

NTNH

nontumor normal hearing

RMS

root mean square

SAT

small acoustic tumor