A Normalization Model of Multisensory Integration

Abstract

Responses of neurons that integrate multiple sensory inputs are traditionally characterized in terms of a set of empirical principles. However, a simple computational framework that accounts for these empirical features of multisensory integration has not been established. We propose that divisive normalization, acting at the stage of multisensory integration, can account for many of the empirical principles of multisensory integration exhibited by single neurons, such as the principle of inverse effectiveness and the spatial principle. This model, which employs a simple functional operation (normalization) for which there is considerable experimental support, also accounts for the recent observation that the mathematical rule by which multisensory neurons combine their inputs changes with cue reliability. The normalization model, which makes a strong testable prediction regarding cross-modal suppression, may therefore provide a simple unifying computational account of the key features of multisensory integration by neurons.

INTRODUCTION

In an uncertain environment, organisms often need to react quickly to subtle changes in their surroundings. Integrating inputs from multiple sensory systems (e.g., vision, audition, somatosensation) can increase perceptual sensitivity, enabling better detection or discrimination of events in the environment ^1–3. A basic question in multisensory integration is: how do single neurons combine their unisensory inputs? Although neurophysiological studies have revealed a set of empirical principles by which two sensory inputs interact to modify neural responses ⁴, the computations performed by neural circuits that integrate multisensory inputs are not well understood.

A prominent feature of multisensory integration is the “principle of inverse effectiveness”, which states that multisensory enhancement is large for weak multimodal stimuli and decreases with stimulus intensity ^4–7. A second prominent feature is the “spatial/temporal principle of multisensory enhancement“, which states that stimuli should be spatially congruent and temporally synchronous for robust multisensory enhancement to occur, with large spatial or temporal offsets leading instead to response suppression ^8–10. Although these empirical principles are well established, the nature of the mechanisms required to explain them remains unclear.

We recently measured the mathematical rules by which multisensory neurons combine their inputs ¹¹. These studies were performed in the dorsal medial superior temporal area (MSTd), where visual and vestibular cues to self-motion are integrated ^12–14. We found that bimodal responses to combinations of visual and vestibular inputs were well described by a weighted linear sum of the unimodal responses, consistent with recent theory ¹⁵. Notably, however, the linear weights appeared to change with reliability of the visual cue ¹¹, suggesting that the neural “combination rule” changes with cue reliability. It is unclear whether this result implies dynamic changes in synaptic weights with cue reliability or whether it can be explained by network properties.

We propose a divisive normalization model of multisensory integration that accounts for the apparent change in neural weights with cue reliability, as well as several other key empirical principles of multisensory integration. Divisive normalization ¹⁶ has been successful in describing how neurons in primary visual cortex (V1) respond to combinations of stimuli having multiple contrasts and orientations ^{17, 18}. Divisive normalization has also been implicated in motion integration in area MT ¹⁹, as well as in attentional modulation of neural responses ²⁰. Our model extends the normalization framework to multiple sensory modalities, demonstrates that a simple set of neural operations can account for the major empirical features of multisensory integration, and makes predictions for experiments that could identify neural signatures of normalization in multisensory areas.

RESULTS

Brief description of the model

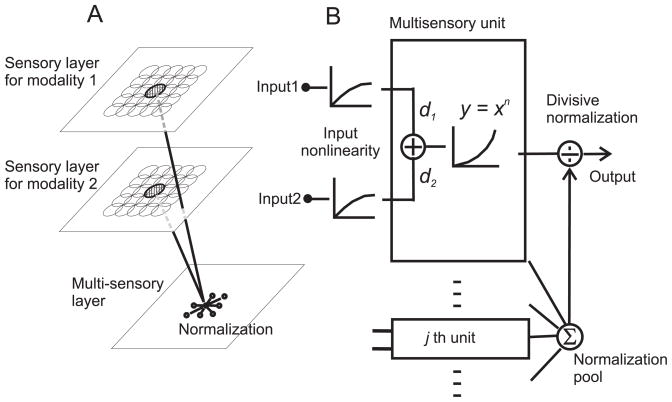
The model consists of two layers of primary neurons, each sensitive to inputs from a different sensory modality (e.g., visual or auditory), and one layer of multisensory neurons that integrate the primary sensory inputs (Fig. 1A). In our basic version of the model, we assume that a pair of primary neurons with spatially overlapping receptive fields (RFs) provides input to the same multisensory neuron. Therefore, each multisensory neuron has spatially congruent RFs, like neurons in the superior colliculus ⁹.

Figure 1.

Schematic illustration of the normalization model of multisensory integration. (A) Overview of network architecture. The model consists of two layers of primary neurons that respond exclusively to sensory modalities 1 and 2. These primary sensory units feed into a layer of multisensory neurons that integrate responses from unisensory inputs with matched receptive fields. (B) Signal processing at the multisensory stage. Each unisensory input first passes through a nonlinearity that could represent synaptic depression or normalization within the unisensory pathways. The multisensory neuron then performs a weighted linear sum of its inputs with modality dominance weights, d₁ and d₂. Following an expansive power-law non-linearity that could represent the transformation from membrane potential to firing rate, the response is normalized by the net activity of all other multisensory neurons.

The unisensory inputs to each multisensory neuron increase monotonically, but sublinearly, with stimulus intensity (Fig. 1B). This input non-linearity models response saturation in the sensory inputs ²¹, which could be mediated via synaptic depression ²² or normalization within the unisensory pathways. This assumption has little effect on the multisensory properties of model neurons, but it plays an important role in the response to multiple unisensory inputs.

Following the input nonlinearity, each multisensory neuron performs a weighted linear sum (E) of its unisensory inputs with weights, d₁ and d₂, that we term modality dominance weights:

$$E=d_1\ast I_1(x_0,y_0)+d_2\ast I_2(x_0,y_0)$$ (1)

Here, I₁(x₀,y₀) and I₂(x₀,y₀) represent, in simplified form, the two unisensory inputs to the multisensory neuron, indexed by the spatial location of the receptive fields (see Methods for a detailed formulation). The modality dominance weights are fixed for each multisensory neuron in the model (they do not vary with stimulus parameters), but different neurons have different combinations of d₁ and d₂ to simulate various degrees of dominance of one sensory modality. Following an expansive power-law output nonlinearity, which simulates the transformation from membrane potential to firing rate ^{17, 23}, the activity of each neuron is divided by the net activity of all multisensory neurons to produce the final response (divisive normalization ¹⁶):

$$R=\frac{E^n}{{\alpha }^n+(1/N)\ast {\sum }_{j=1}^N{E_j}^n}$$ (2)

The parameters that govern the response of each multisensory neuron are the modality dominance weights (d₁ and d₂), the exponent (n) of the output nonlinearity, the semi-saturation constant (α), and the locations of the receptive fields (x₀,y₀). The semi-aturation constant, α, determines the neuron’s overall sensitivity to stimulus intensity, with larger α shifting the intensity-response curve rightward on a logarithmic axis. We show that this simple model accounts for key empirical principles of multisensory integration that have been described in the literature.

Inverse effectiveness

The principle of inverse effectiveness states that combinations of weak inputs produce greater multisensory enhancement than combinations of strong inputs ^4–7. In addition, the combined response to weak stimuli is often greater than the sum of the unisensory responses (super-additivity), whereas the combined response to strong stimuli tends toward additive or sub-additive interactions. Note, however, that inverse effectiveness can hold independent of whether weak inputs produce super-additivity or not ^{7, 24}. The normalization model accounts naturally for these observations, including the dissociation between inverse effectiveness and super-additivity.

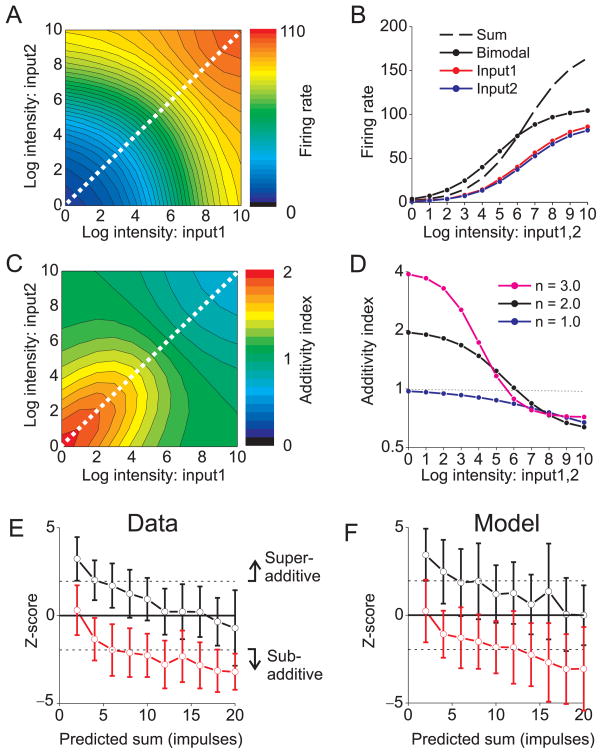
Responses of a representative model neuron (d₁ = d₂) as a function of the intensities of the two unisensory inputs are shown in Fig. 2A. For inputs of equal strength (Fig. 2B), bimodal responses (solid black) exceed the corresponding unimodal responses (red, blue) at all intensities, consistent with physiological results obtained with balanced unisensory stimuli that are centered on the receptive fields ²⁴. For low stimulus intensities, the bimodal response (solid black) exceeds the sum of the unimodal responses (dashed black), indicating super-additivity (Fig. 2B). However, as stimulus intensity increases, the bimodal response becomes sub-additive, demonstrating inverse effectiveness.

Figure 2. Normalization accounts for the principle of the inverse effectiveness.

(A) The bimodal response of a model unit is plotted as a function of the intensities of Input1 and Input2. Both inputs were located in the center of the receptive field. Diagonal line: inputs with equal intensities. Exponent, n = 2.0. (B) The bimodal response (solid black curve) and the unimodal responses (red and blue curves) are plotted as a function of stimulus intensity (from the diagonal of panel A). The sum of the two unimodal responses is shown as the dashed black curve. Red and blue curves have slightly different amplitudes to improve clarity. (C) Additivity index (AI) is plotted as a function of both input intensities. AI > 1 indicates super-additivity, and AI < 1 indicates sub-additivity. (D) AI values (from the diagonal of panel C) are plotted as a function of intensity for three exponent values: n = 1.0 (blue), 2.0 (black), and 3.0 (magenta). (E) Data from cat superior colliculus, demonstrating inverse effectiveness (replotted from ref ²⁶). The z-scored bimodal response (± SD) is plotted against the predicted sum of the two unimodal responses, both for cross-modal (visual-auditory) inputs (black curve) or pairs of visual inputs (red). Z-score values >1.96 represent significant superadditivity, and values <−1.96 denote significant sub-additivity. (F) Model predictions match the data from cat superior colliculus. For this simulation, model neurons had all 9 combinations of dominance weights from the set (d1, d2 = 0.50, 0.75 or 1.00), and the exponent, n, was 1.5.

To quantify this effect, we computed an additivity index (AI), which is the ratio of the bimodal response to the sum of the two unimodal responses. The normalization model predicts that super-additivity (AI > 1) only occurs when both sensory inputs have low intensities (Fig. 2C), which may explain why super-additivity was not seen in previous studies in which one input was fixed at a high intensity ¹¹. Furthermore, the degree of super-additivity is determined by the exponent parameter (n) of the output nonlinearity (Fig. 2D). For an exponent of 2.0, which we used as a default ²⁵, the model predicts AI ≈ 2 for low intensities (Fig. 2D, black). Larger exponents produce even greater super-additivity (Fig. 2D, magenta), whereas the model predicts purely additive responses to low intensities when the exponent is 1.0 (Fig. 2D, dark blue). Thus, the degree of super-additivity is determined by the curvature of the power-law nonlinearity, and greater super-additivity can be achieved by adding a response threshold to the model (not shown).

For large stimulus intensities, responses become sub-additive (AI < 1) regardless of the exponent (Fig. 2D), and this effect is driven by divisive normalization. Thus, all model neurons exhibit inverse effectiveness, but super-additivity is seen only when responses are weak such that the expansive output nonlinearity has a substantial impact. These predictions are qualitatively consistent with physiological data from the superior colliculus, where neurons show inverse effectiveness regardless of whether or not they show super-additivity, and only neurons with weak multisensory responses exhibit super-additivity ²⁴.

To evaluate performance of the model quantitatively, we compared model predictions to population data from the superior colliculus ²⁶. Response additivity was quantified by computing a z-score ⁷ that quantifies the difference between the bimodal response and the sum of the two unimodal responses (a z-score of zero corresponds to perfect additivity, analogous to AI=1). For combined visual-auditory stimuli, significant super-additivity (z-score>1.96) was observed for weak stimuli and additivity was seen for stronger stimuli (Fig. 2E, black curve), thus demonstrating inverse effectiveness. After adding Poisson noise and adjusting parameters to roughly match the range of firing rates, the normalization model produces very similar results (Fig. 2F, black curve). Thus, the model accounts quantitatively for the transition from super-additivity at low intensities to additivity (or sub-additivity) at high intensities, with a single set of parameters.

Although the simulations of Fig. 2 assumed specific model parameters, inverse effectiveness is a robust property of the model even when stimuli are not centered on the receptive fields, or modality dominance weights are unequal (Supplementary Figs. 1 and 2).

Spatial principle of multisensory integration

The spatial principle of multisensory enhancement states that a less effective stimulus from one sensory modality (e.g., a stimulus placed off the RF center) can suppress the response to a highly effective stimulus from the other modality ^{9, 10}. Divisive normalization accounts naturally for this effect, as illustrated in Fig. 3.

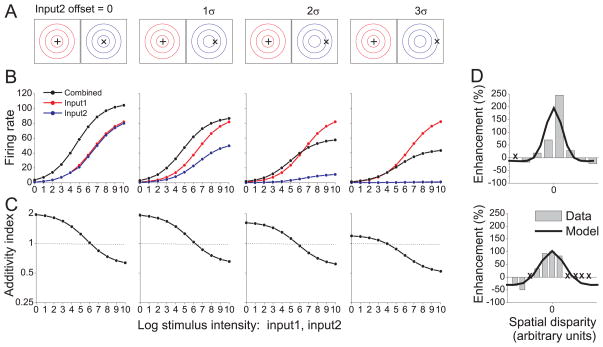
Figure 3. Normalization and the spatial principle of multisensory enhancement.

(A) Schematic illustration of stimulus conditions used to simulate the spatial principle. Input 1 (‘+’ symbol) was located at the center of the receptive field for modality 1 (red contours). Input 2 (’×’ symbol) was offset by various amounts relative to the receptive field for modality 2 (blue contours). Contours defining each receptive field are separated by one standard deviation (σ of the Gaussian. The modality dominance weights were equal (d₁ = d₂ = 1). (B) Responses of the model neuron to the stimuli illustrated in panel A (format as in Fig. 2B). Response is plotted as a function of intensity for Input1 (red), Input2 (blue), and the bimodal stimulus (black). Critically, Input2 can be excitatory on its own (blue) but suppress the response to Input 1 (red) when the two are combined (black, 3^rd column). (C) Additivity Index (AI) as a function of stimulus intensity. (D) Two examples of the spatial principle for neurons from cat superior colliculus, re-plotted from refs ^{9, 27}. The response enhancement index (%) is plotted as a function of the spatial offset between visual and auditory stimuli (gray bars). Locations marked with an “X” denote missing data in the original data set. Predictions of the normalization model are shown as black curves. Model parameters (fit by hand) were: d1, d2 = 1.0, α =1.0 and n = 2.0. Stimulus intensity was set at 16 for the top neuron and 64 for the bottom neuron.

In this simulation, one of the unimodal inputs (Input1, ‘+’ symbol) is presented in the center of the RF, while the other input (Input2, ‘×’ symbol) is spatially offset from the RF center by different amounts (Fig. 3A). When both inputs are centered on the RF (Fig. 3B, left-most column), the combined response exceeds the unimodal responses for all stimulus intensities (as in Fig. 2B). As Input2 is offset from the RF center, the bimodal response decreases relative to that of the more effective Input1. Importantly, when the stimulus offset substantially exceeds one standard deviation of the Gaussian RF profile (two right-most columns of Fig. 3B), the combined response becomes suppressed below the unimodal response to Input1. Hence, the model neuron exhibits the spatial principle. The intuition for this result is simple: the less effective (i.e., offset) input contributes little to the underlying linear response of the neuron, but contributes strongly to the normalization signal because the normalization pool includes neurons with RFs that span a larger region of space. Note that the model neuron exhibits inverse effectiveness for all of these stimulus conditions (Fig. 3C), although super-additivity declines as the spatial offset increases.

Figure 3D shows data from two cat superior colliculus neurons that illustrate the spatial principle ^{9, 27}. Both neurons show cross-modal enhancement when the spatial offset between visual and auditory stimuli is small, and a transition toward cross-modal suppression for large offsets. The normalization model captures the basic form of these data nicely (Fig. 3D, black curves). We are not aware of any published data that quantify the spatial principle for a population of neurons.

For the example neurons of Fig. 3D, responses to the offset stimulus were not presented ^{9, 27}, so it is not clear whether cross-modal suppression occurs while the non-optimal stimulus is excitatory on its own. However, the normalization model makes a critical testable prediction: within a specific stimulus domain, the less effective Input2 evokes a clearly excitatory response on its own (Fig. 3B, 3rd column from left, blue curve) but suppresses the response to the more effective Input1 (red) when the two inputs are presented together (black). Analogous interactions between visual stimuli were demonstrated in V1 neurons and attributed to normalization ¹⁷. Importantly, the cross-modal suppression shown in Fig. 3B appears to be a signature of a multisensory normalization mechanism, as alternative model architectures that do not incorporate normalization ^{28, 29} fail to exhibit this behavior (Supplementary Figs. 3 and 4).

An analogous empirical phenomenon is the temporal principle of multisensory integration, which states that multisensory enhancement is strongest when inputs from different modalities are synchronous, and declines when the inputs are separated in time ⁸. The normalization model also accounts for the temporal principle as long as there is variation in response dynamics (e.g., latency, duration) among neurons in the population, such that the temporal response of the normalization pool is broader than the temporal response of individual neurons (Supplementary Fig. 5). More generally, in any stimulus domain, adding a non-optimal (but excitatory) stimulus can produce cross-modal suppression if it increases the normalization signal enough to overcome the additional excitatory input to the neuron.

Multisensory suppression in unisensory neurons

Multisensory neurons are often much more responsive to one sensory modality than the other. Responses of such neurons to the more effective input can be suppressed by simultaneous presentation of the seemingly non-effective input ^{5, 30}. In the normalization model, each neuron receives inputs from primary sensory neurons with modality dominance weights that are fixed (Fig. 1), but the specific combination of weights (d_1, d₂) varies from cell to cell. We show that normalization accounts for response suppression by the non-effective input.

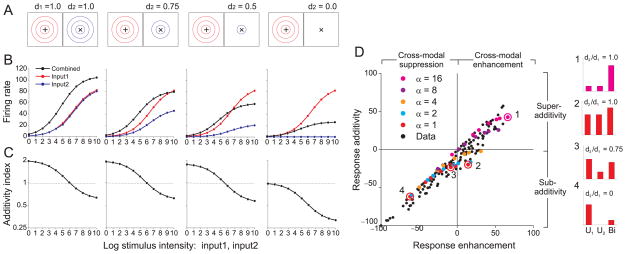
Simulated responses are shown (Fig. 4) for four model neurons with different combinations of modality dominance weights, ranging from balanced inputs (d₁ = 1.0, d₂ = 1.0) to strictly unisensory input (d₁ = 1.0, d₂ = 0.0). When modality dominance weights are equal (d₁ =1.0, d₂ =1.0), the model shows multisensory enhancement (Fig. 4B, left-most column). As the weight on Input2 is reduced, the bimodal response (black) declines along with the unimodal response to Input2 (blue). Importantly, when d₂ is approximately 0.5 or less, the bimodal response becomes suppressed below the best unimodal response (Fig. 4B, two right-most columns). For the “unisensory” neuron with d₂ = 0.0 (right column), Input 2 evokes no excitation (blue) but suppresses the combined response (black). This effect is reminiscent of cross-orientation suppression in primary visual cortex ^{18, 31, 32}.

Figure 4. Multisensory suppression in “unisensory” neurons.

(A) Responses were simulated for four model neurons. The dominance weight for modality 1, d₁, was fixed at unity while the dominance weight for modality 2, d₂, decreased from left to right (denoted by the number of receptive field contours). Input1 (‘+’) and Input2 (‘×’) were presented in the center of the receptive fields. (B) Responses as a function of intensity are shown for Input1 (red), Input2 (blue), and both inputs together (black). Format as in Fig. 3B. (C) Additivity Index is plotted as a function of intensity for the four model neurons; format as in Fig. 3C. (D) Summary of multisensory integration properties for a population of neurons from area VIP (black symbols), re-plotted from ref ³⁰. The ordinate shows a measure of response additivity: (Bi – (U1 + U2)) / (Bi + (U1 + U2)) × 100, for which positive and negative values indicate superadditive and sub-additive interactions, respectively. Bi: bimodal response; U1, U2: unimodal responses. The abscissa represents a measure of response enhancement: (Bi – max (U1, U2)) / (Bi + max (U1, U2)) × 100, for which positive and negative values denote cross-modal enhancement and cross-modal suppression, respectively. Colored symbols represent predictions of the normalization model for units that vary in the ratio of dominance weights (d₂/d₁, ranging from 0 to 1) and the semi-saturation constant, α, ranging from 1 to 16. The exponent, n, was 2.5. Numbered symbols correspond to model neurons for which responses are shown as bar graphs (right).

Normalization accounts for cross-modal suppression in unisensory neurons by similar logic used to explain the spatial principle: although Input2 makes no contribution to the linear response of the neuron when d₂ = 0, it still contributes to the normalization signal via other responsive neurons with non-zero d₂. This effect is robust as long as the normalization pool contains neurons with a range of modality dominance weights. Response additivity (Fig. 4C) again shows inverse effectiveness in all conditions, with super-additivity for weak, balanced inputs.

To assess model performance quantitatively, we compared predictions to an extensive dataset of multisensory responses of macaque ventral intraparietal (VIP) neurons to visual and tactile stimuli ³⁰. In this dataset, a measure of response additivity is plotted against a measure of multisensory enhancement (Fig. 4D). The pattern of data across the population of VIP neurons (black symbols) is largely reproduced by a subset of model neurons (colored symbols) that vary along just two dimensions: the semi-saturation constant (α) and the ratio of dominance weights (d₂/d₁). Increasing the value of α shifts the intensity-response curve to the right and yields greater super-additivity for a fixed stimulus intensity (neuron #1, inset). For a fixed value of α, varying the ratio of dominance weights shifts the data from upper right toward lower left, as illustrated by example neurons #2–4. Model neuron #4 is an example of multi-sensory suppression in a unisensory neuron. Overall, a significant proportion of variance in the VIP data can be accounted for by a normalization model in which neurons vary in two biologically plausible ways: overall sensitivity to stimulus intensity (α) and relative strength of the two sensory inputs (d₂/d₁).

Response to within-modal stimulus combinations

Previous studies have reported that two stimuli of the same sensory modality (e.g., two visual inputs) interact sub-additively whereas two stimuli of different modalities can produce super-additive interactions ²⁶. This distinction arises naturally from the normalization model if each unisensory pathway incorporates a sublinear nonlinearity (Fig. 1B) that could reflect synaptic depression or normalization operating at a previous stage.

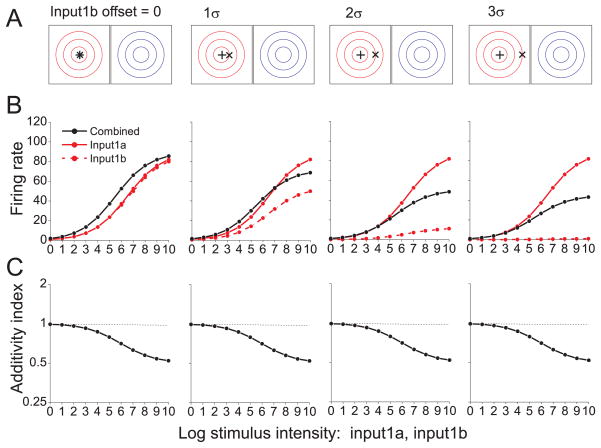
Responses to two inputs from the same modality (Input1a and Input1b) are shown for a model neuron in Fig. 5. Input1a (‘+’ symbol) is presented at the center of the RF, while Input1b (‘×’ symbol) is systematically offset from the RF center (Fig. 5A). When both inputs are centered in the RF (Fig. 5B, left column), the combined response is modestly enhanced. The corresponding AI curve (Fig. 5C) indicates that the interaction is additive for weak inputs and sub-additive for stronger inputs. This result contrasts sharply with the super-additive interaction seen for spatially aligned cross-modal stimuli (Figs. 2B and 3B). As Input1b is offset from the center of the RF (Fig. 5B, left to right), the combined response (black) becomes suppressed relative to the stronger unisensory response (solid red). The AI curves demonstrate that the interaction is either additive or sub-additive for all spatial offsets (Fig. 5C).

Figure 5. Interactions among within-modality inputs.

(A) The stimulus configuration was similar to that of Fig. 3A except that two stimuli of the same sensory modality, Input1a (‘+’) and Input1b (‘×’) were presented, and one was systematically offset relative to the receptive field of modality 1 (red contours). No stimulus was presented to the receptive field of modality 2 (blue contours) (B) Responses of a model neuron are shown for Input1a alone (solid red curve), Input1b alone (dashed red curve) and both inputs together (black curve). (C) Additivity Index as a function of stimulus intensity shows that model responses to pairs of within-modality inputs are additive or sub-additive with no super-additivity.

Presenting two overlapping inputs from the same modality is operationally equivalent to presenting one input with twice the stimulus intensity. Due to the sub-linear nonlinearity in each unisensory pathway, doubling the stimulus intensity does not double the postsynaptic excitation. As a result, the combined response does not exhibit super-additivity for low intensities, even with an expansive output nonlinearity in the multisensory neuron (n = 2.0). For high stimulus intensities, the combined response becomes sub-additive due to normalization. If normalization were removed from the model, combined responses would remain approximately additive across all stimulus intensities (data not shown). For large spatial offsets and strong intensities, the combined response is roughly the average of the two single-input responses (Fig. 5B, right columns). Similar averaging behavior has been observed for SC neurons ²⁶, as well as neurons in primary ¹⁸ and extrastriate ^{33, 34} visual cortex.

In the superior colliculus ²⁶, super-additivity was significantly reduced for pairs of inputs from the same modality (Fig. 2E, red curve) relative to cross-modal inputs (black curve). This difference is reproduced by the normalization model (Fig. 2F) with a single set of model parameters. Hence, the inclusion of an input nonlinearity appears to account quantitatively for the difference in additivity of responses between cross-modal and within-modal stimulation.

Multisensory integration and cue reliability

We have shown that normalization accounts for key empirical principles of multisensory integration. We now examine whether the model can account for quantitative features of the combination rule by which neurons integrate their inputs. We recently demonstrated that bimodal responses of multisensory neurons in area MSTd are well approximated by a weighted linear sum of visual and vestibular inputs, but that the weights appear to change with visual cue strength ¹¹. To explain this puzzling feature of the multisensory combination rule, we performed a “virtual” replication of the MSTd experiment ¹¹ using model neurons. To capture known physiology of heading-selective neurons ^{13, 35}, the model architecture was modified such that each cell had spherical heading tuning, lateral heading preferences were more common than fore-aft preferences, and many neurons had mismatched heading tuning for the two cues (see Materials and Methods and Supplementary Figs. 6 and 7).

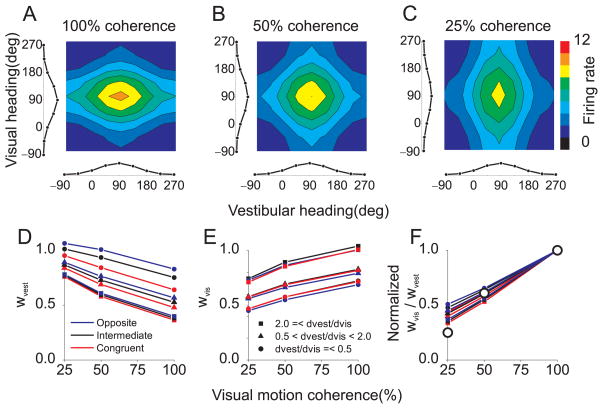
Responses of model neurons were computed for 8 heading directions in the horizontal plane using visual inputs alone, vestibular inputs alone, and all 64 combinations of visual and vestibular headings, both congruent and conflicting. The bimodal response profile of an example neuron, R_bimodal (ϕ_vest,ϕ_vis), is plotted as a color contour map, along with the two unimodal response curves, R_vest(ϕ_vest) and R_vis(ϕ_vest), along the margins (Fig. 6A). The intensity of the vestibular cue was kept constant, while the intensity of the visual cue varied to simulate the manipulation of motion coherence used in MSTd ¹¹. At 100% coherence, the bimodal response is dominated by the visual input, as is typical of MSTd neurons (c.f., Fig. 3 of ref ¹¹). As visual intensity (motion coherence) is reduced, the bimodal response profile changes shape and becomes dominated by the vestibular heading tuning (Fig. 6A–C).

Figure 6. Normalization accounts for apparent changes in the multisensory combination rule with cue reliability.

(A) Responses of a model MSTd neuron to visual and vestibular heading stimuli (100% visual motion coherence). The bimodal response, R_bimodal (ϕ_vest,ϕ_vis), to many combinations of visual (ϕ_vis) and vestibular (ϕ_vest) headings is shown as a color contour plot. Curves along the bottom and left margins represent unimodal responses, R_vest (ϕ_vest) and R_vis(ϕ_vis). This model neuron prefers forward motion (90°). (B) Reponses of the same model neuron when visual stimulus intensity is reduced to 50% coherence. (C) Responses to 25% coherence. Vestibular stimulus amplitude is constant in panels A–C at the equivalent of 50% coherence. (D) Bimodal responses were fit with a weighted linear sum of unimodal responses. This panel shows the vestibular mixing weight, w_vest, as a function of motion coherence. Red, blue and black points denote model neurons with congruent, opposite and intermediate visual and vestibular heading preferences, respectively. Different symbol shapes denote groups of neurons with different ratios of modality dominance weights: d_vest/d_vis <= 0.5, 0.5 < d_vest/d_vis < 2.0, or 2.0 <= d_vest/d_vis. Note that w_vest decreases with coherence. (E) The visual mixing weight, w_vis, increases with coherence. Format as in panel D (F) The ratio of vestibular and visual mixing weights, w_vis/w_vest, normalized to unity at 100% coherence, is plotted as a function of motion coherence. Model predictions are qualitatively consistent with data from area MSTd, replotted from ref ¹¹ as large open symbols.

The bimodal response of each model neuron was fit with a weighted linear sum of the two unimodal response curves:

$$R_{\mathit{bimodal}}({\varphi }_{\mathit{vest}},{\varphi }_{\mathit{vis}})=w_{\mathit{vest}}\ast R_{\mathit{vest}}({\varphi }_{\mathit{vest}})+w_{\mathit{vis}}\ast R_{\mathit{vis}}({\varphi }_{\mathit{vis}})+C$$ (3)

The mixing weights, w_vest and w_vis, were obtained for each of the three visual intensities, corresponding to motion coherences of 25%, 50% and 100%. This analysis was performed for model neurons with different combinations of modality dominance weights (d_vest, d_vis; all combinations of values 0.25, 0.5, 0.75, and 1.0). Note that d_vest, d_vis characterize how each model neuron weights its vestibular and visual inputs, and that these modality dominance weights are fixed for each neuron in the model. In contrast, w_vest and w_vis are weights that characterize the best linear approximation to the model response for each stimulus intensity.

For all visual intensities, the weighted linear fit was a good approximation to responses of model neurons, with average R² values of 0.98, 0.96, and 0.96 for simulated coherences of 25, 50, and 100%, respectively. Importantly, different values of w_vest and w_vis were required to fit the data for different coherences. Specifically, w_vest decreased with coherence (Fig. 6D) and w_vis increased with coherence (Fig. 6E). The slope of these dependencies was similar for all model neurons, whereas the absolute values of w_vest and w_vis varied somewhat with the modality dominance weights assigned to each neuron. To summarize this effect, Figure 6F shows the average weight ratio, w_vis/w_vest, as a function of coherence, normalized to a value of 1 at 100% coherence. The results are strikingly similar to the data from area MSTd (see Fig. 5C–E of ref ¹¹), including the fact that weight changes are similar for cells with congruent and opposite heading preferences (red and blue curves in Fig. 6D,E). Because this result depends mainly on response saturation, it could also be predicted by other models that incorporate a saturating nonlinearity.

The effect of coherence on the visual and vestibular mixing weights can be derived from the equations of the normalization model, with a few simplifying assumptions (including n=1.0). As shown in Methods, the mixing weights, w_vest and w_vis, can be expressed as:

$$w_{\mathit{vest}}=\frac{\alpha +k\ast c_{\mathit{vest}}}{\alpha +k\ast (c_{\mathit{vest}}+c_{\mathit{vis}})},w_{\mathit{vis}}=\frac{\alpha +k\ast c_{\mathit{vis}}}{\alpha +k\ast (c_{\mathit{vest}}+c_{\mathit{vis}})}$$ (4)

Clearly, w_vest declines as a function of visual intensity (C_vis), whereas w_vis rises as a function of C_vis. In the simulations of Fig. 6, the exponent (n) was 2.0. In this case, the mixing weights become functions of the modality dominance weights (d_vest, d_vis) as well as stimulus intensities, resulting in vertical shifts among the curves in Fig. 6D, E.

In summary, normalization simply and elegantly accounts for the apparent changes in mixing weights exhibited by MSTd neurons as coherence was varied ¹¹. For any particular combination of stimulus intensities, the behavior of the normalization model can be approximated as linear summation, but the effective mixing weights appear to change with stimulus intensity due to changes in the net activity of the normalization pool.

DISCUSSION

We propose that divisive normalization can explain many fundamental response properties of multisensory neurons, including the empirical principles described in seminal work on the superior colliculus ^{4, 5} and the effect of cue reliability on the neural combination rule in area MSTd ¹¹. The normalization model is attractive because it relies on relatively simple and biologically plausible operations ³⁶. Thus, the same basic operations that account for stimulus interactions in visual cortex ^17–19 and attentional modulation ²⁰ may also underlie various nonlinear interactions exhibited by multisensory neurons. The normalization model may therefore provide a good computational foundation for understanding multisensory cue integration.

Critical comparison with other models

Despite decades of research, only relatively recently have quantitative models of multisensory integration been proposed ^{28, 29, 37–40}. One of the first mechanistic models of multisensory integration ^{37, 40} is a compartmental model of single neurons that accounts for inverse effectiveness and sub-additive interactions between inputs from the same modality. It was also constructed to account for the modulatory effect of top-down cortical input on multisensory integration in the SC ^{41, 42}. This model shares some elements with ours: it includes a squaring nonlinearity that produces super-additivity for weak inputs and a shunting inhibition mechanism that divides the response by the net input to each compartment. Importantly, this model does not incorporate interactions among neurons in the population. Therefore, it cannot account for the spatial principle of multisensory integration or cross-modal suppression in unisensory neurons. In addition, this model cannot account for the effects of cue reliability on the neural combination rule, as seen in area MSTd ¹¹.

In contrast to this compartmental model ^{37, 40}, a recent neural network architecture ^{28, 29} incorporates lateral interactions among neurons with different receptive field locations. Like the normalization model, this neural network model can account for inverse effectiveness and the spatial principle, but there are important conceptual differences between the two schemes. First, to produce inverse effectiveness, the neural network model _{28, 29} incorporates a sigmoidal output nonlinearity into each model neuron (see also ³⁹). By contrast, in the normalization model, response saturation at strong intensities arises from the balance of activity in the network, not from a fixed internal property of individual neurons. Second, although the neural network model can produce cross-modal suppression, it appears to do so only when the less effective input is no longer excitatory on its own (Fig. 7A of ref ²⁹) but rather becomes suppressive due to lateral connections that mediate subtractive inhibition. We verified this observation by simulating an alternative model containing the key structural features of the neural network model ^{28, 29}. As shown in Supplementary Figs. 3 and 4, this alternative model only produces cross-modal suppression when the non-optimal input is no longer excitatory. Thus, the key testable prediction of the normalization model—that an excitatory non-optimal input can yield cross-modal suppression (Fig. 3)—does not appear to be shared by other models of multisensory integration. The divisive nature of lateral interactions in the normalization model appears to be critical for this prediction. Indeed, the alternative model does not account for the VIP data ₃₀ shown in Fig. 4D as successfully as the normalization model (Supplementary Fig. 8).

A recent elaboration of the neural network model ³⁸ incorporates a number of specific design features to account for the experimental observation ^41–43 that inactivation of cortical areas in the cat gates multisensory enhancement by SC neurons. We have not attempted to account for these results in our normalization model, as it is intended to be a general model of multisensory integration, not a specific model of any one system.

A recent computational theory ¹⁵ has demonstrated that populations of neurons with Poisson-like spiking statistics can achieve Bayes-optimal cue integration if each multi-sensory neuron simply sums its inputs. Thus, nonlinear interactions like divisive normalization are not necessary to achieve optimal cue integration. Because this theory ¹⁵ involves simple summation by neurons, independent of stimulus intensity, it cannot account for various empirical principles of multisensory integration discussed here, including the effects of cue reliability on the neural combination rule ¹¹. It is currently unclear what roles divisive normalization may play in a theory of optimal cue integration, and this is an important topic for additional investigation.

Parallels with visual cortical phenomena

Divisive normalization was initially proposed ¹⁶ to account for response properties in primary visual cortex. Normalization has often since been invoked to account for stimulus interactions in the responses of cortical neurons ^{17, 19, 33, 44} and has been implicated recently in the modulatory effects of attention on cortical responses ²⁰. The apparent ubiquity of divisive normalization in neural circuits ^{36, 45} makes normalization operating at the level of multisensory integration an attractive general model to account for cross-modal interactions.

Perhaps the clearest experimental demonstration of normalization comes from a recent study ¹⁸ that measured responses of V1 neurons to orthogonal sine-wave gratings of various contrasts. This study found that population responses to any pair of contrasts can be well fit by a weighted linear sum of responses to the individual gratings. However, as the relative contrasts of the gratings varied, a linear model with different weights was required to fit the data ¹⁸, as predicted by divisive normalization. This result closely parallels the finding ¹¹ that the multisensory combination rule of MSTd neurons depends on the relative strengths of visual and vestibular inputs. Here, we show that multisensory normalization can account for analogous phenomena observed in multisensory integration ¹¹.

In summary, empirical principles of multisensory integration have guided the field for many years ⁴, but a simple computational account of these principles has been lacking. We demonstrate that divisive normalization accounts for the classical empirical principles of multisensory integration as well as recent findings regarding the effects of cue reliability on cross-modal integration. The normalization model is appealing for its simplicity and because it invokes a functional operation that has been repeatedly implicated in cortical function. Moreover, the model makes a key prediction—that a non-optimal excitatory input can produce cross-modal suppression—that can be tested experimentally. Although this prediction has not yet been tested systematically, a careful inspection of published data (e.g., Fig.1E of ref ³⁰; Fig.7 of ref ¹⁰; Fig.3C of ref ⁴⁶) reveals some examples that may demonstrate cross-modal suppression by a non-optimal excitatory input, although it is generally not clear whether the non-optimal input is significantly excitatory. Ongoing work in our laboratory systematically examines cross-modal suppression in area MSTd and preliminary results support the model predictions (T. Ohshiro, D.E. Angelaki & G.C. DeAngelis, Conference Abstract: Computational and Systems Neuroscience 2010). Thus, normalization may provide a simple and elegant account of many phenomena in multisensory integration.

METHODS

Two different versions of the normalization model were simulated: one to model multisensory spatial integration in the superior colliculus and area VIP (Fig. 1), and the other to model visual-vestibular integration of heading signals in area MSTd (Supplementary Figs. 6, 7). We first describe the spatial integration model in detail, and then consider the modifications needed for the heading model.

Spatial model: primary sensory neurons

Each unimodal input to the spatial integration model is specified by its intensity c and its spatial position in Cartesian coordinates, θ= (x_θ,y_θ). The spatial receptive field (RF) of each primary sensory neuron is modeled as a two-dimensional Gaussian:

$$G(\widehat{\theta };\theta )=\mathit{exp}\left\{-{(\widehat{\theta }-\theta )}^2/(2\ast {\sigma }^2)\right\}$$ (5)

where θ̂ = (x_θ̂,y_θ̂) represents the center location of the RF. Arbitrarily, x_θ̂,y_θ̂ take integer values between 1 and 29, such that there are 29 × 29 =841 sensory neurons with distinct θ̂ in each primary sensory layer. The size of the receptive field, given by σ, was chosen to be 2 (arbitrary units).

The response of each primary sensory neuron was assumed to scale linearly with stimulus intensity, c, such that the response can be expressed as;

$$c\ast G(\widehat{\theta };\theta )$$ (6)

In addition, we assume that two inputs of the same sensory modality, presented at spatial positions θ_1a, θ_1b interact linearly such that the net response is given by;

$$c_{1a}\ast G(\widehat{\theta };{\theta }_{1a})+c_{1b}\ast G(\widehat{\theta };{\theta }_{1b})$$ (7)

where c_1a, c_1b represent the intensities of the two inputs.

We further assume that the linear response in each unisensory pathway is transformed by a nonlinearity, h(x), such that the unisensory input is given by:

$$h(c\ast G(\widehat{\theta };\theta ))$$ (8)

We used a sub-linearly increasing function, $h(x)=\sqrt{x}$ to model this nonlinearity, although other monotonic functions such as log(x + 1) or x/(x+1) appear to work equally well. This nonlinearity models the sublinear intensity response functions often seen in sensory neurons ⁴⁷. It might reflect synaptic depression ²² at the synapse to the multisensory neuron or normalization operating within the unisensory pathways. This input non-linearity, h(x), has little effect on the multisensory integration properties of model neurons, but it plays an important role in responses to multiple unisensory inputs (Fig. 5).

Spatial model: multisensory neurons

Each multisensory neuron in the model receives inputs from primary neurons of each sensory modality, as denoted by a subscript (1 or 2). The multisensory neuron performs a weighted linear sum of the unisensory inputs:

$$E(d_1,{\widehat{\theta }}_1,d_2,{\widehat{\theta }}_2;c_1,{\theta }_1,c_2,{\theta }_2)=d_1\ast h\left(c_1\ast G_1({\widehat{\theta }}_1;{\theta }_1)\right)+d_2\ast h\left(c_2\ast G_2({\widehat{\theta }}_2;{\theta }_2)\right)$$ (9)

The modality dominance weights, d₁ and d₂, are fixed parameters of each multisensory neuron, and each weight takes one of five values: 1.0, 0.75, 0.5, 0.25 or 0.0. Therefore, 5 × 5 =25 multisensory neurons with distinct combinations of modality dominance weights are included for each set of unisensory inputs. The linear response of the i-th neuron E_i (Eqn. 9) is then subjected to an expansive power-law output nonlinearity and divisively normalized by the net response of all other units, to obtain the final output (R_i) of each neuron:

$$R_i=\frac{{E_i}^n}{{\alpha }^n+(1/N)\ast \sum {E_j}^n}$$ (10)

Here, α is a semi-saturation constant (fixed at 1.0), N is the total number of multisensory neurons, and n is the exponent of the power-law nonlinearity that represents the relationship between membrane potential and firing rate ^{17, 23}, The exponent, n, was assumed to be 2.0 in our simulations, except where noted (Fig. 2D). Model responses were simulated for the following stimulus intensities: c₁, c₂ = 0, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, and 1024.

To compare model responses to the physiological literature, an additivity index (AI) was computed as the ratio of the bimodal response to the sum of the unimodal responses:

$$AI=\frac{R_{\mathit{bimodal}}}{R_{\mathit{unimodal}1}+R_{\mathit{unimodal}2}}$$ (11)

R_unimodal1, R_unimodal2 are obtained by setting one of the stimulus intensities, c₁ or c₂, to zero.

In the simulations of Figs. 2–5, the RFs of the two primary sensory neurons projecting to a multisensory neuron were assumed to be spatially congruent (e.g., θ̂₁ = θ̂₂). In total, there were 841 (RF locations) × 25 (modality dominance weight combinations) = 21,025 distinct units in the multisensory layer.

For the simulations of Fig. 2F, the exponent (n) was fixed at 1.5, and responses were generated for all 9 combinations of three dominance weights: d₁, d₂ = 0.50, 0.75 or 1.00. Five neurons having each combination of dominance weights were simulated, for a total population of 45 neurons (similar to that recorded by Alvarado et al. ²⁶), Responses were computed for five stimulus intensities (4, 16, 64, 256, and 1024), Poisson noise was added, and 8 repetitions of each stimulus were simulated. A z-score metric of response additivity was then computed using a bootstrap method ^{7, 26}. Within-modal responses were also simulated (Fig. 2F, red) for pairs of stimuli of the same sensory modality, one of which was presented in the RF center while the other was offset from the RF center by 1 σ.

For the simulations of Fig. 4D, responses were generated for model neurons with all possible combinations of 5 dominance weights (d₁,d₂ = 0.0, 0.25, 0.50, 0.75 or 1.00) except d₁, = d₂ = 0.0, and semi-saturation constants (α) taking values of 1, 2, 4, 8, or 16. The exponent (n) was fixed at 2.5 for this simulation. Two cross-modal stimuli with intensity = 1024 were presented at the RF center to generate responses.

To replot published data (Figs. 2E and 4D), a high-resolution scan of the original figure was acquired and the data were digitized using software (Engauge, http://digitizer.sourceforge.net). To replot the experimental data in Fig. 3D (top panel), peristimulus time histograms from the original figure were converted into binary matrices using the ‘imread’ function in MATLAB. Spike counts were tallied from the digitized PSTHs and used to compute the enhancement index.

Visual-vestibular heading model

To simulate multisensory integration of heading signals in macaque area MSTd (Supplementary Fig. 6), the normalization model was modified to capture the basic physiological properties of MSTd neurons. Because heading is a circular variable in three dimensions ¹³, responses of the unisensory neurons (visual, vestibular) were modeled as:

$$c\ast \left(\frac{1}{100}\right)\ast \left(\frac{1+cos(\mathrm{\Phi })}{2}\right)+\xi \ast \left(\frac{100-c}{100}\right)$$ (12)

Here, c represents stimulus intensity (e.g., the coherence of visual motion) ranging from 0–100, and Φ represents the angle between the heading preference of the neuron and the stimulus heading. Φ can be expressed in terms of the azimuth (ϕ̂) and the elevation (θ̂) components of the heading preference, as well as azimuth (ϕ) and elevation (θ) components of the stimulus:

$$\mathrm{\Phi }=arccos(\widehat{\text{H}}·\text{H})$$ (13)

where Ĥ =[cos θ̂ * cosϕ̂ cosθ̂,* sinϕ̂, sinθ̂], and H =[cosθ * cosϕ, cosθ sinϕ, sinθ]. The dot operator ‘·‘ denotes the inner product of the two vectors.

In the spatial model (Eqns. 5–10), we assumed that stimulus intensity multiplicatively scales the receptive field of model neurons. However, in areas MT and MST, motion coherence has a different effect on directional tuning ^{48, 49}. With increasing coherence, the amplitude of the tuning curve scales roughly linearly, but the baseline response decreases (c.f., Fig. 1C of ref ⁴⁸). To model this effect (see Supplementary Fig. 7D), we included the right-hand term in Eqn. 12, with ξ in the range from 0 to 0.5 (typically 0.1), such that total population activity is an increasing function of c. However, our conclusions regarding changes in mixing weights with coherence (Fig. 6D–F) do not depend appreciably on the value of ξ.

Each model MSTd neuron performs a linear summation of its visual and vestibular inputs:

$$E=d_{\mathit{vest}}\ast \left(c_{\mathit{vest}}\ast \left(\frac{1+cos({\mathrm{\Phi }}_{\mathit{vest}})}{2}\right)+\xi \ast \left(\frac{100-c_{\mathit{vest}}}{100}\right)\right)+d_{\mathit{vis}}\ast \left(c_{\mathit{vis}}\ast \left(\frac{1+cos({\mathrm{\Phi }}_{\mathit{vis}})}{2}\right)+\xi \ast \left(\frac{100-c_{\mathit{vis}}}{100}\right)\right)$$ (14)

where d_vest, d_vis are the modality dominance weights which take values from the array [1.0, 0.75, 0.5, 0.25, 0.0]. In Eqn. 14, the input non-linearity h(x) was omitted for simplicity, because it has little effect on the multisensory integration properties of model neurons, including the simulations of Fig. 6 (data not shown).

In area MSTd, many neurons have heading tuning that is not matched for visual and vestibular inputs ¹³. Therefore, the model included multisensory neurons with both congruent and mismatched heading preferences. Our model also incorporated the fact that there are more neurons tuned to the lateral self-motion than fore-aft motion ^{13, 35}. Specifically, two random vector variables, (ϕ̂ _vest θ̂_vest) and (ϕ̂ _vis, θ̂_vis), were generated to mimic the experimentally observed distributions of heading preferences (Supplementary Fig. 7A, B), and visual and vestibular heading preferences were then paired randomly (200 pairs). To mimic the finding that more neurons have congruent or opposite heading preferences than expected by chance (Fig. 6 of ref ¹³), we added twenty eight units with congruent heading preferences, and another twenty eight with opposite preferences (Supplementary Fig. 7C). Combining these factors, a population of 256 (heading preference combinations) × 25 (dominance weight combinations) = 6400 units comprised our MSTd model. The linear response of each unit (Eqn. 14) was squared and normalized by net population activity, as in Eqn. (10). The semi-saturation constant was fixed at 0.05.

In the simulations of Figure 6, motion coherence took on values of 25, 50, and 100%, while the intensity of the vestibular input was fixed at 50, reflecting the fact that vestibular responses are generally weaker than visual responses in MSTd (Fig.3 of ref ⁵⁰). In Eqn.3, baseline activity (c_vis = c_vest = 0) was subtracted from each response before the linear model was fit. In MSTd ¹¹, the effect of coherence on the mixing weights, w_vest and w_vis, did not depend on the congruency of visual and vestibular heading preferences. To examine this in our model (Fig. 6D–F), we present results for three particular combinations of heading preferences, congruent (ϕ̂ _vest = 90°, ϕ̂ _vis = 90°), opposite (ϕ̂_vest = 90°, ϕ̂_vis =270°), and intermediate (ϕ̂_vest = 90°, ϕ̂_vis =180°), all in the horizontal plane (θ̂_vest = θ̂_vis = 0°). Note, however, that all possible congruencies are present in the model population (Supplementary Fig. 7C). For each congruency type, all possible combinations of modality dominance weights from the set (d₁, d₂ = 1.0, 0.75, 0.5, 0.25) were used. Therefore, we simulated responses for a total of 3 (congruency types) × 16 (dominance weight combinations) = 48 model neurons (Fig. 6D–F). For each congruency type, simulation results were sorted into three groups according to the ratio of dominance weights: d_vest/d_vis <= 0.5, 0.5 < d_vest/d_vis < 2.0, or 2.0 <= d_vest/d_vis. Data were averaged within each group. Thus, results are presented (Fig. 6D–F) as nine curves, corresponding to all combinations of 3 congruency types and 3 weight ratio groups

Derivation of the cue-reweighting effect

Here, we derive the expression for the effective mixing weights of the model MSTd neurons (Eqn. 4) through some simplification and rearrangement of the equations for the normalization model. Assuming that the exponent (n) is one and that tuning curves simply scale with stimulus intensity ( ξ =0), the net population activity in response to a vestibular heading (ϕvest) with intensity c_vest and a visual heading (ϕ_vis) with intensity c_vis, can be expressed as:

$${\sum }_{d_{\mathit{vest}}}{\sum }_{{\widehat{\varphi }}_{\mathit{vest}}}{\sum }_{d_{\mathit{vis}}}{\sum }_{{\widehat{\varphi }}_{\mathit{vis}}}(d_{\mathit{vest}}\ast c_{\mathit{vest}}\ast F_{\mathit{vest}}({\widehat{\varphi }}_{\mathit{vest}};{\varphi }_{\mathit{vest}})+d_{\mathit{vis}}\ast c_{\mathit{vis}}\ast F_{\mathit{vis}}({\widehat{\varphi }}_{\mathit{vis}};{\varphi }_{\mathit{vis}}))={\sum }_{d_{\mathit{vest}}}{\sum }_{{\widehat{\varphi }}_{\mathit{vest}}}{\sum }_{d_{\mathit{vis}}}{\sum }_{{\widehat{\varphi }}_{\mathit{vis}}}(d_{\mathit{vest}}\ast c_{\mathit{vest}}\ast F_{\mathit{vest}}({\widehat{\varphi }}_{\mathit{vest}};{\varphi }_{\mathit{vest}}))+{\sum }_{d_{\mathit{vest}}}{\sum }_{{\widehat{\varphi }}_{\mathit{vest}}}{\sum }_{d_{\mathit{vis}}}{\sum }_{{\widehat{\varphi }}_{\mathit{vis}}}(d_{\mathit{vis}}\ast c_{\mathit{vis}}\ast F_{\mathit{vis}}({\widehat{\varphi }}_{\mathit{vis}};{\varphi }_{\mathit{vis}}))$$ (15)

where F_vest(ϕ̂_vest; ϕ_vest), F_vis (ϕ̂_vis;ϕ_vis) represent vestibular and visual tuning curves with heading preferences at ϕ̂_vest and ϕ̂_vis, respectively. Because heading preferences and dominance weights are randomly crossed in the model population, we can assume that this expression can be factorized:

$$c_{\mathit{vest}}\ast ({\sum }_{d_{\mathit{vis}}}1)\ast ({\sum }_{{\widehat{\varphi }}_{\mathit{vis}}}1)\ast ({\sum }_{d_{\mathit{vest}}}{d}_{\mathit{vest}})\ast ({\sum }_{{\widehat{\varphi }}_{\mathit{vest}}}{F}_{\mathit{vest}}({\widehat{\varphi }}_{\mathit{vest}};{\varphi }_{\mathit{vest}}))+c_{\mathit{vis}}\ast ({\sum }_{d_{\mathit{vest}}}1)\ast ({\sum }_{{\widehat{\varphi }}_{\mathit{vest}}}1)\ast ({\sum }_{d_{\mathit{vis}}}{d}_{\mathit{vis}})\ast ({\sum }_{{\widehat{\varphi }}_{\mathit{vis}}}{F}_{\mathit{vis}}({\widehat{\varphi }}_{\mathit{vis}};{\varphi }_{\mathit{vis}}))$$ (16)

If we make the additional simplification that heading preferences, ϕ̂_vest; and ϕ̂_vis are uniformly distributed, then terms involving sums of tuning curves, Σ_ϕ̂vest F_vest (ϕ̂_vest; ϕ_vest) and Σ_ϕ̂vis F_vis (ϕ̂; ϕ_vis), become constants. Moreover, the summations Σ_dvest d_vest and Σ_dvis d_vis are also constants because d_vest, d_vis are fixed parameters in the model. With these simplifications, Eqn. (15) can be expressed as:

$$k\ast (c_{\mathit{vest}}+c_{\mathit{vis}})$$ (17)

where k is a constant that incorporates the sums of tuning curves and dominance weights. The bimodal response of a model neuron can now be expressed as:

$$R_{\mathit{bimodal}}({\varphi }_{\mathit{vest}},{\varphi }_{\mathit{vis}})=\frac{d_{\mathit{vest}}\ast c_{\mathit{vest}}\ast F_{\mathit{vest}}({\widehat{\varphi }}_{\mathit{vest}};{\varphi }_{\mathit{vest}})+d_{\mathit{vis}}\ast c_{\mathit{vis}}\ast F_{\mathit{vis}}({\widehat{\varphi }}_{\mathit{vis}};{\varphi }_{\mathit{vis}})}{\alpha +k\ast (c_{\mathit{vest}}+c_{\mathit{vis}})}$$ (18)

Unimodal responses can be obtained by setting one of the stimulus intensities, c_vest or c_vis, to zero:

$$\begin{array}{l}{R}_{\mathit{vest}}({\varphi }_{\mathit{vest}})=\frac{d_{\mathit{vest}}\ast c_{\mathit{vest}}\ast F_{\mathit{vest}}({\widehat{\varphi }}_{\mathit{vest}};{\varphi }_{\mathit{vest}})}{\alpha +k\ast c_{\mathit{vest}}}\\ R_{\mathit{vis}}({\varphi }_{\mathit{vis}})=\frac{d_{\mathit{vis}}\ast c_{\mathit{vis}}\ast F_{\mathit{vis}}({\widehat{\varphi }}_{\mathit{vis}};{\varphi }_{\mathit{vis}})}{\alpha +k\ast c_{\mathit{vis}}}\end{array}$$

With these simplifications, the bimodal response (Eqn. 18) can be expressed as a weighted linear sum of the unimodal responses, with weights that depend on stimulus intensity:

$$R_{\mathit{bimodal}}({\varphi }_{\mathit{vest}},{\varphi }_{\mathit{vsi}})=\frac{\alpha +k\ast c_{\mathit{vest}}}{\alpha +k\ast (c_{\mathit{vest}}+c_{\mathit{vis}})}\ast R_{\mathit{vest}}({\varphi }_{\mathit{vest}})+\frac{\alpha +k\ast c_{\mathit{vis}}}{\alpha +k\ast (c_{\mathit{vest}}+c_{\mathit{vis}})}\ast R_{\mathit{vis}}({\varphi }_{\mathit{vis}})$$ (19)

Comparing Eqns.3 and 19, the closed forms of the mixing weights (Eqn.4) are obtained.