Shrinkage Estimation for Robust and Efficient Screening of Single-SNP Association from Case-control Genome-wide Association Studies

SUMMARY

Population-based case-control design has become one of the most popular approaches for conducting genome-wide association scans for rare diseases like cancer. In this article, we propose a novel method for improving the power of the widely used single-SNP two degrees-of-freedom (2 d.f.) association test for case-control studies by exploiting the common assumption of Hardy-Weinberg Equilibrium (HWE) for the underlying population. A key feature of the method is that it can relax the assumed model constraints via a completely data-adaptive shrinkage estimation approach so that the number of false positive results due to the departure of HWE is controlled. The method is computationally simple and is easily scalable to association tests involving hundreds of thousands or millions of genetic markers. Simulation studies as well as an application involving data from a real genome-wide association study illustrate that the proposed method is very robust for large-scale association studies and can improve the power for detecting susceptibility SNPs with recessive effects, when compared to existing methods. Implications of the general estimation strategy beyond the simple 2 d.f. association test are discussed.

1 INTRODUCTION

The identification of large numbers of single-nucleotide polymorphisms (SNPs) across the human genome and the development of technologies for massive multiplex genotyping have now made genome-wide association studies (GWAS) involving hundreds of thousands of markers feasible [Hirschhorn & Daly, 2005; Thomas et al., 2005; Wang et al., 2005]. A number of successful studies have now been able to identify novel susceptibility loci for complex diseases like cancer, heart disease, and diabetes [McPherson et al., 2007; Yeager et al., 2007; Ridderstrale & Nilsson, 2008]. In GWAS, the evaluation of the association between a disease trait and an individual SNP often constitutes the initial analytic step. The lack of statistical significance in this first step may lead to the exclusion of a SNP from further scrutiny. Thus, to reduce the chance of false negatives, it is important to use powerful methods for preliminary screening of associations.

Population-based case-control studies are now being increasingly used for conducting genome-wide association scans. A widely used method for testing single-SNP associations in case-control studies is the Cochran-Armitage (CA) one-degree-of-freedom trend test [Armitage, 1955; Sasieni, 1997; Slager & Schaid, 2001; Freidlin et al., 2002], which is known to be optimal when the mode-of-effect for a SNP is multiplicative. An alternative method, which is known to have robust power under alternative modes-of-effect, is the two-degrees-of-freedom (2 d.f.) chi-square test for independence between case-control and genotype status. The power of the standard 2 d.f. test, however, can be low for detection of SNPs with recessive effects, often because of the lack of sufficient sample size for homozygous variants among the cases and controls. To resolve this sparse data problem, we recently proposed the use of the assumption of Hardy-Weinberg Equilibrium (HWE) for estimation of the genotype frequencies among the controls, then comparing the resulting distribution with the empirical genotype distribution of the cases to obtain a novel 2 d.f. test of association [Chen & Chatterjee, 2007]. We showed that the proposed methodology can increase the power of 2 d.f. tests in a major way under non-multiplicative genetic effects, with the gain being particularly dramatic under the recessive model. A number of other reports had also previously pointed out that “retrospective” methods for analysis of case-control studies can exploit assumptions of HWE or a related population genetics model to gain major power for both genotype- and haplotype-based tests of association [Epstein & Satten, 2003; Satten & Epstein, 2004; Thompson et al., 2004].

A major limitation of all HWE-based tests of genetic association is that they can lead to serious inflation of type-I error when the underlying assumptions of HWE or other genetic models are violated. In Chen & Chatterjee [2007], we characterized the bias of the 2 d.f. test analytically and showed that even modest departure of HWE can lead to an unacceptably high increase in the type-I error of the procedures. The main objective of this article is to develop a 2 d.f. test that can gain power by exploiting the model assumptions of HWE for the underlying population and yet be resistant to bias when the model assumptions are violated. The method involves estimation of genotype-specific disease odds ratio parameters by data-adaptive “shrinkage” of a “model-free” estimator that does not require HWE assumption towards a “model-based” estimator that directly exploits the HWE constraints. The amount of “shrinkage” is sample-size-adaptive and data-adaptive, so that in large samples the method has no bias irrespective of whether the assumptions of HWE hold and yet the method can gain efficiency by shrinking the analysis towards HWE, but only to the extent that the data validate the assumptions. The closed-form expression of the estimator itself and the availability of a simple variance estimator facilitate rapid computation of a corresponding Wald-type 2 d.f. test for GWAS involving hundreds of thousands of SNPs.

We evaluate performance of the proposed method compared with a number of alternative tests, using both simulated and real data. In particular, we use data from the Cancer Genetics Markers of Susceptibility (CGEMS) study to evaluate the ability of the proposed shrinkage estimation procedure to protect against inflated type-I errors due to the departure of HWE that may occur on a genome-wide scale. The study reveals potential problems associated with the application of the so-called “retrospective” methods on a genome-wide scale, even though the underlying assumption of HWE overall may be a good assumption for the genome. These studies together suggest that the proposed novel shrinkage estimation procedure is a promising method for testing genetic association in case-control studies. The method can gain major power over standard case-control analysis by exploiting the possible constraint of HWE for the underlying population and yet can adapt itself to protect against inflation of type-I error when the HWE constraints are violated. We also discuss the potential implications of these findings beyond the context of the simple 2 d.f. test considered in this article.

2 METHODS

The genotype information for an individual SNP in a case-control study can be represented by the 2 × 3 contingency table shown in Table 1. Here D is the indicator of case (D = 1) or control (D = 0) status and G is the number of minor alleles carried by an individual (G = 0, 1, 2). Let P_dg = pr(G = g|D = d), d = 0 and 1, denote the population genotype frequencies for the controls and the cases, respectively. The likelihood L for case-control data is given by the product of two sets of multinomial probabilities, $L=L_1\times L_0={\displaystyle {\prod }_{g=0}^2}{p}_{1g}^{n_{1g}}\times {\displaystyle {\prod }_{g=0}^2}{p}_{0g}^{n_{0g}}$, where n_1g and n_0g denote numbers of cases and controls with genotype g, respectively. In addition, define $n_{d+}={\displaystyle {\sum }_{g=0}^2}{n}_{\mathit{\text{dg}}}$ for d = 0 and 1, i.e., n₁₊ for the number of cases and n₀₊ for the number of controls.

Table 1.

SNP genotype frequencies in diseased (D = 1) and disease-free (D = 0) subjects in the population

	D = 0	D = 1	Total
G=AA	P00	P10	P+0
G=Aa	P01	P11	P+1
G=aa	P02	P12	P+2
Total	1	1

We consider re-parameterizing the likelihood in terms of alternative parameters of interest. Following Lindley [1988], we define

$$\theta =0.5\text{log}\frac{4p_{00}{p}_{02}}{p_{01}^2}\text{ and }\omega =0.5\text{log}\frac{p_{00}}{p_{02}}.$$ (1)

Note that θ and ω characterize the genotype frequencies of the controls according to the formulas $p_{00}=\frac{e^{2\omega }}{1+e^{2\omega }+2e^{\omega -\theta }},p_{01}=\frac{2e^{\omega -\theta }}{1+e^{2\omega }+2e^{\omega -\theta }},\text{ and }{p}_{02}=\frac{1}{1+e^{2\omega }+2e^{\omega -\theta }}$. The Hardy-Weinberg Disequilibrium (HWD) coefficient θ is a measure of the departure from HWE among controls, with θ = 0, θ > 0, and θ < 0 corresponding to HWE, excess homozygosity, and excess heterozygosity, respectively. We note that the HWE assumption is reasonable for the underlying population, which will include both diseased and disease-free subjects. However, for rare diseases like certain cancers, the assumption of HWE is reasonable in the control population, as they approximately represent the underlying whole population. Further, let $\mathit{\psi }=({\psi }_0,{\psi }_1,{\psi }_2)=(1,\frac{P_{11}{P}_{00}}{P_{01}{P}_{10}},\frac{P_{12}{P}_{00}}{P_{02}{P}_{10}})$ be the disease odds ratio parameter vector associated with the genotypes G = 1 and G = 2 relative to the baseline genotype G = 0. Let ${\mathit{\beta }}^T=(\text{log}\frac{P_{11}{P}_{00}}{P_{01}{P}_{10}},\text{ log }\frac{P_{12}{P}_{00}}{P_{02}{P}_{10}})=(\text{log}{\psi }_1,\text{ log }{\psi }_2)$.

Given θ and ω and hence the genotype frequency for the controls, we can characterize the genotype frequencies for the cases by ψ according to the formula

$$p_{1g}=\frac{{\psi }_g{p}_{0g}}{{\displaystyle {\sum }_{g=0}^2}{\psi }_g{p}_{0g}}\text{ for }g=0,1,2,$$ (2)

Thus, the likelihood for case-control data, L = L(β, ω, θ), is a function of ψ, ω, and θ.

Let β̂(θ) denote the maximum-likelihood estimate of β for a fixed value of θ. When θ = 0, i.e., when HWE holds among the controls, the maximum-likelihood estimate of β, denoted by β̂(θ = 0), which we have shown previously [Chen & Chatterjee, 2007], can be expressed in closed form as

$${(\widehat{\mathit{\beta }}(\theta =0))}^T=({\widehat{\beta }}_1(\theta =0),{\widehat{\beta }}_2(\theta =0))=\left(\text{log}(\frac{n_{11}{n}_{00}^E}{n_{10}{n}_{01}^E}),\text{log}(\frac{n_{12}{n}_{00}^E}{n_{10}{n}_{02}^E})\right),$$ (3)

where $n_{00}^E=n_{0+}{(1-\widehat{f})}^2,n_{01}^E=n_{0+}2\widehat{f}(1-\widehat{f}),\text{ and }{n}_{02}^E=n_{0+}{\widehat{f}}^2$ denote the expected genotype counts for the controls computed assuming HWE, with the estimated allele frequency f̂ = (n₀₁+2n₀₂)/2n₀₊. If θ is left completely unconstrained, then the maximum-likelihood estimate of β is given by the standard case-control estimator

$${(\widehat{\mathit{\beta }})}^T=({\widehat{\beta }}_1,{\widehat{\beta }}_2)=\left(\text{log}(\frac{n_{11}{n}_{00}}{n_{10}{n}_{01}}),\text{log}(\frac{n_{12}{n}_{00}}{n_{10}{n}_{02}})\right).$$ (4)

The unconstrained ML estimator can also be expressed as β̂ = β̂ (θ̂), where $\widehat{\theta }=0.5\text{log}\{4n_{00}{n}_{02}/n_{01}^2\}$ denotes the maximum-likelihood estimator of θ.

We propose to combine β̂ (θ = 0) and β̂ (θ̂), the constrained and unconstrained estimators of β, using an empirical-Bayes-type shrinkage estimation approach that we developed earlier for combining alternative estimates of the gene-environment interaction parameter obtained with or without the assumption of gene-environment independence in the underlying population [Mukherjee & Chatterjee, 2008]. In particular, following a very general formulation of the problem we described in that article, we propose to use the composite estimator (referred to as the vector-based shrinkage estimator, EB1) as

$$\begin{array}{cc}{\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}1}\hfill & ={\widehat{\mathrm{\Delta }}}^T\widehat{\theta }{\widehat{\theta }}^T\widehat{\mathrm{\Delta }}{({\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}+{\widehat{\mathrm{\Delta }}}^T\widehat{\theta }{\widehat{\theta }}^T\widehat{\mathrm{\Delta }})}^{-1}\widehat{\mathit{\beta }}+{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}{({\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}+{\widehat{\mathrm{\Delta }}}^T\widehat{\theta }{\widehat{\theta }}^T\widehat{\mathrm{\Delta }})}^{-1}{\widehat{\mathit{\beta }}}^0\hfill \\ \hfill & =\widehat{\mathit{\beta }}-{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}{({\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}+{\widehat{\theta }}^2{\widehat{\mathrm{\Delta }}}^T\widehat{\mathrm{\Delta }})}^{-1}(\widehat{\mathit{\beta }}-{\widehat{\mathit{\beta }}}^0),\hfill \end{array}$$ (5)

where V̂_β̂ denotes the estimated asymptotic variance-covariance matrix of β̂ as in Breslow & Day [1984], and where $\widehat{\mathrm{\Delta }}={\frac{\partial \widehat{\mathit{\beta }}(\theta )}{\partial \theta }|}_{\theta =0}$. We refer the reader to Mukherjee & Chatterjee [2008] for the detailed rationale for the estimator. Intuitively, we note that β̂_EB1 is an weighted average of the constrained and unconstrained estimators. As the sample size increases, and hence V̂_β̂ decreases, the composite estimator puts more weight on the robust unconstrained estimator. The weight also depends on θ̂, the data-driven estimate of the HWD coefficient. If the absolute value of θ̂ increases, i.e., if the data suggest departure of HWE, then less weight is given to the constrained estimator. The influence of θ on the weight depends on Δ̂, which determines the rate of change of β̂(θ) as a function of θ at the point θ = 0. In the Appendix, we derive a closed-form expression for Δ̂. In formula (5), the EB estimator for β = (β₁, β₂) is presented where β is treated as a whole vector. Alternatively, one could derive an EB estimator for each of the two components of β separately. In a vectorized form, we can write the alternative EB estimator (referred to as the component-wise shrinkage estimator, EB2) as

$${\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}2}=\widehat{\mathit{\beta }}-\text{diag}[{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}]{[\text{diag}({\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}+{\widehat{\theta }}^2{\widehat{\mathrm{\Delta }}}^T\widehat{\mathrm{\Delta }})]}^{-1}(\widehat{\mathit{\beta }}-{\widehat{\mathit{\beta }}}^0)=\widehat{\mathit{\beta }}-M(\widehat{\mathit{\beta }}-{\widehat{\mathit{\beta }}}^0),$$ (6)

where diag (A) is the matrix that takes the diagonal of matrix A but sets all the off-diagonal elements to zero, and M = diag(V̂_β̂)[diag(V̂_β̂ + θ̂²Δ̂^TΔ̂)]⁻¹. In the current as well as other applications (see e.g., Chen et al. [2009]), we have found that the component-wise method generally produces more shrinkage compared to its multivariate counterpart. This observation is purely based on extensive empirical studies under several simulation settings. Theoretical justification of the performance advantage of EB2 over EB1 in mean squared error (MSE) and power are still unknown. In the current HWE context with only two parameters, EB2 and EB1 are noted to have very similar MSE, but EB2 has better power properties across all scenarios. With increase in the dimension of the parameter space, as in the haplotype-based estimation context of Chen et al. [2009], the efficiency advantage of EB2 over EB1 becomes more pronounced. Simulation studies indicate that for a large number of parameters, the off-diagonal elements of (V̂_β̂)[(V̂_β̂ + θ̂²Δ̂^TΔ̂)]⁻¹ are quite variable across the samples, which possibly offset the advantages of a full multivariate vector-wise shrinkage. The issue of relative efficiency of EB2 over EB1 merits further theoretical exploration.

In the Appendix, we use the Delta method to obtain an estimate of the variance-covariance matrix (Σ_EB) for the two EB estimators of β = (β₁, β₂). For each of the methods, a 2 d.f. Wald test can be constructed as $T_i=W_{\mathit{\text{EBi}}}={\widehat{\mathit{\beta }}}_{\mathit{\text{EBi}}}^T{\displaystyle {\sum }_{\mathit{\text{EBi}}}^{-1}}{\widehat{\mathit{\beta }}}_{\mathit{\text{EBi}}}$, for i = 1, 2.

We perform simulation studies to compare the type-I error and power for four alternative tests of association: (1) the standard unconstrained 2 d.f. test; (2) the 2 d.f test assuming HWE in the controls; (3) a two-step method that first tests the HWE constraint (i.e., null hypothesis θ = 0) among the controls at a designated significance level, then uses a constrained test if not rejected, or uses a unconstrained test if rejected; and (4) Wald tests based on the proposed EB estimation procedures. In these simulation studies, we assume that the disease susceptibility allele is the less frequent or minor allele. Given the minor allele frequency (MAF) f and HWD coefficient θ, we calculate the genotype frequencies for the controls, p_0g according to formula (1). Further, given the odds ratio parameters ψ₀ = 1 (reference group), ψ₁, and ψ₂, we obtain the genotype frequencies for the cases (i.e., p_1g) using formula (2). The genotypes for the cases and the controls are then generated from the respective multinomial distributions.

3 RESULTS

3.1 SIMULATION STUDIES

In the first set of simulations, we examine the type-I errors of various tests under the null hypothesis of no disease-genotype association. We simulate data in the settings that involve two sample sizes (i.e., n₀ = n₁ = 500 and n₀ = n₁ = 2000) and multiple combinations of coefficients θ (i.e., θ = 0, 0.5 log(1.2), 0.5 log(1.6), and 0.5 log(2.0), referred to as HWE, small, modest, and large deviation from HWE, respectively) and minor allele frequencies f. We choose the significance levels α to be 0.05 for the sample size of 500 and 1.0e–5 for the sample size of 2, 000. We observe from Table 2 that when HWE holds, all of the different procedures, except the two-step method, maintain the desired type-I error level very well. The inflation of the type-I error in the two-step method in this setting is probably due to the fact that the procedure ignores the variability associated with uncertainty in the underlying model selection procedure at the first step. When HWE is violated, we observe that the type-I error of the constrained test rapidly increases with θ and becomes unacceptably high even under modest deviation from HWE. The two-step method, although it reduces the problem of type-I error inflation to a large extent, can still produce a large inflation of the type-I error. The EB procedures provide much better control of type-I error, compared with both the constrained and the two-step method. In particular, it is encouraging to note that when the departure of HWE is small, say |θ| ≤ 0.5 log(1.2), a range where the large majority of HWE departures are likely to appear in practice (see, e.g., Figure 3 in the CGEMS application), the type-I errors of the EB procedures are generally very close to the nominal level. As θ further increases, the type-I errors of the EB procedures initially increase and then eventually again decrease.

Table 2.

The type-I error for alternative tests under the null hypothesis of no disease-genotype association (i.e., ψ_Aa = ψ_aa = 1). Results are obtained based on simulating case-control data sets with either 500 cases and 500 controls (upper panel) or 2000 cases and 2000 controls (lower panel). Desired significance level of the tests are assumed to be α = 0.05 and α = 10⁻⁵ for studies with 500 and 2000 cases, respectively. Empirical significance levels of the tests are obtained by 10, 000 and 1 million simulations, respectively.

HWD coeff (θ)	MAF	Unconstrained	Constrained	Two-step	EB1	EB2
	500 cases and 500 controls, α = 0.05, 10,000 simulations
	0.1	0.03	0.04	0.04	0.03	0.03
θ = 0	0.2	0.05	0.05	0.06	0.04	0.04
	0.3	0.05	0.05	0.06	0.04	0.04
	0.1	0.03	0.07	0.07	0.04	0.04
θ = 0.5log(1.2)	0.2	0.05	0.09	0.09	0.05	0.06
	0.3	0.05	0.11	0.11	0.06	0.07
	0.1	0.03	0.15	0.13	0.06	0.07
θ = 0.5log(1.6)	0.2	0.05	0.31	0.22	0.09	0.11
	0.3	0.05	0.50	0.23	0.08	0.12
	0.1	0.03	0.24	0.18	0.08	0.09
θ = 0.5log(2.0)	0.2	0.04	0.57	0.22	0.07	0.11
	0.3	0.05	0.82	0.13	0.06	0.10
	2000 cases and 2000 controls, α = 1.0e − 5, 1 million simulations
	0.1	3.0e − 6	8.0e − 6	1.0e − 5	3.0e − 6	3.0e − 6
θ = 0	0.2	1.0e − 5	1.4e − 5	1.8e − 5	1.1e − 5	1.3e − 5
	0.3	1.6e − 5	1.1e − 5	2.1e − 5	8.0e − 6	8.0e − 6
	0.1	4.0e − 6	2.6e − 4	2.3e − 4	5.5e − 5	6.5e − 5
θ = 0.5log(1.2)	0.2	1.7e − 5	8.0e − 4	6.1e − 4	1.3e − 4	1.9e − 4
	0.3	1.1e − 5	2.1e − 3	1.3e − 3	2.3e − 4	3.6e − 4
	0.1	1.0e − 6	9.0e − 3	4.9e − 3	6.8e − 4	8.1e − 4
θ = 0.5log(1.6)	0.2	5.0e − 6	0.11	1.1e − 2	4.7e − 4	9.7e − 4
	0.3	8.0e − 6	0.39	3.5e − 3	7.9e − 5	3.7e − 4
	0.1	3.0e − 6	5.9e − 2	1.5e − 2	1.4e − 3	1.7e − 3
θ = 0.5log(2.0)	0.2	5.0e − 6	0.57	2.3e − 3	5.1e − 5	1.8e − 4
	0.3	1.1e − 5	0.95	2.0e − 5	1.0e − 5	3.1e − 5

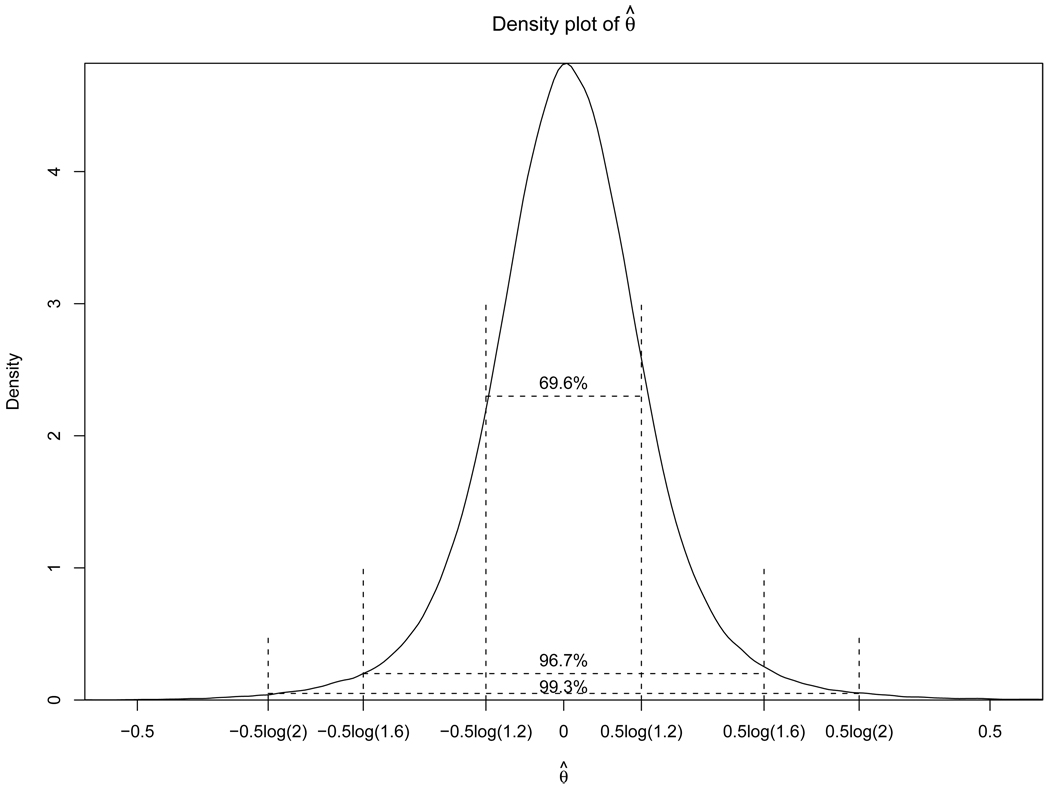
Figure 3.

Histogram of estimates of θ, a log-odds-ratio measure of Hardy-Weinberg Disequilibrium, for the 449, 698 SNPs studied in 22 non-sex chromosomes in the CGEMS study with minor allele frequencies larger than 0.05. The values θ = 0, θ > 0, and θ < 0 correspond to HWE, excess homozygosity, and excess heterozygosity, respectively.

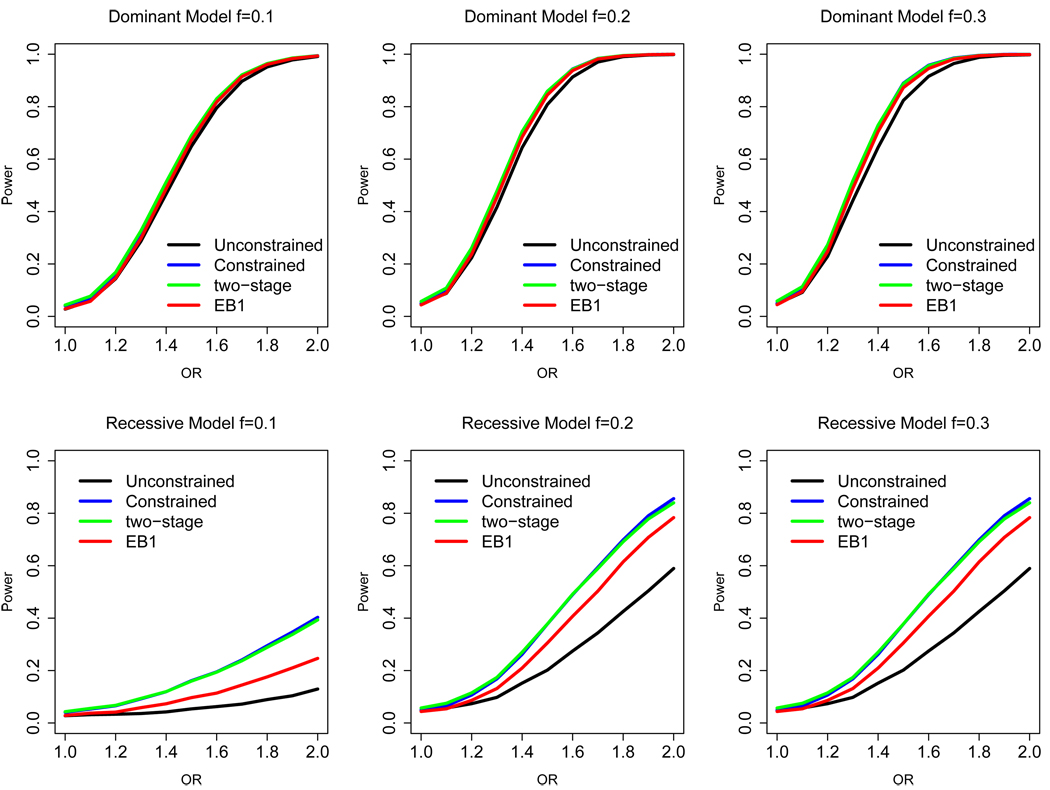
In the next set of simulations, we assume HWE in the control population and explore the power of various test procedures under different combinations of minor allele frequency and odds ratio parameters. Figure 1 displays the power curves estimated from 10, 000 simulated data sets of 500 cases and 500 controls. It is clear that in this setting the constrained test can gain major power over the unconstrained test, especially when the true effect of the genotype is recessive. The EB1 test procedure, although it gives up some efficiency compared with the constrained test, retains a major power advantage over the unconstrained test for detecting recessive genetic effects. The power of EB1 was slightly lower than that of EB2 (not shown in Figure 1). The power of the two-stage test lies between the unconstrained and constrained tests, as expected.

Figure 1.

Power comparison for alternative case-control tests of association: (i) a standard 2 d.f. test (unconstrained), (ii) a 2 d.f. test assuming HWE in controls (constrained), (iii) a two-step test that selects between the constrained and unconstrained tests based on a test of HWE among the controls, and (iv) the proposed EB tests. Data are simulated for a case-control study of 500 cases and 500 controls, assuming that HWE holds for the underlying population. The effect of the SNP on the risk of the disease is assumed to follow either a dominant (upper panel) or a recessive pattern (lower panel). All of the the tests are performed at significance level α = 0.05.

In Table 3, we show the power for various tests of association under the recessive model and different combinations of the minor allele frequency f and the HWE coefficient θ. We observe that when there is small departure from HWE, a scenario that is likely to be common in practice, the EB procedures can maintain desired type-I error levels fairly well (as seen in Table 2) and yet can gain substantial power over the unconstrained test. Similar comparisons for the dominant model are shown in Table 4. Here we observe that under small departures from HWE, the EB procedures generally perform similarly to the unconstrained test. Under large departures from HWE, however, the EB procedures can sometimes have a substantial loss of power compared with the unconstrained test. Since some of the tests we consider do not strictly maintain type-I error under the departure of HWE, we also provide mean squared error (MSE) for the parameter estimates as an alternative way of comparing the performance of the different estimators. The results are similar to those presented in Mukherjee & Chatterjee [2008]. Under HWE, the EB methods produce MSE comparable to the constrained estimator, which has smallest MSE. Under departures from HWE, the EB methods produce the smallest or close to the smallest MSE among all methods we considered (as shown in Tables 3 and 4).

Table 3.

The power for different tests and mean squared error corresponding to the estimate of log(ψ_aa) (in parentheses). The disease-genotype odds ratios are assumed to follow a “recessive” pattern with ψ_Aa = 1, ψ_aa = 1.4². Results are based on 10, 000 simulated case-control data sets, each with 500 cases and 500 controls (upper panel), and on 1, 000, 000 simulated case-control data sets, each with 2, 000 cases and 2, 000 controls (lower panel). All tests are performed at a significance level of α = 0.05 for the study with 500 cases and α = 10⁻⁵ for the study with 2, 000 cases.

Sample Size	HWD coeff (θ)	MAF	Unconstrained	Constrained	Two-step	EB1	EB2
N=500		0.1	0.120 (0.383)	0.379 (0.171)	0.371 (0.205)	0.224 (0.232)	0.233 (0.229)
	θ = 0	0.2	0.556 (0.087)	0.834 (0.056)	0.821 (0.065)	0.707 (0.066)	0.756 (0.063)
		0.3	0.883 (0.043)	0.980 (0.035)	0.973 (0.037)	0.940 (0.037)	0.967 (0.036)
		0.1	0.118 (0.378)	0.517 (0.180)	0.484 (0.211)	0.283 (0.235)	0.306 (0.228)
	θ = 0.5log(1.2)	0.2	0.575 (0.082)	0.945 (0.065)	0.874 (0.071)	0.735 (0.068)	0.809 (0.064)
		0.3	0.893 (0.043)	0.999 (0.042)	0.959 (0.043)	0.930 (0.041)	0.973 (0.040)
		0.1	0.125 (0.367)	0.721 (0.288)	0.598 (0.310)	0.331 (0.276)	0.372 (0.268)
	θ = 0.5log(1.6)	0.2	0.595 (0.082)	0.993 (0.135)	0.754 (0.117)	0.656 (0.089)	0.776 (0.087)
		0.3	0.905 (0.040)	1.000 (0.071)	0.911 (0.053)	0.897 (0.045)	0.963 (0.046)
		0.1	0.126 (0.365)	0.822 (0.435)	0.581 (0.409)	0.322 (0.319)	0.375 (0.310)
	θ = 0.5log(2.0)	0.2	0.605 (0.080)	0.999 (0.228)	0.656 (0.126)	0.619 (0.097)	0.755 (0.096)
		0.3	0.916 (0.038)	1.000 (0.111)	0.916 (0.045)	0.884 (0.043)	0.964 (0.045)
N=2,000		0.1	0.003 (0.082)	0.228 (0.039)	0.218 (0.051)	0.086 (0.054)	0.098 (0.052)
	θ = 0	0.2	0.520 (0.021)	0.965 (0.014)	0.943 (0.016)	0.782 (0.016)	0.859 (0.015)
		0.3	0.986 (0.011)	1.000 (0.009)	0.997 (0.009)	0.994 (0.010)	0.999 (0.009)
		0.1	0.003 (0.081)	0.500 (0.057)	0.438 (0.068)	0.166 (0.062)	0.190 (0.060)
	θ = 0.5log(1.2)	0.2	0.548 (0.020)	0.999 (0.026)	0.808 (0.025)	0.654 (0.020)	0.786 (0.020)
		0.3	0.989 (0.010)	1.000 (0.014)	0.990 (0.013)	0.986 (0.011)	0.997 (0.011)
		0.1	0.003 (0.079)	0.862 (0.174)	0.462 (0.128)	0.123 (0.087)	0.149 (0.087)
	θ = 0.5log(1.6)	0.2	0.585 (0.020)	1.000 (0.093)	0.592 (0.026)	0.505 (0.023)	0.675 (0.024)
		0.3	0.993 (0.010)	1.000 (0.044)	0.993 (0.010)	0.982 (0.011)	0.997 (0.012)
		0.1	0.004 (0.078)	0.968 (0.336)	0.248 (0.134)	0.052 (0.097)	0.071 (0.096)
	θ = 0.5log(2.0)	0.2	0.613 (0.019)	1.000 (0.184)	0.613 (0.019)	0.501 (0.022)	0.682 (0.022)
		0.3	0.995 (0.010)	1.000 (0.085)	0.995 (0.010)	0.978 (0.011)	0.997 (0.010)

Table 4.

The power for different tests and sum of mean squared errors corresponding to the point estimates of log(ψ_Aa) and log(ψ_aa) (in parentheses). The disease-genotype odds ratios are assumed to follow a “dominant” pattern with ψ_Aa = ψ_aa = 1.4. Results are based on 10, 000 simulated case-control data sets, each with 500 cases and 500 controls (upper panel), and on 1, 000, 000 simulated case-control data sets, each with 2, 000 cases and 2, 000 controls (lower panel). All tests are performed at a significance level of α = 0.05 for the study with 500 cases and α = 10⁻⁵ for the study with 2, 000 cases.

Sample Size	HWD coeff (θ)	MAF	Unconstrained	Constrained	Two-step	EB1	EB2
N=500		0.1	0.465 (0.479)	0.498 (0.275)	0.507 (0.308)	0.477 (0.329)	0.482 (0.324)
	θ = 0	0.2	0.637 (0.123)	0.693 (0.089)	0.697 (0.098)	0.664 (0.100)	0.677 (0.096)
		0.3	0.656 (0.069)	0.741 (0.057)	0.740 (0.060)	0.700 (0.060)	0.714 (0.058)
		0.1	0.455 (0.471)	0.460 (0.273)	0.478 (0.308)	0.446 (0.323)	0.437 (0.314)
	θ = 0.5log(1.2)	0.2	0.621 (0.120)	0.600 (0.099)	0.622 (0.107)	0.598 (0.103)	0.593 (0.098)
		0.3	0.651 (0.067)	0.602 (0.066)	0.639 (0.068)	0.610 (0.064)	0.611 (0.062)
		0.1	0.420 (0.472)	0.447 (0.368)	0.473 (0.402)	0.389 (0.362)	0.365 (0.349)
	θ = 0.5log(1.6)	0.2	0.621 (0.119)	0.614 (0.173)	0.658 (0.154)	0.549 (0.124)	0.530 (0.123)
		0.3	0.659 (0.066)	0.629 (0.112)	0.688 (0.084)	0.565 (0.072)	0.580 (0.075)
		0.1	0.384 (0.468)	0.482 (0.519)	0.485 (0.507)	0.351 (0.408)	0.323 (0.395)
	θ = 0.5log(2.0)	0.2	0.600 (0.113)	0.714 (0.273)	0.667 (0.165)	0.489 (0.131)	0.478 (0.133)
		0.3	0.658 (0.064)	0.789 (0.176)	0.686 (0.074)	0.516 (0.071)	0.575 (0.076)
N=2, 000		0.1	0.370 (0.103)	0.428 (0.059)	0.431 (0.071)	0.397 (0.073)	0.417 (0.071)
	θ = 0	0.2	0.690 (0.029)	0.792 (0.021)	0.790 (0.024)	0.744 (0.024)	0.770 (0.023)
		0.3	0.718 (0.017)	0.853 (0.014)	0.847 (0.015)	0.793 (0.015)	0.816 (0.015)
		0.1	0.329 (0.101)	0.314 (0.076)	0.334 (0.087)	0.307 (0.079)	0.297 (0.077)
	θ = 0.5log(1.2)	0.2	0.674 (0.029)	0.614 (0.034)	0.661 (0.034)	0.624 (0.028)	0.612 (0.028)
		0.3	0.723 (0.017)	0.621 (0.022)	0.702 (0.020)	0.651 (0.017)	0.648 (0.018)
		0.1	0.269 (0.099)	0.285 (0.191)	0.301 (0.148)	0.217 (0.106)	0.178 (0.105)
	θ = 0.5log(1.6)	0.2	0.642 (0.028)	0.620 (0.108)	0.651 (0.034)	0.515 (0.032)	0.490 (0.034)
		0.3	0.729 (0.016)	0.671 (0.069)	0.731 (0.016)	0.588 (0.017)	0.641 (0.019)
		0.1	0.225 (0.098)	0.374 (0.354)	0.277 (0.154)	0.152 (0.117)	0.112 (0.118)
	θ = 0.5log(2.0)	0.2	0.613 (0.027)	0.830 (0.210)	0.614 (0.028)	0.400 (0.032)	0.446 (0.032)
		0.3	0.728 (0.016)	0.930 (0.134)	0.728 (0.016)	0.491 (0.018)	0.652 (0.017)

3.2 The CANCER GENETICS MARKERS OF SUSCEPTIBILITY (CGEMS) STUDY

We evaluate the performance of alternative 2 d.f. tests of association using data from the Cancer Genetics Markers of Susceptibility (CGEMS) study, an NCI enterprize initiative to conduct multistage whole-genome association studies to identify genes giving rise to increased risks of prostate and breast cancers. In this article, we will focus on data from the initial scan for the prostate cancer study, involving genotype data on about 550, 000 SNPs from 1, 172 cases and 1, 157 controls. An initial report from the study describing the increased risk of prostate cancer associated with the 8q24 region has been published [Yeager et al., 2007]. Sequential replication studies are now ongoing for about 5% of the SNPs that are considered to be promising based on the data from the initial scan. The details of the CGEMS study design and the results from the initial scan can be found at the website https://caintegrator.nci.nih.gov/cgems/.

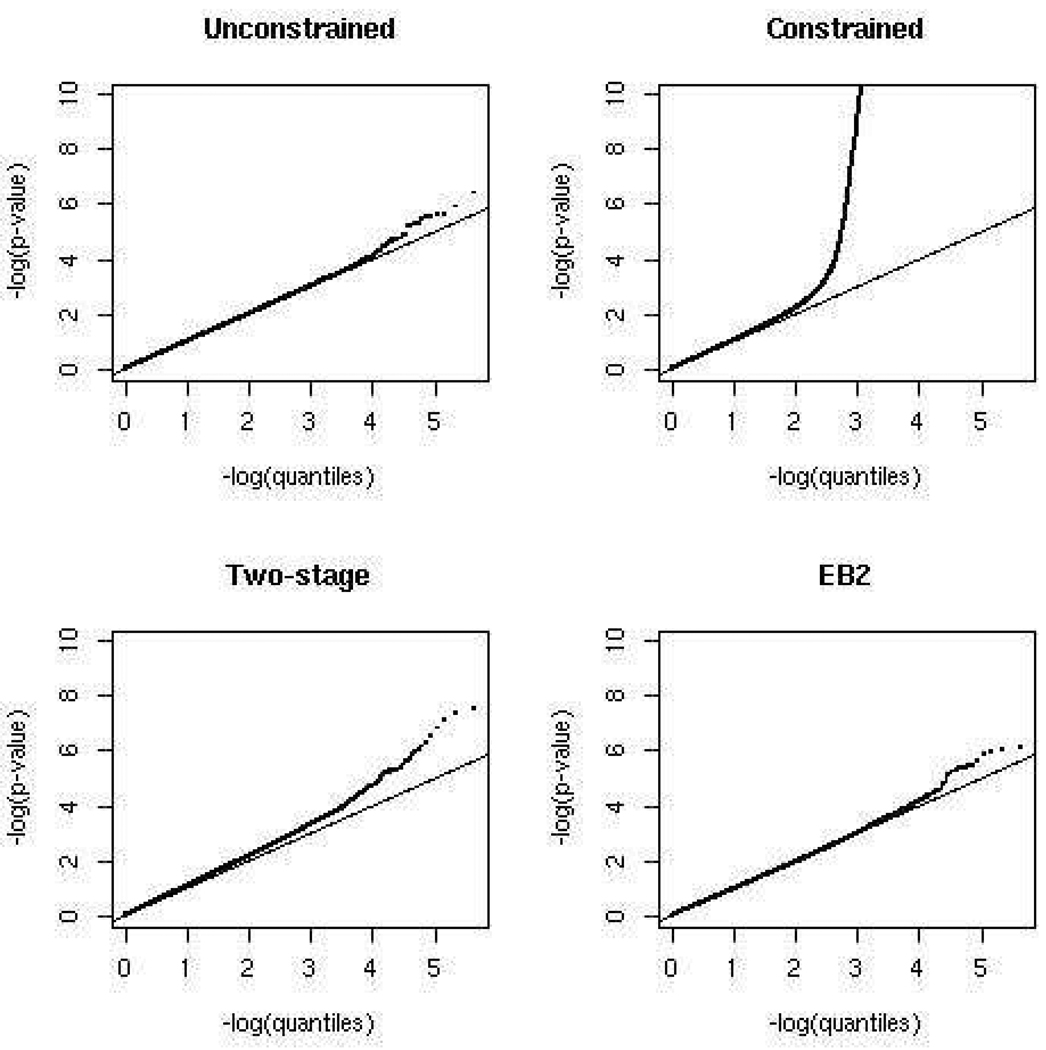
Figure 2 shows the Q-Q plots associated with 449, 698 SNPs from 22 non-sex chromosomes with minor allele frequencies larger than 0.05 for the four different tests of association: (i) unconstrained; (ii) constrained; (iii) two-stage; and (iv) EB2. Each plot in the figure displays the empirical percentile of the p-values associated with one of the four 2 d.f. tests against the percentiles of the expected null distribution. For a well-designed study and a robust analytic method, Q-Q plots for GWAS are expected to follow the diagonal lines closely, given that at most a handful of the SNPs are likely to be truly associated with the disease. Thus, large-scale departure of the Q-Q plot from the expected diagonal is often considered to be indicative of bias in the underlying study design or/and analytic method.

Figure 2.

Q-Q plots for the CGEMS genome-wide association study of prostate cancer. Each panel represents a plot for the percentiles of the observed p-values, obtained from a specific test of association, against those expected under the “null” hypothesis of no association. The solid line represents the diagonal Y = X.

In Figure 2, we observe that the Q-Q plot for the unconstrained test closely follows the diagonal line except at the extreme tail of the distributions, where p < 10⁻⁴. This plot suggests that the CGEMS study does not suffer from any large-scale systematic bias such as those due to population stratification or differential genotyping error. Moreover, the standard 2 d.f. test of association is a robust method for analysis of data from this study. In contrast, we observe that the Q-Q plot for the constrained test departs dramatically from the diagonal line in the range of p < 10⁻². For example, the constrained test finds 1, 716 SNPs to have p-values less than 10⁻³, while under the null hypothesis of no association, only 450 (i.e., 449, 698 × 10⁻³ ≃ 450) such SNPs would be expected in the study. This indicates a major inflation of the type-I error for the constrained test due to departure of the HWE assumption. We observe The Q-Q plot corresponding to the two-step procedure suggests that although the type-I error inflation is substantially reduced compared with the constrained test, it still remains significantly higher than desired. The two-step method, for example, finds 122 SNPs to have p-values less than 10⁻⁴, while under the null hypothesis of no association, only 45 (i.e., 449, 698 × 10⁻⁴ ≃ 45) such SNPs would be expected. The Q-Q plot for the EB2 procedure strikingly resembles that of the robust unconstrained test. The plot closely follows the diagonal line except at the extreme tail of the distribution. The pattern provides empirical evidence that EB-type procedures perform very well in controlling the type-I error rates for the related tests of association under realistic departures from HWE that may arise in GWAS. We refrain from presenting the Q-Q plot for the EB1 procedure in this example as it appears to be very similar to EB2, and EB2 does have a slight edge over EB1 in terms of power for detecting disease-SNP association.

In Figure 3, we show the histogram of the estimated HWD coefficient θ for the 449, 698 SNPs we studied. It is clear that, overall, HWE is a good assumption for the genome, with 69.6% and 96.7% of the estimated coefficients falling between the ±0.5log(1.2) and ±0.5log(1.6) limits, respectively. Nevertheless, a test based on the assumption of HWE can lead to a major inflation of type-I error for large-scale studies.

The CGEMS group has recently reported results from a replication study involving 3, 941 cases and 3, 964 controls [Thomas et al., 2008]. Based on a “joint analysis” of the initial scan and replication study, the report has listed 17 SNPs that have met genome-wide significance for their association with prostate cancer. Given that associations of these SNPs with prostate cancer are now considered to be “replicated”, we can use these SNPs to evaluate the power of alternative methods for the analysis of the initial CGEMS scan. From the results shown in Table 5, we observe that for 12 out of the 17 SNPs (row 1 to 12 of Table 5), both EB-based procedures produce smaller p-values than the standard 2 d.f test, while for 2 other SNPs (rows 13 and 14 of Table 5), one of the EB-based procedures produces smaller p-values. The decrease in p-values, however, is quite modest in general. These results are intuitive, given that none of SNPs shows a genotype odds ratio pattern that resembles a recessive model, under which we would have expected to see a larger gain in power by exploiting the HWE assumption.

Table 5.

The comparison of the p-values of various tests of association for specific target SNPs in the CGEMS study

		Overall
SNP	MAF	Unconstrained	Constrained	Two-step	EB1	EB2
rs4242382	0.100	3.60e − 5	2.71e − 5	2.71e − 5	3.06e − 5	3.17e − 5
rs4242384	0.099	3.42e − 5	2.75e − 5	2.75e − 5	2.82e − 5	2.82e − 5
rs1447295	0.102	1.78e − 4	1.38e − 4	1.38e − 4	1.34e − 4	1.44e − 4
rs7837688	0.097	1.29e − 5	5.24e − 6	5.24e − 6	5.65e − 6	5.67e − 6
rs11988857	0.117	2.30e − 5	2.41e − 5	2.41e − 5	1.84e − 5	1.89e − 5
rs10993994	0.365	2.64e − 3	1.22e − 3	1.22e − 3	2.54e − 3	1.57e − 3
rs9656816	0.088	1.20e − 3	5.22e − 4	5.22e − 4	8.71e − 4	9.80e − 4
rs6983267	0.489	1.04e − 2	7.68e − 3	7.68e − 3	7.65e − 3	7.60e − 3
rs4430796	0.498	9.99e − 3	3.59e − 3	3.59e − 3	3.57e − 3	3.54e − 3
rs7501939	0.421	5.37e − 3	4.32e − 4	4.32e − 4	1.33e − 3	9.07e − 4
rs7014346	0.350	5.50e − 3	4.69e − 3	4.69e − 3	4.84e − 3	4.76e − 3
rs7837328	0.394	2.48e − 3	2.33e − 3	2.33e − 3	2.41e − 3	2.38e − 3
rs1106207	0.428	3.46e − 3	3.97e − 4	3.46e − 4	5.23e − 3	2.32e − 3
rs7017300	0.131	4.83e − 5	6.65e − 5	6.65e − 5	4.21e − 5	5.21e − 5
rs4962416	0.263	9.89e − 5	6.65e − 5	6.65e − 5	1.40e − 4	1.09e − 4
rs1486567	0.231	4.26e − 2	5.13e − 2	5.13e − 2	5.48e − 2	4.91e − 2
rs10896449	0.490	0.024	0.094	0.094	0.064	0.071

4 Discussion

In this article, we propose a powerful test for genetic association in case-control studies by exploiting the common assumption of HWE for the underlying population. Unlike previous methods that have also aimed to gain efficiency for case-control association testing by exploiting HWE for the underlying population, the proposed EB procedure can data-adaptively relax the underlying constraints and thus can reduce the chance of false positive results when the HWE assumption is violated. Simulation studies as well as an application involving a genome-wide association study show that the EB procedure can maintain appropriate control over the type-I error rate for large-scale studies that would have natural deviations from HWE of varying degree across different loci. Further, our studies illustrate that the EB procedure has a major power advantage over standard case-control tests for the detection of susceptibility SNPs with effects resembling a “recessive” pattern. In addition, the closed form expression of the EB estimators and the simple corresponding variance estimation make the computation cost comparable to that of the unconstrained test in the study setting of GWAS.

The pattern of power seen for different methods under different models for genetic effects are intuitive. The constrained test gains power over its unconstrained counterpart by incorporating additional information from the departure of the observed genotype distribution in the case-control sample from the assumed HWE model for the population. If a SNP is under HWE in the population, its genotype distribution approximately follows HWE in the controls, under the assumption of rare disease. Moreover, when the effect of a SNP is multiplicative (log-additive) per copy of an allele, it can be shown that, again assuming rare disease, the HWE for the population implies HWE for the cases [Sasieni, 1997]. It is expected that when the non-multiplicative effect of a SNP is larger, so is the departure for the distribution of its genotypes from HWE, in the cases and hence in the case-enriched case-control sample. Thus, the efficiency gains for the constrained and the EB-type shrinkage procedures over the unconstrained one are expected to be increasing with the magnitude of the non-multiplicative effect of a SNP. In our simulation, under the multiplicative model for the effect of a SNP, we do not see any difference in efficiency among the methods (results not shown). Under the dominant model, which corresponds to modest departure from the multiplicative model, we observe some gain in efficiency for the constrained and the EB procedures. Under the recessive model, which corresponds to large departure from the multiplicative effect, we observe the highest gain in efficiency for the constrained and the EB procedures.

In this article, we have focused on the 2 d.f. single-SNP test of genetic association. The proposed shrinkage estimation strategy, however, can be used to improve the power of other types of genetic association tests in case-control studies. For single-SNP association testing with unknown modes of genetic effect, for example, a popular alternative to the 2 d.f. test is the MAX procedure which uses the maximum of the single-SNP Z-statistics for the additive, dominant, and recessive models as the test statistics for detecting association. For case-control studies, the power of the MAX procedure can potentially be improved by deriving the component Z-statistics by exploiting the HWE constraints for the genotype distribution of the controls. In particular, the proposed shrinkage estimation strategy can be used to estimate the disease-genotype odds ratios and their standard errors under alternative modes of genetic effect and hence to derive the corresponding Wald statistics.

The proposed shrinkage estimation strategy can also potentially be used to improve the power of case-control genetic association tests involving loci with more than two alleles. The general strategy would involve first estimating disease-genotype odds ratios, once using the empirical genotype frequency for the controls, once assuming HWE constraints for the controls, then combining the two estimators using the empirical-Bayes-type weighting strategy proposed here. Further research is merited on the development of such multi-allelic tests, especially in the context of haplotype-based association studies, where the additional complexity arises from the fact that haplotype-phase information is typically missing from the observable genotype data.

In conclusion, we believe that the proposed shrinkage estimation strategy, considering its power, robustness, generalizability, and computational simplicity, overall is a promising approach for detecting genetic associations from case-control studies.

APPENDIX

A.1 DERIVATION OF Δ̂

The likelihood function for controls, L₀, which is proportional to $p_{00}^{n_{00}}{p}_{01}^{n_{01}}{p}_{02}^{n_{02}}$, can be expressed in terms of θ and ω as

$$L_0=\frac{e^{\theta (n_{00}+n_{02})}{e}^{\omega (n_{00}+n_{02})}}{{(1+e^{\theta }\text{cosh}\omega )}^{n_{0+}}},$$

where the hyperbolic cosine $\text{cosh}\omega =\frac{e^{\omega }+e^{-\omega }}{2}$. Taking the derivative of the logarithm of L₀ with respect to ω, we get

$$\frac{\partial \text{log}{L}_0}{\partial \omega }=(n_{00}-n_{02})-\frac{n_{0+}\text{sinh}\omega }{e^{-\theta }+\text{cosh}\omega },$$

where the hyperbolic sine $\text{sinh}\omega =\frac{e^{\omega }-e^{-\omega }}{2}$. Equating the last equation to zero, taking the derivative on both sides with respect to θ, and letting θ = 0, we get

$$k=\frac{\partial \widehat{\omega }}{\partial \theta }(\theta =0)=\frac{n_{00}-n_{02}}{(n_{00}-n_{02})\text{sinh}\widehat{\omega }-n_{0+}\text{cosh}\widehat{\omega }}$$

The unconstrained ML estimator β̂ = β̂(θ = θ̂) in (4) can be expressed in terms of θ̂ and ω̂ as

$${\widehat{\mathit{\beta }}}^T=\left(\widehat{\theta }+\widehat{\omega }+\text{log}(\frac{n_{11}}{2n_{10}}),2\widehat{\omega }+\text{log}(\frac{n_{12}}{n_{10}})\right)$$

Thus we have

$$\widehat{\mathrm{\Delta }}=\frac{\partial {\widehat{\mathit{\beta }}}^T}{\partial \theta }(\theta =0)=(1+k,2k)$$

A.2 VARIANCE CALCULATION FOR THE EB1 ESTIMATOR

We note that the total numbers of cases and controls, n₀₊ and n₁₊, are fixed by the study design. The cell counts for genotype AA, Aa, and aa both in cases and controls follow a multinomial distribution and the cases are independent of the controls. Then the variance-covariance matrix for the cell count vector n = (n₁₁, n₁₂, n₀₁, n₀₂)^T, denoted by B, is given by

$$B=\left(\begin{array}{cccc}\hfill n_{11}(1-\frac{n_{11}}{n_{1+}})\hfill & \hfill -\frac{n_{11}{n}_{12}}{n_{1+}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\frac{n_{11}{n}_{12}}{n_{1+}}\hfill & \hfill n_{12}(1-\frac{n_{12}}{n_{1+}})\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill n_{01}(1-\frac{n_{01}}{n_{0+}})\hfill & \hfill -\frac{n_{01}{n}_{02}}{n_{0+}}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{n_{01}{n}_{02}}{n_{0+}}\hfill & \hfill n_{02}(1-\frac{n_{02}}{n_{0+}})\hfill \end{array}\right).$$ (7)

We notice that the matrix (V̂_β̂ + Δ̂^Tθ̂θ̂^TΔ̂)⁻¹ in (5) is of the form (V + uu^T)⁻¹. From matrix algebra, we know that ${(V+{\mathit{\text{uu}}}^T)}^{-1}=V^{-1}-\frac{(V^{-1}u)(u^T{V}^{-1})}{1+u^T{V}^{-1}u}$. Then we can simplify (5) as

$${\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}1}=\widehat{\mathit{\beta }}-{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}\left({\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}-\frac{{\widehat{\theta }}^2{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}{\widehat{\mathrm{\Delta }}}^T\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}}{1+{\widehat{\theta }}^2\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}{\widehat{\mathrm{\Delta }}}^T}\right)(\widehat{\mathit{\beta }}-{\widehat{\mathit{\beta }}}^0)={\widehat{\mathit{\beta }}}^0+\frac{{\widehat{\theta }}^2{\widehat{\mathrm{\Delta }}}^T\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}}{1+{\widehat{\theta }}^2\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}{\widehat{\mathrm{\Delta }}}^T}(\widehat{\mathit{\beta }}\mathit{-}{\widehat{\mathit{\beta }}}^0).$$ (8)

Since V̂_β̂ and Δ̂ approach zero at the rate of O(1/n), we may ignore the variation in V̂_β̂ and Δ̂ and treat them as constants while computing the variance-covariance matrix of the EB1 estimator. Then the EB1 estimator can be viewed as a fixed function of the cell count vector n. Take the derivative of the EB1 estimator with respect to the cell count vector n. The corresponding gradient matrix A₁ is $A_1=(\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}1}}{\partial n_{11}},\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}1}}{\partial n_{12}},\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}1}}{\partial n_{01}},\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}1}}{\partial n_{02}})$. The relevant derivatives are as follows: for j = 1, 2,

$$\begin{array}{c}\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}1}}{\partial n_{1j}}=\frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{1j}}+\frac{{\widehat{\theta }}^2{\widehat{\mathrm{\Delta }}}^T\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}}{1+{\widehat{\theta }}^2\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}{\widehat{\mathrm{\Delta }}}^T}(\frac{\partial \widehat{\mathit{\beta }}}{\partial n_{1j}}-\frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{1j}})\hfill \\ \frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}1}}{\partial n_{0j}}=\frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{0j}}+{\widehat{\mathrm{\Delta }}}^T\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}\left[\frac{2\widehat{\theta }}{{(1+{\widehat{\theta }}^2\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}{\widehat{\mathrm{\Delta }}}^T)}^2}\frac{\partial \widehat{\theta }}{\partial n_{0j}}(\widehat{\mathit{\beta }}-{\widehat{\mathit{\beta }}}^0)+\frac{{\widehat{\mathit{\theta }}}^2}{(1+{\widehat{\theta }}^2\widehat{\mathrm{\Delta }}{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}}^{-1}{\widehat{\mathrm{\Delta }}}^T)}(\frac{\partial \widehat{\mathit{\beta }}}{\partial n_{0j}}-\frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{0j}})\right];\hfill \\ \frac{\partial \widehat{\mathit{\beta }}}{\partial n_{11}}=\frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{11}}=\left(\begin{array}{c}\frac{1}{n_{11}}+\frac{1}{n_{1+}-n_{11}-n_{12}}\hfill \\ \hfill \frac{1}{n_{1+}-n_{11}-n_{12}}\hfill \end{array}\right);\frac{\partial \widehat{\mathit{\beta }}}{\partial n_{12}}=\frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{12}}=\left(\begin{array}{c}\hfill \frac{1}{n_{1+}-n_{11}-n_{12}}\hfill \\ \frac{1}{n_{12}}+\frac{1}{n_{1+}-n_{11}-n_{12}}\hfill \end{array}\right);\hfill \\ \frac{\partial \widehat{\mathit{\beta }}}{\partial n_{01}}=\left(\begin{array}{c}-\frac{1}{n_{01}}-\frac{1}{n_{0+}-n_{01}-n_{02}}\hfill \\ \hfill -\frac{1}{n_{0+}-n_{01}-n_{02}}\hfill \end{array}\right);\frac{\partial \widehat{\mathit{\beta }}}{\partial n_{02}}=\left(\begin{array}{c}\hfill -\frac{1}{n_{0+}-n_{01}-n_{02}}\hfill \\ -\frac{1}{n_{02}}-\frac{1}{n_{0+}-n_{01}-n_{02}}\hfill \end{array}\right);\hfill \\ \frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{01}}=\left(\begin{array}{c}-\frac{1}{2n_{02}+n_{01}}-\frac{1}{2n_{0+}-n_{01}-2n_{02}}\hfill \\ -\frac{2}{2n_{02}+n_{01}}-\frac{2}{2n_{0+}-n_{01}-2n_{02}}\hfill \end{array}\right);\frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{02}}=\left(\begin{array}{c}-\frac{2}{2n_{02}+n_{01}}-\frac{2}{2n_{0+}-n_{01}-2n_{02}}\hfill \\ -\frac{4}{2n_{02}+n_{01}}-\frac{4}{2n_{0+}-n_{01}-2n_{02}}\hfill \end{array}\right);\hfill \\ \frac{\partial \widehat{\theta }}{\partial n_{11}}=\frac{\partial \widehat{\theta }}{\partial n_{12}}=0;\frac{\partial \widehat{\theta }}{\partial n_{01}}=-\frac{1}{n_{01}}-\frac{1}{2(n_{0+}-n_{01}-n_{02})};\frac{\partial \widehat{\theta }}{\partial n_{02}}=\frac{1}{2n_{02}}-\frac{1}{2(n_{0+}-n_{01}-n_{02})}.\hfill \end{array}$$

The variance-covariance matrix of the EB1 estimator, denoted by Σ_EB1, is given by $A_1{\mathit{\text{BA}}}_1^T$, where T represents the matrix transpose.

A.3 VARIANCE CALCULATION FOR THE EB2 ESTIMATOR

The derivation of the variance for the EB2 estimator follows that of the EB1 estimator. Note that (6) is also a function of the cell count vector n. Take the derivative of the EB2 estimator with respect to the vector n. The corresponding gradient matrix $A_2=(\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}2}}{\partial n_{11}},\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}2}}{\partial n_{12}},\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}2}}{\partial n_{01}},\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}2}}{\partial n_{02}})$. The relevant derivatives are

$$\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}2}}{\partial n_{1j}}=\frac{\partial \widehat{\mathit{\beta }}}{\partial n_{1j}};\frac{\partial {\widehat{\mathit{\beta }}}_{\mathit{\text{EB}}2}}{\partial n_{0j}}=\frac{\partial \widehat{\mathit{\beta }}}{\partial n_{0j}}-[\frac{\partial M}{\partial n_{0j}}(\widehat{\mathit{\beta }}-{\widehat{\mathit{\beta }}}^0)+M(\frac{\partial \widehat{\mathit{\beta }}}{\partial n_{0j}}-\frac{\partial {\widehat{\mathit{\beta }}}^0}{\partial n_{0j}})],$$

and

$$\frac{\partial M}{\partial n_{0j}}=\left(\begin{array}{cc}\hfill -\frac{2{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}\mathit{\text{Aa}}}\widehat{\theta }{\widehat{\mathrm{\Delta }}}_{\mathit{\text{Aa}}}^2}{{({\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}\mathrm{\text{Aa}}}+{\widehat{\theta }}^2{\widehat{\mathrm{\Delta }}}_{\mathit{\text{Aa}}}^2)}^2}\frac{\partial \widehat{\theta }}{\partial n_{0j}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\frac{2{\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}\mathit{\text{aa}}}\widehat{\theta }{\widehat{\mathrm{\Delta }}}_{\mathit{\text{aa}}}^2}{{({\widehat{\mathrm{V}}}_{\widehat{\mathit{\beta }}\mathit{\text{aa}}}+{\widehat{\theta }}^2{\widehat{\mathrm{\Delta }}}_{\mathit{\text{aa}}}^2)}^2}\frac{\partial \widehat{\theta }}{\partial n_{0j}}\hfill \end{array}\right)\text{ for }j=1,2,$$

where $\frac{\partial \widehat{\beta }}{{\partial }_{n_{0j}}},\frac{\partial {\widehat{\beta }}^0}{{\partial }_{n_{0j}}},\text{ and }\frac{\partial \widehat{\theta }}{{\partial }_{n_{0j}}}$ are computed in Appendix A.1.

The variance-covariance matrix of the EB2 estimator, denoted by Σ_EB2, is computed as $A_2{\mathit{\text{BA}}}_2^T$, where B is shown in Appendix A.1.