Quantitative Proton Magnetic Resonance Spectroscopy and Spectroscopic Imaging of the Brain: A Didactic Review

Abstract

This article presents background information related to methodology for estimating brain metabolite concentration from Magnetic Resonance Spectroscopy (MRS) and Magnetic Resonance Spectroscopic Imaging (MRSI) measurements of living human brain tissue. It reviews progress related to this methodology with emphasis placed on progress reported during the past ten years. It is written for a target audience composed of radiologists and MRI technologists. It describes in general terms the relationship between MRS signal amplitude and concentration. It then presents an overview of the many practical problems associated with deriving concentration solely from absolute measured signal amplitudes and demonstrates how a various signal calibration approaches can be successfully used. The concept of integrated signal amplitude is presented with examples that are helpful for qualitative reading of MRS data as well as for understanding the methodology used for quantitative measurements. The problems associated with the accurate measurement of individual signal amplitudes in brain spectra having overlapping signals from other metabolites and overlapping nuisance signals from water and lipid is presented. Current approaches to obtaining accurate amplitude estimates with least squares fitting software are summarized.

1. Introduction

Magnetic Resonance Spectroscopy (MRS) detects magnetic resonance signals produced by atomic nuclei located within molecules in living tissue. Quantification of the MRS signal amplitude can provide a means of estimating the tissue concentration of the signal generating molecules. The molecules that produce readily detected MRS signals tend to have relatively low molecular weight and are able to move freely within the fluid compartments of biological tissues. Many such molecules are components of metabolic pathways and MRS is thereby sensitive to certain aspects of tissue metabolism.

Signal quantitation has increased significance for MRS compared with many other forms of biomedical magnetic resonance. The majority of other MR techniques produce reasonably high resolution images enabling the trained reader to identify image contrast differences that are related to known anatomy or to lesions by visual examination. This form of visual interpretation does not translate well to MRS because of its limited ability to form images. It has never been feasible to perform a sufficient number of single voxel MRS (SV-MRS) acquisitions at different brain regions to build an image. Magnetic resonance spectroscopic imaging (MRSI) provides some improvement in this regard. However MRSI’s spatial resolution and volume coverage are considerably limited compared to other forms of MRI making it difficult to visually interpret MRSI results. Accordingly, the importance of expressing MRS results in a numerical format (e.g. as a table of derived metabolite concentrations) has been emphasized since the emergence of MRS as a medical evaluation technique (1).

This review article will summarize the problems and solutions related to quantitative measurement of MRS signal strength and to the interconversion between MRS signal strength and metabolite concentration. It is written for a target audience of radiologists and MRI technologists. While emphasis is placed on progress made during the past 10 years, considerable attention is devoted to background material to help the target reader understand the many complex issues that are involved. Similar recent articles written by other authors are available (2, 3). The majority of progress related to MRS quantitation has been based on SV MRS technology. Recent years have seen an increased emphasis on the clinical use of MRSI. For this reason this article pays particular attention to MRSI signal quantitation. The presentation will be limited to discussion of ¹H MRS signal quantitation because ¹H MRS is far more routinely performed in a medical imaging context compared with ³¹P- or ¹³C-MRS.

While this article will focus on the problem of deriving numerical estimates of metabolite concentration from MRS, it is worth noting at the outset that reporting of metabolite concentrations may not always be an absolute requirement for clinical utility. Indeed, it is both feasible and useful to develop semiquantitative approaches to MRS evaluation in which the trained reader identifies normal and abnormal patterns of signals in spectra. Disease can sometimes produce large changes in metabolite levels that can be readily identified by a trained reader without conversion of the underlying spectral information into numerical format. Examples are the profound elevation of lactate signal levels in ischemic brain tissue and the elevated choline signal levels produced by some neoplastic or inflamed tissues. Nevertheless, signal level measurement is still important for the following reasons. One must consider that the identification of more subtle disease, such as psychiatric illness, might benefit from quantitative approaches. Living tissues, whether normal or abnormal, tend to use similar metabolism and MRS differences between diseased and normal brain tissues may be very difficult to detect without a complete quantitative approach. MRS signal quantitation is very important in the context of research. The general goals of clinical research are to learn about disease mechanism and to discover effective treatments. For these purposes a reliable metabolite concentration measurement that can be compared between patients and across time points is highly desirable.

2. General approach to metabolite signal quantitation

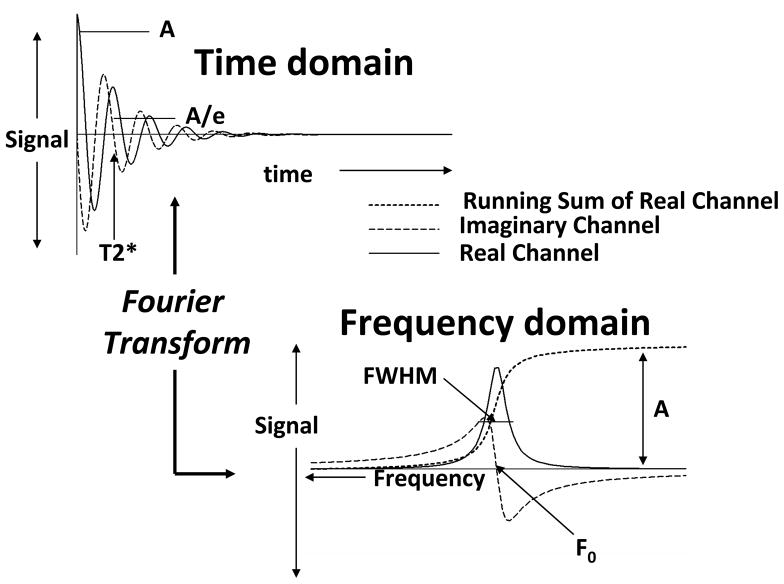
A metabolite’s tissue concentration is related to the integrated amplitude of the MRS signal it produces. Integrated amplitude is the area under the MRS signal curve (Figure 1). The terms “integrated intensity” or “intensity” or “signal level” or simply “signal” are frequently used as synonyms for “integrated amplitude”. While MRS signals are usually acquired in the time domain as free induction decays or echoes, they are usually viewed and analyzed in the frequency domain. The frequency domain representation is derived from the acquired time domain data by the Fourier Transform (FT). This process is convenient because the MRS data collection is most efficient when performed in the time domain but the evaluation and analysis of the results are best done when the data are expressed as a series of signals in a frequency spectrum. The ideal time domain MRS signal (S_R and S_I) is an exponentially decaying function of time (t) with oscillatory modulation at specific frequency (Figure 1).

Figure 1.

Schematic illustration of time domain and frequency domain MRS signals and their properties. See text for further explanation.

$$S_R(t)=Acos(F_{0}t+\phi )e^{-t/T{2}^{\ast }}{S}_I(t)=\pm Asin(F_{0}t+\phi )e^{-t/T{2}^{\ast }}$$ [1]

φ is the phase, which for simplicity is assumed to be zero until phase correction is discussed (see below), and A is the strength of the signal at time zero. The frequency domain representation of this ideal MRS signal has a shape described by the complex-valued “Lorentzian” lineshape

$$S_R(f)=H\frac{W}{W^2+{(F_0-f)}^2}{S}_I(f)=\pm H\frac{F_0-f}{W^2+{(F_0-f)}^2}$$ [2]

H is the height of the signal. The signal’s center position, F₀, identifies the atomic nucleus and the molecule that produced the signal. W is signal’s full width at half maximum (FWHM) is related to the time domain signal decay rate (T2*) as follows.

$$W=\frac{1}{\pi T{2}^{\ast }}$$ [3]

Both the time domain and frequency domain signal representations are “complex” functions that have “real” (S_R(t), S_R(f)) and “imaginary” (S_I(t), S_I(f)) components. “Real”, “imaginary” and “complex” are terms that are widely used in physics and engineering to describe processes that oscillate or have “frequency”. It is usually the real frequency domain signal that it presented on the scanner console, although both the real and imaginary signals have importance for signal quantitation. The integrated signal amplitude is specifically defined as the integral (area under the curve) of the real part of the frequency domain signal (Figure 1), which is equivalent to the initial value (A) of the time domain signal.

The integrated signal amplitude produced by the atomic nuclei of metabolite M is directly proportional to the number (moles) of signal generating molecules (N_M) in the volume of brain (V_B) that is being examined.

$$A_M=K_G{N}_M$$ [4]

K_G is a “global” constant of proportionality that encapsulates a number of factors discussed in the next section. In some instances there can be concern about whether a metabolite is “visible” to MRS. For instance a metabolite that is bound to slowly moving macromolecules may be invisible to MRS because of a very short T2. This visibility problem is not considered at all in this article. When amount (numbers of molecules or concentration) of metabolite is discussed, amount of MRS “visible” metabolite is implied. The tissue concentration of the metabolite is

$$C_M=\frac{N_M}{V_B}$$ [5]

Several different unit systems can be used to report metabolite concentration and certain unit systems work more naturally for specific quantitation procedures (4). Here for the sake of generality V_B can refer to the volume (ml or cm³) or the mass (g) of brain tissue being studied. It could also refer to the volume, mass or amount of water in the brain tissue being studied. A simple expression for the concentration in terms of integrated signal amplitude can be obtained from [4] and [5]

$$C_M=\frac{A_M}{K_G{V}_B}$$ [6]

This summary makes determining a metabolite’s concentration from the area under the MRS signal it produces seem very simple. One needs only to 1) measure the real component signal area, 2) determine the value of the global constant and 3) establish how much brain volume is being sampled. Unfortunately there are a number of very complex matters that must be considered to accomplish each of these steps. Measurement of signal area is very challenging because of complex metabolite signal characteristics and overlap between various signals. Determining the value of the global constant (K_G) is far from trivial because it is dependent on many complex interrelated factors that are specific to the MRI scanner system (both hardware and software) and the pulse sequence that is used to acquire the data and the patient’s physical characteristics. Determining the brain volume is somewhat more straightforward but can still have potential pitfalls related to MRS volume localization procedures.

3. Signal Calibration

The global constant (K_G) defined in the previous section encapsulates a number of multiplicative factors that are described in this section.

MRI scanners are (unfortunately) not designed to measure absolute signal intensity using a standard system of electric measurement units. In many MRI scanners, the electronic receiver system introduces a “receive gain”, or “amplification” (G_A) into the signal before it is converted to digital form. MR systems tend to amplify signals arbitrarily to optimize conversion of the analog signal arriving from the radio frequency (RF) receive coil system into a digital record. The digital processing stream may also incorporate various arbitrary scale factors and this may be considered as a component of G_A. As a result, G_A may vary from study to study, even if the same subject is being studied. This situation is complicated by the fact that the receive gain used in a particular examination is often not directly reported to the user. From an MRS perspective, the use of uncontrolled or hard to find gain factors seems illogical, but one has to remember that the design of the modern MRI scanner is targeted at forming images in which all that practically matters is accurate rendering of relative signal at different points in the imaged space. Because relative signal is all that is necessary for diagnostic MRI, there is no reason to control the receive gain or even to report its value.

A factor, G_RC, expresses that the sensitivity of the receive RF coil system to detect signal produced by a particular brain volume must also be considered. G_RC depends on 1) subject specific parameters 2) Static magnetic field strength (B0), 3) the location of the volume of interest in the brain and 4) the design of the coil system. B1 field imaging allows G_RC to be estimated (5, 6), but such measurements are usually are not made because they are subject specific and consume valuable scanner and patient time.

The increasing popularity of parallel imaging techniques for accelerating the acquisition of MRI data has introduced new technical complications for MRS quantitation. In general each coil in the parallel array has a different distance from the MRS volume element and produces a spectrum having its own unique signal strength and phase characteristics. It remains somewhat unclear how to optimally recombine the spectral information arriving from each of the coils in the array although several approaches have been proposed (7–9).

A very complex factor, G_T, expresses how efficiently the transmitter coil and the RF pulses in pulse sequence excite a particular signal. This factor depends on the detailed designs of all RF pulses in the pulse sequence. These details include the RF pulse amplitudes, shapes (both temporal and phase characteristics) and frequencies relative to the signal’s characteristic frequency. The G_T term encapsulates all pulse sequence design features related to the RF pulses, including volume selection (e.g. spin echo, stimulated echo, volume saturation), water suppression and spectral editing. Usually some form of prescan is performed to optimize the value of G_T before the MRS measurement is run. From this perspective it is sometimes reasonable to assume that G_T equals one, but caution must always be exercised, particularly in MRSI studies. For MRSI studies, it is specifically important to consider that a particular metabolite signal may have an absolute frequency dependent on brain location (because it is usually not possible to make the B0 completely homogeneous over the entire volume of brain being examined), while the RF pulse frequencies will be constant over the entire volume. Furthermore the RF transmitter coil may have relevant spatial dependencies. Therefore variation of G_T with voxel location should be anticipated. An example is that inopportune (anatomy-induced) B0 shift in some location could create a situation in which the entire spectrum is shifted with respect to the water suppression pulse frequency causing the water suppression pulse sequence component to suppress metabolite signal instead of water signal.

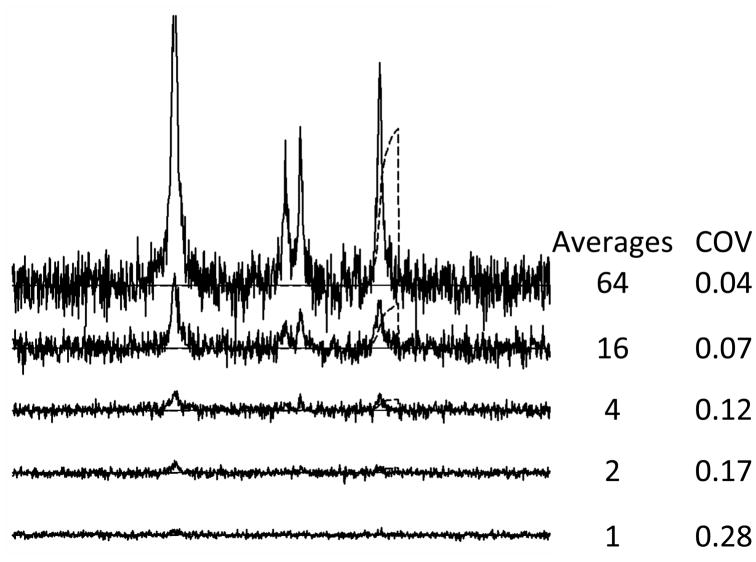
Signal averaging is used in virtually all MRS studies because of the prominence of noise. For typical MRS-acquisition conditions, the noise level is often similar in magnitude to the metabolite signal levels. Noise is thereby a limiting factor in determining metabolite signal amplitude. Here, the term “noise” specifically means randomly fluctuating “signal” that would be present in the absence of artifacts associated physiological characteristics, scanner performance or other nonideal factors. Figure 2 illustrates typical MRS data characteristics with a computer-simulated spectra composed of the principal signals of water (Wat), choline (Cho), creatines (Cre) and N-acetylaspartate (NAA) to which random frequency independent Gaussian noise has been added. It is apparent from the 1 average spectrum shown in the figure that the noise interferes with signal identification and determination of the integrated signal amplitudes. While noise performance can depend on the MRI scanner’s system design, much of the noise detected in the typical MRI or MRS study derives from the electrical properties of living tissue and there is not much that can be done to ameliorate it. The only practical way of dealing with noise is to increase the Signal-to-Noise Ratio (SNR) by averaging the signals obtained in repeated measurements. When this is done the signal grows in proportion to the number of averages and the noise grows in proportion to the square root of the number of averages as is illustrated in Figure 2. Therefore use of signal averaging causes the measured signal level to increase in proportion to the number of individual FIDs or echos (N_AV) that are collected. The figure also illustrates that the precision of the NAA amplitude determination measured with the coefficient of variance (COV) improves as the number of averages increases. One practical limitation to signal averaging arises when substantial physiological motion is present during the collection of the signal averaged data. Motion may produce variations in signal phase and frequency during the averaging process and less than the expected SNR enhancement may be realized due to destructive averaging (10).

Figure 2.

MRS signal averaging. Number of averages used for each simulation are shown to the right of each simulated spectrum. Coefficient of variance (COV) calculated as standard deviation divided by mean. COV values were determined by repeating each simulation 100 times, measuring the amplitude of the simulated NAA signal by integration as shown and then determining the mean and standard deviation over the 100 amplitude measures.

The last of the primary factors, G_RLX, accounts for the T1 and T2 relaxation. In general terms, the signal amplitude depends on pulse sequence’s TE parameter and the T2 according to

$$A(TE)=A(0)e^{-TE/T2}$$ [7]

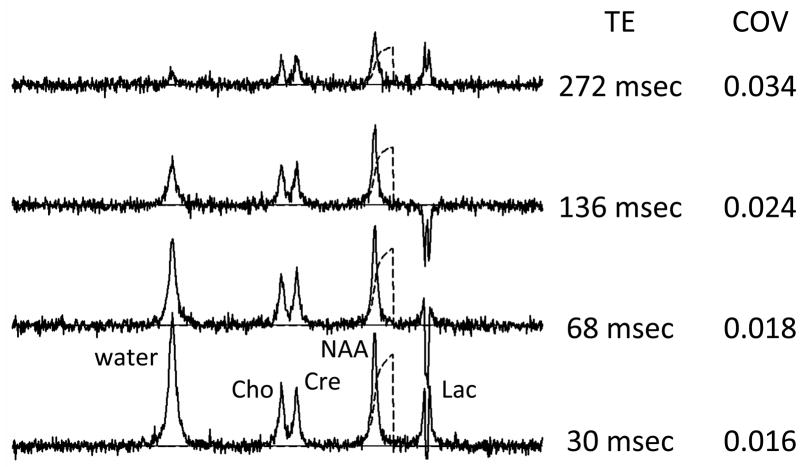
A0 is the signal amplitude that would be measured in the absence of T2 relaxation and TE is the characteristic time to echo for the pulse sequence. Figure 3 illustrates the appearance of TE-related signal decay (T2 relaxation) with a series of computer simulated spectra containing the principal signals of Wat, Cho, Cre and NAA for different TE times. The integrated signal amplitudes decay as TE is increased. The behavior of the lactate signal is discussed below. The noise is independent of TE, so that the SNR decreases with increasing TE. The precision of the NAA amplitude measurement (assessed with the COV) decreases with increasing TE because of the corresponding SNR decrease. For this reason it is generally desirable to acquire brain spectra at the lowest available TE. Several recent publications have demonstrated that very short TE acquisitions have advantages for metabolite concentration quantitation (11–13), but another report comes to a different conclusion (14). This difference undoubtedly is related to the measurement conditions, which underscores the complexity associated with MRS signal amplitude measurements. All signals within the spectrum may not have identical relaxation times and care should be taken with respect to inferring a direct relationship between signal amplitude and metabolite concentration when the pulse sequence has a finite TE. In Figure 3 the water signal decays with TE more quickly than the metabolite signals do because the simulation used a water T2 value that is 3-fold lower than the metabolite T2’s, which is typical for brain. Long TE (eg 136 – 282 msec) was used for some of the first brain MRS studies because system instability created artifact related to the water signal strength and also because of analog to digital conversion limitations. Long TE conditions eliminated the problems because of its water suppression properties. Indeed, long TE is sometimes still used as a means of suppressing unwanted water signal, particularly in MRSI applications (8, 15). However use of this form of water suppression complicates quantitative analysis because knowledge of the metabolite signal T2 value becomes more important and because of SNR loss. The relaxation term G_RLX also includes potential contributions from T1 relaxation that influence signal quantitation.

Figure 3.

Computer-simulated MRS data for various TE settings for a spin echo pulse sequence. COV values were determined as described in Figure 2 caption.

While using T1 and T2 relaxation expressions (e.g. [7]) to correct for the effects of relaxation seems straightforward, there are significant practical limitations. One limitation has to do with the fact that the relaxation correction function must be derived for each pulse sequence. [7] is completely correct only for the specific case of a basic spin echo pulse sequence. It is not even completely correct for the typical volume localizing pulse sequence that is used in SV-MRS. A more accurate rendering requires exact knowledge of all pulse sequence parameters. A second limitation relates to the fact that all metabolite signals may not have identical T1 and T2 relaxation time values. Recent publications report characteristic T1 and T2 values for brain tissue in certain populations and but also give evidence suggesting that metabolite signal relaxation times vary with physiological factors such as age and brain location (16–19). This suggests that T1 and T2 of the relevant signals should be measured to avoid a biased metabolite concentration determination. Approaches for measurements of metabolite signal relaxation times contemporaneously with SV-MRS on an individual subject basis have been reported (6, 20) but are rarely used. Usually it is necessary to use the available time for signal averaging to obtain a single water-supressed spectrum with particular TR and TE settings and there is no additional time available to make measurements with additional TR and TE settings from which metabolite T1 and T2 information could be derived. Note however this is not the case for water strength. The strength of its signal permits relaxation measurements to be completed rather quickly and therefore water signal relaxation properties can be known if necessary.

The foregoing discussion gives a better approximation of the global constant

$$K_G=G_A(p,s,ps)G_{RC}(p,s,r)G_T(p,s,ps,r,F_0^M)G_{\mathit{RLX}}(T{1}^M,T{2}^M,ps)N_{AV}$$ [8]

Many experimental factors including the patient (p), the MRI scanner system (s), the details of the pulse sequence (ps), the brain location being evaluated (r ), the absolute frequency of the metabolite signal being evaluated ( $F_0^M$) and the relaxation times of the metabolite signal being evaluated have a potential influence on the signal amplitude that is actually measured. Only one of the factors (N_AV) in [8] is readily known, readily generalizable, readily measureable, or easy to compute from known experimental parameters for a particular MRS measurement. The complex dependencies in [8] show why quantitation of MRS signal level to obtain metabolite concentration has been so problematic.

The approach to dealing with the complexity described in the previous paragraphs has been to use “signal calibration”. Here the measured brain metabolite signal amplitudes are calibrated against a “reference signal” that is produced by a known concentration of metabolite or some other material. If appropriate care is taken to match the conditions under which the reference signal is acquired to those used for the brain signals, the unknown factors can be eliminated as follows. Expressions for the reference (A_R) and metabolite signal amplitudes (see [4], [5] and [8]) are

$$A_M=G_A(p,s,ps)G_{RC}(p,s,r)G_T(p,s,ps,r,F_0^M)G_{\mathit{RLX}}(T{1}^M,T{2}^M,ps)N_{AV}^M{C}_M{V}_B$$ [9]

$$A_R=G_A(p,s,ps)G_{RC}(p,s,r)G_T(p,s,ps,r,F_0^R)G_{\mathit{RLX}}(T{1}^R,T{2}^R,ps)N_{AV}^R{C}_R{V}_R$$ [10]

If the reference signal and brain signal measurement conditions are closely enough matched, V_B will equal V_R and the terms G_A, G_RC and G_T, will be the same for both measurements. Accordingly ratio of the brain metabolite and reference signals amplitudes will be

$$\frac{A_M}{A_R}=\frac{G_{\mathit{RLX}}(T{1}^M,T{2}^M,ps)N_{AV}^M{C}_M}{G_{\mathit{RLX}}(T{1}^R,T{2}^R,ps)N_{AV}^R{C}_R}$$ [11]

Rearrangement leads to an expression for the brain metabolite concentration in terms of the brain signal to reference signal ratio

$$C_M=\frac{A_M}{A_R}=\frac{G_{\mathit{RLX}}(T{1}^R,T{2}^R,ps)}{G_{\mathit{RLX}}(T{1}^M,T{2}^M,ps)}\frac{N_{AV}^R}{N_{AV}^M}{C}_R$$ [12]

[12] permits estimation of brain metabolite concentration from measured parameters. Knowledge of the relax factors (G_RLX) is sometimes problematic due to practical difficulties associated with relaxation time measurements (see above). Accordingly some calibration approaches report only normalized concentration

$$C_M^{\mathit{NORM}}=\frac{A_M}{A_R}\frac{N_{AV}^R}{N_{AV}^M}{C}_R$$ [13]

which is equivalent to the true concentration multiplied by a relaxation factor (21, 22)

$$C_M^{\mathit{TRUE}}=\frac{G_{\mathit{RLX}}(T{1}^R,T{2}^R,ps)}{G_{\mathit{RLX}}(T{1}^M,T{2}^M,ps)}{C}_M^{\mathit{NORM}}$$ [14]

The reference signal may be generated by a metabolite, by water or by some other chemical compound in a phantom object (23). Relevant literature is somewhat confusing with regard to the terms “internal” and “external” in relation to the reference signal. In this article the term “external reference signal” is used to describe the situation in which the reference signal is produced by a phantom object that is external to the brain. The reference signal may also be generated by a metabolite or by water that is within the brain, in which case the term “internal reference signal” is used.

The phantom object used to generate an external reference signal may be a small object that fits within the RF coil system with the patient’s head or it may be a larger phantom object whose signal is measured before or after the patient examination. This article will use the terms “near-brain phantom” to describe a phantom object that that fits within the RF coil system with the patient’s head and “brain-replacement phantom” to describe a phantom object that is measured before or after the patient examination.

Calibration using near-brain phantoms seems to be a straightforward approach, but is used infrequently. While this method effectively controls for receive coil loading, there is often not sufficient space available inside modern day close fitting head RF coils for a phantom having dimensions on the order of a typical MRS voxel. Furthermore when such RF coil systems are used, near-brain phantoms tend to be placed in close proximity to the RF coil elements where substantial spatial B1 inhomogeneity exists and the reproducibility of the phantom signal level may become limited by the ability to accurately reposition the phantom from study to study. Another negative feature of near-brain phantoms is that they tend to perturb the B0 magnetic field in the space surrounding them and this may introduce difficulty with attaining the necessary B0 homogeneity in regions of brain that are physically close to the phantom. Similarly the head perturbs the B0 magnetic field outside of it and it may not be possible to attain adequate B0 homogeneity within the phantom for accurate reference signal measurements. Many of the negative features of near-brain phantoms can be eliminated with the use of small near-brain phantoms. It is possible to realize the benefits of near-brain phantom signal referencing by the addition of internal water signal referencing approach (see below) even if the near-brain phantom is small compared with the MRS voxel size (24).

Calibration using a brain-replacement phantom object avoids the disadvantages of the internal phantom methodology by using a head-sized phantom that fits within and fills the RF coil. However it suffers from the disadvantage that it may load the RF coil system differently from the head or its signal may be acquired with a different receive gain than the brain spectrum. Care must be taken to avoid either of these problems. The use of a brain-replacement phantom also requires a separate study, which can be suboptimal in busy imaging centers. Furthermore there is no clear understanding about when, with respect to the patient study, or how frequently the calibrating measurement of the brain replacement phantom should be made.

The use of either type of phantom object has additional disadvantages. Even if brain metabolites are used to produce the phantom reference signals, it is difficult to match the phantom signal relaxation times to the brain signal relaxation times and the relaxation correction factor in [12] is not necessarily one for this reason. The use of phantoms of either type may also be limited by the potential for injury or chemical toxicity in the event of breakage or leakage. It is also important to consider whether a phantom is stable over the time period (perhaps years) that is needed to complete a study. The phantom’s solvent may slowly evaporate or the signal generating metabolites in the phantom may change over time as a result of mirco-organism activity. Either of these may lead to undesirable changes in the absolute value of the reference signal amplitude over time. If the phantom will be used in a multiple center study it is also important to control phantom production to assure that the phantoms used at each participating center are equivalent.

Calibration against an internal signal is used far more frequently than is calibration against an external phantom signal. This is undoubtedly due to the many practical disadvantages of phantom calibration that are identified above. Typically the internal reference signal is either the principal Cre signal (3.05 ppm) or the water signal (4.69 ppm). When Cre is used as a reference signal it is more common to report results as signal amplitude ratios (ie NAA/Cre) although it is feasible to estimate the unknown metabolites concentration with [12] and estimates of the brain Cre concentration and relaxation times. If water signal is used as a calibration signal, its amplitude must be measured by performing a separate measurement in the same brain region without using water suppression. This requirement limits the use of brain water signal calibration in MRSI studies that use conventional phase encoding because it mandates the collection of a time-consuming “water reference” MRSI acquisition without water suppression. Recently this limitation has been overcome through the use fast MRSI acquisition technology for both long TE MRSI (21, 25) and short TE MRSI (12). When brain water signal is used as reference signal it is routine to assume a brain water concentration and use this in [12] to estimate the brain metabolite concentrations, although it is also feasible to express the results as signal ratios.

Water and Cre calibration approaches each have their own positive and negative features. Cre referencing has the advantage of using a well-defined and typically very sharp signal that is part of the routinely collected spectrum. Negative features include that the Cre signal amplitude measurement can be limited by overlap with other signals (primarily the Cho signal) or by noise given that it tends to be the weakest of the prominent signals of the water suppressed spectrum. It is also now clear from MRSI studies that Cre signal level is not as uniform throughout the normal brain (22) as once was asserted. More significantly, Cre referencing makes an implicit, but largely unsubstantiated, assumption that the Cre levels do not change with disease or other physiological characteristics. Water referencing has the advantage of using a very strong signal that can be quickly acquired as a reference, although this must be done in a separate measurement without water suppression. At least one MRI manufacturer (GE Medical Systems) provides an MRS acquisition package that automatically collects a water reference signal for SV-MRS and uses this signal for calibration (26). Another positive feature of water referencing is that measurement of water signal can be made so quickly that is possible to measure the water T1 and T2 values and correct for these factors, although this does not fully define the value of the relaxation terms in [12] unless the brain metabolite signal T1 and T2 are known. Negative features of water signal referencing include that water signal level may be altered by disease or may depend on brain location or subject hydration status, that the MRI scanner may change the gain factor (G_A) between the water reference signal acquisition and the brain metabolite signal acquisition, and that it is not all that clear what the true concentration of mobile water is in the brain. There is a great deal of evidence from relaxometry studies and magnetization transfer studies suggesting some fraction of the total brain water is immobile and therefore not detected at the TEs used in a typical MRS study.

Internal reference signals need not be produced by the same brain location that produces the metabolite signals. Water or metabolite signal from a different brain location may be used as a reference signal. For SV-MRS this approach requires study of at least two brain locations. Use of this type of reference signal is more natural for MRSI because the more brain volume is sampled. Such approaches are frequently used when focal brain lesions are present (eg tumor, epilepsy, multiple sclerosis) and some signal produced by normal appearing brain can be used as a reference signal. Of course use of referencing of this type is limited by spatial homogeneity of the B1 fields used for transmit and the spatial uniformity of receive coil sensitivity.

The relevant literature can sometimes be misleading and confusing with respect to the use of the term “absolute concentration” and use of this term is avoided in this article. Some authors use this term in a general sense to mean only that the concentration results are expressed in conventional concentration units (moles per unit mass or moles per unit volume). Other authors are more restrictive and reserve the use of the term for absolute concentration determination by a specific calibration procedure. The use of “absolute” can also give the (untrue) impression that the brain metabolite concentration has been derived without using a signal ratio. In fact [12] shows that all forms of MRS concentration derivation use a signal ratio, but the methods differ with respect to how the reference signal is obtained. Use of “absolute” also conveys the misleading impression that reporting of absolute concentration is more precise than reporting of signal ratios. This may not be true. Data scatter in a measured absolute concentration is implicitly limited by the precision with which both the metabolite and reference signals can be determined. For example, absolute concentration determined by internal water reference calibration may show less pronounced data scatter compared to the scatter in the NAA/Cre signal ratio in the same population. This may not be necessarily true because the absolute methodology is better but because a less noisy reference signal was used. Furthermore the term “absolute” may be confused with “true”. In fact all absolute concentration determinations can be biased by the methodology and assumptions used in the calibration procedure. At best each methodology produces an estimate of the true concentration. Some methodologies may produce a more accurate estimate or a more precise estimate (less scatter) compared with others. Accordingly absolute brain metabolite concentrations determined by two different methods may not agree.

The above described calibration approaches permit the estimation of brain metabolite concentrations or ratios for across-time, across-center and between-patient comparisons. Proof of concept has been demonstrated in small scale studies (4, 23, 27–30). The approach has been used successfully in larger scale studies (22, 26, 31–36).

4. Signal properties and confounds of signal amplitude measurement

This section and the next describe the measurement of the integrated signal amplitude and confounds associated with it. This section introduces key MRS signal properties and describes a few problems that are encountered when MRS signals are qualitatively evaluated. In doing so it lays groundwork for understanding quantitative MRS signal measurement.

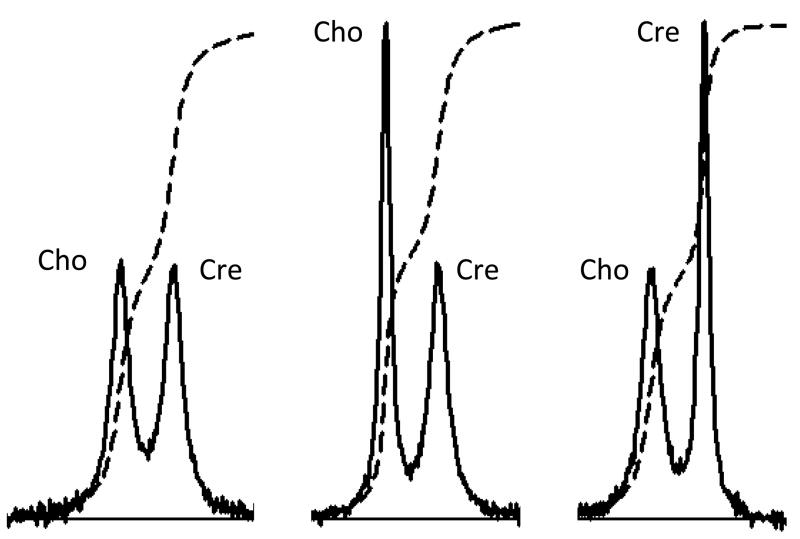
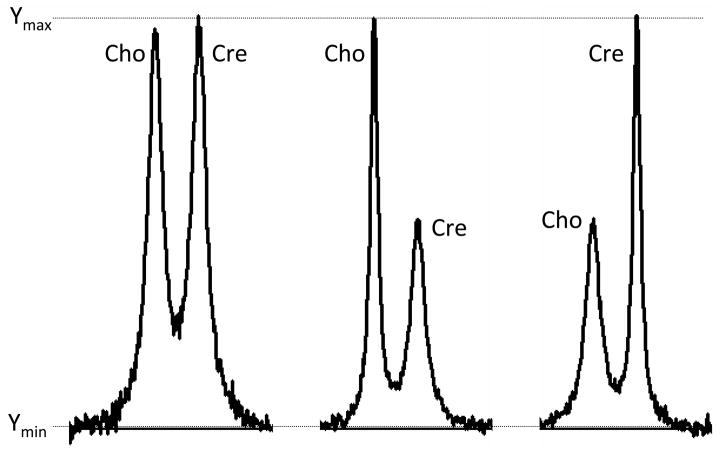
The integrated signal amplitude is not the same as the signal height. Consider the six signals presented in Figure 4. Each pair of signals has been computer-simulated to resemble the principal Cho and Cre signals that might be present in a brain or a brain tumor spectrum. Which of the Cho-Cre signal pairs has the higher Cho signal amplitude? Which of the pairs has the lower Cho signal amplitude? Which of the pairs has the same Cho and Cre signal amplitudes? In fact each pair was simulated using identical Cho and Cre signal amplitudes. All three Cho amplitudes are identical to each other and to all three Cre signal amplitudes. This can be appreciated by review of the signal integral curves that are drawn on each pair signals. This simple example illustrates the importance of identifying differences in signal area as opposed to differences in signal height. Use of signal height or even signal height ratio is therefore not an appropriate way of determining the concentration of metabolites responsible for a particular signal. The correct interpretation of the Figure 4 data is that the FWHM changes. The FWHM of Cho and Cre are identical in the left panel. The Cho signal is sharper than the Cre signal in the middle panel. The Cre signal is sharper than the Cho signal in the right panel. The changes in FWHM may have their own clinical significance, but discussion of this point is beyond the scope of this article.

Figure 4.

Computer-simulation of Cho and Cre signals for three different conditions. See text.

Figure 5 illustrates a related problem. The simulated signals shown in this figure are identical to the ones shown in Fig 4. However each pair has been plotted in a way that scales the plot so the highest point on the spectrum coincides with a fixed maximum point on the paper or computer screen. A reader who is not trained to assess signal area and who is unfamiliar with the characteristics of the plotting software might conclude that the Cre signal is lower in the center panel and Cho signal is lower in the right panel. An inexperienced reader might also incorrectly conclude that both signals in the left panel are larger than those shown in the center or right panels.

Figure 5.

The same data shown in Figure 4 is presented except that a different y-scaling approached is used for display.

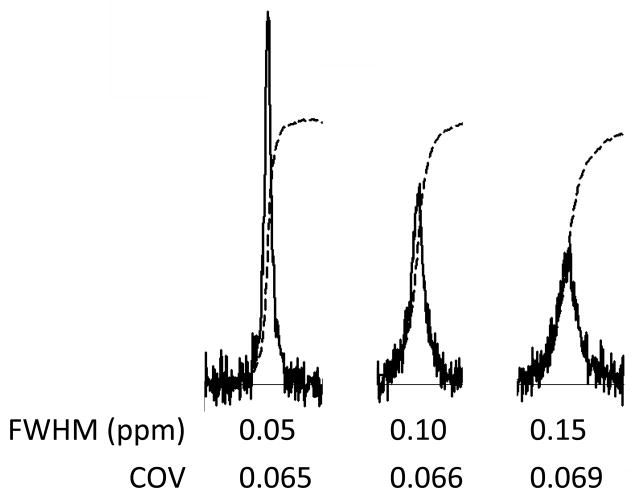
The signal FWHM has an effect on the accuracy of the signal amplitude determination as is illustrated in Fig 6. The three signal traces shown in the figure were computer-simulated using identical signal amplitudes but different FWHM values. As the signal becomes wider, the signal deviation above noise becomes smaller. There is a corresponding subtle deterioration in the precision (the COV) with which the signal area can be measured.

Figure 6.

Computer simulation of the effect of signal broadening in the presence of noise on signal amplitude measurement statistics. COV values were determined as described in Figure 2 caption. See text for further details.

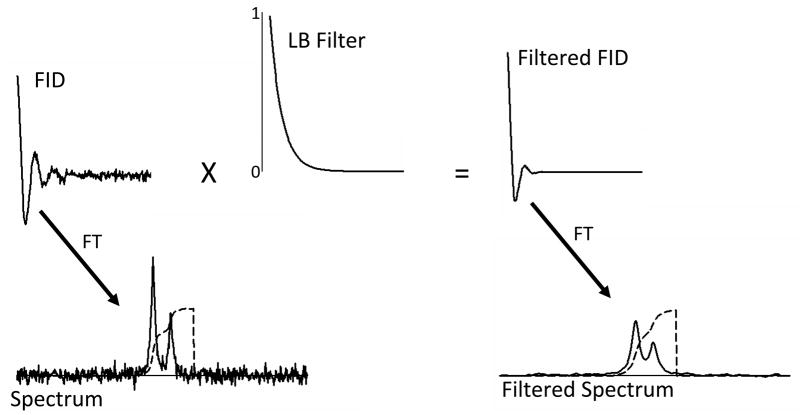
A signal’s FWHM is influenced by noise filtering that occurs during the post acquisition signal processing. Figure 7 illustrates this feature of MRS signal processing with computer simulated signals to which random noise has been added. The unfiltered spectrum (bottom left) shows a greater amount of noise compared to the filtered spectrum (bottom right), but the integral trace illustrates that the determination of the signal amplitudes is feasible even in the presence of this noise. The integration process essentially acts to filter high frequency noise. The filtered spectrum (bottom left) shows that the noise filter processing has two effects on the frequency domain spectra. It filters noise, but does so at the expense of creating wider signals. It is for this reason that this particular filter is often referred to as a “line broadening filter”. The integral trace shows that the determination of the signal integral for the combination of the two signals is equivalent to that determined from the unfiltered spectrum, but that the filtering has added the complication of making it more difficult to determine the two overlapping signal amplitudes independently. This example illustrates that, not only is noise a potential problem, but also that the use of too much noise filter processing can lead to amplitude measurement bias when there are nearby signals that overlap with the signal being evaluated.

Figure 7.

Schematic illustration of noise filtering in the time domain. The top panels of the figure show computer simulated unfiltered FID (left) and the same FID after multiplication by an exponentially decaying filter function (top center and right). The corresponding spectra derived from Fourier transformation are shown in the bottom panels.

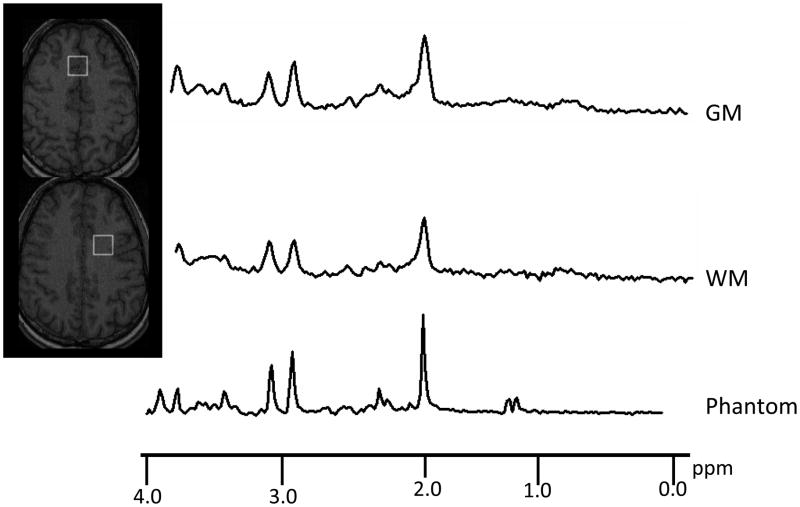
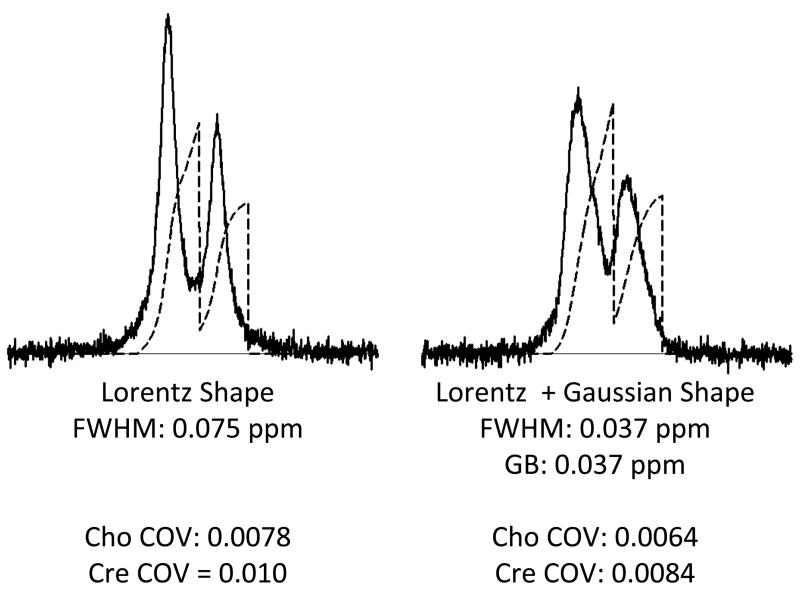
For actual brain spectra the signal shape and FWHM is somewhat more complex than has been implied in the article thus far. In Figure 8 a brain spectrum and the spectrum obtained from a standard phantom are shown. The phantom was made up to contain many of the same metabolites that are present in the brain. Therefore the brain and phantom spectra resemble each other in terms of signal position, but the brain spectrum has wider signals. Furthermore the shapes of the signals in the two spectra differ. The phantom spectrum has sharper more pointed signals. The brain spectrum signals are wider and more rounded. Figure 9 illustrates the widely accepted reason for these differences. The signal broadening and shape change are usually attributed to the existence of a distribution of B0 fields within the voxel (ie B0 field inhomogeneity). The Figure 9 data were computer-simulated assuming Lorentzian line shapes (left panel). Increasing the FWHM term, while maintaining the Lozentzian shape, is not the most accurate way of modeling the effect of B0 inhomogeneity. A more appropriate approach is to construct a family of Lorzentzian shaped signals in which each signal has a subtle frequency shift with respect to the other signals and add then add together the family of signals to form a composite (right panel). Usually a Gaussian distribution of frequency shifts is used to model the distribution of B0 field strengths within the voxel and the signal shape is said to be a Lorzentzian-Gaussian shape. The same integrated signal amplitudes and noise levels were used to computer-simulate the two spectra shown in Figure 9. The figure illustrates that the Gaussian broadening causes the maximum signal deviations relative to noise to be reduced and leads to some loss in the precision of integrated signal amplitude measurement.

Figure 8.

Comparison between 3 Tesla short TE SV-MRS data taken from gray matter (GM), white matter (WM) and a phantom containing brain metabolites.

Figure 9.

Computer simulation of characteristic MRS signal line shapes. Left panel: Cho and Cre signals having Lorentzian shape with FWHM of 0.075 ppm. Right panel: The same Cho-Cre frequency difference was used to simulate signals having the same amplitudes, but mixture of Lorentzian and Gaussian shapes. The data were simulated by repeating the Lorentzian shape calculation 100 times with 1% intensity, a FWHM of 0.037 ppm and a frequency shift that was randomly chosen from a normal (Gaussian) distribution having a FWHM of 0.37 ppm. The data presented are the sum of the 100 simulations. COV values were determined as described in Figure 2 caption.

Signal phase is an important signal property that must be taken into consideration when evaluating spectra qualitatively or quantitatively. The MRS signal is a complex quantity that has real and imaginary components (Figure 1). The integrated signal amplitude is measured only from the real component. However many MRI scanners are not designed to acquire the true real and imaginary signal components independently. Instead it has been typical to acquire two channels of signal information (S₁ and S₂) in which each channel contains a mixture of the true real and imaginary signals

$$S_1(f)=c_1{S}_R(f)+c_2{S}_I(f)$$ [14]

$$S_2(f)=(1-c_1)S_R(f)+(1-c_2)S_I(f)$$ [15]

Where c1 and c2 are positive and the sum of c₁ and c₂ is 1. The true real component signals are then derived by a post-acquisition phase correction procedure that is usually done in the frequency domain. This procedure forms the observed real signal as

$$S_R^{\mathit{obs}}(f)=p_1{S}_1(f)+(1-p_1)S_2(f)$$ [16]

The value of p₁ is then adjusted to create a real signal that resembles the real component of the Lorzentzian signal shown in Figure 1. Frequently this process is done by a trained person. It may also be done automatically by software.

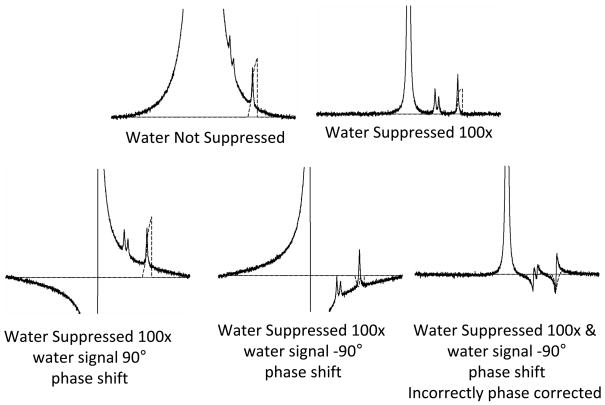
Phase correction is straightforward provided the signal being phase corrected is well separated from other signals, but this is rarely the case in real brain spectra. A commonly encountered problem related to phase correction in the presence of overlapping signals is illustrated in Figure 10. The concentration of brain tissue water protons is more than 3000 times that of the protons that produce the NAA signal. Without the use of a water signal suppression procedure, the spectrum of interest (Cho, Cr, NAA) is superimposed on the curving tail of the water signal even if the spectrum is properly phase corrected (top left panel). It is not possible to adequately determine the areas under the Cho, Cre and NAA signals in this case without assuming a specific curvature for the baseline (which is actually not a baseline, but part of the water signal). Ideally the water suppression works well and the water signal is reduced by many factors (top right panel). Note that the routinely used water suppression method reduces the entire area of the water signal including the signal tail that underlies the spectrum of interest. If the water suppression is less than optimal, a situation resembling that shown in the lower left and lower center panels might be seen. Here in addition to inadequately suppressing the water signal, the water suppression procedure has introduced a phase shift into the water signal that is not present in the metabolite signals. In general, the water suppression procedure shifts water signal phase by an unknown amount. The presence of a poorly suppressed water signal that has been phase shifted by an unknown amount creates a situation in which there is uncertainty about metabolite signal phase correction and the true baseline that underlies the brain metabolite signals. This may then result in errors in determining the integrated signal amplitude. Phase correction software and human experts tend to have difficulty making the appropriate phase corrections when a large poorly suppressed water signal having an arbitrary phase shift is present. The lower right panel shows what happens when the phase correction procedure uses the residual water signal as a reference for phase correction of the entire spectrum. In this situation the metabolite signal amplitude determination becomes totally flawed because the signals are not properly phase corrected. The most useful approach to avoiding such errors is to acquire a second spectrum from the same region without water suppression. The true phase correction can be determined from this “water reference” spectrum and then this correction can be applied to the water suppressed spectrum (26). The water reference acquisition can also be used for signal quantitation (see above), for acquiring information about the signal lineshape and about additional signal imperfections, such as those due to imperfect gradient switching.

Figure 10.

Illustration of a quantitation problem that can arise from the combination of incomplete water suppression and phase correction errors.

Phase correction in MRSI can be a particularly severe problem. The RF pulses used for volume selection in MRSI can impart phase shifts that depend on position and therefore all voxels in the MRSI array do not use the same phase correction. The typical MRSI study has too many voxel spectra for a human expert to manually phase correct and automated phase correction software must be used. Phase correction software works well for voxel spectra in which water signal is fully suppressed, but tends to fail (discussed above) for voxel spectra that have poor water suppression. This in turn leads to errors in signal amplitude measurement and errors in metabolite signal images. For this reason, it is highly desirable to use an MRSI procedure that permits efficient collection of a water reference MRSI.

Errors in metabolite signal amplitude measurement can also result in instances in which there are large signals produced by mobile lipids in the spectrum. Lipid molecules are composed of chains of methylene (CH₂) groups that produce signals at approximately 1.28 ppm terminated by a methyl (CH₃) group that produces a signal at approximately 0.9 ppm. While the brain contains a relatively large amount of lipid, lipid signal is not prominent in brain spectra, because most of the brain’s lipid is molecularly packaged within relatively immobile macromolecular myelin structures. The lipid proton spins associated with such structures have T2 relaxation times that are significantly less than the TE value used by most MRS pulse sequences and the lipid signals are effectively suppressed by T2 relaxation. However this is not true for the tissues that surround the brain. Bone marrow in the cranial bone and the soft tissues of the head and neck contain a significant portion of adipose cells. Such cells store lipid as triacylglyceride. Triglyceride lipid chains are significantly more mobile than is the case for lipid packaged within myelin. Triglyceride lipid proton spins therefore have longer T2 values. Tissues containing adipose cells thereby produce large lipid signals which can obscure brain metabolite signals and render it almost impossible to accurately measure metabolite signal area. This is a particular problem for MRSI. MRSI imaging procedures are far from perfect in avoiding the excitation of the lipid signals the arise from outside the brain (37, 38). As a result, it is not uncommon for MRSI voxel spectra to include detectable “outer volume” lipid signals, which may be phase shifted relative to, and overlap with, metabolite signals, and thereby interfere with signal quantitation. A post processing procedure has been developed to minimize this complicating factor in MRSI and use of this procedure can reduce errors in MRSI signal quantitation (38, 39). Lipid signals may even complicate SV-MRS when a neurodegenerative process causes breakdown of myelin and releases the myelin lipid into a more mobile form. Furthermore it is important to remember that SV-MRS pulse sequences do not always have perfect outer volume lipid suppression and determining whether a lipid signal present in a SV-MRS spectrum arose from within the actual sampled volume or from outside the volume is an ongoing problem. In this regard, it is unfortunate that a widely referenced study that asserted brain MRS lipid signals are biomarkers of neural progenitor cells failed to acknowledge the possibility of accidental detection of lipid signals from the tissues outside the intended volume as a limitation (40, 41).

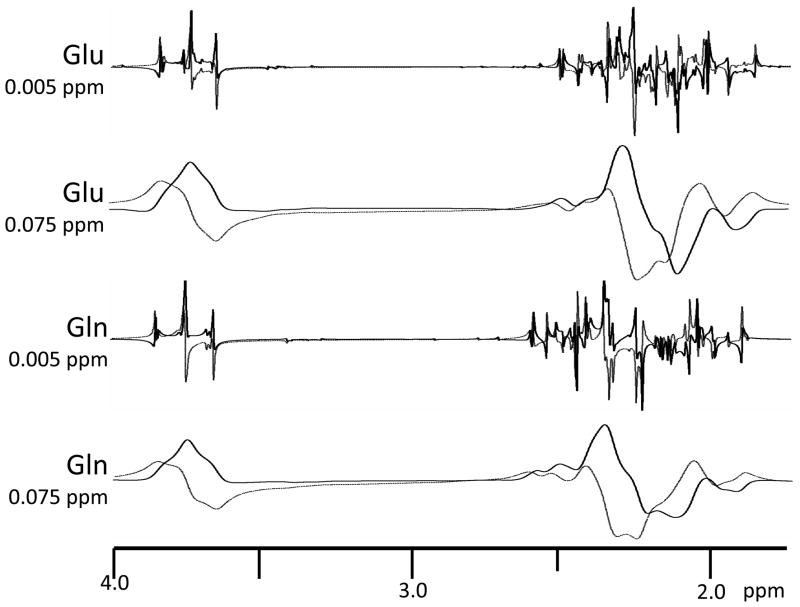
Signal amplitude quantitation is further complicated by “J-modulation” when the typical MRS spin echo pulse sequences are used. The well-known J-modulation of the lactate 1.33 ppm signal is illustrated in Figure 2, which shows that the lactate signal phase changes in a characteristic fashion as TE is changed. The phase modulation is the result of quantum mechanical processes known as “J-coupling” which causes the signal from a particular proton to break apart into a group of signals (i.e. a multiplet) whose positions depend on the presence of other protons on the same metabolite molecule. Furthermore when spin echo pulse sequences are used, each of signals in a multiplet acquires a unique TE-dependent phase. The phase of each signal in the multiplet depends in a complex, but predictable, fashion on type of pulse sequence that is employed and its timing. Software that performs quantum mechanical calculations can be used to predict metabolite multiplet signal patterns (frequencies, phases and relative signal intensities) with a high degree of accuracy (42–46). J-coupling and J-modulation do not occur for the water, or the principal Cho, Cre and NAA signals because the signal-producing molecules do not have other protons that are close enough to the signal generating protons to produce the coupling effect. However many other MRS-detectable metabolites produce similar characteristic TE-dependent patterns of signal phase. Figure 11 illustrates how J-modulation can produce quite complex signal patterns. The figure shows simulated TE = 136 spectra of two commonly sought after brain metabolites, glutamate and glutamine. J-modulation and J-coupling impact on quantitation because they effectively reduce signal relative to noise by breaking a particular signal into a multiplet of smaller signals. Furthermore the signal phase patterns in such situations may take a very bizarre appearance compared to the case of a single signal shown in Figure 1. This is particularly true when there is substantial signal broadening due B0 inhomogeneity and overlap of the multiplet component signals as is illustrated by the broadened signals shown in the Figure 11. At certain TE values the phase modulation may cause much of the signal to be absent from one or the other signal channels. At other TE values inverted and upright signals may cancel each other as a result of close frequency proximity and broadening.

Figure 11.

Glutamine and glutamate MRS signals in the 1.75 – 4.0 ppm region. Data were simulated using the GAVA program. A PRESS localizing pulse sequences with TE = 136 was assumed. Phase corrected real (solid line) and imaginary (dotted line) channels are shown. The data were simulated with a uniform FWHM values of 0.005 ppm and 0.075 ppm. Simulation using narrow FWHM illustrates the complexity of the spectral patterns that underlie the typical in vivo spectrum FWHM (0.075 ppm).

J-modulation is the basis of many spectral editing techniques that are designed to enhance or suppress certain signals relative to overlapping signals in the brain spectrum. Description of such editing pulse sequences are somewhat beyond the scope of this article, but from the standpoint of metabolite concentration measurement, their use has positive and negative features. The primary positive aspect is that spectral simplification enhances quantitation by reducing overlap of the signal of interest with other signals. The primary negative feature is that additional factors that describe how efficiently the pulse sequence detects a particular signal or group of signals must be used to obtain concentration estimates. In many cases, it is quite challenging to derive the values of these factors. Signal referencing approaches as described above that use the particular molecule of interest may be helpful in this regard.

5. Signal Amplitude Measurement though Signal Modeling

In view of the many complexities discussed in the previous paragraphs, it has been recognized that the “running sum” signal integration approach that has been used to illustrate concepts throughout this article can not be used as a means of determining integrated signal amplitude in short TE brain spectra. The situation for long TE spectra is somewhat more relaxed. For long-TE spectra, J-modulation and T2 signal decay tend to produce a situation in which only the prominent singlet signals can be detected above noise and signal integration can be used because there are relatively few overlap problems. For short TE spectra, it has become commonplace to assume that the brain spectrum is represented by a “spectrum model”, which is the sum of many complex valued signals arising from many metabolites. “Optimization” or “fitting” software is then used to repetitively adjust the frequencies, phases and amplitudes of the signals until a simulated model that agrees with the observed data to some prespecified level of accuracy is found. The general fitting process is illustrated in Figure 11. The signal amplitudes that produce the best fit are then used to estimate metabolite concentration. Typically used spectral models include adjustable signal characteristics (phase, frequency and amplitude) of all signals. For metabolites the fitting process can be constrained by the expected phase and frequency signal patterns produced by quantum mechanical calculation or they may come from measuring in vitro spectra of particular metabolites under the same conditions used to obtain brain spectra. In some cases models include “nuisance” signals such as poorly suppressed phase-shifted water and lipid signals. There is also evidence to suggest that small proteins or other macromolecules that are present in brain tissue produce a baseline spectrum composed of rather wide signals that underlies the metabolite spectrum. A practically useful model should also therefore include baseline components (47–49).

Typically spectrum fitting techniques make use of well established linear least squares optimization procedures that are used to solve analogous optimization problems in other scientific and engineering fields, although neural network approaches have also been invstigated (50). MRI manufacturers offer least squares fitting software as a part of their MRS accessories. Alternative software packages are available as freeware and for a cost. The most popular spectrum fitting software is currently LCModel (51, 52). The spectral models used by these software packages fall into two broad categories (48). The model may be a group of individual signals each of which has its own signal frequency, FWHM, phase and amplitude. An alternative is to use a model that recognizes that the individual metabolites are most correctly modeled as a pattern of signals produced by the entire molecule. LCModel was the first software package to use entire molecule approach (51, 52). Spectrum fitting software that takes either time domain (21, 44, 53–55) or frequency domain (56–59) input is available. Efforts to compare results obtained by various methods have been published (60–62). Time domain methods have the advantage of reducing the likelihood that some inappropriate filtering has been used prior to performing the fit. It is also more straightforward to compute the time domain representation non-Lorentzian inhomogeneity broadened lineshape as opposed to the frequency domain representation. Frequency domain fitting does a better job at fitting models that contain wide baseline signals that might arise from water, lipids or macromolecules. Frequency domain fitting tends to do a better job at determining accurate signal positions while time domain methods give better estimates of linewidths. In general either type of fitting may be regarded as adequate.

The use of fitting procedures has some notable shortcomings. Optimizing a fit to a large model containing thousands of signals is sometimes required. This is a very large job even for a modern day computer system. It is not unusual for a fit to require minutes to hours of computer time depending on the level of complexity. While long fitting times are tolerable for SV-MRS, they can severely limiting for MRSI because there are large numbers of voxel spectra to fit. Approaches to breaking the optimization problem into smaller more manageable subproblems is one approach to reducing computing time (54, 63, 64). Fitting methodology requires an initial estimate of the model parameters and the optimal approach for incorporating prior knowledge is rarely clear, although efforts to define optimal approaches are underway (63, 65). The metabolite signal frequencies and phases used in the model as prior information can come from either quantum mechanical calculations or from measurements of metabolite spectra. A recent study indicates that the approaches to obtaining this prior information are equivalent (42). The methodology can be substantially limited by the presence of “nuisance” signals, such as poorly suppressed water signal and outer volume lipid signal. There is a need for better approaches to either filtering these signals for the data prior to fitting or to including these signals into the models to be fit (47, 60, 62, 66–68). Appropriate lineshape estimation must also be included in the model (69). Furthermore there always exists the possibility that the software may fail to arrive at a correct solution and it is sometimes hard to know when this has occurred. Here the problem is that parameters may couple in ways that cause incorrect combinations of signal values to fit the data as well as the correct combinations. Many programs give estimates for the uncertainty of the best fit results (i.e the Cramer-Rao bounds) but these estimates report how well the model fits the data and not necessarily how accurate the result is.

The validity of metabolite concentration estimates determined using the methodology described in this article can be assessed by performing repeated measures on individuals (20, 28, 29, 62, 70–75) or by assessment of variance in cross-sectional studies of normal populations (19, 22, 29, 36, 75, 76). Comparisons between brain and phantom spectra have also been used to assess and validate accuracy, but this validation approach is somewhat circular when an external phantom is used in the calibration approach. These studies suggest that the coefficient of variation for the largest metabolite signal (NAA) is 6% to 15%. It is not well understood what factors or assumptions implicit in the rather complex signal processing chain play a significant role in limiting the accuracy, precision or reproducibility. Investigation of which factors contribute to the variance are underway. Variance depends on the metabolite, its concentration, and on the brain area studied (28). A recent study of metabolite concentrations in the human anterior cingulate found that interindividual differences are more important contributors to the variance than are time of day and voxel and/or subject repositioning (70, 77). On the other hand another recent study found physiologic variability to be an important source of measurement variability for temporal lobe NAA (74). Nevertheless careful repositioning of voxel location may improve reproducibility (75, 76, 78, 79). SNR and linewidths are also an important factors (73, 80).

6. Summary

Metabolite concentration is directly related to the area under an MRS signal produced by the metabolite. While this fact seems to point to a straightforward approach to determining brain metabolite concentration, the approach is actually very complicated due to many complex factors. In general, concentration estimation is achieved by calibrating the measured brain signal levels against a reference signal measurement to control for many factors related to instrumentation and signal detection methodology. Internal signal (Wat or Cre) may be used for this purpose, or signals produced by an external phantom object containing metabolites or other materials may be used. Determining the relative integrated amplitudes of the overlapping signals within a brain spectrum is typically approached by fitting a complex model to the data because of overlapping signals and several complex features related to signal phase and signal overlap. Merging signal calibration with spectral fitting then provides numerical estimates of metabolite concentration. There is often an additional requirement to merge the concentration determination with a tissue content analysis that determines gray, white matter and CSF content within the MRS voxel or voxels as a means of correcting for the fact that different tissue types may have different metabolite concentrations (81). This matter has not been discussed in this article, because tissue segmentation is primarily an MRI quantitation problem. The numerical estimates of metabolite concentration can be used in longitudinal or cross sectional studies.

7. Concluding perspective

Clinical and research applications of proton MRS have grown more slowly than applications involving other MRI techniques. Nevertheless, there has been definite progress in clinical MRS applications development during the past two decades. Several clear clinical uses of MRS have emerged. Most neuroradiologists and neurosurgeons would now agree that MRS provides useful diagnostic and prognostic information about intracerebral neoplastic lesions. Similarly MRS can be valuable for epilepsy, particularly for evaluation of iodiopathic forms of this disease that may or may not originate in the temporal lobes. There is also evidence to suggest that MRS is useful in the diagnostic workup of inborn genetic problems in infants. The further enhancement of MRS quantitation methodology would help to further substantiate the utility of MRS in these important areas of clinical neuroscience. Additional clinical applications of MRS are on the horizon. The present author sees a not too distant future in which MRS and MRSI will play important roles in the differential diagnosis of certain dementias and in the evaluation of functional disorders such as traumatic brain injury and multiple sclerosis. Use of MRS for diagnosing and studying psychiatric disorders may be somewhat more distant, but there is certainly reason to believe that MRS-detectable amino acid metabolites (glutamine, glutamate, NAA) play a role in certain psychiatric conditions. These potential future applications of MRS will require very careful signal quantitation considering that existing studies show that these conditions produce less prominent changes in metabolite levels in comparison with neoplasia and epilepsy.

Difficulty associated with MRS quantitation is sometimes suggested as an impediment to the development of MRS as a clinical tool. It is the present author’s opinion that this is not the primary cause. This review demonstrates that reliable quantitative evaluation of MRS metabolite signal levels is feasible for studies involving groups of subjects or individual patients, although it also shows that accurate quantitation requires significant attention to detail. A more probable explanation for the slow growth of clinical MRS applications is the contemporaneous emergence of other MRI technologies (e.g. magnetic resonance angiography, diffusion MRI, perfusion MRI and blood oxygenation-dependent functional MRI). Some of these alternate technologies could be used with little or no practical quantitation. Such technologies offered more payoff for less work compared with MRS. Resources that would have otherwise been used to perfect MRS technology and develop new clinical MRS applications were directed instead to these competing technologies. Another possible reason for the slow emergence of clinical MRS applications is the relative lack of familiarity with the biochemical aspects of disease within the radiology community. Radiology is largely a non-quantitative anatomically-based discipline in which the majority of the practitioners stop thinking about biochemistry after completing their course work in medical school. The successful use of MRS within this community requires some lateral learning about biochemistry and biochemical quantitation, which many busy radiologists find difficult to undertake.

Looking forward, the academic MRI science community can do a great deal to further enhance MRS quantitation methodology. One important step would be the development of a more rationale framework for performing MRS quantitation and reporting the results. Hopefully this review article has made it clear that the present tendency to classify MRS quantitation in terms of ‘absolute’ or ‘ratio’ is overly simplistic. Wider acceptance of the facts that ‘absolute’ quantitation is largely based on taking ratios and that there can be different forms of ‘absolute’ quantitation is in order. Furthermore the common practice of criticizing findings that use signal ratio measurements needs to be based on the value and validity of the findings as opposed to a categorical decision about a ‘good’ or a ‘bad’ procedure. Sometimes ratio measurements can be more accurate in terms of reporting disease status than absolute measurements. The academic community also needs to focus more on quantitation of individual patient data as opposed to group data. All too frequently mean metabolite level differences between groups (e.g. patients having a particular disease versus normal controls) are reported as statistically significant at the p = 0.05 level and the research stops without further evaluation of what would be needed to apply the findings in an individual patient. Development of practical and statistically sound means of translating such findings to diagnosing and longitudinally following individual patients is needed. The academic community can also offer a great deal more in terms of explaining why certain metabolite levels change in certain diseases. Presently used explanations for observed changes (e.g. ‘NAA has changed because it is a reporter of neuronal function or neuronal density or both’) tend to be largely inferential and somewhat superficial. There is a great deal of room for studies that use modern quantitative cytology and molecular techniques to explain why changes in metabolite levels occur in certain diseases. Such studies might employ animal models of disease or well-characterized patients who provide tissue as a result of neurosurgical procedures or autopsy. In particular, there needs to be a much better understanding of whether disease-related MRS signal level changes result from changes in cellular composition (e.g. cellular atrophy, cell-level immune response, stem cell migration) as opposed to changes in metabolism within a population of existing cells.

The commercial MRI technology community can also do a great deal to enhance the feasibility of MRS quantitation. The introduction of automated acquisition/processing modules for SV MRS into commercial MRI products about 10 years ago was an important first step. A major problem in existing commercial MRI systems is that important information is hidden from the user. Examples of hidden information include transmit and receive gain levels, the excitation profiles of the volume selection and water suppression RF pulses, pulse sequence timing parameters and the exact methodology used for MRS signal fitting and baseline correction. Products that automatically collect a not-water-suppressed reference spectrum, but do not provide the user the opportunity view or otherwise work with this spectrum, is another example of hidden information. Still another ‘hidden information’ problem is the failure to deliver raw MRS information to the user via widely accepted DICOM protocols or to publish information about the formats used to store raw spectral data. Hidden information is highly counterproductive for both the academic and commercial MRI communities. Academic investigators eventually learn how to obtain the hidden information, but doing so consumes valuable resources that could otherwise be devoted to scientific and clinical exploration that, in turn, would be highly valuable in the commercial MRI community. Hidden information also runs contrary to clinical trial design principles, which require keeping verifiable records of the smallest details about the experimental procedures used in a clinical trial. A practical reality is that multicenter clinical trials involving MRS biomarkers will use MRI scanners produced by different manufacturers and manufacturer-specific hidden information severely impedes integrating clinical trial results coming from different scanners. Results presentation is also an area which the commercial MRI community could improve. It has become customary to present MRS results as x-y plots of the spectrum with numerical summaries of signal areas. As is discussed above, such results displays can lead to confusion about vertical scaling and signal area versus signal height. In this context a bar graph that reported the signal areas or metabolite concentrations (including the water reference signal if it is collected) may be more helpful and would also appeal to the visual nature of radiologist training.

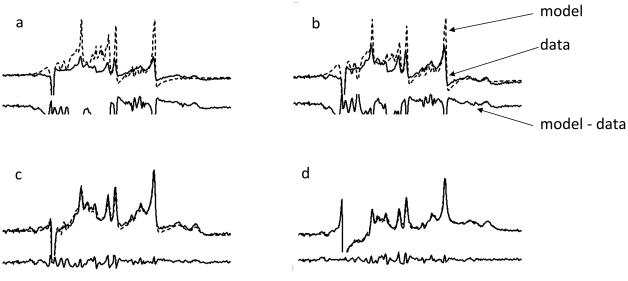
Figure 12.

Illustration of non-linear signal fitting of a 3 T short TE water suppressed human brain spectrum (solid line) to a complex spectral model (dashed line) generated by the GAVA program. The residue (model –data) is shown below each pair. a – d show progressive improvement in the model in terms of agreeing with the data.