Abstract
We develop Bayesian inference methods for a recently-emerging type of epigenetic data to study the transmission fidelity of DNA methylation patterns over cell divisions. The data consist of parent-daughter double-stranded DNA methylation patterns with each pattern coming from a single cell and represented as an unordered pair of binary strings. The data are technically difficult and time-consuming to collect, putting a premium on an efficient inference method. Our aim is to estimate rates for the maintenance and de novo methylation events that gave rise to the observed patterns, while accounting for measurement error. We model data at multiple sites jointly, thus using whole-strand information, and considerably reduce confounding between parameters. We also adopt a hierarchical structure that allows for variation in rates across sites without an explosion in the effective number of parameters. Our context-specific priors capture the expected stationarity, or near-stationarity, of the stochastic process that generated the data analyzed here. This expected stationarity is shown to greatly increase the precision of the estimation. Applying our model to a data set collected at the human FMR1 locus, we find that measurement errors, generally ignored in similar studies, occur at a non-trivial rate (inappropriate bisulfite conversion error: 1.6% with 80% CI: 0.9–2.3%). Accounting for these errors has a substantial impact on estimates of key biological parameters. The estimated average failure of maintenance rate and daughter de novo rate decline from 0.04 to 0.024 and from 0.14 to 0.07, respectively, when errors are accounted for. Our results also provide evidence that de novo events may occur on both parent and daughter strands: the median parent and daughter de novo rates are 0.08 (80% CI: 0.04–0.13) and 0.07 (80% CI: 0.04–0.11), respectively.
Keywords and phrases: Bayesian inference, DNA methylation, transmission fidelity, epigenetics, hairpin-bisulfite PCR, hierarchical models, Markov-chain Monte Carlo (MCMC), measurement error, multi-site models, stationarity
1. Introduction
In this paper we develop statistical models and inference methods to address an important problem in epigenetic biology: inference of the fidelity with which DNA methylation patterns in DNA are preserved over somatic cell divisions in mammals. The double-stranded DNA methylation data we present here have the potential to yield important biological insights. However, due to limitations of current experimental technologies, these data also present challenges. For example, it is difficult to obtain this type of data in large quantities, some key biological variables are unobservable, certain parameters of interest may be confounded, and the data are subject to measurement error at perhaps a non-trivial rate (Genereux et al., 2008). These characteristics put a premium on efficient inference methods that make full use of the data while dealing with complexities intrinsic to the data and to the biological problem. In this section, we introduce, for a statistical audience, relevant biological background on DNA methylation and the hairpin-bisulfite PCR technique (Laird et al., 2004; Miner et al., 2004) used to collect the data. We then state our aim and give overviews of existing methods and our new approach.
A DNA molecule is most commonly described by its sequence of nucleotides, consisting of adenine, cytosine, guanine and thymine; or A, C, G and T. However, this description is incomplete in that it omits some functionally relevant features. An important example is that some nucleotides are methylated — that is, at some nucleotide positions a methyl group has been chemically attached to the DNA. Methylation is an epigenetic mechanism, such that the pattern of methylation along a DNA molecule can profoundly effect its function. Aberrant methylation plays a role in many cancers (Chen and Riggs, 2005; Jones and Baylin, 2002; Laird, 2003) and in several human developmental diseases, including fragile X syndrome (Laird, 1987; Robertson and Wolffe, 2000). In fragile X syndrome, hypermethylation of the FMR1 locus on the X chromosome leads to many manifestations including mental retardation. A critical distinction between methylation patterns and nucleotide sequences is that, whereas the latter are generally assumed to be identical in nearly all cells of an organism, the former can vary considerably from cell to cell within an organism. The processes that govern DNA methylation and its variability across cells are thus of considerable biological interest.
In mammals, methylation of DNA occurs almost exclusively on cytosines (Cs) that are followed by a guanine (G); locations referred to as CpG sites. On average about 70–80% of CpG sites in mammals are methylated (Ehrlich et al., 1982). A key property of DNA molecules is that they are double-stranded, with the two strands complementary to each other, that is, A pairs with T, and C with G. Hence we also refer to CpG sites as CpG/CpG dyads to emphasize their double-strandedness. At a CpG/CpG dyad, methyl groups can be present on both strands (which we call “methylated”), on one strand (“hemimethylated), or on neither strand (“unmethylated”). Our focus here is on the accuracy with which the pattern of methylation on one strand (the parent strand) of a DNA molecule is transferred to the new complementary strand (the daughter strand) produced by DNA replication (see Supplementary Material Section 1 in Fu et al. 2009 for details).
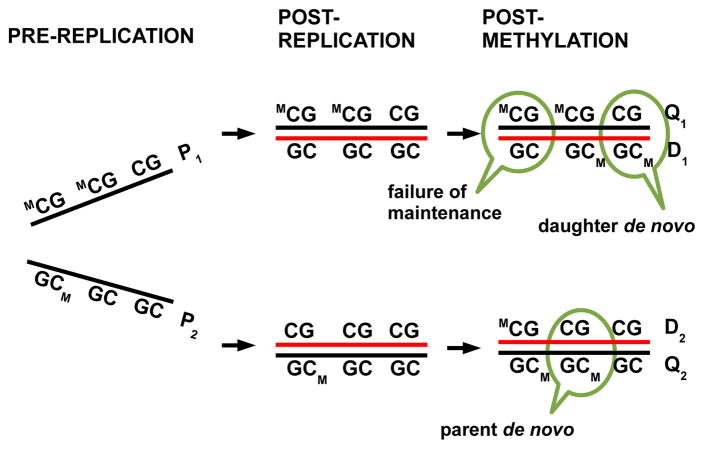
The transmission process of methylation patterns is complex and imperfect: cytosines are first incorporated into DNA and subsequently methylated. Sometimes, however, a cytosine on the daughter strand remains unmethylated even when the parent is methylated, an event we refer to as a failure of maintenance event. Methylation is also sometimes introduced at previously unmethylated locations; we refer to such events as de novo methylation events. Here, as in Genereux et al. (2005), we allow the possibility of de novo events on both parent and daughter strands. Figure 1 illustrates these concepts under a widely-accepted model for the transmission process (Bird, 2007, 2002).
Fig 1.
The transmission process of DNA methylation patterns in mammalian somatic cells. The two strands in a DNA molecule each become parent strands during DNA replication (from left column to middle column), used as a template to synthesize a daughter strand (red lines). During the short, intermediate stage (middle column), daughter strands are completely unmethylated, whereas parent strands have the same methylation patterns as before replication. Subsequently methyl groups are added to cytosines (right column). Failure of maintenance and de novo methylation events can occur, leading to differences in methylation patterns on parent and daughter strands. Binary vectors Pi, Qi and Di, where i = 1, 2, denote methylation patterns on a pre-replication parent strand, on a post-replication parent strand and on a daughter strand, respectively.
Here we consider the problem of using double-stranded DNA methylation patterns to estimate the rates at which failure of maintenance and de novo methylation events occur. We collected these double-stranded data using hairpin-bisulfite PCR (Laird et al. 2004), which was modified as in Miner et al. (2004) to include molecular codes to authenticate each DNA methylation pattern, removing redundant and contaminant patterns (details of the experimental design are in Supplementary Material Section 2 in Fu et al. 2009). Several features of hairpin-bisulfite PCR are particularly relevant to statistical modeling: (i) a short “hairpin” DNA sequence links together complementary parent and daughter strands; (ii) linked strand pairs are subject to bisulfite conversion which reveals their double-stranded methylation patterns; and (iii) errors arise due to imperfections in the bisulfite conversion process (Genereux et al., 2008). Thus, this method yields data, subject to measurement error due to bisulfite conversion, on methylation patterns for parent-daughter pairs from individual molecules. Current experimental technologies, however, cannot determine strand type, i.e. which strand is the parent and which the daughter.
Data on double-stranded methylation patterns obtained by hairpin-bisulfite PCR have previously been analyzed by Laird et al. (2004) and Genereux et al. (2005). The analysis in Laird et al. (2004), which is not explicitly likelihood-based, involves counting the number of events of each type at each site over strands and then averaging the counts over the two possible assignments of strand identity, assuming that de novo events occur only on the daughter strand. Genereux et al. (2005) assumed strict stationarity of the stochastic process that generates the data and based their analysis on a likelihood function for individual CpG sites without incorporating information about which observations at different sites in a double-stranded molecule are on the same strand, and which are on different strands. These existing analyses provide the foundations for our work here.
Here we develop a full statistical model for the data, exploiting information from contiguous sites rather than from individual sites alone. Three additional innovations of our modeling approach are (i) accounting for measurement errors, which are due to imperfections in the bisulfite conversion process; (ii) relaxing the strict stationarity assumption made in Genereux et al. (2005); and (iii) using a hierarchical structure to allow rates of key parameters to vary across sites without greatly increasing the effective size of the parameter space.
2. Models and Methods
2.1. Basic model and key assumptions
We consider data collected using hairpin-bisulfite PCR, on methylation states at S CpG sites on N double-stranded DNA molecules. We denote an unmethylated CpG site by 0, and a methylated CpG site by 1, so the data are N pairs of binary strings, {x1, y1}, …, {xN, yN}, each string being of length S. Current technologies are not able to identify strand type; that is, we do not know which data vector (xi or yi) arose from the parent strand and which from the daughter. Hence, we use {} to represent this lack of ordering in each observed pair. We initially assume that the data are observed without error and then relax this assumption.
Our model introduces latent random variables Qi and Di, each a binary vector, representing patterns of methylation on the parent strand and daughter strand, respectively. These binary vectors may be thought of as potentially-imperfect copies of the patterns of methylation on the unobserved pre-replication parent strand, which we denote by binary vector Pi (Figure 1). Differences between Pi and Di can arise due to failure of maintenance, or de novo methylation on the daughter strand; differences between Pi and Qi can arise due to de novo methylation on the parent strand. We assume that these three types of events occur independently of one another, and independently across individuals and across sites. Denoting the probabilities of these events at site j by 1 − μj, δdj and δpj, respectively, and assuming no spontaneous loss of methylation on the parent strand (explained below), we have
| (2.1) |
| (2.2) |
| (2.3) |
We are interested in estimating failure of maintenance and de novo methylation rates at CpG sites and assessing their variability across sites. We use λ = {μj, δpj, δdj, j = 1, ···, S} to denote the vector of parameters.
To derive the likelihood function for those parameters, we make three key assumptions. The first assumption is that there is no active removal of methyl groups on the parent strand. That is, if the parent strand is methylated before replication, then it will also be methylated after replication:
| (2.4) |
Although recent publications, such as Métivier et al. (2008) and Kangaspeska et al. (2008), suggest the possibility that transcriptionally active loci can have very rapid changes in methylation patterns which may be due to active removal of methyl groups from the template DNA, there is no evidence so far that this active removal occurs at inactive loci in leukocytes, the locus type and the cell type from which our data were collected. This assumption is also consistent with that underlies the models in Laird et al. (2004) and Genereux et al. (2005). The conditional probability in (2.4) then joins those in (2.1) – (2.3) to form a complete probabilistic characterization of the transmission process at a single CpG site.
The second assumption is that methylation events occur independently of one another across sites. Equations (2.1)–(2.4), together with this assumption, determine the conditional distribution of the ordered pair (Qi, Di) given Pi, which we denote hλ (Table 1). To complete the specification of the distribution of (Qij, Dij), we further model Pijs as independent Bernoulli random variables with methylation probability mj:
| (2.5) |
Table 1.
Probabilities of methylation events at site j, hλ(qij, dij; pij) = Pr ((Qij, Dij) = (qij, dij)|Pij = pij). The dagger † indicates cases not possible under the assumption of no active removal of methyl groups on the parent strand.
| (Qij, Dij) = (qij, dij) | Pij = pij | hλ (qij, dij; pij) | Methylation Event |
|---|---|---|---|
| (0, 0) | 1 | 0 | †Assumed not to occur |
| (0, 1) | 1 | 0 | †Assumed not to occur |
| (1, 0) | 1 | 1 − μj | Failure of maintenance |
| (1, 1) | 1 | μj | Maintenance |
| (0, 0) | 0 | (1 − δp;j)(1 − δd;j) | No de novo on parent or daughter |
| (0, 1) | 0 | (1 − δp;j) δd;j | De novo on daughter but not parent |
| (1, 0) | 0 | δp;j(1 − δd;j) | De novo on parent but not daughter |
| (1, 1) | 0 | δp;jδd;j | De novo on parent and daughter |
Under this second assumption, we obtain the likelihood function for a single double-stranded methylation pattern with known strand type as the product of probabilities of methylation patterns at individual sites, each probability summing over two possibilities of the methylation status (represented by pij) on the pre-replication parent strand Pi. Specifically, we give the likelihood for the case where xi contains data from the parent strand and yi contains data from the daughter strand:
| (2.6) |
Since strand type is unobserved, to get the probability of the observed double-stranded methylation pattern i we must sum over the two possible assignments of strand type:
| (2.7) |
where 1(A) is the indicator function, taking value 1 if condition A is true and 0 otherwise.
By making the third assumption that data from the N double-stranded methylation patterns are independent draws from the same distribution with parameter λ, we then obtain a likelihood function of λ for all N patterns:
| (2.8) |
| (2.9) |
2.2. Incorporating measurement error and estimating error rates
As mentioned in Section 1, imperfection in bisulfite conversion is an important source of potential measurement error here and in other applications involving bisulfite conversion. In brief, bisulfite conversion is an experimental technique that aims to convert unmethylated cytosines to a different base, uracil, thus allowing unmethylated and methylated locations to be identified by DNA sequencing. Imperfections during this process can lead to two types of error: failure of conversion, where bisulfite fails to convert an unmethylated cytosine (resulting in a truly unmethylated site being measured as methylated) and inappropriate conversion, where bisulfite converts a methylated cytosine to a thymine (leading to a truly methylated site being measured as unmethylated.) We let b = (b1, …, bS) and c = (c1, …, cS) denote the respective rates at which these two types of errors occur, where the elements bj and cj represent the error rates at site j.
To incorporate these measurement errors into the model, we introduce random variables and to denote the observed methylation states on the post-replication parent strand and the daughter strand, while continuing to use Qij and Dij to denote true methylation states on those two strands. We assume that errors occur independently across CpG sites and DNA strands, so that the conditional distribution of the observed data given the true states is given by
| (2.10) |
where each term on the right hand side is a function of bisulfite conversion error rates bj and cj as in Table 2.
Table 2.
Rates of bisulfite conversion error, which are conditional probabilities of the observed methylation state being different from a given true methylation state. Specifically, bj is the failure of conversion rate at site j and cj the inappropriate conversion rate.
| Observed ( or ) | |||
|---|---|---|---|
| 0 | 1 | ||
| Truth (Qij or Dij) | 0 | 1 − bj | bj |
| 1 | cj | 1 − cj | |
We extend the parameter vector λ to incorporate these measurement error parameters, λ = {μ, δp, δd, b, c}. The likelihood function, allowing for measurement error, becomes
| (2.11) |
where
| (2.12) |
and is defined similarly.
2.3. Hierarchical model for variability in rates across sites
In the above formulation we have allowed that rates may take different values across sites j = 1, …, S. In practice there is limited information about the rates at any given site, so attempting to estimate each of these parameters separately will produce highly variable estimates. To overcome this challenge we employ a hierarchical model to effectively reduce the dimensionality of the parameter space and to borrow strength across sites. In this hierarchical model we assume that the components of the vectors μ, δp, δd, m and c each follow a beta distribution.
In specifying these beta distributions, we find it convenient to use the parameterization Beta(r, g) to denote the beta distribution with mean r and variance gr(1 − r), hence referring to the parameter g as the “scaled” variance. The relationship between this parametrization and the conventional α–β parametrization is:
| (2.13) |
for a Beta(α, β) random variable X with density
| (2.14) |
We prefer the r–g parameterization in our analysis because (i) r and g are easily interpretable; and (ii) this parametrization facilitates specification of sensible priors – in particular it is reasonable to assume r and g to be independent a priori.
Our hierarchical model assumes a separate set of r and g for each of the vectors μ, δp, δd, b and c:
| (2.15) |
| (2.16) |
| (2.17) |
| (2.18) |
| (2.19) |
The methylation probability vector, m, is dealt with slightly differently, as described in the next section.
2.4. Incorporating stationarity
Previous analyses of these types of data (Genereux et al., 2005) have been based on the assumption that the transmission process has attained temporal stationarity; that is, at each site the proportion of methylated CpGs is stable over generations of cell division. Supporting biological evidence for this assumption comes from observations that methylation densities at the FMR1 locus were virtually unchanged over a five-year time span in several human males with fragile X syndrome (Stöger et al., 1997).
The assumption of stationarity in Genereux et al. (2005) imposes the following strict relationship between the methylation probability mj and the failure of maintenance and de novo methylation rates:
| (2.20) |
Requiring strict equality in this equation appears to be a rather strong assumption. Indeed, examples in Fu (2008) illustrate the strong effect this assumption can have on the likelihood surface. Thus, to avoid making this strong assumption, and to improve robustness to departures from strict stationarity, we exploit the exibility of the Bayesian modeling approach to allow for deviations from strict equality in (2.20).
Specifically, to incorporate stationarity we assume that each mj follows a beta distribution,
| (2.21) |
with mean parameter
| (2.22) |
This distribution on mj is centered on its expected value under the stationarity assumption, but allows for deviations, measured by gm: at a CpG site small values of gm represent near-stationarity, whereas large values indicate substantial deviations from stationarity.
2.5. Bayesian inference and choice of priors
We choose to use a Bayesian approach to fit the hierarchical model, specifying priors for the values of mean r and scaled variance g in beta distributions (2.15)–(2.19).
We assign an independent uniform prior to each r: a Uniform(0, 1) prior for each of rμ, rδp and rδd, and a Uniform(0, 0.06) prior for rc because experimental results suggest that measurement error rate cj is likely to be below 0.06. We can use a similar method to estimate rb (and gb) for the other error rate bj, although in our data analysis bj is fixed to an estimate obtained from experiments (see Section 3.)
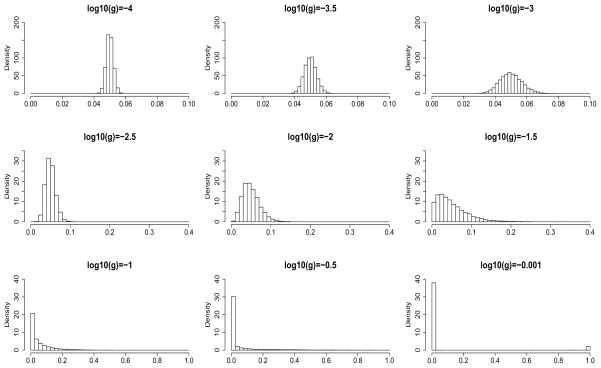
We assign a Uniform(−4, 0) prior to each log10g. This choice of prior has the exibility of capturing a wide range of beta distributions with qualitatively different levels of variability. Figure 2 illustrates this point: for a fixed mean value r, as log10g increases, the beta distribution becomes more and more spread out over the support (0, 1). In other words, this choice of prior on log10g allows us to model cases ranging from little variation (top row in Figure 2), to where a few sites have very different rates from the other sites (for example, bottom right plot in Figure 2). In Table 3 we provide guidelines on the interpretation of log10g.
Fig 2.
Shape of a beta distribution changes with respect to scaled variance g. Data were simulated for beta distributions with mean r = 0.05 and different values of scaled variance g. Ranges of the horizontal and the vertical axes are different between rows. As g increases, the histogram spreads out to the entire support of (0, 1) and a second peak at 1 starts to appear (bottom right panel).
Table 3.
Guidelines on the interpretation of the scaled variance g on the log10 scale.
| log10g | Variability |
|---|---|
| < −3 | very low |
| −3 to −2 | low |
| −2 to −1 | medium |
| > −1 | high |
We fit the model using Markov chain Monte Carlo (MCMC) methods (Supplementary Material Section 3 in Fu et al. 2009). To check the reliability of the output of these methods we applied the algorithm to many simulated datasets, and also confirmed that point estimates of parameters from simpler versions of the model we present here agreed closely with maximum likelihood estimates obtained from an expectation-maximization (EM) algorithm. See Fu (2008) for further details.
2.6. Origins of data
We collected DNA methylation patterns from the FMR1 locus (see Section 1 for associated disease) on the X chromosome in leukocytes using hairpin-bisulfite PCR (experimental conditions as in Laird et al. 2004 and Miner et al. 2004; also briefly discussed in Supplementary Material Section 2 in Fu et al. 2009). Due to cell-cell variation, double-stranded methylation patterns were collected from multiple cells in each individual sampled. The data analyzed here contain 169 double-stranded methylation patterns, each from a single cell, from 6 independent normal females (15–33 cells or patterns per individual) at 22 CpG sites (chrX: 146800867–146801008) in the promoter region of the FMR1 locus. Each female cell has two X chromosomes: one is hypermethylated, hence primarily inactive, and the other hypomethylated and hence primarily active. The data presented here are from the hypermethylated FMR1 locus on the inactive X chromosome in each cell sampled. Although this data set may be considered to be limited in size, the data are unusual in their double-strandedness compared to the single-stranded methylation data commonly produced from high-throughput technologies. A small subset of these data, which contains 33 methylation patterns at 7 CpG sites, was published in Genereux et al. (2005).
3. Results
We applied our model to the FMR1 data described above. Since these data were collected from the primarily hypermethylated (hence inactivated) X chromosome in normal females, the methylation density is high as expected: 81.9% of all CpG dyads are methylated on both strands, 6.4% are methylated on just one strand, and 11.7% are unmethylated on both strands (see Section 1 and Genereux et al., 2005 for previous analysis of a subset of the data).
Here we treat those double-stranded methylation patterns from the six different individuals as independent samples from a single, homogeneous population of methylation patterns. This treatment is effectively equivalent to assuming no variations in mj, μj, δpj and δdj across the individuals. This seems to be a reasonable starting point, given the current absence of evidence for notable variations in at least some of these parameters among individuals (Stöger et al., 1997). In a more elaborate analysis, however, we could relax this assumption by incorporating variability across individuals into our hierarchical model. Furthermore, our model does not distinguish between methylation patterns from X chromosomes inherited from the mother and those inherited from the father. Information on the parental origins of a given methylation pattern is not available for our FMR1 data.
The failure of bisulfite conversion rate, b, is relatively straightforward to estimate directly for the methylation patterns analyzed (Supplementary Material Section 2 in Fu et al. 2009). We estimated b to be 0.003 for our FMR1 data (Laird et al., 2004) and in the analysis here fixed it to be constant across sites. By comparison, the inappropriate conversion rate c is harder to obtain directly. We estimate this rate in our data analysis.
We performed three independent runs of our MCMC fitting procedure, each from a different starting point: two runs of 1.44 million iterations, and a third run of 2.88M iterations (total compute time ~160 hours on a 2.4GHz CPU). We sampled each MCMC run every 2K iterations (or 4K for the third run) after discarding the initial 20% of each run as burn-in. Trace plots displaying MCMC samples versus iterations (not shown) provided no indication of poor mixing. Histograms of key parameters from different runs (not shown) also agreed closely with one another. Results below come from pooling the samples from the three runs. These long runs were carried out to ensure convergence and may have exceeded necessity; in fact, we achieved similar results from much shorter pilot runs of 50K iterations. When using credible intervals to summarize posterior distributions we provide 80% coverage, which is not unduly influenced by long tails of the distributions.
3.1. Rate of measurement error due to inappropriate bisulfite conversion, and its variability
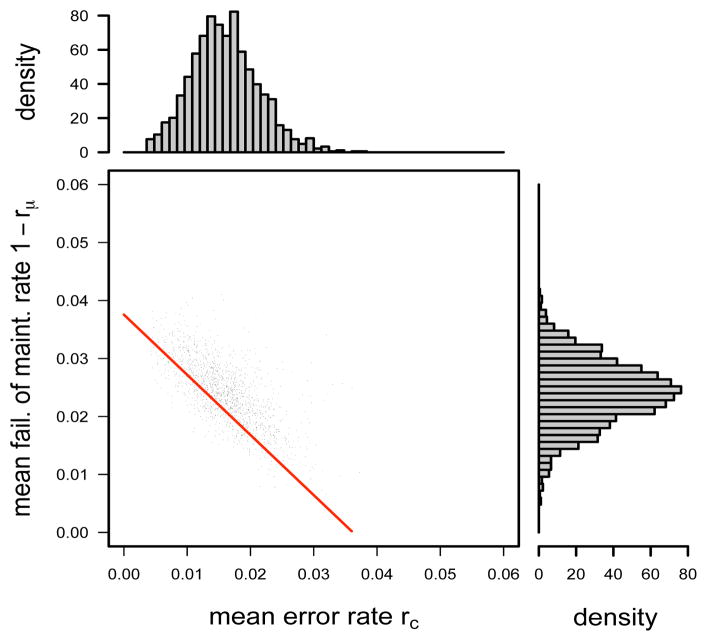
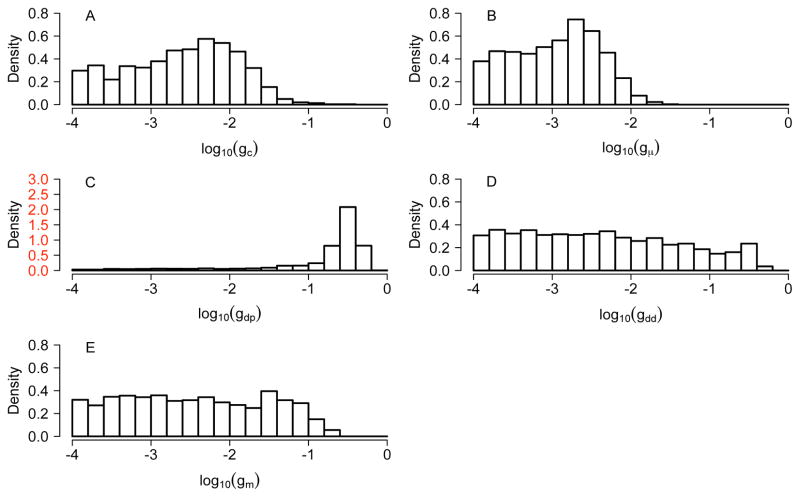
The FMR1 data provide strong evidence for the occurrence of inappropriate conversion error: the posterior distribution for the mean error rate rc across CpG sites is centered on 0.016, with 80% credible interval (CI) of (0.009, 0.023) (top histogram in Figure 3), and there is little probability mass very near 0. The posterior distribution for scaled variance gc is concentrated on small values, suggesting that the error rate c does not vary greatly across CpG sites (Figure 4A), in accord with experimental findings (Genereux et al., 2008).
Fig 3.
Posterior distributions and scatter plot of mean failure of maintenance rate, 1−rμ, and mean error rate, rc, under the multi-site model for the FMR1 data. The red line, 1−μ = 1.04c+0.04, indicates a predicted relationship for these estimates under a much simpler analysis (see Section 3.2).
Fig 4.
Posterior distributions of log10 g for the FMR1 data. g in (A)–(D) is the scaled variance in the beta distribution assumed for (A) measurement error rate c (due to inappropriate bisulfite conversion); (B) failure of maintenance rate 1 − μ; (C) parent de novo rate δp and (D) daughter de novo rate δd. In (E), gm reflects deviation from the stationarity assumption. See Table 3 for guidelines on the interpretation of values of log10g. The y-axis in (C) has a wide range.
3.2. Failure of maintenance rate and its variability
We estimate the mean failure of maintenance rate 1 − rμ across CpG sites to be 0.024 (80% CI: 0.017–0.031; side histogram in Figure 3). MCMC samples of 1−rμ and rc show a striking linear relationship (Figure 3), suggesting a degree of unidentifiability in these parameters. This relationship turns out to conform very closely to predictions under a much simpler analysis based on summarizing the FMR1 data by the overall proportions of methylated, hemimethylated and unmethylated sites (pM, pH, pU) = (0.82, 0.064, 0.116) (red line in Figure 3; see the simple analysis in Supplementary Material Section 4.1 in Fu et al. 2009). This agreement between two very different analysis approaches suggests the robustness of the inference that 1 − rμ and rc lie close to this line. The fact that our MCMC samples are concentrated on only part of this line reflects the additional information we are able to extract from the full data by making more detailed modeling assumptions as stated in Section 2.1. The inference, of course, must then be less robust to deviations from these assumptions.
Regarding variability of 1 − μ across CpG sites, the data suggest that this variability is low, since the posterior for gμ is concentrated around small values (Figure 4B).
3.3. De novo methylation rates and their variability
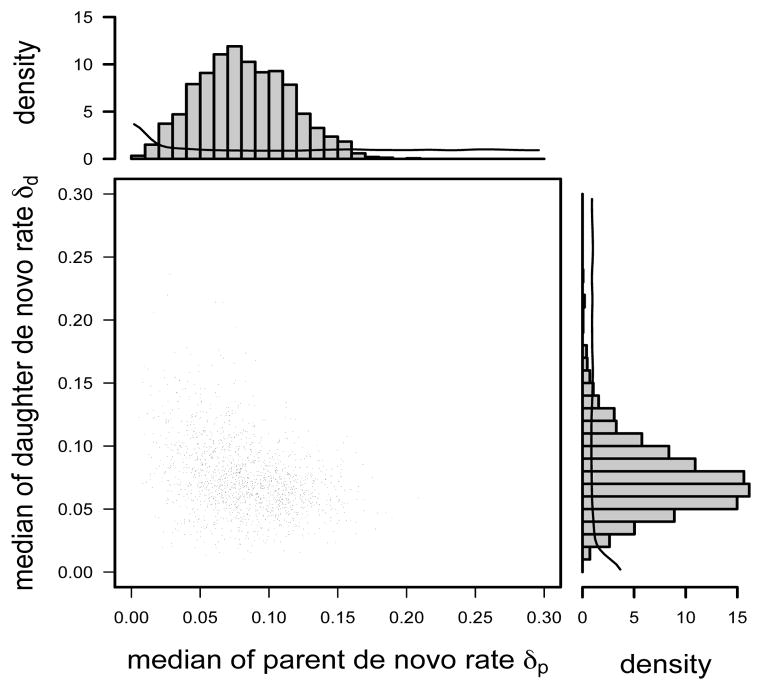
Our results suggest that de novo rates may be substantially larger than failure of maintenance rates (which can happen even at stationarity): the posterior distribution for the median daughter and parent de novo rates are centered on 0.08 and 0.07, respectively, with very low probability mass near 0 (histograms in Figure 5). These high rate estimates are consistent with, and may partly explain, the high overall methylation rates in this genomic region. There is, however, considerable uncertainty in these estimates: 80% CIs are 0.04–0.13 and 0.04–0.11, respectively (histograms in Figure 5). Note that the scatter plot shows that these two parameters are not independent, a posteriori: in particular it is unlikely that both de novo rates are at the upper end of these CIs (no MCMC sample in the scatter plot in Figure 5 has both rates > 0.13).
Fig 5.
Posterior distributions and scatter plot of median de novo rates δp and δd under the multi-site model for the FMR1 data. Smooth curves in the histograms are density functions of the median of 22 beta random variables, each corresponding to a parent (or daughter) de novo rate at a CpG site. The two density curves are identical because the prior distributions for the rates are identical.
One biological question of interest is whether or not de novo events occur on both parent and daughter strands. We do not conduct a formal test of hypotheses here, but we note that the posterior distribution of the median of each de novo rate has little probability mass near 0 (Figure 5), in contrast to the prior distribution, providing informal support for both parent and daughter de novo events occuring.
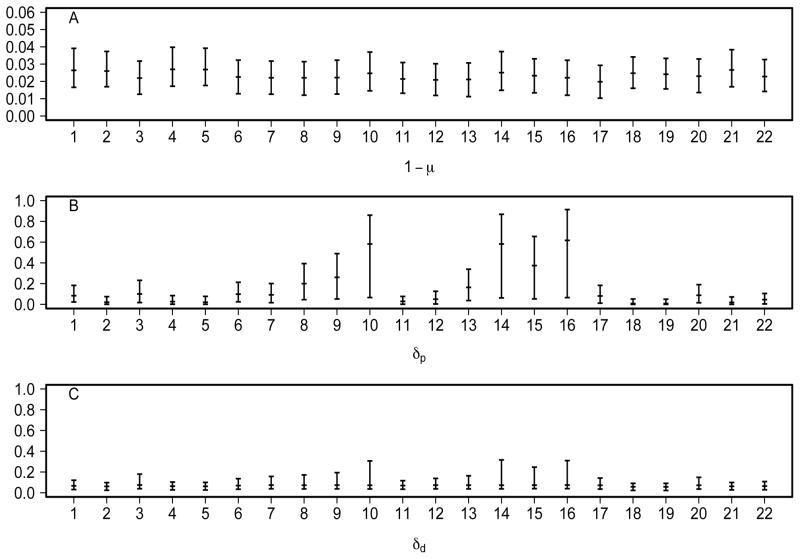
Regarding variability across sites, the data are uninformative for variability in the daughter de novo rate: the posterior for log10gdd is at over the whole support (Figure 4D). In contrast, the parent de novo rate δp may vary considerably across sites: log10gdp is concentrated on large values (see Figure 4C and compare with the bottom right panel in Figure 2). Furthermore, a few outlying sites have possibly high rates (Figure 6B, in contrast to little variation in 1− μ in 6A and in δd in 6C), which may have a strong influence on the mean value across sites. This large variability makes it difficult to estimate mean de novo rates and renders them misleading in summarizing site-specific δps. Therefore we have chosen to report the median de novo rates.
Fig 6.
Median and 80% credible intervals of CpG-site-specific estimates of (A) failure of maintenance rates 1 − μ, (B) parent de novo rates δp and (C) daughter de novo rates δd under the multi-site model for the FMR1 data. The numbering of the CpG sites follows the convention established in Stöger et al. (1997).
The observation that δp may vary considerably across sites brings into question the suitability of our assumption of a single beta distribution for these rates, since this assumption has limited exibility in dealing with potential outliers. To examine this issue we modified our model to allow the de novo rate parameters to follow a mixture of two beta distributions, where the component corresponding to the outlying sites was assumed to be Uniform( 0,1) (i.e. Beta(α = 1, β = 1)). Analyses using this model continued to suggest that some sites (specifically sites 10, 14, 15 and 16) may have substantially higher parent de novo rates than others (see Fu 2008 for further details). Indeed, the data at these four sites are characterized by particularly small numbers of unmethylated CpG dyads (0 at site 16, 1 at sites 10 and 14, and 3 at site 15, in contrast to the median of 20 at other sites).
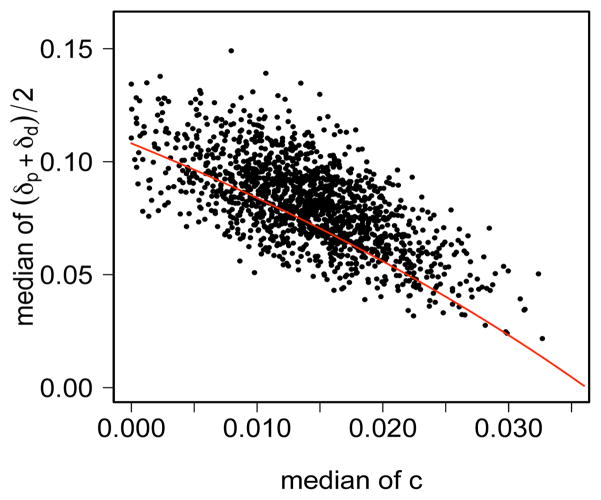
Our analysis differs from previous analyses by accounting for measurement errors which have rate c. To gain insight into how incorporating error rates affects estimated de novo rates, we examined the joint posterior distribution of c and the average de novo rate (Figure 7). As in the analagous plot for failure of maintenance rate (Figure 3), posterior samples here also lie close to a line, which is in close agreement with a simple analysis based on summary statistics (Supplementary Material Section 4.1 in Fu et al. 2009). Remarks made above in Section 3.2 regarding robustness of the conclusions apply equally here.
Fig 7.
Joint posterior distribution of the median of the average of the parent and daughter de novo rates, (δp+δd)=2, and the median of the error rate c for the FMR1 data. The red curve, (δp + δd)=2 = 0.44 + 0.05=(c − 0.15), indicates a predicted relationship for these estimates under a much simpler analysis (see text).
Another important novel contribution of our analysis is that, by modeling the strand information in multi-site data, we can distinguish, at least in principle, between the two different types of de novo events. This novel feature makes it possible to draw several conclusions mentioned above, particularly that the data support the occurrence of both parent and daughter de novo events, and that the data provide different information on the variability of δp and δd. However, due to the relative complexity of our model it is difficult to identify the source of the information that distinguishes daughter de novo events from parent de novo events. To gain insight we examined the multi-site likelihood for a single methylation pattern in some detail (Supplementary Material Section 4.2 in Fu et al. 2009). A conclusion from this investigation is that, assuming stationarity (or, in fact under weaker assumptions) data on methylation patterns where one strand is much more methylated than the other will tend to favor large estimates of δp relative to δd. Additionally, the more methylated strand will tend to be the parent strand. Thus, an intuitive explanation of our inference that sites 10, 14, 15 and 16 have large δp is that some patterns, with large differences in the methylation density on the two strands, are hemimethylated at these sites (with the methylated CpG more likely to be on the overall more methylated strand). The novel insights into the de novo rates we gain here are further discussed in Section 4.
3.4. Stationarity
To examine the extent to which the data are consistent with a stationary model, we consider the posterior distribution of log10 gm, which reflects deviations from stationarity (Figure 4E). This posterior largely follows the uniform prior, except that large values are excluded. We conclude that the data do not exhibit large deviations from stationarity, although they do not provide strong support for the strict stationarity assumption either.
3.5. Impact of bisulfite conversion errors on the estimation of failure of maintenance and de novo methylation rates
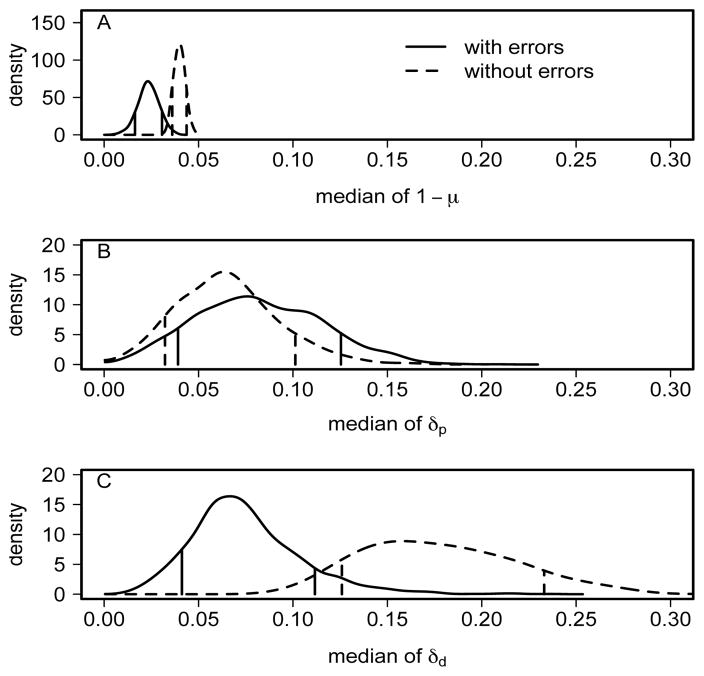
Our analyses above incorporate both types of bisulfite conversion errors, which have not been accounted for in previous analyses of methylation patterns (see, for example, Genereux et al. 2005; Laird et al. 2004; Ushijima et al. 2003; Pfeifer et al. 1990). It seems possible that our incorporation of measurement error may be the main reason for discrepancies between our estimates of rates of methylation events and estimates from these previous analyses. To assess this we reran the multi-site model on the FMR1 data, setting the two measurement error rates b and c to be 0, which corresponds to ignoring both types of bisulfite conversion errors. We carried out three independent runs from different starting points. Each run consisted of 1.44 million iterations, including 20% burn-in, and took about 38 hours. These runs gave consistent results, so we pooled the three runs to produce the posterior distributions.
Our results show that incorporating measurement errors indeed has substantial effects on the inference of failure of maintenance rate 1 − μ and daughter de novo rate δd (Figure 8A and C) but little effects on parent de novo rate δp (Figure 8B). Estimates of these two rates under the no-error model are largely consistent with previous results (Laird et al., 2004; Genereux et al., 2005). This comparison suggests that whether or not measurement error is accounted for may have been an important factor in producing different inferences.
Fig 8.
Impact of measurement errors (due mainly to inappropriate bisulfite conversion error) on the inference of the rates of methylation events. Solid lines incorporate these errors, whereas dashed lines do not. From top to bottom are posterior densities of medians of (A) failure of maintenance rate 1 − μ, (B) parent de novo rate δp and (C) daughter de novo rate δd. Vertical bars indicate the 80% credible interval (10% and 90% percentiles) for each density.
4. Discussion and Conclusions
We have developed a statistical model for double-stranded DNA methylation patterns to investigate a central problem in epigenetic biology: the transmission fidelity of DNA methylation patterns in somatic mammalian cells. Our modeling approach addresses several challenges that are inherent in these data and that have not been approached by previous methods. Key innovations of our model include the incorporation of measurement error and the incorporation of available “phase” information, i.e. which hemimethylated CpG dyads are methylated on the same strand, by examining multiple sites simultaneously. The first innovation is important because, as we have shown, measurement error has a substantial effect on estimates of fidelity rates. The second is important because it allows us both to separately estimate parent and daughter de novo rates, and to relax the strict stationarity assumption that underlies most existing approaches (see, for example, Otto and Walbot 1990; Pfeifer et al. 1990; Genereux et al. 2005).
By applying our new model to the FMR1 data, we gained several new insights into methylation transmission fidelity rates. Below we summarize our findings and compare them with other studies.
Inappropriate bisulfite conversion can be a significant source of measurement error. We estimated the mean rate of this error in our data set to be 0.016 (80% CI: 0.009–0.023). As far as we are aware, ours is the first estimate of this inappropriate conversion rate obtained from genomic methylation pattern data that are double-stranded and molecularly-validated (see Section 1 for detail on data collection). Our estimate of this rate is lower than that obtained by Genereux et al. (2008) using synthetic oligonucleotides (average rate 0.035; 95% confidence interval: 0.027–0.049). This difference may derive, in part, from the different lengths of the DNAs used in the two experiments (Genereux et al., 2008).
We estimated the mean maintenance rate μ to be 0.976 (80% CI: 0.969–0.983). This is higher than previous estimates for similar data (Laird et al., 2004; Genereux et al., 2005), which can be mostly explained by the fact that these previous analyses did not account for bisulfite conversion errors. On the other hand, Pfeifer et al. (1990) estimated the maintenance rate to be much higher (about 0.999), which is mainly due to a high overall methylation density (~ 0.98) at the site analyzed.
We found suggestive evidence that de novo events occur on both parent and daughter strands, in that posterior distributions for both parent and daughter de novo rates have little probability mass near 0. Previous empirical studies have asked whether de novo events can occur on the parent strand (Kappler, 1970; Adams, 1971; Schneiderman and Billen, 1973; Bird, 1978), yielding conflicting conclusions for different cell types. Recent analyses still could not address this question because phase information was either not available (Pfeifer et al., 1990; Ushijima et al., 2003) or not incorporated in their models (Laird et al., 2004; Genereux et al., 2005). To accommodate those limitations, Pfeifer et al. (1990) estimated the total de novo rate as a whole, whereas Laird et al. (2004) and Genereux et al. (2005) imposed additional constraints that are equivalent to estimating the total de novo rates. Potential implifications of a positive parent de novo rate are discussed in Genereux (2009).
We also found some evidence that parent de novo rates vary considerably across sites. In particular sites 10, 14, 15 and 16 in our data may experience unusually high parent de novo rates. Analyses of the data at these sites individually using the single-site approach from Genereux et al. (2005) also suggested potentially large values for the total de novo rate at these sites, although the single-site approach was unable to separately estimate the de novo rates on parent and daughter strands.
Some previous studies estimated an overall methylation transmission fidelity rate, tracking methylation patterns over one (Bird, 1978) or more (Ushijima et al., 2003) rounds of DNA replication. Different experimental techniques and sampling procedures used in these studies led to data of very different types from that of our FMR1 data. A fair comparison of the results is difficult to carry out because of these differences and is therefore not addressed here.
A limitation of our model is the assumption that methylation events occur independently across CpG sites. This assumption does not seem to hold in practice, especially for maintenance events, in light of current research on methylation enzymes (Vilkaitis et al., 2005; Goyal et al., 2006). It is therefore of great interest to study the dependence structure. In separate work we developed statistical models to incorporate the dependence (Fu, 2008). Our preliminary results there yielded similar estimates of at least the mean rates (parameter r) of the methylation events to the estimates in this paper.
As more hairpin-bisulfite PCR data become available, the new statistical analysis methods described here may continue to provide novel biological insights into epigenetic fidelity. The estimation precision will improve as new experimental protocols yield data with lower measurement error rates (Genereux et al., 2008) and lead to better estimates of de novo methylation rates. With our statistical methods one can investigate differences among fidelity rates in different genomic regions. For example, our model can be applied also to sparsely methylated CpG islands where de novo rates may take on a wider range of values than in densely methylated regions (Ushijima et al., 2003; Laird et al., 2004). Furthermore, relaxation of the stationarity condition gives our methods great exibility to examine the transmission of methylation patterns in cases where methylation densities are dynamic rather than stationary. Many of these cases have important clinical and pharmaceutical implications; they include early developmental stages characterized by loss and re-establishment of methylation patterns (Reik et al., 2001), ageing during which methylation patterns may change over time in at least certain cell types (Wilson and Jones, 1983), and in several types of cancer in which methylation patterns change rapidly over cell generations (Foster et al., 1998). These cases will pose new challenges. For instance, sets of methylation patterns collected from cancer patients may be sampled from a mixture of cancer cells and normal cells. Successful analysis of such data must account for the existence of these subpopulations, a challenging yet intriguing research direction for the future.
Supplementary Material
Acknowledgments
The authors would like to acknowledge the invaluable contribution Brooks Miner made to the collection of the FMR1 data analyzed in this paper, a small subset of which was presented and analyzed previously by Genereux, Miner, Bergstrom and Laird (Genereux et al., 2005). Thanks also go to Krista Gile, Peter Hoff, Vladmir Minin and Elizabeth Thompson for stimulating discussions and thought-provoking questions. The authors are grateful to the editor and two anonymous referees for their excellent comments and questions, which have greatly improved this paper.
Footnotes
(doi: ???http://lib.stat.cmu.edu/aoas/???/???). The pdf file contains biological background, experimental design issues, Markov chain Monte Carlo (MCMC) procedures and likelihood analyses for special cases. Other files include the FMR1 data analyzed in this paper, the R code that implements the MCMC procedure and MCMC outputs summarized and displayed in the Results section.
Contributor Information
Audrey Qiuyan Fu, Email: audrey@stat.washington.edu.
Diane P. Genereux, Email: genereux@u.washington.edu.
Reinhard Stöger, Email: Reinhard.Stoger@Nottingham.ac.uk, stoeger@u.washington.edu.
Charles D. Laird, Email: cdlaird@u.washington.edu.
Matthew Stephens, Email: mstephens@uchicago.edu.
References
- Adams RL. Methylation of newly synthesized and older deoxyribonucleic acid. Biochem J. 1971;123:38P. doi: 10.1042/bj1230038pa. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bird A. Use of restriction enzymes to study eukaryotic DNA methylation: II. the symmetry of methylated sites supports semi-conservative copying of the methylation pattern. J Mol Biol. 1978;118:49–60. doi: 10.1016/0022-2836(78)90243-7. [DOI] [PubMed] [Google Scholar]
- Bird A. DNA methylation patterns and epigenetic memory. Genes Dev. 2002;16:6–21. doi: 10.1101/gad.947102. [DOI] [PubMed] [Google Scholar]
- Bird A. Perceptions of epigenetics. Nature. 2007;447:396–398. doi: 10.1038/nature05913. [DOI] [PubMed] [Google Scholar]
- Chen Z, Riggs AD. Maintenance and regulation of DNA methylation patterns in mammals. Biochem Cell Biol. 2005;83:438–448. doi: 10.1139/o05-138. [DOI] [PubMed] [Google Scholar]
- Ehrlich M, Gama-Sosa MA, Huang LH, Midgett RM, Kuo KC, McCune RA, Gehrke C. Amount and distribution of 5-methylcytosine in human DNA from different types of tissues or cells. Nucleic Acids Res. 1982;10(8):2709–2721. doi: 10.1093/nar/10.8.2709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster SA, Wong DJ, Barrett MT, Galloway DA. Inactivation of p16 in human mammary epithelial cells by CpG island methylation. Mol Cell Biol. 1998;18(4):1793–1801. doi: 10.1128/mcb.18.4.1793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu AQ, Genereux DG, Stöger R, Laird CD, Stephens M. Supplement to “Statistical Inference of Transmission Fidelity of DNA Methylation Patterns Over Somatic Cell Divisions in Mammals”. 2009 doi: 10.1214/09-AOAS297SUPPA. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Q. PhD dissertation. University of Washington; 2008. Models and Inference of Transmission of DNA Methylation Patterns in Mammalian Somatic Cells. [Google Scholar]
- Genereux DP. Asymmetric strand segregation: epigenetic costs of genetic fidelity? PLoS Genet. 2009;5(6):e1000509. doi: 10.1371/journal.pgen.1000509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genereux DP, Johnson WC, Burden AF, Stöger R, Laird CD. Errors in the bisulfite conversion of DNA: modulating inappropriate- and failed-conversion frequencies. Nucleic Acids Res. 2008;36(22):e150. doi: 10.1093/nar/gkn691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genereux DP, Miner BE, Bergstrom CT, Laird CD. A population-epigenetic model to infer site-specific methylation rates from double-stranded DNA methylation patterns. Proc Natl Acad Sci USA. 2005;102:5802–5807. doi: 10.1073/pnas.0502036102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goyal R, Reinhardt R, Jeltsch A. Accuracy of DNA methylation pattern perservation by the Dnmt1 methyltransferase. Nucleic Acids Res. 2006;34(4):1182–1188. doi: 10.1093/nar/gkl002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones PA, Baylin SB. The fundamental role of epigenetic events in cancer. Nature Rev Genet. 2002;3:415–428. doi: 10.1038/nrg816. [DOI] [PubMed] [Google Scholar]
- Kangaspeska S, Stride B, Métivier R, Polycarpou-Schwarz M, Ibberson D, Carmouche RP, Benes V, Gannon F, Reid G. Transient cyclical methylation of promoter DNA. Nature. 2008;452(6):112–116. doi: 10.1038/nature06640. [DOI] [PubMed] [Google Scholar]
- Kappler JW. The kinetics of DNA methylation in cultures of a mouse adrenal cell line. J Cell Physiol. 1970;75:21–31. doi: 10.1002/jcp.1040750104. [DOI] [PubMed] [Google Scholar]
- Laird CD. Proposed mechanism of inheritance and expression of the human fragile-X syndrome of mental retardation. Genetics. 1987;117:587–599. doi: 10.1093/genetics/117.3.587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird CD, Pleasant ND, Clark AD, Sneeden JLS, Hassan KMA, Manley NC, Vary JC, Morgan T, Hansen RS, Stöger R. Hairpin-bisulfite PCR: assessing epigenetic methylation patterns on complementary strands of individual DNA molecules. Proc Natl Acad Sci USA. 2004;101:204–209. doi: 10.1073/pnas.2536758100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird PW. The power and the promise of DNA methylation markers. Nature Rev Cancer. 2003;3:253–266. doi: 10.1038/nrc1045. [DOI] [PubMed] [Google Scholar]
- Métivier R, Gallais R, Tiffoche C, Le Péron C, Jurkowska RZ, Carmouche RP, Ibberson D, Barath P, Demay F, Reid G, Benes V, Jeltsch A, Gannon F, Salbert G. Cyclical DNA methylation of a transcriptionally active promoter. Nature. 2008;452(6):45–52. doi: 10.1038/nature06544. [DOI] [PubMed] [Google Scholar]
- Miner BE, Stöger RJ, Burden AF, Laird CD, Hansen RS. Molecular barcodes detect redundancy and contamination in hairpin-bisulfite PCR. Nucleic Acids Res. 2004;32:e135. doi: 10.1093/nar/gnh132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto S, Walbot V. DNA methylation in eukaryotes: kinetics of demethylation and de novo methylation during the life cycle. Genetics. 1990;124:429–437. doi: 10.1093/genetics/124.2.429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeifer G, Steigerwald S, Hansen R, Gartler S, Riggs A. Polymerase chain reaction-aided genomic sequencing of an X chromosome-linked CpG island: methylation patterns suggest clonal inheritance, CpG site autonomy, and an explanation of activity state stability. Proc Natl Acad Sci USA. 1990;87:8252–8256. doi: 10.1073/pnas.87.21.8252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reik W, Dean W, Walter J. Epigenetic reprogramming in mammalian development. Science. 2001;293(5532):1089–1093. doi: 10.1126/science.1063443. [DOI] [PubMed] [Google Scholar]
- Robertson KD, Wolffe AP. DNA methylation in health and disease. Nature Rev Genet. 2000;1:11–19. doi: 10.1038/35049533. [DOI] [PubMed] [Google Scholar]
- Schneiderman MH, Billen D. Methylation rapidly reannealing DNA during the cell cycle of chinese hamster cells. Biochim Biophys Acta. 1973;308:352–360. doi: 10.1016/0005-2787(73)90327-4. [DOI] [PubMed] [Google Scholar]
- Stöger R, Kajimura TM, Brown WT, Laird CD. Epigenetic variation illustrated by DNA methylation patterns of the fragile-X gene FMR1. Hum Mol Genet. 1997;6:1791–1801. doi: 10.1093/hmg/6.11.1791. [DOI] [PubMed] [Google Scholar]
- Ushijima T, Watanabe N, Okochi E, Kaneda A, Sugimura T, Miyamoto K. Fidelity of the methylation pattern and its variation in the genome. Genome Res. 2003;13(5):868–874. doi: 10.1101/gr.969603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilkaitis G, Suetake I, Klimašauskas S, Tajima S. Processive methylation of hemimethylated CpG sites by mouse Dnmt 1 DNA methyltransferase. J Biol Chem. 2005;280(1):64–72. doi: 10.1074/jbc.M411126200. [DOI] [PubMed] [Google Scholar]
- Wilson VL, Jones PA. DNA methylation decreases in aging but not in immortal cells. Science. 1983;220(4601):1055–1057. doi: 10.1126/science.6844925. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.