Theoretical Analysis of Heuristic Search Methods for Online POMDPs

Abstract

Planning in partially observable environments remains a challenging problem, despite significant recent advances in offline approximation techniques. A few online methods have also been proposed recently, and proven to be remarkably scalable, but without the theoretical guarantees of their offline counterparts. Thus it seems natural to try to unify offline and online techniques, preserving the theoretical properties of the former, and exploiting the scalability of the latter. In this paper, we provide theoretical guarantees on an anytime algorithm for POMDPs which aims to reduce the error made by approximate offline value iteration algorithms through the use of an efficient online searching procedure. The algorithm uses search heuristics based on an error analysis of lookahead search, to guide the online search towards reachable beliefs with the most potential to reduce error. We provide a general theorem showing that these search heuristics are admissible, and lead to complete and ε-optimal algorithms. This is, to the best of our knowledge, the strongest theoretical result available for online POMDP solution methods. We also provide empirical evidence showing that our approach is also practical, and can find (provably) near-optimal solutions in reasonable time.

1 Introduction

Partially Observable Markov Decision Processes (POMDPs) provide a powerful model for sequential decision making under state uncertainty. However exact solutions are intractable in most domains featuring more than a few dozen actions and observations. Significant efforts have been devoted to developing approximate offline algorithms for larger POMDPs [1, 2, 3, 4]. Most of these methods compute a policy over the entire belief space. This is both an advantage and a liability. On the one hand, it allows good generalization to unseen beliefs, and this has been key to solving relatively large domains. Yet it makes these methods impractical for problems where the state space is too large to enumerate. A number of compression techniques have been proposed, which handle large state spaces by projecting into a sub-dimensional representation [5, 6]. Alternately online methods are also available [7, 8, 9, 10, 11, 12]. These achieve scalability by planning only at execution time, thus allowing the agent to only consider belief states that can be reached over some (small) finite planning horizon. However despite good empirical performance, both classes of approaches lack theoretical guarantees on the approximation. So it would seem we are constrained to either solving small to mid-size problems (near-)optimally, or solving large problems possibly badly.

This paper suggests otherwise, arguing that by combining offline and online techniques, we can preserve the theoretical properties of the former, while exploiting the scalability of the latter. In previous work [12], we introduced an anytime algorithm for POMDPs which aims to reduce the error made by approximate offline value iteration algorithms through the use of an efficient online searching procedure. The algorithm uses search heuristics based on an error analysis of lookahead search, to guide the online search towards reachable beliefs with the most potential to reduce error. In this paper, we derive formally the heuristics from our error minimization point of view and provide theoretical results showing that these search heuristics are admissible, and lead to complete and ε-optimal algorithms. This is, to the best of our knowledge, the strongest theoretical result available for online POMDP solution methods. Furthermore the approach works well with factored state representations, thus further enhancing scalability, as suggested by earlier work [2]. We also provide empirical evidence showing that our approach is computationally practical, and can find (provably) near-optimal solutions within a smaller overall time than previous online methods.

2 Background: POMDP

A POMDP is defined by a tuple (S, A, Ω, T, R, O, γ) where S is the state space, A is the action set, Ω is the observation set, T: S × A × S → [0, 1] is the state-to-state transition function, R: S × A ℛ is the reward function, O: Ω × A × S → [0, 1] is the observation function, and γ is the discount factor. In a POMDP, the agent often does not know the current state with full certainty, since observations provide only a partial indicator of state. To deal with this uncertainty, the agent maintains a belief state b(s), which expresses the probability that the agent is in each state at a given time step. After each step, the belief state b is updated using Bayes rule. We denote the belief update function b′ = τ(b, a, o), defined as b′(s′) =ηO(o, a, s′) Σ_s∈S T (s, a, s′)b(s), where η is a normalization constant ensuring Σ_s∈S b′(s) = 1.

Solving a POMDP consists in finding an optimal policy, π^*: ΔS → A, which specifies the best action a to do in every belief state b, that maximizes the expected return (i.e., expected sum of discounted rewards over the planning horizon) of the agent. We can find the optimal policy by computing the optimal value of a belief state over the planning horizon. For the infinite horizon, the optimal value function is defined as V^*(b) = max_a∈A [R(b, a) + γ Σ_o∈Ω P(o|b, a)V^*(τ(b, a, o))], where R(b, a) represents the expected immediate reward of doing action a in belief state b and P(o|b, a) is the probability of observing o after doing action a in belief state b. This probability can be computed according to P(o|b, a) = Σ_s′∈S O(o, a, s′) Σ_s∈S T(s, a, s′)b(s). We also denote the value Q^*(b, a) of a particular action a in belief state b, as the return we will obtain if we perform a in b and then follow the optimal policy Q^*(b, a) = R(b, a) + γ Σ_o∈Ω P(o|b, a) V^*(τ (b, a, o)). Using this, we can define the optimal policy π^*(b) = argmax_a∈A Q^*(b, a).

While any POMDP problem has infinitely many belief states, it has been shown that the optimal value function of a finite-horizon POMDP is piecewise linear and convex. Thus we can define the optimal value function and policy of a finite-horizon POMDP using a finite set of |S|-dimensional hyper plans, called α-vectors, over the belief state space. As a result, exact offline value iteration algorithms are able to compute V^*in a finite amount of time, but the complexity can be very high. Most approximate offline value iteration algorithms achieve computational tractability by selecting a small subset of belief states, and keeping only those α-vectors which are maximal at the selected belief states [1, 3, 4]. The precision of these algorithms depend on the number of belief points and their location in the space of beliefs.

3 Online Search in POMDPs

Contrary to offline approaches, which compute a complete policy determining an action for every belief state, an online algorithm takes as input the current belief state and returns the single action which is the best for this particular belief state. The advantage of such an approach is that it only needs to consider belief states that are reachable from the current belief state. This naturally provides a small set of beliefs, which could be exploited as in offline methods. But in addition, since online planning is done at every step (and thus generalization between beliefs is not required), it is sufficient to calculate only the maximal value for the current belief state, not the full optimal α-vector. A lookahead search algorithm can compute this value in two simple steps.

First we build a tree of reachable belief states from the current belief state. The current belief is the top node in the tree. Subsequent belief states (as calculated by the τ(b, a, o) function) are represented using OR-nodes (at which we must choose an action) and actions are included in between each layer of belief nodes using AND-nodes (at which we must consider all possible observations). Note that in general the belief MDP could have a graph structure with cycles. Our algorithm simply handle such structure by unrolling the graph into a tree. Hence, if we reach a belief that is already elsewhere in the tree, it will be duplicated.¹

Second, we estimate the value of the current belief state by propagating value estimates up from the fringe nodes, to their ancestors, all the way to the root. An approximate value function is generally used at the fringe of the tree to approximate the infinite-horizon value. We are particularly interested in the case where a lower bound and an upper bound on the value of the fringe belief states is available. We pay special attention to this case because it allows the use of branch & bound pruning in the tree, thus potentially significantly cutting down on the number of nodes that must be expanded during the search. The lower and upper bounds can be propagated to parent nodes according to:

$$U_T(b)=\{\begin{array}{ll}U(b)\hfill & \text{if}b\text{is}\text{a}\text{leaf}\text{in}T,\hfill \\ {max}_{a\in A}{U}_T(b,a)\hfill & \text{otherwise};\hfill \end{array}$$ (1)

$$U_T(b,a)=R_B(b,a)+\gamma \sum _{o\in \mathrm{\Omega }}P(o\mid b,a)U_T(\tau (b,a,o));$$ (2)

$$L_T(b)=\{\begin{array}{ll}L(b)\hfill & \text{if}b\text{is}\text{a}\text{leaf}\text{in}T,\hfill \\ {max}_{a\in A}{L}_T(b,a)\hfill & \text{otherwise};\hfill \end{array}$$ (3)

$$L_T(b,a)=R_B(b,a)+\gamma \sum _{o\in \mathrm{\Omega }}P(o\mid b,a)L_T(\tau (b,a,o));$$ (4)

where U_T (b) and L_T (b) represent the upper and lower bounds on V^*(b) associated to belief state b in the tree T, U_T (b, a) and L_T (b, a) represent corresponding bounds on Q^*(b, a), and L(b) and U(b) are the bounds on fringe nodes, typically computed offline.

An important motivation for doing an online search is that it allows us to have a value estimate at the current belief which has lower error than the estimate at the fringe nodes. This follows directly from the result by Puterman [14] showing that a complete k-step lookahead multiplies the error bound on the approximate value function used at the fringe by γ^k, and therefore reduces the error bound.

Of course a k-step lookahead search has complexity exponential in k, and may explore belief states that have very small probabilities of occurring (and an equally small impact on the value function) as well as exploring suboptimal actions (which have no impact on the value function). We would evidently prefer to have a more efficient online algorithm, which can guarantee equivalent or better error bounds. In particular, we believe that the best way to achieve this is to have a search algorithm which uses estimates of error reduction as a criteria to guide the search over the reachable beliefs.

4 Anytime Error Minimization Search

In this section, we review the Anytime Error Minimization Search (AEMS) algorithm we had first introduced in [12] and present a novel mathematical derivation of the heuristics that we had suggested. We also provide new theoretical results describing sufficient conditions under which the heuristics are guaranteed to yield ε-optimal solutions.

Our approach uses a best-first search of the belief reachability tree, where error minimization (at the root node) is used as the search criteria to select which fringe nodes to expand next. Thus we need a way to express the error on the current belief (i.e. root node) as a function of the error at the fringe nodes. This is provided in Theorem 1. Let us denote:

• (i) ℱ(T), the set of fringe nodes of a tree T; (ii) e_T (b) = V^*(b) − L_T (b), the error function for node b in the tree T; (iii) e(b) = V^*(b) − L(b), the error at a fringe node b ∈ ℱ(T); (iv) $h_T^{b_0,b}$, the unique action/observation sequence that leads from the root b₀ to belief b in tree T; (v) d(h), the depth of an action/observation sequence h (number of actions); and

• (vi) $P(h\mid b_0,{\pi }^{\ast })={\prod }_{i=1}^{d(h)}P(h_o^i\mid b_0^{h_{i-1}},h_a^i){\pi }^{\ast }(b^{h_{i-1}},h_a^i)$, the probability of executing the action/observation sequence h if we follow the optimal policy π^* from the root node b₀ (where $h_a^i$ and $h_o^i$ refers to the i^th action and observation in the sequence h, and b^hi is the belief obtained after taking the i first actions and observations from belief b. π^*(b, a) is the probability that the optimal policy chooses action a in belief b).

By abuse of notation, we will use b to represent both a belief node in the tree and its associated belief².

Theorem 1

In any tree T, $e_T(b_0)\le {\sum }_{b\in \mathcal{F}(T)}{\gamma }^{d(h_T^{b_0,b})}P(h_T^{b_0,b}\mid b_0,{\pi }^{\ast })e(b)$.

Proof

Consider an arbitrary parent node b in tree T and let’s denote ${\widehat{a}}_b^T={\text{argmax}}_{a\in A}{L}_T(b,a)$. We have e_T (b) = V^*(b) − L_T (b). If ${\widehat{a}}_b^T={\pi }^{\ast }(b)$, then e_T (b) = γ Σ_o∈Ω P(o|b, π^*(b))e(τ(b, π^*(b), o)). On the other hand, when ${\widehat{a}}_b^T\ne {\pi }^{\ast }(b)$, then we know that $L_T(b,{\pi }^{\ast }(b))\le L_T(b,{\widehat{a}}_b^T)$ and therefore e_T (b) ≤ γ Σ_o∈Ω P(o|b, π^*(b))e(τ(b, π^*(b), o)). Consequently, we have the following:

$$e_T(b)\le \{\begin{array}{ll}e(b)\hfill & \text{if}b\in \mathcal{F}(T)\hfill \\ \gamma \sum _{o\in \mathrm{\Omega }}P(o\mid b,{\pi }^{\ast }(b))e_T(\tau (b,{\pi }^{\ast }(b),o))\hfill & \text{otherwise}\hfill \end{array}$$

Then $e_T(b_0)\le {\sum }_{b\in \mathcal{F}(T)}{\gamma }^{d(h_T^{b_0,b})}P(h_T^{b_0,b}\mid b_0,{\pi }^{\ast })e(b)$ can be easily shown by induction.

4.1 Search Heuristics

From Theorem 1, we see that the contribution of each fringe node to the error in b₀ is simply the term ${\gamma }^{d(h_T^{b_0,b})}P(h_T^{b_0,b}\mid b_0,{\pi }^{\ast })e(b)$. Consequently, if we want to minimize e_T (b₀) as quickly as possible, we should expand fringe nodes reached by the optimal policy π^* that maximize the term ${\gamma }^{d(h_T^{b_0,b})}P(h_T^{b_0,b}\mid b_0,{\pi }^{\ast })e(b)$ as they offer the greatest potential to reduce e_T (b₀). This suggests us a sound heuristic to explore the tree in a best-first-search way. Unfortunately we do not know V^* nor π^*, which are required to compute the terms e(b) and $P(h_T^{b_0,b}\mid b_0,{\pi }^{\ast })$; nevertheless, we can approximate them. First, the term e(b) can be estimated by the difference between the lower and upper bound. We define ê(b) = U(b) − L(b) as an estimate of the error introduced by our bounds at fringe node b. Clearly, ê(b) ≥ e(b) since U(b) ≥ V^*(b).

To approximate $P(h_T^{b_0,b}\mid b_0,{\pi }^{\ast })$, we can view the term π^*(b, a) as the probability that action a is optimal in belief b. Thus, we consider an approximate policy π̂_T that represents the probability that action a is optimal in belief state b given the bounds L_T (b, a) and U_T (b, a) that we have on Q^*(b, a) in tree T. More precisely, to compute π̂_T (b, a), we consider Q^*(b, a) as a random variable and make some assumptions about its underlying probability distribution. Once cumulative distribution functions $F_T^{b,a}$, s.t. $F_T^{b,a}(x)=P(Q^{\ast }(b,a)\le x)$, and their associated density functions $f_T^{b,a}$ are determined for each (b, a) in tree T, we can compute the probability π̂_T (b, a) as ${\widehat{\pi }}_T(b,a)={\int }_{-\infty }^{\infty }{f}_T^{b,a}(x){\prod }_{a^{\prime }\ne a}{F}_T^{b,a^{\prime }}(x)dx$. Computing this integral³ may not be computationally efficient depending on how we define the functions $f_T^{b,a}$. We consider two approximations.

One possible approximation is to simply compute the probability that the Q-value of a given action is higher than its parent belief state value (instead of all actions’ Q-value). In this case, we get ${\widehat{\pi }}_T(b,a)={\int }_{-\infty }^{\infty }{f}_T^{b,a}(x)F_T^b(x)dx$, where $F_T^b$ is the cumulative distribution function for V^*(b), given bounds L_T (b) and U_T (b) in tree T. Hence by considering both Q^*(b, a) and V^*(b) as random variables with uniform distributions between their respective lower and upper bounds, we get:

$${\widehat{\pi }}_T(b,a)=\{\begin{array}{ll}\eta \frac{{(U_T(b,a)-L_T(b))}^2}{U_T(b,a)-L_T(b,a)}\hfill & \text{if}{U}_T(b,a)>L_T(b),\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (5)

where η is a normalization constant such that Σ_a∈Aπ̂_T (b, a) = 1. Notice that if the density function is 0 outside the interval between the lower and upper bound, then π̂_T (b, a) = 0 for dominated actions, thus they are implicitly pruned from the search tree by this method.

A second practical approximation is:

$${\widehat{\pi }}_T(b,a)=\{\begin{array}{ll}1\hfill & \text{if}a={\text{argmax}}_{a^{\prime }\in A}{U}_T(b,a^{\prime }),\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (6)

which simply selects the action that maximizes the upper bound. This restricts exploration of the search tree to those fringe nodes that are reached by sequence of actions that maximize the upper bound of their parent belief state, as done in the AO^* algorithm [15]. The nice property of this approximation is that these fringe nodes are the only nodes that can potentially reduce the upper bound in b₀.

Using either of these two approximations for π̂_T, we can estimate the error contribution ê_T (b₀, b) of a fringe node b on the value of root belief b₀ in tree T, as: ${\widehat{e}}_T(b_0,b)={\gamma }^{d(h_T^{b_0,b})}P(h_T^{b_0,b}\mid b_0,{\widehat{\pi }}_T)\widehat{e}(b)$. Using this as a heuristic, the next fringe node b̃(T) to expand in tree T is defined as $\stackrel{\sim }{b}(T)={\text{argmax}}_{b\in \mathcal{F}(T)}{\gamma }^{d(h_T^{b_0,b})}P(h_T^{b_0,b}\mid b_0,{\widehat{\pi }}_T)\widehat{e}(b)$. We use AEMS1⁴ to denote the heuristic that uses π̂_T as defined in Equation 5, and AEMS2⁵ to denote the heuristic that uses π̂_T as defined in Equation 6.

4.2 Algorithm

Algorithm 1 presents the anytime error minimization search. Since the objective is to provide a near-optimal action within a finite allowed online planning time, the algorithm accepts two input parameters: t, the online search time allowed per action, and ε, the desired precision on the value function.

Algorithm 1.

AEMS: Anytime Error Minimization Search

Function SEARCH(t, ε)

Static: T: an AND-OR tree representing the current search tree.

t0 ← TIME()

while TIME() – t0 ≤ t and not SOLVED(ROOT(T), ε) do

b* ← b̃(T)

EXPAND(b*)

UPDATEANCESTORS(b*)

end while

return argmaxa∈A LT (ROOT(T), a)

The EXPAND function simply does a one-step lookahead under the node b^* by adding the next action and belief nodes to the tree T and computing their lower and upper bounds according to Equations 1–4. After a node is expanded, the UPDATEANCESTORS function simply recomputes the bounds of its ancestors according to Equations determining b′(s′), V^*(b), P(o|b, a) and Q^*(b, a), as outlined in Section 2. It also recomputes the probabilities π̂_T (b, a) and the best actions for each ancestor node. To find quickly the node that maximizes the heuristic in the whole tree, each node in the tree contains a reference to the best node to expand in their subtree. These references are updated by the UPDATEANCESTORS function without adding more complexity, such that when this function terminates, we always know immediatly which node to expand next, as its reference is stored in the root node. The search terminates whenever there is no more time available, or we have found an ε-optimal solution (verified by the SOLVED function). After an action is executed in the environment, the tree T is updated such that our new current belief state becomes the root of T; all nodes under this new root can be reused at the next time step.

Since this is an anytime algorithm, overall complexity will be constrained by the time available. Nonetheless we can examine the complexity of a single iteration of the search procedure. The first step is to pick a node to expand. This is in O(1) since it is stored in memory. The EXPAND function has complexity O(|S|²|A||Ω|) since it requires computing τ(b, a, o) for |A||Ω| children nodes (the evaluation of the upper and lower bound is more efficient). The update of the ancestor nodes is in O(D(|Ω|+ |A|C_H)), where D is the maximal depth of the tree, since it requires backing up through at most D levels of the tree, and at each level summing over observations (|Ω|) and evaluating the heuristic (C_H) for each action (|A|).

4.3 Completeness and Optimality

We now provide some sufficient conditions under which our heuristic search is guaranteed to converge to an ε-optimal policy after a finite number of expansions. We show that the heuristics proposed in Section 4.1 satisfy those conditions, and therefore are admissible. Before we present the main theorems, we provide some useful preliminary lemmas.

Lemma 1

In any tree T, the approximate error contribution ê_T (b₀, b_d) of a belief node b_d at depth d is bounded by ê_T (b₀, b_d) ≤ γ ^d sup_b ê(b).

Proof

Since $P(h_T^{b_0,b}\mid b_0,{\widehat{\pi }}_T)\le 1$ and ê (b) ≤ sup_b′ ê (b′) for all belief b, then ê_T (b₀, b_d) ≤ γ^d sup_b ê (b).

For the following lemma and theorem, we will denote $P(h_o\mid b_0,h_a)={\prod }_{i=1}^{d(h)}P(h_o^i\mid b_0^{h_{i-1}},h_a^i)$ the probability of observing the sequence of observations h_o in some action/observation sequence h, given that the sequence of actions h_a in h is performed from current belief b₀, and ℱ̂(T) ⊆ ℱ(T) the set of all fringe nodes in T such that $P(h_T^{b_0,b}\mid b_0,{\widehat{\pi }}_T)>0$, for π̂_T defined as in Equation 6 (i.e. the set of fringe nodes reached by a sequence of actions in which each action maximizes U_T (b, a) in its respective belief state.)

Lemma 2

For any tree T, ε > 0, and D such that γ^D sup_b ê(b) ≤ ε, if for all b ∈ ℱ̂(T), either $d(h_T^{b_0,b})\ge D$ or there exists an ancestor b′ of b such that ê_T (b′) ≤ ε, then ê_T (b₀) ≤ ε.

Proof

Let’s denote ${\widehat{a}}_b^T={\text{argmax}}_{a\in A}{U}_T(b,a)$. Notice that for any tree T, and parent belief b ∈ T, ${\widehat{e}}_T(b)=U_T(b)-L_T(b)\le U_T(b,{\widehat{a}}_b^T)-L_T(b,{\widehat{a}}_b^T)=\gamma {\sum }_{o\in \mathrm{\Omega }}P(o\mid b,{\widehat{a}}_b^T){\widehat{e}}_T(\tau (b,{\widehat{a}}_b^T,o))$. Consequently, the following recurrence is an upper bound on ê_T (b):

$${\widehat{e}}_T(b)\le \{\begin{array}{ll}\widehat{e}(b)\hfill & \text{if}b\in \mathcal{F}(T)\hfill \\ \epsilon \hfill & \text{if}{\widehat{e}}_T(b)\le \epsilon \hfill \\ \gamma \sum _{o\in \mathrm{\Omega }}P(o\mid b,{\widehat{a}}_b^T){\widehat{e}}_T(\tau (b,{\widehat{a}}_b^T,o))\hfill & \text{otherwise}\hfill \end{array}$$

By unfolding the recurrence for b₀, we get ${\widehat{e}}_T(b_0)\le {\sum }_{b\in A(T)}{\gamma }^{d(h_T^{b_0,b})}P(h_{T,o}^{b_0,b}\mid b_0,h_{T,a}^{b_0,b})\widehat{e}(b)+\epsilon {\sum }_{b\in B(T)}{\gamma }^{d(h_T^{b_0,b})}P(h_{T,o}^{b_0,b}\mid b_0,h_{T,a}^{b_0,b})$, where B(T) is the set of parent nodes b′ having a descendant in ℱ̂(T) such that ê_T(b′) ≤ ε and A(T) is the set of fringe nodes b″ in ℱ̂ (T) not having an ancestor in B(T). Hence if for all b ∈ ℱ̂ (T), $d(h_T^{b_0,b})\ge D$ or there exists an ancestor b′ of b such that ê_T (b′) ≤ ε, then this means that for all b in A(T), $d(h_T^{b_0,b})\ge D$, and therefore, ${\widehat{e}}_T(b_0)\le {\gamma }^D{sup}_b\widehat{e}(b){\sum }_{b^{\prime }\in A(T)}P(h_{T,o}^{b_0,b^{\prime }}\mid b_0,h_{T,a}^{b_0,b^{\prime }})+\epsilon {\sum }_{b^{\prime }\in B(T)}P(h_{T,o}^{b_0,b^{\prime }}\mid b_0,h_{T,a}^{b_0,b^{\prime }})\le \epsilon {\sum }_{b^{\prime }\in A(T)\cup B(T)}P(h_{T,o}^{b_0,b^{\prime }}\mid b_0,h_{T,a}^{b_0,b^{\prime }})=\epsilon$.

Theorem 2

For any tree T and ε > 0, if π̂_T is defined such that ${inf}_{b,T\mid {\widehat{e}}_T(b)>\epsilon }{\widehat{\pi }}_T(b,{\widehat{a}}_b^T)>0$ for ${\widehat{a}}_b^T={\text{argmax}}_{a\in A}{U}_T(b,a)$, then Algorithm 1 using b̃(T) is complete and ε-optimal.

Proof

If γ= 0, then the proof is immediate. Consider now the case where γ ∈ (0, 1). Clearly, since U is bounded above and L is bounded below, then êis bounded above. Now using γ ∈ (0, 1), we can find a positive integer D such that γ^D sup_b ê (b) ≤ ε. Let’s denote ${\mathcal{A}}_b^T$ the set of ancestor belief states of b in the tree T, and given a finite set A of belief nodes, let’s define ${\widehat{e}}_T^{\mathit{min}}(A)={\text{min}}_{b\in A}{\widehat{e}}_T(b)$. Now let’s define 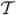_b = {T |T finite, b ∈ ℱ̂(T), ${\widehat{e}}_T^{\mathit{min}}({\mathcal{A}}_b^T)>\epsilon$} and $\mathcal{B}=\{b\mid \widehat{e}(b){inf}_{T\in {\mathcal{T}}_b}P(h_T^{b_0,b}\mid b_0,{\widehat{\pi }}_T)>0,d(h_T^{b_0,b})\le D\}$. Clearly, by the assumption that ${inf}_{b,T\mid {\widehat{e}}_T(b)>\epsilon }{\widehat{\pi }}_T(b,{\widehat{a}}_b^T)>0$, then ℬcontains all belief states b within depth D such that ê (b) > 0, $P(h_{T,o}^{b_0,b}\mid b_0,h_{T,a}^{b_0,b})>0$ and there exists a finite tree T where b ∈ ℱ̂ (T) and all ancestors b′ of b have ê_T (b′) > ∈. Furthermore, ℬis finite since there are only finitely many belief states within depth D. Hence there exist a $E_{\mathit{min}}={\text{min}}_{b\in \mathcal{B}}{\gamma }^{d(h_T^{b_0,b})}\widehat{e}(b){inf}_{T\in {\mathcal{T}}_b}P(h_T^{b_0,b}\mid b_0,{\widehat{\pi }}_T)$. Clearly, E_min > 0 and we know that for any tree T, all beliefs b in ℬ ∩ ℱ̂(T) have an approximate error contribution ê_T (b₀, b) ≥ E_min. Since E_min > 0 and γ ∈ (0, 1), there exist a positive integer D′ such that γ^D′ sup_b ê (b) < E_min. Hence by Lemma 1, this means that Algorithm 1 cannot expand any node at depth D′ or beyond before expanding a tree T where ℬ ∩ ℱ̂ (T) = ∅. Because there are only finitely many nodes within depth D′, then it is clear that Algorithm 1 will reach such tree T after a finite number of expansions. Furthermore, for this tree T, since ℬ ∩ ℱ̂(T) = ∅, we have that for all beliefs b ∈ ℱ̂ (T), either $d(h_T^{b_0,b})\ge D$ or ${\widehat{e}}_T^{\mathit{min}}({\mathcal{A}}_b^T)\le \epsilon$. Hence by Lemma 2, this implies that e∘_T (b₀) ≤ε, and consequently Algorithm 1 will terminate after a finite number of expansions (Solved(b₀, ε) will evaluate to true) with an ε-optimal solution (since e_T (b₀) ≤ ê_T (b₀)).

From this last theorem, we notice that we can potentially develop many different admissible heuristics for Algorithm 1; the main sufficient condition being that π̂_T (b, a) > 0 for a = argmax_{a′ ∈ A} U_T (b, a′). It also follows from this theorem that the two heuristics described above, AEMS1 and AEMS2, are admissible. The following corollaries prove this:

Corollary 1

Algorithm 1, using b̃(T), with π̂_T as defined in Equation 6 is complete and ε-optimal.

Proof

By definition of π̂, ${\widehat{\pi }}_T(b,{\widehat{a}}_b^T)=1$ for all b, T. Hence, ${inf}_{b,T\mid {\widehat{e}}_T(b)>\epsilon }{\widehat{\pi }}_T(b,{\widehat{a}}_b^T)=1$ and therefore it immediately follows from Theorem 2 that Algorithm 1 is complete and ε-optimal.

Corollary 2

Algorithm 1, using b̃(T), with π̂_T as defined in Equation 5 is complete and ε-optimal.

Proof

We first notice that (U_T (b, a) − L_T (b))²/(U_T (b, a) − L_T (b, a)) ≤ e∘_T (b, a), since L_T (b) ≥ L_T (b, a) for all a. Furthermore, ê_T (b, a) ≤sup_b′ ê(b′). Therefore the normalization constant η ≥ (|A| sup_b ê(b))⁻¹. For ${\widehat{a}}_b^T={\text{argmax}}_{a\in A}{U}_T(b,a)$, we have $U_T(b,{\widehat{a}}_b^T)=U_T(b)$, and therefore $U_T(b,{\widehat{a}}_b^T)-L_T(b)={\widehat{e}}_T(b)$. Hence this means that ${\widehat{\pi }}_T(b,{\widehat{a}}_b^T)=\eta {({\widehat{e}}_T(b))}^2/{\widehat{e}}_T(b,{\widehat{a}}_b^T)\ge {(\mid A\mid {({sup}_{b^{\prime }}\widehat{e}(b^{\prime }))}^2)}^{-1}{({\widehat{e}}_T(b))}^2$ for all T, b. Hence, for any ε > 0, ${inf}_{b,T\mid {\widehat{e}}_T(b)>\epsilon }{\widehat{\pi }}_T(b,{\widehat{a}}_b^T)\ge {(\mid A\mid {({sup}_b\widehat{e}(b))}^2)}^{-1}{\epsilon }^2>0$. Therefore it immediatly follows from Theorem 2 that Algorithm 1 is complete and ε-optimal.

5 Experiments

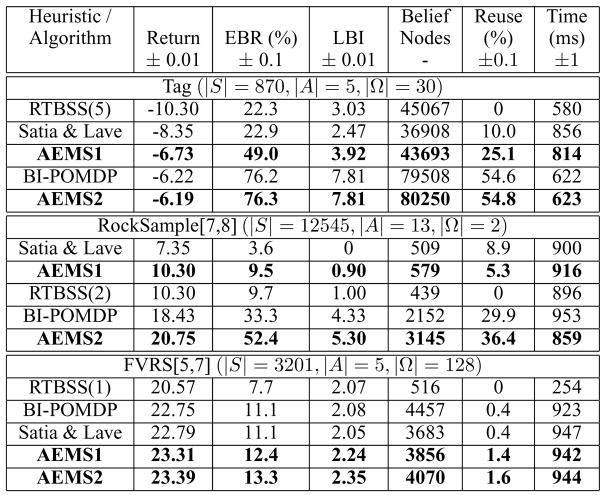
In this section we present a brief experimental evaluation of Algorithm 1, showing that in addition to its useful theoretical properties, the empirical performance matches, and in some cases exceeds, that of other online approaches. The algorithm is evaluated in three large POMDP environments: Tag [1], RockSample [3] and FieldVisionRockSample (FVRS) [12]; all are implemented using a factored state representation. In each environments we compute the Blind policy⁶ to get a lower bound and the FIB algorithm [16] to get an upper bound. We then compare performance of Algorithm 1 with both heuristics (AEMS1 and AEMS2) to the performance achieved by other online approaches (Satia [7], BI-POMDP [8], RTBSS [11]). For all approaches we impose a real-time constraint of 1 sec/action, and measure the following metrics: average return, average error bound reduction⁷ (EBR), average lower bound improvement⁸ (LBI), number of belief nodes explored at each time step, percentage of belief nodes reused in the next time step, and the average online time per action (< 1s means the algorithm found an ε-optimal action)⁹. Satia, BI-POMDP, AEMS1 and AEMS2 were all implemented using the same algorithm since they differ only in their choice of search heuristic used to guide the search. RTBSS served as a base line for a complete k-step lookahead search using branch & bound pruning. All results were obtained on a Xeon 2.4 Ghz with 4Gb of RAM; but the processes were limited to use a max of 1Gb of RAM.

Table 1 shows the average value (over 1000+ runs) of the different statistics. As we can see from these results, AEMS2 provides the best average return, average error bound reduction and average lower bound improvement in all considered environments. The higher error bound reduction and lower bound improvement obtained by AEMS2 indicates that it can guarantee performance closer to the optimal. We can also observe that AEMS2 has the best average reuse percentage, which indicates that AEMS2 is able to guide the search toward the most probable nodes and allows it to generally maintain a higher number of belief nodes in the tree. Notice that AEMS1 did not perform very well, except in FVRS[5,7]. This could be explained by the fact that our assumption that the values of the actions are uniformly distributed between the lower and upper bounds is not valid in the considered environments.

We briefly compared AEMS2 to state of the art offline algorithms. In Tag, the best result in terms of returns comes from the Perseus algorithm which has an average return of −6.17 but requires 1670 seconds of offline time [4], meanwhile AEMS2 obtained −6.19 but only required 1 second of offline time to compute the lower and upper bounds. Again in RockSample[7,8], HSVI, the best offline approach, obtains an average return of 20.6 and requires 1003 seconds of offline time [3], while AEMS2 obtained 20.75 but only requires 25 seconds of offline time to compute the lower and upper bounds.

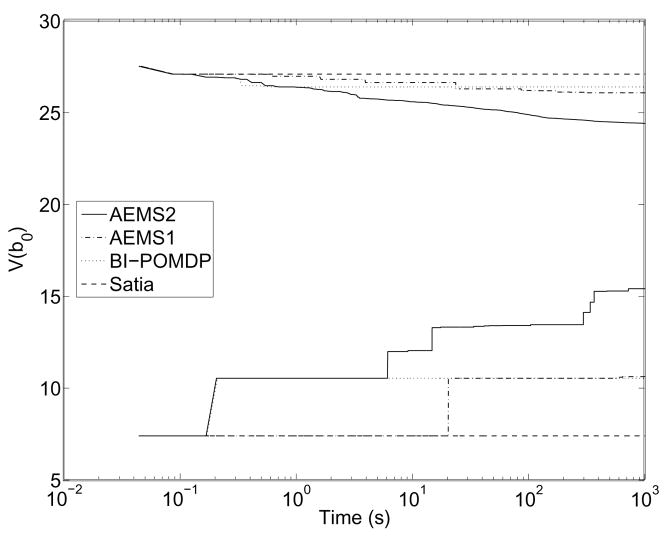
Finally, we can also examine how fast the lower and upper bounds converge if we let the algorithm run up to 1000 seconds on the initial belief state. This gives an indication of which heuristic would be the best if we extended online planning time past 1sec. Results for RockSample[7,8] are presented in Figure 2, showing that the bounds converge much more quickly for the AEMS2 heuristic.

Figure 2.

Evolution of the upper/lower bounds on the initial belief state in RockSample[7,8].

6 Conclusion

In this paper we examined theoretical properties of online heuristic search algorithms for POMDPs. To this end, we described a general online search framework, and examined two admissible heuristics to guide the search. The first assumes that Q^*(b, a) is distributed uniformly at random between the bounds (Heuristic AEMS1), the second favors an optimistic point of view, and assume the Q^*(b, a) is equal to the upper bound (Heuristic AEMS2). We provided a general theorem that shows that AEMS1 and AEMS2 are admissible and lead to complete and ε-optimal algorithms. Our experimental work supports the theoretical analysis, showing that AEMS2 is able to outperform online approaches. Yet it is equally interesting to note that AEMS1 did not perform nearly as well. This highlights the fact that not all admissible heuristics are equally useful. Thus it will be interesting in the future to develop further guidelines and theoretical results describing which subclasses of heuristics are most appropriate.

Figure 1.

Comparison of different online search algorithm in different environments.