Second phase HCV RNA decline during telaprevir based therapy increases with drug effectiveness: implications for treatment duration

Abstract

Hepatitis C virus (HCV) RNA decay during antiviral therapy is characterized by a rapid first phase followed by a slower second phase. The current understanding of viral kinetics attributes the magnitude of the first phase decay to the treatment effectiveness, whereas the second phase decay is attributed to the progressive loss of infected cells. Here we analyzed data from 44 patients treated with telaprevir, a potent HCV protease inhibitor. Using a viral kinetic model that accounts for the pharmacokinetics of telaprevir, we found that the second phase slope of viral decline to be strongly correlated with the treatment effectiveness and to be roughly four-fold more rapid than has been reported with interferon-based therapies. Since telaprevir is not known to increase the death rate of infected cells, our results suggest the second phase slope of viral decline is driven not only by the death of infected cells but may also involve other mechanisms, such as a treatment effectiveness-dependent degradation of intracellular viral RNA. As a consequence of the enhanced viral decay caused by the high antiviral effectiveness of telaprevir, we predict that if drug resistance could be avoided by using an appropriate combination of antiviral agents, treatment duration needed to clear HCV might be dramatically shortened. Indeed, we predict that in 95% of fully compliant patients, the last virus particle should be eliminated by week 7 of therapy. If the remaining infected hepatocytes act as a potential reservoir for the renewal of infection, no more than 10 weeks of treatment should be sufficient to clear the infection in 95% of fully compliant patients. However, if patients miss doses, treatment duration would need to be extended.

Introduction

Chronic hepatitis C virus (HCV) infection has a worldwide prevalence of about 3% (1). Achieving a long-term sustained virologic response (SVR), defined as undetectable HCV RNA in serum 24 weeks after the end of treatment, is the most effective way to prevent disease progression. Currently, treatment outcome with pegylated interferon (peg-IFN) and ribavirin (RBV) is correlated with HCV genotype and SVR is only achieved in approximately 50% of HCV genotype 1 patients.

After initiation of high doses of daily IFN±RBV, viral kinetics is characterized in most patients by a biphasic decline, where a rapid initial decline lasting for 1-2 days is followed by a slower but sustained second phase of viral decay (Fig. 1), where HCV RNA declines 0.42 log₁₀ IU/mL/week on average with high variation among patients (standard deviation 0.36 log₁₀ IU/mL/week) (2-3). Mathematical modeling of viral kinetics has provided valuable insights for the understanding of the determinants of HCV RNA decay after treatment initiation (reviewed in (4)). In particular, it has been proposed that the second phase of viral decline is due to the loss of infected cells and, thus, the high variability in the second phase viral decline could reflect the variability in the strength of the immune response (2). Although several observations support the possibility that the immune response is involved in the second phase of viral decline (2, 5), no means exists to directly quantify the loss rate of infected cells in vivo and the predictions made by mathematical modeling remain to be validated. Whatever the mechanisms involved in the second phase of viral decline, its determination is of great interest because it can ultimately determine the length of time treatment that needs to be given before all virus and infected cells are expected to be cleared (3).

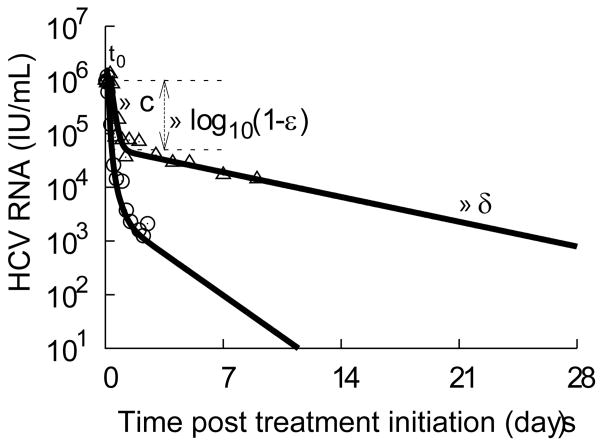
Figure 1.

Typical biphasic HCV RNA decay with daily standard IFN-α (triangles represent data from subject 2D in (ref 2)). After treatment initiation at time t=0, viral load remains equal to its baseline value V₀ for a short time t₀. After that a rapid dose-dependent viral decline lasting for 1-2 days (first phase) followed by a slower but sustained decline (second phase) is typically observed. According to theory (2), the first phase of decline is due to the treatment effectiveness in blocking viral production, ε, and results in a decline of viral load at a rate close to the virion loss rate, c, with the magnitude viral decline depending on ε. With lower amounts of virus, less de novo infection occurs and the infected cells are not efficiently replaced, generating a second phase of viral decline at a rate determined mainly by the loss rate of infected cells, δ. By fitting this model to the data (black line), the parameters can be estimated (2) (t₀=7 h, c=5.6 d^-1, ε=0.95, δ=0.16 d^-1). For comparison, the decline kinetics with telaprevir for a typical subject (circles represent data from subject 1 in the current study) and its best fit using the VE model (t₀=2.4 h, c=12.2 d^-1, ε₁=0.9688, ε₂=0.9978, δ=0.51 d^-1) is also displayed.

Direct-acting antivirals (DAAs) constitute a new stage in HCV therapy. These drugs inhibit specific HCV enzymes important for viral replication, such as the NS3 protease, and thus allow for a more profound antiviral effect than the current IFN-based therapy. Similar to what was observed with IFN based therapy, HCV RNA after initiation of protease inhibitor therapy was found to decline in a biphasic manner, with in most patients a second phase viral decline larger than 1 log₁₀ IU/mL/week (6-9).

In order to gain insights into the faster second phase decline observed with HCV protease inhibitors we reanalyzed data from 44 patients treated with telaprevir (6), using a new viral kinetic model that accounts for the changes in the drug pharmacokinetics/pharmacodynamics. Using the viral kinetic parameters found in this group of patients as a representative sample of naïve genotype 1 patients under telaprevir therapy, and assuming that drug resistance can be avoided, we estimate the treatment time needed to eliminate all virus and infected cells.

Methods

Data

We analyzed data from two phase 1 studies, the first with 28 subjects dosed with varying regimens of telaprevir monotherapy (10) and the second with 8 subjects dosed with telaprevir monotherapy and 8 subjects dosed with telaprevir plus pegylated-IFN-α2a (peg-IFN) (11). Because resistant variants can emerge early, we focused on the first 2.5 days of data in order to avoid the possible perturbation of the HCV RNA decay due to the growth of drug resistant variants.

Viral kinetic models

To explain the biphasic HCV RNA decline observed during daily IFN treatment, Neumann and colleagues proposed the following model:

$$\begin{array}{c}\frac{\mathit{\text{dI}}}{\mathit{\text{dt}}}={\mathit{\text{bVT}}}_0-\delta I\\ \frac{\mathit{\text{dV}}}{\mathit{\text{dt}}}=p(1-\varepsilon )I-\mathit{\text{cV}}\end{array}$$ (Eq.1)

where I represents infected cells, V represents the virus concentration (measured as HCV RNA) and T₀ represents the target cell number at the start of therapy, which is assumed to be constant during the study time, b is the rate at which target cells are infected and p is the viral production rate per infected cell in the absence of treatment. IFN is assumed to be effective after a delay time t₀, and is assumed to reduce the average rate of viral production per cell from p to p(1-ε), where ε represents the constant effectiveness of IFN in blocking viral production, defined such that ε=0.9 means that 90% of the viral production is blocked. As a consequence of this blocking, the model suggests that the initial rate of viral decline is due to the fast clearance of free virus, occurring with rate c. Further, the model predicts that the second phase slope is approximately εδ, where δ denotes the per capita rate of loss of infected cells (2). Hence for potent therapies for which ε is close to 1, the second phase slope will be approximately δ. Because the model (Eq. 1) assumes constant treatment effectiveness, this model has been called the constant effectiveness or CE model (12).

The varying effectiveness model

With dosing every 8 or 12 h, telaprevir plasma concentrations change and an increase in drug area under the curve (AUC) and in drug effectiveness after multiple doses has been reported (13). To account for this feature, we introduce a function that allows the treatment effectiveness, ε, to change over time, t, according to:

$$\varepsilon (t)={\varepsilon }_2+({\varepsilon }_1-{\varepsilon }_2)\left\{1-\text{exp}\left[-\left(\frac{t-t_0}{k}\right)\right]\right\},$$ (2)

where ε₁ and ε₂ are the initial and the final values of the treatment effectiveness, respectively, and k defines the rapidity of the change in effectiveness. This function smooths the variation in drug effectiveness and generates an effectiveness that increases with time (assuming ε₂>ε₁) (Fig. S2), so as to account for the PK/PD of telaprevir (and peg-IFN in patients treated with combination therapy). The use of this function (Eq. 2) combined with the viral dynamics model (Eq. 1) will be called the varying effectiveness (VE) model. Note that if the initial and the final effectiveness are equal (ε₁=ε₂) or if the changes in the drug effectiveness are very rapid (k≈0), the VE model is equivalent to the CE model. In that respect, the CE model is a particular case of the VE model.

Treatment effectiveness in case of partial compliance to treatment

We assume drug is given every τ time units. Before a dose is missed ε(t) is given by Eq. (2). We assume each dose can be missed with an equal probability. When a dose is missed, we set ε=0 until the next dose at time τ later. In reality, residual drug would be present and depending on the drug PK/PD, the effectiveness would decrease. Once dosing is continued ε(t) is again given by Eq. (2) translated in time to the new start time of dosing.

In our simulation study, we will assume that drug is given three times a day and that on average one dose is missed every two days. Thus, τ=8 h and each dose can be missed with probability 1/6.

Data fitting and statistical methods

A non-linear mixed-effects approach was used to estimate the parameters, using the MONOLIX software (http://software.monolix.org) (14). This approach allows to borrow strength from the whole sample to estimate more precisely the mean value of the parameters in the population and their inter-individual variation (IIV) (15) (see supplementary materials). After the population parameters were found, the estimated parameters β̂_i for each individual were deduced using empirical Bayes estimates (15). As found in (6), one subject (subject 11) could not be fitted and was therefore not included in the analysis.

Time to eliminate the last virus particle

For each patient SVR was considered as achieved at time τ_i once the predicted total HCV RNA V(β̂_i;τ_i) was lower than 1 copy in the entire extracellular fluid volume, assumed to be 15L, which corresponds to a viral concentration of 6.7 × 10^-5 HCV RNA/ml. To be conservative we chose V(β̂_i;τ_i) < 3·10^-5 HCV RNA/mL. The time to clear the last infected cell was obtained similarly.

Cumulative distribution function for the time to clear the infection

Using the population approach described above, the distribution of each parameter in the population can be precisely estimated and the cumulative distribution function to eliminate the last virus particle or the last infected cell can be computed. To achieve it, N=10,000 in silico patients were simulated according to the population parameters and their inter-individual variation (IIV) given in Table 1, and for each of them the time τ_i to reach SVR, based on the time to eliminate the last virus particle or the last infected cell, was computed. The probability P̂(t) to achieve SVR by time t was then determined by the fraction of in silico patients that achieved SVR by time t.

Table 1.

Viral parameter estimates obtained using the constant effectiveness (CE) and the varying effectiveness (VE) models.

	V0·106 [ml-1]	δ [d-1]	c [d-1]	ε1	ε2	t0 [d]	k [d-1]	AIC
	Population parameters (standard error)
CE model	2.74 (0.46)	1.19 (0.065)	11.2(0.54)	0.995(0.00083)	-	0.088(0.0059)	-	169.8
VE model	2.68 (0.45)	0.58 (0.11)	13.4(0.87)	0.974(0.0052)	0.999(0.00028)	0.10 (0.0055)	0.35 (0.044)	147.4
	Inter-individual Variation (%)
CE model	108	22.1	21.1	100	-	0 (fixed)	-
VE model	109	24.5	24.8	73.6	61.3	0 (fixed)	63.1

Results

Although both the constant effectiveness (CE) and the varying effectiveness (VE) models provided good fits to the data at all drug doses used (Figs. S1), the VE model yielded significantly better fits when assessed by the Akaike information criterion (AIC), which allows one to compare the ability of models with different numbers of parameters to fit experimental data (Table 1). Because the VE model gave better fits, we only discuss results obtained with the VE model.

In principle, model parameters may vary according to treatment group. In particular, the parameters related to treatment effectiveness (k, ε₁, ε₂) could be different in the telaprevir plus peg-IFN group compared to telaprevir monotherapy group. However, no significant effect was found for any of the viral dynamic or drug effectiveness parameters (all p-values >0.2).

We estimated the initial treatment effectiveness, ε₁=0.974, increased and reached a significantly higher (p<0.0001) effectiveness ε₂=0.999 after about 1 day (Fig. S2). Further, we estimated that there was a small delay, t₀, before drug became effective (see Methods), which was estimated to have nearly the same value in all the patients; t₀ = 0.10 days or 2.4 hours.

As in (6), we found that the mean value of δ was high compared to what has been reported with IFN-based treatments (Fig. 1). However, our estimate of δ is much lower than what was found using the CE model (mean: 0.58 d^-1 vs 1.19 d^-1 in the CE model). Moreover, our estimated value of δ is similar in monotherapy patients (0.58 d^-1) and in patients receiving combination therapy (0.57 d^-1), thus resolving the apparent paradox of a slower second phase decline when peg-IFN was added to telaprevir reported in (6)

Since only the first 3 days of treatment were analyzed, we checked whether our estimates remain unchanged when including later time points (days 6, 10, and 13) in patients treated with telaprevir plus peg-IFN, and in whom no resistant virus was detected (16). Interestingly, we found no significant differences in this subset of patients in the loss rate of infected cells, δ, as compared to the original dataset limited to 3 days of treatment (p-value=0.49, t-test) and the population parameters remained unchanged.

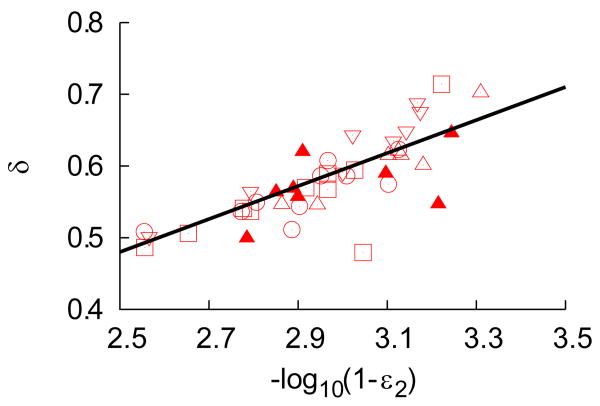
Because the rate of second phase viral decline was larger in this study using telaprevir than in previous studies using IFN-based therapies, we asked if the high effectiveness of telaprevir could play a role. As shown in Fig. 2a, we found that δ was significantly correlated with the final treatment effectiveness ε₂ (r=0.79, p<0.001). Thus for patients in whom the drug effectiveness was higher, not only did the first phase bring viral levels down lower, but also the second phase slope was larger. Adiwijaya et al. (17), although they did not directly explore a correlation between ε and δ, found that allowing δ to increase with the telaprevir effectiveness acccording to a relationship analogous to that shown in Fig. 2a resulted in a better fit of their model to patient viral load data. This finding not only supports the correlation we found, but shows its utility in data analysis.

Figure 2. The loss rate of infected cells increases with drug effectivenees.

(a). Distribution of the loss rate of infected cells, δ, as a function of the final (log-transformed) effectiveness ε₂ in patients dosed with telaprevir. Squares are telaprevir monotherapy 450 mg q8h, upper triangles are 750 mg q8h tablets (filled triangles when used in combination with peg-IFN), reverse triangles are 750 mg q8h suspension and circles are 1250 mg q12h suspension. The black line is the best-fit regression line (r=0.79, p-value<0.001).

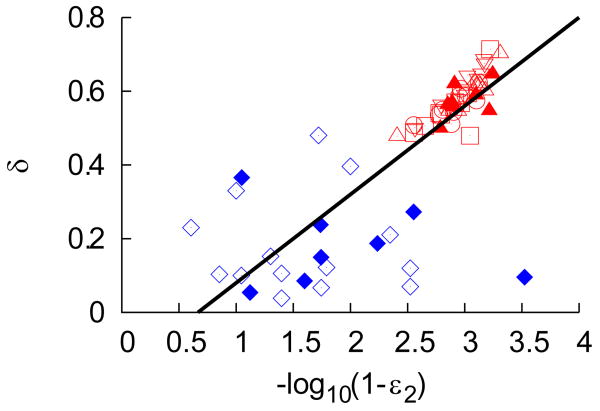
(b). Distribution of the loss rate of infected cells, δ, as a function of the final (log-transformed) effectiveness ε₂ in patients dosed with telaprevir (red symbols) compared to values found in the literature for genotype 1 Caucasian patients treated with 10 MIU of IFN daily (2-3, 18) monotherapy (blue diamond) or in combination with ribavirin (blue filled diamond). The black line is the best-fit regression line (r=0.78, p-value<0.001) where one point, considered as an outlier, has not been taken into account.

Next we asked if this relationship between second phase slope and treatment effectiveness was only true for telaprevir or if it had wider applicability. To assess this, the relationship between drug effectiveness and δ was examined both for the patients in this study and for patients from prior studies involving treatment naïve genotype 1 Caucasian patients receiving a high daily dose of IFN (>10 MIU) (2-3, 18). Recent analyses have demonstrated an association between IL28B genotype and slopes of viral decline (19). Since the samples used here could not be tested for the IL28B genotype, we restricted our analysis to Caucasians, for whom the chances to carry the favorable alleles are the highest (19). Combining the data from these studies with that from the telaprevir studies we encompass a much larger range of drug effectiveness values. As shown in Fig. 2b, we still find a significant positive correlation (r=0.78, p<0.001) between drug effectiveness and δ. However further analyses will be necessary to identify precisely whether polymorphisms in the IL28B gene may affect the relationship between the first and second phases of viral decay in patients treated with IFN.

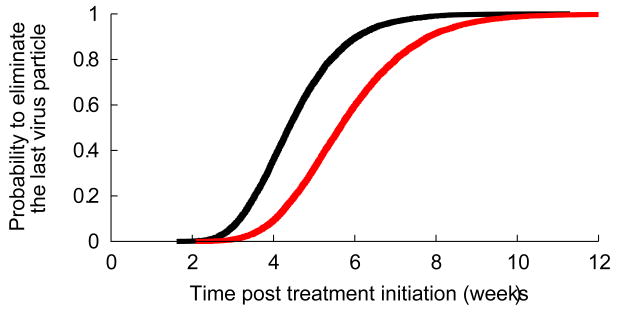
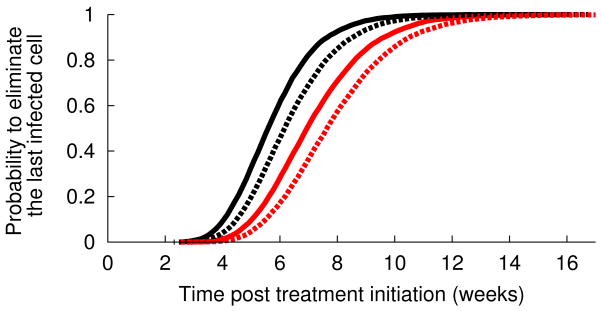
Interestingly, the second phase slope in patients treated with telaprevir is much less variable than what was seen with IFN-based treatment. Since δ almost entirely determines the second phase of viral decline (Methods), this finding suggests that duration of therapy needed to eliminate all virus and infected cells might be considerably shortened as compared to IFN-based therapies. We evaluated empirically the distribution function of the time needed to achieve less than 1 virion in the extracellular body water (Methods). We predict that with full patient compliance 95% of patients could achieve viral clearance within 7 weeks and 99% within 8 weeks (Fig. 3). This time could be significantly delayed if all drug doses are not taken. For patients taking three doses a day, we estimated that if 16% of doses are randomly missed (one every two days on average), the time needed to eradicate the virus in 95% and 99% of the patients would increase to 9 and 11 weeks, respectively (Fig. 3). If more drug doses are missed or if the missed doses are clumped together as in a weekend drug holiday a longer time to eradication should be anticipated (not shown).

Figure 3.

Estimated cumulative probability distribution function (cdf) for the treatment duration needed to eliminate the last remaining (a) virus particle and (b) infected cell. The black line corresponds to perfect treatment adherence whereas the red line represents the case of partial adherence where of three doses per day one dose is randomly missed every two days (Methods). Because the cdf for the time to eliminate the last infected cell depends on the unknown value for the viral production rate in absence of treatment (p in Eq. 1), the solid lines in (b) correspond to p=100 virions/day and the dashed lines correspond to p=10 virions/day.

Under treatment each cell on average may generate less than one HCV RNA per day. Further, the clearance rate of virions is much faster than that of cells and thus when all viruses have been cleared some infected cells may still be present. If SVR is defined as the time to eliminate all infected cells, SVR could be delayed. Since only HCV RNA is observed the estimated number of infected cells is based in part on the rate of viral production per infected cell under treatment, p(1-ε) in Eq. 1. Since only the ratio (1-ε) of the viral production before and during treatment can be estimated but not the viral production rate itself (p in Eq. 1), we considered the values p=10 virions/day and p=100 virions/day that cover the range of p values found in a previous study in patients treated with telaprevir (20). With lower rates of viral production per infected cell, p, more infected cells are needed to explain the observed level of viremia in patients and hence the longer the time needed to eradicate the last infected cell. Based on these values of p, 2 to 3 additional weeks of treatments would be needed in order to eradicate all infected cells (Table 2).

Table 2.

Estimated time to SVR for 95% and 99% of treated patients.

	Length of treatment (in weeks) needed to clear HCV based on eliminating*
	last remaining virus	last infected cell (p=100 virions/day)	last infected cell (p=10 virions/day)
Full compliance
95% cured	7	9	10
99% cured	8	10	11
Three doses/ day - one missed every two days on average
95% cured	9	11	12
99% cured	11	13	14

^*Times (rounded up to the nearest week) to eliminate the last remaining virus or the last remaining infected cell are estimated based on the distribution of first and second phase viral RNA declines oberved with telaprevir. Because the number of infected cells needed to produce the observed levels of HCV RNA depend on the rate of virion production per cell, p, we provide estimates based on two biological reasonable values of p. We also consider the effect of full compliance (all drug dose taken) and partial compliance (1/6 of missed drug doses).

Discussion

Using a new viral kinetic model that allowed for an improved description of the changes in antiviral treatment effectiveness, the second phase of viral decay was found to be very rapid compared with second phases observed in patients treated with IFN alone, with no differences according to the treatment regimen. More precisely, we estimated that telaprevir induced a 4-fold more rapid second phase viral decline than IFN based therapy (2-3). Since the current understanding of HCV RNA decay attributes the second phase of viral decline to the loss rate of infected cells, our result suggests that either cell death is enhanced or mechanisms of infected cell loss other than cell death may be operating. Yet, since no elevation in alanine aminotransferase, a surrogate marker of liver cell death, was reported during telaprevir based therapy, the assumption that the enhanced loss rate of infected cells reflects an elevation in the cell death is unlikely.

The current explanation of HCV RNA decline under therapy comes from studies using moderately potent IFN treatment. In that context, assuming that after a short delay the viral production rate per infected cell is reduced under treatment by a constant factor, (1-ε), has provided excellent fits to viral kinetic data from a variety of studies. Nevertheless, as a consequence of their very high pressure on intracellular replication, the new direct antiviral agents might be able to continuously reduce the levels of intracellular viral RNA and consequently the viral production per infected cell in a treatment effectiveness-dependent manner. This may also be the case for IFN if its effectiveness is high enough. Although this remains speculative, some experiments using the replicon system support the suggestion that intracellular viral RNA not only initially declines by the factor (1-ε) but then continues to decline under protease inhibitor (21) or IFN (22) treatment. If the rate of viral production per infected cell is constantly reduced during therapy, the second slope of viral decline may reflect not only the rate of loss of infected cells, but also the rate at which viral production declines in infected cells (23). Hence the higher chance for attaining SVR observed in patients with an initial rapid viral response (24) could not only be due to a better immune response but also to the progressive elimination of intracellular replication complexes resulting from a more potent antiviral treatment.

No matter what the biological mechanism, the rapid second phase decline observed with telaprevir suggests that the duration of therapy needed to clear the infection might be considerably shortened as compared to IFN-based therapies. Based on the extrapolation of the kinetics of decline estimated in our population study, we estimated that eradication of all virus particles could be reached within 7-9 weeks in 95% of the patients. If SVR is considered to be achieved when the last infected cell has been cleared rather than when the last virus is eliminated, an additional 2 to 3 weeks of therapy may be needed. This estimate is based on the current modeling assumption that the level of viral production under treatment in infected cells is reduced by a constant factor. In the framework of a model considering intracellular viral RNA, the progressive vanishing of viral replicative intermediates could lead to the “curing” of infected cells before infected cells die, which would reduce the time to SVR closer to the estimate based on the last remaining virus particle. Also, our model is deterministic and thus does not consider explicitly the random nature of each possible event (cell infection, cell death, virus clearance). Although an approach that includes the randomness of these processes would more accurately capture the probability distribution function for the time to HCV eradication at the individual level, it would not change the distribution function at the population level, where the law of large numbers applies, and which was our primary object of study.

Although Fig. 2 shows a positive correlation between the treatment effectiveness and the second phase slope, δ, one should not assume second phase slope will continue to increase as drug combinations become more and more effective. In principle, at some point the rate of loss of the infected state will be limited by host cell processes, such as the intrinsic rate at which replication complexes decay, and thus will no longer increase with therapy effectiveness. Also, other viral kinetics studies will be necessary to determine whether the relationship in Fig. 2 is true for other protease inhibitors. The second slope of viral decline has been reported for two other protease inhibitors, TMC-430 and danoprevir and both studies reported a roughly two times slower δ (8-9).

Another limitation of our calculation of treatment duration is that we assume no loss of drug effectiveness throughout the course of treatment. With this assumption the rate of second phase decline is predicted not to decrease during treatment. Is this assumption reasonable with current therapeutic strategies? Based on the high turnover rate of virus and the high error rate of the HCV RNA-dependent RNA polymerase it has been predicted that all possible single and double virus mutants are present at treatment initiation (20). Thus to avoid resistance emergence combination therapy will be needed. Since a single nucleotide substitution can be sufficient to confer resistance to protease inhibitors, the first treatment strategies that are expected to gain regulatory approval will be based on using a protease inhibitor, telaprevir or boceprevir, in combination with the standard of care (SOC). Because only about 50% of genotype 1 patients respond sufficiently strongly to the SOC to attain SVR, about 50% of genotype 1 patients treated with the current generation protease inhibitors and SOC may not have a potent enough regime to fully suppress the growth of protease inhibitor resistance variants. This should also be the case in the majority of patients that already have failed prior regimes with SOC. While resistant virus may not grow rapidly enough to cause viral breakthrough (23), they can slow the second phase decline as suggested by the relationship between ε and δ in Fig. 2, and hence lead to a need for a longer treatment duration. Consistent with this argument, post-treatment relapse with resistant virus has been seen in patients treated with telaprevir and SOC for 12 weeks (25-26). Nucleoside polymerase inhibitors present a high genetic barrier to resistance (reviewed in (27)), but their antiviral activity has tended so far to be much lower than protease inhibitors (27). Using a protease inhibitor and a second DAA constitute the natural next step of anti-HCV treatment strategies. Recent results showed high rates of rapid viral response with no or low prevalence of resistance emergence for up to 4 weeks when the second DAA was a polymerase inhibitor and up to 12 weeks when the second DAA was an NS5A inhibitor (28-31). However, the fact that a resistance related viral breakthrough occurred in some patients when SOC agents were not added to these cocktails hints that resistant virus may not be suppressed but only reduced when two DAAs are used (28-29, 32). Most likely, to attain SVR in 95% of treatment compliant patients with a 10 week course of therapy will require treatments with three or more DAAs including ribavirin. Clearly, at present there are no approved regimes that meet our criteria of high potency and a high enough barrier to resistance.

Even if resistance was avoided by using an appropriate combination of DAAs, other factors might affect our prediction. First, the ability of IFN-sparing antiviral strategies to reach every viral population residing in the liver or in extra-hepatic reservoirs is unknown. Second, the combination of several DAAs might increase toxicity and thus the adherence to treatment. How this may impact treatment duration has only been touched on in this study, and more data are needed to understand how the lack of adherence to treatment may favor the appearance and persistence of resistant virus.

Thus to attain SVR in less than 10 weeks in 95% of fully compliant patients will require combination drug regimes that have a high enough genetic barrier that resistance is avoided, that have high drug penetration into all anatomical sites that contain infected cells, and for which the pharmacokinetics of the drugs in the regime allow the effectiveness of the regime against viral production to be maintained at high levels throughout the course of treatment.

In summary, our finding that the second phase slope increases with the effectiveness of therapy and our expectation that a combination of direct acting antiviral (DAA) agents will suppress the growth of drug-resistant variants holds open the promise that more effective therapies that utilize combinations of DAA agents may one day lead to SVR with treatment durations of two to three months.