Abstract
Pain assessment in patients who are unable to verbally communicate is a challenging problem. The fundamental limitations in pain assessment in neonates stem from subjective assessment criteria, rather than quantifiable and measurable data. This often results in poor quality and inconsistent treatment of patient pain management. Recent advancements in pattern recognition techniques using relevance vector machine (RVM) learning techniques can assist medical staff in assessing pain by constantly monitoring the patient and providing the clinician with quantifiable data for pain management. The RVM classification technique is a Bayesian extension of the support vector machine (SVM) algorithm, which achieves comparable performance to SVM while providing posterior probabilities for class memberships and a sparser model. If classes represent “pure” facial expressions (i.e., extreme expressions that an observer can identify with a high degree of confidence), then the posterior probability of the membership of some intermediate facial expression to a class can provide an estimate of the intensity of such an expression. In this paper, we use the RVM classification technique to distinguish pain from nonpain in neonates as well as assess their pain intensity levels. We also correlate our results with the pain intensity assessed by expert and nonexpert human examiners.
Index Terms: Digital imaging, facial expression recognition, neonates, pain assessment, relevance vector machine (RVM), support vector machine (SVM)
I. Introduction
Pain assessment in patients who are unable to verbally communicate is a challenging problem in patient critical care. This problem is most prominently encountered in sedated patients in the intensive care unit (ICU) recovering from trauma and major surgery, as well as infant patients and patients with brain injuries [1]–[3]. Current practice in patient critical care requires the nursing staff in assessing the pain experienced by the patient, and taking appropriate action to ameliorate the patient's anxiety and discomfort.
Individuals in pain manifest their condition through “pain behavior” [4], [5], which includes facial expressions. The significance of a facial expression as an indicator of pain is discussed and advances in pain assessment using facial expressions are reviewed in [5]. Clinicians regard the patient's facial expression as a valid indicator for pain and pain intensity [6]. Hence, correct interpretation of the facial expressions of the patient and its correlation with pain is a fundamental step in designing an automated pain assessment management system. Of course, other pain behaviors, including head movement and the movement of other body parts, along with physiological indicators of pain, such as heart rate, blood pressure, and respiratory rate responses should also be included in such a system.
Depending on the patient group (e.g., neonates, children, adults, etc.) pain assessment criteria have been developed, and indicators of pain in each group might be different. For example, while the behavioral pain scale for adults focuses on facial expressions, upper limbs, and compliance with ventilation [7], the face, legs, activity, cry, and consolability (FLACC) [8] behavioral pain scale focuses on slightly different set of indicators for postoperative young children. Similarly, the premature infant pain profile (PIPP) [9] considers a special set of pain indicators, including physiological and behavioral indicators for pain assessment in premature infants.
Infants are unable to directly report their level of pain, and hence, medical staff are responsible for pain assessment for neonates. Pain and distress behaviors in neonates, include facial expression, cry, and body movement, and a series of methods have been suggested to objectively assess pain in neonates based on the aforementioned behaviors [5], [8], [9]. In this paper, we focus on the problem of pain assessment in infants using facial expressions.
Although there is a vast potential for using computer vision for agitation and pain assessment, there are very few articles in the computer vision literature addressing this issue. Bonroy et al. [10] have used computer vision for pain assessment in demented elderly patients. An agitation assessment scheme is proposed for patients in the ICU in [11]. The approach of [11] is based on the hypothesis that facial grimacing induced by pain results in additional “wrinkles” (equivalent to edges in the processed image) on the face of the patient, and this is the only factor they use in assessing pain. Although this approach is computationally inexpensive, and especially, appealing for a real-time decision support system, it can be limiting, since it does not account for other facial actions (e.g., smiling, crying, etc.), which may not necessarily correspond to pain. Brahnam et al. [12]–[15] use various face classification techniques, including support vector machines (SVM) and neural networks (NN) to classify facial expressions in neonates into “pain” and “nonpain” classes. Such classification techniques were shown to have reasonable accuracy.
In this paper, we extend the classification technique addressed in [12]–[15] to distinguish pain from nonpain in neonates as well as assess their pain intensity using a relevance vector machine (RVM) classification technique [16]. The RVM classification technique is a Bayesian extension of SVM, which achieves comparable performance to SVM while providing posterior probabilities for class memberships and a sparser model. In a Bayesian interpretation of probability, as opposed to the classical interpretation, the probability of an event is an indication of the uncertainty associated with the event rather than its frequency [17]. If data classes represent “pure” facial expressions, that is, extreme expressions, which an observer can identify with a high degree of confidence, the posterior probability of the membership of some intermediate facial expression to a class can provide an estimate of the intensity of such an expression. This, along with other pain behaviors, can be translated into one of the scoring systems currently being used for assessing pain (e.g., FLACC or PIPP).
The contents of the paper are as follows. In Sections II and III, we review the SVM and RVM classification techniques for pain recognition using facial expressions. Then, in Section IV, we present the results of these classification techniques applied to the infant classification of pain expression (COPE) database [12]. The pain intensity assessment given by the computer classifier shows a strong correlation with the pain intensity assessed by expert and nonexpert human examiners. Finally, we draw conclusions and point to some future research directions in Section V, including opportunities for sedation and agitation assessment using digital imaging in the ICU.
II. Support Vector Machines
As we see in Section IV, the problem of pain and pain intensity assessment using facial images involves a standard problem in machine learning called data classification [17]. Given a series of input variables x1, x2, …, xN in ℝD and their corresponding class labels
 1,
1,
 2, …,
2, …,
 p, where p ≤ N, the data classification problem involves assigning the correct class label to a new input variable x. Kernel-based methods are typically used for data classification and regression [17]. A key limitation of many kernel-based learning algorithms is the computational intensity involved in the training, prediction, and decision-making stages of the algorithm. This is due to the fact that the kernel function, which adds a dimension to the data in order to obtain an optimal classification, has to be computed for all pairs of data points. In sparse kernel machine algorithms, however, only a subset of the training data is used, providing a sparse solution. Sparse kernel machines are faster in the training, and the prediction and decision-making stages. In this paper, we consider two sparse kernel-based classification algorithms, namely, SVMs and RVMs.
p, where p ≤ N, the data classification problem involves assigning the correct class label to a new input variable x. Kernel-based methods are typically used for data classification and regression [17]. A key limitation of many kernel-based learning algorithms is the computational intensity involved in the training, prediction, and decision-making stages of the algorithm. This is due to the fact that the kernel function, which adds a dimension to the data in order to obtain an optimal classification, has to be computed for all pairs of data points. In sparse kernel machine algorithms, however, only a subset of the training data is used, providing a sparse solution. Sparse kernel machines are faster in the training, and the prediction and decision-making stages. In this paper, we consider two sparse kernel-based classification algorithms, namely, SVMs and RVMs.
SVMs [18] involve sparse kernel algorithms used in classification and regression problems, and have their origin in statistical learning theory. Here, we consider the classification problem involving two data classes, namely,
 1 and
1 and
 2. The framework can be generalized to a multiclass label problem using a similar approach as outlined later [17]. Let the training set be given by {x1, x2, …, xN}, with target values given by z1, z2, …, zN, respectively, where xn ∈ ℝD and zn ∈ {−1, 1}, n = 1, …, N, and with xn ∈
2. The framework can be generalized to a multiclass label problem using a similar approach as outlined later [17]. Let the training set be given by {x1, x2, …, xN}, with target values given by z1, z2, …, zN, respectively, where xn ∈ ℝD and zn ∈ {−1, 1}, n = 1, …, N, and with xn ∈
 1 if zn = −1, and xn ∈
1 if zn = −1, and xn ∈
 2 if zn = 1. To classify a new data point x ∈ ℝD, define the classifier function
2 if zn = 1. To classify a new data point x ∈ ℝD, define the classifier function
| (1) |
where ϕ : ℝD → ℝM is a continuous fixed feature-space transformation, w ∈ ℝM is a weight vector, and b ∈ ℝ is a bias parameter. The sign of the classifier function y(x) determines the class of x. More specifically, for a new input variable x, the target value is given by z = sgn(y(x)), where sgn y ≜ y/|y|, y ≠ 0 and sgn(0) ≜ 0.
Next, assume that the training set is linearly separable in the feature space ℝM, that is, there exist a weight vector w ∈ ℝM and a bias parameter b ∈ ℝ, such that y(xn) > 0 for xn ∈ ℝD and zn = 1, and y(xn) < 0 for xn ∈ ℝD and zn = −1, or equivalently, zny(xn) > 0 for all xn ∈ ℝD and zn ∈ {−1, 1}. Later, we will relax the linear separability assumption and consider the more general case of overlapping classes.
Note that the classifier function y(·) separates the feature space ℝM into two disjoint regions characterized by y(x) > 0 and y(x) < 0 for x ∈ ℝD. The affine hyperplane separating the two disjoint regions, namely y(x) = 0, is called the decision boundary and is denoted by
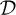 . Note that ϕ(·) can be a nonlinear transformation, which would correspond to a nonlinear decision boundary in the original input space ℝD. The minimum distance between the training set and the decision boundary
. Note that ϕ(·) can be a nonlinear transformation, which would correspond to a nonlinear decision boundary in the original input space ℝD. The minimum distance between the training set and the decision boundary
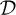 is called the margin. The distance of a point xn ∈ ℝD to the decision boundary
is called the margin. The distance of a point xn ∈ ℝD to the decision boundary
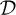 is given by
is given by
| (2) |
where ‖ · ‖ denotes the Euclidean norm on ℝM and dist(x,
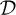 ) ≜ infs∈D ‖x − s‖. Hence, the margin is given by
) ≜ infs∈D ‖x − s‖. Hence, the margin is given by
| (3) |
As in all classification methods, the goal of the SVM algorithm is to classify a new input variable x ∈ ℝD based on the information provided by the training set and the target values. The SVM framework addresses this problem by choosing the decision boundary in such a way so that the margin is maximized. The following problem presents the SVM algorithm as an optimization problem.
Maximum Margin Classification Problem
Consider the training set given by {x1, x2, …, xN} ⊂ ℝD and let the classifier function y : ℝD → ℝ be given by (1). Find the weight vector w ∈ ℝM and the bias parameter b ∈ ℝ such that (3) is maximized.
Theorem 2.1
w* ∈ ℝM and b* ∈ ℝ solve the maximum margin classification problem if and only if w* and b* are the solutions to the optimization problem
| (4) |
Proof
The proof is a direct consequence of the definition of a margin given by (3).
The solution to the nonconvex optimization problem (4) is not unique. To see this, note that scaling the weight vector w ∈ ℝM and the bias parameter b ∈ ℝ by a positive scalar does not change the value of the function to be maximized. The following theorem presents an alternative characterization to the maximum margin classification problem.
Theorem 2.2
w* ∈ ℝM and b* ∈ ℝ solve the maximum margin classification problem if and only if w* and b* are the solutions to the optimization problem
| (5) |
subject to
| (6) |
where xn ∈ ℝD, zn ∈ {−1, 1}, and n = 1, …, N.
Proof
Since rescaling the weight vector w ∈ ℝM and the bias parameter b ∈ ℝ in (4) by a positive scalar does not change the value of the function to be maximized, the optimization problem (4) has a continuum of solutions corresponding to the same optimal value. Hence, introducing the new constraint
| (7) |
where n* = arg minn∈{1, …, N} dist(ϕ(xn),
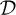 ) does not change the optimal value of the optimization problem (4). Thus, the inequality constraint (6) holds for all xn ∈ ℝD, zn ∈ {−1, 1}, and n = 1, …, N. The proof now follows by noting that the optimization problem (4) subject to (7) is equivalent to the optimization problem (5) subject to (6).
) does not change the optimal value of the optimization problem (4). Thus, the inequality constraint (6) holds for all xn ∈ ℝD, zn ∈ {−1, 1}, and n = 1, …, N. The proof now follows by noting that the optimization problem (4) subject to (7) is equivalent to the optimization problem (5) subject to (6).
The constrained optimization problem given by (5) and (6) is convex and can be solved using Lagrange multiplier methods. Specifically, introducing the Lagrange multipliers λn ∈ ℝ, n = 1, …, N, and forming the Lagrangian
| (8) |
where λ = [λ1, λ2, …, λn]T, it follows from the first-order necessary conditions for optimality that
| (9) |
| (10) |
Note that (9) and (10) can be used to eliminate w and b from the Lagrangian (8) leading to a dual representation of the optimization problem (4). Namely,
| (11) |
subject to
| (12) |
| (13) |
where
| (14) |
and
| (15) |
is the kernel function. Here, we introduced an alternative formulation of the optimization problem (4) in terms of the kernel function k : ℝD × ℝD → ℝ, which allows us to avoid working explicitly in the feature space. Note that the classifier function (1) can be rewritten using the kernel function as follows:
| (16) |
The Kuhn–Tucker (KT) necessary conditions for optimality for the constrained optimization problem (11)–(13) are given by
| (17) |
| (18) |
| (19) |
where n = 1, …, N. Now, it follows from (19) that either λn = 0 or zny(xn) = 1. The input variables xn ∈ ℝD, n = 1, …, N, for which the corresponding Lagrange multiplier λn ∈ ℝ vanishes, do not contribute to the classifier function (16), and hence, can be omitted. The remaining input variables are called support vectors, and by definition, lie on the maximum margin affine hyperplanes w*T ϕ(xn) + b* = ±1, n = 1, …, N. Hence, only the support vectors play a role in the classification of the new input variables and the rest of the training set can be discarded.
Next, we consider the case of overlapping classes. For this case, the SVM algorithm considered earlier identifies the decision boundary so that the training set is separated into two data classes with no input variables being misclassified. This results in poor class assignments for new input variables. The SVM algorithm, however, can be modified by allowing input variables in the training set to lie on the “wrong side” of the margin boundary and penalizing such constraint violations. Specifically, for every input variable xn ∈ ℝD, n = 1, …, N, define the slack variable ξn ≥ 0 such that ξn = 0 if (6) is satisfied, that is, for n ∈ {1, …, N}, xn is on or inside the correct margin boundary, and ξn = |zn − y(xn)| otherwise.
The modified SVM algorithm is given by the following optimization problem:
| (20) |
subject to
| (21) |
| (22) |
where ξ = [ξ1, ξ2, …, ξN]T and
 > 0 is a complexity parameter controlling the tradeoff between the margin and the slack variable penalty. It can be shown that if ξn = 0, then (21) reduces to (6) and the corresponding input variable xn ∈ ℝD will be correctly classified. Moreover, if 0 < ξn ≤ 1, then the input variable xn ∈ ℝD is correctly classified while lying inside the margin boundary, whereas if ξn > 1, then the input variable is misclassified.
> 0 is a complexity parameter controlling the tradeoff between the margin and the slack variable penalty. It can be shown that if ξn = 0, then (21) reduces to (6) and the corresponding input variable xn ∈ ℝD will be correctly classified. Moreover, if 0 < ξn ≤ 1, then the input variable xn ∈ ℝD is correctly classified while lying inside the margin boundary, whereas if ξn > 1, then the input variable is misclassified.
Lagrange multiplier methods can be used to solve the optimization problem (20)–(22) by introducing the Lagrange multipliers λn ∈ ℝ and μn ∈ ℝ, n = 1, …, N, corresponding to the constraints (21) and (22), respectively. In this case, the Lagrangian is given by
| (23) |
where λ = [λ1, λ2, …, λN]T. Now, it follows from the first-order necessary conditions for optimality that
| (24) |
| (25) |
| (26) |
and the KT necessary conditions give
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
where n = 1, …, N. The dual representation of the optimization problem (20) subject to (21) and (22) is given by
| (33) |
subject to
| (34) |
| (35) |
where
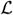 ˜ (λ) is given by (14), the kernel function is given by (15), and where we have used (24)–(32).
˜ (λ) is given by (14), the kernel function is given by (15), and where we have used (24)–(32).
III. Sparse Bayesian Learning
The SVM framework is a powerful classifier, but has a number of limitations. A key deficiency of the approach is the fact that the output of the SVM is the binary classification decision and not the class membership posterior probability. As will be discussed in Section IV, methods which possess an inherent Bayesian structure are more powerful and can provide more information. Such methods not only classify a new input variable, but can also provide a degree of uncertainty (in terms of posterior probabilities) for such a classification. The RVM [16], which is a special case of the sparse Bayesian learning algorithm, can be regarded as the Bayesian extension of the SVM approach.
In this section, we consider a classification problem involving two data classes, namely
 1 and
1 and
 2, using the sparse Bayesian learning approach. The framework can be generalized to a multiclass classification problem using a similar approach as outlined later [16]. Consider the Laplace approximation method [17] involving the random variable υ ∈ ℝM with associated probability density function given by p : ℝM → ℝ. Assume that p(υ) = f(υ)/V, where f : ℝM → ℝ is a function defined on υ ∈ ℝM and V = ∫ℝM f(υ)dυ is the normalization coefficient. The probability density function p(υ) is approximated by a multivariate Gaussian (normal) distribution
2, using the sparse Bayesian learning approach. The framework can be generalized to a multiclass classification problem using a similar approach as outlined later [16]. Consider the Laplace approximation method [17] involving the random variable υ ∈ ℝM with associated probability density function given by p : ℝM → ℝ. Assume that p(υ) = f(υ)/V, where f : ℝM → ℝ is a function defined on υ ∈ ℝM and V = ∫ℝM f(υ)dυ is the normalization coefficient. The probability density function p(υ) is approximated by a multivariate Gaussian (normal) distribution
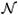 (υ; υ0, Σ) with mean υ0 ∈ ℝM and covariance matrix Σ ∈ ℝM×M, where υ0 = arg maxυ∈ℝM p(υ) and Σ= −∂2/∂υ2 ln f(υ)∣υ=0. The normalization coefficient V can be approximated by [17]
(υ; υ0, Σ) with mean υ0 ∈ ℝM and covariance matrix Σ ∈ ℝM×M, where υ0 = arg maxυ∈ℝM p(υ) and Σ= −∂2/∂υ2 ln f(υ)∣υ=0. The normalization coefficient V can be approximated by [17]
| (36) |
where det(·) denotes the determinant operator.
Next, let the training set be given by {x1, x2, …, xN} ⊂ ℝD, with target values given by z1, z2, …, zN, respectively, where xn ∈ ℝD and zn ∈ {0, 1}, n = 1, …, N, and with xn ∈
 1 if zn = 1, and xn ∈
1 if zn = 1, and xn ∈
 2 if zn = 0. For a new input variable x ∈ ℝD, we predict the associated class membership posterior probability distribution p(
2 if zn = 0. For a new input variable x ∈ ℝD, we predict the associated class membership posterior probability distribution p(
 k∣x, X, Z), k = 1, 2, where p(
k∣x, X, Z), k = 1, 2, where p(
 k∣x, X, Z) is the class membership conditional probability of the data class
k∣x, X, Z) is the class membership conditional probability of the data class
 k given x ∈ ℝD, X = [x1, x2, …, xN], and Z = [z1, z2, …, zN]T. Note that, in contrast to the SVM approach, the sparse Bayesian learning method separates the prediction stage (i.e., finding the posterior class membership probabilities for the new input variable x) from the decision-making stage (i.e., assigning the new input variable x to the appropriate class). This separation is particularly useful when dealing with asymmetric classification costs, where misclassification of input variables belonging to a certain class is more costly [16]. For example, for the problem involving the classification of facial images of patients to pain and nonpain classes discussed in Section IV, the cost of misclassification of a patient in pain to the nonpain class (false negative) is higher than that of a patient with no pain to the pain class (false positive). One of the key advantages of the sparse Bayesian learning approach is its ability to deal with such asymmetric costs.
k given x ∈ ℝD, X = [x1, x2, …, xN], and Z = [z1, z2, …, zN]T. Note that, in contrast to the SVM approach, the sparse Bayesian learning method separates the prediction stage (i.e., finding the posterior class membership probabilities for the new input variable x) from the decision-making stage (i.e., assigning the new input variable x to the appropriate class). This separation is particularly useful when dealing with asymmetric classification costs, where misclassification of input variables belonging to a certain class is more costly [16]. For example, for the problem involving the classification of facial images of patients to pain and nonpain classes discussed in Section IV, the cost of misclassification of a patient in pain to the nonpain class (false negative) is higher than that of a patient with no pain to the pain class (false positive). One of the key advantages of the sparse Bayesian learning approach is its ability to deal with such asymmetric costs.
Define the classifier function
| (37) |
where ϕ: ℝD → ℝM is a continuous feature-space transformation and w = [w1, w2, …, wM]T ∈ ℝM is a weight vector. Note that the RVM algorithm is a special case of the sparse Bayesian learning method. Specifically, in the RVM, wTϕ(x) in (37) has the special form (similar to the SVM algorithm) given by , where k(·, ·) is the kernel function. In the sequel, we consider the general formulation (37).
Following standard statistical practice, we assume that the posterior probability of the target value of an input variable corresponding to the class
 1 is given by p(zn = 1∣xn, w) = σ(y(xn)), n = 1, …, N, where σ(·) is the logistic sigmoidal function defined by σ(s) ≜ 1/(1 + e−s) [16], [17]. Note that, since there are only two classes, p(zn = 0∣xn, w) = 1 − σ(y(xn)). Assuming that the input variables xn, n = 1, …, N, are independent, the likelihood function is given by
1 is given by p(zn = 1∣xn, w) = σ(y(xn)), n = 1, …, N, where σ(·) is the logistic sigmoidal function defined by σ(s) ≜ 1/(1 + e−s) [16], [17]. Note that, since there are only two classes, p(zn = 0∣xn, w) = 1 − σ(y(xn)). Assuming that the input variables xn, n = 1, …, N, are independent, the likelihood function is given by
| (38) |
Each weight parameter wn, n = 1, …, M, in (37) is assumed to have a zero-mean Gaussian distribution, and hence, the weight prior distribution is given by
| (39) |
where αn, n = 1, …, M, is the precision (inverse of the variance of the Gaussian distribution) corresponding to wn and α = [α1, α2, …, αM]T ∈ ℝM. The parameters αn, n = 1, …, M, in the prior distribution (39) are called the hyperparameters. Note that, in contrast to other Bayesian classifiers, each weight parameter wn, n = 1, …, M, has a separate hyperparameter αn.
Given a new input variable x ∈ ℝD, the corresponding target value z ∈ {0, 1} can be predicted using the predictive distribution p(z∣x, X, Z). The predictive distribution is given by
| (40) |
where the distribution is marginalized with respect to the weight vector w ∈ ℝM and the hyperparameters α ∈ ℝM. Since σ(·) is nonlinear, no closed-form solution exists for (40) [16]. Here, we use the type-2 maximum likelihood [19]—also known as the evidence approximation [20]—to approximate (40) by replacing α ∈ ℝM with a constant value α* ∈ ℝM corresponding to the mode (i.e., the maximizer) of the marginal likelihood function p(Z∣X, α). In particular, an approximation to the predictive distribution p(z∣x, X, Z) is given by
| (41) |
The value of α* is found via an iterative process. After initializing α, the posterior distribution p(w∣x, X, Z, α) is approximated by a Gaussian distribution using the Laplace approximation method. The mean of the Gaussian distribution corresponds to the mode (maximizer) of p(w∣x, X, Z, α), which we denote by w*. The maximizer is found using the iterative reweighted least squares (IRLS) method [17], which uses sequential quadratic approximations to find the maximizer. Taking the log of the identity [17]
the maximization problem is equivalent to
| (42) |
or equivalently
| (43) |
where yn = σ(y(xn)) ∈ ℝ, A = diag[α] ∈ ℝM×M, c ∈ ℝ is a variable independent of z (and hence, plays no role in the optimization), and where we have used (38). Note that the covariance matrix of the Gaussian approximation to the posterior distribution p(w∣x, X, Z, α) is equal to the negative Hessian of ln p(w∣x, X, Z, α) evaluated at the maximizer w*. The mean and covariance of the Gaussian approximation are given by
| (44) |
| (45) |
where Φ = [Φ(i,j)] ∈ ℝN × M with Φ(i,j) = ϕj(xi) for i = 1, …, N and j = 1, …, M, B = diag[b1, b2, …, bN] ∈ ℝN × N with bn = yn(1 − yn) ∈ ℝ, n = 1, …, N, and Y = [y1, y2, …, yn]T ∈ ℝN.
Next, using (36), we approximate the marginal likelihood function as follows:
| (46) |
Following the discussion on the type-2 maximum likelihood method, the value of α* is found by maximizing the approximate marginal likelihood function given by (46). Hence, differentiating (46) with respect to αn, n = 1, …, M, and setting the result to zero yields
| (47) |
Solving (47) for αn, n = 1, …, M, gives the updated estimate for αn as follows:
| (48) |
where
n = 1, …, M. Now, using the updated estimate for α, the above steps are repeated until a given convergence criterion is met. The algorithm is summarized in Table I.
TABLE I. Sparse Bayesian Learning Algorithm.
| Step 1. | Initial parameter computation. |
| a. | Set Φ(i,j) = ϕj(xi), i = 1, …, N, j = l, …, M. |
| b. | Set Φ = [Φ(i,j)] ∈ ℝN × M. |
| c. | Set bn = yn(1 − yn), n = 1, …, N. |
| d. | Set B = diag[b1, b2, …, bN]. |
| Step 2. | Initialize the hyperparameters α = [α1, α2, …, αM]T. |
| Step 3. | Find the Gaussian approximation
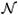 (w; w*, Σ) to the posterior distribution p(w∣x, X, Z, α). (w; w*, Σ) to the posterior distribution p(w∣x, X, Z, α). |
| a. | Set A = diag[α]. |
| b. | Set w* = A−1 ΦT(Z − Y). |
| c. | Set Σ = (ΦT BΦ + A)−1. |
| Step 4. | Compute the approximate marginal likelihood function using . |
| Step 5. | Set γn = 1 − αn Σnn, n = 1, …, M. |
| Step 6. | Update α using . |
| Step 7. | If ‖Δα‖ > Tol1 or ‖Δw*‖ > Tol2, where Δα and Δw* are the changes in the values of α and w* in the current iteration, respectively, and Tol1 and Tol2 are some prespecified tolerances, then go to Step 3. |
| Step 8. | Set α* = α. |
As a result of the maximization of the marginal likelihood function, a number of hyperparameters αn approach infinity, and hence, the corresponding weight parameter wn will be centered at zero with zero variance. Therefore, the corresponding component of the feature-space transformation ϕn(·) plays no role in the prediction, resulting in a sparse predictive model. In the case of the RVM, the input variables xn belonging to the training set {x1, x2, …, xN}, which have a nonzero weight wn, are called relevance vectors. Only the relevance vectors play a role in the classification of new input variables and the rest of the training set can be discarded.
Finally, we note that the posterior probability for the membership of a new input variable x to the class
 1 represented by p(
1 represented by p(
 1 ∣x, X, Z) can be approximated by the logistic sigmoidal function σ(y(x)) using the calculated value of the weight vector w*. This approximatation becomes exact as the number of input variables in the training set approaches infinity [16], [21].
1 ∣x, X, Z) can be approximated by the logistic sigmoidal function σ(y(x)) using the calculated value of the weight vector w*. This approximatation becomes exact as the number of input variables in the training set approaches infinity [16], [21].
IV. Pain and Pain Intensity Assessment in Neonates
In this section, we use the classification techniques described in Sections II and III, in order to assess pain and pain intensity in infants using their facial expressions. For our dataset, we use the infant COPE database [12]. As was shown in [12], the SVM can classify facial images into two groups of “pain” and “nonpain” with an accuracy between 82% and 88%. Here, we extend the results of [12] to additionally assess pain intensity using the class membership posterior probability. Note that although we consider infants, studies have shown that the pain-induced facial expressions in newborns are similar to those observed in older children and adults [22]. However, neonatal facial expressions are characterized by some unique features that are not found in adults, such as “primal face of pain” [23]. In addition, adults can control nonverbal expressions of pain [24].
Before applying the classification techniques to the facial images, we give a brief description of the infant COPE database used in our experimental results.
A. Infant COPE Database
The infant COPE database is composed of 204 RGB color photographs of 26 Caucasian neonates (13 boys and 13 girls) with a resolution of 120 × 100 per photograph and an infant age range of 18 h to 3 days. The photographs were taken after a series of stress-inducing stimuli were administered by a nurse. The stimuli consist of the following [12]:
transport from one crib to another;
air stimulus, where the infant's nose was exposed to a puff of air;
friction, where the external lateral surface of the heel was rubbed with a cotton wool soaked in alcohol;
pain, where the external surface of the heel was punctured for blood collection.
The facial expressions induced by the first three stimuli are classified as nonpain. Four photographs of a typical subject are given in Fig. 1. One of the challenges in the recognition of pain, even for clinicians, is the ability to distinguish an infant's cry induced by pain and some other nonpainful stimulus.
Fig. 1.
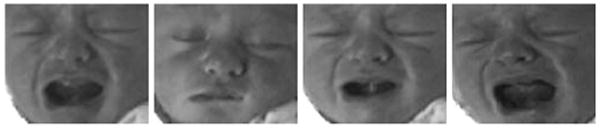
Four different expressions of a subject. The two left images correspond to nonpain, whereas the two right images correspond to pain.
B. Pain Recognition Using Sparse Kernel Machine Algorithms
The classification techniques discussed in Section II were used to identify the facial expressions corresponding to pain. A total of 21 subjects from the infant COPE database were selected such that for each subject at least one photograph corresponded to pain and one to nonpain. The total number of photographs available for each subject ranged from 5 to 12, with a total of 181 photographs considered. We applied the leave-one-out method for validation [17]. In particular, the classifier is trained on all photographs of the subject except for one test photograph, which is used to validate the algorithm. The test photograph corresponds to either a pain or nonpain condition.
In the preprocessing stage, the faces were standardized for their eye position using a similarity transformation. Then, a 70 × 93 window was used to crop the facial region of the image and only the 8-bit grayscale values were used. For each image, a 6510-dimensional vector was formed by column stacking the matrix of intensity values.
We used the MATLAB version R2008a and the OSU SVM MATLAB Toolbox [25] to run the SVM classification algorithm. The classification accuracy for the SVM algorithm with a linear kernel was 90%, where as suggested in [12], we chose the complexity parameter C = 1. The number of support vectors averaged five. Applying the RVM algorithm with a linear kernel to the same dataset resulted in an almost identical classification accuracy, namely, 91%, whereas the number of relevance vectors was reduced to two. However, in 5 out of the 21 subjects considered, the RVM algorithm did not converge. This is due to the fact that in contrast to the SVM algorithm, the RVM algorithm involves a nonconvex optimization problem [17].
C. Pain Intensity Assessment
In addition to classification, the RVM algorithm provides the posterior probability of the membership of a test image to a class. As discussed in Section I, using a Bayesian interpretation of probability, the probability of an event can be interpreted as the degree of the uncertainty associated with such an event. This uncertainty can be used to estimate pain intensity. In particular, if a classifier is trained with a series of facial images corresponding to pain and nonpain, then there is some uncertainty for associating the facial image of a person experiencing moderate pain to the pain class. The efficacy of such an interpretation of the posterior probability was validated by comparing the algorithm's pain assessment with that assessed by several experts (intensivists) and nonexperts.
In order to compare the pain intensity assessment given by the RVM algorithm with human assessment, we compared the subjective measurement of the pain intensity assessed by expert and nonexpert examiners with the uncertainty in the pain class membership (posterior probability) given by the RVM algorithm. Actual pain modes for each infant were used to train the RVM classifier. We chose all 16 infants (out of the total 21) from the COPE database for which the RVM algorithm converged, and for each subject two photographs of the face corresponding to the nonpain and pain conditions were selected. In the selection process, two training photographs were selected, where the infant's facial expression truly reflected the pain intensity condition—calm for nonpain and distressed for pain—and a score of 0 and 100, respectively, was assigned to these photographs to give the human examiner a fair prior knowledge for the assessment of the pain intensity.
Ten data examiners were asked to provide a score ranging from 0 to 100 for each test photograph (i.e., nontraining photograph) of the same subject, using a multiple of ten for the scores. Five examiners with no medical expertise and five examiners with medical expertise in critical care and pain management were selected for this assessment. The medical experts were members of the clinical staff at the ICU of the Northeast Georgia Medical Center, Gainesville, GA, consisting of one medical doctor, one nurse practitioner, and three nurses. The medical doctor has ten years experience as an anesthesiologist and intensivist in pediatric hospitals. The nurse practitioner and nurses have 6 months to 1 year pediatric floor experience in large community hospitals and are also mothers. They were asked to assess the pain for a series of random photographs of the same subject, with the criterion that a score above 50 corresponds to pain, and with an increasing score corresponding to a higher pain intensity. Analogously, a score below 50 corresponds to nonpain, and with a decreasing score corresponding to a lower level of discomfort. The posterior probability given by the RVM algorithm with a linear kernel for each corresponding test photograph was rounded off to the nearest multiple of ten.
The pain scores for five infant subjects are given in Figs. 2–6, where the average score of the expert and nonexpert human examiners are compared to the score given by the RVM algorithm. In order to measure the agreement between the human examiners and the RVM algorithm, we need to quantify the agreement between two raters classifying an observation into different classes. The kappa coefficient [26] is used to measure the agreement between two raters classifying the same observation into two classes. A kappa coefficient of 0 represents chance agreement and a coefficient of 1 represents a perfect agreement between the two raters. The weighted kappa coefficient is an extension of the kappa coefficient to the case, where there are more than two classes and the classes are ordered [27]. In this case, a smaller difference between the chosen classes by the two raters indicates less disagreement between them. The pain intensity assessment can be regarded as a classification process in which a facial expression of a subject is classified into ten ordered classes, where class 1 corresponds to a pain intensity score of 0–9, class 2 corresponds to a pain intensity score of 10–19, etc. A qualitative evaluation of the observed kappa values is given in Table II [28].
Fig. 2.
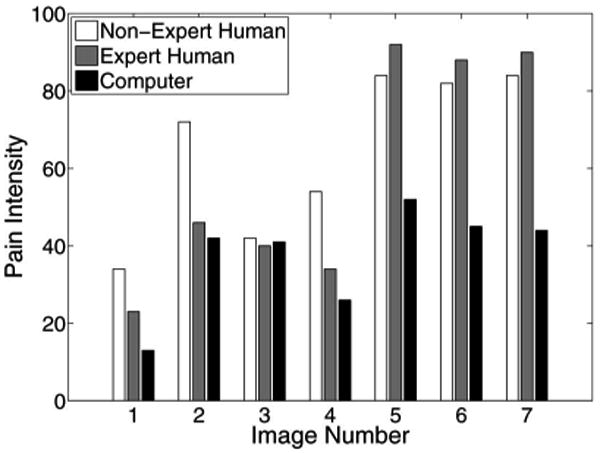
Pain score for subject 1.
Fig. 6.
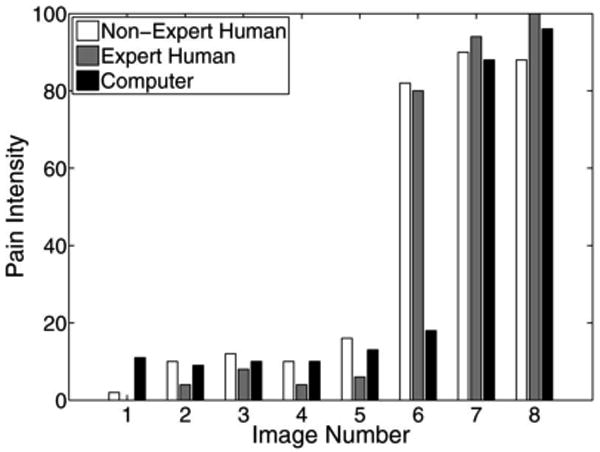
Pain score for subject 5.
TABLE II. Qualitative Evaluation of Observed κ-Values [29].
| κ | Strength of agreement |
|---|---|
| 0.00 | Poor |
| 0.00–0.20 | Slight |
| 0.21–0.40 | Fair |
| 0.41–0.60 | Moderate |
| 0.61–0.80 | Substantial |
| 0.81–1.00 | Almost perfect |
We used the weighted kappa coefficient to measure the agreement in the pain intensity assessment between the human examiners and the RVM algorithm. This coefficient is 0.47 for human expert examiners (with a 95% confidence interval of 0.37 to 0.57) and 0.46 for nonexpert examiners (with a 95% confidence interval of 0.36 to 0.55) as compared with the RVM for the 16 subjects considered in the study. This shows a moderate agreement between the human expert examiners and human nonexpert examiners as compared with the RVM algorithm based on the qualitative evaluation of the observed kappa values given by Table II. It is interesting to note that the weighted kappa coefficient measuring the agreement between human experts and human nonexperts is 0.78 with a 95% confidence interval of 0.73 to 0.82, which indicates a substantial agreement based on Table II. It is important to note, however, that proxy ratings of pain is a highly subjective process [30].
The results show an almost identical classification accuracy for a binary classification (with a score above 50 corresponding to pain). In particular, the nonexpert human examiner, the expert human examiner, and the RVM classification accuracy is given by 79%, 87%, and 91%, respectively. Moreover, the results show that the expert human examiners tend to be more accurate in the binary classification compared to the human nonexperts.
It is worth noting that Fig. 4 shows a poor correlation between the scores given by the RVM algorithm and the data examiners in the first three photographs. The data examiners assessed a high level of pain for subject 3, whereas the subject was not in pain. This highlights the challenge in distinguishing between pain from discomfort, even for human experts. In this case, the RVM algorithm correctly assessed that the infant has some level of discomfort, but is not in pain.
Fig. 4.
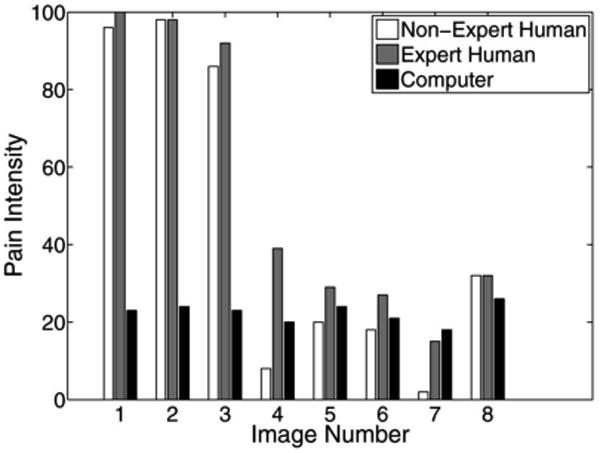
Pain score for subject 3.
Finally, in a repeatability study, the same human expert and nonexpert examiners were asked to assess the intensity of pain for the five subjects considered in Figs. 2–6, after a period ranging from 2 weeks to 4 months. Again, we used the weighted kappa coefficient to measure the agreement between two observations by the same rater. The weighted kappa coefficient in this case can be regarded as a measure of the ability of the human examiner to reproduce his or her own pain scores. The weighted kappa coefficient is 0.79 (with a 95% confidence interval of 0.74 to 0.84) for the human expert examiners and 0.73 (with a 95% confidence interval of 0.68 to 0.78) for the human nonexpert examiners. Based on this analysis, the human expert examiners tend to be slightly more reliable in assessing the pain intensity for the same subjects under the same pain conditions.
V. Conclusion and Opportunities for Future Research
In this paper, the problems of pain and pain intensity assessment using facial expressions in neonates were addressed. Sparse kernel machine algorithms were used to classify the images into pain and nonpain classes. The class membership posterior probability given by the RVM algorithm was interpreted as an estimate of the pain intensity, and this hypothesis was validated by comparing the results with expert and nonexpert human assessments of pain. The results provided by the RVM algorithm can potentially be useful in decision support systems for ICU analgesia, where a reliable objective pain assessment measure is required.
Machine learning techniques, and in particular the RVM algorithm, can potentially be useful in assessing sedation and agitation in the ICU. The fundamental limitations in sedation and agitation assessment in the ICU stem from subjective assessment criteria, rather than quantifiable, measurable data for ICU sedation. This often results in poor quality and inconsistent treatment of patient agitation. Advances in computer vision techniques can potentially assist the medical staff in assessing sedation and agitation by constantly monitoring the patient and providing the clinician with quantifiable data for ICU sedation. An automatic sedation and pain assessment system can be used within a decision support system, which can also provide automated sedation and analgesia in the ICU [31]. In order to achieve closed-loop sedation control in the ICU, a quantifiable feedback signal is required that reflects some measure of the patient's agitation. A nonsubjective agitation assessment algorithm can be a key component in developing closed-loop control algorithms for ICU sedation.
The current clinical standard in the ICU for assessing the level of sedation in adults is an ordinal scoring system, such as the motor activity and assessment scale (MAAS) [32] or the Richmond agitation–sedation scale (RASS) [33], which includes the assessment of the level of agitation of the patient as well as the level of consciousness. For example, the MAAS system evaluates the level of sedation and agitation on a score of 0–6 as follows: 0–unresponsive; 1–responsive only to noxious stimuli; 2–responsive to touch or name; 3–calm and cooperative; 4–restless and cooperative; 5–agitated; and 6–dangerously agitated.
Assessment of the level of sedation and agitation of a patient is, therefore, subjective and limited in accuracy and resolution, and hence, prone to error in assessing the level of sedation, which in turn may lead to oversedation. In particular, oversedation increases risk to the patient since liberation from mechanical ventilation, one of the most common life-saving procedures performed in the ICU, may not be possible due to a diminished level of consciousness and respiratory depression from sedative drugs resulting in prolonged length of stay in the ICU. Prolonged ventilation is expensive and is associated with known risks, such as inadvertent extubation, laryngotracheal trauma, and ventilator-associated pneumonia. Alternatively, undersedation leads to agitation and can result in dangerous situations for both the patient and the intensivist. Specifically, agitated patients can do physical harm to themselves by dislodging their endotracheal tube, which can potentially endanger their life.
While speculative, computer vision techniques offer the possibility to quantify agitation in sedated ICU patients. In particular, such techniques can be used to develop objective agitation measurements from patient motion. In the case of paraplegic patients, whole body movement is not available, and hence, monitoring the whole body motion is not a viable solution. In this case, measuring head motion and facial grimacing for quantifying patient agitation and sedation in critical care can be a useful alternative. Of course, patient occlusions due to medical equipment will need to be accounted for within the machine learning algorithms.
In future research, we will investigate the use of digital imaging and digital video of a patient's entire body movement, as well as facial expressions to assess agitation and sedation in the ICU. In addition, correlations between our objective measurements for agitation and pain intensity using digital imaging and a clinical standard assessment (e.g., MAAS or RASS score) will also be investigated. Furthermore, we will develop an expert control system predicated on digital imaging to emulate a clinician's deductive drug dosing process, that is, the process whereby a clinician successfully infers drug dosing conclusions based on the clinical standard of an assessed MAAS or RASS score. This expert control system can be used within a decision support system to provide closed-loop control for ICU sedation and analgesia, as well as critical care monitoring and lifesaving interventions.
Fig. 3.
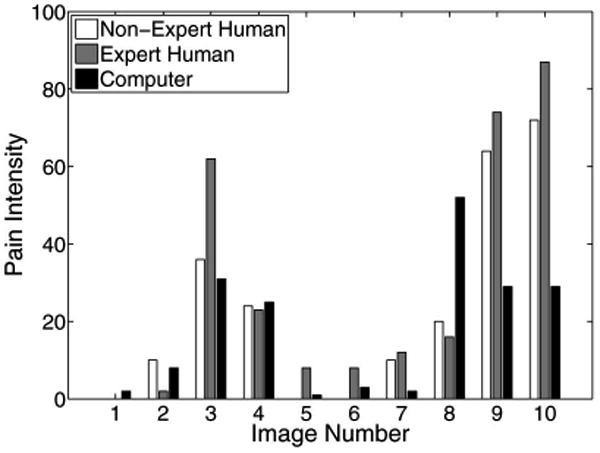
Pain score for subject 2.
Fig. 5.
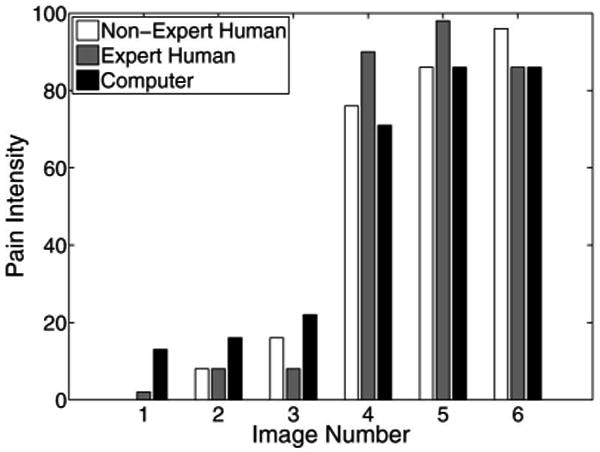
Pain score for subject 4.
Acknowledgments
The authors would like to thank Prof. S. Brahnam for providing the infant COPE database, Dr. J. M. Bailey for assisting in the pain assessment of the infants, and L. K. Haddad for bringing Prof. Brahnam's research to their attention. The first-named author acknowledges several helpful discussions with Prof. J. M. Rehg.
This work was supported in part by the U.S. Army Medical Research and Material Command under Grant 08108002, in part by National Institutes of Health (NIH) under Grant NAC P41 RR-13218 through Brigham and Women's Hospital, and in part by the National Alliance for Medical Image Computing, funded by the NIH through the NIH Roadmap for Medical Research under Grant U54 EB005149.
Biographies

Behnood Gholami (S'04) received the B.Sc. and M.A.Sc. degrees in mechanical engineering from the University of Tehran, Tehran, Iran, and Concordia University, Montreal, Canada, in 2003 and 2005, respectively. In 2009 he received the M.S. degrees in mathematics and aerospace engineering from the Georgia Institute of Technology, Atlanta, GA. He is currently working toward the Ph.D. degree in aerospace engineering at the Georgia Institute of Technology.
In 2007, he was a summer Intern with the Control and Identification Group, The MathWorks, Inc., Natick, MA. His current research interests include computer vision, machine learning, vision-based control, medical image processing, optimal control, robust control, model predictive control, biomedical and biological systems, active control for clinical pharmacology, and image-guided therapy.
Mr. Gholami was a recipient of the Concordia University Graduate Fellowship and a Power Corporation of Canada Graduate Fellowship.

Wassim M. Haddad (S'87–M'87–SM'01–F'09) received the B.S., M.S., and Ph.D. degrees in mechanical engineering from Florida Institute of Technology, Melbourne, FL, in 1983, 1984, and 1987, respectively, with specialization in dynamical systems and control.
From 1987 to 1994, he was a Consultant with the Structural Controls Group, Government Aerospace Systems Division, Harris Corporation, Melbourne, FL. In 1988, he joined the Faculty of the Mechanical and Aerospace Engineering Department, Florida Institute of Technology, where he founded and developed the systems and control option within the graduate program. Since 1994, he has been a member of the Faculty with the School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA, where he is currently a Professor. He has authored or coauthored more than 500 archival journal and conference publications with research contributions in linear and nonlinear dynamical systems and control. He is a coauthor of the books Hierarchical Nonlinear Switching Control Design with Applications to Propulsion Systems (Berlin, Germany: Springer-Verlag, 2000), Thermodynamics: A Dynamical Systems Approach (Princeton, NJ: Princeton University Press, 2005), Impulsive and Hybrid Dynamical Systems: Stability, Dissipativity, and Control (Princeton, NJ: Princeton University Press, 2006), Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach (Princeton, NJ: Princeton University Press, 2008), and Nonnegative and Compartmental Dynamical Systems (Princeton, NJ: Princeton University Press, 2010). His current research interests include nonlinear robust and adaptive control, nonlinear dynamical system theory, large-scale systems, hierarchical nonlinear switching control, analysis and control of nonlinear impulsive and hybrid systems, adaptive and neuroadaptive control, system thermodynamics, thermodynamic modeling of mechanical and aerospace systems, network systems, nonlinear analysis and control for biological and physiological systems, and active control for clinical pharmacology.
Dr. Haddad is a National Science Foundation Presidential Faculty Fellow and a member of the Academy of Nonlinear Sciences.

Allen R. Tannenbaum (M'93–F'09) received the B.A. and Ph.D. degrees in mathematics from Columbia University, New York, NY, and Harvard University, Cambridge, MA, in 1973 and 1976, respectively.
He is currently a Faculty Member with the Schools of Electrical and Computer, and Biomedical Engineering, Georgia Institute of Technology, Atlanta, GA. His research interests include control, image processing, and computer vision.
Contributor Information
Behnood Gholami, Email: behnood@gatech.edu, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA 30332-0150 USA.
Wassim M. Haddad, Email: wm.haddad@aerospace.gatech.edu, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA 30332-0150 USA.
Allen R. Tannenbaum, Email: tannenba@ece.gatech.edu, Schools of Electrical and Computer, and Biomedical Engineering, Georgia Institute of Technology, Atlanta, GA 30332-0150 USA.
References
- 1.Weinert CR, Chlan L, Gross C. Sedating critically ill patients: Factors affecting nurses' delivery of sedative therapy. Amer J Crit Care. 2001;10:156–167. [PubMed] [Google Scholar]
- 2.Aissaoui Y, Zeggwash AA, Zekraoui A, Abidi K, Abouqal R. Validation of a behavioral pain scale in critically ill, sedated, and mechanically ventilated patients. Anesth Analg. 2005;101:1470–1476. doi: 10.1213/01.ANE.0000182331.68722.FF. [DOI] [PubMed] [Google Scholar]
- 3.Gelinas C, Fortier M, Viens C, Fillion L, Puntillo K. Pain assessment and management in critically ill intubated patients: A retrospective study. Amer J Crit Care. 2004;13:126–134. [PubMed] [Google Scholar]
- 4.Keefe FJ, Williams DA, Smith SJ. Assessment of pain behaviors. In: Turk DC, Melzack R, editors. Handbook of Pain Assessment. 2nd. New York, NY: Guilford; 2001. [Google Scholar]
- 5.Prkachin KM. Assessing pain by facial expression: Facial expression as nexus. Pain Res Manag. 2009;14:53–58. doi: 10.1155/2009/542964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Craig KD, Prkachin KM, Grunau RVE. The facial expression of pain. In: Turk D, Melzack R, editors. Handbook of Pain Assessment. New York, NY: Guilford; 2001. [Google Scholar]
- 7.Payen JF, Bru O, Bosson JL, Lagrasta A, Novel E, Deschaux I, Lavagne P, Jacquot C. Assessing pain in critically ill sedated patients by using a behvioral pain scale. Crit Care. 2001;29:2258–2263. doi: 10.1097/00003246-200112000-00004. [DOI] [PubMed] [Google Scholar]
- 8.Merkel SI, Shayevitz JR, Voepel-Lewis T, Malviya S. The FLACC: A behavioral scale for scoring postoperative pain in young children. Pediatr Nurs. 1997;23:293–297. [PubMed] [Google Scholar]
- 9.Stevens B, Johnston C, Petryshen P, Taddio A. Premature infant pain profile: Development and initial validation. Clin J Pain. 1996;12:13–22. doi: 10.1097/00002508-199603000-00004. [DOI] [PubMed] [Google Scholar]
- 10.Bonroy B, Leysens G, Miljkovic D, Schiepers P, Triau E, Wils M, Berckmans D, Colleman P, Maesschalck LD, Quanten S, Vanrumste B. Image acquisition system to monitor discomfort in demented elderly patients. presented at the 3rd Eur. Conf. Use Mod. Inf. Commun. Technol; Ghent, Belgium. 2008. [Google Scholar]
- 11.Becouze P, Hann C, Chase J, Shaw G. Measuring facial grimacing for quantifying patient agitation in critical care. Comp Meth Programs Biomed. 2007;87:138–147. doi: 10.1016/j.cmpb.2007.05.005. [DOI] [PubMed] [Google Scholar]
- 12.Brahnam S, Nanni L, Sexton R. Introduction to neonatal facial pain detection using common and advanced face classification techniques. Stud Comput Intel. 2007;48:225–253. [Google Scholar]
- 13.Brahnam S, Chuang CF, Shih F, Slack M. Machine recognition and representation of neonatal facial displays of acute pain. Artif Intel Med. 2006;36:211–222. doi: 10.1016/j.artmed.2004.12.003. [DOI] [PubMed] [Google Scholar]
- 14.Brahnam S, Nanni L, Sexton R. Neonatal facial pain detection using NNSOA and LSVM. presented at the Int. Conf. Image Proc. Comput. Vis. Pattern Recog; Las Vegas, NV. 2008. [Google Scholar]
- 15.Brahnam S, Chuang CF, Randall S, Shih F. Machine assessment of neonatal facial expressions of acute pain. Decis Support Syst. 2007;43:1242–1254. [Google Scholar]
- 16.Tipping ME. Sparse Bayesian learning and the relevance vector machine. J Mach Learn Res. 2001;1:211–244. [Google Scholar]
- 17.Bishop CM. Pattern Recognition and Machine Learning. New York, NY: Springer-Verlag; 2006. [Google Scholar]
- 18.Vapnik VN. The Nature of Statistical Learning Theory. Berlin, Germany: Springer-Verlag; 1995. [Google Scholar]
- 19.Berger JO. Statistical Decision Theory and Bayesian Analysis. New York, NY: Springer-Verlag; 1985. [Google Scholar]
- 20.MacKay DJC. Bayesian interpolation. Neural Comp. 1992;4:415–447. [Google Scholar]
- 21.Bishop CM. Neural Networks for Pattern Recognition. Oxford, U.K.: Oxford Univ Press; 1995. [Google Scholar]
- 22.Craig KD, Hadjistavropoulos HD, Grunau RVE, Whitfield MF. A comparison of two measures of facial activity during pain in the newborn child. J Pediatr Psychol. 1994;19:305–318. doi: 10.1093/jpepsy/19.3.305. [DOI] [PubMed] [Google Scholar]
- 23.Schiavenato M, Byers JF, Scovanner P, McMahon JM, Xia Y, Lu N, He H. Neonatal pain facial expression: Evaluating the primal face of pain. Pain. 2008;138:460–471. doi: 10.1016/j.pain.2008.07.009. [DOI] [PubMed] [Google Scholar]
- 24.Hadjistavropoulos T, Craig KD. A theoretical framework for understanding self-report and observational measures of pain: A communications model. Behav Res Ther. 2002;40:551–570. doi: 10.1016/s0005-7967(01)00072-9. [DOI] [PubMed] [Google Scholar]
- 25.Ma J, Zhao Y, Ahalt S, Eads D. OSU SVM Toolbox for MATLAB®. 2003 [Online]. Available: http://sourceforge.net/projects/svm.
- 26.Cohen J. A coefficient of agreement for nominal scales. Edu Psychol Meas. 1960;20:37–46. [Google Scholar]
- 27.Cohen J. Weighted kappa: Nominal scale agreement with provision for scale disagreement or partial credit. Psychol Bull. 1968;70:213–220. doi: 10.1037/h0026256. [DOI] [PubMed] [Google Scholar]
- 28.Everitt BS. Statistical Methods in Medical Investigations. London, U.K.: E Arnold; 1994. [Google Scholar]
- 29.Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33:159–174. [PubMed] [Google Scholar]
- 30.Grootendorst PV, Feeny DH, Furlong W. Does it matter whom and how you ask? Inter- and intra-rater agreement in Ontario health survey. J Clinical Epidemiol. 1997;50:127–135. doi: 10.1016/s0895-4356(96)00314-9. [DOI] [PubMed] [Google Scholar]
- 31.Haddad WM, Bailey JM. Closed-loop control for intensive care unit sedation. Best Pract Res Clinical Anaesth. 2009;23:95–114. doi: 10.1016/j.bpa.2008.07.007. [DOI] [PubMed] [Google Scholar]
- 32.Devlin J, Boleski G, Mlynarek M, Nerenz D, Peterson E, Jankowski M, Horst H, Zarowitz B. Motor activity assessment scale: A valid and reliable sedation scale for use with mechanically ventilated patients in an adult surgical intensive care unit. Crit Care Med. 1999;1:1271–1275. doi: 10.1097/00003246-199907000-00008. [DOI] [PubMed] [Google Scholar]
- 33.Sessler C, Gosnell M, Grap MJ, Brophy G, O'Neal P, Keane K, Tesoro E, Elswick R. The Richmond agitation-sedation scale. Amer J Respir Crit Care Med. 2002;166:1338–1344. doi: 10.1164/rccm.2107138. [DOI] [PubMed] [Google Scholar]


