Ridge Structural Equation Modeling with Correlation Matrices for Ordinal and Continuous Data

Abstract

This paper develops a ridge procedure for structural equation modeling (SEM) with ordinal and continuous data by modeling polychoric/polyserial/product-moment correlation matrix R. Rather than directly fitting R, the procedure fits a structural model to R_a = R + aI by minimizing the normal-distribution-based discrepancy function, where a > 0. Statistical properties of the parameter estimates are obtained. Four statistics for overall model evaluation are proposed. Empirical results indicate that the ridge procedure for SEM with ordinal data has better convergence rate, smaller bias, smaller mean square error and better overall model evaluation than the widely used maximum likelihood procedure.

1. Introduction

In social science research data are typically obtained by questionnaires in which respondents are asked to choose one of a few categories on each of many items. Measurements are obtained by coding the categories using 0 and 1 for dichotomized items or 1 to m for items with m categories. Because the difference between 1 and 2 cannot be regarded as equivalent to the difference between m − 1 and m, such obtained measurements only possess ordinal properties. Pearson product-moment correlations cannot reflect the proper association for items with ordinal data. Polychoric correlations are more appropriate if the ordinal variables can be regarded as categorization from an underlying continuous normal distribution. Under such an assumption, each observed ordinal random variable x is related to an underlying continuous random variable z according to

$$x=\{\begin{array}{cc}1& \text{when}z\in (-\infty ,{\tau }_1]\\ 2& \text{when}z\in ({\tau }_1,{\tau }_2]\\ ⋮& ⋮\\ m& \text{when}z\in ({\tau }_{m-1},\infty ),\end{array}$$

where τ₀ = −∞ < τ₁ < … < τ_m−1 < τ_m = ∞ are thresholds. All the continuous variables together form a vector z = (z₁, z₂, …, z_p)′ that follows a multivariate normal distribution N_p(μ, Σ), where μ = 0 and Σ = (ρ_ij) is a correlation matrix due to identification considerations. When such an assumption holds, polychoric correlations are consistent, asymptotically normally distributed and their standard errors (SE) can also be consistently estimated (Olsson, 1979; Poon & Lee, 1987). On the other hand, the Pearson product-moment correlation is generally biased, especially when the number of categories is small and the observed frequencies of the marginal distributions are skewed. Simulation studies imply that polychoric correlations also possess certain robust properties when the underlying continuous distribution departs from normality (see e.g., Quiroga, 1992).

Because item level data in social sciences are typically ordinal, structural equation modeling (SEM) for such data has long been developed. Bock and Lieberman (1970) developed a maximum likelihood (ML) approach to factor analysis with dichotomous data and a single factor. Lee, Poon and Bentler (1990) extended this approach to general SEM with polytomous variables. Because the ML approach involves the evaluation of multiple integrals, it is computationally intensive. Instead of ML, Christoffersson (1975) and Muthén (1978) proposed procedures of fitting a multiple-factor model using pairwise frequencies for dichotomous data by generalized least squares with an asymptotically correct weight matrix (AGLS). Muthén (1984) further formulated a general procedure for SEM with ordinal and continuous data using AGLS, which forms the basis of LISCOMP (an early version of Mplus, Muthén & Muthén, 2007). An AGLS approach for SEM with ordinal and continuous data was developed in Lee, Poon and Bentler (1992), where thresholds, polychoric, polyserial and product-moment correlations were estimated by ML. Lee, Poon and Bentler (1995) further formulated another AGLS approach in which thresholds, polychoric, polyserial and product-moment correlations are estimated by ML using different subsets of variables; they named the procedure partition ML (see also Poon & Lee, 1987). The approach of Lee et al. (1995) has been implemented in EQS (Bentler, 1995) with various extensions for better statistical inference. Jöreskog (1994) also gave the technical details to SEM with ordinal variables, where thresholds are estimated using marginal frequencies and followed by the estimation of polychoric correlations using pairwise frequencies and holding the estimated thresholds constant. Jöreskog’s development formed the basis for ordinal data in LISREL¹ (see e.g., Jöreskog 1990; Jöreskog & Sörbom, 1996). Technical details of the development in Muthén (1984) were provided by Muthén and Satorra (1995). Recently, Bollen and Maydeu-Olivares (2007) proposed a procedure using polychoric instrumental variables. In summary, various technical developments have been made for SEM with ordinal data, emphasizing AGLS.

Methods currently available in software are two-stage procedures where polychoric, polyserial and product-moment correlations are obtained first. This correlation matrix is then modeled with SEM using ML, AGLS, the normal-distribution-based GLS (NGLS), least squares (LS), and diagonally-weighted least squares (DWLS), as implemented in EQS, LISREL and Mplus. We need to note that the ML procedure in software fits a structural model to a polychoric/polyserial/product-moment correlation matrix by minimizing the normal distribution based discrepancy function, treating the correlation matrix as a sample covariance matrix from a normally distributed sample, which is totally different from the ML procedure considered by Lee et al. (1990). We will refer to this ML method in SEM software as the ML method from now on. The main purpose of this paper is to develop a ridge procedure for SEM with ordinal and continuous data that has a better convergence rate, smaller bias, smaller mean square error (MSE) and better overall model evaluation than ML. We next briefly review studies on the empirical behavior of several procedures to identify the limitation and strength of each method and to motivate our study and development.

Babakus, Ferguson and Jöreskog (1987) studied the procedure of ML with modeling four different kinds of correlations (product-moment, polychoric, Spearman’s rho, and Kendall’s tau-b) and found that ML with polychoric correlations provides the most accurate estimates of parameters with respect to bias and MSE, but it is also associated with most nonconvergences. Rigdon and Ferguson (1991) studied modeling polychoric correlation matrices with several discrepancy functions and found that distribution shape of the ordinal data, sample size and fitting function all affect convergence rate. In particular, AGLS has the most serious problem of convergence and improper solutions, especially when the sample size is small. ML generates the most accurate estimates at sample size n = 500; ML almost generates the most accurate parameter estimates at n = 300, as reported in Table 2 of the paper. Potthast (1993) only studied AGLS estimators and found that the resulting SEs are substantially underestimated while the associated chi-square statistic is substantially inflated. Potthast also found that AGLS estimators contain positive biases. Dolan (1994) studied ML and AGLS with polychoric correlations and found that ML with polychoric correlations produces the least biased parameter estimates while AGLS estimators contain substantial biases. DiStefano (2002) studied the performance of AGLS and also found that the resulting SEs are substantially underestimated while the associated chi-square statistic is substantially inflated. There also exist many nonconvergence problems and improper solutions. The literature also shows that, for ML with polychoric correlations, the resulting SEs and test statistic behave badly, because without correction the formula for SEs and test statistics are not correct. Currently, when modeling polychoric/polyserial correlation matrices, software has the option of calculating SEs based on a sandwich-type covariance matrix and using rescaled or adjusted statistics for overall model evaluation (e.g., EQS, LISREL, Mplus). These corrected versions are often called robust procedures in the literature. A recent study by Lei (2009) on ML in EQS and DWLS in Mplus found that DWLS has a better convergence rate than ML. She also found that relative biases of ML and DWLS parameter estimates were similar conditioned on the study factors. She concluded (p. 505)

Table 2.

Averaged bias×10³, variance×10³ and MSE×10³ with 15 dichotomized indicators, based on converged replications.

n	ML			ML.1			ML.2
	Bias	Var	MSE	Bias	Var	MSE	Bias	Var	MSE
100	5.218	12.249	12.305	8.346	11.523	11.608	4.726	11.148	11.175
200	5.319	5.687	5.723	2.930	5.353	5.364	2.211	5.250	5.256
300	3.052	3.647	3.659	2.020	3.481	3.486	1.553	3.420	3.423
400	2.574	2.734	2.743	1.898	2.627	2.631	1.583	2.587	2.590

ML performed slightly better in standard error estimation (at smaller sample sizes before it started to over-correct) while robust WLS provided slightly better overall Type I error control and higher power in detecting omitted paths. In cases when sample size is adequately large for the model size, especially when the model is also correctly specified, it would matter little whether ML of EQS6 or robust WLS of Mplus3.1 is chosen. However, when sample sizes are very small for the model and the ordinal variables are moderately skewed, ML with Satorra-Bentler scaled statistics may be recommended if proper solutions are obtainable.

In summary, ML and AGLS are the most widely studied procedures, and the latter cannot be trusted with not large enough sample sizes although conditional on the correlation matrix it is asymptotically the best procedure. These studies indicate that robust ML and robust DWLS are promising procedures for SEM with ordinal data. Comparing robust ML and robust DWLS, the former uses a weight matrix that is determined by the normal distribution assumption while the latter uses a diagonal weight matrix that treats all the correlations as independent. The ridge procedure to be studied can be regarded as a combination of ML and LS.

One problem with ML is its convergence rate. This is partially because the polychoric/polyserial correlations are obtained from different marginals, and the resulting correlation matrix may not be positive definite, especially when the sample size is not large enough and there are many items. As a matter of fact, the normal-distribution-based discrepancy function cannot take a correlation matrix that is not positive definite because the involved logarithm function cannot take non-positive values. When the correlation matrix is near singular and is still positive definite, the model implied matrix will need to mimic the near singular correlation (data) matrix so that the estimation problem becomes ill-conditioned (see e.g., Kelley, 1995), which results not only in slower or nonconvergence but also unstable parameter estimates and unstable test statistics (Yuan & Chan, 2008). Such a phenomenon can also happen to the sample covariance matrix when the sample size is small or when the elements of the covariance matrix are obtained by ad-hoc procedures (see e.g., Wothke, 1993). Although smoothing the eigenvalues and imposing a constraint of positive definitiveness is possible (e.g., Knol & ten Berge, 1989), the statistical consequences have not been worked out and remain unknown.

When a covariance matrix S is near singular, the matrix S_a = S+aI with a positive scalar a will be positive definite and well-conditioned. Yuan and Chan (2008) proposed to model S_a rather than S, using the normal distribution based discrepancy function. They showed that the procedure results in consistent parameter estimates. Empirical results indicate that the procedure not only converges better, at small sample sizes the resulting parameter estimates are more accurate than the ML estimator (MLE) even when data are normally distributed. Compared to modeling sample covariance matrices, modeling correlations typically encounters more problems of convergence with smaller sample sizes, especially for ordinal data that are skew distributed. Actually, both EQS and LISREL contain warnings about proper application of modeling polychoric correlations when sample size is small. Thus, the methodology in Yuan and Chan (2008) may be even more relevant to the analysis of polychoric/polyserial correlation matrices than to sample covariance matrices. The aim of this paper is to extend the procedure in Yuan and Chan (2008) to SEM with ordinal and continuous data by modeling polychoric/polyserial/product-moment correlation matrices.

When a p × p sample covariance matrix S = (s_ij) is singular, the program LISREL provides an option of modeling S + a diag(s₁₁, ···, s_pp), which is called the ridge option (Jöreskog & Sörbom, 1996, p. 24). With a correlation matrix R, the ridge option in LISREL fits the structural model to R + aI, which is the same as extending the procedure in Yuan and Chan (2008) to correlation matrices. Thus, ridge SEM with ordinal data has already been implemented in LISREL. However, it is not clear how to properly apply this procedure in practice, due to lack of studies of its properties. Actually, McQuitty (1997) conducted empirical studies on the ridge option in LISREL 8 and concluded that (p. 251) “there appears to be ample evidence that structural equation models should not be estimated with LISREL’s ridge option unless the estimation of unstandardized factor loadings is the only goal.” One of the contributions of this paper is to obtain statistical properties of ridge SEM with ordinal data and to make it a statistically sound procedure. We will show that ridge SEM with ordinal data enjoys consistent parameter estimates and consistent SEs. We will also propose four statistics for overall model evaluation. Because ridge SEM is most useful when the polychoric/polyserial/product-moment correlation matrix is near singular, which tends to occur with smaller sample sizes, we will conduct Monte Carlo study to see how ridge SEM performs with respect to bias and efficiency of parameter estimates. We will also empirically identify the most reliable statistics for overall model evaluation and evaluate the performance of formula-based SEs.

Section 2 provides the details of the development for model inference, including consistent parameter estimates and SEs as well as rescaled and adjusted statistic for overall model evaluation. Monte Carlo results are presented in section 3. Section 4 contains a real data example. Conclusion and discussion are offered at the end of the paper.

2. Model Inference

Let R be a p×p correlation matrix, including polychoric, polyserial and Pearson product-moment correlations for ordinal and continuous variables. Let r be the vector of all the correlations formed by the below-diagonal elements of R and ρ be the population counterpart of r. Then it follows from Jöreskog (1994), Lee et al. (1995) or Muthén and Satorra (1995) that,

$$\sqrt{n}(\mathbf{r}-\mathit{\rho })\stackrel{ℒ}{\to }N(\mathbf{0},\mathbf{\Upsilon }),$$ (1)

where $\stackrel{ℒ}{\to }$ denotes convergence in distribution and ϒ is the asymptotic covariance matrix of $\sqrt{n}\mathbf{r}$ that can be consistently estimated. For SEM with ordinal data, we will have a correlation structure Σ(θ). As mentioned in the introduction, popular SEM software has the option of modeling R by minimizing

$$F_{ML}(\mathit{\theta })=\text{tr}[\mathbf{R}{\mathbf{\sum }}^{-1}(\mathit{\theta })]-log\mid \mathbf{R}{\mathbf{\sum }}^{-1}(\mathit{\theta })\mid -p$$ (2)

for parameter estimates θ̂. Such a procedure is just to replace the sample covariance matrix S by the correlation matrix R in the most commonly used ML procedure for SEM. Equations (1) and (2) can be compared to covariance structure analysis when S is based on a sample from an unknown distribution. Actually, the same amount of information is provided in both cases, where ϒ’s need to be estimated using fourth-order moments. Similar to modeling covariance matrices, (2) needs R to be positive definite. Otherwise, the term log |RΣ⁻¹(θ)| is not defined.

For a positive a, let R_a = R + aI. Instead of minimizing (2), ridge SEM minimizes

$$F_{\mathit{MLa}}({\mathit{\theta }}_a)=\text{tr}[{\mathbf{R}}_a{\mathbf{\sum }}_a^{-1}({\mathit{\theta }}_a)]-log\mid {\mathbf{R}}_a{\mathbf{\sum }}_a^{-1}({\mathit{\theta }}_a)\mid -p$$ (3)

for parameter estimates θ̂_a, where Σ_a(θ_a) = Σ(θ_a) + aI. We will show that θ̂_a is consistent and asymptotically normally distributed. Notice that corresponding to R_a is a population covariance matrix Σ_a = Σ + aI, which has identical off-diagonal elements with Σ. Although minimizing (2) for θ̂ with a = 0 for categorical data is available in software, we cannot find any documentation of its statistical properties. Our development will be for an arbitrary positive a, including the ML procedure when a = 0. Parallel to Yuan and Chan (2008), the following technical development will be within the context of LISREL models.

2.1 Consistency

Let z = (x^*′, y^*′)′ be the underlying standardized population. Using LISREL notation, the “measurement model²” is given by

$${\mathbf{x}}^{\ast }={\mathit{\mu }}_x+{\mathbf{\Lambda }}_x\mathit{\xi }+\mathit{\delta },{\mathbf{y}}^{\ast }={\mathit{\mu }}_y+{\mathbf{\Lambda }}_y\mathit{\eta }+\mathit{\epsilon },$$

where μ_x = E(x^*), μ_y = E(y^*), Λ_x and Λ_y are factor loading matrices; ξ and η are vectors of latent constructs with E(ξ) = 0 and E(η) = 0; and δ and ε are vectors of measurement errors with E(δ) = 0, E(ε) = 0, Θ_δ = E(δδ′), Θ_ε = E(εε′). The structural model that describes interrelations of η and ξ is

$$\mathit{\eta }=\mathbf{B}\mathit{\eta }+\mathbf{\Gamma }\mathit{\xi }+\mathit{\zeta },$$

where ζ is a vector of prediction errors with E(ζ) = 0 and Ψ = E(ζζ′). Let Φ = E(ξξ′), the resulting covariance structure of z is (see Jöreskog & Sörbom, 1996, pp. 1–3)

$$\mathbf{\sum }(\mathit{\theta })=\left(\begin{array}{cc}{\mathbf{\Lambda }}_x\mathbf{\Phi }{\mathbf{\Lambda }}_x^{\prime }+{\mathbf{\Theta }}_{\delta }& {\mathbf{\Lambda }}_x\mathbf{\Phi }{\mathbf{\Gamma }}^{\prime }{(\mathbf{I}-{\mathbf{B}}^{\prime })}^{-1}{\mathbf{\Lambda }}_y^{\prime }\\ {\mathbf{\Lambda }}_y{(\mathbf{I}-\mathbf{B})}^{-1}\mathbf{\Gamma }\mathbf{\Phi }{\mathbf{\Lambda }}_x^{\prime }& {\mathbf{\Lambda }}_y{(\mathbf{I}-\mathbf{B})}^{-1}(\mathbf{\Gamma }\mathbf{\Phi }{\mathbf{\Gamma }}^{\prime }+\mathbf{\Psi }){(\mathbf{I}-{\mathbf{B}}^{\prime })}^{-1}{\mathbf{\Lambda }}_y^{\prime }+{\mathbf{\Theta }}_{\epsilon }\end{array}\right).$$

Recall that μ = E(z) = 0 and that Σ = Cov(z) is a correlation matrix when modeling polychoric/polyserial/product-moment correlations. We have μ_x = 0, μ_y = 0,

$$\text{diag}({\mathbf{\Theta }}_{\delta })={\mathbf{I}}_{\delta }-\text{diag}({\mathbf{\Lambda }}_x\mathbf{\Phi }{\mathbf{\Lambda }}_x^{\prime })$$

and

$$\text{diag}({\mathbf{\Theta }}_{\epsilon })={\mathbf{I}}_{\epsilon }-\text{diag}[{\mathbf{\Lambda }}_y{(\mathbf{I}-\mathbf{B})}^{-1}(\mathbf{\Gamma }\mathbf{\Phi }{\mathbf{\Gamma }}^{\prime }+\mathbf{\Psi }){(\mathbf{I}-{\mathbf{B}}^{\prime })}^{-1}{\mathbf{\Lambda }}_y^{\prime }],$$

where diag(A) means the diagonal matrix formed by the diagonal elements of A, and I_δ and I_ε are identity matrices with the same dimension as Θ_δ and Θ_ε, respectively. Thus, the diagonal elements of Θ_δ and Θ_ε are not part of the free parameters but part of the model of Σ(θ) through the functions of free parameters in Λ_x, Λ_y, B, Γ, Φ, Ψ, offdiag(Θ_δ) and offdiag(Θ_ε), where offdiag(A) implies the off-diagonal elements of A.

When Σ(θ) is a correct model for Σ, there exist matrices ${\mathbf{\Lambda }}_x^{(0)},{\mathbf{\Lambda }}_y^{(0)}$, B⁽⁰⁾, Γ⁽⁰⁾, Φ⁽⁰⁾, Ψ⁽⁰⁾, $\text{offdiag(}{\mathbf{\Theta }}_{\delta }^{(0)})$ and $\text{offdiag(}{\mathbf{\Theta }}_{\epsilon }^{(0)})$ such that Σ = Σ(θ₀), where θ₀ is the vector containing the population values of all the free parameters in θ. Let θ_a0 be the corresponding vector of θ_a at ${\mathbf{\Lambda }}_x^{(a)}={\mathbf{\Lambda }}_x^{(0)},{\mathbf{\Lambda }}_y^{(a)}={\mathbf{\Lambda }}_y^{(0)}$, B^(a) = B⁽⁰⁾, Γ^(a) = Γ⁽⁰⁾, Φ^(a) = Φ⁽⁰⁾, Ψ^(a) = Ψ⁽⁰⁾, $\text{offdiag}({\mathbf{\Theta }}_{\delta }^{(a)})=\text{offdiag}({\mathbf{\Theta }}_{\delta }^{(0)})$ and $\text{offdiag}({\mathbf{\Theta }}_{\epsilon }^{(a)})=\text{offdiag}({\mathbf{\Theta }}_{\epsilon }^{(0)})$. In addition, let

$$\text{diag}({\mathbf{\Theta }}_{\delta }^{(a)})=\text{diag}({\mathbf{\Theta }}_{\delta }^{(0)})+{a\mathbf{I}}_{\delta }$$ (4a)

and

$$\text{diag}({\mathbf{\Theta }}_{\epsilon }^{(a)})=\text{diag}({\mathbf{\Theta }}_{\epsilon }^{(0)})+{a\mathbf{I}}_{\epsilon }.$$ (4b)

Thus, θ_a0 = θ₀ and ${\mathbf{\Theta }}_{\delta }^{(a)}$ and ${\mathbf{\Theta }}_{\epsilon }^{(a)}$ are functions of θ_a0 = θ₀ and a. Let the functions in (4a) and (4b) be part of the model of Σ_a(θ_a). Then we have Σ_a = Σ_a(θ_a0) = Σ_a(θ₀). Notice that Σ_a(θ) is uniquely determined by Σ(θ) and a. This implies that whenever Σ(θ) is a correct model for modeling Σ, Σ_a(θ_a) will be a correct model for modeling Σ_a. The above result also implies that for a correctly specified Σ(θ), except for sampling errors, the parameter estimates for Λ_x, Λ_y, B, Γ, Φ, Ψ and the off-diagonal elements of Θ_δ and Θ_ε when modeling R_a will be the same as those when modeling R. The resulting estimates for the diagonals of ${\mathbf{\Theta }}_{\delta }^{(a)}$ and ${\mathbf{\Theta }}_{\epsilon }^{(a)}$ of modeling R_a are different from those of modeling R by the constant a, which is up to our choice. Traditionally, the diagonal elements of Θ̂_δ and Θ̂_ε are estimates of the variances of measurement errors/uniquenesses. When modeling R_a, these can be obtained by

$$\text{diag}({\widehat{\mathbf{\Theta }}}_{\delta })=\text{diag}({\widehat{\mathbf{\Theta }}}_{\delta }^{(a)})-{a\mathbf{I}}_{\delta }$$ (5a)

and

$$\text{diag}({\widehat{\mathbf{\Theta }}}_{\epsilon })=\text{diag}({\widehat{\mathbf{\Theta }}}_{\epsilon }^{(a)})-{a\mathbf{I}}_{\epsilon }.$$ (5b)

The above discussion implies that θ̂_a of modeling R_a may be different from θ̂ of modeling R due to sampling error, but their population counterparts are identical. We have the following formal result.

Theorem 1

Under the conditions (I) Σ(θ) is correctly specified and identified and (II) θ ∈ Θ and Θ is a compact subset of the Euclidean space 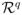, θ̂_a is consistent for θ₀ regardless of the value of a.

The proof of the theorem is essentially the same as that for Theorem 1 in Yuan and Chan (2008) when replacing the sample covariance matrix there by the correlation matrix R. Yuan and Chan (2008) also discussed the benefit of modeling S_a = S + aI from a computational perspective using the concept of condition number; the same benefit holds for modeling R_a. One advantage of estimation with a better condition number is that a small change in the sample will only cause a small change in θ̂_a while a small change in the sample can cause a great change in θ̂ if R is near singular. Readers who are interested in the details are referred to Yuan and Chan (2008).

2.2 Asymptotic normality

We will obtain the asymptotic distribution of θ̂_a, which allows us to obtain its consistent SEs. For such a purpose we need to introduce some notation first.

For a symmetric matrix A, let vech(A) be a vector by stacking the columns of A and leaving out the elements above the diagonal. We define s_a = vech(R_a), σ_a(θ) = vech[Σ_a(θ)], s = vech(R), and σ(θ) = vech[Σ(θ)]. Notice that s_a and s are vectors of length p^* = p(p + 1)/2 while the r in (1) is a vector of length p_* = p(p − 1)/2. The difference between r and s_a is that s_a also contains the p elements of a + 1 on the diagonal of R_a, and s_a = s when a = 0. Let D_p be the duplication matrix defined by Magnus and Neudecker (1999, p. 49), and

$${\mathbf{W}}_a(\mathit{\theta })=2^{-1}{\mathbf{D}}_p^{\prime }[{\mathbf{\sum }}_a^{-1}(\mathit{\theta })\otimes {\mathbf{\sum }}_a^{-1}(\mathit{\theta })]{\mathbf{D}}_p.$$

We will use a dot on top of a function to denote the first derivative or the gradient. For example, if θ contains q unknown parameters, σ̇_a(θ) = ∂σ_a(θ)/∂θ′ is a p^*×q matrix. Under standard regularity conditions, including that θ₀ is an interior point of Θ, θ̂_a satisfies

$${\mathbf{g}}_a({\widehat{\mathit{\theta }}}_a)=\mathbf{0},$$ (6)

where

$${\mathbf{g}}_a(\mathit{\theta })={\stackrel{.}{\mathit{\sigma }}}_a^{\prime }(\mathit{\theta }){\mathbf{W}}_a(\mathit{\theta })[{\mathbf{s}}_a-{\mathit{\sigma }}_a(\mathit{\theta })].$$

In equation (6), because σ_a(θ) and σ(θ) only differ by a constant a, σ̇_a(θ) = σ̇(θ) and s_a − σ_a(θ) = s − σ(θ). So the effect of a on θ̂_a in (6) is only through

$${\mathbf{W}}_a(\mathit{\theta })=2^{-1}{\mathbf{D}}_p^{\prime }\{{[\mathbf{\sum }(\mathit{\theta })+a\mathbf{I}]}^{-1}\otimes {[\mathbf{\sum }(\mathit{\theta })+a\mathbf{I}]}^{-1}\}{\mathbf{D}}_p=\frac{1}{2{(a+1)}^2}{\mathbf{U}}_a,$$ (7)

where

$${\mathbf{U}}_a={\mathbf{D}}_p^{\prime }\{{[\frac{1}{a+1}\mathbf{\sum }(\mathit{\theta })+\frac{a}{a+1}\mathbf{I}]}^{-1}\otimes {[\frac{1}{a+1}\mathbf{\sum }(\mathit{\theta })+\frac{a}{a+1}\mathbf{I}]}^{-1}\}{\mathbf{D}}_p.$$

Notice that the constant coefficient 1/[2(a + 1)²] in (7) does not have any effect on θ̂_a. It is U_a that makes a difference. When a = 0, θ̂_a = θ̂ is the ML parameter estimate. When a = ∞,

$${\mathbf{U}}_a={\mathbf{D}}_p^{\prime }{\mathbf{D}}_p$$

is the weight matrix corresponding to modeling R by least squares. Thus, ridge SEM can be regarded as a combination of ML and LS. We would expect that it has the merits of both procedures. That is, ridge SEM will have a better convergence rate and more accurate parameter estimates than ML and more efficient estimates than LS.

It follows from (6) and a Taylor expansion of g_a(θ̂_a) at θ₀ that

$$\sqrt{n}({\widehat{\mathit{\theta }}}_a-{\mathit{\theta }}_0)=-{[{\stackrel{.}{\mathbf{g}}}_a(\overline{\mathit{\theta }})]}^{-1}{\mathbf{g}}_a({\mathit{\theta }}_0)={({\stackrel{.}{\mathit{\sigma }}}_a^{\prime }{\mathbf{W}}_a{\stackrel{.}{\mathit{\sigma }}}_a)}^{-1}{\stackrel{.}{\mathit{\sigma }}}_a^{\prime }{\mathbf{W}}_a\sqrt{n}({\mathbf{s}}_a-{\mathit{\sigma }}_a)+o_p(1),$$ (8)

where ġ_a(θ̄) is q ×q matrix and each of its rows is evaluated at a vector θ̄ that is between θ₀ and θ̂_a, and o_p(1) represents a quantity that converges to zero in probability as n increases. We also omitted the argument of the functions in (8) when evaluated at the population value θ₀. Notice that the rows of σ̇_a corresponding to the diagonal elements of Σ_a are zeros and the vector (s_a − σ_a) constitutes of (r − ρ) plus p zeros. It follows from (1) that

$$\sqrt{n}({\mathbf{s}}_a-{\mathit{\sigma }}_a)\stackrel{ℒ}{\to }N(\mathbf{0},{\mathbf{\Upsilon }}^{\ast }),$$ (9)

where ϒ^* is a p^* × p^* matrix consisting of ϒ and p rows and p columns of zeros. Obviously, ϒ^* is singular. We may understand (9) by the general definition of a random variable, which is just a constant when its variance is zero. It follows from (8) and (9) that

$$\sqrt{n}({\widehat{\mathit{\theta }}}_a-{\mathit{\theta }}_0)\stackrel{ℒ}{\to }N(\mathbf{0},\mathbf{\Omega }),$$ (10a)

where

$$\mathbf{\Omega }={({\stackrel{.}{\mathit{\sigma }}}_a^{\prime }{\mathbf{W}}_a{\stackrel{.}{\mathit{\sigma }}}_a)}^{-1}{\stackrel{.}{\mathit{\sigma }}}_a^{\prime }{\mathbf{W}}_a{\mathbf{\Upsilon }}^{\ast }{\mathbf{W}}_a{\stackrel{.}{\mathit{\sigma }}}_a{({\stackrel{.}{\mathit{\sigma }}}_a^{\prime }{\mathbf{W}}_a{\stackrel{.}{\mathit{\sigma }}}_a)}^{-1}.$$ (10b)

Let ϒ̂^* be a consistent estimator of ϒ^*, which can be obtained from a consistent ϒ̂ plus p rows and p columns of zeros. A consistent estimate Ω̂ = (ω̂_ij) of Ω can be obtained when replacing the unknown parameters in (10) by θ̂_a and ϒ^* by ϒ̂^*. Notice that the Ω in (10) is the asymptotic covariance matrix. We will compare the formula-based SEs ${\widehat{\omega }}_{jj}^{1/2}/\sqrt{n}$ against empirical SEs at smaller sample sizes using Monte Carlo.

A consistent ϒ̂ can be obtained by the approach of estimating equations (see e.g., Yuan & Jennrich, 1998). Actually, the estimates of ϒ given in Lee et al. (1992, 1995), Jöreskog (1994) and Muthén and Satorra (1995) can all be regarded as using estimating equations.

2.3 Statistics for overall model evaluation

This subsection presents four statistics for overall model evaluation. When minimizing (3) for parameter estimates, we automatically get a measure of discrepancy between data and model, i.e., F_{M La}(θ̂_a). However, the popular statistic T_{M La} = nF_{M La}(θ̂_a) does not asymptotically follow a chi-square distribution even when a = 0. Let

$$F_{\mathit{RLSa}}({\widehat{\mathit{\theta }}}_a)={[{\mathbf{s}}_a-{\mathit{\sigma }}_a({\widehat{\mathit{\theta }}}_a)]}^{\prime }{\mathbf{W}}_a({\widehat{\mathit{\theta }}}_a)[{\mathbf{s}}_a-{\mathit{\sigma }}_a({\widehat{\mathit{\theta }}}_a)]=\frac{1}{2}\text{tr}\{{[{\mathbf{R}}_a{\mathbf{\sum }}_a^{-1}({\widehat{\mathit{\theta }}}_a)-\mathbf{I}]}^2\}$$

and

$$T_{\mathit{RLSa}}={nF}_{\mathit{RLSa}}({\widehat{\mathit{\theta }}}_a)$$ (11)

be the so-called reweighted LS statistic, which is in the default output of EQS when modeling the covariance matrix. Under the assumption of a correct model structure, there exists

$$T_{\mathit{MLa}}=T_{\mathit{RLSa}}+o_p(1).$$ (12)

Notice that σ_a = σ_a(θ₀). It follows from (8) that

$$\begin{array}{l}\sqrt{n}[{\mathbf{s}}_a-{\mathit{\sigma }}_a({\widehat{\mathit{\theta }}}_a)]=\sqrt{n}\{({\mathbf{s}}_a-{\mathit{\sigma }}_a)-[{\mathit{\sigma }}_a({\widehat{\mathit{\theta }}}_a)-{\mathit{\sigma }}_a({\mathit{\theta }}_0)]\}\\ =\sqrt{n}\{({\mathbf{s}}_a-{\mathit{\sigma }}_a)-{\stackrel{.}{\mathit{\sigma }}}_a({\widehat{\mathit{\theta }}}_a-{\mathit{\theta }}_0)\}+o_p(1)\\ ={\mathbf{P}}_a\sqrt{n}({\mathbf{s}}_a-{\mathit{\sigma }}_a)+o_p(1),\end{array}$$ (13)

where

$${\mathbf{P}}_a=\mathbf{I}-{\stackrel{.}{\mathit{\sigma }}}_a{({\stackrel{.}{\mathit{\sigma }}}_a^{\prime }{\mathbf{W}}_a{\stackrel{.}{\mathit{\sigma }}}_a)}^{-1}{\stackrel{.}{\mathit{\sigma }}}_a^{\prime }{\mathbf{W}}_a.$$

Combining (12) and (13) leads to

$$T_{\mathit{MLa}}=n{({\mathbf{s}}_a-{\mathit{\sigma }}_a)}^{\prime }{\mathbf{P}}_a^{\prime }{\mathbf{W}}_a{\mathbf{P}}_a({\mathbf{s}}_a-{\mathit{\sigma }}_a)+o_p(1).$$ (14)

Notice that ϒ^* in (9) has a rank of p_*, there exists a p^* × p_* matrix A such that AA′ = ϒ^*. Let u ~ N_p*(0, I), then it follows from (9) that

$$\sqrt{n}({\mathbf{s}}_a-{\mathit{\sigma }}_a)=\mathbf{Au}+o_p(1).$$ (15)

Combining (14) and (15) yields

$$T_{\mathit{MLa}}={\mathbf{u}}^{\prime }{({\mathbf{P}}_a\mathbf{A})}^{\prime }{\mathbf{W}}_a({\mathbf{P}}_a\mathbf{A})\mathbf{u}+o_p(1).$$ (16)

Notice that (P_aA)′W_a(P_aA) is nonnegative definite and its rank is p_*−q. Let 0 < κ₁ ≤ κ₂ ≤ … ≤ κ_p*−q be the nonzero eigenvalues of (P_aA)′W_a(P_aA) or equivalently of ${\mathbf{P}}_a^{\prime }{\mathbf{W}}_a{\mathbf{P}}_a{\mathbf{\Upsilon }}^{\ast }$. It follows from (16) that

$$T_{\mathit{MLa}}=\sum _{j=1}^{p_{\ast }-q}{\kappa }_j{u}_j^2+o_p(1).$$ (17)

where $u_j^2$ are independent and each follows ${\chi }_1^2$. Unless all the κ_j’s are 1.0, the distribution of T_MLa will not be ${\chi }_{p_{\ast }-q}^2$. However, the behavior of T_MLa might be approximately described by a chi-square distribution with the same mean. Let

$$\widehat{m}=\text{tr}({\widehat{\mathbf{\Upsilon }}}^{\ast }{\widehat{\mathbf{P}}}_a^{\prime }{\widehat{\mathbf{W}}}_a{\widehat{\mathbf{P}}}_a)/(p_{\ast }-q).$$

Then, as n → ∞,

$$T_{\mathit{RMLa}}=T_{\mathit{MLa}}/\widehat{m}$$

approaches a distribution whose mean equals p_* − q. Thus, we may approximate the distribution of T_MLa by

$$T_{\mathit{RMLa}}\stackrel{.}{\sim }{\chi }_{p_{\ast }-q}^2,$$ (18)

parallel to the Satorra and Bentler (1988) rescaled statistic when modeling the sample covariance matrix. Again, the approximation in (18) is motivated by asymptotics, we will use Monte Carlo to study its performance with smaller sizes.

Notice that the systematic part of T_RMLa is the quadratic form

$$Q_{\mathit{RMLa}}=(p_{\ast }-q)\sum _{j=1}^{p_{\ast }-q}{\kappa }_i{u}_j^2/(\sum _{j=1}^{p_{\ast }-q}{\kappa }_j),$$

which agrees with ${\chi }_{p_{\ast }-q}^2$ in the first moment. Allowing the degrees of freedom to be estimated rather than p_* − q, a statistic that agrees with the chi-square distribution in both the first and second moments was studied by Satterthwaite (1941) and Box (1954), and applied to covariance structure models by Satorra and Bentler (1988). It can also be applied to approximate the distribution of T_MLa. Let

$$m_1=\sum _{j=1}^{p_{\ast }-q}{\kappa }_j^2/\sum _{j=1}^{p_{\ast }-q}{\kappa }_j,m_2={(\sum _{j=1}^{p_{\ast }-q}{\kappa }_j)}^2/\sum _{j=1}^{p_{\ast }-q}{\kappa }_j^2.$$

Then T_MLa/m₁ asymptotically agrees with ${\chi }_{m_2}^2$ in the first two moments. Consistent estimates of m₁ and m₂ are given by

$${\widehat{m}}_1=\text{tr}[{({\widehat{\mathbf{\Upsilon }}}^{\ast }{\widehat{\mathbf{P}}}_a^{\prime }{\widehat{\mathbf{W}}}_a{\widehat{\mathbf{P}}}_a)}^2]/\text{tr}({\widehat{\mathbf{\Upsilon }}}^{\ast }{\widehat{\mathbf{P}}}_a^{\prime }{\widehat{\mathbf{W}}}_a{\widehat{\mathbf{P}}}_a),{\widehat{m}}_2={[\text{tr}({\widehat{\mathbf{\Upsilon }}}^{\ast }{\widehat{\mathbf{P}}}_a^{\prime }{\widehat{\mathbf{W}}}_a{\widehat{\mathbf{P}}}_a)]}^2/\text{tr}[{({\widehat{\mathbf{\Upsilon }}}^{\ast }{\widehat{\mathbf{P}}}_a^{\prime }{\widehat{\mathbf{W}}}_a{\widehat{\mathbf{P}}}_a)}^2].$$ (19)

Thus, using the approximation

$$T_{\mathit{AMLa}}=T_{\mathit{MLa}}/{\widehat{m}}_1\stackrel{.}{\sim }{\chi }_{{\widehat{m}}_2}^2$$ (20)

might lead to a better description of T_MLa than (18). We will also study the performance of (20) using Monte Carlo in the next section.

In addition to T_MLa, T_RLSa can also be used to construct statistics for overall model evaluation, as printed in EQS output when modeling the sample covariance matrix. Like T_MLa, when modeling R_a, T_RLSa does not asymptotically follow a chi-square distribution even when a = 0. It follows from (12) that the distribution of T_RLSa can be approximated using

$$T_{R\mathit{RLSa}}=T_{\mathit{RLSa}}/\widehat{m}\sim {\chi }_{p_{\ast }-q}^2$$ (21)

or

$$T_{A\mathit{RLSa}}=T_{\mathit{RLSa}}/{\widehat{m}}_1\sim {\chi }_{{\widehat{m}}_2}^2.$$ (22)

The rationales for the approximations in (21) and (22) are the same as those for (18) and (20), respectively. Again, we will study the performance of T_RRLSa and T_ARLSa using Monte Carlo in the next section.

We would like to note that the o_p(1) in equation (12) goes to zero as n → ∞. But statistical theory does not tell how close T_MLa and T_RLSa are at a finite n. The Monte Carlo study in the next section will allow us to compare their performances and to identify the best statistic for overall model evaluation at smaller sample sizes.

We also would like to note that the ridge procedure developed here is different from the ridge procedure for modeling covariance matrices developed in Yuan and Chan (2008). When treating R_a as a covariance matrix in the analysis, we will get identical T_MLa and T_RLSa as defined here if all the diagonal elements of Σ_a(θ̂_a) happen to be a + 1, which is true for many commonly used SEM models. However, the rescaled or adjusted statistics will be different. Similarly, we may also get identical estimates for factor loadings, but their SEs will be different when based on either the commonly used information matrix or the sandwich-type covariance matrix constructed using ϒ̂^*.

3. Monte Carlo Results

The population z contains 15 normally distributed random variables with mean zero and covariance matrix

$$\mathbf{\sum }=\mathbf{\Lambda }\mathbf{\Phi }{\mathbf{\Lambda }}^{\prime }+\mathbf{\Psi },$$

where

$$\mathbf{\Lambda }=\left(\begin{array}{ccc}\mathbf{\lambda }& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{\lambda }& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{\lambda }\end{array}\right)$$

with λ = (.60, .70, 0.75, .80, .90)′ and 0 being a vector of five zeros;

$$\mathbf{\Phi }=\left(\begin{array}{ccc}1.0& .30& .40\\ .30& 1.0& .50\\ .40& .50& 1.0\end{array}\right);$$

and Ψ is a diagonal matrix such that all the diagonal elements of Σ are 1.0. Thus, z can be regarded as generated by a 3-factor model, and each factor has 5 unidimensional indicators.

Three sets of conditions are used to obtain the observed variables. In condition 1, all the 15 variables in x are dichotomous and are obtained using thresholds

$$\mathit{\tau }={(-0.52,-0.25,0,0.25,0.52,-0.39,-0.25,-0.13,0,0.13,0,0.13,0.25,0.39,0.52)}^{\prime },$$

which corresponds to 30%, 40%, 50%, 60%, 70%, 35%, 40%, 45%, 50%, 55%, 50%, 55%, 60%, 65%, and 70% of zeros at the population level for the 15 variables, respectively. In condition 2, for each factor the first two variables have five categories and the last three variables are dichotomous. The thresholds for the 6 five-category variables are respectively τ₁ = (−0.52, −0.25, 0.25, 0.52)′, corresponding to proportions (30%, 10%, 20%, 10%, 30%) for the five categories of x₁; τ₂ = (−0.84, −0.25, 0.25, 0.84), corresponding to proportions (20%, 20%, 20%, 20%, 20%) for the five categories of x₂; τ₆ = (−0.84, −0.25, 0.25, 0.84), corresponding to proportions (20%, 20%, 20%, 20%, 20%) for the five categories of x₆; τ₇ = (−0.84, −0.52, −0.25, 0.25), corresponding to proportions (20%, 10%, 10%, 20%, 40%) for the five categories of x₇; τ₁₁ = (−0.52, −0.25, 0.25, 0.52), corresponding to proportions (30%, 10%, 20%, 10%, 30%) for the five categories of x₁₁; τ ₁₂ = (−0.25, 0.25, 0.52, 0.84), corresponding to proportions (40%, 20%, 10%, 10%, 20%) for the five categories of x₁₂. The thresholds for the 9 dichotomous variables are τ = (0, 0.25, 0.52, −0.25, 0, 0.13, 0.25, 0.39, 0.52), which correspond to 50%, 60%, 70%, 40%, 50%, 55%, 60%, 65%, 70% of zeros at the population level of x₃, x₄, x₅, x₈, x₉, x₁₀, x₁₃, x₁₄ and x₁₅, respectively. In condition 3, the first two variables for each factor are continuously observed and the last three variables are dichotomous using thresholds

$$\mathit{\tau }={(0,0.25,0.52,-0.25,0,0.13,0.25,0.39,0.52)}^{\prime },$$

which correspond to 50%, 60%, 70%, 40%, 50%, 55%, 60%, 65%, and 70% of zeros at the population level of variables x₃, x₄, x₅, x₈, x₉, x₁₀, x₁₃, x₁₄ and x₁₅, respectively.

Because it is with smaller sample sizes that ML encounter problems, we choose sample sizes³ n = 100, 200, 300 and 400. One thousand replications are used at each sample size. For each sample, we model R_a with a = 0, .1 and .2, which are denoted by ML, ML.₁ and ML.₂, respectively. Our evaluation includes the number of convergence or converging rate, the speed of convergence, biases and SEs as well as mean square errors (MSE) of the parameter estimates; and the performance of the four statistics given in the previous section. We also compare SEs based on the covariance matrix Ω in (10) against empirical SEs.

All the thresholds are estimated using the default probit function in SAS. Pearson product-moment correlations are obtained for continuously observed variables. Fisher scoring algorithms are used to obtain polychoric/polyserial correlations (Olsson, 1979; Olsson, Drasgow & Dorans, 1982) and to solve equation (6) for structural model parameters θ̂_a (Lee & Jennrich, 1979; Olsson, 1979). The convergence criterion in estimating the polychoric/polyserial correlations is set as |r^(k+1) − r^(k)| < 10⁻⁴, where r^(k) is the value of r after the kth iteration; the convergence criterion for obtaining θ̂_a is set as ${max}_{1\le j\le q}\mid {\theta }_j^{(k+1)}-{\theta }_j^{(k)}\mid <{10}^{-4}$, where ${\theta }_j^{(k)}$ is the jth parameter after the kth iteration. True population values are set as the initial value in both estimation processes. We record the estimation as unable to reach a convergence if the convergence criterion cannot be reached after 100 iterations. For each R, the ϒ in (1) is estimated using estimating equations.

Note that not all of the N = 1000 replications converge in all the conditions, all the empirical results are based on N_c converged replications for each estimation method. Let θ̂_ij be the estimate of θ_j in the ith converged replication. For each estimation method at a given sample size we obtained

$${\text{Bias}}_j=\frac{1}{N_c}\sum _{i=1}^{N_c}{\widehat{\theta }}_{ij}-{\theta }_{j0},{\text{Var}}_j=\frac{1}{N_c-1}\sum _{i=1}^{N_c}{({\widehat{\theta }}_{ij}-{\overline{\theta }}_j)}^2,$$

with ${\overline{\theta }}_j={\sum }_{i=1}^{N_c}{\widehat{\theta }}_{ij}/N_c$, and

$${\text{MSE}}_j=\frac{1}{N_c}\sum _{i=1}^{N_c}{({\widehat{\theta }}_{ij}-{\theta }_{j0})}^2.$$

For the performance of the formula-based SE, we also obtained

$${\text{SE}}_{Fj}=\frac{1}{N_c}\sum _{i=1}^{N_c}{\text{SE}}_{ij},$$

where SE_ij is the square root of the jth diagonal element of Ω̂/n in the ith converged replication. In contrast, the empirical SE, SE_Ej, is just the square root of Var_j. Notice that there are 18 free model parameters: 15 factor loadings and 3 factor correlations. With 3 data conditions, 3 estimation methods and 4 sample sizes, there will be too many tables to include in the paper if we report bias, MSE and SEs for each individual parameter. Instead, these are put on the web at “www.anonymous.edu/ridge-item-SEM/”. In the paper, for each sample size and each estimation method, we report the averaged bias, variance and MSE given by

$$\begin{array}{c}\text{Bias}=\frac{1}{18}\sum _{j=1}^{18}\mid {\text{Bias}}_j\mid ,\text{Var}=\frac{1}{18}\sum _{j=1}^{18}{\text{Var}}_j,\text{MSE}=\frac{1}{18}\sum _{j=1}^{18}{\text{MSE}}_j,\\ {\text{SE}}_F=\frac{1}{18}\sum _{j=1}^{18}{\text{SE}}_{Fj},{\text{SE}}_E=\frac{1}{18}\sum _{j=1}^{18}{\text{SE}}_{Ej},\end{array}$$

and the averaged difference

$$\text{AD}=\frac{1}{18}\sum _{j=1}^{18}\mid {\text{SE}}_{Fj}-{\text{SE}}_{Ej}\mid ,$$

which will give us the information of the formula-based SEs when predicting empirical SEs.

Results for data condition 1 with 15 dichotomous indicators are in Tables 1 to 5. All replications reached convergence when estimating R. But more than half replications cannot converge when solving (6) with a = 0 and .1 at n = 100, as reported in the upper panel of Table 1. When a = .2, the number of convergence doubles that when a = 0 at n = 100. When n = 200, there are still about one third of the replications cannot reach convergence at a = 0 while all reach convergence at a = .2. Ridge SEM not only results in more convergences but also converges faster, as reported in the lower panel of Table 1, where each entry is the average of the number of iterations for N_c converged replications.

Table 1.

Number of convergences and average number of iterations with 15 dichotomized indicators, 1000 replications.

	n	ML	ML.1	ML.2
number of convergences	100	438	491	961
	200	688	995	1000
	300	988	1000	1000
	400	1000	1000	1000
average number of iterations	100	18.767	12.112	10.286
	200	9.416	8.085	7.405
	300	7.886	6.949	6.480
	400	7.046	6.348	5.996

Table 5.

Performance of standard errors with 15 dichotomized indicators, based on converged replications.

(a) Averaged empirical standard errors and formula-based standard errors
n	ML		ML.1		ML.2
	SEE	SEF	SEE	SEF	SEE	SEF
100	0.1087	0.0992	0.1060	0.0980	0.1040	0.0964
200	0.0742	0.0709	0.0721	0.0692	0.0714	0.0687
300	0.0595	0.0576	0.0581	0.0567	0.0576	0.0563
400	0.0514	0.0498	0.0504	0.0492	0.0501	0.0489

(b) Averaged difference between empirical standard errors and formula-based standard errors.
n	ML	ML.1	ML.2
100	0.0095	0.0083	0.0076
200	0.0035	0.0032	0.0029
300	0.0021	0.0016	0.0014
400	0.0018	0.0015	0.0013

Tables 2 contains the averaged bias, variance and MSE for the four sample sizes and three estimation methods. Clearly, all the averaged biases are at the 3rd decimal place. Except for n = 100, all the other variances and MSEs are also at the 3rd decimal place. Because the N_c’s for the three different a’s for n = 100 and 200 are so different, it is had to compare the results between different estimation methods. When n = 400, all the three methods converged for all the replications, the averaged bias, variance, and MSE all become smaller as a changes from 0 to .2. At n = 300, both ML.₁ and ML.₂ converged for all the replications, the averaged bias, variance, and MSE corresponding to ML.₂ are also smaller. These indicate that the ridge procedure with a proper a leads to less biased, more efficient and more accurate parameter estimates than ML. The corresponding biases, variances and MSEs for individual parameters are in Tables A1 to A4 at “www.nd.edu~kyuan/ridge-item-SEM/”. From these tables we may notice that most individual biases are also at the 3rd decimal place although they tend to be negative. We may also notice that estimates for smaller loadings tend to have greater variances and MSEs.

Table 3 contains the empirical mean, standard deviation (SD), the number of rejection and the rejection ratio of the statistics T_RMLa and T_AMLa, based on the converged replications. Each rejection is compared to the 95th percentiles of the reference distribution in (18) or (20). For reference, the mean and SD of T_MLa are also reported. Both T_RMLa and T_AMLa over-reject the correct model although they tend to improve as n or a increases. Because the three N_c’s at n = 100 are very different, the rejection rates, means or SDs of the three estimation methods are not comparable for this sample size. Table 3 also suggests that T_MLa cannot be used for model inference because its empirical means and SDs are far away from those of the nominal ${\chi }_{87}^2$.

Table 3.

Performance of the statistics T_RMLa and T_AMLa with 15 dichotomized indicators, based on converged replications (df = p_* − q = 87, RN=reject number, RR=reject ratio).

n	Method	TMLa		TRMLa				TAMLa
		Mean	SD	Mean	SD	RN	RR	Mean	SD	RN	RR
100	ML	497.31	162.63	87.59	32.53	92	21.0%	32.15	13.63	52	11.9%
	ML.1	468.81	140.42	137.47	39.73	363	73.9%	56.23	15.99	284	57.8%
	ML.2	290.74	80.33	121.35	32.71	572	59.5%	51.20	13.47	375	39.0%
200	ML	708.30	228.50	133.40	41.16	474	68.9%	71.03	21.73	388	56.4%
	ML.1	371.14	89.05	109.59	25.27	441	44.3%	62.57	13.85	308	31.0%
	ML.2	236.76	43.25	99.24	17.78	248	24.8%	58.64	10.07	130	13.0%
300	ML	619.56	189.86	116.80	33.29	505	51.1%	71.41	19.72	410	41.5%
	ML.1	335.20	62.25	99.71	18.34	262	26.2%	65.79	11.75	177	17.7%
	ML.2	225.60	37.47	94.77	15.77	156	15.6%	64.52	10.34	95	9.5%
400	ML	549.61	126.47	105.00	23.18	365	36.5%	69.97	15.07	274	27.4%
	ML.1	320.01	55.37	95.55	16.45	189	18.9%	68.30	11.44	123	12.3%
	ML.2	219.34	35.16	92.24	14.85	114	11.4%	67.96	10.62	70	7.0%

Table 4 contains the results of T_RRLSa and T_ARLSa, parallel to those in Table 3. For n = 200, 300 and 400, the statistic T_RRLSa performed very well in mean, SD and rejection rate although there is a slight over-rejection at smaller n. While T_RLSa monotonically decreases with a, T_RRLSa is very stable when a changes. The statistic T_ARLSa also performed well with a little bit of under-rejection.

Table 4.

Performance of the statistics T_RRLSa and T_ARLSa with 15 dichotomized indicators, based on converged replications (df = p_* − q = 87, RN=reject number, RR=reject ratio).

n	Method	TRLSa		TRRLSa				TARLSa
		Mean	SD	Mean	SD	RN	RR	Mean	SD	RN	RR
100	ML	523.60	88.61	90.45	13.47	37	8.4%	32.71	6.17	6	1.4%
	ML.1	280.69	45.27	82.46	12.81	14	2.9%	33.76	5.19	1	0.2%
	ML.2	211.03	32.72	88.19	13.51	64	6.7%	37.24	5.47	5	0.5%
200	ML	443.05	69.13	83.66	12.52	16	2.3%	44.63	7.05	6	0.9%
	ML.1	296.88	48.23	87.74	13.80	65	6.5%	50.13	7.59	23	2.3%
	ML.2	209.50	32.92	87.83	13.61	65	6.5%	51.91	7.67	24	2.4%
300	ML	462.72	77.62	87.51	13.96	66	6.7%	53.63	8.75	29	2.9%
	ML.1	295.39	46.19	87.88	13.67	67	6.7%	57.99	8.74	37	3.7%
	ML.2	209.27	31.91	87.91	13.46	64	6.4%	59.86	8.79	37	3.7%
400	ML	457.14	75.88	87.41	13.94	59	5.9%	58.29	9.18	31	3.1%
	ML.1	292.46	45.10	87.33	13.44	48	4.8%	62.43	9.32	31	3.1%
	ML.2	207.57	31.31	87.29	13.25	46	4.6%	64.32	9.45	29	2.9%

Table 5 compares the averages of the formula-based SEs against the empirical ones. We use 4 decimals to inform the fine differences among the three estimation methods. As expected, within each estimation method, both the averaged SE_E and SE_F become smaller as n increases, as reflected by Table 5(a). They are also smaller at a given n when a changes from 0 to .2, although at n = 100 and 200 they are based on different number of replications. Table 5(a) also implies that formula-based SEs tend to slightly under-predict empirical SEs. The results in Table 5(b) indicate that SE_F predicts SE_E better when either a or n increases. At n = 400, the under-prediction is between 1% and 2% with ML.₂. It is interesting to note that the averaged difference between SE_F and SE_E is smaller at n = 300 and a = .2 than that at n = 400 and a = 0 or .1. The corresponding SEs for individual parameters are in Tables A5 to A8 on the web, where almost all individual SE_Es are slightly under-predicted by the corresponding SE_F s, with only a few exceptions mostly for factor correlations.

Results for data condition 2 with 6 five-category and 9 dichotomous indicators are in Tables 6 to 10. All replications converged when estimating R. But only 294 out of 1000 replications converged when solving (6) with a = 0 at n = 100, as reported in the upper panel of Table 6. At n = 100, the number of convergences almost tripled when a = .1, and only 3 replications could not reach convergence with ML.₂. Nonconvergences still exist for ML at n = 200 and 300 while all replications converged for ML.₁ and ML.₂. The lower panel of Table 6 implies that ridge SEM also converges faster. It is interesting to see that ML at n = 100 in Table 6 enjoys fewer convergences than that in Table 1. Further examination indicates that almost all the nonconvergences are due to nonpositive definite or near singular R. This is because positive definiteness is a function of all the elements in R. One element in R can change the smallest eigenvalue from positive to negative.

Table 6.

Number of convergence and average number of iterations with 6 five-category and 9 dichotomous indicators, 1000 replications.

	n	ML	ML.1	ML.2
number of convergence	100	294	882	997
	200	938	1000	1000
	300	998	1000	1000
	400	1000	1000	1000
average number of iterations	100	16.320	10.249	9.002
	200	8.453	7.317	6.776
	300	7.119	6.433	6.030
	400	6.514	5.958	5.622

Table 10.

Performance of standard errors with 6 five-category and 9 dichotomous indicators, based on converged replications.

(a) Averaged empirical standard errors and formula-based standard errors
n	ML		ML.1		ML.2
	SEE	SEF	SEE	SEF	SEE	SEF
100	0.0989	0.0911	0.0944	0.0886	0.0929	0.0876
200	0.0666	0.0642	0.0650	0.0628	0.0642	0.0624
300	0.0537	0.0523	0.0526	0.0514	0.0521	0.0511
400	0.0464	0.0453	0.0455	0.0446	0.0451	0.0443

(b) Averaged difference between empirical standard errors and formula-based standard errors.
n	ML	ML.1	ML.2
100	0.0080	0.0058	0.0054
200	0.0026	0.0022	0.0020
300	0.0016	0.0013	0.0012
400	0.0014	0.0012	0.0012

Tables 7 contains the averaged bias, variance and MSE for data condition 2. At n = 400 when all the three estimation methods converged on all replications, bias, variance and MSE all become smaller when a changes from 0 to .2. These quantities also become smaller as a increases at n = 100, 200 and 300. These indicate that the ridge procedure with a proper a leads to less biased, more efficient and more accurate parameter estimates than ML. Compared to the results in Table 2, we notice that, except for the averaged bias of ML at n = 100, all the other numbers in Table 7 are smaller. This indicates that having indicators with more categories leads to less biased and more efficient parameter estimates for all the three estimation methods. The exception for the averaged bias with ML at n = 100 is due to the very different convergence rates. The corresponding biases, variances and MSEs for individual parameters are in Tables A9 to A12 on the web. From these tables we may notice that most individual biases are negative. We may also notice that estimates for smaller loadings do not tend to have greater variances or MSEs anymore, due to their corresponding indicators having more categories.

Table 7.

Averaged bias×10³, variance×10³ and MSE×10³, with 6 five-category and 9 dichotomous indicators, based on converged replications.

n	ML			ML.1			ML.2
	Bias	Var	MSE	Bias	Var	MSE	Bias	Var	MSE
100	6.287	10.170	10.230	5.424	9.222	9.259	4.254	8.934	8.957
200	3.714	4.595	4.614	2.306	4.361	4.369	1.806	4.255	4.261
300	2.402	2.985	2.993	1.629	2.854	2.857	1.261	2.798	2.800
400	2.010	2.242	2.247	1.478	2.153	2.156	1.201	2.115	2.117

Parallel to Table 3, Table 8 contains the results for the statistics T_RMLa and T_AMLa, based on the converged replications. Similar to those in Table 3, both T_RMLa and T_AMLa over-reject the correct model although they tend to improve as n or a increases. Among the statistics, T_AMLa performed the best at a = .2. Table 8 also suggests that T_MLa cannot be used for model inference. Table 9 contains the results of T_RRLSa and T_ARLSa, parallel to those in Table 4. Both T_RRLSa and T_ARLSa continue to be stable when n or a changes. But T_RRLSa tends to reject the correct model more than in Table 4 while T_ARLSa slightly under-rejects the correct model. Tables 8 and 9 also suggest that T_MLa and T_RLSa tend to be smaller with indicators having more categories, but they are still too far away from the expected ${\chi }_{87}^2$.

Table 8.

Performance of the statistics T_RMLa and T_AMLa with 6 five-category and 9 dichotomous indicators, based on converged replications (df = p_* − q = 87, RN=reject number, RR=reject ratio).

n	Method	TMLa		TRMLa				TAMLa
		Mean	SD	Mean	SD	RN	RR	Mean	SD	RN	RR
100	ML	504.19	164.86	123.43	43.13	165	56.1%	42.64	16.72	124	42.2%
	ML.1	313.13	94.08	126.18	37.42	565	64.1%	48.27	14.05	378	42.9%
	ML.2	183.64	38.05	106.38	21.63	383	38.4%	42.57	8.43	180	18.1%
200	ML	487.36	169.66	123.47	41.20	522	55.7%	59.69	19.78	404	43.1%
	ML.1	249.16	49.10	101.26	19.62	304	30.4%	53.88	10.19	177	17.7%
	ML.2	164.26	27.54	95.18	15.92	190	19.0%	52.92	8.57	87	8.7%
300	ML	413.77	110.85	106.31	27.42	365	36.6%	59.24	15.15	254	25.5%
	ML.1	234.68	43.58	95.79	17.73	190	19.0%	58.58	10.61	114	11.4%
	ML.2	159.44	27.02	92.41	15.71	129	12.9%	58.98	9.71	75	7.5%
400	ML	383.55	81.45	99.43	20.54	270	27.0%	60.00	12.31	174	17.4%
	ML.1	227.84	39.06	93.19	16.00	144	14.4%	61.52	10.35	88	8.8%
	ML.2	156.81	25.18	90.89	14.68	107	10.7%	62.60	9.84	66	6.6%

Table 9.

Performance of the statistics T_RRLSa and T_ARLSa with 6 five-category and 9 dichotomous indicators, based on converged replications (df = p_* − q = 87, RN=reject number, RR=reject ratio).

n	Method	TRLSa		TRRLSa				TARLSa
		Mean	SD	Mean	SD	RN	RR	Mean	SD	RN	RR
100	ML	361.63	98.63	86.24	17.23	27	9.2%	29.19	5.85	4	1.4%
	ML.1	214.81	33.19	86.67	13.33	44	5.0%	33.21	5.25	8	0.9%
	ML.2	152.91	24.08	88.62	13.78	72	7.2%	35.48	5.40	13	1.3%
200	ML	339.98	57.03	86.41	14.10	55	5.9%	41.88	7.40	13	1.4%
	ML.1	216.18	34.87	87.88	14.05	69	6.9%	46.78	7.35	15	1.5%
	ML.2	151.76	23.60	87.94	13.67	63	6.3%	48.90	7.34	15	1.5%
300	ML	341.33	61.49	87.80	15.29	89	8.9%	48.98	8.71	36	3.6%
	ML.1	215.28	35.77	87.87	14.56	75	7.5%	53.75	8.71	38	3.8%
	ML.2	151.60	24.46	87.87	14.20	67	6.7%	56.08	8.75	35	3.5%
400	ML	337.98	58.18	87.66	14.79	80	8.0%	52.92	8.99	37	3.7%
	ML.1	214.29	34.21	87.65	14.05	70	7.0%	57.87	9.09	34	3.4%
	ML.2	151.23	23.53	87.65	13.74	66	6.6%	60.37	9.19	31	3.1%

Table 10 contains the averages of empirical and the formula-based SEs. Similar to those in Table 5, the SE becomes smaller as either n or a increases. Table 10(a) also implies that formula-based SEs tend to slightly under-predict empirical SEs. The results in Table 10(b) indicate that SE_F predicts SE_E better when either a or n increases. SE_F also predicts SE_E better under ML.₂ at n = 300 than under ML at n = 400. Comparing the results in Table 10 to those in Table 5, we notice that the formula-based SEs predict the empirical ones better when indicators have more categories. The corresponding SEs for individual parameters are in Tables A13 to A16 on the web, where almost all individual SE_Es are slightly under-predicted by the corresponding SE_F s, with only a few exceptions.

Results for data condition 3 with 6 continuous and 9 dichotomous indicators are in Tables 11 to 15. Similar to data conditions 1 and 2, all nonconvergences occurred when solving (6) with a = 0 at n = 100, 200, 300 and with a = .1 at n = 100, as reported in the upper panel of Table 11. Obviously, ridge SEM not only results in more convergences but also converges faster, as reported in the lower panel of Table 1. Similar to being observed previously, the condition with 6 continuous and 9 dichotomous indicators does not necessarily correspond to more positive definite R than the condition with 15 dichotomous indicators when n is small. It is expected that both ML.₁ and ML.₂ perform well.

Table 11.

Number of convergences and average number of iterations with 6 continuous and 9 dichotomized indicators, 1000 replications.

	n	ML	ML.1	ML.2
number of convergence	100	279	919	1000
	200	946	1000	1000
	300	999	1000	1000
	400	1000	1000	1000
average number of iterations	100	13.756	9.950	8.703
	200	8.205	7.121	6.626
	300	6.974	6.278	5.916
	400	6.391	5.847	5.532

Table 15.

Performance of standard errors with 6 continuous and 9 dichotomized indicators, based on converged replications.

(a) Averaged empirical standard errors and formula-based standard errors
n	ML		ML.1		ML.2
	SEE	SEF	SEE	SEF	SEE	SEF
100	0.0940	0.0875	0.0904	0.0844	0.0888	0.0833
200	0.0639	0.0614	0.0620	0.0600	0.0612	0.0595
300	0.0512	0.0501	0.0501	0.0492	0.0495	0.0488
400	0.0445	0.0434	0.0436	0.0426	0.0431	0.0423

(b) Averaged difference between empirical standard errors and formula-based standard errors.
n	ML	ML.1	ML.2
100	0.0067	0.0060	.0054
200	0.0026	0.0021	.0018
300	0.0013	0.0011	.0010
400	0.0012	0.0011	.0010

Tables 12 contains the averaged bias, variance and MSE. Similar to the two previous conditions, bias, variance and MSE all become smaller from a = 0 to a = .2. Compared to the results in Tables 2 and 7, we notice that, except for the averaged bias of ML at n = 100, all the other numbers in Table 12 are smaller. This is expected because more continuous indicators should correspond to less biased and more efficient parameter estimates. The exception for the averaged bias with ML at n = 100 is due to the very different convergence rates. The corresponding biases, variances and MSEs for individual parameters are in Tables A17 to A20 on the web.

Table 12.

Averaged bias×10³, variance×10³ and MSE×10³, with 6 continuous and 9 dichotomized indicators, based on converged replications.

n	ML			ML.1			ML.2
	Bias	Var	MSE	Bias	Var	MSE	Bias	Var	MSE
100	7.939	9.160	9.245	5.000	8.490	8.522	3.918	8.196	8.216
200	3.232	4.264	4.280	2.114	4.004	4.011	1.679	3.896	3.900
300	2.110	2.735	2.741	1.408	2.603	2.606	1.076	2.546	2.548
400	1.771	2.077	2.081	1.323	1.986	1.988	1.091	1.945	1.947

Table 13 gives the results of T_RMLa and T_AMLa, parallel to those in Tables 3 and 8. Similar to being observed earlier, both T_RMLa and T_AMLa over-reject the correct model although they tend to improve as n or a increases. Table 14 contains the results of T_RRLSa and T_ARLSa, parallel to those in Tables 4 and 9. Both T_RRLSa and T_ARLSa continue to be stable to the changes of n and a. But T_RRLSa tends to reject the correct model more often than in previous tables. T_ARLSa performed quite well, only slightly under-rejecting the correct model. Tables 13 and 14 suggest that T_MLa and T_RLSa tend to be smaller with more continuous indicators, but they are still too far away from the expected ${\chi }_{87}^2$.

Table 13.

Performance of the statistics T_RMLa and T_AMLa with 6 continuous and 9 dichotomized indicators, based on converged replications (df = p_* − q = 87, RN=reject number, RR=reject ratio).

n	Method	TMLa		TRMLa				TAMLa
		Mean	SD	Mean	SD	RN	RR	Mean	SD	RN	RR
100	ML	451.83	148.05	125.85	42.36	164	58.8%	42.90	16.17	110	39.4%
	ML.1	276.10	80.09	123.91	35.33	558	60.7%	45.71	12.77	353	38.4%
	ML.2	163.02	35.34	105.92	22.68	372	37.2%	41.06	8.55	174	17.4%
200	ML	427.83	149.16	120.14	39.62	492	52.0%	54.92	17.81	367	38.8%
	ML.1	221.96	45.83	100.88	20.70	304	30.4%	51.14	10.24	184	18.4%
	ML.2	146.32	26.01	95.20	17.00	196	19.6%	50.61	8.76	94	9.4%
300	ML	372.13	124.47	106.17	34.89	366	36.6%	55.62	18.15	242	24.2%
	ML.1	209.60	41.58	95.60	18.85	199	19.9%	55.31	10.71	121	12.1%
	ML.2	142.08	25.63	92.41	16.67	139	13.9%	55.99	9.83	85	8.5%
400	ML	344.34	75.63	99.14	21.14	257	25.7%	55.98	11.86	170	17.0%
	ML.1	203.74	36.01	93.15	16.48	158	15.8%	57.91	10.06	86	8.6%
	ML.2	139.81	23.09	90.95	15.11	107	10.7%	59.21	9.60	61	6.1%

Table 14.

Performance of the statistics T_RRLSa and T_ARLSa with 6 continuous and 9 dichotomized indicators, based on converged replications (df = p_* − q = 87, RN=reject number, RR=reject ratio).

n	Method	TRLSa		TRRLSa				TARLSa
		Mean	SD	Mean	SD	RN	RR	Mean	SD	RN	RR
100	ML	308.96	86.38	84.39	18.34	31	11.1%	28.25	5.96	7	2.5%
	ML.1	195.18	32.15	87.73	14.43	68	7.4%	32.43	5.48	10	1.1%
	ML.2	137.51	22.78	89.39	14.86	96	9.6%	34.68	5.65	14	1.4%
200	ML	308.33	56.25	86.88	15.26	73	7.7%	39.84	7.45	15	1.6%
	ML.1	194.32	33.32	88.33	15.15	92	9.2%	44.80	7.54	33	3.3%
	ML.2	135.86	22.43	88.40	14.70	85	8.5%	47.00	7.56	25	2.5%
300	ML	308.44	60.13	88.09	16.58	103	10.3%	46.20	8.85	46	4.6%
	ML.1	193.14	34.29	88.11	15.57	86	8.6%	50.98	8.85	40	4.0%
	ML.2	135.47	23.21	88.10	15.10	83	8.3%	53.38	8.89	38	3.8%
400	ML	305.32	54.38	87.95	15.30	87	8.7%	49.68	8.72	37	3.7%
	ML.1	192.26	31.58	87.91	14.49	74	7.4%	54.65	8.85	37	3.7%
	ML.2	135.11	21.58	87.90	14.14	72	7.2%	57.22	8.97	35	3.5%

Table 15 compares SE_F against SE_E for data condition 3, parallel to Tables 5 and 10. Both the averaged SE_E and SE_F become smaller as n increases or a changes from 0 to .2. Formula-based SEs still tend to slightly under-predict empirical SEs. The results in Table 15(b) indicate that SE_F predicts SE_E better when either a or n increases. Again, the averaged difference between SE_F and SE_E under ML.₂ at n = 300 is smaller than those under ML and ML.₁ at n = 400. Comparing the numbers in Table 15 with those in Tables 5 and 10 we found that more continuous indicators not only lead to more efficient parameter estimates but also more accurate prediction of empirical SEs by formula-based SEs. The corresponding SEs for individual parameters are in Tables A21 to A24 on the web, where most individual SE_Es are still slightly under-predicted by the corresponding SE_F s.

In summary, for the three data conditions and four sample sizes, ML.₂ performed better than ML.₁, which was a lot better than ML with respect to convergence rate, convergence speed, bias, efficiency, as well as the accuracy of formula-based SEs.

4. An Empirical Example

The empirical results in the previous section indicate that, with a proper a, ML_a performed much better than ML. This section further illustrates the effect of a on individual parameter estimates and test statistics using a real data example, where ML fails.

Eysenck and Eysenck (1975) developed a Personality Questionnaire. The Chinese version of it was available through Gong (1983). This questionnaire was administered to 117 first year graduate students in a Chinese university. There are four subscales in this questionnaire (Extraversion/Introversion, Neuroticism/Stability, Psychoticism/Socialisation, Lie), and each subscale consists of 20 to 24 items with two categories. We have access to the dichotomized data of the Extraversion/Introversion subscale, which has 21 items. According to the manual of the questionnaire, answers to the 21 items reflect a respondent’s latent trait of Extraversion/Introversion. Thus, we may want to fit the dichotomized data by a one-factor model. The tetrachoric correlation matrix⁴ R was first obtained together with ϒ̂. However, R is not positive definite. Its smallest eigenvalue is −.473. Thus, the ML procedure cannot be used to analyze R.

Table 16(a) contains the parameter estimates and their SEs when modeling R_a = R + aI with a = .5, .6 and .7. To be more informative, estimates of error variances (ψ̂₁₁ to ψ̂_21,21) are also reported. The results imply that both parameter estimates and their SEs change little when a changes from .5 to .7. Table 16(b) contains the statistics T_RMLa, T_AMLa, T_RRLSa and T_ARLSa as well as the associated p-values. The estimated degrees of freedom m̂₂ for the adjusted statistics are also reported. All statistics indicate that the model does not fit the data well, which is common when fitting practical data with a substantive model. The statistics T_RMLa and T_AMLa decrease as a increases, while T_RRLSa and T_ARLSa as well as m̂₂ are barely affected by a. Comparing the statistics implies that statistics derived from T_MLa may not be as reliable as those derived from T_RLSa. The p-values associated with T_RRLSa are smaller than those associated with T_ARLSa, which agrees with the results in the previous section where T_ARLSa tends to slightly under-reject the correct model.

Table 16(a).

Parameter estimates θ̂_a and their standard errors for Example 1.

a	θ̂a			SE
	0.5	0.6	0.7	0.5	0.6	0.7
λ1	0.664	0.663	0.663	0.119	0.119	0.119
λ2	0.741	0.741	0.742	0.069	0.070	0.070
λ3	0.827	0.826	0.826	0.063	0.063	0.064
λ4	0.308	0.310	0.311	0.121	0.121	0.121
λ5	0.711	0.713	0.714	0.079	0.079	0.079
λ6	0.551	0.552	0.554	0.089	0.088	0.088
λ7	−0.653	−0.654	−0.655	0.086	0.085	0.085
λ8	0.694	0.695	0.695	0.072	0.072	0.072
λ9	−0.641	−0.643	−0.644	0.078	0.078	0.078
λ10	0.835	0.837	0.838	0.080	0.080	0.080
λ11	0.549	0.549	0.550	0.098	0.098	0.098
λ12	0.595	0.596	0.597	0.095	0.095	0.094
λ13	−0.658	−0.657	−0.657	0.099	0.099	0.099
λ14	0.810	0.809	0.807	0.063	0.064	0.064
λ15	0.651	0.649	0.647	0.160	0.160	0.160
λ16	0.324	0.325	0.325	0.117	0.117	0.117
λ17	0.444	0.443	0.442	0.116	0.116	0.116
λ18	0.234	0.235	0.237	0.138	0.138	0.138
λ19	0.809	0.808	0.806	0.097	0.097	0.098
λ20	0.327	0.329	0.330	0.124	0.124	0.124
λ21	0.812	0.811	0.810	0.075	0.075	0.075
ψ11	0.559	0.560	0.560
ψ22	0.451	0.451	0.450
ψ33	0.316	0.317	0.318
ψ44	0.905	0.904	0.903
ψ55	0.494	0.492	0.490
ψ66	0.697	0.695	0.694
ψ77	0.574	0.573	0.572
ψ88	0.518	0.518	0.517
ψ99	0.589	0.587	0.585
ψ10,10	0.302	0.300	0.298
ψ11,11	0.699	0.698	0.698
ψ12,12	0.646	0.645	0.644
ψ13,13	0.567	0.568	0.569
ψ14,14	0.343	0.346	0.348
ψ15,15	0.576	0.579	0.581
ψ16,16	0.895	0.895	0.894
ψ17,17	0.803	0.804	0.805
ψ18,18	0.945	0.945	0.944
ψ19,19	0.346	0.348	0.350
ψ20,20	0.893	0.892	0.891
ψ21,21	0.340	0.342	0.343

Table 16(b).

Statistics for overall model evaluation for Example 1 (df = p_* − q = 189).

a	TRMLa	p	TAMLa	p	m̂2	TRRLSa	p	TRLSa	p
.5	480.691	0.000	110.491	0.000	43.443	292.675	0.000	67.274	0.012
.6	381.939	0.000	87.791	0.000	43.443	293.880	0.000	67.550	0.011
.7	350.703	0.000	80.597	0.001	43.435	294.895	0.000	67.771	0.011

5. Conclusion and Discussion

Procedures for SEM with ordinal data have been implemented in major software. However, there exist problems of convergence in parameter estimation and lack of reliable statistics for overall model evaluation, especially when the sample size is small and the observed frequencies are skewed in distribution. In this paper we studied a ridge procedure paired with the ML estimation method. We have shown that parameter estimates are consistent, asymptotically normally distributed and their SEs can be consistently estimated. We also proposed four statistics for overall model evaluation. Empirical results imply that the ridge procedure performs better than ML in convergence rate, convergence speed, accuracy and efficiency of parameter estimates, and accuracy of formula-based SEs. Empirical results also imply that the rescaled statistic T_RRLSa performed best at smaller sample sizes and T_ARLSa also performed well for n = 300 and 400, especially when R contains product-moment correlations.

For SEM with covariance matrices, Yuan and Chan (2008) suggested choosing a = p/n. Because p/n → 0 as n → ∞, the resulting estimator is asymptotically equivalent to the ML estimator. Unlike a covariance matrix that is always nonnegative definite, the polychoric/polyserial/product-moment correlation matrix may have negative eigenvalues that are greater than p/n in absolute value, hence choosing a = p/n may not lead to a positive definite R_a, as is the case with the example in the previous section. In practice, one should choose an a that makes the smallest eigenvalue of R_a greater than 0 for a proper convergence when estimating θ̂_a. Once converged, a greater a makes little difference on parameter estimates and test statistics T_RRLSa and T_ARLSa, as illustrated by the example in the previous section and the Monte Carlo results in section 3. If the estimation cannot converge for an a that makes the smallest eigenvalue of R_a greater than, say, 1.0, then one needs to choose either a different set of starting values or to reformulate the model. A good set of starting values can be obtained from submodels where analytical solutions exist. For example, when z_i, z_j and z_k are unidimensional indicators for a factor ξ, with loading λ_i, λ_j and λ_k, respectively; then ρ_ij = λ_iλ_j and λ_i = (ρ_ijρ_ik/ρ_jk)^1/2. Thus, (r_ijr_ik/r_jk)^1/2 gives a good starting value for λ_i. When all the correlations are positive, we may choose .5 for all the free parameters. Actually, all the starting values of factor loadings for the example in the previous section are set at .5 without any convergence problem with a = .5, .6 and .7 even when three of the 21 estimates are negative. The product-moment correlations of the ordinal and continuous data can be used as the starting values when estimating the polychoric and polyserial correlations.

We have only studied ridge ML in this paper, mainly because ML is the most popular and most widely used procedure in SEM. In addition to ML, the normal-distribution-based NGLS procedure has also been implemented in essentially all SEM software. The ridge procedure developed in section 2 can be easily extended to NGLS. Actually, the asymptotic distribution in (10) also holds for the NGLS estimator after changing Σ (θ̂_a) in the definition of W_a to S_a; the rescaled and adjusted statistics parallel to those in (21) and (22) for the NGLS procedure can be similarly obtained. Further Monte Carlo study on such an extension is valuable.

Another issue with modeling polychoric/polyserial/product-moment correlation matrix is the occurrence of negative estimates of error variances. Such a problem can be caused by model misspecification and/or small sample together with true error variances being small (see e.g, Kano, 1998; van Driel, 1978). Negative estimates of error variances can also occur with the ridge estimate although it is more efficient than the ML estimator. This is because Σ_a(θ) will be also misspecified if Σ (θ) is misspecified, and true error variances corresponding to the estimator in (5) continue to be small when modeling R_a. For correctly specified models, negative estimates of error variances is purely due to sampling error, which should be counted when evaluating empirical efficiency and bias, as is done in this paper.

We have only considered the situation when z ~ N (μ, Σ) and when Σ (θ) is correctly specified. Monte Carlo results in Lee et al. (1995), Flora and Curran (2004), and Maydeu-Olivares (2006) imply that SEM by analyzing the polychoric correlation matrix with ordinal data has certain robust properties when z ~ N (μ, Σ) is violated, which is a direct consequence of the robust properties possessed by R, as reported in Quiroga (1992). These robust properties should equally hold for ridge SEM because θ̂_a is a continuous function of R. When both Σ (θ) is misspecified and z ~ N (μ, Σ) does not hold, the two misspecifications might be confounded. Test procedures for checking z ~ N (μ, Σ) under ordinal data exist (see e.g., Maydeu-Olivares, 2006). Further study is needed for their practical use in SEM with a polychoric/polyserial/product-moment correlation matrix.

As a final note, the developed procedure can be easily implemented in a software that already has the option of modeling polychoric/polyserial/product-moment correlation matrix R by robust ML. With R being replaced by R_a, one only needs to set the diagonal of the fitted model to a + 1 instead of 1.0 in the iteration process. The resulting statistics T_ML, T_RML, T_AML and T_RLS will automatically become T_MLa, T_RMLa, T_AMLa and T_RLSa, respectively. To our knowledge, no software currently generates T_RRLSa and T_ARLSa. However, with T_RLSa, m̂₁ and m̂₂, these two statistics can be easily calculated. Although R_a is literally a covariance matrix, except unstandardized θ̂_a when diag(R_a) = Σ (θ̂_a) happen to hold, treating R_a as a covariance matrix will not generate correct analysis (see e.g., McQuitty, 1997).