Structural and dynamic properties of linker histone H1 binding to DNA

Abstract

Found in all eukaryotic cells, linker histones H1 are known to bind to and rearrange nucleosomal linker DNA. In vitro, the fundamental nature of H1∕DNA interactions has attracted wide interest among research communities—from biologists to physicists. Hence, H1∕DNA binding processes and structural and dynamical information about these self-assemblies are of broad importance. Targeting a quantitative understanding of H1 induced DNA compaction mechanisms, our strategy is based on using small-angle x-ray microdiffraction in combination with microfluidics. The usage of microfluidic hydrodynamic focusing devices facilitates a microscale control of these self-assembly processes, which cannot be achieved using conventional bulk setups. In addition, the method enables time-resolved access to structure formation in situ, in particular, to transient intermediate states. The observed time dependent structure evolution shows that the H1∕DNA interaction can be described as a two-step process: an initial unspecific binding of H1 to DNA is followed by a rearrangement of molecules within the formed assemblies. The second step is most likely induced by interactions between the DNA and the H1’s charged side chains. This leads to an increase in lattice spacing within the DNA∕protein assembly and induces a decrease in the correlation length of the mesophases, probably due to a local bending of the DNA.

INTRODUCTION

The linker histone family is a heterogeneous family of highly tissue-specific, basic proteins, which exhibit significant variations in sequence.^{1, 2} However, most eukaryotic linker histones H1 share a similar, tripartite structure consisting of a globular domain flanked by two lysine-rich tails, a shorter amino-terminal domain (N-tail) and a longer carboxyl-terminal one (C-tail).³ Linker histones H1 are known to attach close to the entry and exit sites of linker DNA on the nucleosome core, bringing together two linker DNA segments.^{4, 5, 6} The globular domain with a diameter of 2.9 nm is the only domain that is folded in solution exhibiting three α-helices.⁷ Its most noticeable structural features are the two DNA binding sites situated on opposite sides of the molecule,⁸ which, with the help of the C-terminal domain, render H1-chromatin binding highly dynamic.⁹

Despite positioning along the nucleosome core particle, it is not the globular domain but rather the highly positively charged C-tail that imparts to linker histones their unique ability to bind to linker DNA through nonspecific electrostatic interactions.^{6, 10, 11}In vivo, the absence of C-tails leads to greatly reduced chromatin binding.¹² Binding of linker histones to the linker DNA facilitates the shift of the chromatin structure toward more condensed, higher order forms.¹³ Although a chromatin fiber lacking linker histones is able to fold to a certain extent,¹⁴ there is abundant evidence that the highly ordered chromatin compaction of the 30 nm fiber is only attained in the presence of linker histones.^{5, 13, 15}In vivo studies on H1 depleted chicken cells have shown an altered chromatin structured as well as chromosomal aberrations and increased DNA damage during replication, suggesting that H1 was involved in transcription regulation.¹⁶ Linker histones help select a specific folding state from among the set of compact states reached in its absence by contributing to the free energy of chromatin folding.¹⁷ This suggests that linker histones are of central importance in genome organization and regulation.

Since the linker histone’s position on the nucleosome is still a matter of debate, understanding more closely its interaction with DNA upon condensing is therefore essential for understanding the role H1 plays in gene regulation and chromatin structure. It has been argued that H1∕DNA assemblies are an excellent model system for studying aspects of the interaction of H1 with chromatin. H1∕DNA interaction in vitro^{10, 18, 19, 20} was reported to be dependent on the ionic strength,^{21, 22, 23, 24} suggesting an interaction governed by electrostatics. At high salt concentrations, the screening of interactions was so significant that assembling was no longer reported,²⁵ denoting a rather weak binding in comparison to protamine-DNA assemblies that can still be formed even at monovalent salt concentrations as high as 1.3M.²⁶ Thus, reinforcing the belief that H1 is a highly mobile chromatin component compared to the germinal chromatin, which is made mechanically stable and transcriptionally inactive by strong protamine binding. In a more general context, the H1∕DNA system can be regarded as a model for nonspecific DNA-protein interactions. Herein, using the innovative junction between x-ray scattering and microfluidics, we probed linker histone∕DNA interaction dynamics and structure formation in real-time. A microfluidic channel with a cross geometry provides means to control mixing of H1 and DNA uncovering a two-step assembly process. The nonspecific binding of linker histones to DNA leads to the formation of primary assemblies with columnar structures governed by electrostatic interactions. As the binding reaction evolves and the concentration of H1 histones increases, the columnar structure rearranges to less organized assemblies with smaller correlation lengths. We attribute the latter observation to an additional bending of DNA molecules induced by the interaction of the linker histones tails with DNA.

EXPERIMENTAL SECTION

Materials

Calf thymus linker histone H1 (isolated lysine-rich fraction²⁷) and lyophilized highly polymerized calf-thymus DNA were purchased from Sigma-Aldrich GmbH, Taufkirchen, Germany. Both components were solubilized in 18.2 MΩ cm water (Millipore GmbH, Schwalbach, Germany) to final concentrations of c_H1=10 mg ml⁻¹ and c_DNA=2.5 mg ml⁻¹, respectively. At physiological pH conditions, H1 possesses a molecular weight of M_w=21.5 kDa and 55 positive charges,²² whereas DNA molecules carry two negative charges per base pair.

Microfluidic devices

X-ray compatible Kapton-Steel-Kapton microfluidic devices have been fabricated as described elsewhere.²⁸ Briefly, the microchannel structure is spark eroded in a thin stainless steel plate, resulting in a microchannel structure, which is open on both sides. The thickness of the plate defines the height of the microchannels. Adhesive Kapton foils coated with a poly(siloxane) layer (thickness of 53 μm, Dr. Müller GmbH, Allingen, Germany) are placed on both sides of the steel plate, such that the foils seal the device and serve as x-ray transparent windows to the microchannel. Four holes are punched into the bottom Kapton foil, fitting the channel ends of the steel plate and serving as inlets of the microfluidic device. Using a thin double sided sticking tape with cavities at the inlet positions and the measuring area, the microfluidic device is mounted on a poly(methylmethacrylate) (PMMA) slab assisting the connection to the fluid pumping system. The center region of the PMMA support is milled out to provide an undisturbed pathway for the x-ray beam. The connection to the pumping system is established by Teflon tubing implemented into male nuts (ProLiquid, Überlingen, Germany) that are screwed in the sockets of the PMMA support. The channels we used had a width of 100–150 μm and a depth ranging from 200 to 300 μm.

Microfocused small-angle x-ray measurements

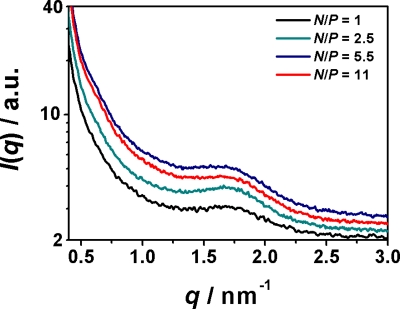
Small-angle x-ray scattering experiments were performed at beamline ID10b at the European Synchrotron Radiation Facility in Grenoble, France. Two-dimensional (2D) scattering patterns were collected using a charge-coupled device (CCD) detector with a fluorescent screen. Beryllium compound refractive lenses focused the x-ray beam of 8 keV (λ=0.155 nm) down to a diameter of 20 μm. The microchannel device was loaded on an x-y stage to probe specific positions using the microfocused x-ray beam. The positional accuracy of absolute coordinates in the microdevice was on the order of the beam size. All CCD images were taken at ambient temperature with exposure times of 30 s∕position and azimuthally averaged to produce one-dimensional intensity profiles I(q). Using a Lorentzian fit, the peak positions and Δq in I(q) are determined. Bulk experiments were performed in quartz capillaries, and a very broad peak has been detected for all measured N∕P ratios (Fig. 1). Local concentrations are translated into assembly compositions given in terms of the relative charge ratio N∕P. N is the total number of positive amine charges of H1 and P is the total number of negatively charged DNA phosphate groups.

Figure 1.

Small angle x-ray scattering profiles of H1/DNA bulk assemblies at different N∕P charge ratios.

Finite element modeling

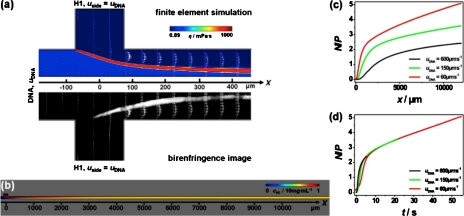
FEMLAB software (Comsol, Inc., Burlington, MA) was used to perform finite element modeling simulations of conditions within the microchannel device. The incompressible Navier–Stokes equation was solved in two dimensions using about 20 000 elements to obtain a solution for the diffusive mixing in the microflow. The velocity fields (and the corresponding strain rates per position) and concentration profiles were subsequently calculated. The viscosity of the formed H1∕DNA assemblies’ η_complex and the diffusion constant D_H1 were used to match the experimentally recorded shape of the hydrodynamically focused DNA stream and of the formed H1∕DNA aggregates. All other parameters, such as channel geometry, flow rates, and the viscosity of the DNA solution, are known. For each flow velocity, two finite element simulations are performed. In order to accurately determine relevant fit parameters, physical conditions in the microchannel device are first simulated with high precision [i.e., high number of finite elements) for a close-up region around the confluence area [x=−200–500 μm, Fig. 3a]. Independent of the flow velocity and throughout all simulations, the viscosity of H1∕DNA aggregates was fitted to η_complex≈3×10³⋅η_water=2.7 Pa s. This result is on the same order of magnitude as the results known from other polymer hydrogels.²⁹ A diffusion constant of D_H1≈2×10⁻¹⁰ m² s⁻¹ was found, which is close to the result one obtained from the Stokes–Einstein relation (r_{globular domain}≈1.5 nm and D_SE≈1.7×10⁻¹⁰ m² s⁻¹) under purely aqueous conditions. To describe physical conditions at positions further down the reaction channel, a second simulation extending over the whole length of the device [x=−200–12 000 μm, Fig. 3b] has been performed using fit parameter values determined in the first set of simulations.

Figure 3.

Real-time monitoring of linker histone H1 induced DNA compaction in a hydrodynamic focusing device. (a) Simulation results (top) and birefringence data (bottom) close to the confluence region are contrasted (u_DNA=600 μm s⁻¹). The product of the assembly reaction appears in the diffusion cone of side and main stream components due to its highly increased viscosity. (b) Simulated H1 concentration profile of the whole device (x=−200–12000 μm). Dependence of the N∕P ratio on the position along x (c) and the time t (d) in the middle of the outlet channel (y=0).

RESULTS AND DISCUSSION

Hydrodynamic focusing device

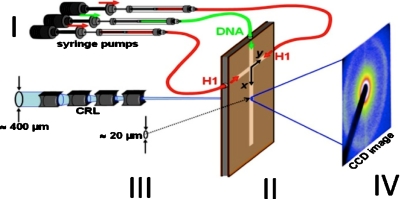
Aside from advantages, such as reduced sample volumes and the possibility of high throughput and parallel operations, microfluidic techniques are particularly useful for the investigation of biomaterials. More importantly, using microfluidics and x rays significantly reduces radiation induced damage of the sample—an important experimental consideration given the damage x rays cause to protein solutions.³⁰ The hydrodynamic focusing device used here consists of two perpendicular microchannels in the form of a cross with three inlets and one outlet. A semidiluted aqueous DNA solution is injected into the reaction channel and hydrodynamically focused by two side streams of aqueous H1 solutions. Figure 2 gives a schematic representation of the experimental setup.

Figure 2.

Schematic representation of the experimental x-ray setup. (I) Syringe pumps with aqueous solutions of DNA and H1. (II) Kapton microfluidic device. (III) Microfocused x-ray beam. (IV) X-ray diffraction pattern.

Laminar flow conditions due to microscale channel dimensions force mixing to occur purely by diffusion. Following the confluence of the microchannels, H1 molecules diffuse into the DNA stream establishing stable concentration gradients. Mixing and concentration distributions in the reaction channel can be adjusted by controlling the main and side channel velocities. Flow velocities are chosen such that concentration gradients of reactants extend along the measurable length of the device. It follows that the composition of the formed assemblies varies at every accessible point along the reaction channel. This allows access to the dynamics of H1∕DNA structure formation in situ, in particular, to transient intermediate states. Thus, it is essential to first quantify concentrations and therefore the composition of the aggregates. This is achieved by a detailed comparison of microscopic images and finite element simulations of flow conditions in the microfluidic device.

Quantifying local conditions in microfluidic devices

Polarized light microscopy has been used widely to study DNA assemblies, which are known to be highly birefringent.^{31, 32} The birefringence signal is increased upon self-assembly of DNA aggregates under conditions of alignment and elongation, which are imposed by using microfluidic devices. Concurrently, combining microfluidics with polarized light microscopy provides a fast and easy access to direct imaging of H1 induced DNA compaction. Data are acquired in the reaction channel (main channel) at three different flow velocities: u_DNA=60, 150, and 600 μm s⁻¹. The flow velocities in the side channels are varied such that a flow velocity ratio u_H1∕u_DNA=1 is maintained.

Finite element simulations of the flow profiles inside the microchannels are performed and compared to experiments in order to elucidate the experimental parameters. In Fig. 3a, simulation data are shown for u_DNA=600 μm s⁻¹ and contrasted to the corresponding experimental results. Owing to the symmetry of the microfluidic device in two dimensions, it is sufficient to simulate half of the device. Following the intersection of the two fluid flows, H1 molecules diffuse into the DNA stream and the H1∕DNA interactions can be observed along the reaction channel. The optically birefringent pattern reflects that DNA chains in the assemblies are orientationally ordered due to the superimposed flow. For direct comparison with the experimental results, the modeled velocity profile white arrows in Fig. 3a in the hydrodynamic focusing device are overlaid to the recorded birefringence image [Fig. 3a (bottom)]. The strong increase in local viscosity connected to the compaction reaction can be exploited to visualize H1∕DNA assemblies in the simulations. Insignificant deviations of simulation results from the experimentally recorded shape are observed in the crossing area, where the center stream is slightly expanding into the side channels. These deviations result from the fact that simulations are performed in two dimensions, whereas the experimental system is affected by additional walls at the top and the bottom of the device. Apart from this detail, experiments and simulations show good agreement. The result of the corresponding simulations over the whole range of the device is given in Fig. 3b.

From simulations, local experimental parameters, such as flow velocities and concentrations, can be obtained at each position. In Fig. 3c, N∕P ratios are plotted for three different flow velocities as a function of the position x along the center of the outlet channel (y=0). Flow velocities result in final charge ratios at the furthest measurable point of the device (x≈12 mm) of N∕P<2.4, 3.3, and 5.1 for u_DNA=60, 150, and 600 μm s⁻¹, respectively. Local flow velocities can be used to translate positional changes along each streamline into corresponding reaction time coordinates t. Figure 3d shows the t dependence of N∕P represented as well for three different flow velocities. For larger t, N∕P ratios unite into a single curve. Deviations at the initial time states reflect differences in the flow velocity depending strain rate, $\dot{\epsilon }=\partial u∕\partial y$.³³ Thus, in Fig. 3d it is clearly emphasized that the composition of the formed assemblies (for three different flow velocities) only depends on the charge ratio N∕P and not on the elapsed time. Once the information concerning the local concentrations and hence assemblies’ compositions is at hand, it is possible to analyze H1∕DNA structure formation in detail.

Small angle x-ray diffraction of H1∕DNA assemblies

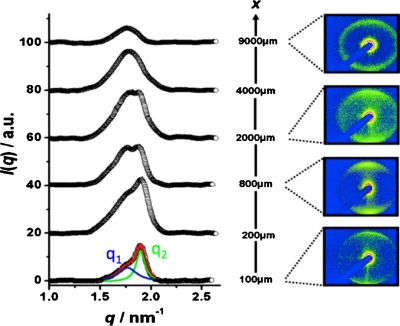
Spatially resolved small-angle x-ray (micro)diffraction is employed as the principle method of analysis to access relevant molecular length scales for the study of biomolecular interactions. Data are obtained at different x-positions along the main channel for all three different flow velocities. In Fig. 4, characteristic 2D diffraction images are shown. The observed alignment is due to the elongational flow at the confluence of the solution streams. Structural information can be obtained by analyzing the radial integrated intensity profiles. The diffraction intensity is plotted as a function of the scattering vector q, which is inversely proportional to the periodic distance between reticular planes d.³⁴ Since DNA has a significantly higher electron density than H1 proteins, the DNA self-assembly promotes or leads to the formation of mesophases that dominate the scattering profile. At positions close to the middle of the cross channels, the diffraction intensity curve is composed of a broad peak with a shoulder in the low q value region. The best decomposition of this broad peak is successfully made by fitting two Lorentzian functions, yielding peak positions q₁ and q₂. In Fig. 4, this is shown for the scattered intensity at x=100 μm.

Figure 4.

Representative 2D x-ray diffraction images (right) obtained at u_DNA=150 μm s⁻¹ in the middle of the outlet channel (y=0) at different positions x and the extracted, radially averaged q-dependence of scattering intensities (left). I(q) plots are offset for clarity.

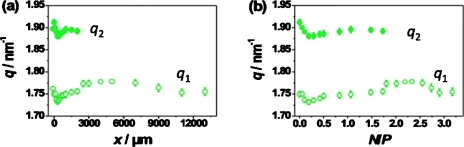
In Fig. 5a, the dependence of the peak positions q₁ and q₂ on the channel position x is given for the data set recorded at u_DNA=150 μm s⁻¹. To elucidate their dependence on assembly composition, it is reasonable to plot quantities of interest versus N∕P obtained from simulations. This is shown for q₁ and q₂ in Fig. 5b.

Figure 5.

Dependence of peak positions q₁ and q₂ on the position x along the outlet channel (a) and on the N∕P ratio (b) shown exemplarily for the data set recorded at a flow velocity of u_DNA=150 μm s⁻¹.

Plotting quantities extracted from x-ray diffraction data obtained at different flow velocities against N∕P allows for the superposition of all data onto a single plot showing their dependence on composition. In Fig. 6a, this is demonstrated for peak positions q₁ (lower curve) and q₂ (upper curve) measured along the streamline at the center of the reaction channel (y=0). The three data sets obtained at u_DNA=60, 150, and 600 μm s⁻¹ show excellent agreement with deviations between different data sets of less than 0.01 nm⁻¹. Local N∕P ratios are highly dependent on the diffusion of H1 molecules. Accordingly, the fact that the data obtained at different flow velocities are in good agreement and collapse onto single curves establishes the validity of the experimental method and the high degree of consistency between experiments and simulations.

Figure 6.

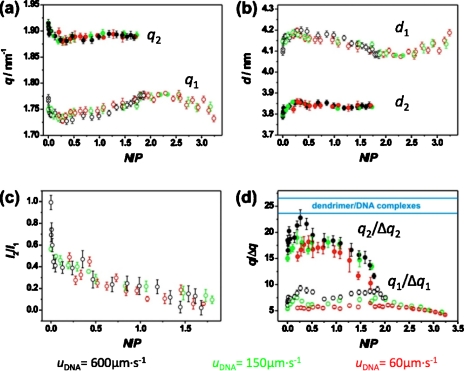
Dependence of the peak position (a), the lattice spacing (b), the intensity ratio of the two peaks (c), and the correlation length given in terms of lattice spacing (for H1 and dendrimers) (d) on the local N∕P ratio.

At low N∕P ratios, peak positions of q₁=1.76 nm⁻¹ and q₂=1.90 nm⁻¹ are observed. With increasing N∕P, q₁ and q₂ are simultaneously shifted toward lower q values with minima at N∕P≈0.2 of q₁=1.73 nm⁻¹ and q₂=1.88 nm⁻¹, respectively. As follows, the peak position q₁ increases monotonically, moving toward higher q values, whereas q₂ levels off at q₂=1.90 nm⁻¹. Eventually, for all the studied velocities, for N∕P>1.8 (corresponding to x>2200 μm) in Fig. 6a, the peak at q₂ disappears, leaving a single peak at q₁. Associated with the disappearance of the peak at q₂, the remaining peak q₁ shows a q_max position at 1.78 nm⁻¹. Increasing H1 concentration even further (i.e., increasing the charge ratio N∕P) results in smaller q values yielding q₁=1.72 nm⁻¹ at the furthermost observable position x=12000 μm along the reaction channel [N∕P≈3.3, Fig. 6a] for a flow velocity of 60 μm s⁻¹.

Structure of H1∕DNA mesophases

Owing to the absence of higher order peaks, the detailed structure of the formed H1∕DNA mesophases cannot be ruled out. This is mainly due to the fact that spatial constrains of the beamline limited the observable q-range to q<2.67 nm⁻¹. Furthermore, correlation lengths of the formed H1∕DNA aggregates are on the order of 10–70 nm (described in Sec. 3E). For systems with such a reduced long-range ordering, scattering peaks of a structure with square symmetry are expected at a position $\left(q_1\cdot \sqrt{2}\approx 2.43{\text{nm}}^{-1}\right)$, which is well situated in the accessible q-range and should be therefore observable. Furthermore, minima of the form factor of the globular domain, which could account for the absence of extra information about a hexagonal or a square phase, are situated at 1.55 and 2.66 nm⁻¹ and are therefore not expected to be of influence. Accordingly, from the absence of peaks at this position, the structure of the mesophase exhibiting the peak at q₁ can be ruled out to be most likely a hexagonal one.^{35, 36} Unfortunately, it is not possible to narrow down the structure of the mesophase exhibiting the peak at q₂. Moreover, it was proven experimentally that the globular domain of H1 (d=2.9 nm) primarily defines distances between neighboring DNA strands;^{37, 38} thus, one can imagine a simplified version of linker histones by approximating them with lower generation dendrimers of similar size and charge (e.g., PAMAM G2). Recently, a systematic structural study has been conducted, which revealed that PAMAM2∕DNA assemble most favorably into hexagonal lattices, their results indicating as well a B conformation maintaining upon interaction.³⁹ Assuming hexagonal ordering, the lattice spacing d can be calculated according to the following relation: $d=4\pi ∕\sqrt{3}q$. In Fig. 6b, lattice spacing’s d₁ and d₂—corresponding to q₁ and q₂—are given and their dependence on H1∕DNA assembly composition is shown in terms of the charge ratio N∕P. The observed lattice spacings are in the range of 3.8–4.2 nm.

The particular three domain structure of the linker histone induces a complex interaction with DNA leading to the formation of unique structures. Although unique, the DNA molecules within these structures are organized in a columnar phase as it was shown in earlier studies using polarizing microscopy for investigating DNA dense phases induced by other polycations.⁴⁰ Previous work using electron microscopy to visualize H1∕DNA complexes on an electron microscopy grid revealed that H1 molecules are sandwiched between two DNA helices forming a tram-track-like pattern⁸ with a diameter of 3.8 nm,²¹ agreeing with interhelical values d₂ plotted in Fig. 6b. However, interhelical distances within complexes formed with poly-L-lysine (PLL) at a N∕P ratio of 1.7 and no added salt were found close to 2.7 nm,³⁴ thus below our experimental values. Although the inner organization of the helices with the linear PLL is hexagonal, the higher lattice values we found are most certainly due to the structured globular domain of the linker histones. In order to enable comparability with results in literature, it is useful to translate N∕P into mass fraction w∕w of H1 to DNA. The x-ray data presented in Fig. 6b exhibit a maximal lattice spacing of both coexisting phases at N∕P≈0.2 (w∕w≈0.2). This is in line with the fact that for linear DNA molecules and low-salt conditions, small amounts of H1, w∕w≈0.15, produce complete incorporation of all DNA molecules into extremely large aggregates.¹⁸

Dynamics of H1∕DNA assembly structure formation

Figure 4 shows the existence of two overlapping diffraction peaks. The evolution of these peaks at different positions along the reaction channel is an evidence of a two-step process. At first, H1 binds electrostatically to DNA and the formed assemblies give rise to the diffraction peak at q₂. A closer study of this diffraction peak reveals columnar packing with DNA helices linked together by H1 molecules. The second step of the process is most probably due to the successive rearrangements of molecules in the formed assemblies, which result in a structure yielding the peak at q₁. Infrared (IR) spectroscopy studies have shown changes in the structure of the C-terminal domain of H1 upon DNA binding.⁴¹ In our experiments, this conformational transition can be monitored in terms of the intensity ratio I₂∕I₁ of the two Bragg reflections [Fig. 6c]. A coexistence regime occurs over a relatively wide range of N∕P ratios and is characterized by an overlapping of the two relatively sharp peaks at q₁ and q₂. With increasing N∕P, I₂∕I₁ is gradually reduced, reaching zero at N∕P≈1.8. This is the assembly composition at which the peak at q₂ is completely lost. The scattering is further characterized by a single peak at q₁ that both shifts to lower q values and broadens in q with a further increase of N∕P.

N∕P≈1.8 corresponds to 15 base pairs (bp) of DNA per H1 molecule. This result is in excellent agreement with sedimentation titration binding data that reported a binding density of one H1 molecule per 10–13 bp (N∕P≈2.5–1.9) (Ref. ⁴²)—a value relatively independent of the salt concentration in the range of c_salt=14–350 mM.^{22, 42} Moreover, our result is also consistent with nuclease digestion studies of chromatin, which have shown that each linker histone protects approximately 10 bp from each end of the chromatosomal DNA.^{15, 23, 43} Furthermore, considering the case of DNA∕PAMAM2 assemblies, each dendrimer has been estimated to cover seven phosphate groups.³⁹

The experimental setup we used did not allow for a complete distinction between reaction time and composition dependent effects. In Fig. 3d, the dependence of N∕P on the reaction time t is given for all three flow velocities. For flow velocities of u=150 and 600 μm s⁻¹, N∕P≈1.8 is reached at t≈2.5 s. For u=60 μm s⁻¹, this assembly composition is only reached at t≈4.1 s. These deviations are due to several factors, such as the complex interaction of the flow fields influenced by the local viscosities and diffusion. However, although the reaction time is almost doubled for u=60 μm s⁻¹, a vanishing of the peak at q₂ is only observed for t≥4.1 s. This indicates that the compaction mechanism of H1 and DNA is rather diffusion limited and conforms to the observations of similar sized dendrimer∕DNA interactions (article in preparation).

Domain size of H1∕DNA assemblies

Based on the combination of microfluidics technology with x-ray microdiffraction, we demonstrate that the interactions of H1 with DNA follow a two-step dynamic process. The efficiency of DNA compaction by H1 is influenced by multiple factors, including flow velocities, diffusion, and viscosity.

In addition to peak positions, average domain sizes of H1∕DNA assemblies can be determined from the full width at half maximum Δq of the reflections at q₁ and q₂. The domain size corresponds to a typical correlation length L_C=2π∕Δq. To ensure comparability, it is useful to analyze q∕Δq, which corresponds to the correlation lengths given in terms of the lattice spacing, q∕Δq=L_C∕d. The N∕P-dependence of q₁∕Δq₁ and q₂∕Δq₂ is shown in Fig. 6d. A clear dependence on the flow velocity of both q₁∕Δq₁ and q₂∕Δq₂ is evident. At low N∕P ratios in the coexistence region, q₂∕Δq₂ is significantly higher than q₁∕Δq₁, exhibiting values of 15–23 (L_C2≈48–73 nm) and 5–9 (L_C1≈19–33 nm), respectively. With increasing N∕P, q₂∕Δq₂ shows a strong decrease starting around the charge neutral point characterized by N∕P=1. For all three flow velocities, maximal values q₁∕Δq₁=6, 7, and 9, respectively, are found at N∕P≈1.8 when the feature at q₂ is disappeared. This finding is consistent with the evolution of the ratio of intensity I₂∕I₁ shown in Fig. 6c. Parallel to the observed shift in peak position q₁ to smaller q values with further increasing H1 concentration, domain sizes decrease to about 4d at the furthest recorded assembly composition (N∕P≈3.3).

The ratio q∕Δq allows for a comparison of H1∕DNA domain sizes to the values obtained in dendrimer∕DNA assemblies. Compared to linker histones, PPI generation 4 and PAMAM generation 3 dendrimers have a similar size and charge. These DNA assemblies have similar lattice spacing (d_PPI4=3.1–3.6 nm, d_PAMAM3=3.8–4.3 nm, and d_H1=3.8–4.2 nm), although the process of structure evolution is not similar (article in preparation). At comparable strain rates$\left({\dot{\epsilon }}_{\text{max}}\approx 1–2{\text{s}}^{-1}\right)$ and charge ratios (N∕P≈1), PPI 4∕DNA and PAMAM 3∕DNA assemblies exhibit domain sizes of approximately 23d and 27d, respectively. The range of these values is added to Fig. 6d (delimited by the blue lines), being comparatively close to those of q₂∕Δq₂ and differing significantly from q₁∕Δq₁.

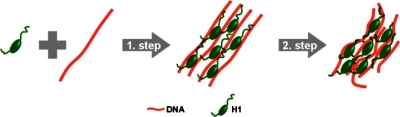
The x-ray diffraction patterns show that at low charge ratios two mesophases coexist within the H1∕DNA assemblies. Since both phases experience identical experimental conditions (N∕P, strain rate, etc.), the differences in correlation lengths of L_C2≈2.5–3⋅L_C1 suggest that the transition from an ordered mesophase (L_C2) corresponding to the columnar organization of helices immediately after binding H1 to a less organized structure (L_C1) is mediated by the rearrangement of the histone tails. For a clearer illustration of the two-step model, we propose a schematic representation that is shown in Fig. 7. As presented in Fig. 6d, the correlation length of domains with extended tails (L_C2) is rapidly reduced after N∕P≈1.1 (28 bp of DNA per each H1 molecule), implying that the tails might distort the order of the columnar phase and bend the DNA. Several studies have previously suggested that chromatosomal linker DNA is bent by the C-terminal domain of H1 forming a stemlike structure.^{44, 45, 46, 47} This structure has also been implicated in the formation of the 30 nm chromatin fiber.⁴⁸ Even though similar condensed DNA structures have been observed with linker histone H1 and polyamines,⁴⁹ the effect on the compaction process seems to be H1 specific since a coexistence of two dense phases is present from the beginning of the diffusive mixing. In order to validate the two-step binding model proposed in this study, future experiments should be performed in physiological conditions using truncated H1 molecules lacking the N and C charged terminal domains. Moreover, assemblies of DNA and H1 have been proven to be more compact at physiological salt (0.2M) rather than at diluted salt (0.05M),⁵⁰ Therefore, we envisage complementary experiments in order to investigate the structure evolution at variable ionic conditions.

Figure 7.

Schematic representation of the H1/DNA interaction mechanism. In a first step, H1 molecules bind unspecifically to DNA with extended tails. In a second step, H1 tails fold upon interaction with DNA, distorting and bending thereby the DNA structure.

CONCLUSIONS

Based on the combination of microfluidics technology with x-ray microdiffraction, we demonstrate that the interactions of H1 with DNA follow a two-step dynamic process. The efficiency of DNA compaction by H1 is influenced by multiple factors, including flow velocities, diffusion, and viscosity. We have seen that by superimposing external strain on biomaterials, it is possible to significantly improve the correlation length of the formed assemblies, underling the advantage of using flow for self-assembling materials compared to the bulk mixing of the components. We show that the first binding step is primarily due to electrostatic interactions between the DNA and the linker histone. Our results suggest that the organization of this phase is columnar hexagonal and is composed of domains with a long correlation length. Furthermore, due to the most certain rearrangement of histone tails within this dense phase, a loss of ordering is observed. Thus, domains with shorter correlation lengths are revealed, which might be attributed to an additional bending of the DNA.

A potential direction for future studies involves monitoring of nucleosome core particle (NCP) arrays∕H1 assembly dynamic formation and structure evolution in microflow. The NCP∕H1 assemblies in microflow may shed light on the 30 nm fibber formation in real-time. Our approach may be generalized and used to access additional relevant biophysical problems of chromatin compaction and decompaction in a single microfluidic experiment.