Accelerating chemical reactions: Exploring reactive free-energy surfaces using accelerated ab initio molecular dynamics

Abstract

A biased potential molecular dynamics simulation approach, accelerated molecular dynamics (AMD), has been implemented in the framework of ab initio molecular dynamics for the study of chemical reactions. Using two examples, the double proton transfer reaction in formic acid dimer and the hypothetical adiabatic ring opening and subsequent rearrangement reactions in methylenecyclopropane, it is demonstrated that ab initio AMD can be readily employed to efficiently explore the reactive potential energy surface, allowing the prediction of chemical reactions and the identification of metastable states. An adaptive variant of the AMD method is developed, which additionally affords an accurate representation of both the free-energy surface and the mechanism associated with the chemical reaction of interest and can also provide an estimate of the reaction rate.

INTRODUCTION

The study of chemical reactions using quantum chemistry calculations is a well established and an active field of research. The general protocol for such studies involves the determination of local energy minima (reactant and product states) and saddle points (transition states) on the potential energy surface (PES). An optimal reaction pathway, the minimum energy path (MEP), connecting the reactant, transition, and product states is then determined along with the associated energy profile.^{1, 2, 3, 4, 5, 6, 7, 8, 9} Despite the fact that these methods are well established, the determination of transition states can be very difficult and computationally expensive. In general, prior knowledge of the PES is required including, at the very least, an accurate representation of the reactant and product states as well as any putative intermediates. Furthermore, these strategies often fail for systems with a large number of degrees of freedom, when entropic effects are important and the free-energy surface needs to be explored. In principle, ab initio molecular dynamics (AIMD) simulations¹⁰ are ideally suited to exploring free-energy surfaces of complex systems, however, the potential of AIMD to study chemical reactions is hindered by the fact that these processes occur on time scales that are significantly longer than those accessible using standard ab initio MD methodologies. Chemical reactions, i.e., the cleavage or formation of one or more covalent bonds, and conformational rearrangements within a molecule occur when a system migrates from one local energy minimum to another. The energy barriers that separate the reactant and product states usually vary from 5 to 20 kcal/mol and therefore chemical reactions occur on time scales ranging from hundreds of nanoseconds to milliseconds. Despite the sustained and rapid increase in the available computational power and the development of efficient simulation algorithms, AIMD simulations of even small isolated molecules are generally limited to time scales of hundreds of picoseconds. In the last two decades, considerable progress has been made in the development of more sophisticated methods to explore both the configurational and reaction space of molecular systems more efficiently,^{11, 12} allowing the study of slow molecular motions and rare events. In general, these methods can be divided into two groups: The first involves the identification of transition pathways between known initial (reactant) and final (product) states or for a known reaction coordinate. Such methods include targeted molecular dynamics^{13, 14} (and constrained dynamics in general,¹⁵) transition path sampling,^{16, 17} and essential molecular dynamics.¹⁸ The second group contains those methods that efficiently explore large areas of the PES without necessarily requiring knowledge of the reaction coordinate and without imposing constraints, allowing for the rapid identification of thermodynamically dominant regions. These methods include replica exchange MD methods,^{19, 20} metadynamics,²¹ hyperdynamics,²² and accelerated molecular dynamics (AMD).²³ The principle behind AMD is to add a continuous, non-negative bias to the actual potential energy surface which raises the low energy regions on the potential energy landscape, decreasing the magnitude of the energy barriers and accelerating the exchange between low energy configurational states, while still maintaining the essential details of the underlying PES. One of the most favorable characteristics of this method is that it yields a canonical average of an observable, so that thermodynamic and other equilibrium properties can be accurately determined.

In the framework of classical molecular dynamics, AMD has already been successfully employed to study the slow time-scale dynamics of polypeptides^{24, 25} and proteins, such as H-Ras,²⁶ ubiquitin,²⁷ and IκBα.²⁸ The enhanced conformational space sampling afforded by AMD in these studies was shown to significantly improve the theoretical prediction of experimental NMR observables, such as residual dipolar couplings,^{27, 28} scalar J-couplings,²⁹ and chemical shifts,³⁰ which are sensitive to dynamic averaging on the micro- to millisecond time scale. As a robust free-energy sampling method, classical AMD has also been successfully combined with molecular modeling approaches to study the conformational behavior of natively unstructured proteins.³¹ AMD used in conjunction with classical MD is however severely limited in its applicability due to the limitations of standard force fields, in particular, their inability to describe chemical reactions.

In this paper, we therefore explore the possibility of using the accelerated molecular dynamics approach in the framework of ab initio molecular dynamics, specifically for the study of chemical reactions. We have employed standard AMD and developed a novel variant of AMD, adaptive AMD (Ad-AMD) in the framework of Car–Parrinello molecular dynamics (CP-MD) to study two chemical reactions: The well-known double proton transfer (DPT) event in formic acid dimer (FAD) and the (hypothetical) adiabatic ring opening and rearrangement reactions of methylenecyclopropane (MCP). The DPT reaction of FAD and the cyclic rearrangement of MCP are depicted diagrammatically in Figs. 1a, 2a, respectively. Using these two test systems, we show that the ab initio AMD approach and its adaptive variant can be used to predict chemical reactions, to obtain accurate free-energy statistics for the chemical reaction of interest, and also to afford a meaningful estimate of the associated reaction rate.

Figure 1.

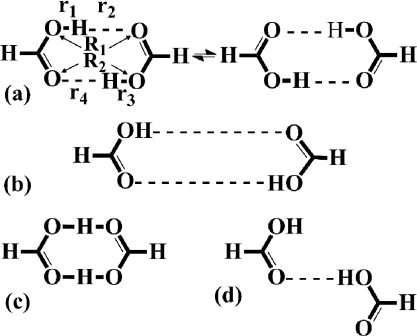
(a) Diagrammatic representation of the DPT reaction in formic acid dimer. The specific interatomic distances required to define the reaction coordinate ρ₁ are labeled (see text for more details). (b) The extended formic acid dimer system. (c) The transition state structure associated with DPT. (d) The twisted formic acid dimer.

Figure 2.

(a) Diagrammatic representation of the ring opening and rearrangement reactions of methylene-cyclopropane. (b) Resonance structures of the biradical TMM intermediate.

METHODS

In the following work, we have employed three ab initio AMD protocols: “Standard ab inito AMD” to explore the reactive PES, “Ad-AMD” to obtain an accurate estimate of the free energy of the chemical reaction, and a specific protocol of Ad-AMD used to obtain a reaction rate constant. These three protocols are discussed in detail below.

Standard Ab Initio AMD

Following the work of Hamelberg et al.,²³ in the standard AMD formalism, a continuous non-negative bias potential, ΔV(r), is defined such that when the true (underlying) potential of the system, V(r), is below a certain, predefined threshold “boost” energy, E_b, the simulation is performed on a modified potential, V*(r) = V(r) + ΔV(r), but when V(r) ≥ E_b, the simulation is performed on the true potential [V*(r) = V(r)]. The modified potential, V*(r), is related to the true potential, V(r), bias potential, ΔV(r), and boost energy, E_b, by²³

$$\begin{array}{c}{V}^{*}\left(r\right)=V\left(r\right),V\left(r\right)\ge E_b,\hfill \\ V^{*}\left(r\right)=V\left(r\right)+\Delta V\left(r\right),V\left(r\right)<E_b,\hfill \end{array}$$ (1)

and the bias potential, ΔV(r), is defined as

$$\Delta V\left(r\right)=\frac{{\left(E_b-V\left(r\right)\right)}^2}{\alpha +E_b-V\left(r\right)}.$$ (2)

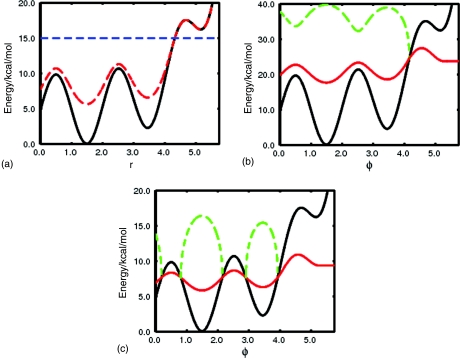
In the framework of CP-MD, the true potential, V(r), is defined as the density functional energy. The application of this bias potential, results in a raising of the potential energy wells and thereby a flattening of the PES, thus enhancing the exchange rate between low energy states. The extent of acceleration (i.e., how aggressively we enhance the configurational space sampling) is determined by the choice of the boost energy, E_b, and the acceleration parameter, α. Configurational space sampling can be enhanced by either increasing the boost energy or decreasing α. A schematic representation of the standard AMD protocol is shown in Fig. 3a. It is important to notice that in the “standard ab initio AMD” protocol, both acceleration parameters, E_b and α, are constants.

Figure 3.

(a) Diagrammatic representation of the “standard AMD” protocol. The true underlying potential is shown in black. Using a fixed boost energy, E_b, at 15.0 kcal/mol (dashed blue line) and an acceleration parameter, α = 25 kcal/mol, the resulting accelerated (modified) potential is shown in red. Both acceleration parameters are kept fixed across the entire configurational space. (b) The adaptive AMD protocol: The modified potential (red line) is defined as a function of a specific reaction coordinate (ϕ) and positioned above the true underlying potential energy surface (black line) across the entire reaction space of interest {0 < ϕ < 4.1}. Keeping the α parameter fixed at 25-kcal/mol, the boost energy (dashed green line) is adapted in a history-dependent fashion to achieve the desired acceleration potential across the reaction coordinate. When ϕ > 4.1, the acceleration is switched off and the system evolves on the true underlying potential. (c) Diagrammatic representation of the adaptive AMD protocol used to estimate reaction rates. The true underlying potential and the desired modified potential are shown in black and red, respectively. In direct comparison to Fig. 3(b), the desired modified potential has been shifted such that it lies below the true underlying potential across the entire transition state region. The adaptive boost energy (dashed green line is only applied to the system when the defined modified potential lies above the true potential. In this way, the acceleration is switched off whenever the system approaches the transition state region and an accurate estimate of the reaction rate can be obtained.

The AMD method also yields correct canonical averages of an observable so that thermodynamic and other equilibrium properties of the system can be accurately determined. The corrected canonical ensemble average of the system is obtained by simply reweighting each point in the configuration space on the modified potential by the strength of the Boltzmann factor of the bias potential, exp(βΔV[r(t_i)]), at that particular point. When the system is on the normal potential, the bias is zero. The reader is referred to Ref. 23 for more details.

Ad-AMD

In the standard AMD methodology, the system evolves on a modified PES which, due to the application of the bias potential, allows for the enhanced configurational space sampling. The standard AMD protocol provides an approximate, albeit somewhat crude representation of the true underlying PES. However, as is demonstrated in the Results section, this protocol does not allow one to specifically focus on a particular rare event or a chemical reaction of importance. Indeed, in most cases, the system samples a large amount of high energy configurational space, much of which is of no particular interest. In order to obtain accurate free-energy statistics for a particular reaction, it is necessary to observe this specific process multiple times over. One means of selectively accelerating a particular event is Ad-AMD. In the Ad-AMD protocol, one defines a specific reaction coordinate, ϕ, that accurately describes the particular reaction of interest, and accelerates the system along the predefined reaction coordinate. Using the approximate representation of the true PES, V(ϕ), obtained from the standard AMD simulation, a specific desired modified potential, V*(ϕ), is defined. Ideally the modified potential reflects all the characteristics of the underlying true PES, however, an exact reproduction of all the characteristics is not necessary to obtain accurate free-energy statistics (as demonstrated below in the case of MCP). In the Ad-AMD protocol, one of the acceleration parameters, α, is held fixed and the other, E_b, is adapted as a function of the reaction coordinate using the approximate representation of the true potential energy, V(ϕ), to obtain the desired, predefined modified potential, V*(ϕ). The functional form for E_b(ϕ) is obtained by simply rearranging Eq. 2 as

$$E_b\left(\phi \right)=\frac{(V^{*}\left(\phi \right)-V\left(\phi \right)\pm \sqrt{{\left(V^{*}\left(\phi \right)-V\left(\phi \right)\right)}^2+4\alpha \left(V^{*}\left(\phi \right)-V\left(\phi \right)\right)}}{2}+V\left(\phi \right).$$ (3)

As can be seen, there are two solutions for E_b(ϕ). In the present work, we always use the solution associated with the positive.

In the Ad-AMD simulation, when the predefined modified potential, V*(ϕ), lies above the true underlying potential, V(ϕ), the system evolves on the modified potential energy surface, V*(ϕ), and the associated adaptive bias potential is given as

$$\Delta V\left(\phi \right)=\frac{{\left(E_b\left(\phi \right)-V\left(\phi \right)\right)}^2}{\alpha +E_b\left(\phi \right)-V\left(\phi \right)}.$$ (4)

However, when the predefined modified potential lies below the true underlying potential, the acceleration is switched off and the system evolves on the true PES, V(ϕ). In this way, during the Ad-AMD simulation, the system is only accelerated across a certain region of the reaction coordinate which defines the reaction subspace of interest. The desired modified potential, V*(ϕ), can be defined and positioned relative to the true potential, V(ϕ), at will in a physically meaningful fashion. In the present examples (FAD and MCP), a simple polynomial function was used to describe the modified potential and an initial estimate of E_b(ϕ) was generated using the results of the standard AMD trajectories. Due to thermal fluctuations and local molecular distortions induced by the application of the bias potential, the initial representation of the true underlying potential across the reaction coordinate, V(ϕ), obtained from the standard AMD simulation is not particularly accurate. As a result of this, the initial estimate of the adaptive boost potential, E_b(ϕ), which is calculated using Eq. 3 does not immediately have the desired effect of the fixed predefined modified potential, V*(ϕ). In order to overcome this problem, both the underlying potential, V(ϕ), and the adaptive boost potential, E_b(ϕ), are updated in a history-dependent fashion during the Ad-AMD simulation: The reaction coordinate, ϕ, is divided into bins, and during the Ad-AMD simulation, the true potential energy, V(ϕ), in each bin is averaged. The enhanced sampling of the reaction space provides an increasingly accurate representation of the true underlying potential, V(ϕ). In the present case, E_b(ϕ) is updated every 500 MD steps using the improved potential energy statistics for V(ϕ), however, the updating frequency is an adjustable parameter. The adaptive AMD approach can be regarded as a generalized extension of the local boost method developed by Wang et. al.³² For the sake of consistency, we have chosen to use the same functional form of the bias potential in both standard and adaptive AMD protocols. However, it should be recognized that having explicitly defined the desired modified potential, any functional form of the bias potential could be implemented. A diagrammatic representation of adaptive AMD is shown in Fig. 3b. Specific details of the modified potential employed for the FAD and MCP systems are described in the Results section.

A free-energy profile for the chemical reaction can be readily calculated from the Ad-AMD trajectory using the canonical ensemble free-energy reweighting protocol: The reaction coordinate that describes the chemical reaction of interest is divided into bins and the structures collected across the Ad-AMD trajectory are allocated to their respective bin, ϕ_j. The effective population statistic for each structure, i, is given by exp(βΔV[ϕ(t_i)]). For each bin, the population statistics are summed across the entire Ad-AMD trajectory to give an effective total population in that bin, pop(ϕ_j). The free-energy profile, ΔG(ϕ_j), is then given as

$$\Delta G\left({\phi }_j\right)=-RT\ln \left[\frac{\mathrm{pop}\left({\phi }_j\right)}{\mathrm{pop}\left({\phi }_{\max }\right)}\right],$$ (5)

where pop(ϕ_max) is the effective total population of the most populated bin.

Using adaptive AMD to estimate reaction rates

In both standard and adaptive AMD the system evolves on a modified potential at an accelerated rate with a nonlinear time scale of Δt^*, given as²³

$$\Delta t_i^{*}=\Delta t\exp \left(\beta \Delta V\left[r\left(t_i\right)\right]\right),$$ (6)

where Δt is the actual time step of the simulation on the modified potential. In principle therefore, it is possible to estimate the time scale of events observed during the AMD simulations as

$$\begin{array}{c}{\displaystyle t^{*}=\sum _i^N\Delta t_i^{*}=\Delta t\sum _i^N\exp \left(\beta \Delta V\left[r\left(t_i\right)\right]\right),}\\ t^{*}=t〈\exp \left(\beta \Delta V\left[r\left(t_i\right)\right]\right)〉,\end{array}$$ (7)

where N is the total number of molecular dynamics steps performed during the whole simulation and 〈exp(βΔV[r(t_i)])〉 is the boost factor.

However, according to the transition state theory (TST),^{33, 34} the above equation is only correct if the boost energy, E_b, lies below the entire transition state region. In the standard AMD protocol, it is rarely possible to achieve a sufficient level of acceleration to observe the desired transition while fulfilling this criterion. However, the same is not true for adaptive AMD. Once the free-energy profile as a function of the chosen reaction coordinate is accurately determined, the adaptive boost energy and acceleration parameter, α, can be readily adjusted, to generate a modified potential with a sufficiently small energy barrier to observe the reaction of interest, while ensuring that the boost energy lies below the entire transition state region. This adaptive AMD protocol is shown schematically in Fig. 3c. Under these conditions, Eq. 7 fulfills the TST criteria and a meaningful estimate of the reaction rate can be obtained.

Computational details

All molecular dynamics simulations were carried out at T = 300 K using an in-house modified version of the CPMD 3.12 package.³⁵ In the case of FAD, the system was placed in the center of a periodically repeating cubic box of side length L = 25 a.u. and the Becke (B) exchange³⁶ and Lee, Yang, Parr correlation³⁷ functional was employed. For MCP, the system was placed in a periodically repeating cubic box of side length L = 20 a.u. and the gradient corrected Perdew-Burke-Ernzerhof (PBE) density functional³⁸ was employed. For both systems, a fictitious electron mass of 400 a.u. was ascribed to the electronic degrees of freedom and the coupled equations of motion were solved using the velocity Verlet algorithm with a time step of 4 a.u. For FAD, core electrons were treated using the norm-conserving pseudopotentials of Troullier and Martins³⁹ and the valence orbitals were expanded in a plane-wave basis up to an energy cut-off of 70 Ry. For MCP, ultrasoft pseudopotentials⁴⁰ were employed and the valence orbitals were expanded in a plane-wave basis set up to an energy cut-off of 25 Ry. Standard CP-MD simulations were performed using a Nosé–Hoover thermostat⁴¹ on the ions. In the case of the ab initio AMD and adaptive AMD simulations, a Nosé–Hoover thermostat was applied to both the electronic and nuclear degrees of freedom. All ab initio AMD and adaptive AMD simulations presented in this work were performed within the framework of CP-MD, however, we would like to point out that the biased potential simulation methods described here could equally well be implemented in the framework of Born–Oppenheimer MD.

The general protocol followed in this work starts with a standard CP-MD simulation. This simulation provides an estimate for the true underlying density functional energy of the system in the thermodynamically stable state at 300 K, V₀, and provides the initial coordinates for the biased potential simulations. Standard AMD simulations are then performed at increasing levels of acceleration in order to explore the configurational space of the system, to identify potential chemical reactions and metastable states, and to acquire an approximate, albeit rather crude representation of the underlying PES. Using this information, a suitable reaction coordinate is defined and an adaptive AMD simulation is performed providing an accurate representation of the free-energy surface for the reaction. Once an accurate description of the free-energy surface is available, the adaptive AMD parameters can be selected in order to obtain an estimate of the reaction rate.

RESULTS

Double proton transfer in formic acid dimer

Exploring the configurational space of FAD using ab initio AMD

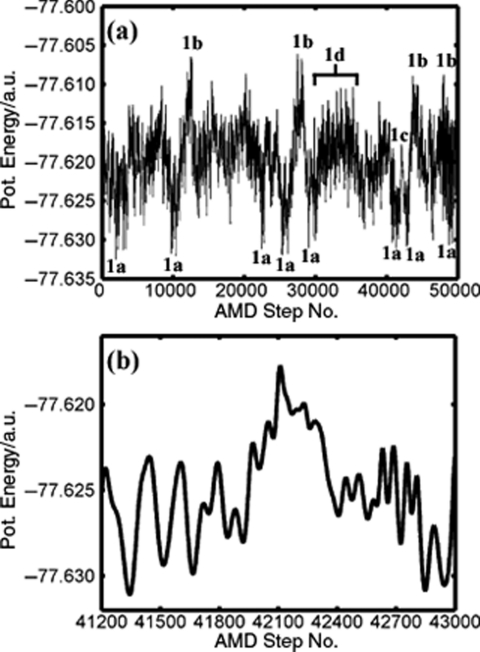
In order to explore the configurational space of FAD, a series of ab initio AMD simulations across a variety of acceleration levels were performed. In all simulations, the acceleration parameter, α, was fixed at 0.016 a.u (10.04 kcal/mol) and the level of acceleration was controlled by varying the boost energy, E_b. The optimal acceleration level for the enhanced configurational space sampling was observed when (E_b – V₀) was set between 0.018 a.u. (11.3 kcal/mol) and 0.024 a.u. (15.1 kcal/mol). Within this acceleration regime, FAD rapidly exchanges between numerous “states” which are depicted in Fig. 1. The variation in the true, underlying potential energy obtained over a 50 000 step segment from a representative AMD trajectory is depicted in Fig. 4a and the different states that are visited are indicated. The system clearly spends a large amount of time exploring high energy regions of configurational space compared to the two thermodynamically stable dimer states [shown in Fig. 1a]. These high energy states include an extended dimer configuration [Fig. 1b], where both hydrogen bonds are longer than 2.5 Å and the system comes close to complete dissociation and a twisted configuration [Fig. 1d], in which one hydrogen bond is maintained and the angle subtended between the two monomer planes increases by more than 90°. Indeed, in one AMD simulation, a complete 360° rotation of one of the monomeric units was observed. In addition to these motions, we also observe the anticorrelated rotation of the two monomeric units in the dimer plane and a “wagging” motion (tilting of the monomers out of the plane of the dimer). All these motions can clearly be identified as extended collective intermonomer vibrational modes that are readily observed in standard CP-MD simulations of FAD. Around step No. 42200 [Fig. 4b], we observe a DPT event.

Figure 4.

(a) Variation of the underlying potential energy of FAD during the standard AMD simulation. The labels across the trajectory refer to the different states and motions depicted in Fig. 1. (b) Variation of the potential energy of FAD across the binary proton transfer event. The estimated energy barrier to DPT is ∼0.009–0.012 a.u. (5.7–7.5 kcal/mol).

Thermal fluctuations combined with the presence of some structural distortions due to the application of the bias potential result in a rather noisy and somewhat crude representation of the underlying PES shown in Fig. 4a. Nevertheless, particularly when averaging the potential energy statistics across the AMD trajectory, it is possible to obtain an approximate, albeit rather crude estimate of the variations in the potential energy of the system as it evolves from one configurational state to another. For example, the thermodynamically stable dimer state at 300 K [Fig. 1a] has an approximate potential energy of –77.629 a.u. (+/– 0.04 a.u.), which is very similar to the average potential energy obtained from the standard CP-MD simulations (–77.630 a.u.) and is referred to from here on as V₀. The potential energy for an extended dimer conformation, as the system approaches dissociation, is seen to lie on average, ∼0.015–0.020 a.u. (9.5–12.5 kcal/mol) above V₀ and the associated potential energy barrier for DPT is ∼0.009–0.012 a.u. (5.7–7.5 kcal/mol). These values obviously only provide an approximate representation of the true underlying PES. For the sake of comparison, the true potential energy barrier to DPT on the minimum energy path is 5.4 kcal/mol. We would like to point out that the aim of the standard AMD simulations is not to obtain accurate energetic statistics, but rather to enhance the configurational space sampling and to identify local energy minima and transition states on the PES.

Despite the relatively low potential energy barrier, the frequency of DPT events in standard AMD simulations is rather low. On average, we observed one DPT event every 250 000 steps. The bias potential obviously has a much stronger effect on the flexible H-bonds, and hence the intermonomer collective vibrational degrees of freedom. Increasing the boost energy to larger values does not afford an increase in the frequency of observed DPT events, but generally results in even larger amplitude fluctuations of the two monomeric units, eventually resulting in dissociation of the dimer. Interestingly, we never observe the formation of a zwitterionic state.

Obtaining an accurate free-energy profile for DPT using Ad-AMD

The standard AMD simulations described above identified the existence of DPT events on slow time scales and also provided an approximate estimate for the associated potential energy barrier for this reaction. In order to obtain an accurate estimate of the free-energy barrier for this process, it is necessary to define a suitable reaction coordinate for the DPT event and perform adaptive AMD. Miura et al. have previously described two reaction coordinates to accurately describe the symmetrized hydrogenic movement (ρ₁) and intermonomer vibrations (ρ₂) in FAD:⁴²

$${\rho }_1=r_1-r_2+r_3-r_4,$$ (8)

$${\rho }_2=R_1+R_2,$$ (9)

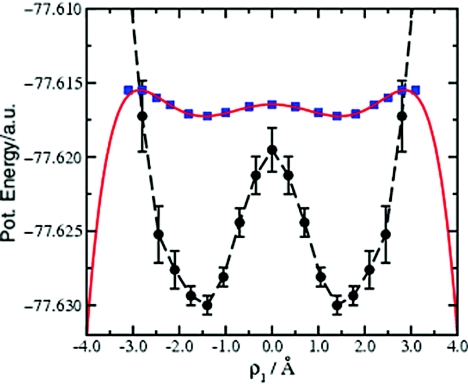
where the relevant interatomic distances, r₁, r₂, r₃, r₄, R₁, and R₂ are defined in Fig. 1a. The single reaction coordinate, ρ₁, is sufficient to describe the DPT event in this system. Using this reaction coordinate and the approximate representation of the underlying PES obtained from the standard AMD trajectory with respect to ρ₁, a desired modified potential was constructed. Ideally, the desired modified potential, V*(ρ₁), should fulfill certain criteria: First, V*(ρ₁) must lie above V(ρ₁) across the entire reaction space of interest. Second, the functional form of V*(ρ₁) should approximately mimic the true underlying PES, at least in terms of the approximate positions of the local energy minima and maxima with respect to the reaction coordinate. In order to achieve efficient configurational space sampling, the activation energy barriers on the modified potential should be ∼0.5 kcal/mol. In a series of initial test Ad-AMD simulations, we found that if the activation energy barrier is defined to be much larger than this value, the frequency of observed reaction events decreases substantially. Alternatively, if the activation energy barrier is set to much smaller values, the modified potential becomes too flat, resulting in the observation of random motion and the system spends a large amount of time exploring high energy, unrealistic regions of the configurational space during the Ad-AMD simulation. Finally, the modified potential should lie below the true potential outside the reaction space of interest. In Fig. 5, we show how the modified potential, V*(ρ₁), was constructed for FAD. The approximate PES obtained from the standard AMD simulation is represented by the dashed black line. The PES is clearly symmetric about ρ₁ = 0 Å, with an energy minima at ρ₁ = +/– 1.4 Å. The upper estimate of the activation energy barrier (located at ρ₁ = 0 Å) lies 7.5 kcal/mol above the thermodynamically stable state (ρ₁ = +/– 1.4 Å) and the reaction space of interest lies in the region {–2.8 Å < ρ₁ < +2.8 Å}. Following the criteria defined above, a series of points describing the desired modified potential were defined manually (Fig. 5, blue squares): At ρ₁ = 0 Å, the modified PES was fixed 8.5 kcal/mol above the true potential energy of the thermodynamically stable state, V₀, and therefore, at least 1 kcal/mol above the estimated true PES at the transition state. The modified potential energy minima were placed at ρ₁ = +/– 1.4 Å, which coincides exactly with the minima on the true underlying PES and were fixed at a value such that the activation energy barrier on the modified potential was 0.5 kcal/mol. Two further points were defined at ρ₁ = +/– 2.8 Å that intercept the underlying PES. A few interstitial points were then manually added, maintaining the symmetric properties of the modified PES and these points were fitted to a simple polynomial function. The resulting desired modified potential (shown in red in Fig. 5) is given by

$$\begin{array}{c}\hfill V^{*}\left({\rho }_1\right)=\left(8.5-V_0\right)-0.517{\left({\rho }_1\right)}^2+0.154{\left({\rho }_1\right)}^4-0.01{\left({\rho }_1\right)}^6,\end{array}$$ (10)

where ρ₁ is in units of angstroms and the polynomial coefficients are in units of kcal/mol.

Figure 5.

Construction of the desired modified potential: The estimated variation of the potential energy of FAD as a function of the reaction coordinate ρ₁ obtained from the standard AMD (cf. Fig. 4) is shown by the dashed black line. A series of points (blue squares) describing the desired modified potential were defined manually and fit to a simple polynomial function [red line, Eq. 10]. The desired modified potential lies above the true potential across the entire reaction space of interest, –2.8 Å < ρ₁ < 2.8 Å.

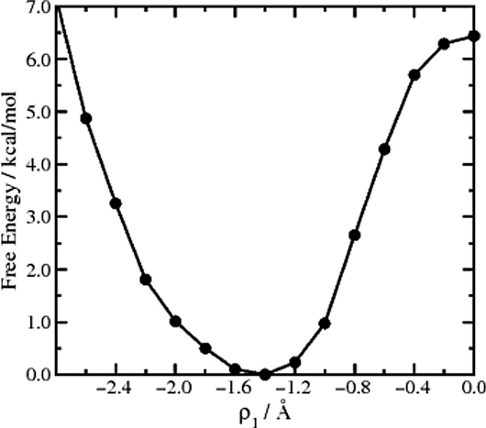
The adaptive boost potential, E_b(ρ₁), necessary to produce the desired modified potential was found to converge exceedingly quickly (within 50 000 steps). Figure 6 depicts the enhanced configurational space sampling obtained from a 250 000-step (unweighted) adaptive AMD simulation of FAD projected onto the two reaction coordinates, ρ₁ and ρ₂, compared to a 250 000-step (∼25 ps) standard CP-MD simulation. Using the adaptive AMD protocol, a DPT event is observed once every 10 000 steps on average. This represents a 25-fold increase in the frequency of observed DPT events compared to the standard AMD simulations discussed above. After performing the free-energy reweighting protocol to obtain the correct Boltzmann canonical ensemble distribution, the resulting free-energy profile as a function of ρ₁ is shown in Fig. 7. The free-energy barrier for DPT is 6.5 kcal/mol, which is in excellent agreement with the value of 6.4 kcal/mol found in a previous study on FAD using the dynamic distance constraint method with the same density functional.⁴³ The structural dynamic changes of the system across the reaction coordinate are also in very good agreement with previous observations.^{14, 43} For example, even before performing the free-energy weighting protocol [Eq. 6], it is clearly apparent that DPT only occurs when the two monomeric units are contracted (giving a low ρ₂ value of 4.8 Å) and that the system becomes considerably more planar on approaching the transition state. The transition state itself is well defined at {ρ₁,ρ₂} = {0.0,4.8} Å and has a very similar structure to the transition state obtained from the MEP.

Figure 6.

Comparison of the conformational space sampling observed for formic acid dimer by standard CP-MD (orange) and adaptive AMD (black). In the (unweighted) adaptive AMD trajectory, the system exhibits multiple DPT events across the transition state located at {ρ₁, ρ₂} = {0.0, 4.8}.

Figure 7.

The free energy of formic acid dimer as a function of the reaction coordinate ρ₁ obtained from the adaptive AMD simulation.

The adaptive AMD simulations discussed above provide a very accurate representation of both the enthalpy and free-energy statistics associated with the DPT reaction. Using this information, a second adaptive AMD simulation of FAD was performed in order to obtain an estimate for the associated DPT reaction rate, as described in the Methods section. The desired modified PES was lowered such that it intersected the true underlying potential at ρ₁ = +/– 0.2 Å and a second set of adaptive AMD simulations were performed. In comparison to the previous AMD simulations, the DPT event in this adaptive AMD protocol was observed considerably less frequently as the system is not being accelerated over the transition state region. The estimated rate constant for DPT was found to be ∼0.077 ns⁻¹ which is slightly slower than the TST predicted rate constant (k_BT/h*exp[βΔG/RT] = 0.108 ns⁻¹, using the value for ΔG determined in the previous Ad-AMD simulation with V* above the true barrier, and assuming a transmission coefficient, κ = 1). This suggests that the transmission coefficient (which is notoriously difficult to calculate) for the DPT reaction is 0.7. We would like to stress that the accuracy of the free-energy barrier and the associated rate constant is, of course, also dependent on the accuracy of the polyelectronic wave-function, i.e., on the quantum chemical electronic structure method employed. The biased potential methods employed in this study do not improve or correct for any inherent errors in the energy function described by the specific density functional.

Cyclic rearrangement of MCP

Before presenting the results for MCP, we would like to point out that this system was chosen as a purely hypothetical study in order to show that the AMD and adaptive AMD approaches can be successfully applied to study transitions across extremely large energy barriers. To the best knowledge of the authors, the ring opening and subsequent rearrangement reactions of MCP, similar to many other cyclic organic systems, proceed via a nonadiabatic mechanism which involves transitions between the ground state and both a singlet excited state and a triplet trimethyl-methane (TMM) biradical state.⁴⁴ The simulations presented in this work have been performed under strict adiabatic (ground electronic state) conditions.

Analogous to the study of FAD described previously, the first step in the investigation into the ring opening and subsequent rearrangement reactions of MCP was to perform a standard CP-MD simulation of the system in the gas phase at 300 K, which afforded an estimate of the average density functional energy of MCP in the stable thermodynamic state. A series of standard AMD simulations were then performed in which the boost energy, E_b, was fixed 60 kcal/mol above this potential energy minimum and the acceleration parameter, α, was systematically decreased in steps of 10 kcal/mol from 60 to 10 kcal/mol. This approach is slightly different to that performed in the case of FAD, where α was held fixed and the level of acceleration was defined by increasing the boost energy. As discussed in the Methods section, the level of acceleration is controlled by both the boost energy, E_b, and α. In the case of MCP, it is clear that the ring-opening mechanism involves a transition over an exceedingly large energy barrier. In such a scenario, it was found that the configurational space sampling could best be controlled by fixing (E_b − V₀) at a large value and using the parameter α to control the level of acceleration. Even at a moderate acceleration level {(E_b − V₀), α} = {60.0, 60.0 kcal/mol}, we observed cleavage of the C3–C4 bond [see Fig. 2a: MCP STATE A] resulting in a partial opening of the cyclopropane ring. The C3–C2–C4 angle, θ, was seen to increase from 66° (equivalent to the thermodynamically stable geometry) to as much as 90° and the underlying (true) potential energy of the system increased by up to 20 kcal/mol. Under more aggressive acceleration conditions (lower values of α), the ring-opening mechanism was even more pronounced, however, at such aggressive acceleration levels, we also observed some intramolecular distortions, particularly involving C–H bond cleavage events. In order to overcome this problem, a second set of standard AMD simulations were performed where the acceleration (and associated force modification) was only applied to the heavy C-atom frame of the molecule. The (partial) standard AMD simulations identified two chemical reactions: The first involved the ring opening and subsequent ring closure via a trigonal-planar TMM biradical intermediate and the underlying potential energy barrier for this chemical reaction was found to be ∼40 kcal/mol. The second chemical reaction involved cleavage of the C2–C3 bond, leading to the formation of an exceedingly high energy vinyl-radical system.

In order to study the lower energy chemical reaction, the ring opening and subsequent rearrangement of the MCP system via the biradical TMM intermediate in more detail, a series of adaptive AMD simulations were performed. Making use of the observed planar symmetry of the C-atom frame in the standard AMD simulations, the reaction coordinate for the adaptive AMD simulations was defined as the smallest angle, θ, subtended between two peripheral atoms over the central C-atom (C2) forming the heavy atom frame: In this way, acceleration was constantly applied to the system as it evolved between the different isomeric states, each of which, while being chemically identical, differs in respect to the specific C-atoms that form the cyclopropane ring. The desired modified potential as a function of θ, was therefore defined within the boundary conditions (0°< θ < 120°). Similar to the case of FAD, an approximate representation of the underlying PES, V(θ), was obtained by averaging the potential energy statistics from the standard AMD trajectory with respect to θ. The modified potential, V*(θ), was then constructed by manually defining an initial set of points. The underlying PES obtained from the standard CP-MD and AMD simulations had a single energy minimum at θ = 66°. The upper estimate of the activation energy barrier for ring opening and subsequent ring closure, located broadly at θ = 120°, was found to be ∼40 kcal/mol above the thermodynamically stable state. For small values of θ, particularly, θ < 40°, the system was energetically highly unstable. Based on this potential energy function, the transition state for the modified potential was positioned at θ = 120° and was fixed 41 kcal/mol above the true potential energy of the thermodynamically stable state, V₀ (located at θ = 66°), more than 1 kcal/mol above the true PES at the assumed transition state (θ = 120°). The modified potential energy minimum was placed at θ = 66°, which coincides with the minimum on the true underlying PES and was fixed at a value such that the activation energy barrier on the modified potential was 0.5 kcal/mol. A third point for the modified potential was defined at θ = 40°, which intercepted the true underlying PES. Similar to the case of FAD, a few interstitial points were manually added and these points were fitted to a simple polynomial function. The resulting predefined fixed modified potential is given by

$$\begin{array}{ccc}\hfill V^{*}\left(\theta \right)& =& \left(41.522-V_0\right)+1.21\theta -4.27{\theta }^2\hfill \\ & & +3.30{\theta }^3-0.7352{\theta }^4,\hfill \end{array}$$ (11)

where the angle θ is in radians and the polynomial coefficients are given in kcal/mol.

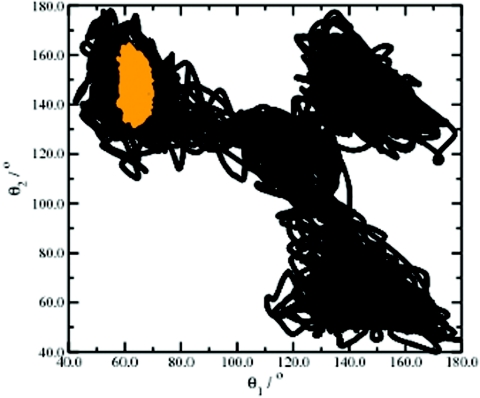
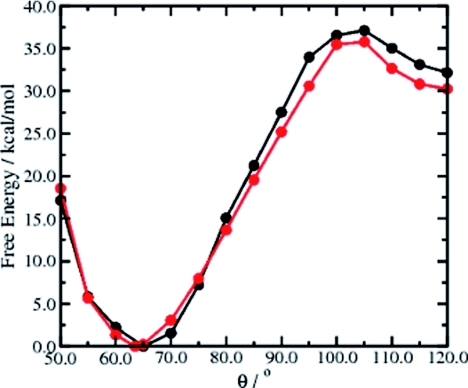
Two C–C–C angles {θ₁, θ₂} are sufficient to accurately describe the configurational space of the MCP system. Figure 8 depicts the enhanced configurational space sampling obtained from a 500 000-step (unweighted) adaptive AMD simulation of MCP projected onto the two internal degrees of freedom, {θ₁, θ₂}, compared to a 500 000-step (∼50 ps) standard CP-MD simulation. While the standard CP-MD simulation samples a very limited region of the configurational space centered approximately around {θ₁, θ₂} = {65°, 150°}, the adaptive AMD trajectory readily samples all three isomeric states of MCP and the interconversion between these states proceeds via a metastable trigonal planar biradical TMM state located at {θ₁, θ₂} = {120°, 120°}. The associated free-energy profile for ring opening as a function of θ is depicted in Fig. 9 and shows a transition state located at θ = 105°. The free energy for ring opening is found to be ∼36 kcal/mol and the metastable TMM intermediate state lies ∼32.5 kcal/mol above the thermodynamically stable energy minimum located at {θ = 66°}. In order to assess the accuracy of this result, we calculated the free-energy profile for the ring opening of MCP using an established method:^{15, 45, 46} A series of CP-MD simulations were performed in which the C3–C2–C4 angle that defines the propane ring was constrained and the associated free-energy profile was obtained by thermodynamic integration of the average constraint force over this reaction coordinate, (θ), including a correction for the metric effects on the associated Lagrangian. The free-energy profile obtained from this constrained CP-MD approach is shown with the present adaptive AMD result in Fig. 9. A remarkable agreement between the two different free-energy methods is observed, confirming the fact that ab initio adaptive AMD is a robust protocol for determining accurate free-energy statistics, even in the case when the associated free-energy barriers are extremely large. Under the strict constraints of this (hypothetical) adiabatic study, the associated reaction path for ring opening and subsequent ring closure of MCP possesses two transition states. This free-energy profile can be well understood when one considers that as the system approaches trigonal-planar symmetry, the resonance hybridization effect [Figure 2b] results in energetic stabilization of the biradical TMM intermediate. Despite the fact that the functional form of the predefined modified potential, V^*(θ), employed in the adaptive AMD simulations does not resemble the true free-energy profile for this reaction, it is important to recognize that the free-energy weighting procedure still provides extremely accurate free-energy statistics. This observation underlines the fact that it is not necessary to define a modified potential that contains all the characteristics of the true underlying energy landscape: Accurate free-energy statistics are consistently produced via the subsequent free-energy weighting protocol. As was previously mentioned in the Methods section, the predefined modified potential only has to mimic the true underlying PES accurately enough to ensure that it lies above the true potential across the entire reaction space of interest, thereby ensuring that the system is constantly under the influence of the acceleration potential, resulting in more efficient configurational space sampling.

Figure 8.

Comparison of the conformational space sampling observed in MCP by standard CP-MD (orange) and adaptive AMD (black). In the (unweighted) adaptive AMD trajectory, the system rapidly exchanges between all three isomeric states of MCP located at ∼{θ₁, θ₂} = {65, 150}°, {150, 150}°, and {150, 65}°. The TMM metastable intermediate is located at {120, 120}°.

Figure 9.

The free-energy profile for ring opening of MCP as a function of the C–C–C angle, θ obtained from the adaptive AMD method (black line), and the standard constrained CP-MD approach (red line). The closed ring system has a free-energy minimum at 66° and the transition state is located approximately at θ = 105°.

The adaptive AMD approach does not only provide an accurate estimation of the free-energy profile associated with the ring opening and subsequent rearrangement of MCP, but also affords a very accurate description of the associated reaction mechanism. The transition state identified in the adaptive AMD simulations is almost identical to that observed in the constrained CP-MD protocol: As the cylcopropane ring opens, the two C–C bonds that originally formed the cyclopropane ring increase in length from 1.5 to 1.8 Å, as does the C=C ethylene bond. Both ring-opening and ring-closure events on the (hypothetical) adiabatic PES involve a disrotatory motion of the two CH₂ groups. These structural geometric changes are observed in both the adaptive AMD simulations and the constrained CP-MD analysis.

DISCUSSION

The results presented above demonstrate how the application of the accelerated molecular dynamics approach in the framework of ab initio molecular dynamics can be used to study chemical reactions and to obtain an accurate representation of both the free-energy surface and the associated reaction mechanism. It is important to note that the two bias potential methods (standard AMD and adaptive AMD) serve different purposes: The primary purpose of the standard AMD simulations is to explore the configuration and reactive free-energy surface of the system, to identify stable and metastable states, and to predict chemical reactions of interest. For example, the standard AMD simulations performed on FAD readily identified the dissociated state [Fig. 1b] and the twisted state [Fig. 1d] and predicted the DPT chemical reaction via the transition state [Fig. 1c]. In the case of MCP, the standard AMD simulations identified two chemical reactions: Ring opening and subsequent ring closure via a TMM intermediate and cleavage of the C2–C3 bond leading to the formation of a high energy vinyl-radical state. For both systems it was possible to obtain an approximate representation of the underlying PES. The primary purpose of the adaptive AMD method is to obtain accurate free-energy statistics for a specific chemical reaction of interest and, when appropriate, an estimate of the associated reaction rate.

In general, one faces the following dilemma concerning enhanced configurational space sampling and obtaining accurate free-energy statistics: Ideally, we would like to explore large areas of the PES of a system as efficiently as possible and at the same time extract accurate free-energy statistics. However, these two aims are often mutually exclusive, as the more widely we explore the PES, the less accurate the free-energy statistics will be in the narrow regions of interest. The different roles of the two bias potential methods presented in this paper reflect this mutual exclusivity. While the standard AMD approach is much more efficient at exploring the total PES of the system, identifying a large number of high energy states or activated processes, the associated free-energy statistics are not very accurate. Having identified a particular chemical reaction of interest, the application of the bias potential can then be adapted in order to focus more on the specific associated reacting degrees of freedom, enhancing the specific sampling of that particular process and thereby affording more accurate free-energy statistics. This forms the basis of adaptive AMD. We would like to point out that a similar argument can be made for other contemporary enhanced configurational space sampling methods. For example, in the constrained CP-MD approach, having defined a reaction coordinate, it is possible to obtain an accurate free-energy profile with respect to that specific reaction coordinate, but only a very small part of the total PES of the system is sampled.

As discussed above, the primary aim of the standard AMD approach is to efficiently explore the PES of a system and to identify activated processes and chemical reactions. The efficiency of the enhanced configurational space sampling in AMD simulations depends strongly on the choice of the acceleration parameters, E_b (or more specifically [E_b − V₀]) and α. In practice, the “optimal” choice of these AMD parameters is extremely system-specific and depends on many factors, including the size of the system and the nature of the underlying potential energy landscape. Nevertheless, based on the work presented here, it is possible to construct some general guidelines. The boost energy, E_b, represents the potential energy ceiling: Any activated process that involves a transition over an energy barrier greater than [E_b − V₀] will not generally be observed in the standard AMD simulations. While initial estimates of the energy barriers (and hence the magnitude of [E_b − V₀]) can be made using our understanding of different classes of chemical reactions, in the case where one has no prior knowledge of the underlying PES for a given system, a suitable choice for [E_b − V₀], in general, is 10–15 kcal/mol, which, according to TST, will allow the prediction of chemical reactions occurring on the micro- to millisecond time scale. Nevertheless, when approaching extremely rare events or reactions mediated by nonadiabatic mechanisms (such as that observed in MCP) that involve transitions over exceedingly large energy barriers (usually in excess of 30 kcal/mol), a significantly larger initial estimate of [E_b − V₀] is required. Based on the work presented here, we have identified that the optimal value for the acceleration parameter, α, generally lies between 0.7*[E_b – V₀] and 0.1*[E_b – V₀]. Obviously, when approaching a system for which one has no prior understanding of the underlying PES, an initial series of test AMD simulations across a variety of acceleration levels is necessary in order to identify the optimal acceleration parameters. For example, in the case of FAD, we performed six initial short AMD simulations using a fixed value of α (0.016 a.u.) and varying the value of [E_b – V₀] between 0.016 and 0.026 a.u. in steps of 0.002 a.u. We would like to note that even when performing very short initial test AMD simulations (such as 100 000 steps which is the equivalent of ∼10 ps), the appropriate acceleration level can be readily identified: If the acceleration level is too low, ostensibly no enhanced configurational space sampling is observed. In contrast, applying too high an acceleration level, results in a molecular explosion or dissociation of the system. The initial test AMD simulations also provide valuable qualitative information about the associated activation energies for different processes occurring in the system. It should be recognized that the efficiency of the standard ab initio AMD approach to predict chemical reactions is dependent on the size and inherent flexibility of the system under study. AMD amplifies the motion of all the vibrational degrees of freedom in the system, including low energy, large amplitude molecular motions, and not just those degrees of freedom associated with the chemical reaction. In some cases, the acceleration of these low energy vibrational fluctuations (such as the intermonomer breathing mode of FAD) brings the system toward the chemical transition state, thereby facilitating the observation of the chemical reaction of interest. However, whether a particular chemical reaction is sufficiently accelerated by AMD also depends on the number of alternative dynamical pathways. Therefore, the efficiency of the AMD method to predict chemical reactions may be compromised to some extent when applied to larger, more flexible systems than those reported in this paper.

In addition to their ability to predict chemical reactions of interest, the standard AMD simulations also provide an approximate representation of the underlying variation in the PES for these processes (as demonstrated specifically in the Results section for FAD). As such, these simulations allow us to formulate a suitable reaction coordinate for the specific reaction of interest which is then used in the adaptive AMD simulations to obtain accurate free-energy statistics. The initial definition of the magnitude and functional form of the boost energy (for a fixed value of α) employed in the adaptive AMD simulations can be obtained using the approximate representation of the underlying PES. It is therefore clear that defining the initial acceleration parameters in the adaptive AMD approach is much simpler than in the case of standard AMD, where no information about the PES is available. The adaptive AMD method presented here was developed to show that it is possible to obtain accurate free-energy statistics and reaction rates for chemical reactions in the general framework of ab initio AMD. However, it is clear that having predicted a chemical reaction and formulated a suitable reaction coordinate from the standard AMD simulations, alternative methods to obtain the associated free-energy profile, such as metadynamics or constrained MD can be employed and in some cases may be more favorable. This is certainly true when dealing with systems where the reactant and product states do not exist in dynamic equilibrium. An objective comparison of the efficiency and accuracy of the enhanced configurational space sampling and free-energy methods is difficult to perform as certain methods are more suited to some systems than to others. In terms of exploring the PES and predicting activated processes and chemical reactions, the standard AMD approach has significant advantages over other methods (such as metadynamics and constrained CP-MD) as it does not require any a priori understanding of the underlying PES, nor does it require the specific prior definition of a reaction coordinate or a set of collective variables. As such, we consider that the standard AMD approach could be particularly useful when studying larger, more complex systems where the specific construction of an appropriate reaction coordinate or a suitable definition of the appropriate collective variables might not be readily apparent. In terms of obtaining accurate free-energy statistics, the relative efficiency of the different methods is not so clear: A direct comparative analysis of the adaptive AMD and constrained MD approaches applied to the systems presented in this work suggests that the two methods are equally efficient. We would like to stress that this observation is based on just two systems and as such, it is inappropriate to draw general conclusions about the relative efficiency of methods. In particular, we note once again that the test systems studied here are small and possess a limited number of internal degrees of freedom. The relative efficiency of the two methods when applied to larger and inherently more flexible systems remains unclear. Nevertheless, the Ad-AMD approach does not require a correction for metric effects on the associated Lagrangian, which is often necessary and tedious in the constrained CP-MD method. Furthermore, the Ad-AMD approach affords an estimate of the reaction rate constant, including a meaningful estimate of the associated transmission coefficient, which is notoriously difficult to obtain using any standard method for enhanced configurational space sampling. In general therefore, we consider that the ab initio AMD methods presented here can be readily used alone, or to complement existing methods to study chemical reactions and reactive free-energy surfaces.

CONCLUSIONS

We have demonstrated that the accelerated molecular dynamics approach, which has previously been successfully applied to the study of conformational transitions in polypeptides and proteins, can also be implemented in the framework of ab initio molecular dynamics to study chemical reactions. A two-step procedure is proposed: In step 1, the standard AMD approach is applied, which allows one to efficiently explore the reactive subspace of molecular systems, identifying a variety of high energy states and predicting potential chemical reactions. In step 2, a new variant, adaptive AMD, is introduced which allows one to focus on a particular chemical reaction or rare event of interest, providing a detailed description of the reaction mechanism, an accurate representation of the associated free-energy statistics, and an approximate estimate of the associated reaction kinetics.

In the standard ab initio AMD method, the application of the bias potential raises and flattens the global PES. As a result, all the vibrational degrees of freedom are accelerated or “activated”. This includes both the low energy modes associated with large amplitude collective fluctuations, as well as the high frequency localized vibrations. In order to observe a chemical reaction, the system must approach the chemical transition state geometry. In standard ab initio MD, this is usually a very rare event as it involves the system moving to a high energy region on the PES. By activating all the vibrational modes, the frequency of these rare events is dramatically enhanced in ab initio AMD, and therefore the effective time taken to visit the transition state is reduced by many orders of magnitude. This general principle holds true for any system and any class of chemical reaction. In comparison to other methods, ab initio AMD allows for the exploration of the reaction space of a molecular system without any a priori understanding of the underlying free-energy surface, nor does it involve the specific definition of a predefined reaction coordinate. However, the efficiency of the ab initio AMD approach for the prediction of chemical reactions will most certainly be system dependent: The size of the system (i.e., the number of degrees of freedom), the flexibility of the system, and the magnitude of the energy barriers on the PES will all have an effect on the efficiency of the method.

The biased potential ab initio MD simulations presented here have been performed in the framework of Car–Parrinello MD, but the application of this method in the framework of Born–Oppenheimer MD is equally viable. Our present study of chemical reactions in simple systems, the DPT event in FAD and the ring opening and subsequent rearrangement of MCP have demonstrated that both ab initio AMD and adaptive ab initio AMD methods are readily applicable to the study of chemical reactions involving transitions over intermediate to large free-energy barriers up to 25-kcal/mol. The study of chemical reactions involving transitions over substantially larger energy barriers is possible (as demonstrated by the example of MCP in this work), but is somewhat more challenging. However, we would like to point out that such high energy processes are usually mediated by more complex nonadiabatic mechanisms that require more elaborate methods.^{47, 48} Most chemical reactions of interest, particularly, biochemical reactions, generally occur on micro- to millisecond time scales and have associated free-energy barriers ranging up to a magnitude of 15-kcal/mol. We believe that standard ab initio AMD is a powerful and general tool for searching for any reactive pathways in an unbiased fashion. It can be readily applied to highly complex systems, retaining its predictive power. In fact, we are presently implementing these ab initio AMD methods in a Quantum Mechanical∕Molecular Mechanical (QM/MM) manifold in order to study enzymatic reactions in a realistic biomolecular environment. Accurate free-energy landscapes are readily obtained using the new, adaptive AMD method, i.e., by selectively accelerating the reactive modes identified in the standard AMD simulation. Generalization of Ad-AMD to many-dimensional reaction coordinates in more complex systems is straightforward once they have been identified. In conclusion, we consider that the ab initio AMD methods presented here can be readily used alone, or to complement existing methods to study chemical reactions and reactive free-energy surfaces.