Constraining local structure can speed up folding by promoting structural polarization of the folding pathway

Abstract

The pathway which proteins take to fold can be influenced from the earliest events of structure formation. In this light, it was both predicted and confirmed that increasing the stiffness of a beta hairpin turn decreased the size of the transition state ensemble (TSE), while increasing the folding rate. Thus, there appears to be a relationship between conformationally restricting the TSE and increasing the folding rate, at least for beta hairpin turns. In this study, we hypothesize that the enormous sampling necessary to fold even two-state folding proteins in silico could be reduced if local structure constraints were used to restrict structural heterogeneity by polarizing folding pathways or forcing folding into preferred routes. Using a Gō model, we fold Chymotrypsin Inhibitor 2 (CI-2) and the src SH3 domain after constraining local sequence windows to their native structure by rigid body dynamics (RBD). Trajectories were monitored for any changes to the folding pathway and differences in the kinetics compared with unconstrained simulations. Constraining local structure decreases folding time two-fold for 41% of src SH3 windows and 45% of CI-2 windows. For both proteins, folding times are never significantly increased after constraining any window. Structural polarization of the folding pathway appears to explain these rate increases. Folding rate enhancements are consistent with the goal to reduce sampling time necessary to reach native structures during folding simulations. As anticipated, not all constrained windows showed an equal decrease in folding time. We conclude by analyzing these differences and explain why RBD may be the preferred way to constrain structure.

Introduction

For a protein to function its polypeptide chain must overcome the difficult task of finding the native structure in a vast configurational space. Proteins accomplish this feat by employing a folding mechanism, which guides the ordering of structure during the folding reaction. Mechanisms are determined in protein engineering experiments by analyzing a large number of mutations to generate phi-values.¹ For small single domain proteins, there are in general two folding mechanisms. The diffusion-collision model is followed when local structures are formed independently and their collisions lead to the native state.² With increasing secondary structure propensity, folding proceeds more hierarchically. On the other hand, the nucleation-condensation model is more likely to occur when the secondary structure is inherently unstable.³ Collapse around an extended nucleus is followed by the simultaneous formation of secondary and tertiary structure.⁴ Ultimately, the shape and roughness of the energy landscape will determine the folding mechanism for a protein.

The native structure for a protein resides at a deep energy minimum in the funnel-shaped folding landscape.⁵ Roughness in the funnel can result from both non-native interactions and incomplete compensation of entropy loss to enthalpy gained during folding.⁶ The latter energy landscapes are considered to be topologically frustrated. It has been shown that for many small single domain proteins, topological frustration plays a primarily role in determining their folding mechanism.⁷ Thus folding seems only minimally affected by sequence. The relationship between folding rates for many two-state proteins and the number of nonlocal contacts in their native structure supports this theory.⁸ In general, proteins with more complex topologies fold slower because the entropic penalty to form nonlocal contacts is greater than for local ones. Additionally, models that incorporate only native interactions, thus leaving out sequence-dependent frustration, can reproduce many important features in the folding mechanisms of small single domain proteins.⁹

Sampling long time scale phenomena such as protein folding in detailed atomistic simulations is not currently possible without the use of massively parallel or distributed computing clusters.¹⁰ However, Gō models using simplified protein representations biased toward the native structure have helped to understand the folding process and identify important interactions that drive folding.¹¹ Off-lattice Gō models typically employ a Lennard-Jones function to model nonlocal interactions using a strictly repulsive term to block the formation of non-native contacting. While adding energetic frustration into a Gō model through a small amount of non-native contacting can speed up the folding reaction, ¹² other evidence suggests that frustration may disrupt folding rates, stability, and cooperativity.¹³ When using a Gō model, simulations are typically started from native and unfolded at high temperature to generate uncorrelated initial structures. Simulations are then jumped to the temperature of interest to yield the relevant statistics.^{7 14} The simple protein representation allows one to perform equilibrium folding/unfolding simulations thus sampling high energy intermediates such as transition state structures.¹⁵

Gō models have also been used to explore the conformational dynamics of the TSE. In one particular study, it was shown that increasing the stiffness of a beta hairpin turn (by changing the position of the hydrophobic cluster) decreased the time necessary to fold.¹⁶ Stiffening the beta turn also restricted the size of the TSE based on the number of clusters for member structures of the transition state. Thus, there appears to be a relationship between the size of TSE and the folding rate for beta hairpin turns. Based on these results, it is theorized that the conserved folding mechanism across SH3 domains results from the conserved stiffness in the distal hairpin loop. These results were supported experimentally with hydrophobic core mutants of the alpha-spectrin SH3 domain. Although these mutants were unstable, they still folded properly. After destabilizing the distal hairpin, mutants became molten globule-like.¹⁷ Therefore, an intact distal hairpin can conformationally restrict the SH3 TSE by inducing structural polarization of the folding pathway (see the section on the src SH3 domain for an explanation of the TSE and folding pathway). Consequently, constraining the distal hairpin should not alter the TSE. On the other hand, the nature of the TSE for proteins with little loop rigidity and primarily nonlocal contacts cannot be easily determined using this metric. The phi-value distribution for these proteins is relatively broad indicating they fold mostly through a nonhierarchical mechanism. Differences in the degree of transition state polarization implies that folding mechanisms and rates are dependent on the type, propensity, and burial of the secondary structural elements.

Building on this idea with the goal to reduce sampling time for folding two-state proteins, we introduce native local structure constraints at all possible sequence windows for the proteins CI-2 and src SH3 and monitored both their folding pathway and folding time changes. Based on the results of previous studies, we attempt to show that constraining local structure to native can induce structural polarization of the folding pathway thus reducing the conformational size of the ensemble and sampling necessary to reach the folded state. Additionally, constraining local structure to native that is not formed in the TSE can still increase the folding rate by inducing structural polarization along a folding pathway that is different from native. Results of this study present an opportunity to improve structure prediction sampling based on the relationship between local sequence and structural stability. Correctly predicting local structure and constraining it, should increase the folding rate by restricting the structural heterogeneity during simulations. Effective local structure prediction makes this approach particularly attractive as a way to encode a hierarchical structure prediction program.¹⁸

Results and Analysis

Src SH3 domain

The src SH3 domain is a 56 residue portion of a protein tyrosine kinase that associates into complexes typically by binding proline-rich peptide sequences. It is composed of five beta strands in an antiparallel arrangement plus one short 3-10 helical turn. The three loops connecting those strands are the functional RT loop, by far the longest and most disordered, the n-src loop connecting strands 3/4 and the distal hairpin loop [Fig. 1(a)]. Experimental evidence indicates that the domain folds by diffusion-collision and exhibits two-state folding behavior.¹⁹ Based on phi-value analysis, the transition state is formed when the distal hairpin and diverging turn are structured and docked.²⁰ This polarized transition state can be seen in the large phi-values for these two regions [Fig. 2(a)]. Other SH3 domains with significant differences in sequence have been shown to fold by a conserved folding mechanism.²² This has been used to support the theory that topological frustration plays a primary role in the folding mechanisms of small single domain proteins. It also explains the usefulness of topological folding models, which incorporate only native interactions.

Figure 1.

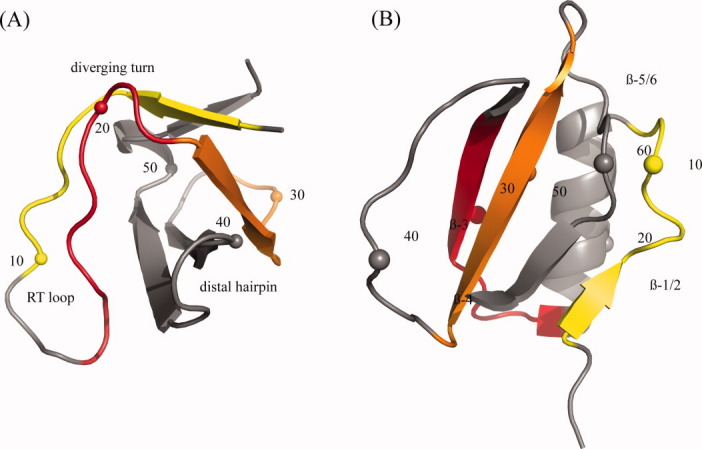
Structures for (A) src SH3 domain [1SRL] and (B) CI-2 [2CI2] with every tenth residue numbered. In the online version, residue windows in (A) are colored yellow 2–10, red 14–22, and orange 23–31. Residue windows in (B) are colored yellow 4–12, red 25–33, and orange 45–53. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 2.

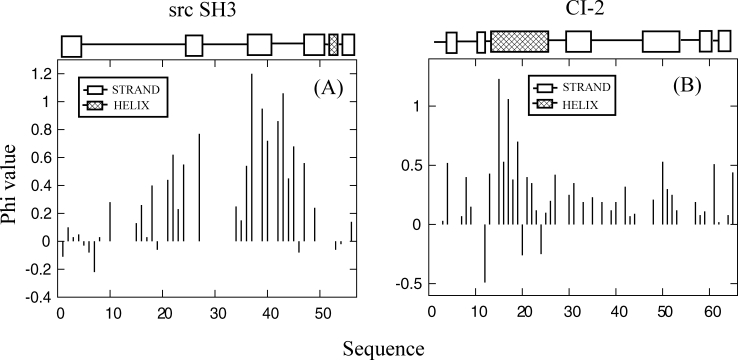
Experimentally determined phi values for (A) src SH3 (Ref. ²⁰) with the distal hairpin centered at residue 42 and diverging turn centered at residue 23 and (B) CI-2 (Ref. ²¹).

Comparing constrained with unconstrained simulations for the src SH3 domain, 41% of constrained windows show at least a two-fold decrease in folding time and no window shows a significant (more than two-fold) increase in folding time [Fig. 3(a)]. 90% confidence intervals for folding times were determined by 10,000× resampling with replacement of folding times for the 100 runs within each window. As expected, only three constrained windows show an increase in median folding time compared with unconstrained simulations. Confidence intervals for two of these windows overlap with the unconstrained median folding time indicating that folding was mostly unaffected by the local constraint. The folding time for window 7 however does not overlap with the unconstrained median time. Given the large confidence interval for this window, the result is probably not significant.

Figure 3.

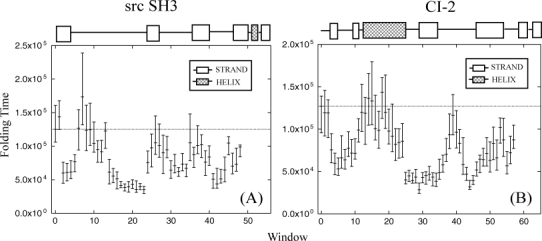
(A) src SH3 and (B) CI-2 median first passage folding times (in simulation steps) with 90% confidence intervals for all constrained windows. The unconstrained median first passage folding time is shown in window zero. Data are plotted at the first position of the 9-residue window.

Two of the local sequence areas, which show the greatest decrease in folding time are windows 2-5 and 14-17 (window 2 contains residues 2-10, window 3 residues 3-11, etc.). Windows in these areas show at least a two-fold increase in folding time and cover the most disordered region of the native structure, the RT loop. Between these two local sequence areas (windows 7-10), the same folding time increases are not seen. Residues for these windows are located in the turn region of the RT loop, which makes their local contacts more likely to form given the spatial proximity to one another. Thus preforming these contacts does not significantly alter the folding time for two reasons. (1) Local contacts in the turn region stabilize the loop compared with strands or other disordered structures that have no local contacts. Constraining it to be formed will have only a marginal effect on the secondary structure propensity. (2) Since there are relatively few nonlocal contacts made to the loop, the local structure does not provide an ideal position to induce structural polarization along the folding pathway. Therefore folding time is decreased by constraining local structure that has little secondary structure propensity and provides a position for structural polarization during folding. The turn of the RT loop does not fit this description but constraining either extended portion does.

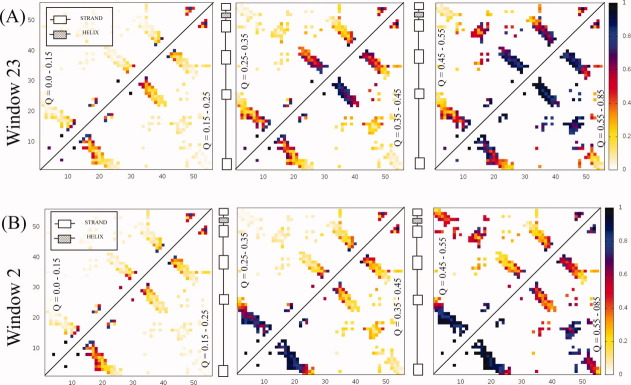
Structural polarization around the first strand of the n-src loop (residues 23-31, window 23) can be seen in Figure 4(a), which shows a sequence of contact probability maps as a function of the reaction coordinate Q. In the contact probability map generated from structures with Q = 0.35–0.45, the n-src loop is almost completely ordered. Surprisingly, it adopts structure even before the tighter turning distal hairpin. Folding proceeds down the native pathway with the formation of the distal hairpin and docking to the diverging turn (Q = 0.45–0.55). Interactions between the termini and RT loop are the last to form. Structural polarization around another disordered region, the first extended portion of the RT loop (window 2), can be seen in Figure 4(b). In these simulations, the RT loop forms first while docking between the distal hairpin and diverging turn occurs much later. Instead, early structuring of the loop promotes contacting between the termini. The folding pathway for this constrained window is considerably different from the native pathway.

Figure 4.

Contact probability maps for src SH3 simulations constraining (A) residues 23-31 as a function of the reaction coordinate Q. The color bar indicates the probability that a contact is formed for structures with a Q-value shown inside the triangle. The sequence runs along both the x and y axes. The constraint promotes the early formation of the n-src loop. Interactions within the RT loop and termini are formed after the distal hairpin (residue 42) and diverging turn (residue 22) contact. The constrained simulation retains many features of the native folding pathway based on experimental results. (B) Constraining residues 2-10 as a function of the reaction coordinate Q. Early contacting between the termini is a result of constraining the N-terminus.

Folding rate changes for the rest of the structure follow the criteria outlined above (Table I). In the turn region of the n-src loop (windows 25–29), folding times do not decrease significantly. Secondary structure propensity is only partially affected by the constraint since there are local contacts in the turn. Constraining these windows does not promote structural polarization because there are few nonlocal contacts to the turn. For windows in the turn region of the distal hairpin (windows 36–37), folding times also did not decrease significantly. Constraining the strands that made up the turn however (windows 34 and 41), decreased folding times at least two-fold. The native folding pathway is polarized around the strands of the hairpin when they dock to the diverging turn. Since there are very few nonlocal contacts in the turn region itself, constraining leaves the folding time unchanged. Window 35 does not follow this trend, but the confidence interval indicates that noise has affected the median folding time.

Table I.

Comparison of Folding Time Changes, Contacts, and ln(k_f) for Different Regions of CI2 and src SH3 Domain

	CI2					Src SH3
Window	Structure	Locala	Nonlocalb	%Δc	ln (kf)d	Structure	Local	Nonlocal	%Δ	ln (kf)
0	unconstrained			100	−11.8	unconstrained			100	−11.7
1		2	5	94	−11.7		1	4	115	−11.9
2		3	4	94	−11.7		1	9	48	−11
3		3	5	59	−11.2	RT loop (extended 1)	1	11	49	−11
4	strands 1/2	2	9	47	−11.0		2	12	49	−11
5		3	10	42	−10.9		1	13	62	−11.3
6		3	12	52	−11.1		2	12	101	−11.8
7		2	15	50	−11.1		5	9	138	−12.1
8		5	13	61	−11.3		8	6	99	−11.7
9		7	12	56	−11.2	RT loop (turn)	9	5	100	−11.7
10		6	15	56	−11.2		9	7	83	−11.6
11		8	14	78	−11.5		4	14	76	−11.5
12		10	14	94	−11.7		2	16	73	−11.4
13	helix	9	14	93	−11.7		0	17	98	−11.7
14		9	22	107	−11.8	RT loop (extended 2)	2	15	49	−11
15		9	22	105	−11.8		3	13	44	−10.9
16		9	22	79	−11.5		5	8	41	−10.8
17		9	20	78	−11.5		5	5	33	−10.6
18		9	17	113	−11.9		4	3	31	−10.6
19		9	15	94	−11.7		2	5	31	−10.6
20		9	13	77	−11.5		0	10	34	−10.7
21		9	10	72	−11.4		0	14	28	−10.5
22		6	11	64	−11.3		1	14	32	−10.6
23		1	14	66	−11.3	n-src loop (strand)	1	13	28	−10.5
24		1	12	67	−11.4		1	12	60	−11.2
25	strand 3	1	12	31	−10.6		2	9	78	−11.5
26		0	12	35	−10.7		4	7	84	−11.6
27		0	10	31	−10.6	n-src loop (turn)	8	3	81	−11.5
28		0	8	34	−10.7		9	2	72	−11.4
29		1	5	22	−10.3		6	7	76	−11.5
30		2	2	34	−10.7		2	16	51	−11.1
31		3	0	36	−10.7		1	20	57	−11.2
32		3	1	37	−10.7		0	22	50	−11
33		3	3	34	−10.7	distal hairpin (strand 1)	0	22	59	−11.2
34		1	7	30	−10.6		1	20	54	−11.1
35		0	10	38	−10.8		3	16	84	−11.6
36		0	12	45	−11.0		7	7	70	−11.4
37		0	12	55	−11.2	distal hairpin (turn)	10	2	81	−11.5
38		0	11	73	−11.4		10	2	82	−11.5
39	functional loop	4	6	91	−11.7		5	7	61	−11.2
40		5	4	76	−11.5		1	14	67	−11.3
41		8	1	65	−11.3		0	15	41	−10.8
42		6	4	46	−11.0		0	15	35	−10.7
43		4	9	37	−10.8		0	14	41	−10.8
44		2	16	25	−10.4		1	11	52	−11.1
45	strand 4	0	21	31	−10.6		3	6	84	−11.6
46		0	21	41	−10.9		6	2	56	−11.2
47		0	21	51	−11.1		6	0	58	−11.2
48		1	16	50	−11.1		6	0	79	−11.5
49		4	12	56	−11.2
50		8	4	50	−11.1
51		10	2	65	−11.3
52		8	4	52	−11.1
53		3	9	80	−11.5
54		1	12	69	−11.4
55	strands 5/6	1	12	45	−10.9
56		1	12	57	−11.2
57		1	11	69	−11.4

^aNumber of local contacts made within the window.

^bNumber of nonlocal contacts made between the window and outside residues.

^cMedian folding time as a percent of unconstrained median folding time.

^dk_f is in units of simulation steps.

Chymotrypsin inhibitor 2 (CI-2)

Chymotrypsin Inhibitor-2 (CI-2) is 65 residue protein containing six strands in a parallel/antiparallel beta-sheet packed against an alpha-helix to form a hydrophobic core [Fig. 1(b)]. Experimental evidence indicates that it folds with two-state behavior.^{23 24} Based on a broad range of phi-values, the TSE appears as an expanded version of the native [Fig. 2(b)]. Larger phi-values have been determined for residues in the helix, mini-core (strands 3/4 and loop between them), and the turn between strands 4 and 5. Otzen and Fersht ²⁵ have found that strands 1, 5, and 6 are in general not structured at the transition along with strand 2. It is believed that the transition state contains a loose hydrophobic cluster formed between the mini-core and helix. Evidence suggests that after the formation of strands 3/4 and the helix, both strands dock to the C-terminus of the helix.²¹ Condensation then takes places around this nucleating hydrophobic cluster. CI-2 is a representative example of nucleation-condensation folding.

No constrained window for CI-2 has a significant increase in folding time and 45% of constrained windows show at least a two-fold decrease in folding time [Fig. 3(b)]. There are two sequence regions, which do not show a change in folding time compared with unconstrained simulations. Windows centered directly on the helix (windows 12-19) have folding times that are approximately equal to unconstrained simulations. Even though the helix forms several nonlocal contacts with strands of the termini, most of the contacts in the helix are local. Folding rate changes for these windows are not expected to increase since preforming these contacts does not significantly alter the secondary structure propensity (Table I). The functional loop connecting strands 3 and 4 (window 39) is another constrained window that shows no decrease in folding time. This part of the structure is mostly disordered in the native state and has few nonlocal contacts since it is mostly floating outside the surface of the protein. Although the local structure propensity changes considerably after constraining the loop, structural polarization near the window will not occur given the lack of nonlocal contacts for this structure.

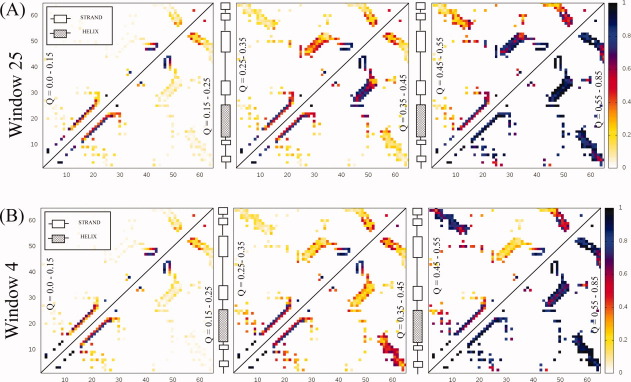
Constrained windows which show the greatest decrease in folding times are in the strands that make up the beta-sheet [Fig. 3(b)]. In the sequence of contact probability maps for simulations constraining window 25, strand 3 from CI-2, contacts are stabilized between strands 3 and 4 shortly after the helix appears [Fig. 5(a)]. The turn between strands 4 and 5 is formed next while nonlocal contacts between the termini are the last to occur. Overall the sequence of contact formation retains many features of the native folding pathway. The rate increase appears to be a result of mini-core stabilization, which enhances polarization near the constrained local structure. Constraining window 4 which covers strands 1 and 2 is another local structure that decreases folding time two-fold. The sequence of contact probability maps shows that the helix forms early as expected [Fig. 5(b)]. The next fastest forming contacts are located between the termini. Folding proceeds with contacting between strands 4 and 5 while the major part of the beta-sheet is the last to form. In this case, structural polarization near the termini decreases folding time by making a major change to the folding pathway.

Figure 5.

Contact probability maps for CI-2 simulations (A) constraining residues 25-33 as a function of the reaction coordinate Q. The color bar indicates the probability that a contact is formed for structures with a Q-value shown inside the triangle. The sequence runs along both the x and y axes. The constraint stabilizes early interactions within the mini-core (strands 3/4). Contacting between the mini-core and helix forms next indicating that folding retains many features of the native pathway based on experimental results. (B) Constraining residues 4-12 as a function of the reaction coordinate Q. Early contacting between the termini is a result of constraining strands 1/2.

Rigid body constraints

Constraining local structure in off-lattice continuum-based simulations is similar to Monte Carlo algorithms such as fragment assembly and lattice-based methods. In fragment assembly, secondary structure is inserted randomly into the chain.^{26 27} Although successful in structure prediction, the algorithm allows chain crossings, which may lose pathway information that could improve sampling. Lattice-based Monte Carlo simulations also benefit by allowing multiple residue concerted movements. ^{28 29} However, sampling on lattice grid points can cause local structure deformations, which may lead to unwanted barrier crossings or off-pathway sampling. The strength of these two Monte Carlo approaches lies in their ability to sample constrained local structure. By averaging out the local fluctuations, tertiary interactions that depend on the formation of local structure can occur more often. This idea has shown to be useful in hierarchical structure prediction algorithms, which attempt to fold sequences from local to global. ^30–32

The question remaining then is how to average out local structure fluctuations in off-lattice continuum-based simulations? One simple way is to add distance restraints onto sequence local contacts. There are two conditions that need to be satisfied to make the restraint effective. The restraint must be stronger than all other local interactions, otherwise it will not be maintained continuously. Second, the time step must be kept sufficiently small to prevent spring-like waves when restraints are tested. Reducing the time step however is counterproductive if the total CPU time for sampling increases. Another way to average out local fluctuations is to constrain structure using one of the various Lagrangian multiplier routines.^{33 34} In these algorithms, atomic positions are updated as if no constraint existed. Afterwards a corrective force is computed and applied to satisfy the constraint condition. Often the procedure needs to iterate several times. The cost of computing these corrective forces is only justified if longer time scale behavior is simulated given the same CPU time.

In this work, we utilize rigid body dynamics (RBD) as a local constraint method for off-lattice continuum based Gō model simulations. RBD treats one or more sets of atoms as independent rigid bodies. Fixing local windows using this method promotes folding near constrained regions early on during simulations. Furthermore, applying local constraints in the presence of the entire chain promotes nonlocal contacting to the fixed window when nonlocal contacts are present in the native structure for that window. This result presents an opportunity to improve the protein structure prediction algorithm Zipping & Assembly (Z & A).^{32 35} In Z & A, distant restraints are used in absence of the entire chain. It would be interesting to investigate whether nonlocal contacting observed using this Gō model is reproduced in molecular dynamics simulations of the entire chain. Given the results of this study, the tendency for Z & A to produce low contact order predictions may be overcome.

Conclusion

In summary, we have shown that using a Gō model and constraining local sequence windows to their native structure by RBD affects both the kinetics and folding pathways for CI-2 and the src SH3 domain. Constraining local structure decreases folding time two-fold for 41% of src SH3 windows and 45% of CI-2 windows. For both proteins, folding times are never significantly increased after constraining any window. Rate increases are dependent on the local structure propensity before adding the constraint and whether the window provides an ideal position for structural polarization during folding. In agreement with others, constraining native local structure found in the TSE does not alter the native folding pathway. However, constraining native local structure not found in the TSE can cause entropically disfavored contacts to form early, which increases the folding rate. Rate enhancements result from lowering the entropic penalty for these nonlocal contacts to form since the enthalpy of the native state is the same for constrained and unconstrained simulations. All folding rate increases are consistent with the goal to reduce sampling time necessary to reach native structures during folding simulations.

Although the observed variability is significant, no single constrained window decreases folding time more than three-fold for src SH3 or four-fold for CI-2 while experimental folding times can span orders of magnitude for proteins with different topologies and similar length sequences. This suggests that differences in local structure propensity and burial may not affect folding rates as much as differences in contact order or topological complexity. On the other hand, the range of folding times for unconstrained Gō model simulations is compressed (Table II). Experimental folding times for 1PGB and 1SRL are separated by a 16-fold decrease while there is a two-fold decrease in unconstrained Gō model simulations. This known feature of Gō models implies a lack of sufficient cooperativity.⁴⁰ However, there is a correlation between the rank order of folding times between experiment and Gō model simulations. Considered in this context, a two-fold folding time change may be more important than first suggested.

Table II.

Comparison of Experimental and Unconstrained Gō Folding Times

PDB Code	Name	Fold	N	Unconstrained Gō folding timea	Experimental folding time	Experimental ln(kf)	Relative contact order	Reference number
1PRB	Albumin binding domain	3 Helical Bundle	53	27,000	2.5 μs	12.9	11.1	36
1PGB	Protein G	Alpha+Beta Mixed Sheet	56	62,000	1.7 ms	6.4	17.6	37
1SRL	src SH3	SH3 barrel	56	125,200	17.4 ms	4.05	19.5	23
2CI2	Chymotrypsin Inhibitor-2	Alpha+Beta Sandwich	65	127,200	20.8 ms	3.87	16.4	38
1TEN	TnFN3	2 Sheet Beta Sandwich	89	429,600	346.4 ms	1.06	17.4	39

^aMeasured in units of simulation steps.

In an experiment by the Baker group, engineering a disulfide bond across the base of the distal hairpin of the src SH3 domain caused a 30-fold decrease in folding time.⁴¹ In constrained simulations for window 41 (the second strand of the distal hairpin), there is a two-fold decrease in folding time compared with unconstrained simulations. Although it is difficult to make a direct comparison of these folding time decreases, given the compression in the simulated range of folding rates, this result is intriguing. It is also interesting to consider how the experimental folding rate for the src SH3 domain would change if the strand of the n-src loop (window 23) were forced into the native conformation in the denatured state. In simulations, there is nearly a four-fold change in folding time. However, there is no experiment to our knowledge that can constrain the polypeptide backbone in an extended conformation.

Methods

We use the Gō model first proposed by Clementi et al.⁷ Readers are encouraged to review the paper for background on using this model to reproduce the TSE for proteins studied in this work. To describe the model briefly, each residue is represented as a single interaction point located at the position of the alpha-carbon. The energy of a configuration Γ with a native configuration of Γ₀ is given by the following function:

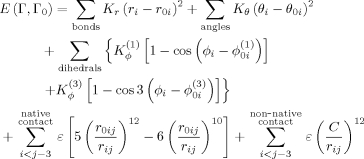(1)

The variables r_0i, θ_0i, and φ_0i, correspond the native values for bond length, bond angle, and dihedral angle, respectively. The nonlocal 12-10 Lennard-Jones function was set to minimize the distance r_0ij between any two natively contacting residues. All residues not contacting in the native structure are given a repulsive energy where C = 4.0 Å. The following energy constant values were used K_r = 100, K_θ = 20, 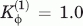, , 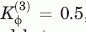and ɛ = 1.0. A native contact was declared between any two residues separated by a sequence separation of at least four residues when any heavy atom from one residue was less than 6.5 Å of any heavy atom from the other residue using the PDB coordinate file. During folding simulations, the reaction coordinate Q was calculated as the percentage of native contacts formed. A native contact between two residues was considered made if the distance between their alpha-carbons was less than 1.2 times the native contacting distance r_0ij. Simulations were run using constant temperature Langevin dynamics and total system momentum was kept constant using a Berendsen thermostat.⁴²

Local structures were constrained to native using RBD. The total translational force for each rigid body was taken as the sum over all individual forces for constrained residues 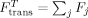. Similarly, the total rotational force on the rigid body was the sum of all the individual torques 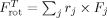. At each simulation step, forces were computed the same way for all residues regardless of whether they were constrained or not using the derivative of the Gō energy function. Forces were then rigidified for the constrained region using the equations shown above. Rigid body momentum and position were updated and stored separately. Using a sufficiently small time step ensures that bond stretching is minimal between constrained and unconstrained portions of the chain.

To demonstrate that constraining local sequence windows can increase the folding rate (shown by a decrease in folding time) compared with unconstrained sequences, constant temperature simulations were run at the transition temperature identified in unconstrained simulations. Transition temperatures are located by running long simulations and identifying the temperature at which structures are 50% folded/unfolded (Fig. 6). Although the transition temperature in constrained simulations may be different from unconstrained, it is still consistent with the goal of studying the effects of constraining local structure on the rate of folding. Median first passage studies were conducted for all 9 residue sliding windows along the length of the sequence by constraining the local sequence window to its native structure. For each constrained window, 100 folding simulations were started from native and unfolded at high temperature to generate uncorrelated initial structures. Simulations were then jumped to the transition temperature. Configurations were considered folded and simulations stopped if at any time Q was 0.85 or greater.

Figure 6.

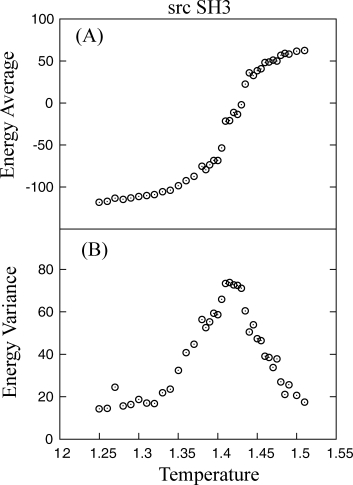
(A) Melting curve for src SH3 constant temperature simulations is shown. (B) The transition temperature is located at the peak in energy variance (1.415). At the transition temperature, Q-values between 0.3 and 0.7 were observed only transiently, indicating 2-state behavior.

Glossary

Abbreviations:

CI-2

Chymotrypsin Inhibitor 2

RBD

rigid body dynamics

TSE

transition state ensemble

Z & A

zipping and assembly.