Modulating repeat protein stability: The effect of individual helix stability on the collective behavior of the ensemble

Abstract

Repeat proteins are tandem arrays of a small structural motif, in which tertiary structure is stabilized by interactions within a repeat and between neighboring repeats. Several studies have shown that this modular structure is manifest in modular thermodynamic properties. Specifically, the global stability of a repeat protein can be described by simple linear models, considering only two parameters: the stability of the individual repeated units (H) and the coupling interaction between the units (J). If the repeat units are identical, single values of H and J, together with the number of repeated units, is sufficient to completely describe the thermodynamic behavior of any protein within a series. In this work, we demonstrate how the global stability of a repeat protein can be changed, in a predictable fashion, by modifying only the H parameter. Taking a previously characterized series of consensus tetratricopeptide repeats (TPR) (CTPRa) proteins, we introduced mutations into the basic repeating unit, such that the stability of the individual repeat unit was increased, but its interaction with neighboring units was unchanged. In other words, we increased H but kept J constant. We demonstrated that the denaturation curves for a series of such repeat proteins can be fit and additional curves can be predicted by the one-dimensional Ising model in which only H has changed from the original fit for the CTPRa series. Our results show that we can significantly increase the stability of a repeat protein by rationally increasing the stability of the units (H), whereas the interaction between repeats (J) remains unchanged.

Introduction

Repeat proteins are composed of tandem arrays of a small structural unit of defined secondary structure, which can be alpha helical, beta strand, or a mixture of the two.^1,2 The length of the individual repeat varies between 18 and 47 amino acids among different repeat protein families.^3,4 Two of the most abundant and well-studied classes of repeat proteins are tetratricopeptide repeats (TPR) and ankyrin repeats (ANK).^5,6 A defining feature of all classes of repeat proteins is that each repeat interacts with only its two nearest-neighbor repeats. There are no long-range interactions. As a consequence, repeat proteins tend to be linear, modular, extended structures. Thus, repeat proteins present a simple system in which to study protein folding, and allow a dissection of the contribution to the folding free energy of each structural element.^6–8

Previous studies have shown that the modular structure of repeat proteins translates into modular thermodynamics.⁹ For different types of repeat proteins, it has been experimentally demonstrated that it is reasonable to treat repeat proteins as linear polymers, where each monomer unit is a repeat.^10–12

Nearest-neighbor linear models based on the classical Ising model¹³ consider only two possible states: folded or unfolded and the interaction between neighboring units. Zimm and Bragg successfully described the helix-coil transition for peptides with a formalism based on the Ising model.¹⁴

The most simplified approach to test the modular nature of the repeat protein thermodynamics is the application of homopolymeric linear models for the description of their folding/unfolding transitions. These models can be appropriate for consensus repeat proteins, composed of repeat units identical in sequence.

We have previously shown that the behavior of a series of designed, consensus TPR proteins is well described by a one-dimensional (1D) Ising model.^6,11,15,16 Specifically, we created a series of consensus proteins with different numbers of tandem repeats (CTPRa2 to CTPRa20) of an identical TPR unit.^15,17,18 The thermal and chemical denaturation behavior of this entire series is well described by a 1D Ising model in which a single value of H for the intrinsic stability of each repeat, a single value of J for the coupling energy of two adjacent repeats and N the number of tandem repeats are the only variables.

It follows that one should be able to rationally modify the properties of the array, that is, the thermodynamic behavior of the proteins by changing H, J, or N. We have already demonstrated the predictable dependence of array stability (midpoint and sharpness of the denaturation transition) on N.^11,15 Here, we show how the stability can be changed, in a predictable fashion, by varying H.

Our design goal was to change the value of H without simultaneously changing the value of J. In practice, this means mutating only residues that are on the solvent exposed surface, and which do not interact with buried residues. Although one can envision designs that either decrease or increase the value of H, we considered it desirable to use exclusively designs, which increase stability, so that the structure of the protein is not compromised.

H corresponds to the intrinsic stability of a single repeat unit. Because the TPR repeat is virtually entirely α-helical, we can make use of the vast amount of data on “intrinsic helix propensity,” derived from experimental studies of short peptides.¹⁹ In addition, the stabilizing effect of i – i + 4 salt bridges in alpha helices is well documented,^20–22 and we can use such information in our designs. Such data is collated in the program AGADIR, an algorithm for the prediction of α-helical contents based on the helix-coil transition theory and using values based on experimental determinations of helical contents for peptides.^23,24

We were able to make such designs and to show that when repeats with redesigned helices were incorporated into tandem arrays, the thermodynamic behavior of the protein was predictable, with J kept the same as in previous designs, N indicating the number of repeats and H as the only variable.

Results and Discussion

The design of proteins in which H is changed but J is not was based the following criteria: (1) redesign the helices to increase H, rather than decrease H; (2) change only solvent-exposed residues; (3) change residues that are located in helices, not in turns; (4) change residues within the helices that have low helix propensity;¹⁹ and (5) make changes at positions where a substitution to Alanine (highest helix propensity residue) would be conservative based on amino acid frequency analysis of all TPR sequences. Examination of the sequence and structure of the CTPR repeat allowed us to identify several positions that satisfied these criteria.

Position 8 in helix A of all TPR sequences is highly conserved; Gly is the most common residue, then Ala (Fig. 1).¹⁷ This residue is partially solvent exposed (Fig. 1), so it is reasonable to change from Gly to Ala to increase intrinsic helix propensity without affecting the coupling between adjacent repeats.

Figure 1.

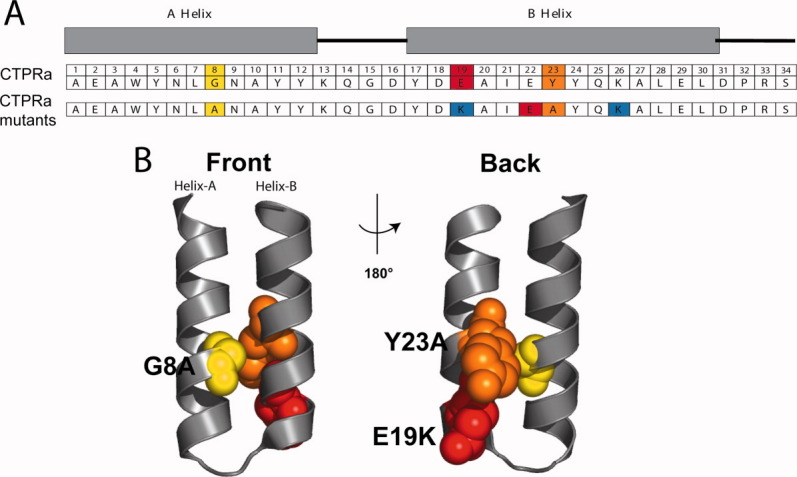
(A) A schematic of the CTPRa unit sequences indicating the amino acid positions in a TPR repeat and nomenclature of the helices. The residue identity at each position corresponds to the TPR consensus sequence (CTPRa).^9,11 The residues that are mutated in this work are highlighted and the identity of the mutated residues is shown in the lower row (G8A in yellow; E19K in red; and Y23A in orange). The i – i + 3 and i − i + 4 charge-charge interaction network introduced by the E19K mutation is shown below being the negatively charged residues colored in red and the positively charged colored in blue. (B) Ribbon representation of the structure of the parent protein, CTPRa3 (PDB ID: 1na0) depicting in space filling representation the three residues that were mutated (G8 colored in yellow, E19 colored in red, and Y23 colored in orange). The structure on the right is rotated 180° around the vertical axis relative to the structure on the left.

Position 23 in helix B of all TPR sequences is also conserved; Tyr is the most common residue based on global propensity (Fig. 1),¹⁷ but when a straight conservation analysis is applied Ala is the residue that shows maximum frequency at this position.²⁵ Mutation of the solvent exposed Try 23 to Ala should increase the intrinsic helix propensity without compromising the TPR structure.¹⁹

We used the program AGADIR^23,24 to predict the helical content corresponding to each helix (A or B helix) and the effect of the proposed mutations on this helical content. The relative helical content calculated by AGADIR for the A and B helices of the consensus TPR repeat are 0.20 and 2.23, respectively. The Gly8Ala (G8A) mutation in helix A is predicted to increase the helical content from 0.20 to 0.73 and the Tyr23Ala (Y23A) in helix B, is predicted to increase the helical content from 2.23 to 6.14. Although the AGADIR calculations pertain to monomeric helical peptides, it is appropriate to apply them to assess the effect of mutations on the stability of helices in a TPR repeat, because we are considering exclusively surface-exposed residues but only in a qualitative not a quantitative fashion.

'In previous studies, we have shown that the back/convex face of CTPR3 can be redesigned to introduce a network of complementary charge–charge interactions, which significantly stabilize the protein.²⁶ Of relevance for this study is that substituting a negatively charged residue (E) for a positive charged residue (K) at position 19, results in an increase in stability. Introducing the E19K mutation should, therefore, provide another route by which to increase H.

The genes encoding three different CTPRa2 proteins with the appropriate mutations were synthesized. We chose CTPRa2 as the “host” protein, because it is the smallest fully folded CTPR protein.¹⁷ The three CTPRa2 proteins generated are: CTPRa2-G8A, CTPRa2-Y23A, and CTPRa2-E19K (Fig. 2). Each of these proteins carries the indicated point mutation in each of the two tandem repeats.

Figure 2.

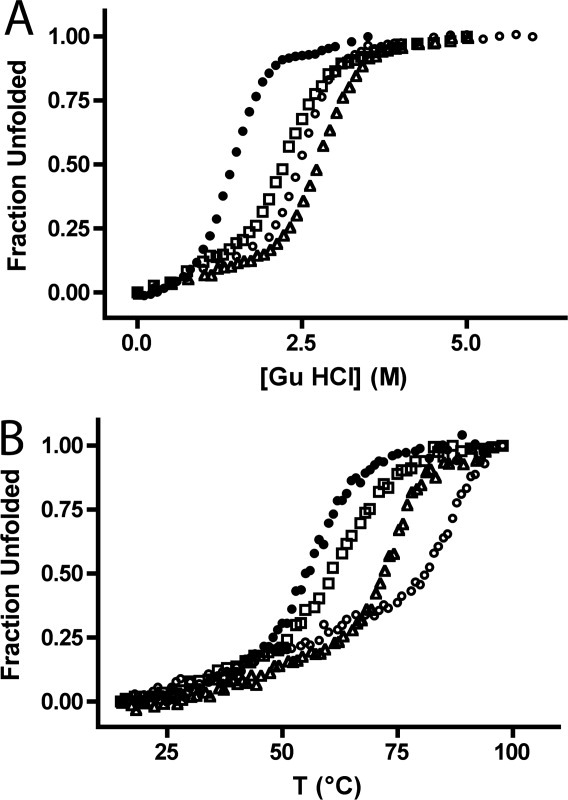
Thermodynamic stability of CTPRa2 variants. Chemical (A) and thermal (B) denaturation curves of CTPRa2 variants: CTPRa2 (filled circles), CTPRa2-G8A (empty squares), CTPRa2-Y23A (empty triangles), and CTPRa2-E19K (empty circles). The chemical denaturation studies (A) were performed by titrating a solution at 3 μM protein concentration in 50 mM phosphate pH 6.5, 150 mM NaCl and 7M GuHCl into an identical protein solution with 0M GuHCl. Thermal denaturation (B) was monitored at 12 μM protein concentration following the ellipticity at 222 nm from 15 to 95°C in 1°C steps. Only the “ramp-up” curves are displayed in the figure. The “ramp-down” curves were recorded and all the thermal denaturation curves displayed 85 to 95% reversibility (data not shown).

The stability of each CTPRa2 variant was assessed using thermal and chemical denaturation, monitoring the transition by circular dichroism (CD) (Fig. 2). Both datasets indicate that all three CTPRa2 variants are significantly more stable than the original CTPRa2. We also compared the CD wavelength scans of CTPRa2 with the three redesigned proteins. The CD spectra of CTPRa2-Y23A and CTPRa2-E19K were essentially identical to that of the parent CTPRa2. Unexpectedly, the spectrum of CTPRa2-G8A was noticeably different from the spectrum of the parent CTPRa2 protein (data not shown). Because the intention of our designs was to not perturb protein structure, we did not continue our studies with this variant.

Having established that two of the mutations do not perturb the structure, and that they increase the stability of the proteins, we went forward to characterize their thermodynamics in greater detail. Specifically, we investigated if the increase in stability that they exhibit could indeed be accounted for solely by a change in the intrinsic stability (H).

To perform a reliable fit of denaturation data to the 1D Ising model, a minimum of three proteins with different numbers of tandem repeats of the same TPR unit are required. We, therefore, created two sets of proteins with 2, 3, and 4 identical repeats of either CTPRa-Y23A or CTPRa-E19K and assessed their stability by both chemical and thermal denaturation, monitored by CD. For CTPRa-E19K series the proteins with 3 and 4 repeats were not fully denatured at 98°C (data not shown), therefore, we could not obtain the full unfolding dataset by thermal denaturation. For all proteins, therefore, we only present chemical denaturation data from this point onward.

Figure 3 shows chemical denaturation curves for the parent proteins CTPRa2, CTPRa3, and CTPRa4, and these same proteins carrying the mutations indicated in each repeat: CTPRa2-Y23A, CTPRa3-Y23A and CTPRa4-Y23A; CTPRa2-E19K, CTPRa3-E19K, and CTPRa4-E19K. The data for each set of three proteins were globally fit to the 1D-Ising model.¹¹ The 1D Ising model describes and predicts the folding/unfolding transition of these TPR proteins in terms of H and J. H is the intrinsic folding energy of one repeat unit, given by H = m₁(x−x_c), where x is the denaturant concentration, x_c represents the denaturant concentration at the transition midpoint, and m₁, assumed independent of x, is analogous to the m-value (slope of the plot of folding energy vs. denaturant concentration). J is the coupling energy between nearest neighboring repeats. The free energy of folding for a TPR with N repeats is given by:

Figure 3.

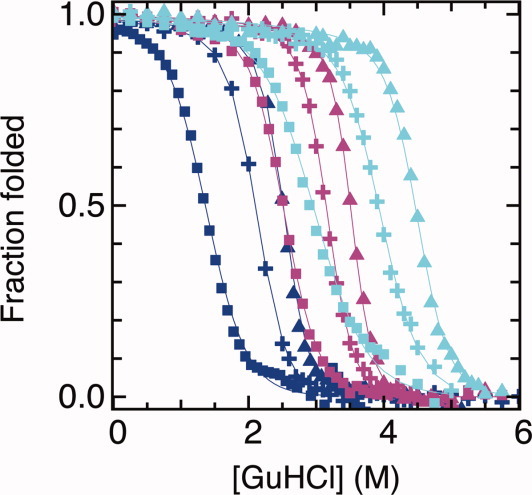
Thermodynamic stability of the parent and two redesigned CTPRa2, 3, 4 series and the fit to the 1D Ising model. The fraction unfolded (monitored by CD) is plotted versus the concentration of GuHCl for CTPRa2, CTPRa3 and CTPRa4 (dark blue); CTPRa2-E19K, CTPRa3-E19K and CTPRa4-E19K (magenta); and CTPRa2-Y23A, CTPRa3-Y23A and CTPRa4-Y23A (cyan) are shown in squares, crosses, or triangles for proteins in each series with two, three, or four repeats. The best fit of the data to the Ising model is shown in solid lines of corresponding color. The 1D-Ising model parameters for the fit are: J = 2.3 is constant value for all the curves in the plot, x_c = 3.79 ± 0.01 and m₁ = 0.37 ± 0.01 for CTPRa series, x_c = 6.14 ± 0.01 and m₁ = 0.28 ± 0.01 for Y23A series, and x_c = 4.61 ± 0.02 and m₁ = 0.42 ± 0.01 for E19K series. The goodness-of-fit parameter χ² obtained was 0.0005924 for CTPRa series, 0.0003965 for CTPRa-Y23A series, and 0.0003224 for CTPRa-E19K series. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

When the coupling constant is held constant at the value that well describes the parent, CTPRa, series (J = 2.3), and x_c and m₁ are allowed to vary, good fits to the data are obtained for all three series of proteins (Fig. 3). The values obtained from the fit are the following: x_c = 3.79 ± 0.01 and m₁ = 0.37 ± 0.01 for CTPRa, x_c = 6.14 ± 0.01 and m₁ = 0.28 ± 0.01 for Y23A, and x_c = 4.61 ± 0.02 and m₁ = 0.42 ± 0.01 for E19K. Therefore, the increased in stability can be accounted by the change in intrinsic stability (H = x_c × m₁; H = 1.40 kcal mol⁻¹ for CTPRa, 1.71 kcal mol⁻¹ for Y23A, and 1.93 kcal mol⁻¹ for E19K) with J, the coupling energy, held constant.

Conclusions

We have demonstrated that simple design principles can be used to increase protein stability in a defined fashion. Specifically, our goal was to change the thermodynamic profile of a repeat protein by increasing the stability of the individual repeat elements without changing the interrepeat interaction energy. In the nomenclature of the Ising model, we aimed to change H (intrinsic stability) while keeping J (coupling energy) constant. We tested our designs by creating a sets of proteins with different repeat units and tracked their behavior by measuring denaturation curves and fitting to the Ising model. Their increased stability, and change in thermodynamic profile can be fully described by the increase in stability of the helical repeat unit, with no change in the interrepeat interaction energy. In future studies, it may be of interest to study the effects of such mutations on protein folding kinetics.

In summary, a homopolymer model well describes the modular stability of repeat proteins, and repeat unit stability and interrepeat interactions can be decoupled and experimentally modified independently.

Materials and Methods

Molecular biology and cloning

Single point mutations, G8A, E19K, and Y23A were introduced independently in the CTPRa1 gene cloned into the pProEX-HTb vector (Invitrogen, Carlsbad, CA)²⁷ using the Quick-change Site-directed mutagenesis kit (Stratagen, La Jolla, CA). Clones were sequenced to confirm the mutations.

The series of CTPRa mutant genes with two, three, and four repeats were generated from the CTPRa1 mutated gene comprised of one repeat. A deoxyribonucleic acid (DNA) fragment encoding one TPR repeat with the desired mutation is extracted by digestion with BamHI and BglII restriction enzymes of CTPRa1 encoding plasmid. The digestion with BamHI and BglII generates compatible sticky ends. The gene encoding CTPRa2 was created by ligation of the one-repeat fragment into the pPROEX-HTb vector containing the CTPRa1 gene singly digested with BamHI.¹⁵ The orientation of the added one-repeat fragment after ligation was verified by sequencing. In the same manner, by successive rounds of digestion and ligation steps were generated the genes encoding the CTPRa3 and CTPRa4 proteins.

Protein purification

CTPRa proteins were over-expressed in Escherichia coli BL21(DE3) cells. An overnight saturated cell culture was diluted and grown to an OD₆₀₀ = 0.6–0.8 at 37°C and induced with 0.6 mM IPTG and grown for 5 h at 30°C. CTPRa mutant proteins were all purified as Hig-tagged fusions following standard protocols using Nickel-nitrilotriacetic acid (Ni-NTA) affinity chromatography as described before.^18,26 The his-tag was cleaved by Tabacco Etch Virus (TEV) protease digestion (Invitrogen, Carlsbad, CA) and the His-tag and the tagged protease removed by a second Ni-NTA column. Protein concentration was estimated based on their extinction coefficient calculated from their amino acid composition. Purified proteins were stored frozen at −80°C.

Circular Dichroism unfolding measurements

CD experiments were performed using an AVIV Model 215 CD spectophotometer (AVIV Instruments, Lakewood, NJ) in 150 mM NaCl, phosphate 50 mM pH 6.8 buffer at 25°C.

Chemical denaturations of CTPRa proteins with GuHCl were acquired using an automatic titrator (Microlab 500) by monitoring the ellipticity at 222 nm at different GuHCl concentrations. The equilibrium denaturation studies were performed by preparing two stock solutions at 3 μM protein concentration in 150 mM NaCl, phosphate 50 mM pH 6.8 buffer with 0 or 7M GuHCl. After each CD measurement, the titration apparatus removed a set volume of solution from the cuvette and injected an equivalent volume of the protein solution at 7M GuHCl, thus the protein concentration was kept constant during the course of the experiment. At each titration point, the concentration of GuHCl was increased by 0.1M and the ellipticity at 222 nm was monitored after 30-min equilibration time. Measurements were performed in a 1-cm path-length cuvette with constant stirring at 25°C. Under our experimental conditions, we always obtain a very good reproducibility of the denaturation curves. The curves obtained from independent denaturation experiments of the same protein overlay perfectly (data not shown).

Thermal denaturations of CTPRa proteins were monitored at 12 μM protein concentration following the ellipticity at 222 nm from 15 to 95°C and in the reverse direction from 95 to 15°C in a 0.1-cm pathlength cuvette. The temperature ramp was performed in 1°C steps with an equilibration time at each temperature of 1 min.

Application of the 1D Ising model

The 1D Ising model was applied to describe the stability of CTPRa protein series as described before.^11,15 The model considers each helix as an individual Ising spin, with +1 and −1 spins corresponding to the folded and unfolded states, respectively. The fraction folded corresponds to the experimental data obtained from the circular dichroism denaturation curves. The model fits all the data within a complete CTPRa series considering only three variable parameters J, x_c, and m₁. The unfolding/folding behavior of all the CTPRs in a series is described by the same J, x_c, and m₁ values and it is only distinguished by the change on N (number of repeats).