Assessment of flexible backbone protein design methods for sequence library prediction in the therapeutic antibody Herceptin–HER2 interface

Abstract

Computational protein design methods can complement experimental screening and selection techniques by predicting libraries of low-energy sequences compatible with a desired structure and function. Incorporating backbone flexibility in computational design allows conformational adjustments that should broaden the range of predicted low-energy sequences. Here, we evaluate computational predictions of sequence libraries from different protocols for modeling backbone flexibility using the complex between the therapeutic antibody Herceptin and its target human epidermal growth factor receptor 2 (HER2) as a model system. Within the program RosettaDesign, three methods are compared: The first two use ensembles of structures generated by Monte Carlo protocols for near-native conformational sampling: kinematic closure (KIC) and backrub, and the third method uses snapshots from molecular dynamics (MD) simulations. KIC or backrub methods were better able to identify the amino acid residues experimentally observed by phage display in the Herceptin–HER2 interface than MD snapshots, which generated much larger conformational and sequence diversity. KIC and backrub, as well as fixed backbone simulations, captured the key mutation Asp98Trp in Herceptin, which leads to a further threefold affinity improvement of the already subnanomolar parental Herceptin-HER2 interface. Modeling subtle backbone conformational changes may assist in the design of sequence libraries for improving the affinity of antibody–antigen interfaces and could be suitable for other protein complexes for which structural information is available.

Introduction

Computational design methods aim to predict low-energy sequences compatible with a given structure or interaction^1,2 and can provide information on the diversity of sequences tolerated in proteins and protein–protein interfaces.^3–5 In particular, for the latter application, incorporating backbone flexibility in design simulations⁶ has been shown to expand the predicted sequence diversity^7–12 by capturing amino acid substitutions that require small backbone adjustments.^13–15 Recently, our laboratory developed a computational design method that incorporates backbone flexibility by generating near-native conformational ensembles.^16,17 When applied to the human growth hormone in complex with its receptor, the computational predictions were found to be in good qualitative agreement with the tolerated sequence space observed experimentally.¹⁶

Here, we use a similar computational strategy that first generates an ensemble of backbone conformations and then searches the tolerated sequence space, but we employ it to investigate two new aspects: first, how do different protocols for modeling conformational ensembles compare in terms of correctly identifying functional protein sequences? While different flexible backbone design methods have been applied to a variety of applications,^{7,8,11,16,18–23} no direct comparison has been made within the context of the same general design protocol on the same experimental dataset. Second, we test whether flexible backbone computational design is useful to predict sequence libraries to increase the affinity of an antibody–antigen interface, an important application given the considerable success of therapeutic antibodies.²⁴

To address the first question, we compare computational design predictions obtained using three different protocols to generate conformational ensembles, in each case employing RosettaDesign^16,19 in the subsequent sequence space simulations. The first two methods use Monte Carlo sampling strategies to generate conformations with small deviations from the native input crystal structures. The “backrub” protocol models subtle conformational changes observed in high-resolution structures by considering local backbone rotations about axes between Cα atoms of protein segments.^15,25 The “kinematic closure (KIC) refinement” protocol iterates backbone moves on protein segments that adjust all torsional degrees of freedom together with N–Cα–C bond angles.²⁶ In this work, a new KIC option is used to sample near-native backbone conformations (see Methods section). The third method uses snapshots from a molecular dynamics (MD) simulation for modeling backbone flexibility, as also done in Ref. 23.

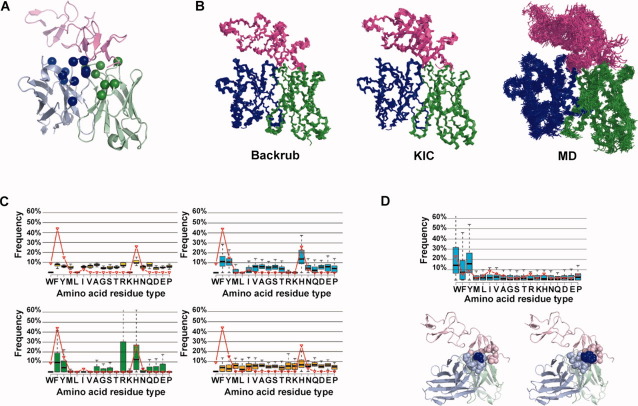
To address the second question, we use the therapeutic antibody Herceptin (trastuzumab) bound to the proto-oncogene human epidermal growth factor receptor 2 (HER2) as a model system, because an experimental analysis of the tolerated amino acid mutations at the interface of this complex [Fig. 1(A) and Supporting Information Table S1] by phage display is available.²⁷ In this manner, we can directly compare experimentally and computationally selected sequences.

Figure 1.

Comparison of flexible backbone protein design methods to predict the sequence tolerance in the Herceptin antibody interface with its target HER2. (A) Structure of the Herceptin antibody–HER2 complex (pink: HER2 C-terminal domain; green: antibody Fv light chain; blue: antibody Fv heavy chain; spheres: Cα atoms of the residues chosen for design). (B) Conformational ensembles generated by the backrub and KIC methods and MD snapshots. For clarity, only 20 snapshots were included in the MD ensemble depicted (100 ensemble members were used in simulations for all methods). (C) Comparison of the amino acid tolerance profile determined experimentally by phage display²⁷ (red lines, library B) and predicted computationally using the different design protocols for position H91V_L; shown are boxplots for the fixed backbone (yellow), backrub (cyan), KIC (green), and MD (orange) methods. (D) Upper: Comparison of the amino acid tolerance profile determined experimentally (red lines) and predicted computationally (boxplots) using backrub for the position D98V_H; Lower: Mutation of residue D98V_H on the Herceptin heavy chain from Asp to Trp likely increases packing interactions in the interface with HER2. Left panel: native structure of the Herceptin-HER2 complex (PDB 1nz8). Right panel: structural model of the lowest energy designed sequence for the top scoring backrub conformer. Residues located within 6 Å from the residue at position 98 (dark blue) are shown as spheres. Figures were made using Pymol http://www.pymol.org/.

Results and Discussion

The computational protocol to predict sequences tolerated at the interface of protein complexes¹⁶ consists of two stages: (1) model protein conformational variability by generating an ensemble of backbone conformations over the entire protein–protein complex and (2) search sequence space using fixed backbone design on each ensemble member to generate a “tolerance profile,” which lists the predicted amino acid residue types for each of the designed positions. Figure 1(B) depicts the conformational diversity of ensembles generated using the backrub, KIC refinement, and MD protocols (see Methods section). The first two methods generate near-native ensembles, where the different ensemble members have conformations close to the starting crystal structure, while the ensemble obtained by MD is more diverse (Table I).

Table I.

Comparison of Predictions to Phage Display Data

	Phage display	KIC ensemble	Backrub ensemble	Fixeda backbone	MD ensemble	Nativeb	Naïvec
AFRd	≡1.00	0.69 (0.71)	0.62 (0.69)	0.43 (0.64)	0.22 (0.51)	0.46	0.66
Library Sizee	n.a.	1 × 108 (2 × 108)	7 × 106 (5 × 107)	9 × 105 (1 × 107)	240 (1 × 103)	1	2 × 108
Sensitivity	≡1.00	0.65	0.55	0.43	0.22	0.34	0.64
PPV	≡1.00	0.49	0.49	0.43	0.47	0.82	0.51
Ensemble RMSD [Å]f	n.a.	0.3 (0.1–0.7)	0.3 (0.2–0.4)	0	1.8 (0.9–3.3)	n.a.	n.a.
Missed Positionsg	0	2	3	5	11	3	2

Abbreviations: AFR, average amino acid frequency recovered; KIC, kinematic closure; MD, molecular dynamics; n.a., not applicable; PPV, positive predictive value; RMSD, root mean square deviation.

^aIncluding an initial side chain repacking step.

^bIncluding only the wild-type amino acid present in the starting complex structure.

^cIncluding the wild-type amino acid and chemically similar residues (groups: [D,E,N,Q], [R,K,H], [L,I,V,M], [F,Y,W], [P,A,G], and [S,T] as in Ref. 16).

^dAverage amino acid frequency recovered, as defined in the main text. The numbers in parentheses give AFR values when the wild-type amino acid type is added to the predictions.

^eCalculated for the 17 positions analyzed (for the four positions randomized in two libraries, the average was calculated; cysteine residues are excluded in the simulations; the upper limit for library size is 19¹⁷ ∼ 5 × 10²¹. The numbers in parentheses include the native amino acid residue.

^fMedian pairwise ensemble backbone root mean square deviation (minimum and maximum RMSDs in parentheses).

^gNumber of positions at which none of the amino acids experimentally observed (those with experimental frequency ≥ 10%) were identified computationally in any of the libraries (supporting Information Table S3).

We define an amino acid residue type as predicted to be tolerated at a given position of the Herceptin–HER2 interface if its frequency in the computational tolerance profile is above a cutoff value (an adjustable parameter). Previous work in our laboratory selected a cutoff of 10% for the interface between human growth hormone and its receptor.¹⁶ We used the same value here for the Herceptin–HER2 interface (for assessment of the influence of cutoff values, see Supporting Information text and Table S2). Because we perform design simulations over ensembles of backbones, we obtain distributions of frequencies from these ensembles, which we represent as boxplots [Fig. 1(C)]. We apply the 10% cutoff to the third quartile value of these distributions, as in Ref. 16 (i.e., an amino acid is set to be tolerated if the 75th percentile of the predicted distribution (from the boxplot) is at least 10%; see Methods section for details).

Figure 1(C) shows an example of an amino acid tolerance profile predicted computationally (boxplots) when compared with the tolerance profile obtained by phage display in Ref. 27 (red lines) at one position in the Herceptin–HER2 interface. Boxplots for all positions randomized in each of the libraries for the different protocols are shown in Supporting Information Fig. S1–S4.

To assess the overall agreement between computationally and experimentally selected sequences, we used the following metrics (see Methods section for details).

Average amino acid frequency recovered (AFR)

Experimental amino acid frequencies from phage display recovered by considering all computationally predicted amino acid types at a sequence position, averaged over all 17 randomized positions.

Sensitivity (true positive rate)

Ratio of the number of computationally predicted amino acid types that are present in the phage display profile (with ≥10% frequency) to the total number of amino acid types observed in the phage display profile.

Positive predictive value

Ratio of the number of computationally predicted amino acid types that are present in the phage display profile (with ≥10% frequency) to the total number of amino acid types predicted computationally.

The protocols using near-native conformational ensembles generated by the KIC and backrub methods recover a considerable fraction [69% and 62% average amino acid frequency recovered (AFR), respectively] of the tolerated sequence space observed experimentally for the Herceptin–HER2 complex (Table I). Supporting Information Figure S5 depicts the conformational diversity modeled for the antibody binding site loops in the near-native ensembles. When only the crystal structure backbone was used for design simulations (fixed backbone protocol), the sensitivity was reduced (see below). Using MD snapshots, which have greater conformational diversity [Fig. 1(B)], led to lower sensitivity and AFR. In this case, the predicted profiles for many of the designed positions are flat (frequencies of nearly all amino acids are less than 10%) with no particular amino acids preferred (Supporting Information Fig. S4). Incorporation of appropriate filters improved the performance of the MD method (see Supporting Information text for further details). Although not tested here, it is possible that using restraints in the MD simulations to reduce modeled conformational diversity would improve design predictions. For a list of all amino acids predicted using the different computational approaches and experimentally observed at each position by phage display in Ref. 27, see Supporting Information Table S3.

We also compared the design predictions to the divergence from the native sequence, and a control model (“naïve” prediction) considering only chemically similar amino acid substitutions (Table I). As the affinity of the starting Herceptin sequence for HER2 is already high (K_D = 0.35nM²⁷), the experimentally observed sequence divergence from the starting amino acid is modest: in 10 of 17 randomized positions, wild-type amino acid residues were strongly preferred (frequency ≥ 45%²⁷). Employing the KIC or backrub protocols predicted sequence profiles that contained the wild-type amino acid in 10 or 9 of these cases, respectively (Supporting Information Table S3). In contrast, the fixed backbone protocol predicted wild-type residues in fewer (seven) of these positions. This somewhat counterintuitive observation could be explained by the limitations of the discrete rotamer libraries used for computational design: small adjustments to the backbone may be required to select native-like rotamers that are missed when using the crystallographic backbone and excluding the native side chain coordinates from the simulation. To test this idea, we performed fixed backbone design simulations that included the native side chain conformations. As expected, the wild-type residue is now captured in 9 of 10 of the positions above and the AFR value improves to 0.61 from 0.43 (Supporting Information Table S4).

The “naïve” control model performs equally well to the ensemble simulations for many positions (Table I). However, phage display²⁷ identified some positions with preferences for amino acids with significantly different size and chemical properties from the Herceptin starting sequence (Supporting Information Table S3, positions 30V_L, 94V_L, 98V_H, and 102V_H). The most prominent case is the Herceptin heavy chain position 98, in which the wild-type aspartate residue was replaced by a tryptophan in 23% of phage display selected sequences.²⁷ Moreover, a single Asp98Trp mutation led to a threefold improvement in Herceptin affinity for HER2. This substitution was successfully captured in the design simulations when the backbone was retained fixed or subtle backbone conformational changes were introduced by the KIC or backrub methods (Supporting Information Table S3). A predicted structural model of the Asp98Trp mutation suggests that the increase in binding affinity is likely a result of improved packing interactions across the interface [Fig. 1(D)]. This mutation would not be detected when considering only conservative substitutions (as in the naïve model). Interestingly, MD was the only method that captured another non-conservative substitution observed in the dataset: a replacement of the wild-type threonine at position 94 in the light chain with a tryptophan (Supporting Information Fig. S6). Thus, in some cases ensembles with larger conformational variability may be required to capture tolerated mutations. For the other two positions (30V_L and 102V_H), none of the computational methods captured observed nonconservative substitutions. It should be noted that water molecules are not explicitly represented in the RosettaDesign method; thus, small residues forming water-mediated hydrogen bonds could be missed, with larger amino acid residues being selected instead. This may be the case for the asparagine at light chain position 30 (Supporting Information Table S3).

Conclusions

We have compared computational design predictions for the binding site of a high-affinity therapeutic antibody using different protocols for modeling backbone conformational flexibility. We found that the KIC refinement and backrub protocols, which are fast and introduce subtle backbone changes, capture a considerable fraction of the sequence diversity experimentally observed by phage display (Table I). Furthermore, these methods lead to better predictions than those obtained by allowing larger backbone conformational changes by MD. The fixed and flexible backbone Monte Carlo methods were also able to predict the key Asp98Trp substitution that leads to a threefold improvement in the already subnanomolar affinity of the Herceptin antibody for HER2.²⁷ Thus, computational design can help to reduce the complexity of experimental libraries and, at the same time, enrich the sequence pools for functional variants.^16,28,29 This strategy could facilitate the engineering of protein variants with new or modified functions, such as improved therapeutic antibodies that bind with higher affinity to their protein target.

Methods

Source of experimental sequence tolerance data

Experimental sequence tolerance data for the Herceptin–HER2 interface were taken from Ref. 27. The authors screened antibody positions [Fig. 1(A)] in groups of five to seven positions, using four different phage display libraries (Supporting Information Table S1). Note that some positions were randomized in more than one library.

Generation of backbone ensembles

Rosetta command lines for ensemble generation methods are given in the Supporting Information text.

Backrub protocol

A backrub move²⁵ is a local backbone motion, that consists of rotating a peptide segment (up to 40°) around the axis defined by the Cα atoms of the segment's first and last residues; the rotation is followed by optimization of the positions of the branching Cβ and hydrogen atoms.¹⁵ Within Rosetta, backrub moves are iterated with side chain rotamer changes in a Monte Carlo protocol, as described in Ref. 15. As an initial equilibration step, a backrub Monte Carlo simulation for the starting crystal structure of the Herceptin–HER2 complex (PDB code 1n8z) was performed over all sequence positions (excluding disulfides) at kT = 0.1 for 10,000 steps with a maximum segment length of 12, as described in Ref. 30. The lowest energy structure from this simulation was used as the starting conformation for 100 randomly seeded backrub simulations at kT = 0.6 for 10,000 steps, using the full-atom Rosetta scoring function as in Ref. 16. The last structure from each of these simulations was retained. This protocol resulted in an ensemble of 100 structures, with a median pairwise backbone root mean square deviation (RMSD) of 0.3 Å (Table I).

KIC refinement protocol

KIC also samples conformations of protein segments while keeping the two segment endpoint Cα atoms fixed in space.²⁶ A KIC move begins with selection of a random segment in a protein containing at least three and at most 12 residues. The Cα atoms of the first, last, and middle residues of this segment are defined as “pivots.” In the implementation used in this study, torsions around the remaining non-pivot Cα atoms are then sampled from a normal distribution up to three degrees above or below the values before the KIC move (this is termed “vicinity sampling,” which was not used in the original KIC implementation described in Ref. 26 for de novo loop reconstruction) and N–Cα–C bond angles are set to random values within one-half the standard deviation (σ = 2.48°) above and below the mean (110.86°) observed in ultrahigh-resolution crystal structures (<1.0 Å resolution) in the PDB. This step perturbs the segment and breaks its continuity. KIC then determines the possible rotations about the pivot phi/psi torsions that restore the continuity of the segment and place it into a new conformation.²⁶

For generating a near-native conformational ensemble, we used the refinement mode (high-resolution stage) of the KIC protocol after an initial step of repacking all side chains (Metropolis Monte Carlo simulated annealing of rotameric conformations excluding the native side chain coordinates), as described in Ref. 26. Different from the original protocol, the entire complex (and not just a loop region) was considered for KIC moves. A total of 200 Monte Carlo iterations within the KIC refinement procedure were applied, consisting of: (1) execution of a KIC move (as above) on randomly selected overlapping subsegments of the complex, with a constant temperature equal to 1.2 kT and (2) side chain repacking (every 20 steps) and rotamer trials (each side-chain is set to the most favorable rotamer conformation, while all other side chains remain fixed, until the energies converge), each within 10 Å of the moved segment. Rotamer trials are followed by energy minimization using the Davidon–Fletcher–Powell method³¹ on the segment backbone and side chains within 10 Å of the new segment conformation. This procedure resulted in an ensemble of 100 structures, with a median pairwise backbone RMSD of 0.3 Å (Table I).

Molecular dynamics

A MD simulation was performed for 10 ns at 300 K using the GROMACS package v3.3³² with the GROMOS96 force field.³³ A leap-frog algorithm was used for integrating the equations of motion. The Protein Local Optimization Program³⁴ was used to build the missing segment formed by residues 581–590 in the HER2 protein. For segment building, only heavy atoms of flanking residues (580 and 591) were allowed to move, but hydrogen optimization was performed for all residues in the complex. Then, the complex was placed in an octahedron box filled with simple point charge water molecules.³⁵ The minimum distance between the protein complex and the wall of the unit cell was set to 0.1 nm. Two positive counter ions were incorporated for a zero net charge of the system. The SHAKE algorithm,³⁶ with the default tolerance value (10⁻⁴), was used to constrain all bonds involving hydrogen atoms. Periodic boundary conditions were applied to avoid edge effects. Long-range electrostatic interactions were calculated using particle-mesh Ewald. The temperature was maintained constant by coupling the protein and solvent to an external heat bath with a Berendsen thermostat³⁷ at 300 K. The pressure was coupled to an isotropic pressure bath (1 bar). Following steepest descent minimization, the system was heated up to 300 K during 50 ps, then the pressure and temperature were kept constant for 25 ps and finally the system was equilibrated for 125 ps. Production runs were carried out for 10 ns with a 2 fs time step. The MD trajectory is shown in Supporting Information Figure S6. Conformational ensembles were generated by writing out frames every 125 ps during the last 5 ns of the MD simulation. Finally, each of the retained 100 structures was repacked (Metropolis Monte Carlo simulated annealing of rotameric conformations) using Rosetta to equilibrate the system to the Rosetta force field used in the design simulations. The simulation resulted in an ensemble of 100 structures with a median pairwise backbone RMSD of 1.8 Å (Table I).

Generation of sequence tolerance profiles

Predicted sequence tolerance profiles for the Herceptin–HER2 interface were produced from computational design simulations with Rosetta as in Ref. 16, except that here the sequences were propagated for 10 generations by the genetic algorithm rather than 5. Computational design runs were performed on four different groups representing the four experimental libraries described in Ref. 27.

We searched the tolerated sequence space by performing a fixed backbone design simulation for each of the conformers of a structural ensemble. As described in Ref. 16, all sampled sequences with binding and folding scores within 1% of the score of the input ensemble member with the starting sequence were recorded. The frequencies of each amino acid (excluding cysteine, which was never allowed to be sampled) were then obtained at each designed position for each of the ensemble structures to generate a position-specific tolerance profile. This step ignores possible experimental or computational covariations between positions. Then, the sequence profiles for all ensemble structures were combined, and the distributions of frequency values over the ensemble members were represented as boxplots. We defined an amino acid type as “computationally predicted” when it had a third quartile frequency value ≥10% obtained from the boxplots.

Performance metrics for comparing computational and experimental sequence tolerance

Assignment of frequencies to each of the amino acid types predicted computationally

For each computationally predicted amino acid type at each position, the experimental frequency of the amino acid type was retrieved from the phage display data, as in Ref. 16. These frequency values were added for each position.

Computationally predicted AFR

The frequency values obtained for each of the positions in the computational profiles (as defined above) were summed (for positions occurring in more than one library, the average value of the occurrences was calculated). Then, this sum was divided by 17 (the number of randomized positions) to obtain the AFR.

For calculating the sensitivity and positive predictive value (as defined in the results section), the 10% frequency cutoff was used for both computational and experimental profiles. Thus, an amino acid was considered as “predicted” if its third quartile frequency from the boxplots was ≥10% (as above) and considered as “observed” if its experimental frequency in the phage display data was ≥10%.

Glossary

Abbreviations:

AFR

average amino acid frequency recovered

AUC

area under the ROC curve

Fv

variable region

HER2

human epidermal growth factor receptor 2

KIC

kinematic closure

MD

molecular dynamics

PDB

potein data bank

ROC

receiver–operator curve

RMSD

root mean square deviation

V_L

light chain variable region

V_H

heavy chain variable region.