Summary
In this paper, we propose a multivariate growth curve mixture model that groups subjects based on multiple symptoms measured repeatedly over time. Our model synthesizes features of two models. First, we follow Roy and Lin (2000) in relating the multiple symptoms at each time point to a single latent variable. Second, we use the growth mixture model of Muthén and Shedden (1999) to group subjects based on distinctive longitudinal profiles of this latent variable. The mean growth curve for the latent variable in each class defines that class’s features. For example, a class of “responders” would have a decline in the latent symptom summary variable over time. A Bayesian approach to estimation is employed where the methods of Elliott et al (2005) are extended to simultaneously estimate the posterior distributions of the parameters from the latent variable and growth curve mixture portions of the model. We apply our model to data from a randomized clinical trial evaluating the efficacy of Bacillus Calmette-Guerin (BCG) in treating symptoms of Interstitial Cystitis. In contrast to conventional approaches using a single subjective Global Response Assessment, we use the multivariate symptom data to identify a class of subjects where treatment demonstrates effectiveness. Simulations are used to confirm identifiability results and evaluate the performance of our algorithm. The definitive version of this paper is available at onlinelibrary.wiley.com.
1. Introduction
Interstitial Cystitis (IC) is a chronic syndrome characterized by multiple urinary symptoms in the absence of any identifiable cause. The cause of the disease and effective treatments have both remained elusive (Mayer et al., 2005). Analysis of data from IC studies presents several challenges. First, due to the complex nature of the disease, it is difficult to determine one primary endpoint that would indicate improvement with treatment over time. In the clinical trial that motivated this work, multiple symptoms were recorded at multiple time points, however the primary outcome for the trial was the final Global Response Assessment (GRA), which records how a subject feels overall relative to the beginning of treatment. Thus, the information in each patient’s multiple symptom profiles was ignored in favor of a more subjective outcome for the efficacy analysis.
An additional challenge is the extreme heterogeneity of the population diagnosed as having IC. As is the case with other conditions of unknown etiology (e.g., fibromyalgia, chronic prostatitis/chronic pelvic pain syndrome), heterogeneity of experienced symptoms suggests the possibility of distinct disease subgroups. In the case of IC, there is also pathological evidence that there are different disease processes at work in different individuals and that these different disease processes are associated with different expressed symptoms (Leiby et al., 2007). Consequently, not all subjects diagnosed with IC would be expected to respond to a given treatment. A model that accounts for the full range of symptoms reported over time while grouping subjects based on their reported multivariate symptom profiles would be crucial in identifying clinically important subgroups for further study. Such a model could be useful in identifying subjects for whom certain treatments are effective.
Statistical models for longitudinal studies typically evaluate the behavior of a single continuous outcome over time (e.g., mixed effects models Laird and Ware, 1982). When there are several outcomes of interest measured repeatedly over time, modeling becomes more complicated. Several authors have suggested approaches for jointly modeling multivariate longitudinal profiles through the use of correlated random effects (Shah et al., 1997; Gueorguieva, 2001; Fieuws and Verbeke, 2006). Roy and Lin (2000) proposed a latent variable model to address the situation where the multiple outcomes are not only correlated but may be measuring the same underlying quantity of interest. Their model combines features of the factor analytic model (Bartholomew and Knott, 1999) with the mixed effects model. That is, the multiple manifest variables at each time point are reduced to a single normally-distributed latent variable which is then assumed to follow a mixed effects model. As several authors have noted, both factor analytic models and mixed effects models are types of latent variable models (Muthén and Curran, 1997; Palta and Lin, 1999). In factor analysis, the variance of the latent variable is fixed in order to estimate its coefficients or factor loadings. In mixed effects models, the coefficients of the latent variable are fixed (the random effects design matrix) and the covariance matrix of the random effects is estimated. The Roy and Lin model utilizes both types of latent variables.
Latent variable models using categorical latent variables can be used to estimate unobserved population stratification or clustering. Verbeke and Lesaffre (1996) extended the mixed effects model to allow for finite mixtures of normal distributions for the random effects thus implying a categorical latent variable. Among the most widely used models with categorical latent variables are latent class models (see Clogg, 1995; Garrett and Zeger, 2000) where the focus is to identify the latent groups or classes and predictors of those classes. In the past decade, many researchers have focused on the integration of categorical and continuous latent variable models using categorical latent variables to account for unobserved population heterogeneity while accounting for correlation among observed variables not represented by the latent classes through the use of random effects (Bauer and Curran, 2004). When applied to longitudinal data, these models are often referred to as growth mixture models as they model mixtures of longitudinal trajectories or growth curves. Roeder et al. (1999) used a latent class model to group subjects based on the observed longitudinal trend of a single outcome where conditional on class membership a subject’s observations are assumed to be independent across time. Muthén and Shedden (1999) and Muthén et al. (2002) developed a general framework which allows for correlation among the repeated measurements in addition to that induced by the latent class structure. That is, the continuous outcomes are assumed to follow a mixed effects model conditional on class membership.
Other authors have proposed models for classification of subjects with multivariate longitudinal data. Nagin and Tremblay (2001) developed a model with two sets of latent classes for two longitudinal outcomes. Correlation between the two outcomes is modeled by allowing for correlation between the latent class variables. Elliott et al. (2005) developed a Bayesian growth curve mixture model to combine two items that were measured repeatedly over time where conditional on latent class membership, the items follow independent mixed effects models.
In this paper, we extend recent models for continuous and categorical latent variables to the case of correlated multivariate continuous outcomes measured repeatedly over time. The proposed model incorporates the model of Roy and Lin (2000) into a latent class structure, allowing for model parameters to vary by class, and it extends the model of Muthén and Shedden (1999) to allow for growth mixture modeling of a latent summary variable of multivariate manifest variables. Estimation proceeds using a Bayesian approach adapted from Elliott et al. (2005). Our approach differs from that of Nagin and Tremblay and Elliott et al. in that it allows for correlation among the multiple outcomes conditional on latent class membership. In addition, our focus is on the trajectory of an unobserved underlying variable which we view as the real measure of interest. We apply our model to data from a randomized clinical trial evaluating the efficacy of Bacillus Calmette-Guerin (BCG) in treating symptoms of Interstitial Cystitis. In contrast to conventional approaches using a single subjective GRA, we use the multivariate symptom data to identify a class of subjects where treatment demonstrates effectiveness.
This paper is organized as follows: Section 2 presents the proposed model and describes the method of estimation. Section 3 presents results from application of the proposed model as well as from existing models to data from a randomized trial in IC. Section 4 presents results of a simulation study to assess model identifiability and validate our estimation procedure. Finally, section 5 discusses our results and suggests some extensions for future research.
2. A Multivariate Growth Curve Latent Class Model
In this section, we describe a growth curve mixture model for repeated measurements of multivariate outcomes over time. At each time point, the multivariate outcome is summarized by a single latent variable through an extended factor analytic model. The latent variable is then assumed to follow a mixed effects model to account for within subject correlation of the repeated measures and to describe its behavior over time. The factor analytic and fixed effects parameters are allowed to vary by latent class membership allowing for different trajectories and different relationships among the multivariate outcomes in each class. We implement the model in a Bayesian framework by specifying prior distributions for all parameters and computing the posterior distribution using Markov chain Monte Carlo (MCMC) methods.
2.1. Model Notation
Define Yijm to be the mth variable (m = 1,…,M) measured at the jth time point (j = 1,…,ni) for the ith subject (i = 1,…,N). The Yijm are the manifest or observed outcome data. Let Ci be the latent class membership of subject i with Ci = k if subject i belongs to class k (k = 1,…,K). Conditional on Ci = k, Yijm follows the modified factor analytic model of Roy and Lin such that
| (1) |
where and . Conditional on the latent variable Zij, the M outcomes at each time point are assumed to be independent, and conditional on Zij and bim, the ni repeated measures of the mth outcome are also independent. The outcome-specific intercepts (αmk) and factor loading parameters (λmk) vary by class but are static with respect to time. The factor loading parameters express the strength of association between the latent variable and the manifest variables and are a function of the correlation among the manifest variables.
Conditional on Ci = k, Zij is assumed to follow a mixed effects model:
| (2) |
| (3) |
where is an r × 1 vector of observed covariates for Zij and γk is the mean of ηi, the vector of coefficients. In a typical growth curve model the covariates will include an intercept and polynomials in time and may contain other baseline or time-varying covariates or possibly interaction terms. The vector ai ~ N (0, Ψa) specifies the random effects while fixed effects are specified by setting the appropriate variance components equal to 0. The probability of class membership, πik, follows a reference category multinomial logistic regression model:
| (4) |
where δK ≡ 0 and is a p × 1 vector of observed subject-level covariates.
By assuming that the mean of the vector of coefficients varies by class, we allow for different trajectory shapes for the latent variable. Allowing for different factor loadings in each class admits the possibility that the observed outcomes may be more strongly related to the latent variable in one class than another. For example, it may be that in one class all outcomes have relatively large factor loadings and are thus strongly correlated and equal contributors to the definition of the latent trajectory shape. Another class may have one outcome with a factor loading much larger than the others in which case the variables would be less strongly correlated and only the variable with the large factor loading would contribute to the definition of the latent trajectory.
2.2. Identifiability
As is the case with all latent variable models, not all parameters are simultaneously identifiable, and therefore, the following constraints have been applied. For the loading parameters λmk and outcome-specific intercepts αmk to be identified, we assume , λ1k is constrained to be positive, and the mean of the intercept in the model for Z is fixed at 0. These constraints should provide for identifiability of all remaining parameters provided that the number of manifest variables (M) is 3 or greater. For the case of 2 manifest variables other conditions apply. In a one class model with a random intercept in the model for Z, all parameters should be identified if γ ≠ 0. In our application, this means that the trajectory of the latent symptom variable would not be flat, having nonzero slope. When γ ≠ 0 the factor loading λmk appears in both the mean and variance of the observed data. When γ = 0, the mean of the latent variable Zij is 0, λmk disappears from the mean of Y, and all information about λmk must come from the covariance matrix of Y (see appendix A for a more detailed discussion of this issue). When there are two or more classes the variance components , and Ψa are the same across classes, and the model may still be identified if γk ≠ 0 for some classes. However, if the class with mean zero is also the largest class, there may not be enough information in the covariance matrix to fully identify all variance parameters and computation problems may result. We explore some of these issues further with simulations (see section 4).
2.3. Estimation
The hierarchical nature of latent variable problems suggests a Bayesian approach to estimation which we apply here. MCMC methods including the Gibbs sampler (Gelfand and Smith, 1990; Gelman and Rubin, 1992; Gilks and Wild, 1992) and the Metropolis-Hastings algorithm (Hastings, 1970) can be used to obtain the posterior distribution of the model parameters and the latent variables quite easily. We implement a Gibbs sampler with Metropolis draws where necessary for non-conjugate distributions. The Bayesian approach eliminates the need for numerical integration and provides for more straightforward interval estimation.
When the number of classes (K) is two or greater, informative, proper priors are required for all class-specific parameters (αmk, λmk, γk, and δk) to allow for the possibility of empty classes in the computation of the posterior distribution and to ensure a proper posterior distribution. Following Elliott et al. (2005), we specify data-based priors for αmk, λmk, and γk. The priors are centered at the median posterior estimates ( , and ) for the 1-class (i.e., Roy and Lin) model. The variance of the prior distributions is specified by multiplying the variance of the posterior distribution from the one-class model by the sample size (N) so that with moderate sample sizes the priors are relatively non-informative. For the one-class model, we specified p(α1,…,αM; λ1,…,λM;γ) ∝ 1. For the k-class models we specified the following priors:
where ψαm and ψλm are the variances of the posterior distribution for the appropriate parameter from a one-class model and Ψ0 is a diagonal matrix of variances of the γ parameters from the one-class model. Following Garrett and Zeger (2000), we specify the priors for δk as
when class probability model 4 contains more than an intercept. Otherwise, we place a Dirichlet prior directly on the class probabilities.
To ensure proper posterior distributions, we specify independent, proper non-informative inverse-chi-square (1 df) priors for the variance components of the factor model (1) and an inverse-Wishart prior for the variance of the random effects in 3:
where ν = 1 and S = diag(1).
The posterior distribution of all model parameters is computed via a Gibbs sampler. We view Zi, bi, ai, and Ci as missing data and treat them as additional parameters to be estimated. Each parameter is drawn sequentially from its full conditional distributions:
| (5) |
where Θ = (θ1; θ2,…,θq) is the vector of all model parameters. For the parameters δk, the full conditional distribution does not have a closed form and so we use a Metropolis-Hastings step within the Gibbs chain. (See Appendix B more details on the Gibbs sampler.)
Because the subjects are reassigned to a class at each iteration without regard to the class labels (e.g., class 1 in one iteration may more resemble class 2 at another iteration), it is sometimes necessary to reassign labels to properly associate similar classes across iterations. When necessary, the decision-theoretic approach of Stephens (2000a) was applied to sort class labels. Multiple chains of substantial length were run to achieve convergence to the posterior distribution which was assessed using visual checks of traceplots and calculation of the Gelman-Rubin statistic ( ) (Gelman and Rubin, 1992). Values of were considered to indicate adequate convergence.
All models were fit using SAS macros written utilizing SAS/STAT and SAS/IML software, Version 9.1 of the SAS System for Windows. Copyright 2002–2003, SAS Institute Inc., Cary, NC, USA.
2.4. Model selection and goodness of fit
Model selection is challenging in all latent variable models, regardless of the method of estimation. This is particularly the case with determining the dimension of the latent categorical variable, as standard likelihood ratio methods are inappropriate because of the non-nested model structure. In most frequentist applications, the number of classes is chosen by comparing summary statistics of fit such as the χ2 statistic or likelihood-based criteria such as AIC and BIC. The Deviance Information Criterion (DIC), proposed by Spiegelhalter et al. (2002), is a similar measure of complexity and fit within the Bayesian setting. Like the AIC and BIC, the DIC is based on the likelihood. The DIC estimates the “effective” number of parameters for the penalty term using the deviance function (D(θ) = −2L(θ) + 2 log(f(y))). We evaluated the DIC at the median of the posterior distribution and chose the model yielding the smallest DIC value. In addition, we applied graphical methods such as the Latent Class Identifiability Display (LCID) of Garrett and Zeger (2000) to assess the ability of our data to identify parameters. To assess goodness-of-fit, we used an omnibus posterior predictive check (Gelman et al., 1996). We generated yrep|θj for each vector of parameters Θj in a random sample of draws from the posterior distribution and calculated the Chi-square statistic
for the replicated data and the observed data y at each θj. We plotted and calculated the Bayesian p-value . Small or large values of p̂ indicate poor fit to the data.
3. Application to data from an IC clinical trial
In this section the proposed model is applied to data from a multi-center clinical trial to evaluate the efficacy of Bacillus Calmette-Guerin (BCG) in treating IC symptoms. Two hundred sixty-five (265) subjects were randomized to receive intravesical BCG or intravesical placebo. Symptoms and other variables were recorded at baseline and 4 subsequent visits (approximately 8, 18, 26, and 34 weeks after randomization). At the end of the trial 21% of BCG subjects and 12% of placebo subjects identified themselves as moderately or markedly improved since the initiation of treatment (“responders”) as measured by the GRA. This difference did not achieve the prespecified threshold for statistical significance (p=0.06). Longitudinal analyses of the two secondary outcomes pain and urgency to void showed that the interaction between treatment assignment and time was not significant for either outcome, giving further evidence that treatment was not effective (Mayer et al., 2005). The goal of our analysis was to use the multivariate symptom profiles to classify patients in hopes of identifying a subset of true treatment responders. We applied our model to the symptoms pain and urgency. Both symptoms are measured on a 10-point (0–9) Likert scale with 9 indicating the most severe symptoms, and we model both as normally distributed random variables as was done in Mayer et al. (2005). In section 3.1 we report results from preliminary analyses which considered each outcome separately. In section 3.2 we report results from the application of the multivariate model to the bivariate repeated measurements of pain and urgency. In section 3.3 we compare the results from the univariate and multivariate analyses.
3.1. Application of a Univariate Growth Curve Mixture model
Each symptom was analyzed using a simplified version of the model of Muthén and Shedden (1999) (the “univariate” models). Each subject’s symptom profile was assumed to follow a quadratic curve in time adjusted for age (centered at the mean) and log10 transformed duration of symptoms with the intercept and slope allowed to vary with treatment assignment. A quadratic curve was chosen based on the plots of raw data means over time. Such a curve allows for the possibility that symptoms may rebound after treatment ended between weeks 6 and 10. Models with subject-specific random intercepts and random intercepts and slopes were considered. Curves were grouped into latent classes by allowing for the mean growth curve parameters (intercept, slope, quadratic effect, age, duration of symptoms, treatment, and treatment by time interaction) to vary by class. No covariates were included in the model for the probability of class membership. Bayesian models were fit using a simplified version of the Gibbs sampler described above. For the univariate models, chains of 10000 iterations, discarding the first 500 iterations for “burn-in”, were sufficient for convergence. Two-, three-, and four-class models were considered for each outcome.
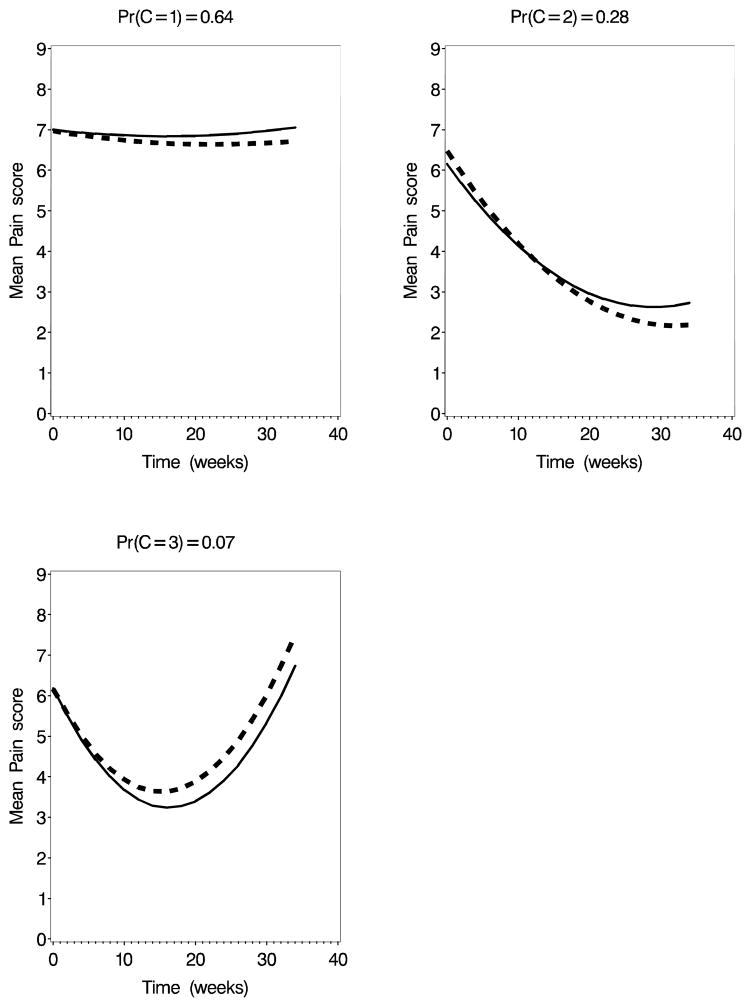
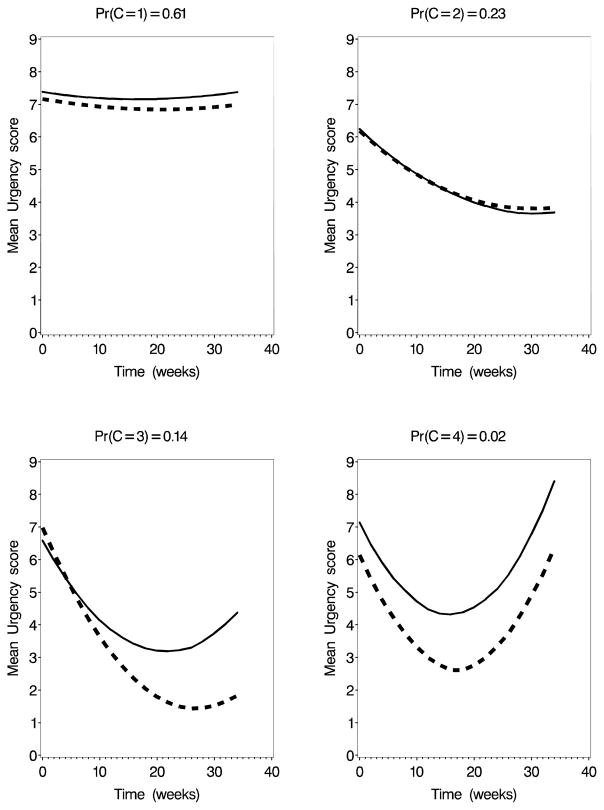
The DIC values for the 2-, 3-, and 4-class models for random-intercept only models for pain were, respectively, 4891, 4859, and 4861. When a random slope was included the values were 4897, 4869, and 4870. For urgency, the values were 4768, 4751, and 4743 for the random-intercept model and 4766, 4755, and 4748 for the random-slope model. Based on the DIC, the three-class model is favored for pain while the four-class model is favored slightly for urgency. In both cases, the random-intercept models are favored over the random-slope models. Figures 1 and 2 show the mean curves by class for the best-fitting models. For both pain and urgency, the two-class models identify a “non-responder” and a “responder” class. For the three class model for pain, the non-responder classes remains and the responder class was divided into “responders” and “temporary responders” (U-shaped profiles). The four-class model for urgency also produces a large non-responder class, two responder classes, and one small class of temporary responders. In the first class of responders (class 2), placebo and treatment arms had similar symptom trajectories while in the second class (class 3), treated subjects had a greater improvement in urgency than did those randomized to placebo.
Fig. 1.
Mean symptom growth curves at the median of the posterior distribution for the 3-class univariate model for Pain. Solid line=Placebo; Dashed line=Active Treatment.
Fig. 2.
Mean symptom growth curves at the median of the posterior distribution for the 4-class univariate model for Urgency. Solid line=Placebo; Dashed line=Active Treatment.
Using the median of the posterior for all model parameters, subjects were assigned to classes based on the posterior probability of class membership (i.e., Pr(Ci = k|y; Θ)). A significant number of subjects (41) belonged to one of the responder classes on one of the symptoms but were classified as non-responders on the other.
3.2. Application of the Multivariate Growth Curve Mixture Model
In considering the two symptoms simultaneously, pain and urgency were modeled as a bivariate manifestation of Z, which we call the underlying IC symptom severity (see equation 1). This latent variable was assumed to follow a quadratic curve over time. Fixed effects for treatment arm and treatment by time interaction were included to allow for the possibility that treatment may impact symptoms in one or more classes. Age and log10-transformed duration of symptoms were included as clinically important variables. Models with random intercepts only and random intercept and random slopes (see equations 2 and 3) were considered. Initial models were fit with only an intercept in the class membership model (4) as the metropolis step required when covariates are present in the logistic model greatly slows the algorithm. Given the results of the univariate analyses, two- and three-class models were considered. In addition to the quadratic curve in time, we considered a “saturated” model where we included fixed effects for each time and treatment group combination, again adjusting for age and log10 duration. As in Muthén et al. (2002), we assume that each subject belongs to a certain latent class and that this membership does not change over time. Active treatment is assumed to modify the class-specific trajectory from that expected under placebo.
Longer chains were needed to achieve convergence to the posterior distribution in the multivariate models. Multiple chains of 200,000 iterations were run assuming different sets of starting values for each chain for each model. Converged chains were combined to calculate posterior medians and measures of fit (DIC). The first 100,000 iterations from each chain were discarded when calculating the posterior distribution for quantities of interest. When necessary, the online algorithm of Stephens (2000b) was applied to correct for label-switching.
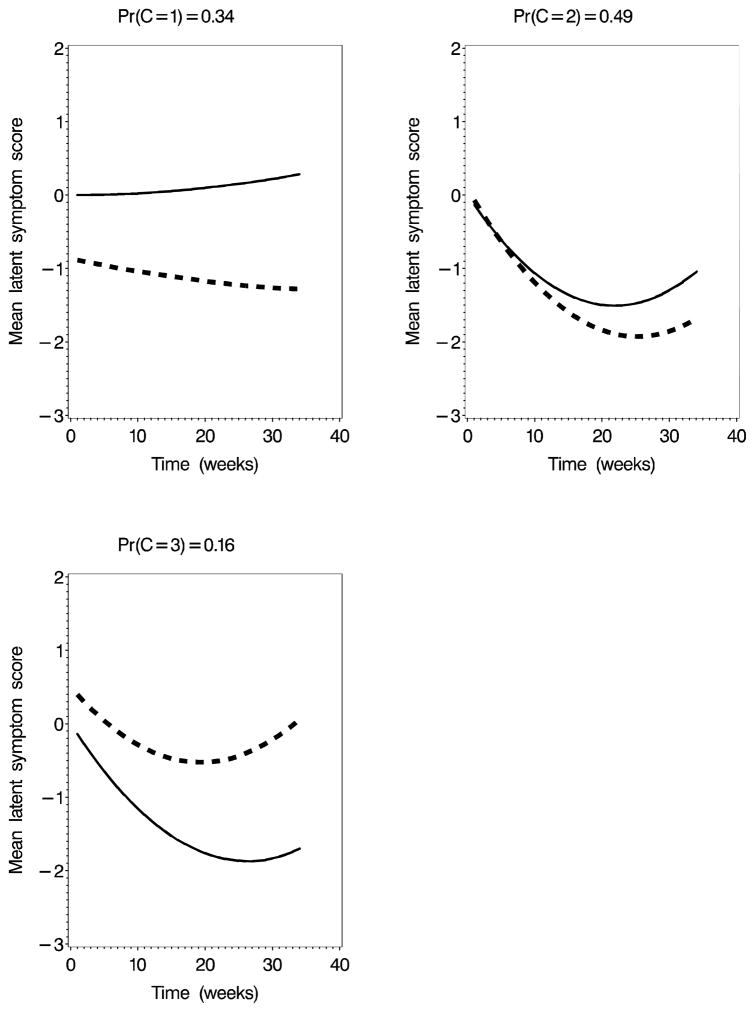
As in the univariate models, the two-class model yielded a flat and a responder class. The three-class model had the smallest DIC among those considered and is the one that is presented in detail (see Table 1. Figure 3 shows the mean curves for the latent variable by class at the median of the posterior distribution. Lower levels of the latent variable indicate greater improvement in symptoms. In the three-class model, the largest class is class 2 (Pr(C=2)=0.49) which includes both placebo and treatment responders. Response occurs early, during the intervention period, and levels off during the post-treatment follow-up period. The next largest class (class 1 Pr(C=1)=0.34) displayed relatively flat symptoms over the entire study period in both treatment arms. The third class (Pr(C=3)=0.16) exhibited substantial improvement in the placebo group but not the treatment group. The latent class identifiability display (figure not shown) indicated that the classes are well-identified by our data and the posterior predictive check yielded a “p-value” of 0.66 for the three-class model indicating that there is little evidence of poor fit for this model using the omnibus fit statistic. In addition, to check the assumption of normality of residual errors, we assigned each subject to its most likely class and calculated the residual between the predicted mean symptom score and observed symptom score. Histograms and q-q plots (not shown) gave no evidence of lack of normality.
Table 1.
DIC values for the multivariate models.
| Fixed Effects and number of classes | Random Effects | |
|---|---|---|
| Random Intercept | Random Intercept and Slope | |
| One-Class Quadratic | 9229 | 9057 |
| Two-Class Quadratic | 8933 | 8873 |
| Three-Class Quadratic | 8813 | 8771 |
| Three-Class Saturated | 8820 | |
Fig. 3.
Mean latent variable growth curves at the median of the posterior distribution: three-class multivariate model for pain and urgency. Solid line=Placebo, Dashed line=Active Treatment.
Table 2 gives the median of the posterior distribution and 95% credible intervals for all parameters for the three-class multivariate model. The responder class for the three-class model includes both placebo and treatment responders, with those randomized to the treatment arm improving faster than those in the placebo arm γ6 = −0.21 95% credible interval=[−0.43,−0.0047]). In classes 1 and 2 pain and urgency contribute roughly the same amount of information to the latent variable. The responder class (class 2) had the strongest association between the observed variables and the latent variable (λpain = 1.31, λurgency = 1.30). Class 1 had the lowest association between the observed and latent variables λpain = 0.39,λurgency = 0.49). Class 3 differed from the other two in that there was a strong association for pain but a weak association for urgency λpain = 1.31, λurgency = 0.41). Plots of the symptom-specific predicted curves (not shown) suggest that class three is composed of subjects randomized to placebo whose pain improved but whose urgency did not and subjects randomized to treatment who had a small temporary relief in pain, but no improvement in urgency. There is substantial evidence that subjects in class 2 had more improvement the longer they had been experiencing symptoms prior to entering the study (γ4 = −0.39 95% CI=[−0.84,0.034]). In class 3, there was evidence that older subjects had greater improvement (γ3 = −0.13 95% CI=[−0.31,0.025]).
Table 2.
Median posterior estimates and 95% posterior intervals
| Parameter | Class 1 Non-responder | Class 2 Responder | Class 3 Mixed | |
|---|---|---|---|---|
| Pr(Ci = k) | 0.34 (0.25,0.43) | 0.49 (0.40,0.59) | 0.16 (0.098,0.24) | |
| αpain | 7.49 (7.19,7.78) | 6.40 (6.04,6.77) | 6.35 (5.61,7.09) | |
| αurgency | 7.25 (6.90,7.60) | 6.44 (6.06,6.84) | 7.58 (7.17,8.02) | |
| λpain | 0.39 (0.22,0.54) | 1.31 (1.20,1.42) | 1.31 (1.10,1.53) | |
| λurgency | 0.49 (0.30,0.65) | 1.30 (1.20,1.41) | 0.41 (0.24,0.54) | |
| γ1 (time x 10−1) | −0.0040 (−0.57,0.60) | −1.38 (−1.72,−1.05) | −1.43 (−2.21,−0.75) | |
| γ2 (time2 x 10−2) | 0.025 (−0.13,0.19) | 0.31 (0.23,0.40) | 0.27 (0.11,0.46) | |
| γ3 (age) | −0.13 (−0.31,0.025) | −0.016 (−0.085,0.052) | 0.061 (−0.091,0.22) | |
| γ4 (log10(duration)) | 0.61 (−0.81,1.70) | −0.39 (−0.84,0.034) | −0.52 (−1.23,0.22) | |
| γ5 (trt. arm) | −0.87 (−2.17,0.14) | 0.084 (−0.29,0.45) | 0.50 (−0.35,1.41) | |
| γ6 (trt. x time x 10−1) | −0.21 (−0.63,0.15) | −0.21 (−0.43,−0.0047) | 0.37 (−0.025,0.82) | |
|
| ||||
| Ψa11 | 0.22 (0.10,0.43) | |||
| Ψa12 | 0.055 (−0.015,0.12) | |||
| Ψa22 | 0.15 (0.10,0.23) | |||
|
|
0.30 (0.16,0.48) | |||
|
|
0.59 (0.43,0.80) | |||
|
|
0.50 (0.37,0.63) | |||
|
|
0.58 (0.49,0.69) | |||
After selecting the number of classes, subjects were assigned to the class with the highest subject-specific posterior probability of class membership (i.e., Pr(Ci = k|Yi, Θ)). Potential predictors of class membership were evaluated using logistic regression. No potential predictors of class membership were identified, and so the extended model was not run.
3.3. Comparison of Univariate and Multivariate Models
Table 3 gives the cross-tabulation of the classes assigned in the 3-class multivariate model with those from both univariate models. For simplicity, the class assignments from the univariate models were grouped as non-responders (class 1 for both variables) vs. responders (classes 2–3 for pain and 2–4 for urgency). The multivariate responder class appears to reflect the union of the both groups of univariate responders rather than an intersection of the two groups and captures most of the responders identified by either univariate model. In addition, the multivariate model identified 38 additional subjects as responders who were classified as non-responders by both univariate models.
Table 3.
Multivariate 3-class model vs. univariate models for pain and urgency.
| Multivariate Non-Responders
| |||
|---|---|---|---|
| Pain Class | Urgency Non-Responder | Urgency Responder | Total |
| Non-Responder | 100 | 1 | 101 |
| Responder | 0 | 0 | 0 |
|
| |||
| Total | 100 | 1 | 101 |
|
| |||
| Multivariate Responders
| |||
| Pain Class | Urgency Non-Responder | Urgency Responder | Total |
|
| |||
| Non-Responder | 38 | 20 | 58 |
| Responder | 8 | 68 | 76 |
|
| |||
| Total | 46 | 88 | 134 |
|
| |||
| Multivariate Mixed
| |||
| Pain Class | Urgency Non-Responder | Urgency Responder | Total |
|
| |||
| Non-Responder | 18 | 0 | 18 |
| Responder | 12 | 0 | 12 |
|
| |||
| Total | 30 | 0 | 30 |
The growth trajectories from the univariate models and the multivariate models show some similarities. All two-class models indicate the presence of a “responder” class whose symptoms improved over time. The three-class models indicate that there is some evidence of a small class that improves over time and then worsens towards the end of the study. This is most evident with pain in the univariate models.
Table 4 compares class assignments from the multivariate models to treatment assignment and to the primary study endpoint, the Global Response Assessment. The distribution of class assignments for subjects randomized to BCG is roughly the same as that of Placebo. For the comparison with GRA, any subject missing the GRA at the final visit (n=19) was classified as a GRA non-responder. In the three-class model, 96 subjects who did not report improvement in their subjective assessment of their condition were assigned to the responder class based upon their multivariate profile for pain and urgency. Subjects experiencing actual improvement in symptoms may be underestimating their improvement at the end of the study. The multivariate model identified the largest number of responders (134 vs. 43 using GRA and 109 when combining the univariate responders).
Table 4.
Class assignment from multivariate models vs. treatment assignment and subjective response assessment.
| Multivariate Three-Class | Treatment Arm | GRA | ||
|---|---|---|---|---|
| Placebo | BCG | Non-responder | Responder | |
| Non-Responder | 55 | 46 | 99 | 2 |
| Responder | 65 | 69 | 96 | 38 |
| Mixed | 14 | 16 | 27 | 3 |
4. Simulations
Data were simulated under five scenarios to explore the conditions necessary for model identifiability (scenarios 1–3) and to test the ability of our algorithm to correctly identify model parameters and classify subjects. In the first scenario, data were generated under a one-class model for two observed symptom scores. The latent variable underlying the symptom scores had mean zero (i.e., no trend over time). The second and third scenarios were similar to the first, except the slope of the mean growth curve for the latent variable was assumed non-zero. In the fourth scenario, data were generated under a three-class model with two observed symptom scores where the slope of the latent variable in all classes was non-zero. The final scenario considered data generated from a three-class model with three observed symptom scores. In this simulation, the slope and quadratic effects for the largest class were specified to be zero. For each scenario 100 data sets were considered, each with 200 subjects measured at 5 time points. Results of the simulation study are given in tables 5–7. Average bias and nominal 95% coverage are reported for all model parameters.
Table 5.
Simulation results. Data generated under one-class model.
| Simulation 1
| |||||
|---|---|---|---|---|---|
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
| α1 | 6.89 | 6.91 (0.15) | 0.019 | 88 | |
| α2 | 6.79 | 6.80 (0.14) | 0.007 | 93 | |
|
| |||||
| λ1 | 1.10 | 1.06 (0.11) | −0.04 | 87 | |
| λ2 | 1.22 | 1.28 (0.13) | 0.058 | 92 | |
|
| |||||
| γ1 | 0 | 0.00021 (0.01) | 0.00021 | 93 | |
| γ2 | 0 | −0.00002 (0.00033) | −0.00002 | 91 | |
|
| |||||
| Ψa | 1 | 1.00 (0.17) | 0.0036 | 95 | |
|
|
1 | 1.07 (0.27) | 0.078 | 91 | |
|
|
1 | 0.85 (0.32) | −0.15 | 93 | |
|
|
1 | 1.06 (0.23) | 0.06 | 88 | |
|
|
1 | 0.85 (0.31) | −0.15 | 88 | |
|
| |||||
| Simulation 2
| |||||
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
|
| |||||
| α1 | 6.89 | 6.92 (0.15) | 0.027 | 87 | |
| α2 | 6.79 | 6.80 (0.14) | 0.01 | 94 | |
|
| |||||
| λ1 | 1.10 | 1.10 (0.056) | 0.001 | 92 | |
| λ2 | 1.22 | 1.23 (0.056) | 0.0009 | 95 | |
|
| |||||
| γ1 | −0.05 | −0.049 (0.011) | 0.00066 | 96 | |
| γ2 | 0.0003 | 0.0003 (0.00033) | −0.00004 | 95 | |
|
| |||||
| Ψa | 1 | 1.01 (0.18) | 0.0099 | 96 | |
|
|
1 | 1.03 (0.22) | 0.031 | 92 | |
|
|
1 | 0.97 (0.24) | −0.03 | 93 | |
|
|
1 | 0.99 (0.10) | −0.013 | 97 | |
|
|
1 | 0.99 (0.13) | −0.0074 | 92 | |
|
| |||||
| Simulation 3
| |||||
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
|
| |||||
| α1 | 6.89 | 6.89 (0.16) | 0.0011 | 91 | |
| α2 | 6.79 | 6.79 (0.14) | 0.002 | 95 | |
|
| |||||
| λ1 | 1.10 | 1.10 (0.043) | 0.002 | 91 | |
| λ2 | 1.22 | 1.23 (0.049) | 0.0069 | 94 | |
|
| |||||
| γ1 | −0.20 | −0.20 (0.013) | 0.0015 | 97 | |
| γ2 | 0.0003 | 0.0003 (0.00033) | −0.00004 | 93 | |
|
| |||||
| Ψa | 1 | 1.01 (0.18) | 0.014 | 97 | |
|
|
1 | 1.03 (0.18) | 0.031 | 98 | |
|
|
1 | 0.98 (0.21) | −0.02 | 96 | |
|
|
1 | 0.99 (0.087) | −0.011 | 99 | |
|
|
1 | 1.00 (0.12) | −0.0020 | 87 | |
Table 7.
Simulation results. Data generated under three-class model with three manifest variables. Zero mean for latent variable in largest class
| Class 1
| |||||
|---|---|---|---|---|---|
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
| Pr(Ci = k) | 0.50 | 0.52 (0.07) | 0.019 | 91 | |
| α1 | 7.0 | 6.99 (0.15) | −0.006 | 96 | |
| α2 | 7.0 | 7.05 (0.15) | 0.05 | 94 | |
| α3 | 2.0 | 2.03 (0.10) | 0.03 | 92 | |
| λ1 | 1.2 | 1.20 (0.05) | 0.001 | 98 | |
| λ2 | 1.2 | 1.18 (0.07) | −0.015 | 95 | |
| λ3 | 0.4 | 0.40 (0.03) | 0.003 | 95 | |
| γ1 | 0 | −0.0034 (0.01) | −0.0034 | 95 | |
| γ2 | 0 | 0.00009 (0.0004) | 0.00009 | 94 | |
|
| |||||
| Class 2
| |||||
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
|
| |||||
| Pr(Ci = k) | 0.33 | 0.33 (0.035) | −0.007 | 94 | |
| α1 | 6.0 | 6.01 (0.18) | 0.008 | 92 | |
| α2 | 6.0 | 5.99 (0.15) | −0.014 | 98 | |
| α3 | 1.5 | 1.49 (0.14) | −0.008 | 96 | |
| λ1 | 1.0 | 1.01 (0.05) | 0.01 | 93 | |
| λ2 | 1.0 | 1.01 (0.05) | 0.01 | 93 | |
| λ3 | 0.8 | 0.81 (0.04) | 0.0056 | 94 | |
| γ1 | −0.25 | −0.24 (0.020) | 0.0052 | 95 | |
| γ2 | 0.0034 | 0.0033 (0.0005) | −0.0001 | 95 | |
|
| |||||
| Class 3
| |||||
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
|
| |||||
| Pr(Ci = k) | 0.17 | 0.15 (0.066) | 0.015 | 89 | |
| α1 | 6.5 | 6.42 (0.35) | −0.085 | 96 | |
| α2 | 8.0 | 7.89 (0.34) | −0.11 | 93 | |
| α3 | 3.0 | 2.89 (0.28) | −0.11 | 98 | |
| λ1 | 1.10 | 1.15 (0.14) | 0.05 | 95 | |
| λ2 | 0.50 | 0.60 (0.18) | 0.10 | 92 | |
| λ3 | 0.50 | 0.54 (0.12) | 0.04 | 91 | |
| γ1 | −0.10 | −0.09 (0.028) | 0.0096 | 98 | |
| γ2 | 0.0032 | 0.0028 (0.0009) | −0.00038 | 96 | |
|
| |||||
| Variance Parameters
| |||||
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
|
| |||||
| Ψa | 0.40 | 0.40 (0.10) | 0.002 | 91 | |
|
|
0.50 | 0.53 (0.11) | 0.029 | 96 | |
|
|
0.60 | 0.62 (0.097) | 0.021 | 96 | |
|
|
0.30 | 0.32 (0.043) | 0.02 | 97 | |
|
|
0.40 | 0.40 (0.039) | 0.0049 | 96 | |
|
|
0.40 | 0.40 (0.040) | 0.0049 | 93 | |
|
|
0.30 | 0.30 (0.018) | −0.0002 | 95 | |
Our simulation results provide evidence for the non-identifiability of some parameters in the one-class model for two outcomes when the mean of the latent variable is zero. While the bias and coverage for the mean parameters (α and γ) are acceptable, as expected, there is substantial bias for the variance parameters. This bias is substantially reduced when the slope of the mean growth curve for the latent variable is nonzero. The results for both sets of three-class simulations show that our estimation procedure performs well with regard to the criteria of average bias and nominal coverage in a multi-class setting.
The results presented in Table 6 show that with two outcomes and non-zero means in all classes, our procedures was able to identify all parameters accurately with moderate sample sizes. Table 7 shows that for the case of 3 manifest variables, even with a large class with zero mean, all parameters are identified with fairly good bias and coverage.
Table 6.
Simulation results. Data generated under three-class model with non-zero mean for latent variable in each class
| Class 1
| |||||
|---|---|---|---|---|---|
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
| Pr(Ci = k) | 0.50 | 0.49 (0.06) | −0.009 | 92 | |
| α1 | 7.0 | 6.97 (0.11) | −0.031 | 95 | |
| α2 | 6.5 | 6.51 (0.19) | 0.013 | 95 | |
| λ1 | 0.8 | 0.81 (0.12) | 0.010 | 96 | |
| λ2 | 0.9 | 0.88 (0.09) | −0.020 | 93 | |
| γ1 | −0.10 | −0.099 (0.013) | 0.0009 | 97 | |
| γ2 | 0.002 | 0.002 (0.0004) | −0.000038 | 97 | |
|
| |||||
| Class 2
| |||||
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
|
| |||||
| Pr(Ci = k) | 0.33 | 0.33 (0.029) | 0.001 | 96 | |
| α1 | 6.0 | 6.02 (0.15) | 0.021 | 92 | |
| α2 | 6.0 | 6.00 (0.15) | 0.004 | 96 | |
| λ1 | 1.2 | 1.21 (0.05) | 0.0077 | 97 | |
| λ2 | 1.2 | 1.21 (0.05) | 0.0057 | 96 | |
| γ1 | −0.25 | −0.25 (0.016) | 0.0029 | 95 | |
| γ2 | 0.0034 | 0.0033 (0.00047) | −0.00007 | 98 | |
|
| |||||
| Class 3
| |||||
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
|
| |||||
| Pr(Ci = k) | 0.17 | 0.17 (0.055) | 0.0056 | 96 | |
| α1 | 6.5 | 6.47 (0.25) | −0.035 | 96 | |
| α2 | 7.5 | 7.47 (0.17) | −0.028 | 94 | |
| λ1 | 1.60 | 1.59 (0.16) | −0.012 | 88 | |
| λ2 | 0.30 | 0.31 (0.095) | 0.011 | 94 | |
| γ1 | −0.15 | −0.15 (0.021) | 0.0046 | 95 | |
| γ2 | 0.0032 | 0.0031 (0.0006) | −0.00014 | 96 | |
|
| |||||
| Variance Parameters
| |||||
| Parameter | True Value | Mean (SD) | Average Bias | Coverage | |
|
| |||||
| Ψa | 0.20 | 0.21 (0.047) | 0.014 | 98 | |
|
|
0.20 | 0.21 (0.041) | 0.011 | 97 | |
|
|
0.20 | 0.21 (0.038) | 0.008 | 96 | |
|
|
0.30 | 0.30 (0.034) | 0.0016 | 97 | |
|
|
0.30 | 0.30 (0.029) | 0.0017 | 96 | |
5. Discussion
In this paper we have presented a Bayesian latent variable mixture model that jointly models multivariate outcomes repeatedly measured over time. This method provides a way of characterizing population heterogeneity in observed responses by clustering subjects based on their unobserved latent growth curve profiles. This model was applied to clinical trial data and identified a class of subjects who showed substantial improvement in their symptom scores. The 49% “response” rate for the three-class model was substantially higher than the response rate reported for the primary endpoint in the original clinical trial (16%) indicating that a subjective evaluation of improvement may not capture all actual improvement in experienced symptoms and argues for a more complete assessment of symptom data as presented here. Our method also identified more responders than either of the univariate growth curve mixture models including 38 subjects who were not identified as responders in either outcome individually. This suggests that there may be a substantial advantage in considering outcomes together rather than separately if the goal is to identify all subjects with potential for response. In contrast to conventional longitudinal analyses of individual symptoms stratified by subjective response status, we were able to identify a class of subjects where active treatment was more effective than placebo in reducing the symptom severity as summarized by the latent variable.
This framework allows for joint modeling of the multivariate normal longitudinal outcomes while simultaneously clustering subjects based on their underlying latent variable growth curves thus properly accounting for uncertainty in all parameter estimates. The joint model for the multivariate outcomes can flexibly account for within subject correlation through the combined latent variable and mixed effects structure similar to Roy and Lin (2000). Study subjects were also classified into groups based on their underlying latent variable growth curve while accounting for the uncertainty in the class assignment through the use of a mixture model. We allow for the probability of class membership and the growth curve trajectory to depend on covariates and could easily incorporate covariates into the factor analytic model. While we did not identify any potentially interesting predictors of class membership in our post-hoc analysis, these tests are known to be biased toward the null. When covariates of interest can be specified a priori, they should be included in the joint model to avoid this bias.
Our use of the Gibbs sampler provides a full posterior distribution for the model parameters which is a more complete picture of the uncertainty in parameter estimates when compared with the alternative EM algorithm which identifies only the mode of the posterior distribution. Use of Gibbs samplers for finite mixture models has been criticized as they have difficulty moving among the potentially multiple modes of the posterior distribution (Celeux et al., 2000). We did not observe these problems in our data application, and our simulations showed that given an identifiable model, the Gibbs sampler performed well.
The proposed model allows for missing data under the assumption that the data are missing at random which seemed appropriate for this application as the missing data does not appear to be related to response, i.e. subjects with missing data appear in all classes. Also, less than 10% of the subjects withdrew before the end of the study, and any bias caused by data missing not at random will likely be minimal. Roy and Lin (2000) extended their model for the case of nonignorable missing data and there may be situations where a latent class extension of that model would be useful. Allowing for non-normally distributed outcomes is a subject of future work.
The proposed models require a priori specification of the number of classes. The DIC was used to guide our selection of the number of latent classes. The DIC is attractive as it is easy to compute and can be used to compare models of varying types. Some authors have suggested that the DIC may not correctly adjust for additional parameters when applied to mixture models and may favor overly complex models (Richardson, 2002). This was apparent in our univariate models where the DIC favors more classes. A fully Bayesian approach (e.g., see Richardson and Green, 1997) to selecting the number of classes is challenging both conceptually and computationally but warrants further research.
Acknowledgments
This research was partially supported by grant R01-DK59601 from the National Institute for Diabetes and Digestive and Kidney Diseases, National Institutes of Health. We thank the investigators of the Interstitial Cystitis Clinical Trials group for use of their data. We thank Drs. Kathleen Joy Propert and Michael Elliott for their helpful comments and discussions.
APPENDIX
A. Identifiability of model parameters
In this section we show that the variance parameters and factor loadings in the two-variable, one-class model with a random intercept for the latent variable are not simultaneously identifiable if the mean of the latent variable is zero. The variance parameters and factor loadings for the three-variable, one-class model are identifiable regardless of the mean of the latent variable. Consider the case of two manifest variables measured at three times. For j = 1, 2, 3, and m = 1, 2 we have:
If γ = 0 then E(Yijm) = αm and there is no information about λm available from the mean. Define to be the variance of the mth variable at the jth timepoint and to be the covariance of the mth at the jth timpoint with the m′th outcome at the j′th timepoint. For three repeated measurements we have 21 observed covariance parameters.
Using the model specification, there are only six unique covariance terms. They are:
Thus, when solving for moment estimators this yields a system of six equations in seven unknowns indicating that one of the variance components is not identifiable using information from the observed covariance matrix alone.
When three manifest variables are observed, there are 12 covariance terms with 10 parameters:
Thus, all parameters involved in the variance can be identified from the covariance matrix alone.
For a model with K classes, the covariance terms involve functions of the class-specific means. For example, with two classes, k = 1, 2:
If at least one γk ≠ 0 and E(Yijm|Ci = 1) ≠ E(Yij′m′|Ci = 2) for all combinations of j; j′, m and m′, then for a two-class model with two variables measured at 3 time points and one column in Xz (the fixed effects matrix design matrix in 2), the mean and covariance equations form a system of 27 equations in 16 unknowns and the model is identifiable. If γk = 0 or E(Yijm|Ci = 1) = E(Yij′m′|Ci = 2) for all (or a sufficiently large number of) combinations of j; j′, m and m′, the model will not be identifiable. Difficulties in estimation may result if class-specific means are not well-differentiated.
B. Details of the Gibbs Sampler for the multivariate model with continuous outcomes
Parameters are drawn from their full conditional distributions as follows:
Draw βmk = (αmk, λmk)T from N2(μβkΣβk) where and . Here , and Θβm = N*diag(ψαmψβm).
Draw γk from N(μγkΣγk) where and . Here .
Draw zij from N(μzij;σzij) where and . Here .
Draw ai from Nq(μaiΣai) where and
Draw Ψa from Inv - Wishart(N + 1, Sa) where
Draw bim from where and . Here . Jni is an ni × 1 vector of 1’s
Draw from Inv - χ2(N +1 Sbm) where .
Draw from where .
- Draw Ci from where and
(6) -
When the class probability model contains only an intercept, draw the class probabilities directly from the full conditional distribution
(7) where .
When the probability of class membership is a function of covariates, draw δk via a Metropolis algorithm where the proposal distribution is . is the mode of the full conditional posterior distribution of δ found using a Newton-Raphson routine and is R times the inverse of the Hessian at the mode. R inflates the variance and is chosen to achieve an acceptance rate of 15–20%. Each complete iteration in the Gibbs chain includes 20 iterations of the Metropolis algorithm to ensure that at least one new δk is accepted.
All chains were started with different initial estimates for the parameters.
Contributor Information
Benjamin E. Leiby, Division of Biostatistics, Thomas Jefferson University, Philadelphia, PA, USA.
Mary D. Sammel, Department of Biostatistics and Epidemiology, University of Pennsylvania School of Medicine, Philadelphia, PA, USA
Thomas R. Ten Have, Department of Biostatistics and Epidemiology, University of Pennsylvania School of Medicine, Philadelphia, PA, USA
Kevin G. Lynch, Department of Psychiatry, University of Pennsylvania School of Medicine, Philadelphia, PA, USA
References
- Bartholomew DJ, Knott M. Latent variable models and factor analysis. Edward Arnold Publishers Ltd; 1999. [Google Scholar]
- Bauer DJ, Curran PJ. The integration of continuous and discrete latent variable models: Potential problems and promising opportunities. Psychological Methods. 2004;9(1):3–29. doi: 10.1037/1082-989X.9.1.3. [DOI] [PubMed] [Google Scholar]
- Celeux G, Hurn M, Robert CP. Computational and inferential difficulties with mixture posterior distributions. Journal of the American Statistical Association. 2000;95(451):957–970. [Google Scholar]
- Clogg CC. Handbook of statistical modeling for the social and behavioral sciences. Plenum Publishing Corporation; 1995. p. 592. [Google Scholar]
- Elliott MR, Gallo JJ, Ten Have TR, Bogner HR, Katz IR. Using a bayesian latent growth curve model to identify trajectories of positive affect and negative events following myocardial infarction. Biostatistics. 2005;6(1):119–143. doi: 10.1093/biostatistics/kxh022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fieuws S, Verbeke G. Pairwise fitting of mixed models for the joint modeling of multivariate lonigtudinal profiles. Biometrics. 2006;62:424–431. doi: 10.1111/j.1541-0420.2006.00507.x. [DOI] [PubMed] [Google Scholar]
- Garrett ES, Zeger SL. Latent class model diagnosis. Biometrics. 2000;56:1055–1067. doi: 10.1111/j.0006-341x.2000.01055.x. [DOI] [PubMed] [Google Scholar]
- Gelfand AE, Smith AFM. Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association. 1990;85:398–409. [Google Scholar]
- Gelman A, Meng XL, Stern H. Posterior predictive assessment of model fitness via realized discrepancies. Statistica Sinica. 1996;6:733–760. [Google Scholar]
- Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statistical Science. 1992;7:457–472. [Google Scholar]
- Gilks WR, Wild P. Adaptive rejection sampling for Gibbs sampling. Applied Statistics. 1992;41:337–348. [Google Scholar]
- Gueorguieva R. A multivariate generalized linear mixed model for joint modelling of clustered outcomes in the exponential family. Statistical Modelling: An International Journal. 2001;1(3):177–193. [Google Scholar]
- Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
- Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
- Leiby BE, Landis JR, Propert KJ, Tomaszewski JE. Discovery of morphological subgroups that correlate with severity of symptoms in interstitial cystitis. Journal of Urology. 2007;177:142–148. doi: 10.1016/j.juro.2006.08.096. [DOI] [PubMed] [Google Scholar]
- Mayer R, Propert KJ, Peters KM, Payne CK, Zhang Y, Burks D, Culkin DJ, Diokno A, Hanno P, Landis JR, Madigan R, Messing EM, Nickel JC, Sant GR, Warren J, Weign AJ, Kusek JW, Nyberg LM, Foster HE the Interstitial Cystitis Clinical Trials Group. A randomized controlled trial of intravesical bacillus calmette-guerin for treatment refractory interstitial cystitis. Journal of Urology. 2005;173(4):1186–1191. doi: 10.1097/01.ju.0000152337.82806.e8. [DOI] [PubMed] [Google Scholar]
- Muthén B, Brown CH, Masyn K, Jo B, Khoo ST, Yang CC, Wang CP, Kellam SG, Carlin JB, Liao J. General growth mixture modeling for randomized preventive interventions. Biostatistics. 2002;3:459–475. doi: 10.1093/biostatistics/3.4.459. [DOI] [PubMed] [Google Scholar]
- Muthén B, Shedden K. Finite mixture modeling with mixture outcomes using the EM algorithm. Biometrics. 1999;55:463–469. doi: 10.1111/j.0006-341x.1999.00463.x. [DOI] [PubMed] [Google Scholar]
- Muthén BO, Curran PJ. General longitudinal modeling of individual differences in experimental designs: A latent variable framework for analysis and power estimation. Psychological Methods. 1997;2:371–402. [Google Scholar]
- Nagin D, Tremblay R. Analyzing developmental trajectories of distinct but related behaviours: a group-based method. Psychological Methods. 2001;6:18–34. doi: 10.1037/1082-989x.6.1.18. [DOI] [PubMed] [Google Scholar]
- Palta M, Lin CY. Latent variables, measurement error and methods for analysing longitudinal binary and ordinal data. Statistics in Medicine. 1999;18:385–396. doi: 10.1002/(sici)1097-0258(19990228)18:4<385::aid-sim25>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- Richardson S. Comment on “Bayesian measures of model complexity and fit”. Journal of the Royal Statistical Society, Series B, Methodological. 2002;64(4):626–627. [Google Scholar]
- Richardson S, Green PJ. On Bayesian analysis of mixtures with an unknown number of components. Journal of the Royal Statistical Society, Series B, Methodological. 1997;59:731–758. [Google Scholar]
- Roeder K, Lynch KG, Nagin DS. Modeling uncertainty in latent class membership: A case study in criminology. Journal of the American Statistical Association. 1999;94:766–776. [Google Scholar]
- Roy J, Lin X. Latent variable models for longitudinal data with multiple continuous outcomes. Biometrics. 2000;56(4):1047–1054. doi: 10.1111/j.0006-341x.2000.01047.x. [DOI] [PubMed] [Google Scholar]
- Shah A, Laird N, Schoenfeld D. A random-effects model for multiple characteristics with possibly missing data. Journal of the American Statistical Association. 1997;92:775–779. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society, Series B, Methodological. 2002;64(4):583–616. [Google Scholar]
- Stephens M. Bayesian analysis of mixture models with an unknown number of components: alternative to reversible jump methods. The Annals of Statistics. 2000a;28(1):40–74. [Google Scholar]
- Stephens M. Dealing with label switching in mixture models. Journal of the Royal Statistical Society, Series B. 2000b;62(4):795–809. [Google Scholar]
- Verbeke G, Lesaffre E. A linear mixed-effects model with heterogeneity in the random-effects population. Journal of the American Statistical Association. 1996;91:217–221. [Google Scholar]