Mechanisms of fluid production in smooth adhesive pads of insects

Abstract

Insect adhesion is mediated by thin fluid films secreted into the contact zone. As the amount of fluid affects adhesive forces, a control of secretion appears probable. Here, we quantify for the first time the rate of fluid secretion in adhesive pads of cockroaches and stick insects. The volume of footprints deposited during consecutive press-downs decreased exponentially and approached a non-zero steady state, demonstrating the presence of a storage volume. We estimated its size and the influx rate into it from a simple compartmental model. Influx was independent of step frequency. Fluid-depleted pads recovered maximal footprint volumes within 15 min. Pads in stationary contact accumulated fluid along the perimeter of the contact zone. The initial fluid build-up slowed down, suggesting that flow is driven by negative Laplace pressure. Freely climbing stick insects left hardly any traceable footprints, suggesting that they save secretion by minimizing contact area or by recovering fluid during detachment. However, even the highest fluid production rates observed incur only small biosynthesis costs, representing less than 1 per cent of the resting metabolic rate. Our results show that fluid secretion in insect wet adhesive systems relies on simple physical principles, allowing for passive control of fluid volume within the contact zone.

1. Introduction

Adhesive pads of insects, both of the smooth and hairy types, are known to secrete fluids on their surface [1–7]. While some studies concluded that this pad secretion generally enhances adhesion [8,9], recent work showed that accumulation of secretion on a smooth surface actually leads to a significant loss of adhesion and friction [10]. However, it was demonstrated that the tarsal fluid can increase adhesion on rough substrates, where it helps to maximize contact area. This behaviour is consistent with predictions for capillary adhesion: forces are maximal when there is just enough fluid to fill in the gaps resulting from surface roughness [11,12]. The gaps to be filled with fluid are smaller for soft adhesive pads that deform under the influence of negative capillary pressure [13]. Therefore, a biological adhesive pad could maximize forces by secreting an optimal amount of fluid into the contact zone, which will depend both on its stiffness and on surface roughness. It has been hypothesized that insects are able to control adhesion by regulating the amount of injected liquid via a neuronal feedback mechanism [14]. However, there are still no quantitative data on the secretion rate of adhesive fluid in insects and it is unclear whether and how it can be controlled.

Smooth adhesive pads are characterized by a special morphology, which is very similar in different insect orders [15–19]. The arolium cuticle of stick insects and cockroaches consists of cuticular rods that are oriented perpendicular to the surface and branch into finer fibres towards the epicuticle [16,19]. As in other types of insect cuticle, the epicuticle consists of the outer cuticulin layer and an amorphous inner layer that is penetrated by pore canals [15,16,19–22].

The role of the specialized cuticle of smooth adhesive pads in the secretion of adhesive fluid is unclear. Epidermal cells associated with adhesive pads often contain secretory vesicles [18,23,24]. As for other types of cuticle, it is thought that epicuticular lipids are released onto the cuticle surface via pore canals, which are visible in the amorphous inner epicuticle of smooth adhesive pads [19,25]. Other supposed mechanisms include the transport of fluid on the surface of the cuticle, from the more proximal parts of the leg towards the adhesive pads [24] or from glands in the femur and tibia along the hollow apodeme of the claw retractor muscle [26]. For all of these proposed mechanisms, it is unclear whether and how the secretion rate could be controlled and what forces are responsible for the release of fluid into the contact zone.

Insects with smooth pads have been observed to secrete an emulsion, consisting of volatile, aqueous droplets within a persistent, hydrophobic phase [3]. It has been shown for stick insects that this emulsion increases friction forces, possibly based on its non-Newtonian properties [2]. Chemical analyses of insect adhesive secretions have found long-chained hydrocarbons, alcohols, alkanes, alkenes, fatty acids, saccharides, amino acids and proteins [1,6,27–32].

The constant loss of adhesive fluid with every step could be metabolically costly in the long term. It is possible that insects minimize this loss by using only as much adhesive contact area as is necessary [33]. Freely running Phytolacca americana cockroaches were observed to deposit no visible footprints, while arolia and euplantulae manually placed on a substrate left ‘greasy’ imprints [34]. This suggests that insects are able to recover secretion after each step.

In this study, we investigate the following questions: (i) What is the maximum rate of adhesive fluid secretion in simulated, consecutive steps? (ii) How is secretion released in pads that are in stationary contact? (iii) How much fluid do freely running insects leave behind?

2. Methods

2.1. Experimental setup

We used adult female Indian stick insects (Carausius morosus: 370 ± 55 mg, 64 ± 1.7 mm, n = 7, means ± s.e.) and adult cockroaches (Nauphoeta cinerea: 372 ± 33 mg, 25 ± 1.0 mm, n = 7) from laboratory colonies kept at 24°C and fed on ivy (Carausius), dog food (Nauphoeta) and water ad libitum. To restrain insects and immobilize their adhesive pads, stick insects were enclosed in a hollow glass tube, with front or hind legs protruding from the open end. Cockroaches were anaesthetized using CO₂ and fastened to a mount using parafilm tape. The tarsal segments and the dorsal side of the hind leg pretarsus were fixed to a protruding soldering wire using dental cement (ESPE, Protemp). The tips of the claws were carefully clipped with microscissors to prevent them from touching the substrate and interfering with the measurements.

2.2. Interference reflection microscopy

Interference reflection microscopy (IRM) measures the reflectivity of a specimen under monochromatic illumination; it can be used to quantify the thickness of thin films with nanometre resolution and to achieve a three-dimensional reconstruction of thin transparent objects such as droplets [35–37]. IRM has been previously used to reconstruct the shape of small insect footprint droplets [3]. We used a Leica DMR-HC upright microscope equipped with a 100×/1.25 oil objective and switchable bandpass interference filters in the epi-illumination path to isolate the 546 or 436 nm lines from the spectrum of a 100 W mercury arc lamp. The illuminating numerical aperture (INA) can be set to 0.27, 0.79 or 1.27 using a home-built pinhole slider. Images were captured using a QIC-FM12 camera.

2.3. Footprints in simulated steps

To perform series of consecutive press-downs (‘steps’) with a controlled normal force, a custom-built force-feedback setup was used [10]. The arolium of N. cinerea was brought into contact with a clean glass coverslip (18 × 18 × 0.1 mm) attached to the distal end of a two-dimensional bending beam force transducer equipped with 350 Ω foil strain gauges (Vishay SR-4). The transducer recorded to a data acquisition board (PCI-6035E, National Instruments) and was moved by a computer-controlled three-dimensional positioning stage (M-126PD, C-843, Physik Instrumente). Positioning stage and force recording were synchronized using a LabVIEW program (National Instruments). The contact area of the pads was recorded under reflected light before each trial using a Redlake PCI 1000 B/W camera at 10 Hz.

The arolia were pressed down for 1 s with a feedback-controlled normal force of 1 mN, and pulled off with 0.7 mm s⁻¹. The time between steps was 1.1, 5.6 or 10.6 s (resulting in step frequencies of 0.476, 0.152 and 0.086 s⁻¹). To control for any effects of experimental order, the trials with different time delays were varied in a random order for each insect; a pause of at least 15 min was left between different step series for each insect.

The glass surfaces with the footprints were analysed immediately after the trials by removing the force transducer from the setup and investigating the glass plate using IRM. We analysed images of footprints taken at 5× magnification (INA 0.15, λ = 546 nm). The area covered with adhesive fluid was marked on the images.

The volume V of each single marked droplet was calculated from its area A and contact angle α, assuming that it is a spherical cap:

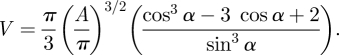2.1

The contact angle on glass was measured using IRM as 17.55 ± 0.6° for C. morosus (n = 10), and 17.03 ± 0.8° for N. cinerea (means ± s.e.). The overall volume of each footprint was calculated as the sum of all single droplet volumes. We found that large droplets (diameter more than ca 9 µm) were mostly non-spherical and flattened; their height rarely exceeded 1.3 µm. This effect may be due to contact angle hysteresis when during pull-off, droplets do not fully contract to their equilibrium shapes. Applying equation (2.1) would therefore lead to an overestimation of the volume in larger droplets. To correct for this error, we restricted the fluid heights to a maximum of 1.3 µm.

To control for different pad sizes of larger and smaller insects, we calculated the footprint volume secreted per unit adhesive contact area. Area-specific footprint volumes were fitted with a three-parameter exponential model (equation (A 4), for derivation, see appendix A). From the parameters of the fit, we calculated the area-specific storage volume V₀, the area-specific influx rate Q and the proportion k of the fluid volume that is deposited at each step (appendix A).

2.4. Measurement of fluid volume in stationary contact

To study the pad contact zone of stick insects (n = 6) and cockroaches (n = 4) in vivo, pads were carefully brought into contact with clean glass coverslips using a micromanipulator. Images of the edge of the pad contact zone were taken 10, 60, 120 and 180 s after initial contact with an INA of 0.27. Images of the entire contact area of pads were captured at 5× magnification.

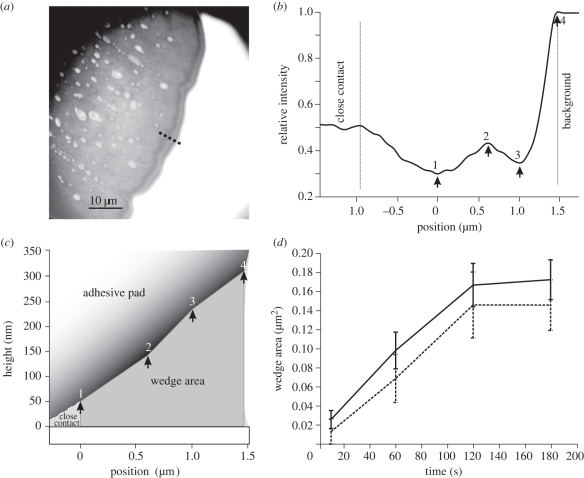
The interference fringes at the edge of the contact zone (see figure 2a) show that there is a wedge of fluid, which increases in thickness towards the outer meniscus. As in a previous study [3], we used these patterns to estimate the thickness of the fluid wedge between the pad cuticle and the substrate. For a small illuminating numerical aperture of 0.27, the height difference between an interference minimum and the adjacent maximum is

2.2

where λ is the wavelength and n_L ≈ 1.47 the refractive index of the hydrophobic phase of the secretion. In our previous study, we assumed a three-layer optical model consisting of the surface (glass), the adhesive fluid and the pad cuticle. However, our recent findings indicate that the thin cuticulin envelope acts as a fourth optical layer that shifts the interference pattern, so that the fluid thickness at the first visible interference minimum is approximately 50 nm. We used this value and equation (2.2) to estimate the fluid film height in the wedge. The positions of the visible interference maxima and minima were measured from the recorded images along a line perpendicular to the edge of the pad. The film thickness at these extrema was used to reconstruct the cross-sectional area of the fluid wedge from the first interference minimum to the edge of the pad (‘wedge area’, see figure 2c). The fluid film height at the outer meniscus was estimated by linearly extrapolating the visible extrema. The perimeter of the entire contact zone was measured and used to calculate the overall volume of the surrounding fluid wedge (‘wedge volume’ = perimeter × ‘wedge area’).

Figure 2.

Fluid secretion volume of pads in stationary contact with glass. (a) 100× IRM image of the adhesive contact zone (Nauphoeta cinerea) in contact, showing hydrophilic droplets (asterisks) and a wedge of hydrophobic fluid at the edge of the contact zone. The dotted line indicates the position of the line plot. (b) Intensity (relative to the background) along the line shown in (a). Positions of the interference maxima and minima are indicated by arrows. (c) Reconstructed cross section of the fluid wedge. Arrows correspond to the positions marked in (b). (d) Comparison of the increase in wedge area during stationary contact in stick insects (solid line, C. morosus, n = 6) and cockroaches (dashed line, N. cinerea, n = 4).

2.5. Measurement of fluid deposition of freely running stick insects

Adult stick insects were allowed to walk freely on clean glass surfaces (100 × 500 mm) upright and upside down (n = 117 steps from six insects). The insects were filmed using a 12 bit monochrome digital camera (QIC-FM12, QImaging). From the recordings, the exact position of each footprint on the glass substrate was reconstructed; the resolution of the camera view was 73 µm per pixel. The glass surfaces were then checked for the presence of fluid droplets at the reconstructed positions with a Leica DMR-HC microscope at 5× and 20× magnification. A calibrated motorized positioning stage (LSTEP, Märzhäuser) was used to locate the reconstructed positions on the glass substrate.

3. Results

3.1. Fluid loss during consecutive simulated steps

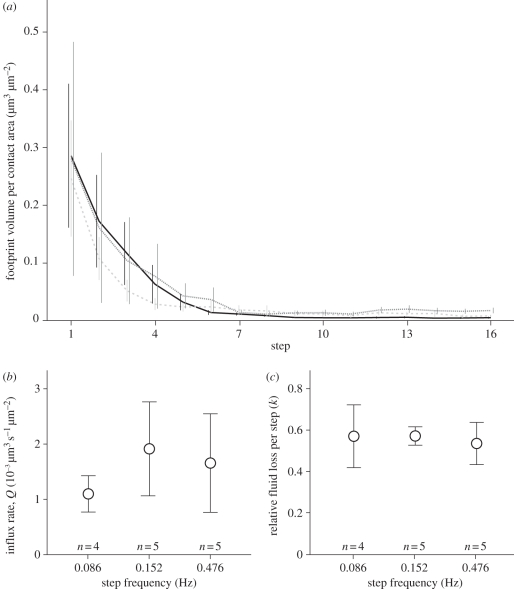
Adhesive pads of cockroaches repeatedly pulled off glass surfaces left footprints with exponentially decreasing volumes (see figure 1a). The droplet volumes decreased to a non-zero steady state. This behaviour indicates that the pad initially contained a large volume of fluid, which was then depleted over consecutive steps. The observed exponential decay is consistent with a simple model, where fluid is secreted at a steady rate into a ‘storage volume’, of which a constant proportion is deposited on the surface with every step (see appendix A). The assumption of a constant proportion of fluid deposited is physically plausible, as this condition would be observed for the separation of a simple fluid meniscus between two surfaces. We fitted the measured footprint droplet volumes with the predicted three-parameter exponential model (equation A 4). Fit and data were in excellent agreement, suggesting that the simple model describes the essential principles of footprint deposition (mean R² = 0.97 ± 0.01, n = 14). From the three parameters of the exponential fit, we calculated estimates for the steady influx rate Q, the initial storage volume V₀ (both per unit contact area; mean contact area was 46 351 ± 6256 µm²), and the proportion k of the storage volume that is deposited with every step (see appendix A).

Figure 1.

Volume and rate of fluid deposition during consecutive pad press-downs in Nauphoeta cinerea. (a) Volumes of adhesive fluid deposited at different step frequencies (data show means ± s.e.) (black line, 0.476 Hz (n = 5); grey dashed line, 0.152 Hz (n = 5); grey dotted line, 0.086 Hz (n = 4)). (b) Influx rate Q of adhesive fluid in depleted adhesive pads, for different frequencies of simulated steps (means ±s.e.). (c) Relative fluid loss per step (k) for different step frequencies (means ±s.e.).

The influx rate Q into the storage volume was 0.00159 ± 0.00043 µm³ s⁻¹ per µm² contact area. With each step, the insects lost k = 56 ± 5 per cent of the available adhesive fluid. The initial storage volume V₀ calculated from the fit parameters was 0.60 ± 0.19 µm³ per µm² contact area (all n = 14 trials from six cockroaches, medians ± 95% CI).

We tested whether the influx rate is stimulated and increased by a higher step frequency (see figure 1b,c). However, we did not find any significant correlation between influx rate per unit contact area and step frequency (Spearman's rank, ρ = 0.028, t₁₂ = 0.097, p > 0.2). The relative fluid loss was also not significantly correlated with step frequency (Spearman's rank, ρ = − 0.016, t₁₂ = −0.056, p > 0.2).

3.2. Fluid secretion volume of pads in stationary contact

After bringing pads into contact with glass, the volume of adhesive fluid in the outer wedge of the adhesive contact zone at first rapidly increased but then appeared to approach an asymptote, where little or no further increase was observed (figure 2). This pattern was found both for cockroaches and stick insects, suggesting a similar mechanism. For the measurements of pads in stationary contact, the mean contact area of cockroaches was 87 942 ± 29 856 µm² and the perimeter 2696 ± 878 µm (n = 4, mean ± s.e.), whereas contact area and perimeter of stick insects were 114 519 ± 12 835 µm² and 1836 ± 42 µm, respectively (n = 6). Within 180 s, the volume increased from 22 ± 22 to 351 ± 103 µm³ in cockroaches (n = 4) and from 47 ± 17 to 393 ± 63 µm³ in stick insects (n = 6, mean ± s.e.).

3.3. Fluid deposition in freely running stick insects

To compare the footprints deposited by simulated steps (with a perpendicular attachment and detachment) with those left during natural walking movements, stick insects were allowed to walk upright and upside down on clean glass plates while filmed with a digital camera. Compared with the footprints from simulated steps, freely running stick insects deposited only very small amounts of adhesive fluid. From 117 analysed steps (n = 6 insects, 85 inverted, 32 upright steps) only 7 footprints with traces of adhesive secretion were detected on the surface (all from inverted trials).

4. Discussion

Our study shows that adhesive pads of cockroaches repeatedly pressed onto a smooth surface deposited footprints of adhesive fluid with exponentially decreasing volumes. This behaviour indicates that the pad possesses a storage volume of adhesive fluid which is depleted over consecutive steps. However, the droplet volumes decreased to a non-zero steady state, providing evidence for a steady influx of secretion into the storage volume. Our results suggest that this influx rate is independent of press-down frequency. The mean storage volume of the pad (0.60 µm³ per µm² contact area) and the mean influx rate (0.00159 µm³ s⁻¹ per µm² contact area) indicate that it should take ca 6 min for a pad to ‘refill’. Our observation that completely depleted pads recovered initial footprint volumes after a pause of 15 min is consistent with this estimate, but it also suggests that the insects possess an ‘overflow’ feedback mechanism that limits further influx when the storage volume is full. It is unclear whether this overflow feedback mechanism is active (neuronal) or passive (mechanical).

A previous study on the chemical composition of insect adhesive fluid showed that locust tarsi, manually pressed several times onto a smooth glass surface, deposited between 53 000 and 74 000 µm³ of adhesive fluid [6]. Although measured under different conditions and in another insect (of similar size), these observations are in good agreement with a mean storage volume (V₀ × contact area) of 26 035 µm³ measured here for cockroaches.

The total volume of fluid stored in the pad is relatively small in comparison to the volume of the adhesive cuticle. The area-specific storage volume V₀ (0.60 µm³ per µm² contact area in cockroaches) is much smaller than the thickness of the specialized fibrous procuticle of smooth adhesive pads (in cockroaches it varies between 14.5 and 61 µm [16,19]). Thus, the cuticle provides more than sufficient space for holding the required volume of adhesive fluid.

Our results show that the steady-state influx rate into the storage volume was approximately constant, independent of the speed at which the pads were depleted.

4.1. Mechanism of fluid release

Our results show that smooth adhesive pads in contact with a glass surface continuously accumulated adhesive fluid in the perimeter of the contact zone. Once in contact with the surface, fluid built up at the edge of the pad. However, the increase gradually slowed down so that the volume of adhesive fluid remained approximately constant after 120 s.

It is unlikely that this slow change in deposition rate is the result of a neuronal feedback, as normal stepping frequencies would require a much faster reaction. It is also unclear whether and how the volume of the fluid can be monitored by tarsal sensors.

Instead, our results indicate that the secretion of adhesive fluid into the contact zone and its accumulation are driven by capillary forces. In the initial contact phase, the fluid volume in the contact zone is small so that the meniscus at the edge of the contact zone will have a small radius of curvature, giving rise to a strongly negative Laplace pressure. As a consequence, adhesive fluid will be sucked into the contact zone and will accumulate at the edge of the contact zone. This transport may be very fast initially, when capillary suction pulls fluid out of the channel-like cuticular folds [38]. The removal of fluid from the channels may deform the cuticle until the resisting elastic force balances the capillary suction. This equilibrium may be reached quickly, due to the facilitated flow of fluid through the channels. The very slow increase of fluid volume during stationary contact observed in our experiment is therefore unlikely to reflect this rapid flow of fluid. Instead, we assume that it is determined by the slowest link in the transport chain, which is either the secretion of fluid from epidermal cells into the cuticle or the transport of fluid through cuticular pore canals. In fact, even the highest flow rates observed during stationary contact were 30 times smaller than the ‘steady state’ flow rates observed in the footprint experiment, where the pad was fully depleted and where all fluid was secreted anew into the contact zone. This difference shows that the force driving the fluid was much smaller during stationary contact than when the pad was depleted of fluid.

Further accumulation of fluid along the perimeter of the pad increases the meniscus radius of curvature and thus reduces the capillary suction. As a consequence, fluid transport is slowed down. As shown in appendix B, a capillary suction model for a linear wedge predicts fluid volume to scale with (contact time)^2/3, approximately consistent with our observations (figure 2d).

Capillary suction can also explain the re-filling of the storage volume when the pad is not in contact. After depletion, secretion may be driven by capillarity into the cuticular folds on the pad surface until they are largely filled. However, we cannot exclude that internal pad pressure also contributes to secretion transport.

Capillary suction thus provides a simple non-neuronal mechanism controlling the release of adhesive fluid into the contact zone. The mechanism implies that both surface roughness and wettability of the substrate should increase the amount of substance released into the contact zone; further experiments are needed to test this prediction.

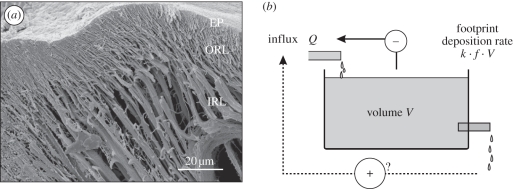
4.2. Secretion from a ‘sponge-like’ cuticle

The ‘sponge-like’ morphology of smooth adhesive pads in insects (figure 3a) suggests a mechanically controlled fluid release, similar to what was suggested for the pulvilli of Calliphora by Bauchhenss [27]. Adhesive fluid is driven into the contact zone by compression of the pad or by capillary suction when in contact with the surface. This will probably result in a deformation of the soft pad cuticle. When detaching from the surface, the pad will partly reabsorb adhesive fluid. It is probable that the pad can recover more fluid than would be expected from the balance of surface tension forces between surface and cuticle. This recovery may be driven by suction due to elastic recoil of the compressed cuticle. It will depend on the detailed mechanism of detachment, in particular on the detachment speed and the presence or absence of peeling, to what extent the compressed pad will be able to reabsorb adhesive fluid into the storage volume. For example, slow peeling will result in the accumulation of fluid at the peeling edge, thereby reducing capillary suction (see appendix B) and facilitating reabsorption.

Figure 3.

Structure of adhesive pad cuticle and model for fluid secretion. (a) SEM image of a freeze-fractured Nauphoeta cinerea arolium showing the branched fibrous structure of the procuticle (IRL, inner rod layer; ORL, outer rod layer; EP, epicuticle). (b) Schematic of the discrete-step compartmental model, which includes a storage volume V, a steady influx Q and an efflux (footprint deposition) that linearly depends on volume and step frequency. The dotted arrow shows a hypothesized positive effect of step frequency on influx rate (not confirmed by our experiments); the solid arrow indicates an overflow feedback mechanism limiting the influx when the storage volume is full. The model predicts an exponential decay of droplet volume down to a non-zero steady state (see appendix A).

The amount of adhesive fluid lost in freely running insects observed in this study was indeed very small, much less than the footprint volumes measured for simulated steps with perpendicular pull-offs. This discrepancy can be explained by the specific detachment movements of adhesive pads during locomotion [3,34,39–42] and by the ability of insects to control adhesive contact area. Many insects make very little contact with their adhesive organs when walking upright and use their soft pads primarily while climbing when adhesive forces are required [16,34,41,43]. Even when pads are in surface contact, insects can control the size of the adhesive contact area. For example, Oecophylla smaragdina ants were found to use only 14 per cent of their available contact area when walking upside down [33]. This control of adhesive contact area may not only be important for reducing wear of adhesive pads and facilitating detachment, but also for limiting fluid loss [33]. It is probable that capillary suction leads to more fluid deposition on rough surfaces [38], but the magnitude of this effect is still unknown.

We estimated the metabolic costs of adhesive fluid production using the approach of Penning de Vries [44]. Even the high footprint fluid production rates observed for simulated steps correspond to only small biosynthesis costs, which represent less than 1 per cent of the resting metabolic rate (see appendix C). Nevertheless, it is possible that a weak selection pressure acts against unnecessary losses of adhesive fluid.

Our results suggest that a passive, mechanically controlled release of secretion is sufficient to ensure that the right amount of fluid reaches the contact zone. A lack of fluid in the contact zone will give rise to very negative capillary pressures, drawing in more fluid. Conversely, larger volumes of fluid will result in less capillary suction, stopping further fluid release and promoting fluid reabsorption. Such a passive control of fluid release has the advantage that it is fast and reliable and does not require any neuronal feedback, a principle commonly found in biological systems.

Appendix A. Discrete-step compartmental model for fluid secretion

One of the simplest models to explain the observed exponential decay of footprint volume is a simple wash-out from a storage volume. We assume that there is a constant fluid production (influx) Q into a storage space V₀, from which fluid is then released into the contact zone (see figure 3b). This ‘compartment’ may be located within the fibrous procuticle and on the surface of the adhesive pads. To correct for different pad sizes, we define V₀ as the storage volume per µm² contact area and Q as the corresponding area-specific influx rate. We further assume that with every step, a constant proportion k (0 < k < 1) of the fluid volume V in the storage space is deposited on the surface. The remaining storage volume after the nth step is given by

A1

where 1/f is the time for one step (inverse of step frequency f). This model has the solution

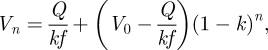A2

where V₀ is the fluid volume at the start of the experiment. Substituting c =−ln (1 − k) > 0, equation (A 2) can be rewritten for the droplet volume D_n as

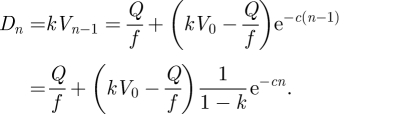A3

Thus, the model predicts an exponential decay of droplet volume D_n down to a steady state volume (after depletion) of Q/f.

Therefore, the measured droplet volumes were fitted by a three-parameter exponential model:

A4

From the fitting parameters a, b and c, we calculated Q, k and V₀ as

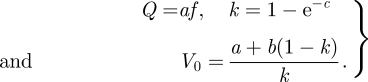A5

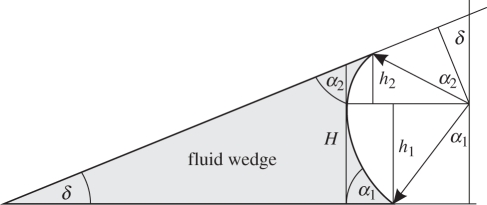
Appendix B. Fluid secretion by laplace pressure

Assuming a simple, linear-shaped fluid wedge surrounding the perimeter of the adhesive pad (see figure 4), the generated Laplace pressure depends on the height if the wedge H, the wedge angle δ, the fluid's contact angles α to pad and substrate and the fluid's surface tension γ with

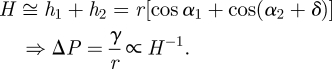B1

Figure 4.

Diagram of fluid wedge at the edge of the adhesive contact zone. H, maximum wedge height; α₁, α₂, contact angles; δ, wedge angle.

This model predicts a decreasing pressure p with an increasing height of the fluid wedge. Assuming a negative Laplace pressure driving the secretion of adhesive fluid from the inner procuticle through fine pores onto the surface of the adhesive pad, the fluid transport rate Q should linearly depend on the Laplace pressure p according to the Hagen–Poiseuille law with

B2

If the outer shape of the wedge is linear, then the wedge area scales with H², so that (for a constant perimeter) the volume V scales with

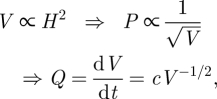B3

where c is a constant. Integration yields

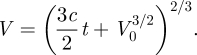B4

Assuming a small initial wedge volume V₀, V follows a power law and should approximately scale as

B5

Appendix C. Estimation of metabolic costs of adhesive fluid synthesis

To estimate the metabolic costs of adhesive fluid production, we follow the approach of Penning de Vries [44] and calculate the total glucose requirement, both for the carbon skeleton and the energy to synthesize the compounds. We ignore costs arising from transport within or between cells. The most detailed chemical analysis available for the composition of footprint secretion in smooth pads is the study by Vötsch et al. on Locusta migratoria [6], who found that the fluid contained amino acids (53%), long chained hydrocarbons (32.8%), fatty acids (7.8%) and carbohydrates (6.3%). For each of these substance classes, we calculated the ‘production value’ (PV), defined as the ratio of the end product mass and the mass of glucose required for carbon skeletons and energy [44]. As shown in table 1, the synthesis of 1 g of the fluid's organic matter would require 1.945 g of glucose. Thus, with a steady-state fluid secretion rate of 0.44 ng s⁻¹ for the whole insect (6 legs × 0.00159 µm³s⁻¹µm⁻² × 46 351 µm² mean contact area × density of water), the synthesis should cost 0.86 ng glucose s⁻¹.

Table 1.

Composition of the adhesive fluid of Locusta migratoria [6] and metabolic costs of biosynthesis [44]. Production value (PV) is the mass of the end product divided by the mass of glucose required for carbon skeletons and energy.

substance class	main substance	molecular weight (g mol−1)	production value (PV)	mass per 1 g organic matter (g)	glucose requirement (g)
amino acids	glutamate	147.13	1.107	0.530	0.479
hydrocarbons	C29-hydrocarbon	408.60	0.282	0.328	1.163
fatty acids	stearic acid	284.48	0.333	0.078	0.234
carbohydrates	di- and trisaccharides	342.30a	0.914	0.063	0.069
total					1.945

^aValue for sucrose.

A N. cinerea cockroach with a body weight of 370 mg has a resting metabolic rate (RMR) of approximately 0.45 mJ s⁻¹ (calculated from RMR = 0.217 ml O₂ g⁻¹ h⁻¹ [45]), corresponding to the combustion of 88 ng glucose s⁻¹. Thus, the cost of producing adhesive fluid at the measured rate corresponds to 0.97 per cent of the insect's resting metabolic rate. If, however, only 10 per cent of the adhesive fluid's mass is organic matter, as suggested by Vötsch et al. [6], this value would further decrease by one order or magnitude.