Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2011 Jan 12;8(60):934–941. doi: 10.1098/rsif.2010.0672

Interpretation of the human skin biotribological behaviour after tape stripping

C Pailler-Mattei 1,2,*, C Guerret-Piécourt 1, H Zahouani 1, S Nicoli 3
PMCID: PMC3104339  PMID: 21227961

Abstract

The present study deals with the modification of the human skin biotribological behaviour after tape stripping. The tape-stripping procedure consists in the sequential application and removal of adhesive tapes on the skin surface in order to remove stratum corneum (SC) layers, which electrically charges the skin surface. The skin electric charges generated by tape stripping highly change the skin friction behaviour by increasing the adhesion component of the skin friction coefficient. It has been proposed to rewrite the friction adhesion component as the sum of two terms: the first classical adhesion term depending on the intrinsic shear strength, τ0, and the second term depending on the electric shear strength, τelec. The experimental results allowed to estimate a numerical value of the electric shear strength τelec. Moreover, a plan capacitor model with a dielectric material inside was used to modelize the experimental system. This physical model permitted to evaluate the friction electric force and the electric shear strength values to calculate the skin friction coefficient after the tape stripping. The comparison between the experimental and the theoretical value of the skin friction coefficient after the tape stripping has shown the importance of the electric charges on skin biotribological behaviour. The static electric charges produced by tape stripping on the skin surface are probably able to highly modify the interaction of formulations with the skin surface and their spreading properties. This phenomenon, generally overlooked, should be taken into consideration as it could be involved in alteration of drug absorption.

Keywords: biotribology, electric charge, friction model, stratum corneum, tribo-electricity, tape stripping

1. Introduction

Human skin is a stratified tissue composed of three different layers, which are from the bottom to the top: hypodermis, dermis and epidermis. The outermost layer of epidermis, called stratum corneum (SC), arises from the sequential differentiation of cells migrating from the basal epidermal layer to the surface. The SC consists of about 15 tightly stacked layers of flattened dead cells full of keratin, embedded in a lipidic intercellular matrix, mainly composed of ceramides, long-chain free fatty acids and cholesterol [1]. The water content of the SC is low, compared with viable tissues, and it is characterized by a gradient that increases from the skin surface to the viable epidermis [2–7]. Due to its peculiar structure and composition, the SC represents the main barrier against the penetration of exogenous substances and also against transepidermal water loss.

Tape stripping is a minimally invasive procedure for the removal and sampling of SC. It consists in the sequential application and removal of adhesive tapes onto the skin surface, in order to collect microscopic layers of SC. Since skin stripping results in barrier disruption, this procedure is used, besides other applications, as an in vivo model for those skin diseases characterized by skin barrier weakening; for the same reason, it can be used to evaluate the effect of the application of skin care products on barrier restoration [8–10].

The SC, despite its limited thickness (between 10 and 20 µm), and even if its mechanical properties are very different from those of viable skin [11–14], is the layer that mainly controls the skin biotribological behaviour [12]; it follows that the removal of this layer (for instance by tape stripping) will dramatically affect them. Moreover, the static electric charges produced by tape stripping on the skin surface, are probably able to modify the interaction of formulations with the skin surface and their spreading properties. This phenomenon, generally overlooked, should be taken into consideration as it may be involved in alteration of drug absorption.

The aim of this paper is to propose a new method to describe and explain the skin tribological behaviour in vivo after the tape-stripping procedure. In this study an original method is proposed to estimate the surface electric charge produced by tape stripping on the skin surface based on a tribological analysis.

In fact, because of the production of electric charges on the skin surface, the skin friction coefficient is highly modified, especially the adhesion component of the friction coefficient. To explain this modification, a new assumption about the classical friction law has been made. It consists in inserting into the adhesion component of the friction force an electric shear strength term, τelec, due to the electric charges on the skin surface. The value of the electric charge on the skin surface has been measured using a fieldmeter device and the electric shear strength has been experimentally estimated. The experimental value of the electric shear strength has been compared with the theoretical value obtained with a physical model consisting in a plan capacitor with dielectric material inside.

2. Material and methods

2.1. Bio-tribometer device and measurement of electric charges

The use of an original light load indentation/friction device to study the mechanical and tribological properties of human skin in vivo has been previously reported [15]. Traditionally, the indentation test consists in recording the penetration depth, δ, of a rigid indenter as a function of the applied normal load, Fz, during a loading/unloading experiment. The friction test consists in applying a constant normal load and sliding velocity on the skin surface and in measuring the resulting friction force, Fx. In the present study, the indentation/friction tests are performed in controlled displacement mode. The displacement is obtained from the National Instrument displacement tables and controlled by a displacement sensor (figure 1a). The indentation tests are realized with the z-displacement table, whereas the x-displacement table enables the friction tests. The maximum displacement during the loading/unloading cycle can reach about 15 mm with a resolution of 10 µm, and the experimental device offers a wide range of indenting/sliding velocities from 5 to 1500 µm s−1. In the present paper, the normal load was applied for a constant indentation speed 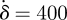Inline graphic µm s−1 and friction tests were performed for a constant friction velocity V = 400 µm s−1. The used probe was a spherical steel probe, with a radius of curvature R = 6.35 mm.

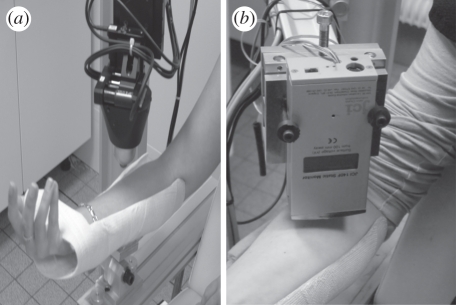
Figure 1.

Figure 1.

Open in a new tab

(a) Skin tribometer device; (b) fieldmeter device (JCI 140 Static Monitor). This allows us to measure the voltage of surfaces at a distance h (h is the distance between the charged skin surface and the fieldmeter device).

The electric charge value on the skin surface was measured by using a fieldmeter device (JCI 140 Static Monitor). It is a compact sensitive ‘field mill’ instrument to measure the voltage of surfaces at a distance h. The fieldmeter is fixed on a z-displacement table to control the distance, h, between the charged skin surface and the fieldmeter device (figure 1b). All the measurements were performed using h = 1 mm.

2.2. In vivo skin indentation/friction test

The friction tests were carried out on the inner forearm, at 5 cm from the elbow, of three healthy Caucasian women, from 28 to 34 years old. This location is easily accessed, relatively flat and there are few disturbances by the natural movements of the body. In order to facilitate reading of the results, the results of a unique volunteer, which approximately correspond to average behaviour among the three volunteers, will be chosen to illustrate the analysis. The tests were made at controlled temperature (22–24°C) and relative humidity (20–30%).

The tests were carried out in controlled normal load, which will allow us to include all the adhesion effects within the normal load (adhesion, electric charges effect, etc.).

All tests were repeated five times for each subject.

2.3. Tape-stripping test

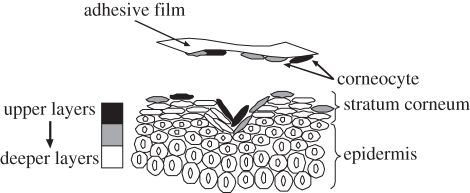
Tape stripping is a minimally invasive procedure for SC removal and sampling. It consists in the sequential application and removal of an adhesive tape-strip onto the skin surface, in order to collect microscopic layers (0.2–1 µm) of SC [16,17] (figure 2).

Figure 2.

Figure 2.

Open in a new tab

Schematic of the tape-stripping test.

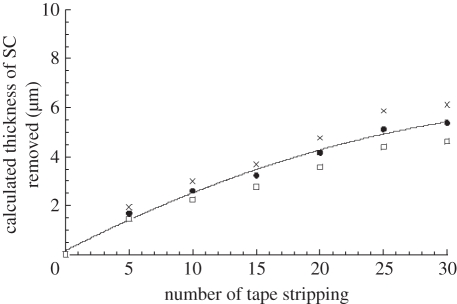
Scotch 3 M, precut to 1.9 cm × 2.5 cm, was used to realize the tape stripping. To estimate the quantity of the SC removed, each tape was weighed before and after the tape-stripping test. The mass variation obtained, Δm, corresponds to the mass of SC removed by each tape. The average thickness of the SC removed, e, was then calculated from the cumulative mass and the density of the SC, ρSC, from 1 to 1.33 g cm−3 [2,18] (figure 3). The evolution of the thickness of the SC removed from each tape stripping is reported in figure 3.

Figure 3.

Figure 3.

Open in a new tab

Average thickness of the removed stratum corneum versus number of tape strippings, for a representative subject. Thickness of removed stratum corneum, e, was calculated for both values of stratum corneum density (1 and 1.33 g cm−3 as 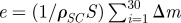Inline graphic, where S is the stripping surface, Δm the mass of stratum corneum removed from each tape stripping and ρSC the stratum corneum density (grey cross symbols, thickness of SC removed for SC density 1 g cm−3; black squares, average thickness of SC removed; open squares, thickness of SC removed for SC density 1.33 g cm−3).

3. Classical skin friction theory

Traditionally, the friction coefficient, μ, is defined as the ratio between the friction force, Fx, and the normal load applied on the material, Fz: μ = Fx/Fz. It is usually admitted that the friction force, Fx, is the sum of two components: a deformation term, Fdef, and a interfacial adhesion term, Fint, thus Fx = Fdef + Fint [19]. The skin biotribological behaviour has been widely studied in the literature [20]. In the case of skin, the deformation component of the friction force, Fdef, is negligible compared with the interfacial adhesion term [19,21], so in first approximation Fx = Fint.

The interfacial adhesion component of the frictional force is given by [22–24]

3. 3.1

where τ(p) is the average interfacial shear strength, depending on the applied pressure and defined as τ(p) = τ0 + αp [23,24]. τ0 is the intrinsic shear strength, p the average contact pressure and α represents the material properties controlling friction [19,23]. A is the projected contact area.

Dividing relation (3.1) by the normal load, Fz, and considering that p is the average contact pressure defined by the ratio between normal load, Fz, and contact area A, as p = Fz/A, the skin friction coefficient is given by

3. 3.2

4. Results and discussion

4.1. Analysis of the skin friction force curve as a function of the thickness of the removed stratum corneum

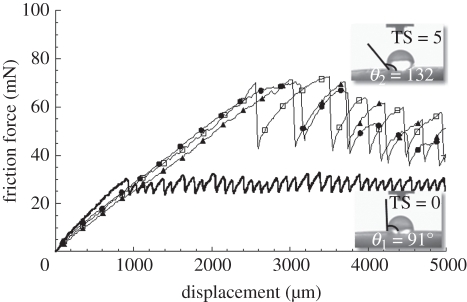
The variation of the skin friction force as a function of the amount of SC removed has been studied (figure 4). The obtained results indicate that the skin friction force and the amplitude of stick-slip phenomena greatly increase when removing layers of SC. The lateral stiffness, which corresponds to the slope of the friction curve in the sticky zone, decreases after the tape-stripping procedure, as previously observed in the literature [12]. Moreover, the distance necessary before the sliding phase between the skin and the steel spherical probe increases after the tape stripping. These substantial modifications of cutaneous friction force are explained by an increase in the adhesion force between the skin and the probe [12], which is due to a relevant change of the skin physico-chemical surface properties. To understand the interfacial skin property modifications after the tape stripping, wettability tests were realized with distilled water on the skin-stripped zone. The wettability tests were realized with the ‘pocket goniometer’. To measure the contact angle, a camera is integrated to the ‘pocket goniometer’. The volume of water micro-droplets placed onto skin surface was 1.5 µl. The contact angles between the distilled water and the skin surface were measured before (TS = 0) and after five (TS = 5) tape strippings (figure 4). The values of the contact angles measured before the tape stripping (TS = 0) (θ1 = 91°) confirm the values previously observed in the literature [25–27]. However, the shape of the distilled water micro-droplet after five tape strippings (TS = 5) (θ2 = 132°) are not in good agreement with the water gradient inside the epidermis [2–7]. The contact angle between the stripped skin and the distilled water should decrease, contrary to what is observed (figure 4).

Figure 4.

Figure 4.

Open in a new tab

Evolution of the skin friction force versus friction length for different values of tape stripping (TS). The friction tests were carried out for normal load equal to 40 mN and a constant friction velocity V = 400 µm s−1. Variations in the skin contact angle for distilled water before tape stripping (TS = 0) (θ1 = 91°) and after five tape strippings (TS = 5) (θ2 = 132°) were also reported (black line, 0 TS; open square, 5 TS; filled triangle, 15 TS; filled circle, 30 TS).

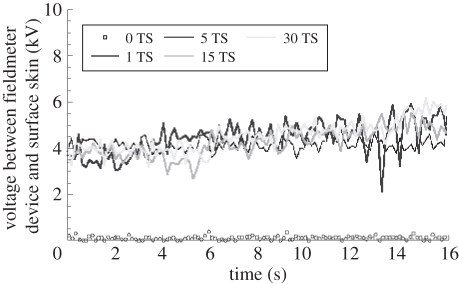
To explain the distilled micro-droplet shape and the skin friction force behaviour after tape stripping, the voltage between the fieldmeter device and the surface skin was measured as a function of time and for different tape-stripping values (figure 5). All the measurements were realized for a distance h = 1 mm (h is the distance between the fieldmeter device and the surface skin). The obtained voltage values are practically constant whatever the thickness of the removed SC. The average value of the voltage is between 4 and 5 kV. Small variations in the voltage are mainly due to the natural movement of the forearm during the measurements.

Figure 5.

Figure 5.

Open in a new tab

Voltage between fieldmeter device and skin surface versus time for different tape-stripping values. All the measurements were realized for a distance h = 1 mm (h is the distance between fieldmeter device and surface skin).

4.2. New assumption about skin friction theory

The increase in the skin friction force after tape stripping may be due to the electrical phenomenon at the interface between skin and probe. Electric charges may increase the adhesion component of the skin friction force. As a consequence, the friction force (3.1) can be re-written by adding an electric shear strength, τelec, as

4.2. 4.1

This means that the friction coefficient can be re-written as

4.2. 4.2

4.3. Experimental estimation of the electric shear strength

To evaluate experimentally the electric shear strength, τelec, the variation of the friction coefficient as a function of the inverse of the contact pressure has been reported in figure 6. The contact pressure is the average contact pressure, p, and it has been calculated with the Hertzian theory [28] for a measured skin reduced Young's modulus from 10 kPa to 14 kPa as a function of penetration depth [11], as

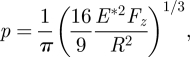4.3. 4.3

where E* is the measured skin reduced Young's modulus, Fz is the normal load and R is the radius of curvature of the spherical probe equal to 6.35 mm.

Figure 6.

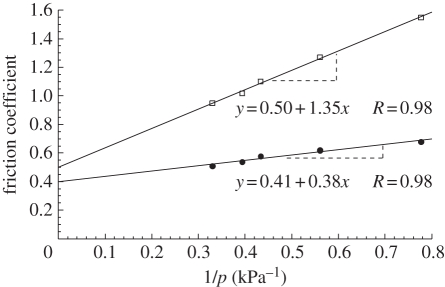
Figure 6.

Open in a new tab

Variation in skin friction coefficient before tape stripping (TS = 0) and after five tape strippings (TS = 5) as a function of inverse contact pressure (filled circle, TS = 0; open square, TS = 5).

The results indicate that the skin friction coefficient increases as a function of the inverse of the contact pressure before and after the tape-stripping procedure. The intrinsic shear strength, τ0, and the electric shear strength, τelec, were calculated using equations (3.2) and (4.2). The intrinsic shear strength, τ0, which is the slope of the curve before the tape stripping (figure 6), was calculated on the curve before the tape stripping with equation (3.2): τ0 = 0.38 kPa. The electric shear strength, τelec, was obtained with the curve after five tape strippings (figure 6). The slope of the curve after five tape strippings is τ0 + τelec and it is equal to 1.35 kPa; therefore, the value of the electric shear strength is τelec = 1.35 − τ0 = 0.97 kPa.

The small variation in the α parameter is probably due to the modification of the skin surface roughness after tape stripping [29].

4.4. Theoretical estimation of the electric shear strength

In this section, a physical model is proposed to link the electric shear strength to the electric charge onto surface skin generated by tape-stripping procedures.

4.4.1. Physical model to estimate the electric charge, Q, onto the stripped skin area

Human forearm can be considered as a dielectric material with dielectric constant ɛ1. During the friction experience the forearm is fixed on a metallic support and it was assumed that only the tape-stripping (TS) area, S, is electrically charged (S = 1.9 × 2.5 cm) (figure 7a). The fieldmeter device is above the forearm at a distance h equal to 1 mm. To estimate the electric charge, Q, on the stripped skin surface, an electric physical model is suggested to modelize the experimental problem. The equivalent model consists in a plan capacitor with a dielectric material inside and a dielectric constant, ɛ1 (figure 7b). The thickness, e1, of the dielectric material inside the plan capacitor, which symbolizes the human forearm, is chosen: e1 = 5 cm, which is the average thickness of the forearm of the volunteers in this study. The surface of the dielectric material is S, which corresponds to the surface of the tape-stripping area. The distance between the dielectric material and the fieldmeter device is noted, h, and equal to 1 mm as previously indicated. The environment between the dielectric material and the fieldmeter device is the air with the dielectric constant ɛ ≈ ɛ0, since the relative dielectric constant, ɛr(air), of the air is around 1 (ɛ = ɛ0ɛr(air)).

Figure 7.

Figure 7.

Open in a new tab

(a) Schematic of the measurement of the voltage between fieldmeter device and stripped skin; (b) electric physical equivalent model to estimate the total electric charge Q on stripped skin surface. The physical model is a plan capacitor with dielectric material inside.

If we neglect the boundary effect, the electric charge, Q, on the stripped skin surface has been estimated using the plan capacitor with dielectric material inside the model.

The electric field intensity between the fieldmeter device and the dielectric material, E0, and inside the dielectric material, E1, are, respectively [30]:

4.4.1. 4.4

and

4.4.1. 4.5

where σ is the surface charge density on the fieldmeter device.

The electrical potential difference, V, between the metallic support for the forearm and the fieldmeter device is given as

4.4.1. 4.6

where V1 and V2 are, respectively, the potential on the fieldmeter device and on the metallic support.

Using equations (4.4) and (4.5) in equation (4.6), the electrical potential difference is written as

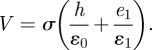4.4.1. 4.7

The surface charge density, σ, is defined as σ = Q/S; therefore, the potential difference can be written as a function of electric charge, Q, as

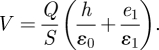4.4.1. 4.8

As a consequence the electric charge, Q, on the stripped skin surface is

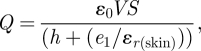4.4.1. 4.9

where ɛr(skin) is the skin relative permittivity given by ɛ1 = ɛ0ɛr(skin).

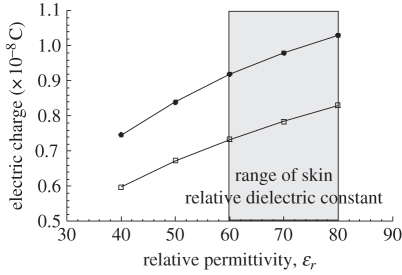
The variation in the electric charge, Q, on the stripped skin, calculated with relation (4.9), for different values of relative skin dielectric constant,ɛr(skin), is shown in figure 8. The results are indicated for two values of voltage, which correspond to the range of the voltage values previously measured with the fieldmeter device (figure 5). In the literature, there are few papers describing skin dielectric constant, ɛr(skin) [31,32]. The values of skin relative permittivity are influenced by the humidity rate and skin hydration. Human living tissues are mainly composed of water and there is a water gradient inside the epidermis. The tests were realized on the stripped skin in vivo; therefore, we assumed that the skin relative dielectric constant was very close to the water relative dielectric constant (ɛr(water) = 80), and, as a consequence, it has been assumed that the range of the skin relative dielectric constant was 60 < ɛr(skin) < 80 (figure 8).

Figure 8.

Figure 8.

Open in a new tab

Value of the electric charge, Q, generated by tape-stripping procedure on skin surface S (1.9 × 2.5 cm) as a function of relative permittivity, ɛr, for two values of voltage (4 kV and 5 kV) previously measured on stripped skin with a fieldmeter device (figure 5; filled square, V = 5 kV; open square, V = 4 kV).

The electric charges, Q, obtained with the average skin relative dielectric constant (ɛr(skin) = 70) are Q = 9.8 × 10−9 C for V = 5 kV or Q = 7.85 ×10−9 C for V = 4 kV (figure 8).

4.4.2. Relation between the electric charge, Q, on the skin surface and the electric shear strength, τelec

By using the previous plan capacitor model and by replacing the fieldmeter device with the spherical probe, the previous physical model can be used to evaluate the electrical variation energy for a displacement of the spherical probe from D to D + d. The electrical energy change lifts the spherical probe and the skin from a separation D to a separation D + d, and is expressed as

4.4.2. 4.10

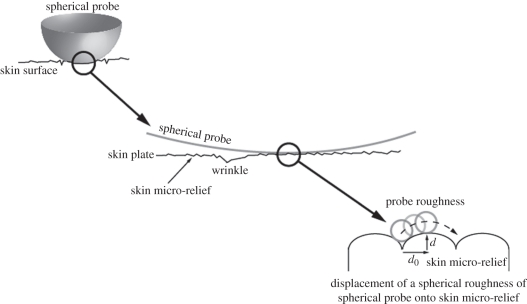
where D is the intermolecular distance between the two surfaces and d is the critical vertical displacement to initiate the sliding (figure 9a).

Figure 9.

Figure 9.

Open in a new tab

Schematic multi-scale two-dimensional representation of the sliding of the spherical probe on the skin surface. The cutaneous surface is not smooth, but has a specific relief. The skin relief can be observed at two different scales: the macroscopic scale, where the skin is composed of cutaneous plates and primary lines (or wrinkles) which separate the cutaneous plates; and the microscopic scale, which corresponds to the skin micro-relief and is composed of the secondary lines on the cutaneous plates. Like skin, in the microscopic scale, the spherical probe is not smooth. The probe roughness has been assimilated to spherical roughness for the model. The parameters d and d0 are the skin micro-relief parameters. d is the critical vertical displacement to initiate sliding and d0 is the lateral critical distance to initiate sliding [33]. The spherical geometry of the probe roughness has been chosen arbitrarily.

The electrical energy for the plan capacitor model is Eelec = (1/2)QV (V is given by relation (4.8)); as a consequence, the electrical variation energy from h = D to h = D + d, using relation (4.10), is given by

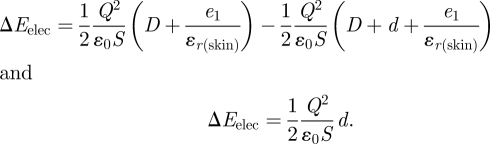4.4.2. 4.11

By using the classical friction model, the classical frictional energy, ΔEFx, between two surfaces in contact is the sum of two terms [33]:

4.4.2. 4.12

where ΔEad is the van der Waals frictional adhesion energy and ΔEload the frictional load energy due to the normal load applied.

By adding the electrical friction energy term in the previous classical frictional energy (4.12), the total frictional energy is written as

4.4.2. 4.13

By dividing the electrical friction energy by d0, which corresponds to the lateral critical distance to initiate sliding, the friction force, Fx, is obtained:

4.4.2.

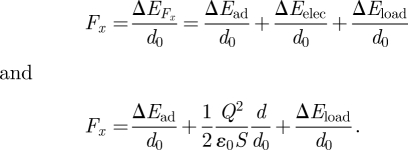The new global adhesion component of the friction force is

4.4.2. 4.14

By dividing relation (4.14) by the average contact area, A, which is the contact area between the spherical probe and the skin, the theoretical electric shear strength, linked to the electric charge on the skin surface, is obtained and defined as

4.4.2. 4.15

The parameters d and d0 are characteristics of the skin micro-relief. Therefore, the ratio d/d0 is a roughness parameter, approximately equal to 1 for skin aged about 30 years.

The average contact area, A, between the spherical probe and the skin is calculated with the Hertizian theory: A = πδR, where δ is the average penetration depth of the probe on the skin (δ ≈ 1 mm) and R is the radius of curvature of the spherical probe, R = 6.35 mm [28]. The average contact area is around 20 mm2.

Therefore, the theoretical electric shear strength calculated with equation (4.15) for both values of previously calculated Q are reported in table 1.

Table 1.

Results of the theoretical electric shear strength as a function of the values of electric charge, Q, on skin surface for a stripped skin surface S ≈ 4.7 cm2 and for contact area between skin and probe A ≈ 20 mm2.

electric charge, Q (C) 9.8 × 10−9 7.85 × 10−9
theoretical electric shear strength, τelec (kPa) 0.87 0.56
Open in a new tab

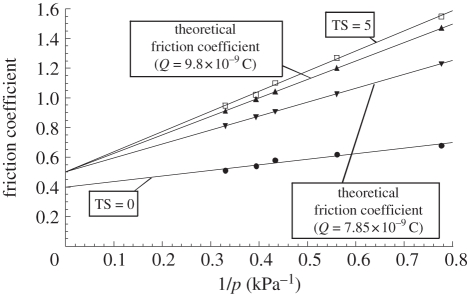
The comparison between the measured electric shear strength (τelec = 0.97 kPa) and the theoretical values of the electric shear strength, obtained with the electrical physical model (table 1), are in the same order of magnitude. The theoretical friction coefficient was calculated with equation (4.2), using the theoretical values of electric shear strength (table 1) and reported in figure 10. After tape stripping, the skin friction behaviour is highly modified (figure 10). The electric charges generated by tape stripping add an electric component to the adhesive component of the friction force, which increases significantly the friction coefficient value (figure 10). The proposed physical model seems to modelize the effect of the tape stripping on the skin friction behaviour, integrating and defining an electric shear strength, τelec, in the adhesive component of the friction force (4.1) or the friction coefficient (4.2).

Figure 10.

Figure 10.

Open in a new tab

Comparison between the measured friction coefficient after TS = 5 and the theoretical friction coefficient calculated with the two theoretical values of electric shear strenght previously obtained (Q = 9.8 × 10−9 C and Q = 7.85 × 10−9 C) as a function of inverse contact pressure. The friction coefficient has been calculated with α = 0.5, which is the value obtained after tape stripping (figure 6). The variation of the friction coefficient before tape stripping (TS = 0) is also indicated.

5. Conclusion

It has been shown that the tape-stripping procedure generates electric charges on the skin surface, which greatly change the skin biotribological behaviour and modify the physico-chemical properties of the skin surface. It has been proposed to add to the friction adhesion component a term depending on the electric charge created by tape stripping, which is the electric shear strength, τelec. The value of the electric shear strength has been experimentally estimated. A physical model has been proposed to theoretically estimate the value of the electric shear strength and to link the electric shear strength to the electric charge on the skin surface. Both values have been compared and they are in the same order of magnitude.

This model is very interesting because it allows us to obtain an analytical solution about the observed physical phenomena. However, the plan capacitor model with a dielectric inside presents some limitations. It does not separate the effect of the electric charges and the effect of the physico-chemical modifications after tape stripping on the skin friction behaviour. Moreover, the physical model requires some experimental parameters to obtain the electric shear strength. The measurements of the experimental parameters generate some errors on the theoretical physical model.

Tape stripping can be used to disrupt the SC and to evaluate the effect of the application of skin care products on barrier restoration. The static electric charges produced by tape stripping on the skin surface are probably able to greatly modify the interaction of formulations with the skin surface and their spreading properties. This phenomenon, generally overlooked, should be taken into consideration as it could be involved in alteration of drug absorption.

The results presented are very interesting since they show that the SC, after being damaged by tape stripping, partially preserves a sort of barrier function. In fact, the electric charges created by tape stripping greatly change the chemico-physical properties of the SC surface, hindering the spreading of water and its penetration inside the epidermis.

References

  • 1.Elias P. M. 1983. Epidermal lipids, barrier function, and desquamation. J. Invest. Dermatol. 80, 44–49 10.1038/jid.1983.12 (doi:10.1038/jid.1983.12) [DOI] [PubMed] [Google Scholar]
  • 2.Blank I. H., Moloney J., Emslie A. G., Simon I., Apt C. 1984. The diffusion of water across the stratum corneum as a function of its water content. J. Invest. Dermatol. 82, 188–194 10.1111/1523-1747.ep12259835 (doi:10.1111/1523-1747.ep12259835) [DOI] [PubMed] [Google Scholar]
  • 3.Crowther J. M., Sieg A., Blenkiron P., Marcott C., Matts P. J., Kaczvinsky J. R., Rawlings A. V. 2008. Measuring the effects of topical moisturizers on changes in stratum corneum thickness, water gradients and hydration in vivo. Br. J. Dermatol. 159, 567–577 10.1111/j.1365-2133.2008.08703.x (doi:10.1111/j.1365-2133.2008.08703.x) [DOI] [PubMed] [Google Scholar]
  • 4.Egawa M., Tagami H. 2008. Comparison of the depth profiles of water and water-binding substances in the stratum corneum determined in vivo by Raman spectroscopy between the cheek and volar forearm skin: effects of age, seasonal changes and artificial forced hydration. Br. J. Dermatol. 158, 251–260 10.1111/j.1365-2133.2007.08311.x (doi:10.1111/j.1365-2133.2007.08311.x) [DOI] [PubMed] [Google Scholar]
  • 5.Pirot F., Berardesca E., Kalia Y. N., Singh M., Maibach H. I., Guy R. H. 1998. Stratum corneum thickness and apparent water diffusivity: facile and noninvasive quantification in vivo. Pharm. Res. 15, 492–494 10.1023/A:1011996903513 (doi:10.1023/A:1011996903513) [DOI] [PubMed] [Google Scholar]
  • 6.Kalia Y. N., Pirot F., Guy R. H. 1996. Homogeneous transport in a heterogeneous membrane: water diffusion across human stratum corneum in vivo. Biophys. J. 71, 2692–2700 10.1016/S0006-3495(96)79460-2 (doi:10.1016/S0006-3495(96)79460-2) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Darlenski R., Sassning S., Tsankov N., Fluhr J. W. 2009. Non-invasive in vivo methods for investigation of the skin barrier physical properties. Eur. J. Pharm. Biopharm. 72, 295–303 10.1016/j.ejpb.2008.11.013 (doi:10.1016/j.ejpb.2008.11.013) [DOI] [PubMed] [Google Scholar]
  • 8.Loden M., Barany E. 2000. Skin-identical lipids versus petrolatum in the treatment of tape-stripped and detergent-perturbed human skin. Acta Derm. Venereol. 80, 412–415 10.1080/000155500300012774 (doi:10.1080/000155500300012774) [DOI] [PubMed] [Google Scholar]
  • 9.Gerritsen M. J., van Erp P. E., van Vlijmen-Willems I. M., Lenders L. T., van de Kerkhof P. C. 1994. Repeated tape stripping of normal skin: a histological assessment and comparison with events seen in psoriasis. Arch. Dermatol. Res. 286, 455–461 10.1007/BF00371571 (doi:10.1007/BF00371571) [DOI] [PubMed] [Google Scholar]
  • 10.Hachem J. P., et al. 2006. Serine protease signaling of epidermal permeability barrier homeostasis. J. Invest. Dermatol. 126, 2074–2086 10.1038/sj.jid.5700351 (doi:10.1038/sj.jid.5700351) [DOI] [PubMed] [Google Scholar]
  • 11.Pailler-Mattei C., Bec S., Zahouani H. 2008. In vivo measurements of the elastic mechanical properties of human skin by indentation tests. Med. Eng. Phys. 30, 599–606 10.1016/j.medengphy.2007.06.011 (doi:10.1016/j.medengphy.2007.06.011) [DOI] [PubMed] [Google Scholar]
  • 12.Pailler-Mattei C., Pavan S., Vargiolu R., Pirot F., Falson F., Zahouani H. 2007. Contribution of stratum corneum in determining bio-tribological properties of the human skin. Wear 263, 1038–1043 10.1016/j.wear.2007.01.128 (doi:10.1016/j.wear.2007.01.128) [DOI] [Google Scholar]
  • 13.Pailler-Mattei C., Zahouani H. 2004. Study of adhesion forces and mechanical properties of human skin in vivo. J. Adhes. Sci. Technol. 18, 1739–1758 10.1163/1568561042708368 (doi:10.1163/1568561042708368) [DOI] [Google Scholar]
  • 14.Pailler-Mattei C., Zahouani H. 2006. Analysis of adhesive behaviour of human skin in vivo by an indentation test. Tribol. Int. 39, 12–21 10.1016/j.triboint.2004.11.003 (doi:10.1016/j.triboint.2004.11.003) [DOI] [Google Scholar]
  • 15.Pailler-Mattei C., Nicoli S., Pirot F., Vargiolu R., Zahouani H. 2009. A new approach to describe the skin surface physical properties in vivo. Colloid. Surface. B 68, 200–206 10.1016/j.colsurfb.2008.10.005 (doi:10.1016/j.colsurfb.2008.10.005) [DOI] [PubMed] [Google Scholar]
  • 16.Jui-Chen T., Weiner N. D., Flynn G. L., Ferry J. 1991. Properties of adhesive tapes used for stratum corneum stripping. Int. J. Pharm. 72, 227–231 10.1016/0378-5173(91)90112-2 (doi:10.1016/0378-5173(91)90112-2) [DOI] [Google Scholar]
  • 17.Lademann J., Jacobi U., Surber C., Weigmann H.-J., Fluhr J. W. 2009. The tape stripping procedure—evaluation of some critical parameters. Eur. J. Pharm. Biopharm. 72, 317–323 10.1016/j.ejpb.2008.08.008 (doi:10.1016/j.ejpb.2008.08.008) [DOI] [PubMed] [Google Scholar]
  • 18.Anderson R. L., Cassidy J. M. 1973. Variations in physical dimension and chemical composition of human stratum corneum. J. Invest. Dermatol. 61, 30–32 10.1111/1523-1747.ep12674117 (doi:10.1111/1523-1747.ep12674117) [DOI] [PubMed] [Google Scholar]
  • 19.Adams M. J., Briscoe B. J., Johnson S. A. 2007. Friction and lubrication of human skin. Tribol. Lett. 26, 239–253 10.1007/s11249-007-9206-0 (doi:10.1007/s11249-007-9206-0) [DOI] [Google Scholar]
  • 20.Sivamani R. K., Goodman J., Gitis N. V., Maibach H. I. 2003. Coefficient of friction: tribological studies in man—an overview. Skin Res. Technol. 9, 227–234 10.1034/j.1600-0846.2003.02366.x (doi:10.1034/j.1600-0846.2003.02366.x) [DOI] [PubMed] [Google Scholar]
  • 21.Wolfram L. J. 1983. Friction of skin. J. Soc. Cosmet. Chem. 34, 465–476 [Google Scholar]
  • 22.Bowers R. C., Zisman W. A. 1968. Pressure effects in the friction of thin solid film lubricant. J. Appl. Phys. 39, 5385–5395 10.1063/1.1655987 (doi:10.1063/1.1655987) [DOI] [Google Scholar]
  • 23.Briscoe B. J. 1981. Wear of polymers: an essay on fundamental aspects. Tribol. Int. 14, 231–243 10.1016/0301-679X(81)90050-5 (doi:10.1016/0301-679X(81)90050-5) [DOI] [Google Scholar]
  • 24.Singer I. L., Bolster R. N., Wegand J., Fayeulle S., Stupp B. C. 1990. Hertzian stress contribution to low friction behaviour of thin MoS2 coating. Appl. Phys. Lett. 57, 995–997 10.1063/1.104276 (doi:10.1063/1.104276) [DOI] [Google Scholar]
  • 25.Ginn M. E., Noyes C. M., Jungermann E. 1968. The contact angle of water on viable human skin. J. Colloid Interf. Sci. 26, 146–151 10.1016/0021-9797(68)90306-8 (doi:10.1016/0021-9797(68)90306-8) [DOI] [PubMed] [Google Scholar]
  • 26.Mavon A., Zahouani H., Redoules D., Agache P., Gall Y., Humbert P. 1997. Sebum and stratum corneum lipids increase human skin surface free energy as determined from contact angle measurements: a study on two anatomical sites. Colloid. Surface. B 8, 147–155 10.1016/S0927-7765(96)01317-3 (doi:10.1016/S0927-7765(96)01317-3) [DOI] [Google Scholar]
  • 27.Mavon A., Redoules D., Humbert P., Agache P., Gall Y. 1998. Changes in sebum levels and skin surface free energy components following skin surface washing. Colloid. Surface. B 10, 243–250 10.1016/S0927-7765(98)00007-1 (doi:10.1016/S0927-7765(98)00007-1) [DOI] [Google Scholar]
  • 28.Johnson K. L. 2001. Contact mechanics, 2 edn. Cambridge, UK: Cambridge University Press [Google Scholar]
  • 29.Guerret-Piecourt C., Bec S., Treheux D. 2001. Electrical charges and tribology of insulating materials. C. R. Acad. Sci. 2, 761–774 10.1016/S1296-2147(01)01218-5 (doi:10.1016/S1296-2147(01)01218-5) [DOI] [Google Scholar]
  • 30.Bruhat G. 1959. Cours de Physique Generale: Electricité 7th edn. Paris, France: Masson & Cie [Google Scholar]
  • 31.Pethig R. 1987. Dielectric properties of body tissues. Clin. Phys. Physiol. Meas. 8, 5–12 10.1088/0143-0815/8/4A/002 (doi:10.1088/0143-0815/8/4A/002) [DOI] [PubMed] [Google Scholar]
  • 32.Yamamoto T., Yamamoto Y. 1976. Dielectric constant and resistivity of epidermal stratum corneum. Med. Biol. Eng. Comput 14, 494–500 [DOI] [PubMed] [Google Scholar]
  • 33.Israelachvili J. N., Chen Y.-L., Yoshizawa H. 1994. Relationship between adhesion and friction forces. J. Adhes. Sci. Technol. 8, 1231–1249 10.1163/156856194X00582 (doi:10.1163/156856194X00582) [DOI] [Google Scholar]

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES