de Bruijn cycles for neural decoding

Abstract

Stimulus counter-balance is critical for studies of neural habituation, bias, anticipation, and (more generally) the effect of stimulus history and context. We introduce de Bruijn cycles, a class of combinatorial objects, as the ideal source of pseudo-random stimulus sequences with arbitrary levels of counter-balance. Neuro-vascular imaging studies (such as BOLD fMRI) have an additional requirement imposed by the filtering and noise properties of the method: only some temporal frequencies of neural modulation are detectable. Extant methods of generating counterbalanced stimulus sequences yield neural modulations that are weakly (or not at all) detected by BOLD fMRI. We solve this limitation using a novel “path-guided” approach for the generation of de Bruijn cycles. The algorithm encodes a hypothesized neural modulation of specific temporal frequency within the seemingly random order of events. By positioning the modulation between the signal and noise bands of the neuro-vascular imaging method, the resulting sequence markedly improves detection power. These sequences may be used to study stimulus context and history effects in a manner not previously possible.

Introduction

Neuroscience experiments routinely examine the relationship between a set of stimuli and the neural responses they evoke. When presented sequentially and repeatedly, the ordering of the stimuli is fundamental to the inferences drawn. For the neuroimaging modality of BOLD fMRI, methodological advancement has been tied to novel orderings of stimuli, with increasingly sophisticated inferences following the introduction of “blocked” (Bandettini et al, 1993), sparse and rapid “event-related” (Dale and Buckner, 1997), and “adaptation” (Grill-Spector and Malach 2001; Henson and Rugg, 2003) designs. While multi-voxel pattern analysis (MVPA; Haxby et al., 2001) can use data derived from any of these sequencing approaches, stimulus ordering still has important consequences for inference and reproducibility (Aguirre, 2007).

Stimulus ordering plays an especially critical role in studies of “carry-over effects” (Aguirre, 2007): the impact of stimulus history and context upon neural response. All studies of neural adaptation (Desimone 1996) are measures of carry-over effects, as are studies of anticipation, priming, bias (Kahn et al, 2010), contrast (Gescheider, 1988), and temporal non-linearity. These effects are measured efficiently and without bias in the setting of counter-balanced stimulus sequences (Aguirre, 2007).

A sequence in which every stimulus appears immediately before every other stimulus is counterbalanced at the n=2 level, meaning that every possible sequential pairing of stimuli is included an equal number of times. Higher-level counterbalancing is possible, in which every triplet (or n-tuple) of possible sequential stimulus orderings are present. In fact, n=3 counterbalancing or greater is preferred in BOLD fMRI studies that seek to measure carry-over effects. This requirement derives from the ability to model only the history of stimuli, as opposed to the history of neural states of the system (see Appendix A for a complete examination of this issue).

Experiments using BOLD fMRI (and other neuroimaging methods based on vascular response; e.g. near-infrared optical tomography) face an additional challenge. The neural signal must be detected in the presence of both a low-pass hemodynamic response function and pink (1/f) autocorrelation in the noise (Zarahn et al., 1997). As a consequence, only neural modulations at certain temporal frequencies are detectable.

Extant methods of generating counter-balanced stimulus sequences yield neural modulations that are weakly (or not at all) detected by BOLD fMRI, and this limitation grows with ever higher levels of counter-balance. There is no way currently to design neuro-vascular imaging experiments that provide both statistical power and the inferential power of higher levels of stimulus counter-balance.

Here we describe a new foundation for the design of imaging studies, based upon the guided construction of de Bruijn cycles. De Bruijn cycles are a class of combinatorial objects that provide arbitrary levels of stimulus counter-balance in a maximally compact sequence. The ordering of the stimuli can be pseudo-random and therefore not predictable by the subject. They are generally useful for any neuroscience study that examines or controls the influence of stimulus order upon neural response.

To fully realize the potential of de Bruijn cycles for BOLD fMRI, however, an additional development is needed. We have created a novel, “path-guided” algorithm for the creation of deBruijn cycles which solves the problem of poor statistical power. The resulting sequence encodes in the seemingly random order of stimuli a neural modulation at one or more specific frequencies. These second-order temporal fluctuations may be positioned to be optimal for the signal and noise properties of the imaging technique. In application, the encoded modulation will only be detected if the hypothesized neural representation is present. This solution provides a many-fold improvement in statistical power over extant approaches.

Using path-guided sequences, an entire domain of study of the representation and effect of stimulus context and history is rendered tractable. We begin with the properties of de Bruijn cycles and our path-guided algorithm before considering an example experiment.

Theory

de Bruijn cycles

Consider an experiment with kdifferent stimuli (including any “blank” or null stimuli, which themselves constitute an experimental condition). We consider the order in which stimuli are presented by assigning each a label; for convenience we will use the natural numbers (0,1,2,3,…,k−1). De Bruijn sequences are a cyclic ordering of k-labels of order-n such that travel through the sequence yields every possible sub-sequence of length n ordering of the labels. Equivalent statements of this property are that de Bruijn sequences contain every “word” of length n in the alphabet of k labels, or that de Bruijn sequences are counterbalanced at the level of n. The sequence has a length of kⁿ. Cyclic sequences of this kind are a subject of study in discrete mathematics and have been discovered independently many times. It was Nicolaas Govert de Bruijn (pronounced roughly “duh-BROUN”) who formalized their description and determined that the number of distinct sequences for a given k and n is:

$$\frac{k{!}^{k^{(n-1)}}}{k^n}$$

which is clearly vast for even small values of k and n.

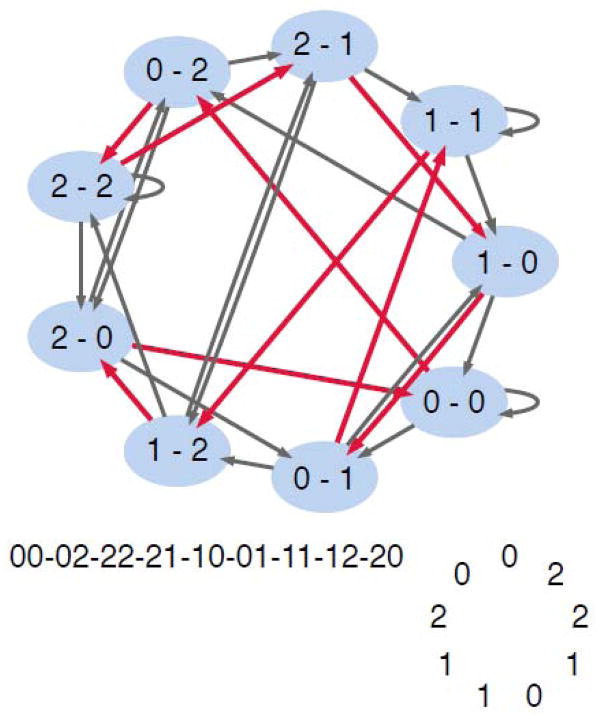
De Bruijn sequences may be represented, and thus constructed, as the path through a de Bruijn graph: a network of kⁿ connected nodes in which each node is one of the length n words that may be assembled from the k labels (Fig. 1). Two nodes are connected if their words are an available sequential transition. The de Bruijn cycle is given by a Hamiltoniancircuit through the graph, which is a path that visits each vertex once and returns to the starting vertex.

Fig. 1.

A k=3, n=2 de Bruijn graph and cycle. For an alphabet of three letters [0,1,2], there are 9, two-letter words. Each node (light blue) in the de Bruijn graph is a possible two-letter word. The directed edges between the nodes indicate available sequential transitions between one word and the next, each of which shifts the word by one register and adds a new letter. The red lines indicate one of 24 possible Hamiltonian circuits through the graph. Below the graph is the necklace of nodes indicated by the red path. In the bottom-right is the de Bruijn cycle, derived from the last register of each bead on the necklace. Travel about the cycle yields every possible two-letter word in the three-letter alphabet.

Finding Hamiltonian circuits is an NP-complete problem (Karp 1972), and thus solved by brute-force search algorithms. One approach begins at a random node in the graph and then selects randomly amongst the available neighboring nodes to trace a path. If a dead-end is reached from which there is no available next node, a “backtracking” process is used to re-route. This search approach is guaranteed to produce a valid Hamiltonian path (and thus a de Bruijn) cycle within a de Bruijn graph.

The de Bruijn cycle for a given k and n defines the sequential presentation of k different stimuli with the guarantee of nth-order counter-balance. Cycles of this form are of utility to a broad range of neuroscience experiments, although there has been only limited use of general de Bruijn cycles for this purpose (Brimijoin and O’Neill, 2010; Appendix B describes a taxonomy of de Bruijn sequences, encompassing counter-balanced sequences that have been used previously in neuroimaging studies). De Bruijn cycles hold the same potential benefits for neuro-vascular imaging studies, providing both rigor and flexibility in experimental design to support more robust and subtle inferences. To realize this potential, however, the idiosyncratic signal and noise properties of the measure must be addressed.

Detection Power

The properties of BOLD fMRI (and other neuro-vascular methods) render some experimental designs more statistically powerful than others. Specifically, variations in neural activity which approximate sinusoids of ~0.01–0.1 Hz are well detected (Zarahn et al., 1997). Higher frequencies are attenuated by the dispersed hemodynamic response, while lower frequencies are lost within the pink (1/f) noise of the system.

Several techniques have been used to search for, or iteratively craft, sequences with improved detection power while retaining a pseudo-random order (Aguirre 2007; Wager and Nichols 2003; Liu 2004). These approaches provide at most n=2 counter-balance (or an approximation thereof; Wager and Nichols 2003; optseq2; http://www.nitrc.org/projects/optseq/).

Ideally, we would use a stimulus ordering defined by a de Bruijn cycle with the desired level of counter-balance, and pick a particular cycle that provides for optimal detection power. The vast space of possible de Bruijn sequences renders a random search inefficient. We describe here a novel approach to the generation of de Bruijn cycles, in which the Hamiltonian circuit through the de Bruijn graph may be guided to craft a sequence with the desired properties.

Path-Guided sequences to increase decoding detection power

Given variation in the amplitude of expected responses for different stimuli or transitions, a sequence of stimuli may be created that will produce a modulation of neural activity within the band of temporal frequencies that are optimal for the imaging method. This is done by defining a guide function, which concentrates power within the desired band of temporal frequencies, and then biasing the path through the de Bruijn graph to follow that function. The guide function may be simply a sinusoid of the desired frequency, or the sum of sinusoids of random phases within a frequency range.

A path-guided sequence is generated by ranking the nodes that are available as the next point in the growing Hamiltonian path. The ranking favors nodes (and thus transitions) predicted to produce larger or smaller neural responses and this bias varies over the course of the sequence according to the guide function. (See Appendix C for details of the algorithm; code available for download at http://cfn.upenn.edu/aguirre).

The resulting sequences are ideal for a great many neuroimaging experiments: pseudo-random, with arbitrary levels of counter-balance, but with a tailored statistical power many times greater than that obtained by even extensive computational searches of possible stimulus orders.

Example experiment

We consider an example experiment designed to detect neural habituation (adaptation) that is proportional to stimulus dissimilarity (or distance within a stimulus space) (Jiang et al 2006; Drucker and Aguirre 2009; Drucker et al 2009). As is discussed in Appendix A, this is best examined with at least n=3 counterbalance. We will show that this is not possible with extant methods, but can be achieved using path-guided de Bruijn sequences. We begin with an example of the n=2 case—as this is more readily illustrated and compared to existing methods—before considering a third-level counter-balanced design.

Second-level counter-balance

Consider a set of 16 stimuli drawn from a two-dimensional stimulus space. We wish to test if the response to a given stimulus is modulated in proportion to its similarity to the preceding stimulus, as has been examined in many studies (e.g., Jiang et al 2006; Drucker and Aguirre 2009; Drucker et al 2009); such an experiment examines population codes for stimulus properties. Including a blank or “null” trial yields 17 different experimental states, requiring a k=17 sequence for presentation order. If each stimulus is to be presented for 1.5 seconds, a first-order counter-balanced (n=2) sequence yields ~8 minutes of data collection.

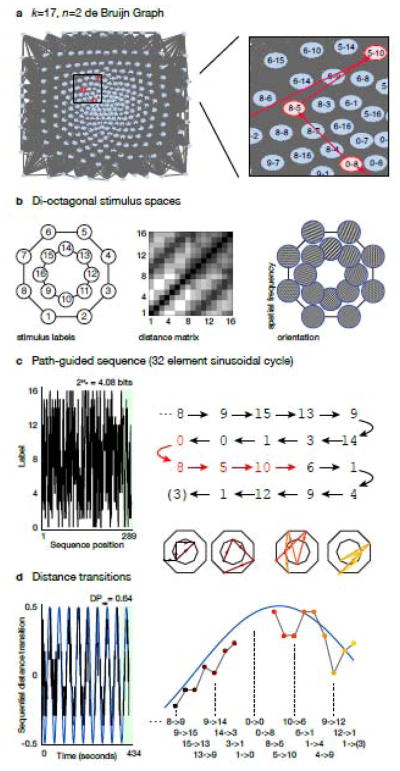
A k=17, n=2 de Bruijn cycle may be defined as the Hamiltonian circuit through the corresponding de Bruijn graph (Fig. 2a). There are over 8 × 10²⁴⁴ possible cycles, rendering a search for sequences with good detection power inefficient. Instead, we will guide a Hamiltonian circuit predicted to induce a sinusoidal modulation of the neural response with a period of 32 seconds (0.02 Hz).

Fig. 2.

An example experiment with a path-guided de Bruijn sequence. (a) The experiment calls for 17 stimuli (16 and a null-trial) and n=2 counter-balance. The corresponding de Bruijn graph is shown, with an enlargement to the right of a small portion. In the enlargement, a segment of a Hamiltonian circuit is shown in red (the entire path visits every node). The grey background is the web of the connections between nodes. (b) The example experiment uses sixteen stimuli drawn from a di-octagonal sampling of a two-dimensional space. The labels for each of the sixteen stimuli in the space are shown, along with the matrix that is the distance between each stimulus in the space (black near, white far). An example stimulus set—gratings varying in spatial frequency and orientation—is shown to the right. (c) The Hamiltonian circuit through the de Bruijn graph was guided by a sinusoidal function with a period of 32 elements (48 seconds). The sequence generated is pseudo-random. The sequence of labels for the portion of the plot shaded in green is shown to the right. The sequence elements marked in red correspond to the nodes and path indicated in red in panel a. The final value of the sequence is enclosed in parentheses as it is also the first value of the sequence, completing the cycle. (d) Given the distance matrix in panel b, the path-guided de Bruijn cycle encodes a series of sequential stimulus transitions that vary systematically in their distance. The plot demonstrates the sinusoidal modulation encoded in the seemingly random sequence. The green portion of the plot is expanded to the right, and corresponds to the sequence elements shown in panel c. The di-octagonal schematics show the location and sizes of the transitions through the stimulus space that produce overall sinusoidal modulation. Note that some transitions (e.g., between “blank” stimuli, or from a “blank” to a stimulus) have an undefined distance, and so are omitted from the plot.

The stimuli are sampled from the two-dimensional space on a di-octagonal grid (Drucker et al 2009) (Fig. 2b; the demonstration does not depend in any special way upon this sampling). The particular stimuli studied could be faces that differ in features, or shapes that vary in aspect ratio or curvature, or, as illustrated, gratings that vary in orientation and spatial frequency. The perceptual distance between any pairing of the stimuli is defined by a dissimilarity matrix. We bias the search along the growing Hamiltonian circuit to rank neighboring nodes by perceptual dissimilarity following the sinusoidal guide function.

A resulting path-guided sequence (Fig. 2c) is n=2 counterbalanced across the 17 stimuli. The sequence is pseudo-random, with essentially no sequential predictability (conditional entropy, 2^H₂ = 4.08 bits; Liu 2004). Encoded in this ordering of stimuli is the guide function, which is revealed by plotting the perceptual distance between sequential stimuli (Fig. 2d). A sinusoidal modulation of sequential distance is readily apparent. Relative detection power (DP_rel; Liu 2004; Friston et al 1999) is calculated with respect to a hemodynamic response function (Aguirre et al 1998) and a model of low-frequency noise (here a 0.01 Hz high-pass filter). If neural adaptation is proportional to perceptual distance in this experiment, this example provides DP_rel=0.64 (a perfect sinusoidal modulation at this frequency is an eigenmode of the system and has a DP_rel of 1.0). Varying the frequency of encoded sinusoid and searching across path-guided sequences, we have found sequences for this experimental design with a DP_rel as high as 0.74.

Experimental measurement of the sinusoidal signal modulation proportional to stimulus dissimilarity would be the target of a study of neural adaptation and population coding. Perhaps surprisingly, this sequence also has important utility in an MVPA study of the distributed pattern of voxel responses to the stimuli themselves. Using this sequence, the nuisance carry-over effects may be efficiently modeled and removed from the data, revealing the neural coding of the individual stimuli free of preceding context.

Table 1 presents the best performance of sequences obtained using extant methods for generating counter-balanced sequences. The best sequence had less than half of the relative detection power of the path-guided de Bruijn sequence. Additional measures of sequence randomness and balance are presented, and it can be seen that the path-guided de Bruijn sequence does not differ in any substantial way from the randomly generated de Bruijn sequences or an m-sequence in these measures.

Table 1. Properties of k=17, n=2 sequences.

Sequence properties calculated for a single, path-guided de Bruijn sequence, as well as the best performing of each of 1,000,00 randomly sequences of each type. The random de Bruijn sequences were generated from random Hamiltonian circuit; the type 1 index 1 and m-sequences were produced by searching across permutations of the assignment of labels to stimuli. DP_rel-adapt calculated by taking the variance of the hypothesized neural modulation proportional to sequential stimulus distance as the denominator, and the numerator as the variance of that modulation following application of a 0.01 Hz high-pass notch filter and convolution with a hemodynamic response function (Aguirre et al 1998). DP_rel-main was calculated for the main (direct) effect of presentation of any of the 16 stimuli versus the null-trials. Autocorrelation is the square root of the SSQ of the correlation of a sequence with itself at every lag except zero. Balance is a measure of the even distribution of labels across the sequence; small numbers indicate more balance (Hsieh et al 2004). Uniformity is a measure of spacing of labels across the sequence; small numbers indicate a more uniform distribution of labels (Hsieh et al 2004).

Sequence	DPrel-adapt	DPrel-main	Autocorrelation	Balance	Uniformity
path-guided de Bruijn	0.74	0.31	1.09	1918	95
random de Bruijn	0.29	0.34	0.99	1309	96
type 1, index 1	0.28	0.34	1.03	293	26
m-sequence	0.32	0.32	1.22	1135	94

Third-level counter-balance

The advantage of the path-guided de Bruijn approach becomes more apparent with higher levels of stimulus counter-balance. As sequence length increases geometrically with n, shorter stimulus presentation times are needed if the experiment is to be of practical duration. Continuing with our example, n=3 counter-balance for the 17 stimuli would require a ~20 minute study if each stimulus were presented for 250 msecs. Stimulus presentations of this brevity readily produce neural adaptation along the visual pathway (Kourtzi & Huberle, 2005), and may enhance early adaptive neural responses, which have greater stimulus specificity (Verhoef et al., 2008).

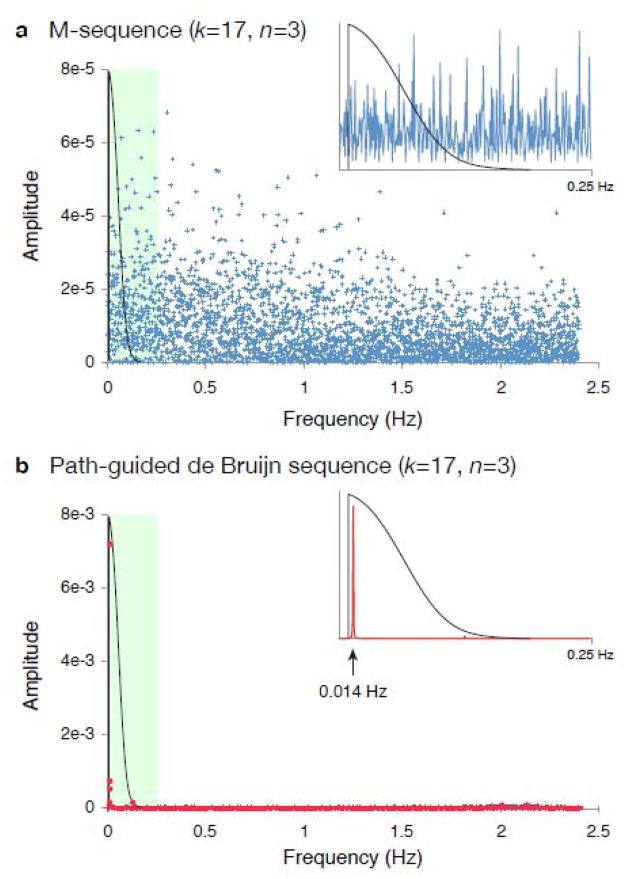
Previously, this experiment could only be conducted by defining an m-sequence of the appropriate length. The flaw of such a design is that the rapid stimulus presentation and requirement for counter-balance places the bulk of signal modulation at high temporal frequencies relative to the hemodynamic response function (Fig. 3a). Searching across 1,000,000 k=17, n=3, m-sequence variations (permuting the assignment of sequence label to stimulus; Aguirre 2007, Appendix A.3) we find the best DP_rel is 0.048. This is sufficiently low to render the experiment infeasible.

Fig. 3.

Power spectra of k=17, n=3 sequences. (a) 1,000,000 label permutations of an m-sequence were searched for the sequence with the greatest DP_rel-adapt for the stimulus space shown in Fig. 2b, given a stimulus presentation time of 250 msecs. The power spectrum of the distance transitions for this best sequence is shown in blue. In black is the transfer function of the hemodynamic response, which also incorporates a 0.01 Hz high-pass notch filter to represent the loss of sensitivity for the elevated 1/f noise range. Effectively, only neural variance under the curve of the black line will be represented in the BOLD fMRI signal. The shaded green region (0–0.25 Hz) is expanded in the inset. (b) A path-guided de Bruijn sequence was created, encoding a 0.014 Hz modulation in the distance transitions. The power spectrum is shown in red. Experimental variance is concentrated at the ideal location with respect to the filtering properties of the system.

With the path-guided approach, however, we may encode a lower-frequency modulation within the pattern of rapid presentations of stimuli. We guided a de Bruijn sequence with a sinusoidal period of 289 elements (0.014 Hz). The resulting sequence has DP_rel=0.32, a nearly 7-fold improvement over the best extant technique for stimulus ordering. The power-spectrum of the path-guided sequence shows the encoded sinusoidal modulation positioned between the filtering and noise properties of the BOLD fMRI system (Fig. 3b).

Discussion

Context is a key determinant of neural representation. Stimulus carry-over is therefore either quarry or confound in essentially every neuroscience experiment. De Bruijn cycles, providing arbitrary control of counter-balance for any number of stimuli, are of fundamental utility in decoding neural representation.

The characterization of a neural response function measures the “direct effect” of each stimulus upon neural activity, theoretically independent of stimulus context. In such studies, carry-over is a nuisance which can bias the results if not properly modeled (Kahn et al 2010). Stimulus counter-balance allows the direct and carry-over effects to be modeled independently and without bias (Kemptonn et al 2001), providing the opportunity to resolve the confound.

Multi-voxel pattern analysis makes use of the distribution of direct effects across brain locations. Un-modeled carry-over effects decrease the reproducibility and statistical power of the technique if different stimulus sequences are used during “training” and “test” phases. Incorrect inferences result if sequence patterns are repeated across phases. More generally, the attribution of neural coding to the effect of the stimuli themselves, as opposed to their status within the context of the other stimuli, requires attention to counter-balance.

Finally, carry-over effects are themselves the target of study in many neuroscience experiments. Our example experiment was tailored to detect a hypothesized neural adaptation effect. Carryover effects can take many other forms (bias, contrast, etc), and the techniques we have introduced may be used to create sequences optimized for the study of any of these phenomena.

The implementation of path-guided sequence construction may be expanded greatly beyond that presented here. Using a guide function composed of a range of sinusoids, the encoded (second order) modulation may be rendered more stochastic without substantial loss of detection power. Moreover, different modulations may be guided at different carrier frequencies, creating a sequence simultaneously optimized for the detection of two orthogonal neural response patterns.

The construction of sequences that encode multiple possible response patterns can provide greater generality and flexibility than our example design. The example study is designed to test for the presence of neural adaptation that is proportional to stimulus similarity. In this case, the design is precise: it is optimized to test a particular hypothesis, and has less power to detect other forms of neural response. This precision should not be mistaken for “bias”, in that the experiment will only detect the encoded pattern to a degree that reflects its match to the neural response.

It should further be understood that this specificity is a feature of the example experiment, and not of carry-over designs or path-guided de Bruijn sequences in general. The entire space of possible influences of stimulus history upon response is captured in a carry-over matrix (Aguirre 2007), and may be decomposed into a basis set of matrices that represent particular hypothesized influences of stimulus properties and timing upon neural response. A path-guided de Bruijn sequence may be generated that is sensitive to a set of these matrices, thus providing the ability to flexibly estimate the space of possible responses. Unavoidably, the more flexible and general an experimental design, the less power it has to test for any particular type of neural response.

Despite their flexibility and power, path-guided de Bruijn sequences have limits. In general, the fidelity of the encoded modulation to the guide function will be related to the range and distribution of steps possible in the distance matrix. Another limitation is that provision of ever higher levels of counter-balance will reduce the fidelity of the modulation for shorter (higher frequency) cycles, as the available neighbors in the Hamiltonian circuit become further constrained by the path history. Fortunately, this limitation is ameliorated by using a lower-frequency guide function, which is required regardless by the use of shorter stimulus presentations in long sequences.

A deeper limitation relates to the distribution of higher, uncontrolled levels of counter-balance. Our method establishes counter-balance at a specified level and encodes a particular modulation of stimuli in that sequence. To encode the modulation, however, the sequence will necessarily induce imperfect counter-balance at still higher levels. This is not a limitation of our method in particular, but is instead an unavoidable property of any sequence which is not infinitely long and utterly uncorrelated.

The application of de Bruijn cycles to decode neural states follows from their use in cryptography. For example, a de Bruijn cycle provides an efficient brute-force attack upon certain kinds of digital locks (those that do not use an “enter” key and accept the last n digits entered). The efficiency that a de Bruijn cycle provides in traversing the space of possible input states to a system is the basis for its usefulness in a neuroscience context. Beyond the general application of these sequences for neuroscience experiments, the path-guided approach dramatically improves the statistical power of neuro-vascular studies by tailoring experimental design to the signal and noise properties of the imaging method. The resulting sequences permit previously unachievable experiments, in which higher-order counterbalance reveals the effect of stimulus history and context on neural response.

Appendix A - The level of counterbalance in neuro-vascular studies

Generally, neuro-vascular imaging studies require stimulus counter-balance at a level one greater than the level at which inference is made. That is, measures of direct-effects should be made in the context of a n=2 counterbalanced sequence, while the carry-over effects of immediately preceding stimuli (e.g., in a study of neural adaptation) are ideally obtained in a sequence that is at least n=3 counter-balanced.

This additional level of counter-balance is mandated by a modeling limitation in neuro-vascular studies. While one can model the carry-over effects of the prior stimulus (t-1) upon the current stimulus (t), it is actually the prior neural state of the system that modulates the response to the current stimulus. In BOLD fMRI studies, an independent measure of the prior neural state of the system is generally not available. A possible concern is that the same prior stimulus (t-1) might leave the neural system in two different amplitude states (perhaps, dependent upon the effect of the stimulus that preceded the prior stimulus; e.g., the stimulus two back, t-2). For example, the t-1 stimulus may have been the same (along some relevant modeled dimension) as the t-2 stimulus, and thus the neural state is relatively adapted. Presentation then of the current (t) stimulus may result in a different signal response depending upon the prior neural state. If this effect were unbalanced across the possible stimulus pairings, it could introduce bias (the effect being dependent upon the particular sequence used and how second-order transitions were distributed across first-order transitions).

This issue is best addressed by employing a sequence with an additional level of counter balance. This will ensure that the neural amplitude state of the system prior to the current stimulus is always balanced across the possible transitions from the prior to current stimulus (presuming that the systematic neural state of the system prior to the current stimulus is entirely determined by the t-2 stimulus).

Appendix B - Specific forms of de Bruijn cycles

Specific forms of cyclic, counterbalanced sequences are contained within the larger class of de Bruijn sequences.

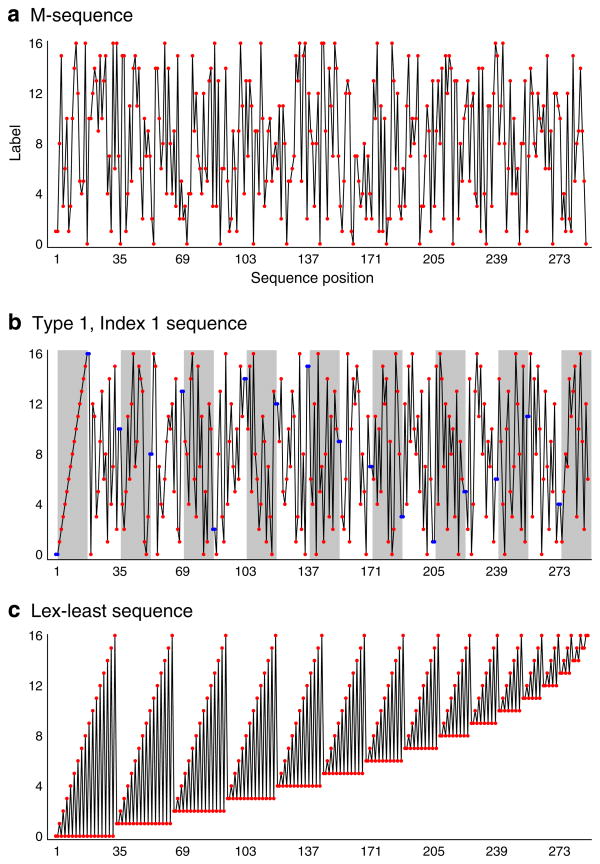
A modified (or “punctured”) de Bruijn sequence is created by removing one label (by convention, the label “zero”) from the single occurrence of the length n word composed of all zeros, yielding a sequence of length kⁿ 1. The set of Maximum Length Sequences (or m -sequences) are contained within this set of punctured de Bruijn sequences. In addition to the counter-balance properties of all de Bruijn sequences, m-sequences have the additional property of a nearly flat power spectrum (alternatively stated, the autocorrelation function of the sequence approaches a delta function). Introduced for use in BOLD fMRI studies by Buracas and Boynton (2002), m-sequences provide ideal efficiency for estimating the shape of the hemodynamic transfer function, although relatively weak detection power. M-sequences are generated with maximal linear feedback shift registers, and exist only for alphabets in which k is the power of a prime number; there are no constraints upon n. An example m-sequence for the k=17, n=2 case is shown in Figure B1a.

Fig. Appendix B1.

Examples of particular k=17, n=2 de Bruijn sequences. Note that the apparent “ordering” at the start some of the sequences is a consequence of the use of the natural numbers as sequence labels. In application, there is no requirement that the initial stimuli presented to a subject will have a perceptual ranking, as the assignment of labels to stimuli may be arbitrary. (a) M-sequence. (b) Type 1, index 1 sequence. Gray bars indicate the permuted “blocks” of the labels, and the repeated labels at the borders of the blocks are indicated by blue points. (c) Lexicographically-least sequence.

Type 1, Index 1 (T1I1) sequences are n=2 counterbalanced sequences of k labels. T1I1 sequences have the property of presenting permuted blocks of the labels over the course of the sequence, with repetition of the labels at the boundaries of each block. The sequences were described by Finnery and Outhwaite in 1956, and in 2008 Aletta Nonyane and Chris Theobald presented an algorithm for the production of T1I1 sequences with 6 or more labels. T1I1 sequences have some desirable properties for BOLD fMRI experiments (Aguirre 2007). T1I1 sequences have excellent balance and uniformity (Hsieh et al 2004), meaning that labels are evenly distributed across the sequence. Consequently, neural effects are relatively insensitive to order effects across the entire experiment. In other words, the T1I1 sequence has relatively little power at very low frequencies, thus avoiding the elevated (1/f) noise range of BOLD fMRI. Limitations include the non-stochastic structure of the sequence (each stimulus is guaranteed to appear twice within 2k 2 trials, and there is a stimulus repetition every k trials), the restriction to n=2 (i.e., no higher-order counterbalancing is possible as, for example, the word [010] is prohibited), and the absence of T1I1 sequences for k=3, 4, or 5. An example T1I1 for the k=17, n=2 case is shown in Figure B1b.

In contrast to T1I1 sequences which have a nearly even distribution of labels across the sequence, the lexicographically-least de Bruijn sequence (also known as a “Ford” sequence) is highly discrepant (Cooper 2010). This sequence is generated as the concatenation of the primitive parts of the Lyndon words of the k-label alphabet in lexicographic order (Arndt 2010). There exists a “lex-least” de Bruijn sequence for every k and n. An example lex least sequence for the k=17, n=2 case is shown in Figure B1b.

A Kautz sequence (Kautz 1968) is a non-de Bruijn sequence which is essentially a de Bruijn cycle without self-adjacency of labels. It is created by finding a Hamiltonian circuit through a Kautz Graph, which is a modified de Bruijn graph that eliminates those vertices that would lead to repetition of the final register of the nodes.

Appendix C - An algorithm for guided-path sequences

The pair-wise distances between k labels is specified in a k × k matrix D. We wish to create a de Bruijn sequence of k labels containing every word of length n in which the distances corresponding to sequential transitions in the sequence approximate a guide function G of length kⁿ. This may be done by guiding a Hamiltonian circuit through the de Bruijn graph composed of kⁿ directionally connected nodes.

We first discretize the guide function G into b values. Next, the values in D are ranked and then divided into b bins, such that each bin has an equal (or as close as possible) number of values. If the current node in the growing path is i, then:

1. Start at a random node (i=1)

2. Identify the m available neighbors (where 0 ≤ m ≤ k). If m=0 then initiate a back-track algorithm (Vandegriend 1998).

3. If m=1, select the only available node. If m>1, select the bin corresponding G_i. If there are no available nodes in that bin, select the next closest bin (randomly choose in the event of a tie).

4. Travel to a random neighbor within the selected bin, increment i.

5. If i=kⁿ and the current node is connected to the i=1 node, then the sequence is finished. Otherwise, continue with step 2.

Some minor stochasticity in node selection is desirable. This avoids the generation of a sequence which closely conforms to guide function early in the sequence, with a progressive departure from desired form as the path progresses and the set of available nodes decreases. For transitions between some stimuli (e.g., the stimuli that follow “null” trials or target stimuli), the distance matrix value may be undefined; these transitions can be randomly distributed throughout the sequence without disrupting the primary sinusoidal variation that is the target of optimization. The approach may also be described as assigning lengths to the connections in the de Bruijn graph equal to the predicted distances in D. The path-guiding algorithm then favors “trips” of certain lengths following the guide function G.