Design and Implementation of an Automated Partial Volume Correction in PET: Application to Dopamine Receptor Quantification in the Normal Human Striatum

Abstract

The considerable effort and potential lack of reproducibility of human-driven PET quantification and partial volume correction (PVC) can be alleviated by use of atlas-based automatic analysis. The present study examined the application of a new algorithm designed to automatically define 3-dimensional regions of interest (ROIs) and their effect on dopamine receptor quantification in the normal human brain striatum, both without and with PVC.

Methods

A total of 90 healthy volunteers (age range, 18–46 y) received a single injection of ¹¹C-raclopride, and automatic segmentation of concomitant structural MR images was performed using a maximum-probability atlas in combination with a trained neural network. For each identified tissue segment considered homogeneous for the tracer (or volumes of interest [VOIs]), an a priori criterion based on minimum axial recovery coefficient (RC_zmin = 50%, 75%, and 90%) was used to constrain the extent of each ROI.

Results

With ROIs essentially overlapping the entire VOI volume (obtained with RC_zmin = 50%), the binding potential (BP_ND) of ¹¹C-raclopride was found to be around 2.2 for caudate and 2.9 for putamen, an underestimation by 35% and 28%, respectively, according to PVC values. At increased RC_zmin, BP_ND estimates of ¹¹C-raclopride were increased by 12% and 21% for caudate and 8% and 15% for putamen when the associated ROIs decreased to around 65% and 43% of total tissue volume (VOI) for caudate and 67% and 31% for putamen. After PVC, we observed relative increases in BP_ND variance of 12% for caudate and 20% for putamen, whereas estimated BP_ND values all increased to 3.4 for caudate and 4.0 for putamen, regardless of ROI size. Dopamine receptor concentrations appeared less heterogeneous in the normal human striatum after PVC than they did without PVC: the 25%–30% difference in BP_ND estimates observed between caudate and putamen remained significant after PVC but was reduced to slightly less than 20%. Furthermore, the results were comparable with those obtained with a manual method currently in use in our laboratory.

Conclusion

The new algorithm allows for traditional PET data extraction and PVC in an entirely automatic fashion, thus avoiding labor-intensive analyses and potential intra- or interobserver variability. This study also offers the first, to our knowledge, large-scale application of PVC to dopamine D₂/D₃ receptor imaging with ¹¹C-raclopride in humans.

Accuracy of PET is greatly reduced by the limited spatial resolution of the scanner and the resulting partial volume (PV) effects. Although various methods have been proposed for PV correction (PVC) in emission tomography (1), a major limiting factor in applying PVC to brain PET data remains the amount of manual intervention needed. As for routine PET data analysis, region-of-interest (ROI) definition might still be performed in a manual or semi-automatic fashion; however, ROI drawing is tedious, time consuming, and questionable for reproducibility. Furthermore, differences in ROI size and placement lead to much greater differences in corresponding physiologic parameter estimates (2).

By automating PET data extraction, sources of variability associated with manual ROI definition can be eliminated, making it, in theory, easier to detect subtle changes in tracer concentrations. Several groups have proposed to automate regional activity extraction by using some atlas-based approaches in rodents (3), nonhuman primates (4), and humans (5–7). Although the method of Svarer (7) uses a threshold of tissue probability maps to define ROIs, our approach uses a threshold of the probability of detection within each PET slice, achieved through automated MRI segmentation from the ANIMAL+INSECT algorithm (8), and application of the concept of a minimum axial recovery coefficient (RC_zmin) for constraining ROI extent. We studied the impact of automatic 3-dimensional ROIs of decreasing sizes (increasing RC_zmin) on ¹¹C-raclopride binding-potential measurements in the normal human striatum, both without and with PVC. Although our projection-based PET simulator was validated for the Advance system (GE Healthcare) with a sphere phantom, we also assessed recovery coefficient (RC) values with an image-space dataset to compare projection-and image-space–based simulations (9).

MATERIALS AND METHODS

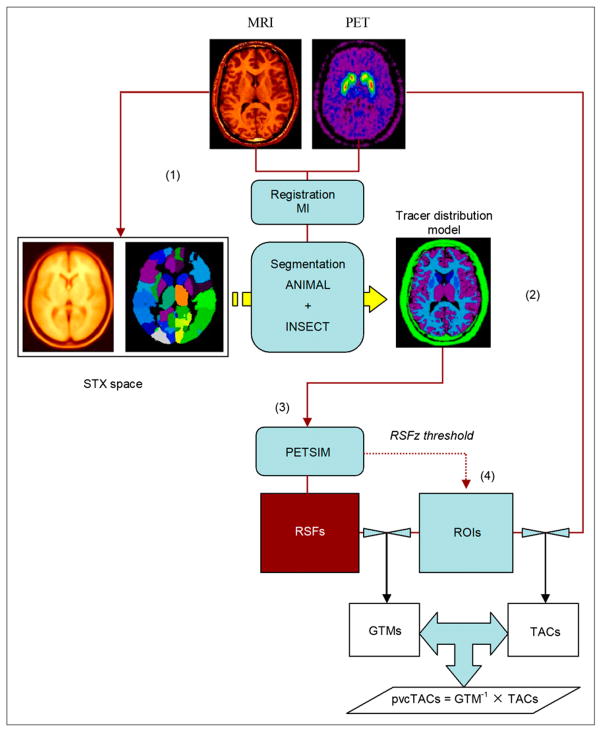
A c-shell script takes as sole input a numbered list of subjects with identifying fields pointing to the MRI and PET image data location. This algorithm (4PVC) can be broken into the following 4 steps (Fig. 1): image registration, tissue segmentation, simulation of resolution effects, and data extraction and PVC.

FIGURE 1.

Synopsis of automatic 4PVC algorithm. After spatial normalization of MRI in stereotactic (STX) space (1), max-proba brain atlas is used to segment MRI into specific brain regions that are mapped back to PET space according to computed spatial transformations (2). Resulting tracer distribution model is processed through PET simulator (3) to create individual RSFs. ROIs (4) are derived from thresholding axial component of RSF (RSF_z) and applied to RSF images to extract regional PV coefficients of GTM matrices and to dynamic PET images to generate regional time–activity curves. PV-corrected time–activity curves are obtained by GTM inversion and multiplication by observed time–activity curves.

Human Data Collection

We analyzed data from 90 healthy volunteers recruited for several ongoing research protocols at the Johns Hopkins Medical Institutions for the past 3 y, ranging in age from 18 to 46 y (18 women, mean age ± SD, 25.2 ± 7.5; and 72 men, mean age ± SD, 30.0 ± 7.5). A subgroup (n = 50) for which manual ROI time–activity curves were available was used for comparison with the fully automatic procedures.

A thermoplastic mask (Tru-Scan Imaging) was fitted to each patient to minimize head movement during scanning and optimize head placement in both MRI and PET scanners.

MRI

A sequence using spoiled gradient-recalled echo in the steady state was applied to acquire 124 transaxial images with a 1.5-T imaging system (Signa; GE Healthcare), using the following parameters: repetition time (TR), 35 ms; echo time (TE), 6 ms; flip angle (α) 45°; number of excitations (NEX), 1; slice thickness point-spread function (PSF_z), 1.5 mm, with no gap; field of view, 24 × 18 cm; and image acquisition matrix, 256 × 192, reformatted to 256 × 256, with a final voxel size of 0.9375 × 0.9375 × 1.5 mm.

PET

Each subject received a single 185- to 370-MBq bolus intravenous injection of high-specific-activity ¹¹C-raclopride, a D₂/D₃ dopamine receptor antagonist radioligand. Thirty frames were collected over 90 min on the Advance imaging system: 4 × 15, 4 × 30, 3 × 60, 2 × 120, 5 × 240, and 12 × 300 s. Data were acquired in the 3-dimensional mode, and images were reconstructed after correction for attenuation, scatter, randoms, dead-time, and isotope decay, to yield a 35-slice volume with final voxel size of 2 × 2 × 4.25 mm.

Tracer Distribution Model

Anatomy-based PVC methods such as geometric transfer matrix (GTM) PVC (10) require the identification of tissue components assumed to take up the tracer homogeneously. Digital models of tracer distribution throughout the brain can be built on high-resolution anatomic information such as structural MRI. Image segmentation methods are used to parcellate the gray-scale MR images into a limited number of meaningful anatomic components that represent the a priori anatomic (i.e., spatial) distribution of the tracer within the brain. Whether using hard or fuzzy segmentation, the assumption is made that the tracer is evenly distributed within each tissue component. This anatomic-to-functional topology mapping can usually be derived from known distributions assessed with postmortem and autoradiographic studies (11).

The tracer distribution model used here is built on a maximum-probability brain atlas (12), combined with a trained neural network for fine gray/white/cerebrospinal fluid classification (13). The maximum-probability (max-proba) atlas contains individual statistical parametric anatomic maps derived from 305 individual MRI datasets used to create the average brain, known as the MNI305 (14).

Both linear and nonlinear transformations were computed between each individual MR image (source volume) and the MNI305 target volume, by maximizing the cross-correlation between voxel intensities, and applied to the max-proba atlas to create a customized max-proba atlas for each subject (12). We complemented this low-resolution segmentation by application of a neural-network algorithm trained over large clusters of fixed landmarks for major tissue classification (gray, white, and cerebrospinal fluid) and originally developed for multiple sclerosis lesion detection (13). By masking of the high-resolution, 3-cluster classified volume provided by INSECT (13) by the low-resolution region parcellation provided by ANIMAL (12), we established 3-dimensional boundaries to provide a final high-resolution segmented volume (8). In addition to cerebral segmentation, the cerebellum was segmented after extraction in MNI space by a binary mask and application of a fuzzy c-means classification algorithm (15). The remaining soft tissues, including scalp, were also obtained by masking in MNI space and then assigned a common tissue code (“other”).

Depending on the tracer used, the number of regions originally present in the atlas is reduced by combining brain regions with known or a priori identical tracer distribution and metabolism, thus performing an anatomofunctional mapping. This final step was performed according to spatial MRI/PET normalization through mutual information (16), together with the previously computed transformations used for the MRI spatial normalization. In the particular case of ¹¹C-raclopride, we chose to test our algorithm with a 7-tissue system (cortical gray plus thalamus [gray], caudate nuclei [caudate], putamina [putamen], white matter [white], brain stem, cerebellum, and scalp plus other nonbrain tissue [other]).

Resolution Effects

On the basis of the known characteristics of the PSF of the PET system, the noise-free image of each tissue component VOI_i, or regional-spread function (RSF) (10), can be used to provide either correction maps or regional correction factors (1). The RSF of a given VOI_i is therefore expressed as (10):

$${\mathit{RSF}}_i(r)={\int }_{{\mathit{VOI}}_i}h(r,r^{\prime })d{r}^{\prime },$$ Eq. 1

where r and r′ represent 3-dimensional vectors in the image/object spaces and h(r,r′) is the PSF of the PET scanner. In the GTM PVC method, the observed activity concentration t_j within a region ROI_j is given by (10):

$$t_j=\sum _{i=1}^N{\omega }_{ij}{T}_i,$$ Eq. 2

where T_i represents the true activity concentration of VOI_i, and the weighting factors ω_ij represent the contribution of tissue component VOI_i into ROI_j, which in turn can be expressed as:

$${\omega }_{ij}=\frac{1}{v_j}{\int }_{RO{I}_j}{\mathit{RSF}}_i(r)dr,$$ Eq. 3

where v_j represents the total volume of ROI_j. The ω_ij factors make up a matrix of regional geometric transfer coefficients, or GTM. PV-corrected regional concentrations are obtained by GTM inversion and multiplication by the observed measurements obtained with the same set of ROIs (10).

In our current approach, a projection-based (analytic) PET simulator is used to reproduce finite sampling and resolution. We have modified the simulator originally developed for the previous-generation SCX2048 and SCX4096 scanners (17) and adapted it to match the higher resolution and better sampling characteristics of the GE Advance scanner (18). The blurring effects introduced during acquisition for a linear PET system can be decomposed into axial and in-plane components. In this work, each individual tissue component was first convolved with a gaussian function of 4.6-mm full width at half maximum (FWHM) along the z direction to simulate the effect of the axial resolution of the scanner to yield an RSF_z image; that is, the axial component of the RSF image (10). During this step, ROIs were automatically defined by applying an image threshold to the resulting RSF_z images to constrain the spatial extent of each regional mask (see “Human Data Extraction and Correction”). The second step in PSF simulation is the generation of projection sinograms computed for each slice of the RSF_z volume (17) and smoothing with a 2-dimensional gaussian kernel of 5.0-mm FWHM to simulate the GE Advance in-plane resolution (18). Images were then reconstructed with the same reprojection algorithm used for the clinical data, ensuring the same amount of smoothing. The 4PVC algorithm generates a 35-slice PET volume containing the RSF image of each tissue segment, arranged in a time series to simplify data storage and GTM extraction.

Validation of Chosen PSF

To test the accuracy of our simulated PSF used for 4PVC, 6 spheres (internal diameter, 8–33 mm) were filled with a homogeneous aqueous solution of ¹¹ CO₂ + H₂O (236 kBq/mL⁻¹), placed with their equator in a common plane and their center 7 cm from the center of a 20-cm water-filled flood phantom and scanned in the 3-dimensional acquisition mode for 1 h on the GE Advance system. Emission sinograms were corrected for photon attenuation by means of a transmission scan using 2 external ⁶⁸Ga line sources and for scatter, random, dead time, and isotope decay. The corrected data were finally reconstructed using the reprojection algorithm, which includes 2-dimensional (radial and axial) square filtering (cutoff at the Nyquist frequencies) before 3-dimensional backprojection (19). Second, simulated sphere images derived from concomitant segmented MR images were generated with our PET simulator. Maximum RC was computed for each sphere in 5-pixel ROIs. Assuming a gaussian “image” PSF, the global 3-dimensional FWHM of the GE Advance and that of the projection-based PET simulator were independently searched for minimizing the root-mean-square (RMS) distance between the theoretic computed RC curve (20) and the sphere RC data. A third set of sphere data was generated using an image-space convolution with an isotropic 3-dimensional convolution kernel of equivalent size to assess whether an image-space convolution would provide similar characteristics in the blurring of digitized objects (9).

Human Data Extraction and Correction

In the present study, ROIs used for data extraction were automatically defined during the PET simulation procedure described above and involved applying an image threshold to each individually produced RSF_z image resulting from simulation of the axial PSF. This criterion constrains the ROI to incorporate only voxels with values above a certain minimum (RC_zmin) of the maximum possible 100% axial RC; that is, voxels in RSF_z exhibiting values greater than RC_zmin are all set to unity, whereas all others are set to zero, thus creating a binary regional mask (i.e., ROI) for regional data extraction. We applied a 50% threshold as suggested in previous work (21) and performed data extraction with ROIs defined with RC_zmin values of 75% and 90%. In the 50% case, this is equivalent to resampling the high-resolution VOIs to the lower PET resolution with a gaussian weighting function of FWHM equal to axial PET resolution, followed by nearest-neighbor interpolation.

In all cases, the cerebellar ROI was defined using a unique RC_zmin threshold of 60%, which seemed to provide the best trade-off between limited PV and signal statistics to supply a smooth time–activity curve suitable for mathematic modeling. Each set of defined ROIs was applied to the computed RSF images for GTM extraction and to the original PET images to provide observed regional time–activity curves. The PV-corrected time–activity curves were then obtained by GTM inversion and multiplication by the observed time–activity curves (10).

Analysis of the 50-subject group compared BP_ND values obtained by the manual segmentation method with those obtained by automatic ROI definition with the RC_zmin = 50% threshold. We further compared BP_ND estimates across RC_zmin thresholds for the complete 90-subject group to assess the level of agreement between each pair of ROI definition methods (50%–75%, 75%–90%, and 50%–90%), both without and with PVC. We also calculated the differences between BP_ND values across each RC_zmin threshold pair to assess the variability of BP_ND estimates after PVC.

Physiologic Modeling

We applied the simplified reference tissue method (22) with the cerebellum considered as devoid of dopaminergic receptors and taken as the reference region. We computed the nondisplaceable component of the binding potential, BP_ND = f_ND × (B_avail/K_d), where f_ND is the free fraction of the nondisplaceable component of the signal, B_avail is the concentration of available receptors, and K_d is the dissociation constant (23) for each individual ROI both before and after PVC.

RESULTS

Resolution

Real and simulated images of the set of 6 hot spheres are presented in Figures 2A and 2B. To obtain the best fit—in a least-square sense—of the theoretic RC curve (20) to the observed RC values from the real sphere phantom experiment, the PSF for the GE Advance in 3-dimensional acquisition mode was found to be equivalent to a 3-dimensional gaussian function of 7.5-mm FWHM (% RMS = 3.5%), a value that is consistent with previously reported values (24). When searching for the equivalent FWHM in the case of the simulated data obtained with the projection-based simulator, the minimum RMS distance between the data points and the theoretic RC curve was also achieved for FWHM = 7.5 mm (% RMS = 3.8%). This value of 7.5-mm FWHM was subsequently taken as the kernel size for the image-based simulation used to provide another set of sphere images for which RC values were also computed. The resulting 3 sets of RC values as a function of sphere diameter normalized to the computed FWHM, together with the theoretic RC curve (20), are reported in Figure 2C. These results indicate that the resolution scheme of the projection-based simulator is satisfactory in reproducing the GE Advance limited spatial resolution and that an image-based simulation achieves similar results to those achieved by projection-based simulation, as previously reported (9).

FIGURE 2.

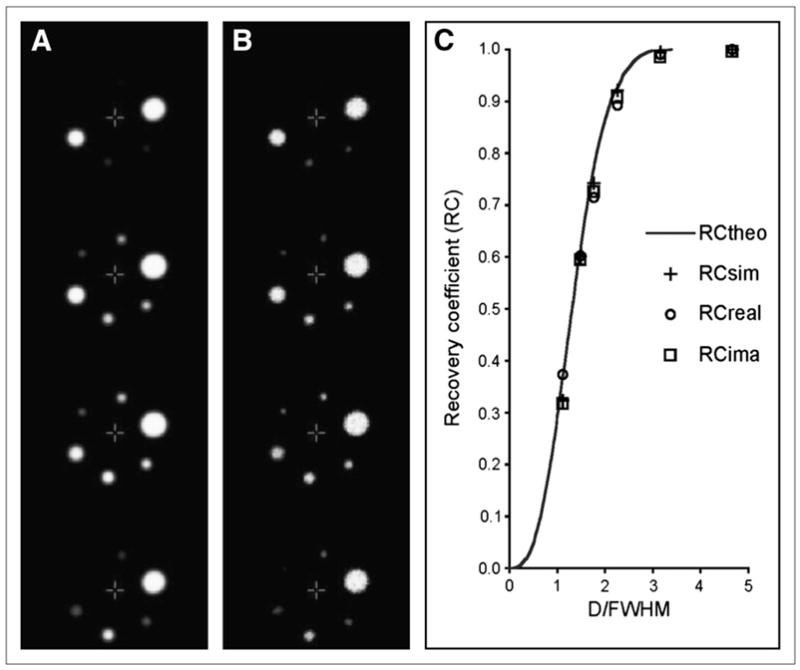
Slice-by-slice comparison of PET images of sphere phantom obtained by projection-based simulation (A) and in the case of real data (B) and RC curves for spheric objects (C) as function of their diameter D normalized to equivalent resolution (FWHM, 7.5 mm) of scanner. Peak values (maximum RC) are for real PET sphere images (open circles) and those generated with projection-based simulator (crosses) and by means of image-based convolution (squares), whereas solid curve represents theoretic RC curve given gaussian PSF of FWHM of 7.5 mm.

VOI and ROI

An example of the tracer distribution model used in the characterization of the PV effects in normal ¹¹C-raclopride studies is presented in Figure 3. For each subject, the MRI-derived tracer distribution model results from the automatic segmentation in standardized (MNI) space and subsequent spatial realignment with the time-weighted average distribution of the ¹¹C-raclopride tracer obtained with the GE Advance scanner over 90 min. Of the 90 datasets originally processed, 2 failed to reach completion because of apparent bad MR image quality that impaired the automatic MRI/PET registration algorithm and were therefore rejected for further analysis.

FIGURE 3.

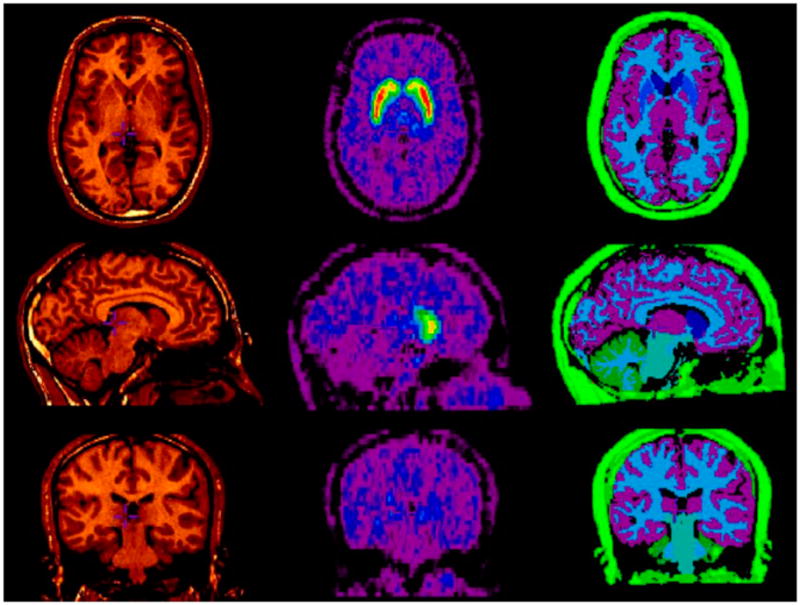
Typical definition of tracer distribution model (right) for healthy subject with 7 distinct tissue segments, or VOIs, obtained by MRI (left) automatic segmentation, together with corresponding time-weighted average PET image volume of distribution of tracer ¹¹C-raclopride (middle) used for MRI/PET spatial normalization.

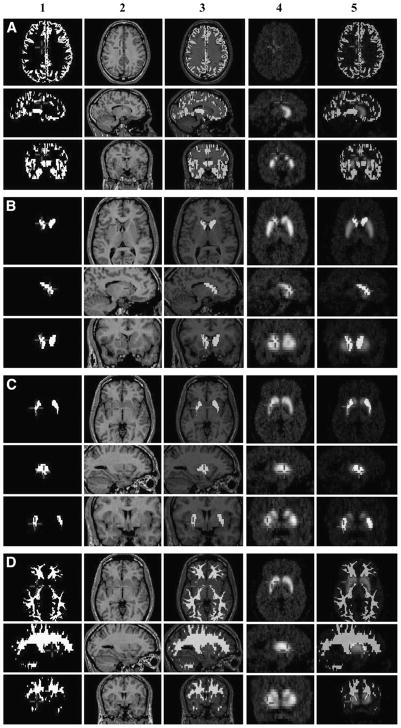
Typical automatic ROIs for gray, caudate, putamen, and white segments derived during the PET simulation process and used to extract both the observed regional time–activity curves from the PET images and the GTMs from the simulated RSF images are presented in Figure 4. The fraction of total structure volume (VOI) present in each ROI for the various threshold values (RC_zmin = 50%, 75%, and 90%) are summarized in Table 1. For comparison between the manual and automatic segmentation methods, caudate and putamen volumes computed for the subgroup of 50 subjects are presented in Table 2.

FIGURE 4.

Typical ROIs for gray (A), caudate nucleus (B), putamen (C), and white matter (D), taken as examples and used to extract both observed regional time–activity curves from ¹¹C-raclopride PET images and regional PVC factors constituting GTM. (A1–D1) Actual ROI defined after 75% threshold of RSF_z image; (A2–D2) central MRI slice in PET native space; (A3–D3) superimposition of ROI and MR; (A4–D4) corresponding time-weighted average ¹¹C-raclopride PET image; (A5–D5) superimposition of ROI and PET.

TABLE 1.

Total Structure Volume (VOI) and Associated ROI Volume of Tissue Components Identified by Automatic Segmentation

Tissue	Total VOI (mL)	Percentage of VOI* contained in ROI for an RCzmin of…
		50%†	75%†	90%†
Caudate	10.25 ± 1.46	96.5 ± 9.7	65.1 ± 7.6	42.7 ± 5.7
Putamen	8.74 ± 1.16	95.4 ± 1.6	67.2 ± 2.1	30.5 ± 1.8
Gray	555.20 ± 82.81	99.5 ± 5.5	56.3 ± 6.5	30.0 ± 5.0
White	484.81 ± 83.60	95.8 ± 4.4	66.8 ± 4.2	45.8 ± 2.8
Brain stem	25.49 ± 3.89	96.3 ± 12.0	72.1 ± 9.0	56.6 ± 7.5
Cerebellum	70.69 ± 19.53	84.5 ± 9.8	34.6 ± 10.7	13.0 ± 9.4

^*Mean ± SD for 88-subject group.

^†RC minimum voxel value for inclusion in ROI.

TABLE 2.

Striatal Volume Obtained in Subgroup of 50 Subjects

Segmentation method	Tissue volume (mL)*
	Caudate	Putamen
Manual	8.78 ± 1.37†	10.24 ± 1.03†
Automatic	10.40 ± 1.46†	8.57 ± 1.17†

^*Mean ± SD across 50-subject group.

^†Significant difference (t test, P < 0.01).

¹¹C-Raclopride Data

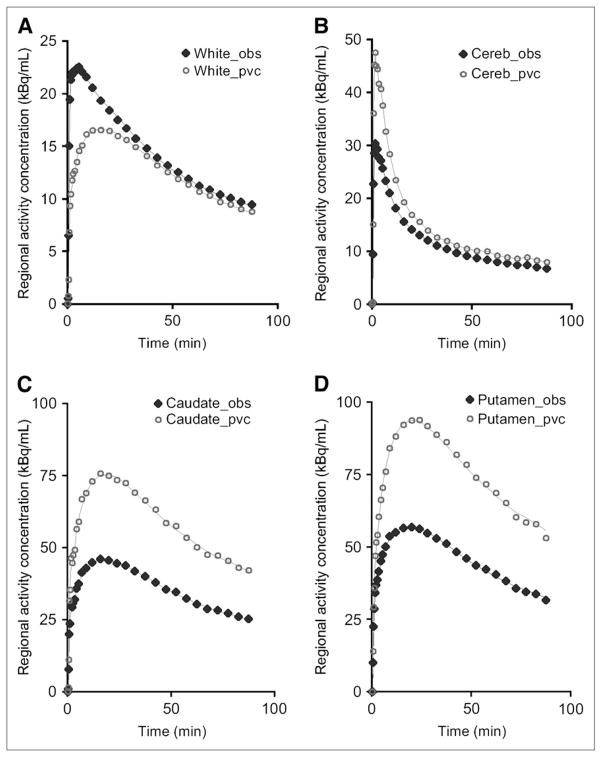
Figure 5 illustrates the typical regional time–activity curves automatically extracted from the real PET images for 4 of the individual brain regions studied, together with their PV-corrected counterparts, in the case where a 50% threshold was used as the spatial extent criterion. BP_NP values obtained for the 3 different values of the RC_zmin criterion used for the automatic definition of the ROIs are summarized in Table 3; Table 4 regroups the BP_NP values estimated for the subgroup of 50 subjects with ROIs obtained from both the manual segmentation and the automatic segmentation, using a 50% threshold.

FIGURE 5.

Observed (obs; solid diamonds) and PV-corrected (pvc; open circles) time–activity curves typically obtained in healthy subject who received single bolus injection of ¹¹C-raclopride. ROIs were defined with 50% RC_zmin threshold, in white matter (white) (A), cerebellum (cereb) (B), caudate (C), and putamen (D).

TABLE 3.

BP_ND Estimates of ¹¹C-Raclopride Before and After PVC in Normal Human Striatum for Various RC_zmin Thresholds Used to Define ROI Spatial Extent

Threshold (%)	BPND*
	Caudate		Putamen
	Observed	After PVC	Observed	After PVC
50	2.18 ± 0.35†	3.34 ± 0.60‡	2.87 ± 0.49†	3.96 ± 0.82‡
75	2.45 ± 0.39†	3.37 ± 0.60‡	3.09 ± 0.54†	3.97 ± 0.83‡
90	2.64 ± 0.43†	3.37 ± 0.60‡	3.30 ± 0.60†	3.93 ± 0.83‡

^*Mean ± SD over 88-subject group.

^†Significant difference across observed values (t test, P < 0.01).

^‡No significant difference across PVC values (t test, P > 0.95).

TABLE 4.

Measured BP_ND of ¹¹C-Raclopride in Normal Human Striatum Using ROI Defined from Coregistered MRI (Manual) and Automatically at RC_zmin = 50% Threshold (Auto)

ROI method	Tissue BPND*
	Caudate	Putamen
Manual	2.21 ± 0.32†	3.02 ± 0.35†
Auto	2.21 ± 0.37†	2.95 ± 0.45†

^*Mean ± SD over 50-subject group.

^†No significant difference (t test, P < 0.01).

DISCUSSION

Resolution Simulation

The sphere phantom results presented in Figure 2 indicate that although the projection-based PET simulation accurately reproduces the GE Advance limited spatial resolution, the 3-dimensional convolution in image space achieves comparable performance (Fig. 2C), in agreement with previous findings (9). Although projection-based simulations are superior in reproducing PET scanner geometric interaction (25), this finding strongly supports the potential of image-space GTM PVC methods that offer great improvement in processing speed over projection-based analytic simulations and that are, in practice, far easier to implement.

Segmentation and ROIs

The same threshold (RC_zmin = 50%, 75%, or 90%) was used to define the extent of each ROI derived from the automatically segmented MRI, with the exception of the cerebellum, for which RC_zmin was maintained at 60% throughout. This was done to reduce the number of variables involved in final BP_ND estimates. It appears that the cerebellar ROI decreases rapidly with increasing threshold (Table 1). The cerebellum is particularly prone to PV effects because of its particular “sandwiched” anatomy of gray-and white-matter components. In addition, the mathematic model used for the calculation of the BP_ND is heavily dependent on the cerebellar time–activity curve, which needs to be appropriate for accurate fitting. Hence, we have investigated the effect of ROI size specification on BP_ND estimates only with the cerebellar time–activity curve obtained with the 60% threshold throughout. At this value, we found 62.6% ± 10.8% of cerebellar gray total volume to be included in the cerebellar ROIs used (data not shown). This appeared to provide a good trade-off between a small ROI in favor of limiting the PV effects and that of a larger ROI to increase the statistics of the measurements to facilitate modeling. When RC_zmin was set at 50%, all ROIs showed an almost complete overlapping with corresponding tissue segments, with ROIs including more than 95% of total VOI volume (Table 1). At increasing RC_zmin, ROI volume decreased linearly for gray: ROI retained 56% of total VOI volume at the 75% threshold and 30% at the 90% threshold (Table 1), making for a 1.75% linear decrease in gray ROI volume per percentage increase in RC_zmin. Similar reductions were observed for the other tissue components, but without the linear trend observed with gray; the putamen appeared the second tissue most susceptible to RC_zmin increase, followed by caudate and white matter (Table 1).

When looking at the subgroup of 50 subjects, volumetric analysis of the striatum obtained by manual segmentation and that obtained automatically using the combination of ANIMAL+INSECT (8) indicates significant differences between corresponding volumes (Table 2). We found differences of volume of 13.7% ± 13.6% for the caudate nuclei and of 16.3% ± 9.4% for the putamen between the manual and automatic segmentations. However, these observed differences in structure total volume do not translate into differences in corresponding average BP_ND, which appear not significantly different between the manual and automatic ROI definitions (Table 4). However, one might question the impact of segmentation discrepancies on PV-corrected estimates because correction factors are directly dependent on the shape and volume of the structure. To address this issue, we performed an experiment in one particular dataset in which the original caudate was eroded by 1 pixel all around, leading to a 17% reduction in total volume, and another experiment in which this structure was dilated by 1 pixel to yield a 23% increase in total volume, more than covering the range of volume difference found between the automatic and the manual segmentations. We then generated RSF images of the original, eroded, and dilated caudate volumes. The resulting RCs were found to be 0.70 for the original caudate, 0.65 for the eroded caudate, and 0.73 for the dilated caudate, yielding an uncertainty in RC (∂RC) of about ± 5%. Such discrepancy is believed not to significantly impair the accuracy of the PV-corrected estimates (T), as the associated error will be of the form:

$$\partial T=\left(\frac{1}{RC}-\frac{1}{RC+\partial RC}\right)\times t,$$ Eq. 4

where t is the observed radioactivity concentration in the target (caudate) region. This calculation yields a value ∂T< 0.1 × t for the given value of ∂RC of 5%. Hence, the error associated with the corrected estimates T_i can be considered to be less than ± 10% of observed values. Although the study of the exact impact of such a discrepancy on the final BP_ND values is beyond the scope of the current work, it could be easily performed by simulation of dynamic images of the ¹¹C-raclopride tracer with the various normal, eroded, or dilated volumes of structures such as the caudate nucleus or putamen. However, we consider that the effect of missegmentation error on the final corrected estimates is much smaller than the error associated with regional activity measurements in the absence of PVC, hence justifying its application. Still, the choice of the image-segmentation method remains the most critical aspect of PVC accuracy and is an active field of research (26).

Although we considered the caudate and putamen as the 2 sole distinct regions of the striatum, tracer inhomogeneity is likely to be present in both the normal and diseased brains. Refined atlases, whether by adding the statistical parametric anatomic maps of the subregions (14) or by being more disease-specific (27), have become increasingly promising for small deep-structure segmentation (28). The atlas-based nonlinear deformation and segmentation algorithm (12) has shown good performance in cortical segmentation in the presence of atrophy (29) and has compared favorably with manual segmentation of deep structures such as the hippocampus, also in the presence of atrophy (30).

BP_ND

Before PVC, the present estimates of BP_ND in healthy subjects (Table 3) are in the range of earlier estimates (31,32). In the study of the 50-subject subgroup, we have not found significant differences in observed BP_ND values between the 2 methods of ROI definition (Table 4), indicating that the proposed automated approach is suitable for routine PET data analysis (i.e., without PVC). The analysis of the difference in BP_ND estimates obtained with the manual segmentation and those obtained by automatic segmentation reveals a small systematic bias between the 2 methods (BP_ND difference [mean ± SD], 0.07 ± 0.17), suggesting slightly smaller ROIs used for the manual definition. However, no detectable trend indicating a dependence on BP_ND values, which signifies good agreement between manual and automatic ROI definition, is demonstrated. Not surprisingly, higher BP_ND estimates were obtained with increasing threshold, yielding smaller ROIs (Table 3). Average BP_ND increased 12.0% in the caudate between ROIs defined with a 75% threshold, compared with time–activity curves obtained with a 50% threshold. Average BP_ND values were further increased by 7.9% when the threshold was increased to 90%, making a 20% difference in BP_ND estimate for the caudate between the 2 extreme thresholds (Table 3). Putaminal regions were slightly less affected, with a 7.7% and 6.7% increase in apparent BP_ND when the threshold values were increased from 50% to 75% and from 75% to 90%, respectively (Table 3).

After PVC, the corresponding significant increase in BP_ND (Table 3) was more pronounced for the caudate (range, 27%–52%) than for the putamen (range, 19%–38%). This increase is consistent with larger PV effects affecting the caudate because of the nearness of the third ventricle, whereas nonzero background activity completely surrounds the putamen. Although PV-corrected estimates have slightly larger variance than the original values (Table 3), the corresponding noise magnification factor, defined as the ratio of coefficient of variation after PVC divided by coefficient of variation before PVC (10) and easily derived from Table 3, was found to be 1.08–1.12 for the caudate and 1.15–1.20 for the putamen, depending on the threshold used. This indicates a limited effect of PVC on data dispersion and that data variance might reflect a large percentage of the true variability in dopamine receptor levels across the healthy population.

Regression analysis of BP_ND values obtained in the caudate and putamen across the various thresholds before PVC indicated a linear increase (R² > 0.96) in BP_ND estimates with increasing thresholds (Table 3). Conversely, linear regression analysis of BP_ND estimates obtained across thresholds after PVC presented no significant deviation from the identity line (R² > 0.95), consistent with the modeling of resolution effects with ROI size built into the GTM PVC method. The variability of the differences in BP_ND estimates across thresholds was slightly increased with increasing threshold after PVC: from an SD of 0.16 across the 50%–75% thresholds to an SD of 0.18 across the 75%–90% thresholds, further increasing to 0.23 across the 50%–90% thresholds (not shown). On the basis of these observations and that after PVC, larger ROIs exhibit no increased bias relative to smaller ROIs (while having better precision due to inclusion of more voxels), we feel that the lower 50% threshold provides superior PV-corrected BP_ND estimates. Although the 50% threshold worked well for structures such as the striatum observed with the GE Advance PET scanner (Table 1), even lower thresholds maximizing ROI–VOI overlap should be considered when analyzing smaller structures such as the ventral striatum, to retain sufficiently high statistics to limit noise amplification during PVC.

CONCLUSION

We have designed, implemented, and tested an automatic PVC algorithm (4PVC) capable of analyzing multiple dynamic PET data without any user intervention. We have shown that the systematic bias encountered with variable ROI size disappears after 4PVC, making this algorithm a potentially powerful tool for large dataset analyses where reproducibility is important.