Direct 4D reconstruction of parametric images incorporating anato-functional joint entropy

Abstract

We developed an anatomy-guided 4D closed-form algorithm to directly reconstruct parametric images from projection data for (nearly) irreversible tracers. Conventional methods consist of individually reconstructing 2D/3D PET data, followed by graphical analysis on the sequence of reconstructed image frames. The proposed direct reconstruction approach maintains the simplicity and accuracy of the expectation-maximization (EM) algorithm by extending the system matrix to include the relation between the parametric images and the measured data. A closed-form solution was achieved using a different hidden complete-data formulation within the EM framework. Furthermore, the proposed method was extended to maximum a posterior reconstruction via incorporation of MR image information, taking the joint entropy between MR and parametric PET features as the prior. Using realistic simulated noisy [¹¹C]-naltrindole PET and MR brain images/data, the quantitative performance of the proposed methods was investigated. Significant improvements in terms of noise versus bias performance were demonstrated when performing direct parametric reconstruction, and additionally upon extending the algorithm to its Bayesian counterpart using the MR-PET joint entropy measure.

1. Introduction

Dynamic PET imaging provides the capability to extract important physiological and biochemical parameters of interest (Rahmim and Zaidi 2008). The conventional process starts with reconstructing activity images from individual dynamic frames, after which kinetic parameters are estimated from the time-activity response of each voxel via compartmental analysis (Gunn et al 2001, Bentourkia and Zaidi, 2007). The conventional approach, however, generates noisy images as information from other frames is not included within the reconstruction task for a given dynamic frame. The emerging field of spatiotemporal 4D PET image reconstruction aims to obtain an improved noise property for a given temporal sampling scheme through incorporation of information from more than one frames in the reconstruction task (Rahmim et al 2009). An important class of spatiotemporal reconstruction techniques is to directly estimate the kinetic parameters from the projection data (e.g. Carson and Lange 1985,Meikle et al 1998, Kamasak et al 2005). The direct approach, also reviewed in Tsoumpas et al (2008b), benefits from the advantages of (i) collectively including the data from all dynamic frames in the reconstruction process compared to frame-by-frame reconstruction, and (ii) modeling the Poisson noise distribution in the projection space, as opposed to a need for noise modeling in the image domain, the latter confounded by space-dependent noise variance and inter-voxel correlations (Barrett et al 1994, Qi 2003).

The majority of parametric reconstruction methods in the past utilized nonlinear kinetic models to estimate individual kinetic parameters. By contrast, a number of graphical modeling methods have been developed that yield simple linear/visual techniques for the estimation/evaluation of the kinetic properties of various PET tracers (e.g. see Logan (2000) as a review). The Patlak linear model for irreversible tracers was recently included in a direct parametric estimation task, wherein the authors expanded the objective function for the reconstruction task to directly relate the Patlak parameters across the image to measured data, and used a preconditioned conjugate gradient algorithm to find the optimum solution (Wang et al 2008). Closed-form iterative expectation-maximization (EM) techniques were also developed independently by Tsoumpas et al (2008a) and Tang et al (2008); the latter elaborated and expanded in this work. In essence, we have extended the system matrix formulation and derived a direct closed-form 4D EM parametric reconstruction algorithm based on a new hidden complete-data formulation.

Furthermore, an area of interest has been to develop reconstruction algorithms incorporating anatomical information obtained from MR/CT measurement with a higher spatial resolution. Conventional techniques utilized segmented anatomical images, in which regional boundaries or labels were produced, to penalize inter-voxel intensity variations within the regions (e.g. Lipinski et al 1997, Comtat et al 2002). More flexible techniques allowing incorporation of differences between anatomical and functional segmentation (e.g. hot spots in brain stimulation studies or cold spots in arterial stenosis or occlusions) have also been proposed (e.g. Bowsher et al 1996, Rangarajan et al 2000). Within this context, more recent techniques tend to apply no segmentation of the anatomy but involve similarity measures that work directly on image features. In particular, Somayajula et al (2005) proposed to use the mutual information (MI) between features (e.g. intensities or intensity gradients) of MR/CT and PET images as priors. It was later suggested that the use of only the joint entropy (JE) component of the MI metric was better conditioned to minimize bias in the reconstructed images (Nuyts 2007). In Tang and Rahmim (2009a), we designed and investigated a one-step-late (OSL) maximum a posterior (MAP) algorithm with the JE between intensities of the anato-functional image pairs as the regularization, while the application of the JE between spatial feature images as generated using wavelets was proposed in Tang and Rahmim (2009b). In this work, we have extended the JE-MAP reconstruction methodology to direct parametric PET imaging within the proposed 4D image reconstruction framework.

2. Methods

2.1. Direct 4D reconstruction algorithm

Patlak and Blasberg (1985) presented a linear model for the time-activity curves in a region of interest (ROI) and the blood-input function, which applies to a tissue-compartment model that contains at least one irreversible compartment. Based on this Patlak model, the relation between the time-activity curve in a voxel j, C_j(t), and the plasma-input function, C^p(t), can be written as

$$C_j(t)={\kappa }_j{S}^p(t)+b_j{C}^p(t),t>t^{*},$$ (1)

where

$$S^p(t)={\displaystyle {\int }_0^t}{C}^p(\tau )\mathrm{d}\tau ,$$ (2)

t^* is the time for the tracer to reach steady state (determined visually) and κ_j and b_j are the Patlak slope and intercept parameters (as seen when dividing both sides of (1) by C^p(t)), respectively. In particular, the parameter of interest κ_j indicates the fractional rate of uptake from the plasma to the tissue. Next, note that the cumulated image $x_j^n$ in the voxel j and frame n can be written as

$$x_j^n={\displaystyle {\int }_{t_{s,n}}^{t_{e,n}}}{C}_j(\tau )\mathrm{d}\tau ={\kappa }_j{\overline{S}}^p(n)+b_j{\overline{C}}^p(n),$$ (3)

where t_s,n and t_e,n are the starting and ending times for the frame n (decay factors are not written here for simplicity, but need to be taken into account), and

$${\overline{S}}^p(n)={\displaystyle {\int }_{t_{s,n}}^{t_{e,n}}}{S}^p(\tau )\mathrm{d}\tau ,{\overline{C}}^p(n)={\displaystyle {\int }_{t_{s,n}}^{t_{e,n}}}{C}^p(\tau )\mathrm{d}\tau .$$ (4)

Using the standard system matrix P relating the image vector xⁿ at a particular frame n = (1, …, N) to the measured data yⁿ for that frame yⁿ = Pxⁿ, we can arrive at the following overall 4D relation:

$$\mathbf{Y}=\overline{\mathbf{P}}\mathbf{M},$$ (5)

where

$$\begin{array}{cccc}\hfill \mathbf{Y}=\left(\begin{array}{c}\hfill {\mathbf{y}}^1\hfill \\ \hfill \cdots \hfill \\ \hfill {\mathbf{y}}^N\hfill \end{array}\right),\hfill & \hfill \mathbf{M}=\left(\begin{array}{c}\hfill \mathit{\kappa }\hfill \\ \hfill \mathbf{b}\hfill \end{array}\right),\hfill & \hfill \text{and}\hfill & \hfill \overline{\mathbf{P}}=\left(\begin{array}{cc}\hfill {\overline{S}}^p(1)\mathbf{P}\hfill & \hfill {\overline{C}}^p(1)\mathbf{P}\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill {\overline{S}}^p(N)\mathbf{P}\hfill & \hfill {\overline{C}}^p(N)\mathbf{P}\hfill \end{array}\right).\hfill \end{array}$$ (6)

Thus, this approach effectively composes an extended system matrix P̄ relating the combined parametric image M to the overall 4D measured data Y.

It was first noted that the application of the direct parametric EM scheme proposed by Carson and Lange (1985) to this problem did not turn out to result in a closed-form solution. The standard, physically intuitive voxel contributions to each bin i were used as the hidden complete data in Carson and Lange (1985). Implementing a different underlying framework, we then derive a closed-form algorithm for direct 4D parametric reconstruction. In the present work, we employ the contributions of each of the κ_j and b_j elements to each bin i as the complete data, which forms an unobservable complete-data space. Implemented through the EM steps (Hebert and Leahy 1989), the above-mentioned complete data framework can be shown to first result in the following Q-function in the E-step:

$$Q((\mathit{\kappa },\mathit{b});({\mathit{\kappa }}^{\text{old}},{\mathbf{b}}^{\text{old}}))={\displaystyle \sum _j}\left[-{\kappa }_j{s}_j{\displaystyle \sum _{n=1}^N}{\overline{S}}^p(n)-b_j{s}_j{\displaystyle \sum _{n=1}^N}{\overline{C}}^p(n)+{\kappa }_j^{\text{old}}\frac{{\displaystyle {\sum }_{n=1}^N}{\overline{S}}^p(n){[{\mathbf{P}}^T{\mathbf{y}}^n]}_j}{{\overline{y}}_j^n({\mathit{\kappa }}^{\text{old}},{\mathbf{b}}^{\text{old}})}\text{log}{\kappa }_j+b_j^{\text{old}}\frac{{\displaystyle {\sum }_{n=1}^N}{\overline{C}}^p(n){[{\mathbf{P}}^T{\mathbf{y}}^n]}_j}{{\overline{y}}_j^n({\mathit{\kappa }}^{\text{old}},{\mathbf{b}}^{\text{old}})}\text{log}{b}_j\right],$$ (7)

where ȳⁿ (κ^old, b^old) = P[κ^oldS̄^p(n) + b^oldC̄^p(n)] (of which ${\overline{y}}_j^n$ is an element) is the estimated data based on the given parameter estimates and s (of which s_j is an element) is the standard sensitivity image. The maximization of the above formulation results in the 4D maximum-likelihood (ML) EM iterative algorithm:

$${\mathit{\kappa }}^{\text{new}}=\frac{{\mathit{\kappa }}^{\text{old}}}{\mathbf{s}{\displaystyle {\sum }_{n=1}^N}{\overline{S}}^p(n)}{\displaystyle \sum _{n=1}^N}{\overline{S}}^p(n){\mathbf{P}}^T\left[\frac{{\mathbf{y}}^n}{{\overline{\mathbf{y}}}^n({\mathit{\kappa }}^{\text{old}},{\mathbf{b}}^{\text{old}})}\right],$$ (8)

$${\mathbf{b}}^{\text{new}}=\frac{{\mathbf{b}}^{\text{old}}}{\mathbf{s}{\displaystyle {\sum }_{n=1}^N}{\overline{C}}^p(n)}{\displaystyle \sum _{n=1}^N}{\overline{C}}^p(n){\mathbf{P}}^T\left[\frac{{\mathbf{y}}^n}{{\overline{\mathbf{y}}}^n({\mathit{\kappa }}^{\text{old}},{\mathbf{b}}^{\text{old}})}\right].$$ (9)

It is worth noting that Fessler and Hero (1994) demonstrated that it is possible and sometimes helpful to use alternative complete-data formulations to arrive at more effective reconstruction algorithms. The present work proposes one such approach with significant potential benefits in the area of direct parametric EM reconstruction, as will be demonstrated in the following sections.

2.2. Incorporation of anato-functional joint entropy

We designed and investigated a OSL MAP algorithm with the JE between features (such as intensity) of the anato-functional image pairs as the prior (Tang and Rahmim 2009a). In the present work, we seek to implement and study direct 4D Bayesian parametric reconstruction incorporating the JE between the parametric image itself (u = κ or b) and the MR anatomical image (v). The feature vectors u and v are considered as realizations of the random feature variables U and V (when only the image intensity is considered), respectively. The JE of these two feature variables H_U,V is evaluated by constructing the vector random variable Z = [U,V]^T. The entropy of the random variable H_Z may be expressed as

$$H_{\mathbf{Z}}=-E_{\mathbf{Z}}[\text{ln}p(\mathbf{Z})]=-{\displaystyle \sum _{\mathbf{Z}}}p(\mathbf{Z})\text{ln}p(\mathbf{Z}),$$ (10)

where the summation is performed over all possible values of the vector random variable Z. The probability density p(Z) is approximated by a superposition of Gaussian densities centered on the realizations z_j of a sample Ω drawn from Z (Viola 1995, Duda et al 2001):

$$\widehat{p}(\mathbf{Z})=\frac{1}{N_{\mathrm{\Omega }}}{\displaystyle \sum _{j\in \mathrm{\Omega }}}{G}_{{\mathit{\psi }}_{\mathbf{Z}}}(\mathbf{Z}-{\mathbf{z}}_j)=\frac{1}{N_{\mathrm{\Omega }}}{\displaystyle \sum _{j\in \mathrm{\Omega }}}[{(2\pi )}^{\frac{-n}{2}}|{\mathit{\psi }}_{\mathbf{Z}}{|}^{-\frac{1}{2}}\text{exp}\left(-\frac{1}{2}{(\mathbf{Z}-{\mathbf{z}}_j)}^T{\mathit{\psi }}_{\mathbf{Z}}^{-1}(\mathbf{Z}-{\mathbf{z}}_j)\right)],$$ (11)

where N_Ω is the number of realizations of Z in the sample Ω, and n is the dimension of Z.

Assuming the covariance matrix is diagonal ψ_Z = DIAG(ψ_UU,ψ_VV), and ψ_UU and ψ_VV are diagonal, with the measured functional and anatomical intensity realizations u and v, the joint probability density p(U,V) is approximately evaluated as

$${\widehat{p}}_{\mathbf{u},\mathbf{v}}(U,V)=\frac{1}{N_{\mathrm{\Omega }}}{\displaystyle \sum _{j\in \mathrm{\Omega }}}[{(2\pi )}^{-1}{({\psi }_{\mathit{\text{UU}}}^j{\psi }_{\mathit{\text{VV}}}^j)}^{-\frac{1}{2}}\text{exp}\left(-\frac{1}{2}\frac{{(U-u_j)}^2}{{\psi }_{\mathit{\text{UU}}}^j}-\frac{1}{2}\frac{{(V-{\upsilon }_j)}^2}{{\psi }_{\mathit{\text{VV}}}^j}\right)].$$ (12)

With p(U,V) expressed in (12), the JE metric can be expressed as

$$H_{U,V}=-{\displaystyle \sum _U}{\displaystyle \sum _V}{\widehat{p}}_{\mathbf{u},\mathbf{v}}(U,V)\text{ln}{\widehat{p}}_{\mathbf{u},\mathbf{v}}(U,V).$$ (13)

The derivative of the JE metric was then incorporated within the OSL MAP algorithm, as we first proposed in Tang and Rahmim (2009a), but here for parametric image reconstruction. Specifically, applying the JE regularization to (8) (u = κ, where κ is a realization of random variable K) results in

$${\mathit{\kappa }}^{\text{new}}=\frac{{\mathit{\kappa }}^{\text{old}}}{\mathbf{s}{\displaystyle {\sum }_{n=1}^N}{\overline{S}}^p(n)+\beta \frac{\partial H_{K,V}}{\partial \mathit{\kappa }}{|}_{\mathit{\kappa }={\mathit{\kappa }}^{\text{old}}}}·{\displaystyle \sum _{n=1}^N}{\overline{S}}^p(n){\mathbf{P}}^T\left[\frac{{\mathbf{y}}^n}{{\overline{\mathbf{y}}}^n({\mathit{\kappa }}^{\text{old}},{\mathbf{b}}^{\text{old}})}\right],$$ (14)

where β is the weighting factor on the JE regularization, which strongly affects the performance of the proposed MAP reconstruction algorithm. It is optimized based on the evaluation metrics described in subsection 2.4. The JE between the functional and anatomical intensity realizations b and v is also incorporated within (9) for the b estimation.

2.3. Simulated tracer study

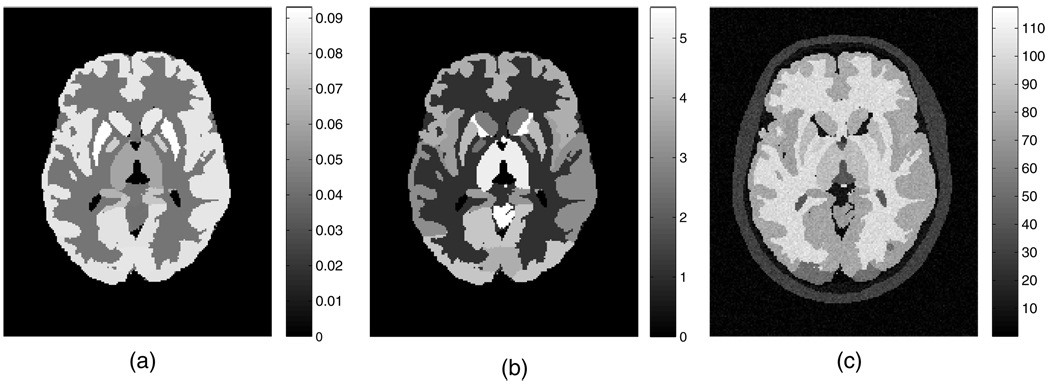
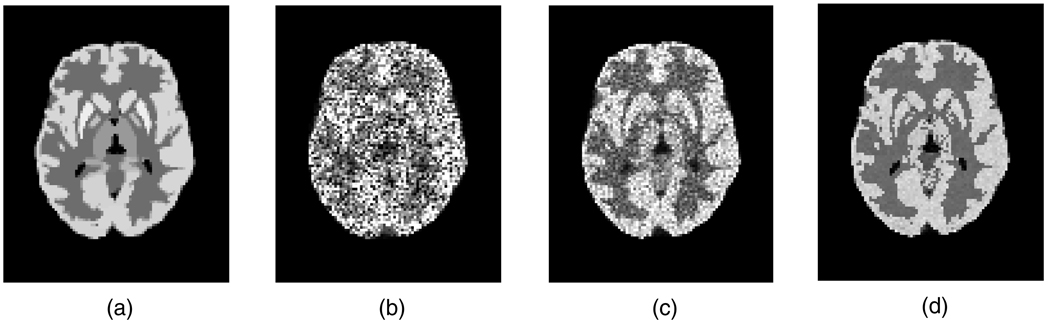
Aside from the widely utilized tracer FDG, which is irreversibly phosphorylated (k₄ = 0), some other tracers of interest also exhibit complete or near irreversibility (within the scanning periods). These tracers include [¹⁸F]-spiperone, [¹⁸F]-CFT (WIN 35428), 2-[¹⁸F]-FA and [¹¹C]-naltrindole, the last of which targeting the delta opioid receptor was simulated in this work. We used parametric brain images with the mean regional parametric slope and intercept estimates from a human naltrindole brain study as the starting truth in the simulations. The plasma tracer concentration as measured from the patient was employed with the parametric images to generate the set of dynamic image implementations on a mathematical brain phantom (Rahmim et al 2008a). Six 8-min frames covering the data acquisition starting from 18 to 66 min of the patient study were simulated. To achieve reconstructed (activity and parametric) images of 128 × 128 × 47 voxels with each voxel size as 2.34 × 2.34 × 3.27 mm³, the brain phantom was generated with a reduced voxel size by a factor of 2 in each dimension (Patlak slope and intercept images as shown in figures 1(a) and (b), respectively) for realistic data simulation. The corresponding MR image (the same size as the finer grid PET phantom images) was generated based on actual patient MR intensity measurement². Gaussian noise with zero mean and the standard deviation as the maximum image value divided by 25 (i.e. peak SNR = 25) was added to the MR image, after which the absolute value of the noisy image was acquired (resulted image shown in figure 1(c)) so that for small intensity values the image noise was Rayleigh distributed.

Figure 1.

Transaxial slice of the human brain phantoms simulating activities of (a) the Patlak slope, (b) the Patlak intercept and (c) the noisy MRI.

The simulated dedicated-brain PET scanner had 323 projection angles and 315 radial bins, and covered transaxial and axial fields-of-view (FOVs) of 35.0 cm and 15.3 cm, respectively. After projection of each image of the dynamic image sets, 30 noise realizations were implemented with the Poisson noise levels of the projection data consistent with routine [¹¹C]-naltrindole brain PET count rate levels. Attenuation and normalization effects were incorporated within the simulations; these effects were also incorporated within the reconstruction. Parametric images were obtained using (i) conventional dynamic image reconstruction, followed by graphic modeling analysis, (ii) the proposed 4D direct parametric reconstruction algorithm and (iii) the proposed 4D direct parametric MAP algorithm incorporating JE between parametric PET and MR images. The noisy MR image with a fine grid as described in the last paragraph was collapsed to the same size as the to-be-reconstructed parametric images, before it was used in the anato-functional JE calculation. We used 21 ordered subsets in all the reconstructions.

2.4. Evaluation metrics

To compare the parametric Patlak slope images estimated from the different algorithms described in the last subsection, we use the quantitative evaluation criterion, which is the tradeoff between normalized mean squared error (NMSE) and normalized standard deviation (NSD) for individual regions of the brain. The NMSE for each ROI on the brain was calculated using NMSE

$$\text{NMSE}=\frac{1}{m}{\displaystyle \sum _{j=1}^m}{\left(\frac{{\overline{\kappa }}^j-\overline{\mu }}{\overline{\mu }}\right)}^2,$$ (15)

where ${\overline{\kappa }}^j=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n}{\kappa }_i^j$ with ${\kappa }_i^j$ denoting the ith estimated voxel intensity from the j th noise realization; $\overline{\mu }=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n}{\mu }_i$ with μ_i representing the ith reference true Patlak slope value; n is the number of voxels in the ROI and m is the number of noise realizations. Note that the phantom Patlak slope image with a finer grid than the reconstructed images was collapsed to the size of the reconstructed image before the NMSE described above was calculated. For each ROI, the NSD was calculated across noise realizations using

$$\text{NSD}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\frac{\sqrt{\frac{1}{m-1}{\displaystyle {\sum }_{j=1}^m}{({\kappa }_i^j-{\overline{\kappa }}_i)}^2}}{{\overline{\kappa }}_i},$$ (16)

where ${\overline{\kappa }}_i=\frac{1}{m}{\displaystyle {\sum }_{j=1}^m}{\kappa }_i^j$. The change of the estimated Patlak slope NSD versus NMSE along with the reconstruction iteration number was plotted for each of the reconstruction/estimation algorithms for performance comparison.

3. Results

We applied the parametric image reconstruction/estimation algorithms, i.e. conventional image reconstruction followed by graphic modeling analysis, the proposed direct 4D parametric reconstruction, and the proposed anatomy-guided direct 4D parametric reconstruction to the 30 noisy dynamic brain PET dataset described in subsection 2.3. For the anatomy-guided 4D reconstruction, the algorithm (including the weight factor β) was first optimized using a particular noise realization before application to other noise realizations distinct from the former (as elaborated in Tang and Rahmim (2009a)). As side information, the dynamic 3D and the 4D (ML) parametric estimations take a comparable amount of time on a quad-core Intel Xeon (2.33 GHz; 8 GB RAM), namely ~1.5 min per iteration (each iteration containing 21 subsets), the latter involving more projection operations while the former requiring regression of the dynamic images. The 4D MAP estimation by comparison takes ~15 min per iteration with the JE calculation code remaining to be enhanced. The memory requirements (with the particular scanner simulated) for the 3D, 4D ML and 4D MAP algorithms are ~70 MB, 330 MB and 350 MB, respectively.

We first evaluated the performance of the direct 4D reconstruction algorithm with respect to conventional reconstruction followed by graphical analysis, and then compared the JE-incorporated 4D MAP reconstruction algorithm against the 4D ML reconstruction algorithm. Note that we evaluated both the estimated Patlak slope images and the estimated Patlak intercept images. As the Patlak intercept parameters are not of much interest in the application of dynamic analysis and the results for the intercept images are similar to the slope images (in terms of improvement led by the proposed algorithms), we only show the results for the Patlak slope images hereafter.

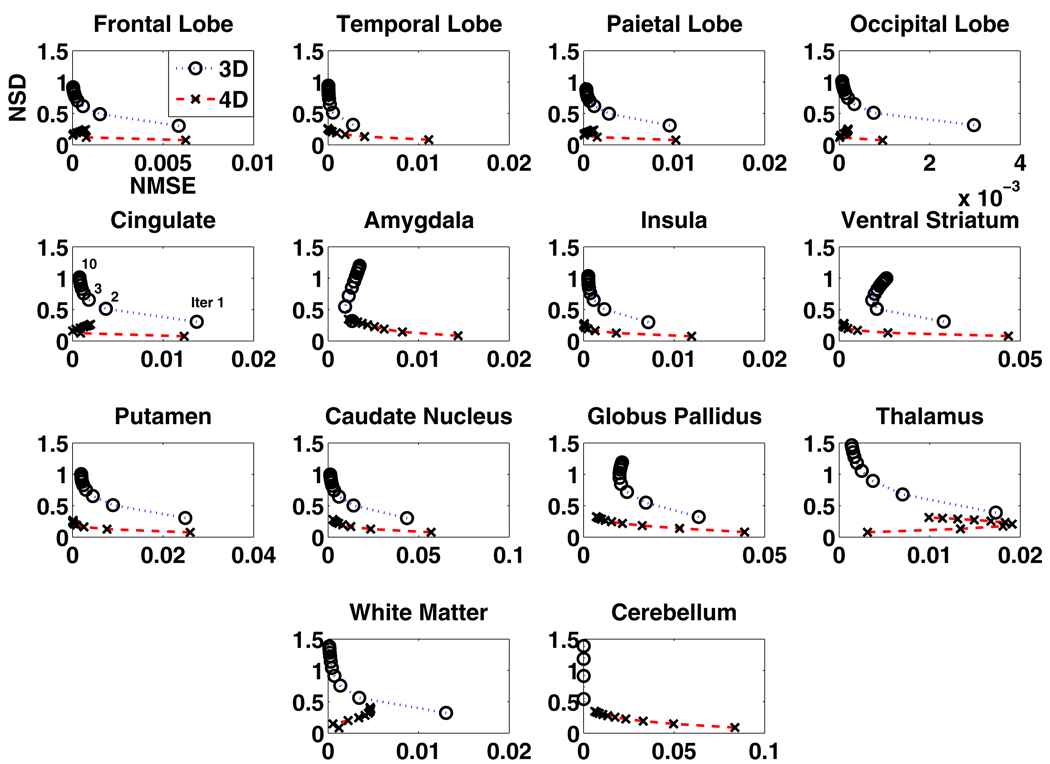
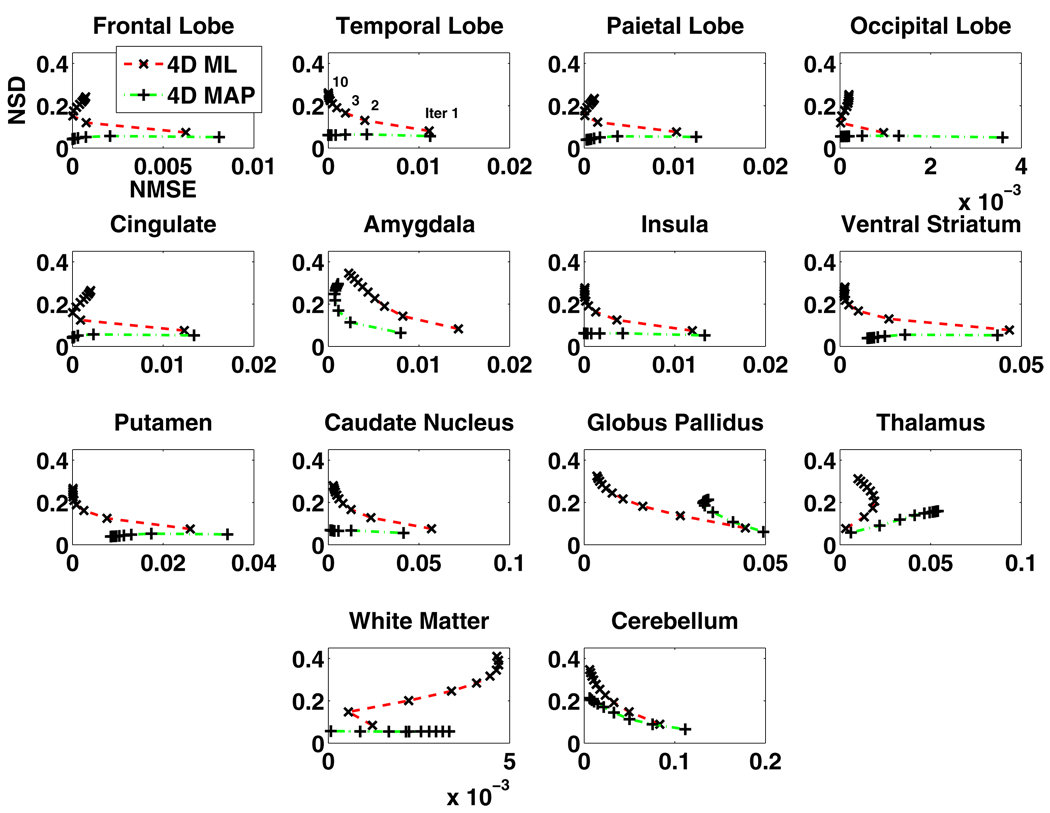
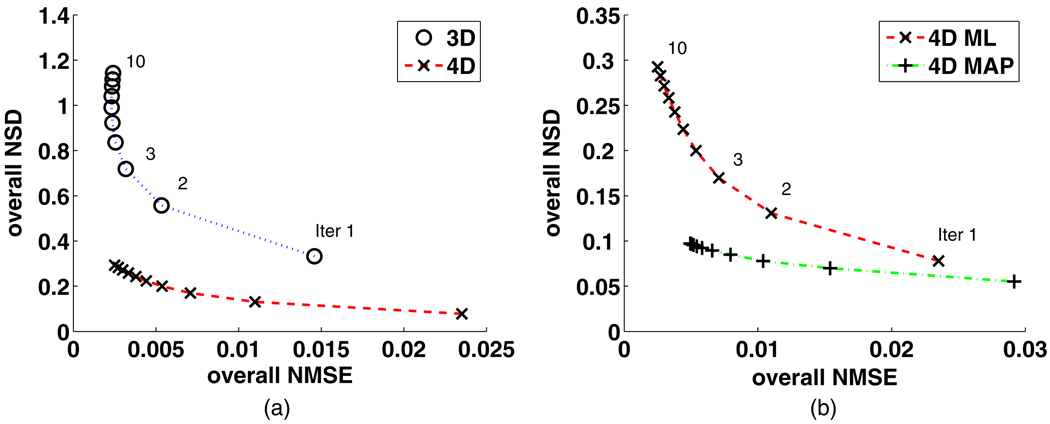
The regional NSD versus NMSE tradeoffs (14 regions) of the Patlak slope images estimated from the 3D reconstruction followed by modeling technique and the proposed 4D direct parametric image reconstruction technique are shown in figure 2, while the tradeoffs estimated from the latter technique and those from the JE-incorporated 4D MAP reconstruction technique are presented in figure 3. As depicted in figure 2, in the majority of the ROIs, the proposed 4D direct parametric image reconstruction technique noticeably outperforms the conventional technique, by lowering the noise (NSD) while achieving comparable bias (NMSE). The tradeoffs of regional NSD versus NMSE are further improved when the anatomical information from the noisy MR image is incorporated in the 4D reconstruction through the MAP algorithm, as demonstrated in figure 3. For a direct impression of the performance of the reconstruction algorithms across the brain, the overall NSD versus NMSE tradeoffs (averaged regional NSD versus averaged regional NMSE) corresponding to those shown in figure 2 are plotted in figure 4(a) and the overall tradeoffs corresponding to those shown in figure 3 are plotted in figure 4(b).

Figure 2.

The NSD versus NMSE of the estimated Patlak slope changing with the iteration number (from 30 noise realizations of projection data) for different regions of brain images reconstructed from the standard 3D reconstruction followed by graphical modeling (3D) and from the proposed 4D direct parametric reconstruction (4D) (14 brain regions).

Figure 3.

The NSD versus NMSE of the estimated Patlak slope changing with the iteration number (from 30 noise realizations of projection data) for different regions of brain images reconstructed, from the 4D direct parametric reconstruction without (4D ML) and with (4D MAP) incorporating the MR image information (14 brain regions).

Figure 4.

Overall NSD versus overall NMSE of the estimated Patlak slope changing with the iteration number from (a) the standard 3D reconstruction followed by graphical modeling (3D) and the 4D direct parametric reconstruction (4D), and (b) the 4D direct parametric reconstruction without (4D ML) and with (4D MAP) incorporating the MR image information.

While the reduction of the noise is obvious in the proposed direct estimation algorithms, we also note that, for example, it takes more iterations for the proposed 4D techniques to achieve the same NMSE as the conventional 3D technique (i.e. ~5 iterations for the 4D reconstruction algorithm as ~2 iterations for the 3D reconstruction followed by modeling). As reported before, slower convergence rates for more advanced reconstruction techniques are commonly observed (Rahmim et al 2008b).

For a visual comparison of the estimated Patlak slope images, we presented the center slice through parametric images (not post-filtered) obtained by the three algorithms together with the phantom image in figure 5. These estimated images were from different iterations (specified in the figure caption) of the reconstruction algorithms in order that they have comparable bias for a fair and easy comparison of their noise levels. Having comparable bias, the parametric images estimated from the proposed 4D direct reconstruction technique are clearly seen to be much less noisy than those from the conventional reconstruction followed by graphical modeling analysis. With the guidance of the noisy MR image, the 4D MAP reconstruction technique demonstrated further reduction of the noise than its counterpart without the MR anatomical information.

Figure 5.

Transaxial slice of the Patlak slope image of (a) the phantom image, (b) the image estimated from 3D reconstruction followed by modeling (the second iteration), (c) the direct 4D parametric reconstruction (the fifth iteration) and (d) the 4D direct MAP parametric reconstruction incorporating the MR image information (the fifth iteration).

4. Discussion

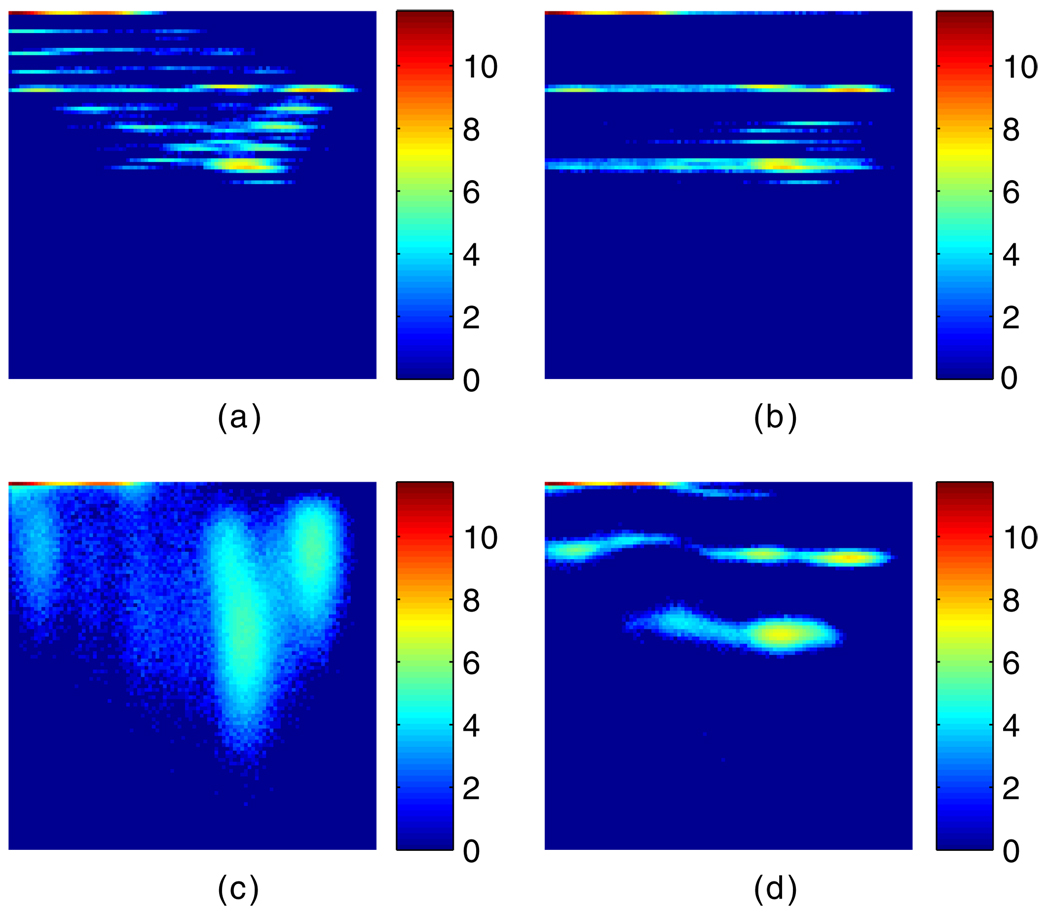
In previous studies on anatomy-guided PET reconstruction (e.g. Somayajula et al 2005, Nuyts 2007, Tang and Rahmim 2009a), noise-free MR images were simulated. In this work, as stated in subsection 2.3, we investigated the use of the noisy MR image as anatomical reference information. The effect of incorporating MR images on the reconstructed PET images can be well demonstrated by plotting a number of joint histograms for the anatomical and functional images (true or estimated; with or without noise), as we show below.

The joint histogram of the true noise-free PET Patlak slope image (i.e. uptake rate image) and the noisy MR image is shown in figure 6(a) (both images collapsed from the grids two times finer, as described in subsection 2.3). Figure 6(b) shows the joint histogram of the true noise-free PET Patlak slope image (this time created with the grid as coarse as the reconstructed image) and the noisy MR image. The difference between the two PET images used in figure 6(a) versus (b) is that the one used in (a) has regional edge voxel values that are different from non-edge voxel values, due to the 2-to-1 collapse process. The PET image used in (b), however, has uniform regions with edge voxel values the same as non-edge voxel values, since the phantom is created on a coarse grid to begin with. The joint histogram of the 4D ML reconstructed Patlak slope image with no MR guidance and the noisy MR image is plotted in figure 6(c). Finally, the joint histogram of the noisy-MR-image-guided 4D MAP reconstructed Patlak slope image and the noisy MR image is shown in figure 6(d). The horizontal axis in each of these figures corresponds to the MR image intensity and the vertical axis corresponds to the Patlak slope PET image intensity. Log scale was used in all the histograms shown.

Figure 6.

Joint histograms of (a) the true PET Patlak slope image collapsed from finer grid and the noisy MR image, (b) the true PET Patlak slope image created in coarse grid and noisy MR image, (c) the PET Patlak slope image reconstructed without incorporation of MR image and the noisy MR image and (d) the noisy-MR-image-guided reconstructed PET Patlak slope image and the noisy MR image. The horizontal axis corresponds to the MR image intensity while the vertical axis corresponds to the PET Patlak slope image intensity.

Comparing figures 6(c) and (d), we can see that when anatomical information was incorporated in the reconstruction, more concentrated peaks formed in the joint histogram (to lower the JE) than the case without the MR image as a guidance. Since the MR image, as noisy as it is, does not change during the reconstruction process, the PET images were tuned to take on fewer intensity values (less noisy). The joint histogram in figure 6(d) resembles figure 6(b), meaning that the noisy MR image guides the reconstruction process to result in PET images with edge voxel values pushed to take non-edge voxel values as could be identified by the PET image resolution. Although incorporation of the collapsed noisy MR image in the MAP reconstruction does not result in PET images with a finer resolution (as shown in figure 6(a)), it does reduce the noise compared to the ML algorithm.

Aside from the noisy MR image incorporation discussed above, we would also like to touch base on the irregular regions, such as thalamus and white matter, in terms of NSD versus NMSE pattern in figures 2 and 3. The unexpected pattern of NSD versus NMSE is related to the partial volume effect (PVE) the reconstructed PET images experience, with respect to the image applied as the truth. In the 3D or the 4D ML reconstruction, the PVE could be such that the bias may increase sometimes along with iteration. This is especially the case for regions such as those mentioned above with early estimates happening to be very close to the truth. In the case of MR guidance, the effect is also not always ideal greatly due to the fine-grid to coarse-grid MR image collapsing process, which creates more intensity levels on edges of regions, additionally complicating the task of MR guidance of PET image reconstruction at regional edges. In general, these are issues on which we seek to improve in our ongoing investigations toward patient data application.

5. Summary

We have developed a closed-form 4D algorithm to directly reconstruct parametric images from dynamic PET datasets for (nearly) irreversible tracers. Using the Patlak linear model, the proposed approach was implemented through composing a system matrix relating the combined parametric images directly to the measured 4D data. The closed-form solution of the 4D reconstruction problem was achieved from using a different complete-data formulation within the EM method. Instead of using the standard, physically intuitive activity image voxel contributions to each projection bin i as the hidden complete data, the present framework effectively employs the contributions of each of the Patlak elements (κ_j and b_j) to each bin i as the complete data. Furthermore, the method was extended to MAP reconstruction via incorporating anatomic information from noisy MR images, making use of the JE between the parametric PET and MR image features. The NSD (noise) versus NMSE (bias) tradeoff of the directly estimated Patlak slope image was shown to be significantly improved compared to that estimated from graphical analysis on 3D reconstructed images. Additional improvement on the NSD versus NMSE tradeoff was achieved when the proposed anatomy-guided 4D MAP algorithm was employed.